Fixed-Time Aircraft Spin Recovery Control Based on a Nonsingular Integral Terminal Sliding Mode Approach

Abstract

This paper introduces a control strategy to recover from various spin motions to level trim flight conditions, utilizing a fixed-time nonsingular terminal sliding mode approach to minimize altitude loss. Firstly, an integral terminal sliding mode surface is constructed to guarantee the tracking errors of the spin recovery system converge to the origin within a fixed time and avoid the singularity problem. Next, a fixed-time type reaching law is proposed to weaken the chattering phenomenon and guarantee terminal sliding hyperplanes converge to zero in a fixed time. Furthermore, the stability analysis indicates the fixed-time convergence stability of the spin recovery control system and provides an accurate calculation of the settling time. Finally, comparative simulations are performed to validate the effectiveness and superiority of the developed spin recovery control scheme.

1. Introduction

Aircraft spin, as a highly nonlinear and dangerous flight condition, is characterized by a supercritical angle of attack, a large sideslip angle, and a significant yaw rate. Recovering from aircraft spin to avoid ground collisions is a challenging task that has attracted considerable attention [1,2,3,4].

The spin characteristics of an aircraft can be researched through rotary balance tests, vertical spin tunnels, bifurcation analysis, radio-controlled flight tests, and real aircraft flight tests. Recovering from aircraft spin is difficult and depends on its spin characteristics, including entry speed, intensity, and recovery time. The combination of a steep descent, delayed recognition of the spin mode, and inadequate recovery actions creates a situation where it becomes almost improbable for the pilot to achieve a successful recovery before colliding with the ground [5,6]. Hence, research on control technology for automatic recovery from aircraft spin is of utmost importance.

The first critical issue in recovering from an aircraft spin is predicting and identifying the spin state. Bifurcation analysis techniques have been widely used to investigate the spin solutions of the open-loop aircraft dynamics model. The open-loop bifurcation results have been used to provide the reference inputs for the spin recovery controller [7,8,9]. Therefore, to address the spin recovery control problem within a reasonable time, several control techniques have been investigated. Ref. [5] introduced a spin automatic recovery flight control system, minimizing altitude loss. The study highlighted the importance of initiating recovery within the first turn and quantified the relationship between altitude loss and recovery delay. In Ref. [10], a reinforcement learning intelligent control approach has been applied for fully developed spin recovery that demonstrated time optimality. In Ref. [11], spin recovery was formulated as a trajectory optimization problem, with time and altitude loss serving as cost functions to be minimized and addressed through the utilization of the direct multiple shooting method. Ref. [12] delved into the application of nonlinear dynamic inversion (NDI) techniques for resolving the spin recovery problem. However, controllers based on NDI have been criticized in [13] for their lack of robustness and inability to handle control saturation limits.

Sliding mode control (SMC) has attracted significant interest due to its simplicity, efficiency, remarkable adaptability to external disturbances, and insensitivity to fluctuations in system parameters [14]. Therefore, in Ref. [15], linear sliding mode (LSM) control was used to spin recovery, which was achieved at low trim state without thrust vectoring. Refs. [16,17] improved SMC controller design by incorporating the TSM-type reaching law, enabling direct spin recovery through aerodynamic forces, and thrust utilization. Moreover, through repetitive altitude simulations, the altitude loss allowance to prevent ground collisions was achieved [18]. In Ref. [19], an investigation was conducted to examine the influence of open-closed loop thrust control on spin recovery, employing SMC. The findings of the study revealed that the implementation of a closed-loop thrust controller effectively mitigated altitude loss during the spin recovery process, showcasing its efficacy in enhancing control precision and system performance. Furthermore, in Ref. [20], the thrust vectoring control command was strategically designed as a function of the angle of attack in both pitch and yaw directions, and its optimal integration with the aircraft’s primary control system was explored. Ref. [17] investigated the impact of fin positioning on SMC spin recovery, finding that optimal fin placement notably reduced altitude loss. In addition, Ref. [21] discusses the problem of spin recovery in aircraft and proposes a robust SMC control solution to address the issue of improper feedback data.

Altitude loss is considered a metric in spin flight, requiring swift control to avert collisions with the ground. Faster convergence speed in altitude control results in smaller altitude losses. To achieve faster convergence and higher control accuracy, an extension of finite time stability, fixed time stabilization, has received much attention for providing a predefined convergence time toward equilibrium independent of initial conditions [22]. Thus, to minimize altitude loss during spin recovery, fixed-time SMC emerges as a potential candidate for automated spin recovery.

The main innovations and merits of this paper are:

(1)

Unlike the finite-time controller in [23], the proposed fixed-time spin recovery controller based on the nonsingular integral terminal sliding mode (NITSM) approach has a faster convergence rate, which has helped the aircraft recover from spin motions in a shorter time and with less altitude loss. In addition, the convergence time of the proposed spin recovery controller is independent of the initial states. Thus, the success rate of spin recovery has increased remarkably.

(2)

Different from the conventional fixed-time control methods that depend on piecewise continuous or saturation functions, this study presents an enhanced fixed-time NITSM spin recovery strategy that avoids singularity issues. It directly constructs the NITSM surface, thus simplifying fixed-time convergence analysis with reduced computational complexity.

(3)

The introduced fixed-time spin recovery controller is designed to effectively mitigate the undesirable chattering phenomenon associated with SMC. Moreover, the continuity of the control law presents practical advantages, thus facilitating its implementation in engineering applications.

2. Preliminaries and Notations

2.1. Notations

Throughout this context, the following notation is adopted: For any $x\in ℝ$ and a positive constant $\alpha$, $si{g}^{\alpha }\left(x\right)$ is defined as $si{g}^{\alpha }\left(x\right)=\left[sign\left(x\right){\left|x\right|}^{\alpha }\right]$. For a vector $x\in {ℝ}^n$, $si{g}^{\alpha }\left(x\right)={\left[sign\left(x_1\right){\left|x_1\right|}^{\alpha },\dots ,sign\left(x_n\right){\left|x_n\right|}^{\alpha }\right]}^T$.

2.2. Some Definitions and Lemmas

Before the control system is designed, some necessary preliminaries regarding fixed-time stability are introduced. Consider the differential equation:

$$\dot{x}\left(t\right)=f\left(x\left(t\right)\right), x\left(0\right)=x_0$$

(1)

where $x={[x_1,\dots x_n]}^T\in {ℝ}^n$ denotes the state vector, and $f\left(x\right):{ℝ}^n\to {ℝ}^n$ represents a known vector field.

Definition 1.

The equilibrium point of (1) is globally finite-time stable, and it there exists a finite time $T\left(x_0\right)$ that is uniformly bounded and independent of initial states, i.e., for all $x_0\in {ℝ}^n$, there exists $T_{\max }>0$, then $T\left(x_0\right)<T_{\max }$. Thus, it is globally fixed-time stable [22].

Lemma 1.

A continuously differentiable, positive-definite, radially unbounded function V satisfying ${ℝ}^n\to {ℝ}^{+}\cup \left\{0\right\}$, thus [24]:

(1) $V\left(x\right)=0\Rightarrow x=0$

(2) Any solution $x$ of system (1) satisfies:

$$\dot{V}\left(x\right)\le -aV{\left(x\right)}^p-bV{\left(x\right)}^q$$

(2)

where $a>0$, $b>0$, and $0<p<1$, $q>1$. The origin is globally fixed-time stable for the system (1), and the reaching time satisfies the following:

$$T\left(x_0\right)\le T_{\max }=\frac{1}{a\left(1-p\right)}+\frac{1}{b\left(q-1\right)},\forall x_0\in {ℝ}^n.$$

(3)

Lemma 2.

Consider the system [25]:

$$\dot{y}=-asi{g}^p\left(y\right)-bsi{g}^q\left(y\right), y(0)=y_0$$

(4)

The equilibrium point of the above system (4) is fixed-time stable, and its setting time depends on Equation (3).

3. Aircraft Flight Dynamics Model

3.1. Aircraft Dynamic Model

The fixed-time spin recovery control law is founded on the nonlinear dynamic model of the F-18/HARV [12]. The aircraft dynamic model with twelve state variables ${\left[u,v,w,p,q,r,\varphi ,\theta ,\psi ,H,X,Y\right]}^T$ can be written as follows:

$$\left\{\begin{array}{l}\dot{u}=rv-qw-g\sin \theta +\frac{\rho V^{2}S\left(C_L\left(\alpha ,q,{\delta }_e\right)\sin \alpha -C_D\left(\alpha ,q,{\delta }_e\right)\cos \alpha \right)}{2m}+\frac{T_{\mathrm{m}}{\delta }_t}{m}\\ \dot{v}=pw-ru+g\sin \varphi \cos \theta +\frac{\rho V^{2}S{C}_Y\left(\beta ,p,r,{\delta }_e,{\delta }_a,{\delta }_r\right)}{2m}\\ \dot{w}=qu-pv+g\cos \theta \cos \varphi -\frac{\rho V^{2}S\left(C_L\left(\alpha ,q,{\delta }_e\right)\cos \alpha +C_D\left(\alpha ,q,{\delta }_e\right)\sin \alpha \right)}{2m}\end{array}\right.$$

(5)

$$\left\{\begin{array}{l}\dot{p}=I_{1}pq-I_{2}qr+\frac{\rho V^{2}S}{2m}\left(I_3{C}_l\left(\beta ,p,r,{\delta }_e,{\delta }_a,{\delta }_r\right)+I_4{C}_n\left(\beta ,p,r,{\delta }_e,{\delta }_a,{\delta }_r\right)\right)\\ \dot{q}=I_{5}pr-I_6\left(p^2-q^2\right)+\frac{\rho V^{2}S\overline{c}}{2m}{C}_m\left(\alpha ,q,{\delta }_e\right)\\ \dot{r}=I_{7}pq-I_{1}qr+\frac{\rho V^{2}Sb}{2m}\left(I_4{C}_l\left(\beta ,p,r,{\delta }_e,{\delta }_a,{\delta }_r\right)+I_8{C}_n\left(\beta ,p,r,{\delta }_e,{\delta }_a,{\delta }_r\right)\right)\end{array}\right.$$

(6)

$$\left\{\begin{array}{l}\dot{\varphi }=p+q\sin \varphi \tan \theta +r\cos \varphi \tan \theta \\ \dot{\theta }=q\cos \varphi -r\sin \varphi \\ \dot{\psi }=\sec \theta \left(r\cos \varphi +q\sin \varphi \right)\end{array}\right.$$

(7)

$$\left\{\begin{array}{l}\dot{H}=u\sin \theta -v\sin \varphi \cos \theta -w\cos \varphi \cos \theta \\ \dot{X}=u\cos \theta \cos \psi +v\left(\sin \varphi \sin \theta \cos \psi -\cos \varphi \sin \psi \right)+w\left(\cos \varphi \cos \psi \sin \theta +\sin \varphi \sin \psi \right)\\ \dot{Y}=u\cos \theta \sin \psi +v\left(\sin \varphi \sin \theta \sin \psi +\cos \varphi \cos \psi \right)+w\left(\cos \varphi \sin \psi \sin \theta -\sin \varphi \cos \psi \right)\end{array}\right.$$

(8)

where u, v, and w denote velocity components, respectively. p, q, and r are roll, pitch, and yaw angular velocities. $\varphi$, $\theta$, and $\psi$ represent roll, pitch, and heading angles. X and Y are the positions of the aircraft. H is aircraft altitude. $I_{xx}$, $I_{yy}$, $I_{zz}$, and $I_{xz}$ represent roll, pitch, yaw, and cross-product moment of inertia. Let $I=I_{xx}{I}_{zz}-I_{xz}^2$, then the inertia parameters $I_i$, $i=1,2,\dots 8$ in Equation (7) can be defined as $I_1=I_{xz}\left(I_{xx}-I_{yy}-I_{xz}\right)/I$, $I_2=\left(I_{zz}\left(I_{xx}-I_{yy}\right)+I_{xz}^2\right)/I$, $I_3=I_{zz}/I$, $I_4=I_{xz}/I$, $I_5=\left(I_{zz}-I_{xx}\right)/I_{yy}$, $I_6=I_{xz}/I_{yy}$, $I_7=\left(I_{xx}\left(I_{xx}-I_{yy}\right)+I_{xz}^2\right)/I$, and $I_8=I_{xx}/I$. $T_{\mathrm{m}}$ denotes maximum available thrust.

The aerodynamic model can be represented by the following nonlinear equations:

$$\left\{\begin{array}{l}{C}_i\left(\alpha ,q,{\delta }_e\right)=C_i\left(\alpha \right)+C_{iq}\left(\frac{q\overline{c}}{2V}\right)+C_{i_{{\delta }_e}}{\delta }_e,i=L,D,m\\ C_j\left(\beta ,p,r,{\delta }_e,{\delta }_a,{\delta }_r\right)=C_{j_0}+C_{j_{\beta }}\beta +C_{j_p}\left(\frac{pb}{2V}\right)+C_{j_r}\left(\frac{rb}{2V}\right)+C_{j_{{\delta }_e}}{\delta }_e+C_{j_{{\delta }_a}}{\delta }_a+C_{j_{{\delta }_r}}{\delta }_r,j=Y,l,n\end{array}\right.$$

(9)

where $C_Y$, $C_L$, and $C_D$ denote coefficients of lateral force, lift force, and drag force, respectively. $C_l$, $C_m$, and $C_m$ represent coefficients of roll, pitch, and yaw moment. The nonlinear models of aerodynamical coefficients are the functions of variables $\alpha$, $\beta$, ${\delta }_e$, ${\delta }_a$, ${\delta }_r$ p, q, and r, which can be obtained from Refs. [12,15].

3.2. Model Transformation

NDI, which stands for feedback linearization [26,27], is a control approach that harnesses the system model to achieve precise control. To facilitate the NDI-based fixed-time NITSM spin recovery control design, the flight dynamic Equations (5)–(8) can be transformed into control-oriented MIMO affine form [28].

$$\left\{\begin{array}{l}{\dot{x}}_1=F\left(x\right)+G\left(x\right)u\\ y_1=x_1\end{array}\right.$$

(10)

In Equation (10), $x={\left[u,v,w,p,q,r,\varphi ,\theta ,\psi ,H,X,Y\right]}^T\in {ℝ}^{12\times 1}$, $x_1={\left[\varphi ,\theta ,\dot{\psi },\dot{H}\right]}^T\in {ℝ}^{4\times 1}$ is the state vector, $u={\left[{\delta }_e,{\delta }_a,{\delta }_r,{\delta }_t\right]}^T\in {ℝ}^{4\times 1}$ is the control vector, and $y_1$ is the system output vector, the system matrix $F\left(x\right)$ represents the nonlinear system dynamics and is defined as follows:

$$F\left(x\right)={[f^{\varphi },f^{\theta },f^{\dot{\psi }},f^{\dot{H}}]}^T$$

(11)

We denote control matrix $G\left(x\right)$ as follows:

$$G\left(x\right)=\left[\begin{array}{cccc}{G}_{{\delta }_e}^{\varphi },& G_{{\delta }_a}^{\varphi },& G_{{\delta }_r}^{\varphi },& G_{{\delta }_t}^{\varphi }\\ G_{{\delta }_e}^{\theta },& G_{{\delta }_a}^{\theta },& G_{{\delta }_r}^{\theta },& G_{{\delta }_t}^{\theta }\\ G_{{\delta }_e}^{\dot{\psi }},& G_{{\delta }_a}^{\dot{\psi }},& G_{{\delta }_r}^{\dot{\psi }},& G_{{\delta }_t}^{\dot{\psi }}\\ G_{{\delta }_e}^{\dot{H}},& G_{{\delta }_a}^{\dot{H}},& G_{{\delta }_r}^{\dot{H}},& G_{{\delta }_t}^{\dot{H}}\end{array}\right]$$

(12)

System matrix elements in Equation (11) and control matrix elements in Equation (12) are provided in Appendix A.

4. Fixed-Time NITSM Controller Formulation

4.1. Controller Design

This study aims to develop a spin recovery controller leveraging the fixed-time NITSM control methodology. Once $\varphi$, $\theta$, and $\dot{\psi }$ reach their desired values, then $p$, $q$, $r$ will converge to zero, resulting in a successful recovery from the spin state. When $\dot{H}$ converges zero, the aircraft will attain level flight trim condition. This is equivalent to the control objective of steering $y_{1d}$ towards the desired values $y_{1d}={[{\varphi }_d,{\theta }_d,{\dot{\psi }}_d,{\dot{h}}_d]}^T$ within a fixed time.

Instead of using a linear sliding function in [17], the nonsingular integral terminal sliding manifold (NITSM) based on $e=y_1-y_{1d}$ is designed.

$$s=e+C_1{\displaystyle \int si{g}^m\left(e\right)}dt+C_2{\displaystyle \int si{g}^n\left(e\right)}dt$$

(13)

where $e={[e_{\varphi },e_{\theta },e_{\dot{\psi }},e_{\dot{h}}]}^T\in {ℝ}^4$, $s={\left[s_{\varphi },s_{\theta },s_{\dot{\psi }},s_{\dot{h}}\right]}^T\in {ℝ}^4$, $C_1=diag\left(c_{11},c_{12},c_{13},c_{14}\right)$ and $C_2=diag\left(c_{21},c_{22},c_{23},c_{24}\right)$ are two positive definite diagonal matrixes, and $0<m<1$, $n>1$ are defined positive constants.

Taking the time derivative of $s$, we have the following:

$$\dot{s}=\dot{e}+C_{1}si{g}^m\left(e\right)+C_{2}si{g}^n\left(e\right)=F\left(x\right)+G\left(x\right)u-{\dot{y}}_{1d}+C_{1}si{g}^m\left(e\right)+C_{2}si{g}^n\left(e\right)$$

(14)

To guarantee that the states of the spin recovery system (10) approach the sliding mode manifold within a fixed time, regardless of initial conditions. A fixed-time type of reaching law is chosen as follows:

$$\dot{s}=-k_{1}si{g}^p\left(s\right)-k_{2}si{g}^q\left(s\right)$$

(15)

where $k_1=diag\left(k_{11},k_{12},k_{13},k_{14}\right)$ and $k_2=diag\left(k_{21},k_{22},k_{23},k_{24}\right)$ are diagonal positive definite matrices, $0<p<1$ and $q>1$.

Based on fixed time and NDI theory, the spin recovery algorithm is designed as follows:

$$u=-G^{-1}\left(x\right)\left[F\left(x\right)+C_{1}si{g}^m\left(e\right)+C_{2}si{g}^n\left(e\right)+k_{1}si{g}^p\left(s\right)+k_{2}si{g}^q\left(s\right)-{\dot{y}}_{1d}\right]$$

(16)

where $G\left(x\right)$ is invertible.

4.2. Fixed-Time Stability Analysis

Subsequently, we will provide the main result regarding the stability proof of the spin recovery system (10), as stated in Theorem 1.

Theorem 1.

For system (10), if the proposed fixed-time NITSM is chosen as (13), the spin recovery algorithm is designed as (16), and the reaching law is given by (15), it is concluded that.

(1) The ITSM (13) converges to $s=0$ in a fixed time.

(2) The tracking error vector$e$ in $\varphi$, $\theta$, $\dot{\psi }$, and $\dot{H}$ converges to the origin in a fixed time.

Two applications of Lemma 2 yield that the convergent time is bounded by:

$$T<T_{\max }=T_1+T_2$$

(17)

where $T_1=\frac{1}{{\mu }_1}\frac{2}{1-p}+\frac{1}{{\mu }_2}\frac{2}{q-1}$ and $T_2=\frac{1}{{\mu }_3}\frac{2}{1-m}+\frac{1}{{\mu }_4}\frac{2}{n-1}$.

Proof of Theorem 1.

(1) The quadratic Lyapunov function, expressed through sliding functions, is expressed as follows:

$$V_1=\frac{1}{2}{s}^{T}s>0$$

(18)

Taking the time derivative of $V_1$ along the dynamics (10) yields

$${\dot{V}}_1=s^T\dot{s}=-s^T{k}_{1}si{g}^p\left(s\right)-s^T{k}_{2}si{g}^q\left(s\right)$$

(19)

This is equivalent to

$${\dot{V}}_1\le -{\mu }_1{V}_1^{\frac{p+1}{2}}-{\mu }_2{V}_1^{\frac{q+1}{2}}$$

(20)

where ${\mu }_1=\min \left\{2^{\frac{p+1}{2}}{k}_{1i}\right\}$ and ${\mu }_2=\min \left\{2^{\frac{q+1}{2}}{k}_{2i}\right\},i=1\cdots 4$.

Referring to Lemma 1, the spin recovery system (10) reaches $s=0$ in a fixed time, satisfying:

$$T_1=\frac{1}{{\mu }_1}\frac{2}{1-p}+\frac{1}{{\mu }_2}\frac{2}{q-1}$$

(21)

(2) As soon as the system’s trajectories reach $s=0$, we have

$$s=e+C_1{\displaystyle \int si{g}^m\left(e\right)}dt+C_2{\displaystyle \int si{g}^n\left(e\right)}dt=0$$

(22)

By defining a Lyapunov function $V_2=\frac{1}{2}{e}^{T}e$, ${\dot{V}}_2$ is given by

$${\dot{V}}_2=e^T\left(-C_{1}si{g}^m\left(e\right)-C_{2}si{g}^n\left(e\right)\right)$$

(23)

which is equivalent to the following:

$${\dot{V}}_2=-2^{\frac{m+1}{2}}{\displaystyle \sum _{i=1}^4{c}_{1i}}{\left|e_i\right|}^{m+1}-2^{\frac{n+1}{2}}{\displaystyle \sum _{i=1}^4{c}_{2i}}{\left|e_i\right|}^{n+1} \le -{\mu }_3{V}_2^{\frac{m+1}{2}}-{\mu }_4{V}_2^{\frac{n+1}{2}}$$

(24)

where ${\mu }_3=\min \left\{2^{\frac{m+1}{2}}{c}_{1i}\right\}$ and ${\mu }_4=\min \left\{2^{\frac{n+1}{2}}{c}_{2i}\right\},i=1\cdots 4$. □

By using Lemma 1 again, it is deduced that $e$ reaches the origin in a fixed time satisfying

$$T_2=\frac{1}{{\mu }_3}\frac{2}{1-m}+\frac{1}{{\mu }_4}\frac{2}{n-1}$$

(25)

Finally, the system state reaches the origin in a fixed time that is obtained by Equation (17).

Remark 1.

The control variables, namely $\varphi ,$, $\theta$, $\dot{\psi }$, and $\dot{H}$, of the spin recovery system (10) can uniformly converge to their desired values within a fixed time T. To decrease the convergence time, appropriate adjustments to the gain parameters of the controller are required. However, the convergence time is also subject to saturation limits, and the control saturation constraint presents an unavoidable challenge during the spin recovery process [29].

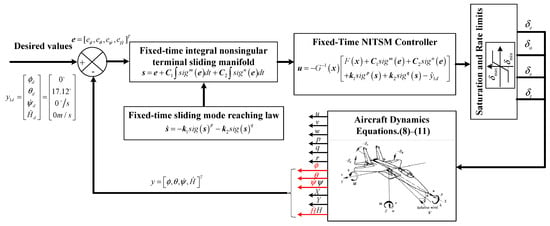
To offer a clearer summation of the control design procedure, a block diagram illustrating the control architecture is presented in Figure 1.

Figure 1. The proposed fixed-time NITSM spin recovery control architecture.

Remark 2.

The variables highlighted in red in Figure 1 are regarded as the input states to design controller.

5. Discussions

To validate the efficacy and superiority of the proposed spin recovery controller, numerical simulations are conducted in this section using the F-18 HARV model. Parameter values are borrowed from [12]. The initial and final conditions for simulation are obtained from bifurcation analysis results. In Ref. [12], the spin solutions of the aircraft have been obtained by bifurcation analysis. As a result, the findings obtained from this analysis are not reiterated in the present paper. The initial and final reference points are listed in Table 1 and Table 2.

Table 1. Initial and final state variables.

State Variables	Initial Spin States		Final Level Flight States
	Oscillatory	Steady
V (m/s)	194.39	221.16	67.3
$\alpha$ (rad)	1.23	1.07	0.3
$\beta$ (rad)	0.037	0.02	0
p (rad/s)	−0.48	−0.37	0
q (rad/s)	0.052	0.13	0
r (rad/s)	−1.36	−0.74	0
$\varphi$ (rad)	−0.038	−0.17	0
$\theta$ (rad)	−0.34	−0.46	0.3

Table 2. Initial and final control variables.

Control Variables	Initial Spin States		Final Level Flight States
	Oscillatory	Steady
${\delta }_e$ (rad)	−0.16	−0.43	−0.058
${\delta }_a$ (rad)	0	0	0.41
${\delta }_r$ (rad)	0	0	−0.076
${\delta }_t$	0.43	0.59	0.54

To evaluate the performance of the spin recovery control approach, we use the NDI and finite-time SMC spin recovery methods as comparative methods [12,18]. The simulations are conducted under two different initial spin values (oscillatory and steady).

Spin recovery control is attempted after 10 s of spin motion. During the first 10 s, the control inputs are held in the fixed position, referring to Table 2. Then, the control inputs in Equation (18) are applied at t = 10 s to converge the control variables $\left(\varphi ,\theta ,\dot{\psi },\dot{h}\right)$ to their desired states $\left({\varphi }_d,{\theta }_d,{\dot{\psi }}_d,{\dot{h}}_d\right)$. The spin recovery simulation results are exhibited in Figure 2 and Figure 3, while the computed control commands are shown in Figure 4.

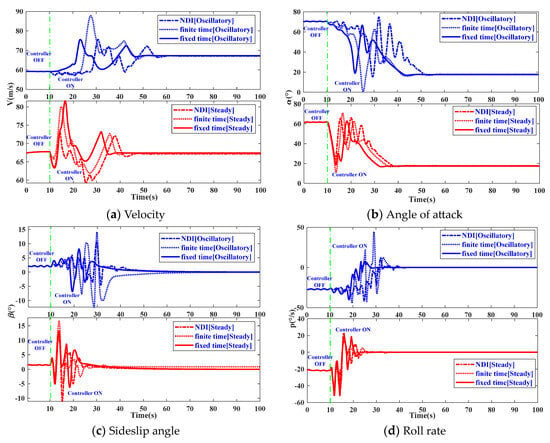
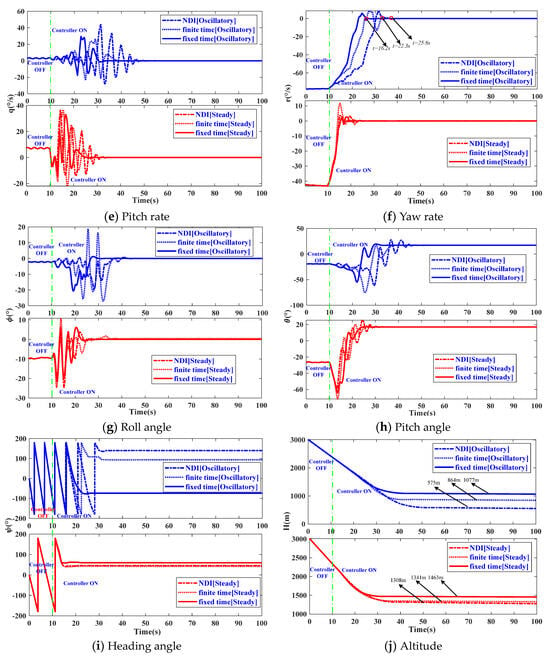
Figure 2. System response under two different initial spin states.

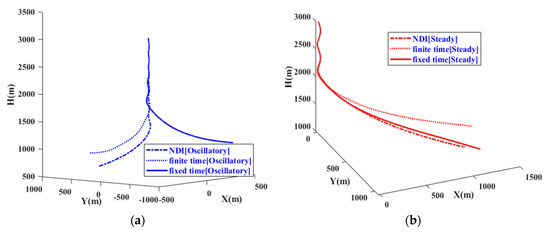
Figure 3. Aircraft trajectory under two different (a,b) initial spin states.

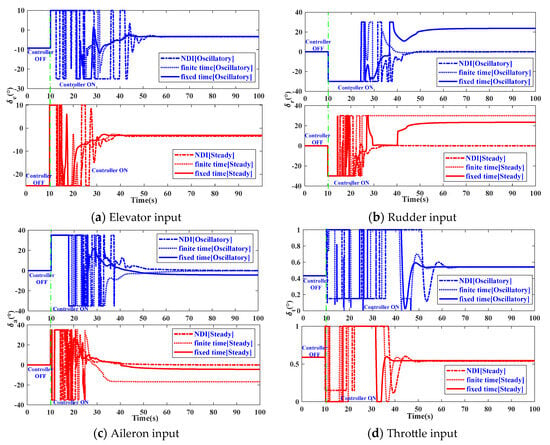
Figure 4. Control commands under two different initial spin states.

It is apparent from Figure 2 that the proposed spin recovery controller can provide a faster convergence rate compared to NDI and the finite-time SM spin recovery control method. It can be observed that the convergence time for two initial conditions is very close to each other, indicating that the characteristic is independent of the initial conditions. It is observed from Figure 2g–i that the response curves of $\varphi$, $\theta$, and $\dot{\psi }$ can effectively track the desired values. For the oscillatory spin recovery, the $\varphi$ and $\theta$ converge to the desired states at t = 28.92 s and t = 30.37 s, respectively. For the steady spin recovery, the $\varphi$ and $\theta$ converge to the desired states at t = 23.51 s and t = 24.8 s, respectively. In the case of the oscillatory spin recovery, the aircraft spin rotation stops after completing 1.75 left turns at t = 23.35 s, as shown in Figure 2i. For the steady spin recovery, the aircraft spin rotation stops after completing 0.75 left turns at t = 14.01 s, as shown in Figure 2i. Thus, it is evident that the convergence time of $\dot{\psi }$ is less than that of $\varphi$ and $\theta$, indicating that the aircraft spin rotation stops well before achieving level flight. More explicitly, $\dot{H}$ achieves the desired altitude rate for oscillatory and steady spin recovery as shown in Figure 2j at H = 1077 m and H = 1463 m, respectively. As depicted in Figure 2j, the aircraft, subjected to two distinct spin motions, maintains a reference altitude of 3 km for 10 s, subsequently experiencing altitude losses of approximately 592 m and 677 m, respectively. The descent rates are approximately 59.2 m/s and 67.7 m/s, respectively. This indicates that aircraft require altitude margins of 1331 m and 860 m to reach the desired α, respectively. In conclusion, the proposed spin recovery controller mitigates the altitude loss compared to NDI spin recovery and the finite-time SMC method. This reduction is significant for avoiding ground collisions.

The control command curves are shown in Figure 4. The control inputs of elevator, aileron, rudder, and throttle are simultaneously applied at t = 10 s, and the control commands are constrained [17]. Figure 4 reveals that the controller is manipulating the ${\delta }_e$ surface downwards to reduce the $\alpha$, controlling the ${\delta }_r$ to restrain the yaw rotation, and employing ${\delta }_a$ in the roll direction to sustain a flight at a constant altitude. Additionally, it is evident that the aerodynamic control surfaces (${\delta }_e$, ${\delta }_r$, ${\delta }_a$, and ${\delta }_t$) exhibit a reduced time to withdraw from their permissible limits. To sum up, the superiority of the explored fixed-time spin recovery approach over finite time and NDI methods is clearly demonstrated through simulation results.

6. Conclusions

A novel fixed-time NITSM controller for spin recovery is exploited. Based on the conducted simulations, the proposed spin recovery controller demonstrates a superior convergence rate compared to NDI and finite-time SMC spin recovery schemes. Consequently, the aircraft can recover from spin motions in a shorter time with less altitude loss. The fixed-time NITSM spin recovery controller has exhibited satisfactory performance under two different initial spin conditions. This method of spin recovery is expected to render substantial aid in the evolution of upcoming technologies designed for automated spin recovery. Given that the saturation control problem represents a significant hindrance to minimizing convergence time, future research will aim to explore the allocation of control between aerodynamic surfaces and thrust vectors.