Abstract
Federated learning is a new paradigm where multiple data owners, referred to as clients, work together with a global server to train a shared machine learning model without disclosing their personal training data. Despite its many advantages, the system is vulnerable to client compromise by malicious agents attempting to modify the global model. Several defense algorithms against untargeted and targeted poisoning attacks on model updates in federated learning have been proposed and evaluated separately. This paper compares the performances of six state-of-the art defense algorithms—PCA + K-Means, KPCA + K-Means, CONTRA, KRUM, COOMED, and RPCA + PCA + K-Means. We explore a variety of situations not considered in the original papers. These include varying the percentage of Independent and Identically Distributed (IID) data, the number of clients, and the percentage of malicious clients. This comprehensive performance study provides the results that the users can use to select appropriate defense algorithms to employ based on the characteristics of their federated learning systems.
1. Introduction
In recent years, federated learning has emerged as an innovative machine learning paradigm due to its ability to facilitate the training of a machine learning model without having direct access to data [1]. In a basic federated learning architecture, clients train their local machine learning models using their own data and send their local models to a central server, which then aggregates the local models to update the global model and sends the updated global model to the clients to use. The same process is repeated in the following rounds. This approach opens up new ways to leverage privacy-sensitive data for many applications, such as training next word prediction models on text message data, training image classifiers on secure smartphone images, or training a model collaboratively between companies without either revealing proprietary data.
While federated learning offers exciting opportunities, it also introduces unique vulnerabilities [2,3,4,5]. Because the model is iteratively trained on client devices, and because only clients have access to their own data, the system is vulnerable to client compromise by malicious actors seeking to influence the global model. Malicious clients could manipulate the updates that they send to the server to install a “backdoor” subtask in the global model. For example, a company could inject its brand name into a next word prediction model. Some malicious clients might add fake news in federated learning systems for news recommendations, making the system promote misinformation. Similarly, in a federated learning context for healthcare applications, malicious clients could provide deceptive health data, influencing the global model to suggest ineffective or potentially harmful personalized treatment recommendations, ultimately jeopardizing the well-being of users.
This paper presents a comprehensive comparison of six state-of-the-art algorithms that are designed to defend against targeted model poisoning attacks. The algorithms under examination include PCA + K-Means [6], KPCA + K-Means [7], CONTRA [8], KRUM [9], and COOMED [10], and RPCA + PCA + K-Means.
To the best of our knowledge, this is the first work that provides a thorough performance evaluation of a comprehensive set of the best algorithms available for defending against model attacks in federated learning. The evaluation model considers a wide variety of client numbers and proportions of malicious clients, and both types of data—IID (Independent and Identically Distributed) and non-IID. The evaluation results help the users decide which algorithms to use in their own systems, based on which experiments most closely resemble their own applications.
In addition, we extend previous research by experimenting with four other datasets—the UCI Adult Census and Epileptic Seizure Recognition datasets are used in addition to Fashion-MNIST and CIFAR-10. A more realistic and varied investigation of poisoning attacks in different FL situations is made possible by our study’s unique variation of other parameters, such as the degree of data IID, the total number of customers, and the number of malicious customers. Our work offers new perspectives for modifying and improving defense mechanisms in federated learning systems by modeling situations that more closely resemble real-world applications, where the number of clients and data distribution differ significantly.
The main contributions of this paper are the following:
- Provides comprehensive discussions of the background and the existing algorithms relating to attack defense in federated learning;
- Introduces a unique defense approach against model attacks in federated learning that combines RPCA with PCA and clustering, which has not been seen in other studies;
- Presents comprehensive experimental evaluations of six state-of-the-art defense algorithms against model attacks in federated learning using four different datasets, providing insights into their performance.
The remainder of this paper is structured as follows. Section 2 introduces the details of the federated learning paradigm. Section 3 discusses related work and makes a comparison of previous studies on poisoning attacks in federated learning systems. Section 4 presents the attack models and Section 5 details the defense methods investigated. Section 6 discusses the simulation model and performance metrics. Section 7 details the experimental results, and finally, Section 8 concludes the paper and proposes directions for future work.
2. Federated Learning
The concept of federated learning (FL) was first introduced by [11]. It represents a decentralized machine learning paradigm that has gained prominence in recent years. Unlike traditional centralized models, federated learning distributes the learning process across multiple devices or nodes, such as smartphones or edge devices, allowing them to collaboratively train a shared model without exchanging raw data. This unique approach addresses privacy concerns associated with data sharing, as model updates occur locally on each device, and only aggregated model updates are transmitted to a central server.
This collaborative learning strategy not only enables the development of robust models that generalize well across diverse datasets, but also prioritizes user privacy. In addition, federated learning introduces the concept of communication efficiency, which emphasizes the need to minimize the communication costs between devices and the central server [6,8].
At the intersection of machine learning, privacy, and efficient communication, federated learning offers a promising way to train models on decentralized data sources while maintaining privacy and security principles.
Applied in a variety of real-world scenarios, federated learning systems demonstrate their versatility and practical utility. In healthcare, it enables collaborative model training on patient data from multiple institutions without compromising individual privacy. This can facilitate the development of predictive models for diseases such as diabetes and cancer. In the financial sector, federated learning systems can also be used for loan risk assessment and for fraud detection, allowing multiple banks to collaboratively improve their models while keeping sensitive transaction data decentralized. In the transportation sector, federated learning systems enable collaborative model training in vehicular networks, enhancing vehicle and traffic management [1,12].
As shown in Figure 1, a federated learning system consists of a central server that attempts to develop a global model and multiple clients that own private data. The clients perform local model updates based on their respective datasets. After training, each client sends its model update back to the central server. The server then aggregates these updates and iteratively refines the global model and sends the updated global models to the clients. This decentralized process ensures collaborative learning while maintaining individual data privacy [13].
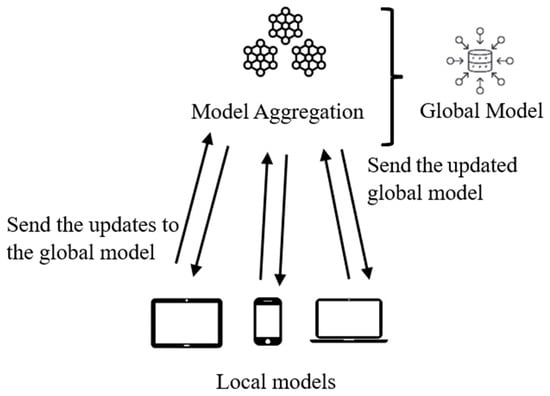
Figure 1.
Training process of a federated learning system.
We present a step-by-step algorithm proposed by Yang et al. [14] to better understand the machine learning training process on distributed data, as follows:
- The server randomly initializes the global model parameters;
- The global model is distributed to a random subset of the clients;
- Each selected client performs standard stochastic gradient descent on its own data for a given number of epochs;
- Each selected client computes the difference between the model after this round of training and the model it received at the beginning of this round of training;
- Each client sends this difference back to the server;
- The server aggregates all the model updates using the FedAvg algorithm [11];
- The server applies the aggregated update to the global model;
- Steps 2–7 are repeated for a given number of time steps (T).
While this approach is powerful, it introduces vulnerabilities in the event that one or more clients are compromised, an issue that will be discussed in Section 4. In addition, critical issues remain in the area of federated learning. One issue is scalability in terms of number of clients increases. Another issue is robustness against adversarial attacks, which requires the development of better defense mechanisms to secure federated learning systems against malicious entities that seek to manipulate model updates.
Addressing non-IID data is another critical issue because the data samples on each participating device are typically not IID. This introduces significant challenges associated with statistical heterogeneity in federated learning [12].
3. Related Work
In addition to the specific algorithms studied in this paper, which we discuss in detail in Section 5, there is also research aimed at improving the security of federated learning.
Bagdasaryan et al. [2] proposed an attack model that installs a “backdoor” malicious subtask into a classification model. The inclusion of a malicious client allows it to “replace” the global model with one designed by the adversary. Additionally, the size of the update can be reduced to avoid detection by a naive defense scheme.
Fung et al. [15] introduced a method for defending against sybils (a large number of fraudulent clients attempting to achieve the same goal) called FoolsGold. The method is based on examining the similarities between client updates to identify a group of “suspiciously similar” updates, with the assumption that these updates are from malicious clients instead of from naturally varying legitimate clients. This approach forms the basis of the CONTRA algorithm that we analyze in this paper [8].
Tolpegin et al. [6] investigated data poisoning attacks in the context of federated learning systems, using the CIFAR-10 and Fashion-MNIST datasets for testing. These attacks involve the malicious insertion of data on participants’ devices, which adversely affects the overall performance of the model. In response to this attack, the paper proposes a defense mechanism based on the identification of malicious participants using gradient analysis and Principal Component Analysis (PCA). This defense enables the FL system to detect and restrict the participation of suspicious participants. The research demonstrates the effectiveness of PCA in separating and identifying malicious and benign clients into distinct groups. Although this paper also examined the impact of varying the number of malicious clients ranging from 0% to 50%, our work additionally considers the resulting impact of varying the number of clients and the type of data, including both IID and non-IID scenarios.
Li et al. [7] proposed a new defense strategy using Kernel Principal Component Analysis (KPCA) [16] to combat data poisoning attacks. This new approach aims to improve the security of FL systems in the face of malicious data manipulation, thereby expanding the repertoire of defense strategies available in this domain. The performance evaluation of PCA, and KPCA combined with the K-means clustering algorithm [16] shows that the KPCA + K-means algorithm outperforms the others, demonstrating its effectiveness in securing FL systems, especially for the CIFAR-10 and Fashion-MNIST datasets. While our paper explores the impact of malicious clients, our research goes beyond that by investigating the impact of numbers of clients and different types of data, including both IID and non-IID scenarios.
The research conducted by Bhagoji et al. [17] investigated the vulnerability of federated learning to adversarial model poisoning attacks. Using two different datasets, Fashion MNIST and UCI Adult Census, the study examined attack strategies, including explicit boosting model poisoning, stealth model poisoning, and alternating minimization method. In addition, the impact of these attacks on Byzantine-resilient aggregation algorithms, such as KRUM [9] and coordinate-wise median (COOMED) [10], was evaluated by Bhagoji et al. [17]. The results show the effectiveness of these adversarial attacks, even against Byzantine defense mechanisms, highlighting the need for more sophisticated detection strategies and robust approaches to protect federated learning against such threats. While this paper explored the KRUM and COOMED algorithms using the Fashion MNIST and UCI Adult Census datasets, our research goes further. We include two additional datasets, CIFAR-10 and Epileptic Seizure Recognition, and explore a broader range of algorithms beyond KRUM and COOMED.
Other works has been useful in establishing the severity of the vulnerability [10,18]. Another type of attack, Byzantine attacks, attempts to prevent the global model from converging, and [15] demonstrated that defenses against Byzantine attacks are not effective against model poisoning, and proposed two defense methods. However, neither of the methods showed consistent success, so they are not considered in our paper. Shejwalkar and Houmansadr in [19] produced a similar result regarding the vulnerability of Byzantine-robust systems to model poisoning, and proposed an effective defense against an untargeted model poisoning attack.
More recently, in 2024, Kiran Purohit et al. [20] introduced the “LearnDefend” defense mechanism designed for federated learning to combat poisoning attacks. This approach uses an external defense dataset to detect poisoned data and evaluates the likelihood of malicious updates from clients. It significantly reduces attack success rates, especially for edge-case model poisoning attacks.
Also in 2023, the AgrAmplifier algorithm was introduced by Zirui Gong et al. [21]. This algorithm is designed to improve the defense of Federated Learning (FL) systems against poisoning attacks by amplifying updates from benign clients, thus reducing the influence of malicious updates. The authors developed a set of variants and integrated them with existing aggregation mechanisms, demonstrating improved robustness, fidelity, and efficiency compared to traditional methods. These attacks occur when malicious clients manipulate their local data or updates to degrade the global model. AgrAmplifier addresses this problem by amplifying the contributions of benign clients, which helps minimize the impact of malicious updates. The algorithm uses two key techniques to accomplish this—AGRMP and AGRXAI.
AGRMP organizes gradient updates into patches and extracts the most significant values, which are then amplified to better distinguish between benign and malicious updates. On the other hand, AGRXAI uses explainable AI methods to focus on the most activated features of the gradients, improving the interpretability of the decision-making process and identifying discrepancies that may indicate malicious behavior. Combined, these two methods enhance the filtering process and improve the effectiveness of existing Byzantine-robust aggregation rules (AGR) in detecting and mitigating poisoning attacks.
The effectiveness of AgrAmplifier has been demonstrated through extensive experiments, where it was shown to improve robustness, fidelity, and efficiency by an average of 40%, 39%, and 10%, respectively, across multiple datasets and attack scenarios. These improvements make AgrAmplifier a promising solution for protecting federated learning systems from malicious perturbations, especially in scenarios involving Byzantine attacks.
Table 1 summarizes recent studies and highlights the limitations of the metrics used by Awan et al. [8], Li et al. [7], and Tolpegin et al. [6] to assess the impact of poisoning attacks in federated learning (FL) systems. In this table, the parameters and metrics used in each study are marked with an "X". These studies have largely focused on assessing model effectiveness through Accuracy and Attack Success Rate (ASR) metrics. However, they have not included additional critical metrics—such as Precision, Recall, F1-Score, and Malicious Confidence (MC)—that are essential to understanding the complexities involved in defending against these attacks. These additional metrics are particularly valuable for evaluating a model’s ability to more accurately distinguish between honest and malicious updates, and could provide deeper insight into the defensive robustness of FL models.

Table 1.
Comparison of previous studies on poisoning attacks in federated learning systems; evaluation metrics and experimental parameters.
Our study aims to address this gap by adopting a broader, more comprehensive set of metrics that includes Precision, Recall, F1-Score, and Malicious Confidence in addition to the traditional Accuracy and ASR metrics. This expanded approach provides a more nuanced view of the defense effectiveness, allowing for a more detailed evaluation of how attacks impact model performance. We also extend previous studies by conducting experiments on four different datasets; in addition to Fashion-MNIST and CIFAR-10, we use the UCI Adult Census and Epileptic Seizure Recognition datasets. Our study also uniquely varies additional parameters, including the degree of data IID (Independent and Identically Distributed), the total number of clients, and the number of malicious clients, allowing for a more realistic and diverse analysis of poisoning attacks in different FL contexts. By simulating scenarios closer to real-world applications, where data distribution and client numbers vary significantly, our work contributes new insights for adapting and refining defense mechanisms in federated learning systems.
4. Attack Model
The attacks discussed in this paper are examples of adversarial learning, a technique in which attackers manipulate the learning process to influence the behavior of a machine learning model [22]. In the context of federated learning, adversarial learning attacks are realized through the potential compromise of participating clients by malicious actors. Because federated learning works by applying an aggregation function to the model updates received from the clients, a malicious client has the ability to influence the resulting global model to achieve specific goals. These goals could include degrading the overall model performance or inserting a “subtask” into the global model without noticeably degrading the performance of the main task. For example, an attack may aim to compromise the global model’s ability to identify specific patterns, directly impacting the main task of image classification. The attack could be achieved by modifying the malicious client’s training data or labels, or it could be accomplished by directly manipulating the updates that the client sends to the server. The following subsections enumerate different types of adversarial learning attacks on federated learning, and explain the implementations of the specific attacks on which this work focuses.
4.1. Classification of Attacks
Malicious clients in a federated learning environment can attempt to use their inclusion in the training process to influence the final global model. However, different adversaries may have different goals for the global model. Here are the main categories of poisoning attacks against federated learning:
Untargeted Attacks (Byzantine Attacks). These attacks aim to prevent the global model from converging to an effective classifier. Techniques include data poisoning, where false labels are introduced during training to negatively affect the performance of the global model [18]. A model update poisoning attack can be more powerful because it exploits the fact that the agent has direct control over the model updates it sends to the server. It can thus increase the amount of its contribution in order to dominate the global model after aggregation.
Targeted Attacks. Also known as “backdoor” attacks, targeted attacks seek not to degrade the performance of the global model, but to insert a backdoor subtask into the global model. For example, an organization might attempt to inject marketing messages into a next word prediction model. This can also be accomplished through data poisoning or model poisoning [1].
There are two main approaches to model poisoning for a targeted attack—boosting the entire contribution of the malicious client to replace the global model [2], or boosting only the malicious component of the update [17].
In this paper, we only consider a targeted model update poisoning attack with selective boosting.
4.2. Attack Implementation
The attack model considered here is similar to the one proposed by Bhagoji et al. in [17], where the following pertains:
- The malicious actor controls at least one client;
- The malicious clients have access to some of the legitimate training data, as well as the auxiliary data that will be used to create the adversarial subtask.
The goal of the adversary is to cause the global model to perform the targeted misclassification of the auxiliary data while still converging to good performance on the main task. The adversary aims to induce a specific misclassification in the auxiliary data for the main task while ensuring that the overall performance on the main task remains good. The term subtask here can be understood as the manipulation introduced into the auxiliary data to achieve a specific desired outcome in the main task.
This is accomplished by using the explicit boosting technique. It first trains on the legitimate data and the mislabeled auxiliary data to obtain an estimate of what it wants the parameters of the global model to be after aggregation (i.e., with the subtask installed). It then computes the difference between these desired weights and the global model provided at the beginning of the communication round. It then multiplies this difference by a “boosting factor” before sending it back to the server. This ensures that the expected global model after the attack behaves as the attacker desires, even after the attacker’s contribution is aggregated with those of many other clients.
The attack implementation also includes a stealth strategy called “alternating minimization” [17]. This strategy identifies two objectives: the targeted objective and the stealth objective. The targeted objective is the objective of the global model, which performs the malicious subtask after aggregating the update from the malicious client. The stealth objective seeks to minimize the distance between the malicious update and a benign update (which the attacker can compute from its portion of the benign data). The attacker then alternates between training its local model for each of these objectives (the targeted objective and the stealth objective) until both are achieved to the attacker’s satisfaction. Without this strategy, malicious updates are easily detectable by defense algorithms as they exhibit significantly greater magnitude compared to benign updates.
5. Defense Methods
In this section, we explore the diverse landscape of aggregation algorithms within federated learning systems: PCA + K-Means [6], KPCA + K-Means [7], CONTRA [8], KRUM [9], COOMED [10], and RPCA + PCA + K-Means. The efficiency and effectiveness of aggregating model updates from multiple clients are critical to the success of federated learning. We investigate and compare several state-of-the-art aggregation techniques, each being designed to improve the federated model training process. Each of the defenses explored in this paper has a similar goal—to identify likely malicious clients and prevent them from impacting the global model. This is accomplished by analyzing patterns in benign updates versus malicious updates.
5.1. PCA + K-Means
Principal Component Analysis (PCA) is a widely used dimensionality reduction technique in machine learning and statistics [6]. Its primary goal is to transform high-dimensional data into a lower-dimensional representation that captures the most important information while minimizing loss. PCA accomplishes this by identifying the principal components, which are linear combinations of the original features, ordered by the amount of variance they explain. By retaining a subset of these components, PCA allows for a more compact representation of the data, aiding in visualization, analysis, and, in this context, the identification of potential patterns or clusters, such as those indicative of malicious activity in federated learning systems [23].
The use of dimensionality reduction combined with a clustering algorithm has been proposed as a method to identify and remove malicious clients that perform both targeted and untargeted poisoning attacks [6].
The central insight underlying this method of defense is that updates from malicious clients will “look different” than updates from benign clients. Benign clients are simply trying to improve the overall accuracy of the global model on their training data, while malicious clients have some other goals, such as to degrade the performance of the global model or to covertly install a backdoor subtask.
We do not need to know how to quantify what characteristics we might expect malicious updates to have. We can develop a method to identify a cluster of updates that are “generally different” from the mass of benign updates.
The algorithm is similar to that used for typical federated learning, except that a dimensionality-2 PCA is performed on a subset of the local updates. The algorithm, as presented below, then plots these two-dimensional points to identify the malicious cluster, but the cluster can also be identified using the K-means clustering algorithm with two centroids, identifying the smaller cluster as malicious [6,7].
The algorithm for the federated learning system using PCA + K-means as the aggregation model works as follows (Algorithm 1):
| Algorithm 1. Identifying malicious model updates using PCA + K-means |
| Input: numberOfAgents, T (number of iterations) |
| Output: globalWeights |
| // Step 1: Initialization and Configuration |
| Initialize agents with indices [1, 2, …, numberOfAgents] |
| Initialize globalWeights |
| Set t = 0 |
| // Step 2: Main Training Loop |
| while t < T do |
| // Step 2a: Calculate probabilities for agent selection |
| probabilities = CalculateSelectionProbabilities(agents) |
| // Step 2b: Start parallel training and wait for completion |
| selectedAgents = SelectAgents(probabilities) |
| updates = ParallelTraining(selectedAgents) |
| // Step 2c: Data Collection and Preprocessing |
| updateMatrix = CollectUpdates(updates) |
| // Step 2d: Dimensionality Reduction with PCA |
| reducedData = PCA(updateMatrix) |
| // Step 2e: Cluster Analysis using K-Means |
| clusters = KMeansClustering(reducedData) |
| // Step 2f: Cluster Selection to identify anomalies |
| selectedClusters = IdentifyAnomalousClusters(clusters) |
| // Step 2g: Weighted Aggregation within clusters |
| aggregatedUpdates = WeightedAggregate(selectedClusters, clusterSizes) |
| // Step 3: Evaluation and Updating |
| globalWeights = UpdateGlobalWeights(globalWeights, aggregatedUpdates) |
| EvaluateModel(globalWeights) |
| // Step 4: Close Loop |
| StoreEvaluationResults(globalWeights) |
| t = t + 1 |
| end while |
| return globalWeights |
5.2. KPCA + K-Means
Kernel Principal Component Analysis (KPCA) is a robust extension of PCA, which is widely used in machine learning and statistics [7]. Similar to PCA, KPCA excels in reducing the dimensionality of high-dimensional data, with the goal of retaining important information while minimizing loss. What sets KPCA apart is its ability to handle non-linear relationships within the data by using a kernel function. This enhanced capability makes KPCA particularly effective at capturing complex patterns that may be missed by linear methods.
The key improvement of KPCA over PCA is its ability to reduce the dimension of data nonlinearly, as demonstrated in Figure 2 [6,7,16]. The linear green lines (on the right side) represent the linear reduction of data, where only a straight line is traced. In contrast, the curved green lines (on the left side) demonstrate the non-linear reduction achieved by KPCA, allowing for a more flexible representation of the underlying data. This figure emphasizes KPCA’s capability to capture intricate patterns and relationships that may be overlooked by traditional linear methods like PCA.
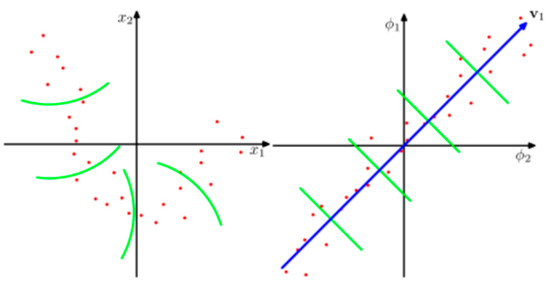
Figure 2.
Demonstration of the benefit of non-linear dimensional reduction.
The algorithm for the federated learning system using KPCA + K-means as the aggregation model works as follows (Algorithm 2):
| Algorithm 2. Identifying malicious model updates using KPCA + K-means |
| Input: numberOfAgents, T (number of iterations) |
| Output: globalWeights |
| // Step 1: Initialization and Configuration |
| Initialize agents with indices [1, 2, …, numberOfAgents] |
| Initialize globalWeights |
| Set t = 0 |
| // Step 2: Main Training Loop |
| while t < T do |
| // Step 2a: Calculate probabilities for agent selection |
| probabilities = CalculateSelectionProbabilities(agents) |
| // Step 2b: Start parallel training and wait for completion |
| selectedAgents = SelectAgents(probabilities) |
| updates = ParallelTraining(selectedAgents) |
| // Step 2c: Data Collection and Preprocessing |
| updateMatrix = CollectUpdates(updates) |
| // Step 2d: Kernel Transformation with KPCA |
| kernelTransformedData = KPCA_Transform(updateMatrix) |
| // Step 2e: Kernel-Based Cluster Analysis using K-Means |
| clusters = KMeansClustering(kernelTransformedData) |
| // Step 2f: Cluster Selection and Weighted Aggregation |
| selectedClusters = IdentifyDistinctiveClusters(clusters) |
| aggregatedKernelUpdates = WeightedAggregate(selectedClusters, clusterSizes) |
| // Step 2g: Inverse Kernel Transformation |
| globalUpdate = KPCA_InverseTransform(aggregatedKernelUpdates) |
| // Step 3: Evaluation and Updating |
| globalWeights = UpdateGlobalWeights(globalWeights, globalUpdate) |
| EvaluateModel(globalWeights) |
| // Step 4: Close Loop |
| StoreEvaluationResults(globalWeights) |
| t = t + 1 |
| end while |
| return globalWeights |
5.3. CONTRA
CONTRA, presented by Awan et al. in [8], is a distinctive defense mechanism in federated learning that takes a novel approach to defending against potential malicious clients. Instead of outright identification and exclusion, CONTRA implements a reputation system. Each client is assigned a reputation score, and is penalized for suspicious behavior detected by assessing the similarity of updates to historical data. The algorithm aims to limit the impact of malicious agents and reduce their chances of being chosen in subsequent training rounds [8].
The algorithm for the federated learning system using CONTRA as the aggregation model works as follows (Algorithm 3):
| Algorithm 3. Identifying malicious model updates using CONTRA |
| Input: numberOfAgents, T (number of iterations) |
| Output: globalWeights |
| // Step 1: Initialization and Configuration |
| Initialize agents with indices [1, 2, …, numberOfAgents] |
| Initialize globalWeights |
| Set t = 0 |
| // Step 2: Main Training Loop |
| while t < T do |
| // Step 2a: Calculate probabilities for agent selection |
| probabilities = CalculateSelectionProbabilities(agents) |
| // Step 2b: Start parallel training and wait for completion |
| selectedAgents = SelectAgents(probabilities) |
| updates = ParallelTraining(selectedAgents) |
| // Step 2c: Calculate Offsets |
| for each agent in selectedAgents do |
| offset[agent] = CalculateOffset(agent.update, referenceUpdate) |
| end for |
| // Step 2d: Similarity Measurement |
| for each agent in selectedAgents do |
| similarityScore[agent] = MeasureSimilarity(offset[agent], referenceUpdate) |
| end for |
| // Step 2e: Weighted Aggregation |
| globalUpdate = 0 |
| totalWeight = 0 |
| for each agent in selectedAgents do |
| if similarityScore[agent] is High then |
| weight = AssignHigherWeight(similarityScore[agent]) |
| globalUpdate += weight * agent.update |
| totalWeight += weight |
| end if |
| end for |
| globalUpdate = globalUpdate/totalWeight |
| // Step 3: Evaluation and Updating |
| globalWeights = UpdateGlobalWeights(globalWeights, globalUpdate) |
| EvaluateModel(globalWeights) |
| // Step 4: Close Loop |
| StoreEvaluationResults(globalWeights) |
| t = t + 1 |
| end while |
| return globalWeights |
5.4. KRUM
KRUM, initially designed to combat “Byzantine” attacks, stands out as a robust aggregation algorithm in the realm of federated learning. Unlike traditional approaches, KRUM strategically evaluates the reliability of models by considering the distances between them. It takes a discerning stance, excluding models that deviate significantly from the majority, thereby prioritizing the creation of a dependable global model [9].
This algorithm finds particular significance in the federated learning landscape, where its application serves as a defense against the introduction of malicious or poisoned models by specific clients. KRUM’s primary goal is to minimize the potential impact of these models on the collaborative training process, contributing to the overall security and effectiveness of federated learning endeavors. Through its selective model inclusion based on proximity, KRUM enhances the global model’s resilience against harmful contributions, reinforcing the integrity of federated learning systems [8].
The algorithm of the federated learning system using KRUM as the aggregation model works as follows (Algorithm 4):
| Algorithm 4. Identifying malicious model updates using KRUM |
| Input: numberOfAgents, T (number of iterations) |
| Output: globalWeights |
| // Step 1: Initialization and Configuration |
| Initialize agents with indices [1, 2,..., numberOfAgents] |
| Initialize globalWeights |
| Set t = 0 |
| // Step 2: Main Training Loop |
| while t < T do |
| // Step 2a: Calculate probabilities for agent selection |
| probabilities = CalculateSelectionProbabilities(agents) |
| // Step 2b: Start parallel training and wait for completion |
| selectedAgents = SelectAgents(probabilities) |
| updates = ParallelTraining(selectedAgents) |
| // Step 2c: Calculate Distance |
| distanceMatrix = InitializeDistanceMatrix() |
| for each agent_i in selectedAgents do |
| for each agent_j in selectedAgents, where j ≠ i do |
| distanceMatrix[i][j] = CalculateDistance(agent_i.update, agent_j.update) |
| end for |
| end for |
| // Step 2d: Select Models |
| selectedDistances = SelectSmallestDistances(distanceMatrix) |
| // Step 2e: Calculate Score |
| for each agent in selectedAgents do |
| score[agent] = Sum(selectedDistances[agent]) |
| end for |
| // Step 2f: Choose Final Model |
| krum_index = AgentWithLowestScore(score) |
| globalUpdate = updates[krum_index] |
| // Step 3: Evaluation and Updating |
| globalWeights = UpdateGlobalWeights(globalWeights, globalUpdate) |
| EvaluateModel(globalWeights) |
| // Step 4: Close Loop |
| StoreEvaluationResults(globalWeights) |
| t = t + 1 |
| end while |
| return globalWeights |
5.5. COOMED
The coordinate-wise median (COOMED) algorithm stands out as a significant aggregation strategy in federated learning systems [10]. Handling sets of updates in different dimensions, COOMED calculates a coordinate median to strengthen the formation of the global model. COOMED uses information from all agents, and promotes robust and efficient coordination to achieve effective global models. COOMED’s functioning is characterized by its coordination mechanism, where it incorporates information from all participating agents. Instead of favoring one specific update, COOMED collaboratively leverages insights from multiple agents [17].
In essence, COOMED enhances the global model’s formation by ensuring that each dimension is influenced by the coordinated median, creating a more comprehensive and resilient representation of the aggregated updates.
The algorithm for the federated learning system using COOMED as the aggregation model works as follows (Algorithm 5):
| Algorithm 5. Identifying malicious model updates using COOMED |
| Input: numberOfAgents, T (number of iterations) |
| Output: globalWeights |
| // Step 1: Initialization and Configuration |
| Initialize agents with indices [1, 2, …, numberOfAgents] |
| Initialize globalWeights |
| Set t = 0 |
| // Step 2: Main Training Loop |
| while t < T do |
| // Step 2a: Calculate probabilities for agent selection |
| probabilities = CalculateSelectionProbabilities(agents) |
| // Step 2b: Start parallel training and wait for completion |
| selectedAgents = SelectAgents(probabilities) |
| updates = ParallelTraining(selectedAgents) |
| // Step 2c: Calculate Median (COOMED Aggregation) |
| medianUpdates = InitializeMedianUpdates() |
| for each coordinate in globalWeights do |
| values = [] |
| for each agent in selectedAgents do |
| values.append(agent.update[coordinate]) |
| end for |
| medianUpdates[coordinate] = CalculateMedian(values) |
| end for |
| // Step 2d: Global Update |
| globalWeights = medianUpdates |
| // Step 3: Evaluation and Updating |
| EvaluateModel(globalWeights) |
| // Step 4: Close Loop |
| StoreEvaluationResults(globalWeights) |
| t = t + 1 |
| end while |
| return globalWeights |
5.6. RPCA + PCA + K-Means
This is an algorithm we propose that combines Robust Principal Components Analysis (RPCA) with the PCA + K-Means algorithm. RPCA is a technique designed to decompose a matrix into two distinct components: a low-rank matrix (L) representing dominant and essential patterns, and a sparse matrix (S) capturing sparse and potentially disruptive elements. This approach is particularly useful for identifying significant patterns and handling sparse elements, such as outliers or malicious updates, in contexts like federated learning [24].
The decomposition of low-rank matrix (L) and sparse matrix (S) is achieved by solving a complex optimization problem. Essentially, the objective is to find the best combination of L and S that, when added together, reconstructs the original matrix (M). The optimization involves balancing the trade-off between maintaining the essential patterns (low-rank) and identifying sparse disruptive elements. The process aims to discern regularities in the data (L) while singling out irregular or sparse occurrences (S) [25].
This defense mechanism is a combination of RPCA with PCA and clustering. This combination in federated learning introduces a multi-step approach to processing and analyzing updates from participating agents. Initially, RPCA is applied to decompose the update matrix into a low-rank matrix (L) and a sparse matrix (S), allowing for the identification of dominant patterns and potential sparse or disruptive elements, which may include outliers or malicious updates. Subsequently, the low-rank matrix (L) undergoes dimensionality reduction using PCA, aiming to represent the identified patterns in a more compact form. The reduced matrix is then subjected to a clustering algorithm, such as K-Means, to group similar update patterns. This step helps identify clusters of agents contributing similar updates, helping to identify potential malicious activity or anomalous behavior. It enhances the system’s ability to robustly aggregate updates in federated learning, while addressing outliers and identifying patterns indicative of irregularities.
The algorithm for the federated learning system using RPCA + PCA + K-means as the aggregation model works as follows (Algorithm 6):
| Algorithm 6. Identifying malicious model updates using RPCA + PCA + K-means |
| Input: numberOfAgents, T (number of iterations) |
| Output: globalWeights |
| // Step 1: Initialization and Configuration |
| Initialize agents with indices [1, 2,..., numberOfAgents] |
| Initialize globalWeights |
| Set t = 0 |
| // Step 2: Main Training Loop |
| while t < T do |
| // Step 2a: Calculate probabilities for agent selection |
| probabilities = CalculateSelectionProbabilities(agents) |
| // Step 2b: Start parallel training and wait for completion |
| selectedAgents = SelectAgents(probabilities) |
| updates = ParallelTraining(selectedAgents) |
| // Step 2c: Data Collection and Preprocessing |
| updateMatrix = CollectUpdates(updates) |
| // Step 2d: Robust Principal Component Analysis (RPCA) |
| // Decompose matrix into low-rank (L) and sparse (S) |
| [L, S] = RPCA(updateMatrix) |
| // Step 2e: Dimensionality Reduction with PCA |
| reducedData = PCA(L) |
| // Step 2f: Cluster Analysis with K-Means |
| clusters = KMeansClustering(reducedData) |
| // Step 2g: Cluster Selection |
| selectedClusters = IdentifyAnomalousClusters(clusters) |
| // Step 2h: Weighted Aggregation within Clusters |
| aggregatedUpdates = InitializeAggregatedUpdates() |
| for each cluster in selectedClusters do |
| clusterSize = SizeOf(cluster) |
| for each update in cluster do |
| weightedUpdate = WeightUpdate(update, clusterSize) |
| aggregatedUpdates = AddWeightedUpdate(aggregatedUpdates, weightedUpdate) |
| end for |
| end for |
| // Step 3: Evaluation and Updating |
| globalWeights = UpdateGlobalWeights(globalWeights, aggregatedUpdates) |
| EvaluateModel(globalWeights) |
| // Step 4: Close Loop |
| StoreEvaluationResults(globalWeights) |
| t = t + 1 |
| end while |
| return globalWeights |
6. Experimental Setup
In this section, we detail the setup of our experiments, examining the simulation model and the performance metrics. In addition, we examine the datasets used and explain the specific neural network architectures tailored to the requirements of each dataset.
6.1. Simulation Model
The simulation model used in our experiments is based on the repository provided by [17], as previously described in Section 4.2.
The experiments for the classification task used the Fashion-MNIST dataset along with the CIFAR-10, UCI Adult Census, and Epileptic Seizure Recognition datasets, which are described in Section 6.3. The impact of the following three dynamic parameters on performance metrics is also analyzed: (i) the percentage of Independent and Identically Distributed (IID) data in clients, (ii) the total number of clients, and (iii) the percentage of malicious clients.
The extent of IID in the data is quantified in a manner similar to that described in McMahan’s original paper [11]. First, the training data to be distributed among the clients are sorted using class labels. Then, they are divided as evenly as possible into a number of slices that lies between the number of clients and the number of training examples. Then, an equal number of slices are randomly distributed to the clients. If the number of slices is equal to the number of clients, the data are maximally non-IID because each client is likely to receive data from only one or two labels. If the number of slices is equal to the number of training examples, the data are maximally IID, since this is equivalent to randomly distributing the data among the clients. These two extremes are linearly mapped to the values 0 and 1 of the parameter called IID, where 0 is completely non-IID and 1 is IID. Each run consisted of 20 communication rounds, as detailed in the subsequent section, and the performance metrics were averaged over the 10 experimental runs. This approach aligns with the methodology utilized by [7] for computing performance metrics across different scenarios listed in Table 2.

Table 2.
Parameters and variation ranges used in experimental evaluation.
6.2. Performance Metrics
In the experiments, the performance is measured after each round of communication and consists of the following six metrics: Accuracy, Precision, Recall, F1-Score, Malicious Confidence, and Attack Success Rate. A communication round in federated learning is a cycle where clients train models locally and send their updates to the server, and the server aggregates these updates to refine the global model and sends the updated global model to the clients, completing one iteration of the collaborative learning process.
The server retains a portion of the data as a test set to evaluate performance. Then, at the end of the federated learning process, the metrics of the global model are extracted from the test data. As mentioned above, this is computed after 20 rounds of communication.
The Malicious Confidence (MC) measures the accuracy of the model specifically in predicting malicious examples. It is calculated by dividing the number of correct malicious predictions by the total number of predictions that the model classified as malicious (see Equation (1)). This metric provides insights into the model’s confidence in making malicious classifications. A higher Malicious Confidence indicates a greater tendency for the model to identify malicious instances that manage to go unnoticed by being misclassified as benign. A robust defense algorithm should ideally exhibit a low MC, indicating a reduced likelihood of misclassifying malicious instances as benign.
The Attack Success Rate (ASR) [8] evaluates the effectiveness of malicious attacks on the model. It is calculated by dividing the number of successful malicious attacks by the total number of attempted malicious attacks (see Equation (2)). The ASR provides a measure of the adversary’s success in manipulating the model to misclassify examples as malicious.
In this equation the “Number of Successful Malicious Attacks” represents the number of test data instances that were successfully tampered with (mislabeled), and the “Total Number of Attempted Malicious Attacks” is the total number of test data instances on which malicious attacks were attempted [8]. The higher the ASR, the worse the algorithm’s performance in preventing attacks. Therefore, we aim for a good algorithm to have a low ASR.
Before discussing the additional metrics, we must first clarify the meanings of true positive (TP), true negative (TN), false positive (FN), and false negative (FN). TP is the number of instances correctly predicted to be malicious. TN is the number of instances correctly predicted to be benign. FP is the number of instances falsely predicted to be malicious (benign instances misclassified). FN is the number of instances misclassified as benign [21].
Accuracy is a general metric that measures the overall correctness of the model’s predictions. It is the ratio of the correct predictions (both benign and malicious) to the total number of predictions (see Equation (3)). High accuracy indicates a well-performing model.
Precision measures the correctness of the model’s malicious predictions. It is calculated by dividing the number of true positives (correctly predicted) by the sum of true positives and false positives (see Equation (4)). Precision is critical when minimizing false positives or misclassifying benign examples as malicious.
Recall, also known as Sensitivity or True Positive Rate, measures the ability of the model to identify all malicious examples. It is calculated by dividing the number of true positives by the sum of true positives and false negatives (see Equation (5)). A high recall indicates the effective detection of malicious instances.
The F1-Score is the harmonic mean of Precision and Recall (see Equation (6)). It provides a balanced measure between precision and recall, especially in situations where there is an imbalance between classes (e.g., more benign examples than malicious ones). The F1-Score is useful for evaluating the overall performance of the model.
In the experiments, the malicious subtask consists of several examples that the attacker tries to get the global model to misclassify. Thus, Malicious Confidence is the value that the global model assigns to the attacker’s target class in the model’s output layer when classifying the attacker’s example.
A good defense method will maintain high global accuracy while minimizing the attack success rate and minimizing the confidence the model assigns to the malicious subtask by correctly identifying and penalizing the malicious clients.
Another performance metric we looked at was execution time to measure how long it takes each algorithm to run. By evaluating the execution time, we gain insights into the algorithms’ computational efficiency.
6.3. Datasets and Deep Neural Networks Architectures
In order to evaluate the performance of the different defense algorithms, we tested them on four different datasets: the Fashion-MNIST [26], the CIFAR-10 [27], the UCI Adult Census [28], and the Epileptic Seizure Recognition [29].
6.3.1. The Fashion-MNIST Dataset
The Fashion-MNIST dataset is a classification dataset consisting of images. Each image has dimensions of 28 pixels in height and 28 pixels in width, for a total of 784 pixels. Each pixel is assigned a pixel-value that represents its level of lightness or darkness, with higher values indicating darker shades. These pixel-values are integers between 0 and 255.
This dataset is divided into a training set, consisting of 60,000 examples, and a test set of 10,000 examples. As mentioned before, each image is characterized by a total of 784 pixels, corresponding to 784 attributes. Due to its classification nature, the dataset is structured into 10 classes representing a particular fashion category: T-shirt, trousers, pullover, dress, coat, sandal, shirt, sneaker, bag, and ankle boot.
The following deep neural network, shown in Table 3, follows a convolutional structure for classification, and is designed for the Fashion-MNIST dataset. The network uses ReLU activation for learning and dropout to prevent overfitting.

Table 3.
The DNN architecture used in Fashion-MNIST dataset.
6.3.2. The CIFAR-10 Dataset
The CIFAR-10 dataset is a classification dataset consisting of images. Each image has dimensions of 32 pixels in height and 32 pixels in width, for a total of 1024 pixels.
This dataset is divided into a training set, consisting of 50,000 examples, and a test set comprising 10,000 examples. As mentioned before, each image is characterized by a total of 1024 pixels, since the image is colored with three color channels (RGB format), and each pixel has three values corresponding to the color components (red, green, and blue), corresponding to 3072 attributes. Given its classification nature, the dataset is structured in 10 classes, with 6000 images per class, each representing a different category (airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck).
The following deep neural network, shown in Table 4, follows a convolutional structure for classification, and is designed for the CIFAR-10 dataset. The model uses Batch Normalization and Leaky ReLU activation to improve training stability and introduce non-linearity. The final dense layer produces the output for classification.

Table 4.
The DNN architecture used in the CIFAR-10 dataset.
6.3.3. The UCI Adult Census Dataset
The UCI Adult Census dataset is a classification dataset that aims to predict whether income exceeds USD 50 K/year based on the 1994 census data. The dataset consists of 45,222 instances, with 14 features (age, work class, education, education-num, marital status, occupation, relationship, race, sex, capital gain, capital loss, final weight, hours per week, and native country), and two classes (>USD 50 K/year or <USD 50 K/year).
The training set consists of 30,162 instances and the test set consists of 15,060 instances. The following deep neural network, shown in Table 5, was designed to train the UCI Adult Census dataset. The use of densely connected layers with ReLU activation facilitates effective feature learning, and the dropout layer helps prevent overfitting during the training process. The output layer, with neurons equal to the number of classes (2), is used to generate predictions for the income classification task.

Table 5.
The DNN architecture used in UCI Adult Census dataset.
6.3.4. The Epileptic Seizure Recognition Dataset
The Epileptic Seizure Recognition dataset consists of 11,500 instances, each with 179 attributes. These attributes correspond to the amplitude of electroencephalogram (EEG) signals recorded at different electrodes and times. The test set consists of 2300 instances and the train set consists of 9200 instances.
The dataset is composed of five classes: (1) the epileptic seizure occurred in the EEG, (2) the epileptic seizure did not occur, but the EEG showed abnormal activity, (3) the EEG was recorded outside the brain, (4) the epileptic seizure did not occur, and the EEG was in a normal state and, (5) the epileptic seizure did not occur, but there was abnormal activity in the EEG.
The following deep neural network, shown in Table 6, was designed to train the Epileptic Seizure Recognition dataset. The network uses ReLU activation for learning and dropout to prevent overfitting.

Table 6.
The DNN architecture used in the Epileptic Seizure Recognition dataset.
7. Experimental Results and Discussion
In this section, we present the experimental performance results of the six defense algorithms used. Through a detailed discussion, we explore the strengths and weaknesses of each algorithm, providing valuable insights into their effectiveness in federated learning systems.
7.1. Overall Performance
In this subsection, we present in Table 7 the average results of 10 tests conducted on the Fashion-MNIST dataset, using the default values of the dynamic parameters, as follows: IID = 0.4, number of clients = 100, and percentage of malicious clients = 10%.

Table 7.
The average test results with the default dynamic parameter values for the Fashion-MNIST dataset.
The KPCA + K-means algorithm achieved the best performance in terms of accuracy, and COOMED achieved the best performance in terms of Precision, Recall, and F1-Score. This can be attributed to the combination of the two techniques Kernel Principal Component Analysis and K-Means. KPCA allows data projection into a higher-dimensional space, where nonlinear patterns can be more easily separated. Subsequently, the K-means algorithm groups the projected data into clusters, helping identify distinct patterns and make more precise decisions. This results in a more robust and effective model for data classification.
On the other hand, KRUM showed the lowest global model performance, considering the metrics Accuracy, Precision, Recall, and F1-Score. This is due to its sensitivity to the presence of outliers and its inability to effectively handle nonlinear or highly complex data, which are common in real-world datasets.
The global model performances of the algorithms vary according to their ability to handle the complexity of the data and extract relevant patterns for the classification task. KPCA + K-means stood out in this specific case due to its ability to handle nonlinear data and find more complex patterns in the Fashion-MNIST dataset.
Based solely on the metrics of Precision, Recall, and F1-Score, the best algorithm is COOMED, followed by CONTRA, RPCA + PCA + K-means, PCA + K-means, KPCA + K-means, and KRUM. Considering just the metric accuracy, the best algorithm is KPCA + K-means, followed by RPCA + PCA + K-means, CONTRA, PCA + K-means, KRUM, and COOMED.
Considering the Attack Success Rate (ASR) and the Malicious Confidence (MC), where lower values indicate better performance, the experiments show that the best algorithms are PCA + K-means, KPCA + K-means, and RPCA + PCA + K-means, which have an ASR and MC of 0%, and COOMED is the worst algorithm with the highest ASR and MC.
In terms of the execution time, the fastest algorithm is CONTRA, and RPCA + PCA + K-means is the slowest algorithm. CONTRA is 1.06, 1.07, 1.11, 1.13, and 1.14 times faster than KRUM, PCA + K-means, KPCA + K-means, COMMED, and RPCA + PCA + K-means, respectively.
7.2. Impacts of the Percentage of Independent and Identically Distributed Data
To study the impacts of the percentage of IID data on the performances of the defense algorithms, we vary the percentage of the IID parameter between 0% and 100%, as shown in Table 1. This provides insights into the robustness of the algorithms under different data distribution scenarios. By examining the results across all datasets, as shown in Figure 3, Figure 4 and Figure 5, a trend emerges that shows an improvement in the model’s performance and a significant reduction in the Attack Success Rate and Malicious Confidence as the percentage of IID parameter increases.
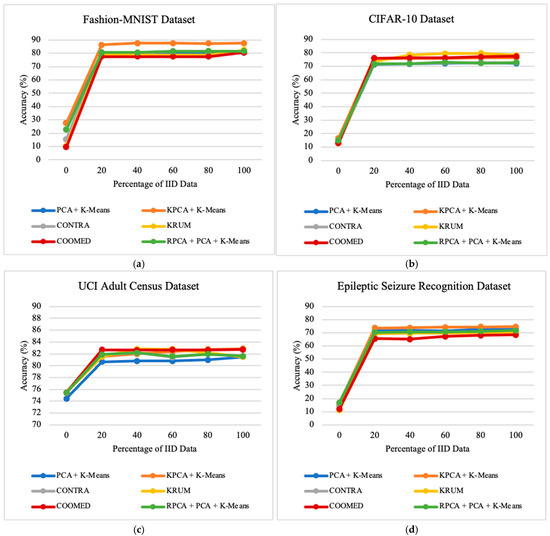
Figure 3.
The impact of the percentage of IID data on the prediction accuracy of the global model on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
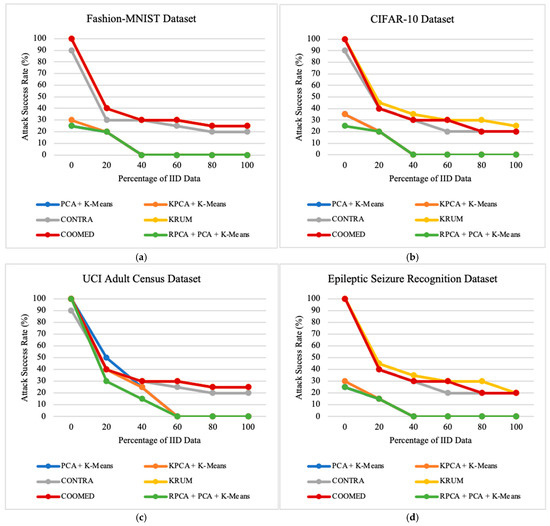
Figure 4.
The impact of the percentage of Independent and Identically Distributes data on the attack success rate on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
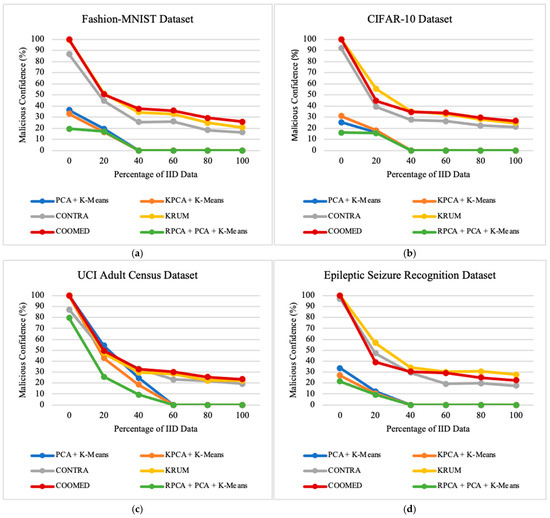
Figure 5.
The impact of the percentage of Independent and Identically Distributes data on malicious confidence on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
Regardless of the defense algorithm employed, the overall accuracy remains consistently stable across all datasets, as depicted in Figure 3. This indicates that the choice of defense algorithm has minimal impact on the system’s overall accuracy across varying datasets. For instance, for the Fashion-MNIST dataset, the algorithm with the highest average precision is COOMED with 73.00%, followed by KPCA + K-means with 72.40%, RPCA + PCA + K-means with 71.81%, PCA + K-means with 71.73%, CONTRA with 70.22%, and lastly KRUM with 66.33%.
As for average recall, considering only the Fashion-MNIST dataset, the algorithm with the highest recall was KPCA + K-means with 93.51%, followed by PCA + K-means with 93.41%, RPCA + PCA + K-means with 92.81%, CONTRA with 91.32%, COOMED with 89.52%, and lastly KRUM with 89.11%.
In terms of average accuracy, and considering only the Fashion-MNIST dataset, the algorithm with the highest accuracy was KPCA + K-means with 77.34%, followed by PCA + K-means with 71.45%, RPCA + PCA + K-means with 71.37%, CONTRA with 70.17%, COOMED with 66.68%, and lastly KRUM with 67.88%.
The results obtained from Precision, Recall, and F1-Score as the number of clients varies can be found in Appendix A—Figure A1, Figure A2 and Figure A3, respectively.
Of particular note is the low performance seen when the data are completely non-IID (percentage of IID data = 0%). However, as the percentage of IID data increases, the overall accuracy improves rapidly, stabilizing in the percentage of IID data range of 20% to 100%. This behavior is intuitively expected as a higher percentage of IID data indicates that each client has data points drawn from the same underlying distribution, independently of each other. Thus, the local models are trained on datasets that are more representative of the global dataset, facilitating easier convergence.
Figure 4 and Figure 5 show that CONTRA, KRUM, and COOMED have relatively worse performances in minimizing Malicious Confidence (MC) and Attack Success Rate (ASR) compared to other algorithms. PCA + K-means, KPCA + K-means, and RPCA + PCA + K-means perform quite similarly in attempting to minimize malicious confidence. In certain cases, non-IID data can result in malicious updates that are difficult to distinguish from benign updates. This consistency is observed across different datasets.
The reductions in MC and ASR as the percentage of IID data increases is intuitive, as non-IID data can make a malicious update more detectable among more similar benign updates. This observation is particularly pronounced in the presence of the alternating minimization stealth strategy. When the data are IID, and the attacker optimizes for the stealth objective, a malicious update can apparently share a very similar direction with a benign update, making it less detectable. This suggests that malicious updates, even when optimized for stealth, can form distinctive clusters, regardless of whether the data are IID or not. However, this phenomenon is not entirely reliable and depends on the nature of the classification task.
These results underscore the critical importance of considering the percentage of the IID data parameter when selecting and evaluating defense algorithms in federated learning systems. They highlight the need for a tailored approach for different data configurations and potential threats. In addition, the detailed analysis of the ASR and MC metrics provides valuable insights into the algorithms’ ability to withstand adversarial attacks in federated environments, contributing to the development of more robust and effective strategies. As we can observe in Figure 4 and Figure 5, both ASR and MC tend to decrease as the data become more independent and identically distributed (increasing the percentage of IID data), and the performance of the model tends to increase.
When the percentage of IID data varies from 0% to 100%, RPCA + PCA + K-means becomes the most effective algorithm in defending the federated learning system, followed by KPCA + K-means, PCA + K-means, CONTRA, KRUM, and finally COOMED.
Comparing the execution times of the algorithms on the Fashion-MNIST dataset, the results presented in Table 8 show that the fastest algorithm is CONTRA, followed by KRUM, PCA + K-means, KPCA + K-means, COOMED, and finally RPCA + PCA + K-means. RPCA + PCA + K-means is the slowest because it involves more complex computations and additional processing steps compared to the other algorithms.

Table 8.
The execution time (in minutes) when varying the percentage of IID data.
In the CIFAR-10 dataset, the algorithms have almost the same order in terms of execution time as in the Fashion-MNIST dataset, with CONTRA being the fastest, followed by KRUM, COOMED, PCA + K-means, KPCA + K-means, and finally RPCA + PCA + K-means.
For the UCI Adult Census dataset, the execution time in our tests was so fast that it was not possible to identify the fastest and slowest algorithms.
Lastly, for the Epileptic Seizure Recognition dataset, the fastest algorithm is COOMED, followed by KRUM, then PCA + K-means and CONTRA with the same execution time, followed by KPCA + K-means, and finally RPCA + PCA + K-means.
7.3. Impact of Number of Clients
We investigate the impacts of number of clients on the performance of the defense algorithms by varying the number of clients between 20 and 100. This provides insights into how the algorithms perform in scenarios with many clients. Looking at the results in Figure 6, Figure 7 and Figure 8, we can see a clear pattern that shows the relationship between the number of clients and how well the defense algorithms work.
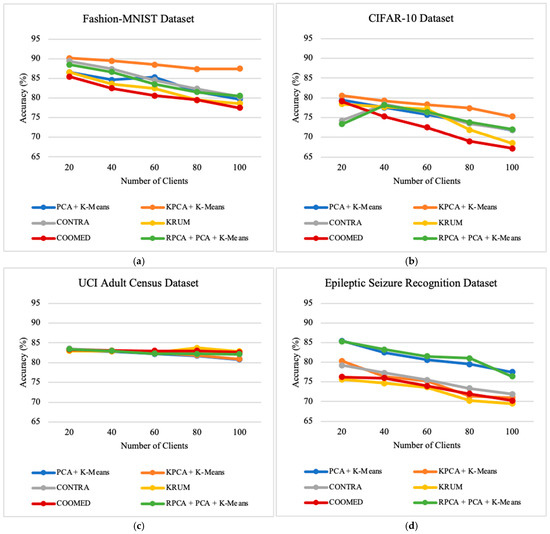
Figure 6.
The impact of the number of clients on the prediction accuracy of the global model on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
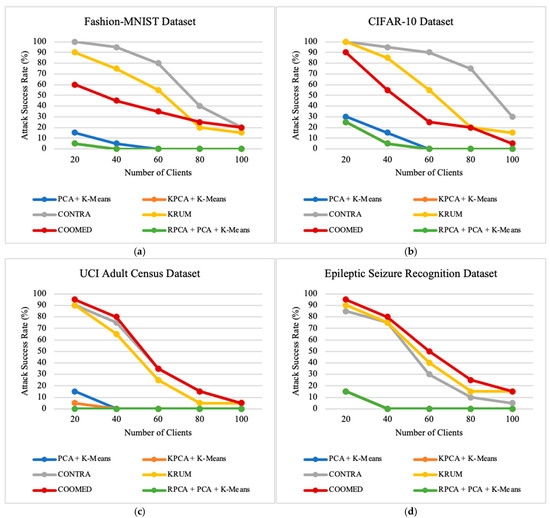
Figure 7.
The impact of the number of clients on attack success rate on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
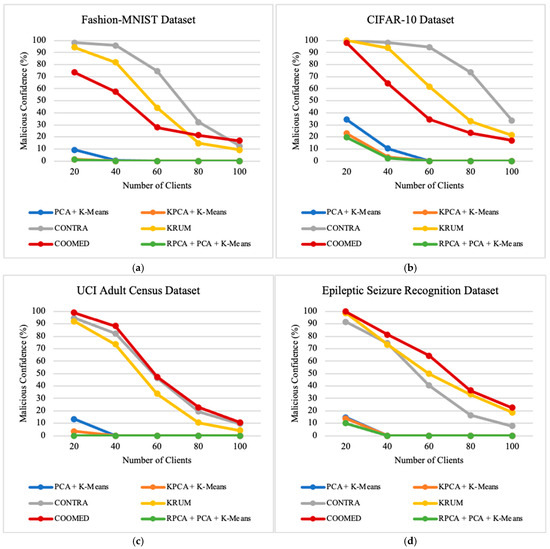
Figure 8.
The impact of the number of clients on malicious confidence on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
First, we notice that as the number of clients increases, the overall accuracy gradually decreases along with precision and recall, except for with the UCI Adult Census dataset, where the recall metric increases when the number of clients also increases. Another factor observed across all datasets is that recall is higher than precision and accuracy. This makes sense because each client gets a smaller portion of the data when there are more clients, making the local models more specialized. This makes it harder to combine these specialized models together into one strong global model that can work well with different datasets.
For instance, for the Fashion-MNIST dataset, the algorithm with the highest average precision was COOMED with 86.92%, followed by CONTRA with 84.14%, RPCA + PCA + K-means with 83.87%, PCA + K-means with 83.36%, KPCA + K-means with 83.29%, and lastly KRUM with 80.06%.
As for average recall, considering only the Fashion-MNIST dataset, the algorithm with the highest recall is COOMED with 97.74%, followed by PCA + K-means with 97.67%, RPCA + PCA + K-means with 97.66%, CONTRA with 97.63%, KPCA + K-means with 97.61%, and lastly KRUM with 96.67%.
In terms of average accuracy, and considering only the Fashion-MNIST dataset, the algorithm with the highest accuracy was KPCA + K-means with 88.59%, followed by CONTRA with 84.78%, RPCA + PCA + K-means with 84.12%, PCA + K-means with 83.56%, KRUM with 82.13%, and lastly COOMED with 81.11%.
The results obtained from Precision, Recall, and F1-Score as the number of clients varies can be found in Appendix A—Figure A4, Figure A5 and Figure A6, respectively.
In terms of MC and ASR, we see a consistent decrease in all algorithms as the number of clients increases. This is because the local models become more specialized with fewer data per client, making it easier for these algorithms to see the “suspicious similarity” between malicious updates and benign updates. In general, CONTRA, KRUM, and COOMED typically have an Attack Success Rate above 90% with 20 clients, but with 100 clients, they consistently maintain an Attack Success Rate below 30%.
On the other hand, PCA + K-means, KPCA + K-means, and RPCA + PCA + K-means perform more consistently and better than the other algorithms; their MC and ASR levels may increase slightly for a few clients, but they typically remain below 15%. This suggests that the total number of clients does not have a big impact on how distinct clusters are formed between malicious and benign updates.
In addition, as shown in Figure 7 and Figure 8, ASR and MC are higher in some datasets, which may be related to the nature of the dataset itself. However, they all follow the same trend of decreasing ASR and MC as the number of clients increases. This suggests that, despite variations in datasets, the positive influence of increasing clients on reducing ASR and MC is a consistent trend across different scenarios.
Moreover, all algorithms perform well as the number of clients increases, indicating that they are well suited to handling a large number of clients.
When increasing the number of clients from 20 to 100 clients, the experiments show the following results: for the Fashion-MNIST and CIFAR-10 datasets, RPCA + PCA + K-means is the best algorithm, followed by KPCA + K-means, PCA + K-means, COOMED, KRUM, and CONTRA; for the UCI Adult Census dataset, RPCA + PCA + K-means is the best algorithm, followed by KPCA + K-means, PCA + K-means, KRUM, CONTRA, and COOMED.; and for the Epileptic Seizure Recognition dataset, RPCA + PCA + K-means is the best algorithm, followed by KPCA + K-means, PCA + K-means, CONTRA, KRUM, and COOMED.
Comparing the execution times of the algorithms on the Fashion-MNIST dataset (presented in Table 9), we can determine that the fastest algorithm is the COOMED, followed by CONTRA, KRUM, PCA + K-means, KPCA + PCA + K-means, and finally RPCA + PCA + K-means.

Table 9.
Execution time with variation in the number of clients (in minutes).
For the CIFAR-10 dataset, COOMED is the fastest, followed by KRUM, CONTRA, PCA + K-means, KPCA + K-means, and finally RPCA + PCA + K-means.
For the UCI Adult Census dataset, the execution time in the tests was so fast that it was not possible to identify the fastest and slowest algorithms.
Lastly, for the Epileptic Seizure Recognition dataset, the fastest algorithm is COOMED, followed by CONTRA, then KRUM and RPCA + K-means with the same execution time, followed by PCA + K-means, and finally KPCA + PCA + K-means.
7.4. Impact of the Percentage of Malicious Clients
To study the impact of the percentage of clients who are malicious, we vary the percentage of malicious clients parameter. In our experiments, the variation of this parameter, ranging from 0% to 50%, provides valuable insights into the robustness of the algorithms in scenarios with the presence of malicious clients. These insights influence the performance and security of federated learning systems. Upon examining the results across all datasets, as presented in Figure 9, Figure 10 and Figure 11, a trend emerges that shows a decrease in the prediction accuracy of the global model as the number of malicious clients increases. Additionally, there is a very pronounced increase in ASR and MC, especially when 20% or more of the clients are malicious clients.
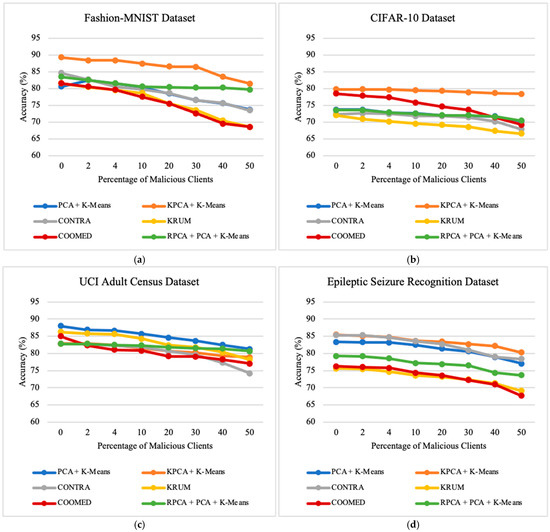
Figure 9.
The impact of the percentage of malicious clients on the prediction accuracy of the global model on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
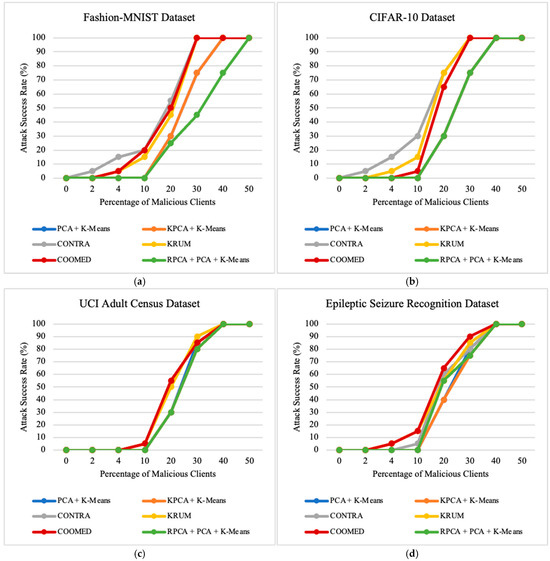
Figure 10.
The impact of the percentage of malicious clients on attack success rate on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
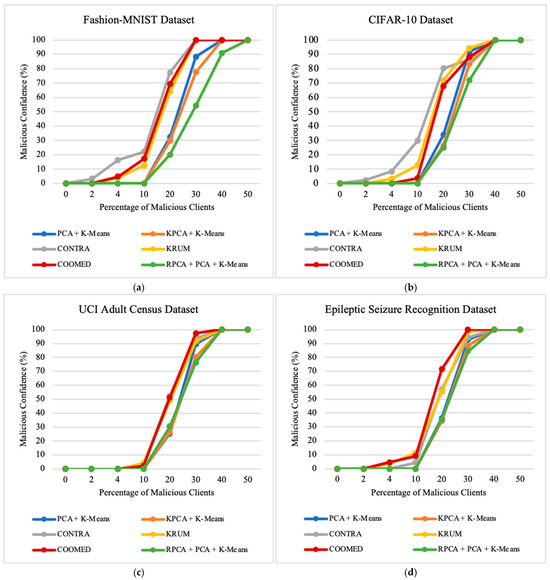
Figure 11.
The impact of the percentage of malicious clients on malicious confidence in: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
This observation highlights the sensitivity of federated learning systems to the presence of malicious clients. The negative impact on the global model becomes more prominent beyond the threshold of 20% malicious clients. At this point, ASR and MC experience a sharp increase, indicating a significant compromise in the integrity and security of the federated learning process. When the percentage of malicious clients reaches 40%, none of the algorithms can provide effective defense as they all consistently produce an ASR and MC close to 100%.
All algorithms perform well in terms of ASR and MC when the percentage of malicious clients is low (from 0% to 4%). However, the performance of the PCA + K-means, KPCA + K-means, and RPCA + PCA + K-means algorithms is excellent at 10% and 20% malicious clients, but deteriorates rapidly, reaching a plateau at 100% ASR and MC. This observation suggests that the clusters of malicious and benign updates remain fairly distinct as long as the proportion of malicious clients is small. As the percentage of malicious clients increases, the likelihood of a malicious client being included in the larger “benign” cluster increases, giving it full access to the global model.
Furthermore, even if malicious and benign updates form separate clusters, these algorithms are prone to failure when malicious updates form a larger cluster than benign updates. This failure occurs because the algorithms simply discard the smaller cluster, assuming it could be malicious. To improve robustness against a large fraction of malicious clients, these algorithms would need to be integrated with additional defense methods.
These findings highlight the critical importance of implementing robust defense mechanisms to detect and mitigate the influence of malicious clients in federated learning environments.
Analyzing Figure 9, Figure 10 and Figure 11 in more detail, we can conclude the following results when the percentage of malicious clients increases from 0% to 50% of the total number clients. For the Fashion-MNIST dataset, RPCA + PCA + K-means has the least average loss of accuracy, with the average loss of accuracy on PCA + K-means, KPCA + K-means, CONTRA, KRUM, COOMED, and RPCA + PCA + K-means being 6.87%, 7.83%, 11.18%, 12.96%, 12.96%, and 3.82%, respectively.
On the other hand, for the CIFAR-10 dataset, KPCA + K-Means has the least average loss of accuracy, with the average loss of accuracy on PCA + K-means, KPCA + K-means, CONTRA, KRUM, COOMED, and RPCA + PCA + K-means being 3.46%, 1.41%, 4.55%, 5.49%, 9.21%, and 3.15%, respectively.
For the UCI Adult Census dataset, RPCA + PCA + K-means has the least average loss of accuracy, with the average loss of accuracy on PCA + K-means, KPCA + K-means, CONTRA, KRUM, COOMED, and RPCA + PCA + K-means being 6.70%, 3.99%, 8.60%, 8.04%, 7.94%, and 2.08%, respectively.
For the Epileptic Seizure Recognition dataset, KPCA + K-means has the least average loss of accuracy, with the average loss of accuracy on PCA + K-means, KPCA + K-means, CONTRA, KRUM, COOMED, and RPCA + PCA + K-means being 6.35%, 5.17%%, 6.96%, 6.58%, 8.61%, and 5.57%, respectively.
Across all datasets, the overall Accuracy, Precision, Recall, and F1-Score decrease as the percentage of malicious clients increases, regardless of the defense algorithm employed. In all datasets used, we achieve higher recall than Precision, Accuracy, and F1-Score.
For instance, for the Fashion-MNIST dataset, when the number of malicious clients increases from 0% to 50%, the algorithm with the highest average precision is COOMED followed by RPCA + PCA + K-means, CONTRA, PCA + K-means, KRUM, and lastly KPCA + K-means with 85.16%, 79.38%,78.77%,78.52%,78.50%, and 78.32%, respectively.
As for average recall, considering only the Fashion-MNIST dataset, when the number of malicious clients increases from 0% to 50%, the algorithm with the highest recall is COOMED, followed by PCA + K-means, CONTRA, RPCA + PCA + K-means, KPCA + K-means, and lastly KRUM, with 97.55%, 97.44%, 97.44%, 97.40%, 97.40%, and 94.09%, respectively.
The results obtained for Precision, Recall, and F1-Score as the number of malicious clients varies can be found in Appendix A—Figure A7, Figure A8 and Figure A9, respectively.
In terms of average accuracy, and considering only the Fashion-MNIST dataset, when the number of malicious clients increases from 0% to 50%, the algorithm with the highest accuracy is KPCA + K-means, followed by RPCA + PCA + K-means, CONTRA, PCA + K-means, KRUM, and lastly COOMED, with 86.42%, 81.08%, 78.96%, 78.63%, 75.99%, and 75.66%, respectively.
For all the algorithms, regardless of the dataset used, when reaching 50% malicious clients, these malicious clients were able to achieve 100% successful attacks, as can be observed in Figure 10. All algorithms, when reaching 20% malicious clients, already exhibit some failure in mitigating attacks, and as the percentage of malicious clients grows, the number of successful attacks increases. Only PCA + K-means, KPCA + K-means, and RPCA + PCA + K-means show successful attacks in all four datasets starting from 20% malicious clients, while below 20%, they do not exhibit successful attacks. In the case of CONTRA, for the FMNIST and CIFAR-10 datasets, successful attacks occur even with only 2% malicious clients. Considering all four datasets, CONTRA, KRUM, and COOMED start showing successful attacks with 4% to 10% malicious clients. Taking these into account, we can say that no algorithm is 100% effective in mitigating attacks. Still, PCA + K-means, KPCA + K-means, and RPCA + PCA + K-means demonstrate greater resilience, unlike CONTRA, KRUM, and COOMED, and this observation holds across all datasets.
As observed in Figure 10 and Figure 11, the defense algorithms PCA + K-means, KPCA + K-means, and RPCA + PCA + K-means consistently achieve a very similar Attack Success Rate. The primary distinction among them lies in the Malicious Confidence metric, where RPCA + PCA + K-means predominantly exhibits lower Malicious Confidence compared to the other algorithms, which indicates a lower probability of misclassification of malicious instances as benign. In summary, COOMED often shows the largest decreases in the model performance (Accuracy, Precision, Recall, and F1-Score) while KPCA + K-means and RPCA + PCA + K-means tend to show more resilient performance across different datasets, as we can observe in the Attack Success Rate and Malicious Confidence metrics.
When increasing the percentage of malicious clients from 0% to 50% of the clients, as shown in Figure 10 and Figure 11, the following results are obtained: for the Fashion-MNIST dataset, our proposed algorithm RPCA + PCA + K-means is the most effective algorithm in defending the federated learning system, followed by KPCA + K-means, PCA + K-means, KRUM, COOMED, and CONTRA; for the CIFAR-10 dataset, RPCA + PCA + K-means remains the most effective algorithm, followed by KPCA + K-means, PCA + K-means, COOMED, KRUM, and CONTRA; for the UCI Adult Census dataset, RPCA + PCA + K-means is still the most effective algorithm, followed by KPCA + K-means, PCA + K-means, KRUM, CONTRA, and COOMED; and for the Epileptic Seizure Recognition dataset RPCA + PCA + K-means remains the most effective, followed by KPCA + K-means, PCA + K-means, CONTRA, KRUM, and COOMED.
Comparing the execution times of the algorithms presented in Table 10, when the number of malicious clients increases from 0% to 50%, the experiments show the following results: for the Fashion-MNIST dataset, the fastest algorithm is COOMED, followed by KRUM, PCA + K-means, CONTRA, KPCA + K-means, and finally RPCA + PCA + K-means; for the CIFAR-10 dataset, KRUM is the fastest algorithm, followed by CONTRA, PCA + K-means, COOMED, KPCA + K-means, and finally RPCA + PCA + K-means; for the UCI Adult Census dataset, the execution time in the tests was so fast that the only conclusion we can draw is that PCA + K-means, CONTRA, KRUM, and COOMED seems to be faster than KPCA + K-means and RPCA + PCA + K-means; and lastly, for the Epileptic Seizure Recognition dataset, the fastest algorithm is COOMED, followed by KRUM, then PCA + K-means, and CONTRA, KPCA + PCA + K-Means, and finally RPCA + PCA + K-Means.

Table 10.
The execution time (in minutes) when varying the number of malicious clients parameter.
8. Conclusions and Future Work
This paper presents experimental studies comparing the following six state-of-the-art algorithms designed to defend against model update attacks in a federated learning setting: PCA + K-means, KPCA + K-means, CONTRA, KRUM, COOMED, and RPCA + PCA + K-means. Each algorithm aims to detect updates originating from malicious clients and mitigate their impact on the classification performance of the global model. The evaluation of these algorithms involves running experiments that vary three parameters, the percentage of IID data in the training data, the total number of clients, and the percentage of malicious clients, using four popular datasets existing in the literature.
Overall, our results show that regardless of the dataset used, the percentage of IID training data, changes in the number of clients, or changes in the percentage of malicious clients, the three algorithms that use clustering, PCA + K-Means, KPCA + K-means, and RPCA + PCA + K-means, consistently performed better in detecting and mitigating attacks, but also consistently performed worse in execution time than the other algorithms that do not use clustering, CONTRA, KRUM, and COOMED. The difference between these two groups of algorithms suggests that the use of clustering provides additional benefits in improving the identification of groups of malicious clients, but incurs additional time overhead.
Another conclusion to draw is that, across the variations in the three parameters (percentage of IID data, number of clients, and percentage of malicious clients), KPCA + K-means consistently yielded better prediction accuracy for the global model, and COOMED consistently outperformed others in terms of Precision, Recall, and F1-Score metrics in most cases.
In general, RPCA + PCA + K-means was shown to be the most effective algorithm in defending federated learning systems when varying the percentage of IID data, the number of clients, and the percentage of malicious clients, considering the ASR and MC metrics. It was usually followed by KPCA + K-means and PCA + K-means.
As future work, we intend to investigate the effectiveness of these algorithms against other types of attacks in federated learning systems, beyond the adversarial attacks considered so far. Extending this research to cover a wider range of threats would help develop more robust strategies to protect federated learning systems against different types of attacks.
Author Contributions
Conceptualization, L.G. and J.B.; Methodology, L.G. and J.B.; Software, I.C. and K.H.; Validation, I.C.; Investigation, I.C.; Resources, K.H.; Writing—original draft, I.C.; Writing—review & editing, L.G. and J.B.; Visualization, J.B.; Supervision, L.G. and J.B.; Project administration, L.G. and J.B.; Funding acquisition, J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
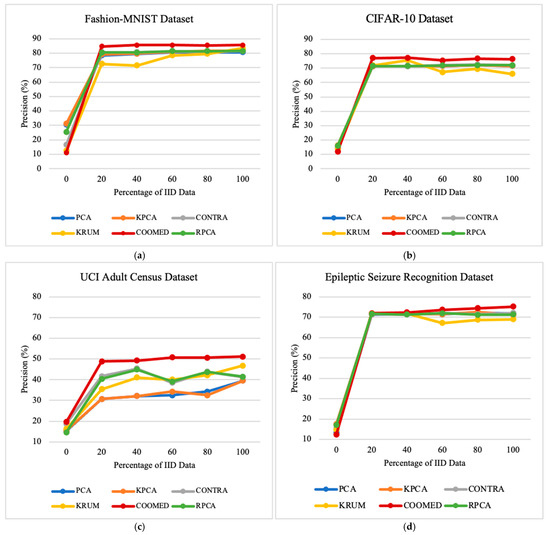
Figure A1.
The impact of the percentage of IID data on precision on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
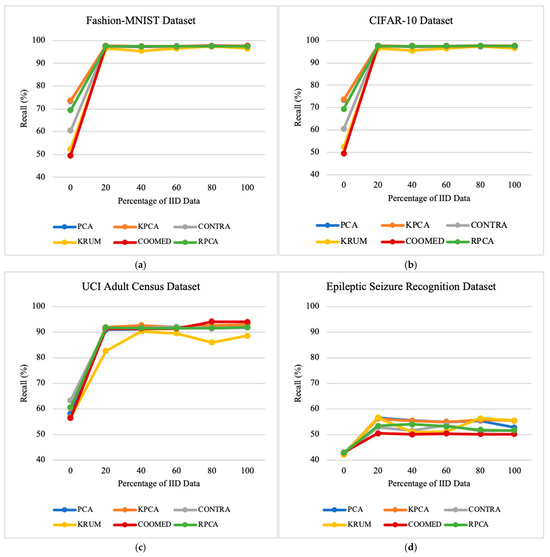
Figure A2.
The impact of the percentage of IID data on recall on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
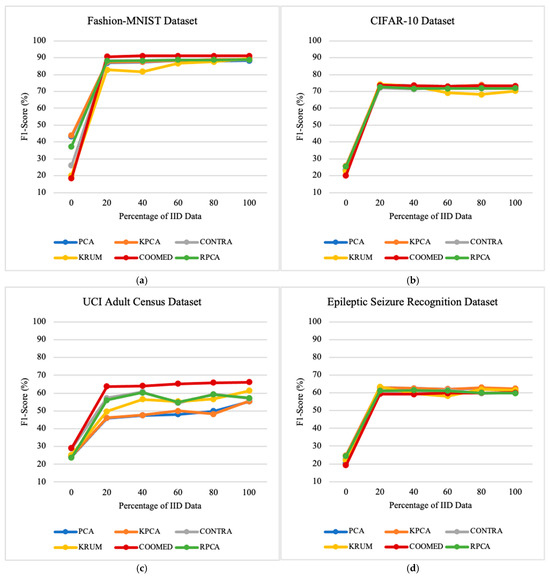
Figure A3.
The impact of the percentage of IID data on F1-Score in: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
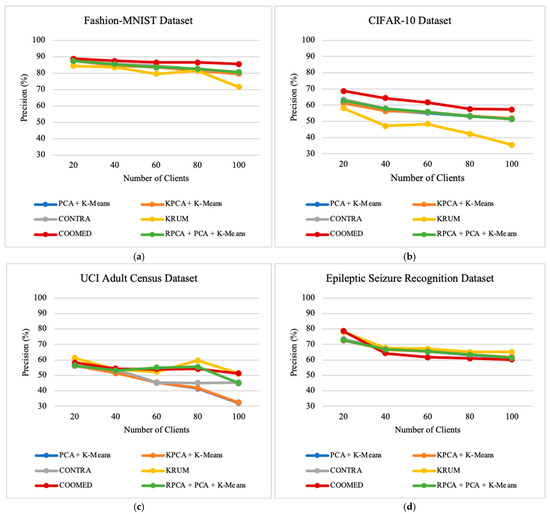
Figure A4.
The impact of the number of clients on precision on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
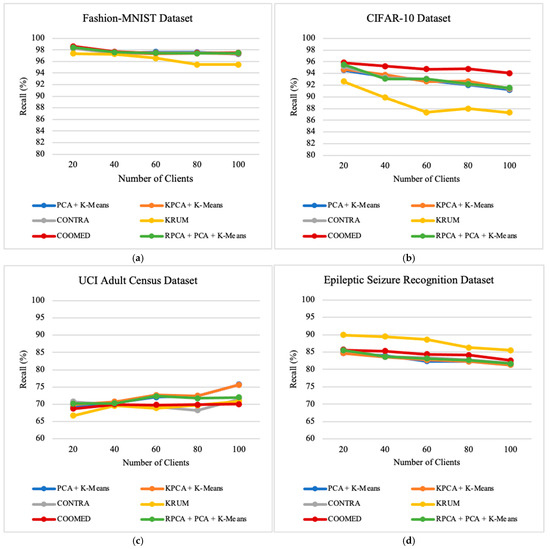
Figure A5.
The impact of the number of clients on recall on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
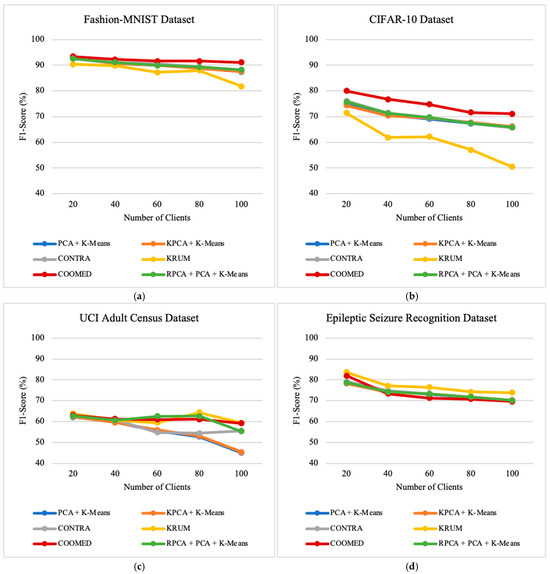
Figure A6.
The impact of the number of clients on F1-Score on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
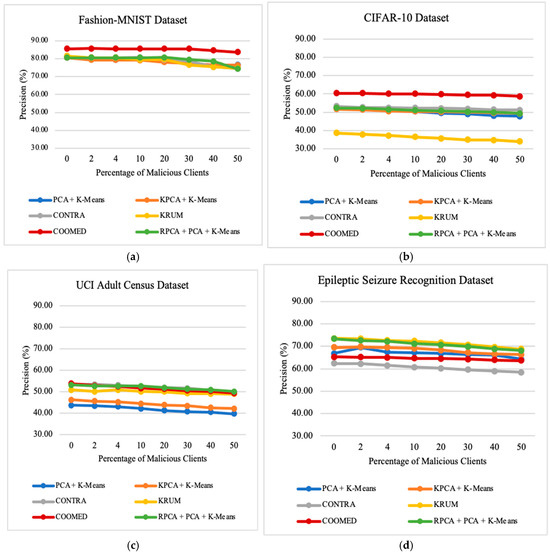
Figure A7.
The impact of the number of malicious clients on precision on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
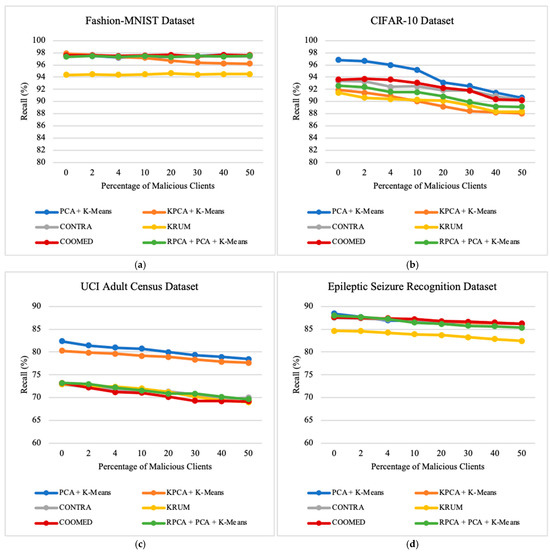
Figure A8.
The impact of the number of malicious clients on recall on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
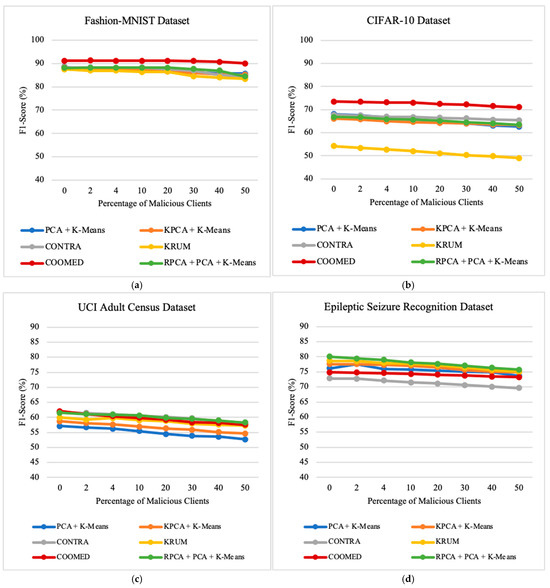
Figure A9.
The impact of the number of malicious clients on F1-Score on: (a) Fashion-MNIST dataset; (b) CIFAR-10 dataset; (c) UCI Adult Census dataset; (d) Epileptic Seizure Recognition dataset.
References
- Mammen, P. Federated Learning: Opportunities and Challenges. arXiv 2021, arXiv:2101.0542. [Google Scholar]
- Bagdasaryan, E.; Veit, A.; Hua, Y.; Estrin, D.; Shmatikov, V.; Tech, C. How To Backdoor Federated Learning. In Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; Machine Learning Research: New York, NY, USA, 2020; Volume 108, pp. 2938–2948. [Google Scholar]
- Bouacida, N.; Mohapatra, P. Vulnerabilities in federated learning. IEEE Access 2021, 9, 63229–63249. [Google Scholar] [CrossRef]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and Open Problems in Federated Learning. In Foundations and Trends® in Machine Learning; Now Publishers: Hanover, NH, USA, 2021; Volume 14. [Google Scholar]
- Park, S.; Han, S.; Wu, F.; Kim, S.; Zhu, B.; Xie, X.; Cha, M. Feddefender: Client-side attack-tolerant federated learning. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 1850–1861. [Google Scholar]
- Tolpegin, V.; Truex, S.; Gursoy, M.E.; Liu, L. Data Poisoning Attacks Against Federated Learning Systems. arXiv 2020. [Google Scholar] [CrossRef]
- Li, D.; Wong, W.E.; Wang, W.; Yao, Y.; Chau, M. Detection and Mitigation of Label-Flipping Attacks in Federated Learning Systems with KPCA and K-Means. In Proceedings of the 2021 8th International Conference on Dependable Systems and Their Applications, DSA, Yinchuan, China, 5–6 August 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 551–559. [Google Scholar] [CrossRef]
- Awan, S.; Luo, B.; Li, F. CONTRA: Defending against Poisoning Attacks in Federated Learning. In Proceedings of the European Symposium on Research in Computer Security, Darmstadt, Germany, 4–8 October 2021. [Google Scholar]
- Blanchard, P.; El Mhamdi, E.M.; Guerraoui, R.; Stainer, J. Machine Learning with Adversaries: Byzantine Tolerant Gradient Descent. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Austrália, 6–11 August 2017. [Google Scholar]
- Yin, D.; Chen, Y.; Ramchandran, K.; Bartlett, P. Byzantine-Robust Distributed Learning: Towards Optimal Statistical Rates. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- McMahan, H.B.; Moore, E.; Ramge, D.; Hampson, S.; Arcas, B. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Ma, X.; Zhu, J.; Lin, Z.; Chen, S.; Quin, Y. A state-of-the-art survey on solving non-IID data in Federated Learning. Future Gener. Comput. Syst. 2022, 135, 244–258. [Google Scholar] [CrossRef]
- Lo, S.K.; Lu, Q.; Zhu, L.; Paik, H.; Xu, X.; Wang, C. Architectural Patterns for the Design of Federated Learning Systems. arXiv 2021. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Fung, C.; Yoon, C.J.M.; Beschastnikh, I. Mitigating Sybils in Federated Learning Poisoning. arXiv 2018. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2016; Available online: https://link.springer.com/book/10.1007/978-0-387-45528-0 (accessed on 21 April 2023).
- Bhagoji, A.N.; Chakraborty, S.; Mittal, P.; Calo, S. Analyzing Federated Learning through an Adversarial Lens. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Al Mallah, R.; López, D.; Badu-Marfo, G.; Farooq, B. Untargeted Poisoning Attack Detection in Federated Learning via Behavior AttestationAl. IEEE Access 2023, 11, 125064–125079. [Google Scholar] [CrossRef]
- Shejwalkar, V.; Houmansadr, A. Manipulating the byzantine: Optimizing model poisoning attacks and defenses for federated learning. In Proceedings of the Network and Distributed Systems Security (NDSS) Symposium, Online, 21–25 February 2021; Available online: https://www.ndss-symposium.org/wp-content/uploads/ndss2021_6C-3_24498_paper.pdf (accessed on 14 November 2024).
- Purohit, K.; Das, S.; Bhattacharya, S.; Rana, S. A Data-Driven Defense against Edge-case Model Poisoning Attacks on Federated Learning. arXiv 2024. [Google Scholar] [CrossRef]
- Gong, Z.; Shen, L.; Zhang, Y.; Zhang, L.Y.; Wang, J.; Bai, G. AgrAmplifier: Defending Federated Learning Against Poisoning Attacks Through Local Update Amplification. IEEE Trans. Inf. Forensics Secur. 2023, 19, 1241–1250. [Google Scholar] [CrossRef]
- Huang, L.; Joseph, A.; Nelson, B.; Rubinstein, B.; Tygar, J.D. Adversarial Machine Learning. In Proceedings of the ACM Conference on Computer and Communications Security, Chicago, IL, USA, 17–21 October 2011; pp. 43–58. [Google Scholar]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python, 5th ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2016. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data Driven Science & Engineering Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- GitHub. Fashion-Mnist. Fashion-Mnist Dataset. 2017. Available online: https://github.com/zalandoresearch/fashion-mnist (accessed on 26 June 2023).
- Kaggle. CIFAR-10—Object Recognition in Images. 2015. Available online: https://www.kaggle.com/c/cifar-10 (accessed on 26 June 2023).
- UCI—Machine Learning Repository. Adult. 1996. Available online: https://archive.ics.uci.edu/dataset/2/adult (accessed on 13 September 2023).
- Kanggle. Epileptic Seizure Recognition. 2019. Available online: https://www.kaggle.com/code/maximkumundzhiev/epileptic-seizure-recognition (accessed on 14 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).