Research on Kalman Filter Fusion Navigation Algorithm Assisted by CNN-LSTM Neural Network

Abstract

In response to the challenge of single navigation methods failing to meet the high precision requirements for unmanned aerial vehicle (UAV) navigation in complex environments, a novel algorithm that integrates Global Navigation Satellite System/Inertial Navigation System (GNSS/INS) navigation information is proposed to enhance the positioning accuracy and robustness of UAV navigation systems. First, the fundamental principles of Kalman filtering and its application in navigation are introduced. Second, the basic principles of Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) networks and their applications in the navigation domain are elaborated. Subsequently, an algorithm based on a CNN and LSTM-assisted Kalman filtering fusion navigation is proposed. Finally, the feasibility and effectiveness of the proposed algorithm are validated through experiments. Experimental results demonstrate that the Kalman filtering fusion navigation algorithm assisted by a CNN and LSTM significantly improves the positioning accuracy and robustness of UAV navigation systems in highly interfered complex environments.

1. Introduction

With the rapid advancement of unmanned aerial vehicle (UAV) technology [1], the application domains of UAVs continue to expand, posing higher demands on the accuracy and stability of UAV navigation systems. Traditional UAV navigation algorithms often rely on single-sensor data sources such as GPS and Inertial Measurement Units (IMUs) [2]. However, in complex environments, these sensor data are susceptible to noise, interference, and errors, leading to a decrease in navigation accuracy. To ensure that UAVs can efficiently and accurately execute tasks in complex environments, the performance of their navigation systems becomes crucial. Therefore, research on UAV navigation algorithms based on the fusion of multisensor data holds significant practical significance and application value.

During the execution of tasks, UAV navigation systems typically adopt a fusion navigation approach integrating the Global Navigation Satellite System (GNSS) and Inertial Navigation System (INS) [3]. While GNSS offers long-term high-precision capabilities and cost-effectiveness, its inherent drawback lies in susceptibility to severe electromagnetic interference in battlefield environments, leading to disturbances in the GNSS receiver signals. Conversely, INS provides a higher sampling rate, enabling continuous signal output for recursive estimation. However, when used alone, the INS system’s navigation computation results may suffer from increased errors due to noise introduction through integration operations, leading to divergence over time. The advantages and disadvantages of INS and GNSS are complementary. Integrating the strengths of both technologies provides a continuous, high-bandwidth, comprehensive, and high-precision navigation solution. This integration not only overcomes performance issues of individual sensors but also yields a system performance surpassing that of a single sensor. Therefore, in practical navigation computations, employing Kalman-filter-based theory to integrate INS computed data with GNSS information offers a more continuous and reliable navigation solution, enhancing navigation parameter computation results.

Kalman filtering [4], as a classical estimation theory method, is widely employed in UAV navigation systems. It estimates and corrects the state of the UAV through prediction and update steps, thereby enhancing navigation accuracy. El-Sheimy [5] and others proposed that under the assumption of process and measurement noises following zero-mean Gaussian distributions with known covariance matrices, the Kalman filter can achieve optimal estimation solutions. However, this assumption does not always hold in practical systems. Therefore, some scholars have proposed alternative methods from the perspectives of noise modeling and adaptive estimation.

The first method involves a thorough analysis of the composition mechanism of noise and utilizes mathematically interpretable models to accurately describe the noise characteristics. Kalman filtering often adopts such mechanistic models as the core models of the system during state estimation. For example, Nirmal et al. [6] ingeniously utilized Allan variance to analyze noise in IMUs in their 2016 study and successfully identified different noise components within the IMU. It is noteworthy that the dynamic Allan variance [7] was originally designed to assess the stability of atomic clocks but was later extended to capture nonstationary components in signals. Although this noise analysis method can provide targeted explanations for each system, its generalizability is relatively weak and is significantly affected by sensor differences, thus requiring further refinement. Recently, scholars have proposed an innovative nonlinear optimization method [8,9,10], which combines gradient search and Newton search strategies, aiming to more accurately identify noise using Gaussian activation functions.

Another strategy focuses on the adaptive estimation of noise based on data characteristics. In this field, scholars have proposed various adaptive techniques, including but not limited to Adaptive Kalman Filtering [11,12] (AKF), Adaptive Finite Impulse Response Filters [13], and Adaptive Square Root EKF [14]. The common goal of these methods is to intelligently adjust the parameters or structural elements of the system model according to changes in system performance and different operating conditions. However, traditional analytical methods often struggle to extract valuable features when dealing with highly nonlinear or noisy data, as they may overlook certain key information during the estimation process.

The core challenge in system modeling lies in how to simplify its structure as much as possible while ensuring model accuracy. In practical applications, identifying noise model parameters is particularly challenging, primarily because the noise generated by actual systems is often highly complex. These noises do not follow a single distribution pattern but rather consist of mixed distributions formed by multiple distributions [15,16]. Therefore, it is difficult to accurately describe this highly nonlinear relationship solely from a mechanistic or data feature perspective.

However, with the significant improvement in computer computational power, machine learning methods have regained widespread attention from researchers. Artificial Neural Networks (ANNs) have demonstrated outstanding fitting capabilities [17] when dealing with highly nonlinear problems. Particularly, derivative models based on Recurrent Neural Networks (RNNs), such as Long Short-Term Memory (LSTM) networks [18] and Gated Recurrent Units (GRUs) [19], have gained favor among many scholars for handling highly nonlinear problems.

ANNs offer robust solutions for system modeling and noise parameter identification within the Kalman filtering framework. Currently, researchers are delving into the integration of Kalman filtering and neural networks, focusing primarily on two subfields: external interaction fusion of Kalman filtering and neural networks and internal deep fusion of Kalman filtering and neural networks. Research in these two subfields holds promise for providing new insights and methods for handling complex systems and noise issues. By combining neural networks with Kalman filtering, it is possible to fully leverage the advantages of neural networks in handling complex nonlinear problems and extracting features, as well as the benefits of Kalman filtering in state estimation and noise suppression. Particularly, the combination of Convolutional Neural Networks (CNNs) and LSTM networks demonstrates significant advantages in sequence data processing and feature extraction. CNNs automatically learn and extract spatial features from input data, while LSTMs excel in handling data with temporal dependencies, capturing long-term dependencies, thereby enhancing the accuracy and stability of UAV navigation.

Therefore, this paper proposes a Kalman filtering UAV fusion navigation algorithm assisted by CNN and LSTM. The algorithm extracts spatial features from multiple sensor data using CNNs, processes temporal data using LSTMs, and integrates the extracted feature information into the Kalman filtering framework. This algorithm effectively utilizes the complementary nature of multisensor data to improve the accuracy and robustness of UAV navigation systems.

This paper first introduces the basic principles of Kalman filtering and its current applications in UAV navigation. Then, it elaborates on the design and implementation process of the Kalman filtering UAV fusion navigation algorithm assisted by a CNN and LSTM, including data preprocessing, feature extraction, and the construction of the neural network framework. Finally, the effectiveness and performance of the algorithm are validated through experiments, and the experimental results are analyzed and discussed. Through this research, it is hoped to provide new insights and methods for the development of UAV navigation algorithms, thereby promoting the further application and development of UAV technology.

2. Kalman Filtering GNSS/INS Fusion Navigation Basic Principles

2.1. Basic Principles of Kalman Filtering

The Kalman filtering algorithm [20] minimizes mean square error as its core estimation principle, cleverly combining current observation data with the previous moment’s predicted value to achieve optimal estimation at the current moment. The primary formula of the Kalman filter is as follows:

Prediction Equation:

$$\left\{\begin{array}{l}{X}_t^{-}=F{X}_{t-1}^{+}+B{U}_t\\ P_t^{-}=F{P}_{t-1}^{+}{F}^T+Q\end{array}\right.$$

(1)

State Update Equation:

$$\left\{\begin{array}{l}\Delta Z_t=Z_t-H{X}_t^{-}\\ S_t=H{P}_{t-1}^{-}{H}^T+R\\ K_t=P_{t-1}^{-}{H}^T{S}_t^{-}\\ X_t^{+}=X_t^{-}+K_t\Delta Z_t\\ P_t^{+}=\left(I-K_{t}H\right)P_{t-1}^{-}\end{array}\right.$$

(2)

In this context, X represents the initial state, P denotes the covariance matrix indicating uncertainty, B is the control matrix, U is the control vector, F stands for the system transition matrix representing the system’s recursive process, Q represents process noise, H is the sensor transformation matrix, Z is the sensor measurement vector, R denotes sensor noise, and K signifies the Kalman gain.

The Kalman filter algorithm is typically categorized into two processing modes: loosely coupled and tightly coupled [21].

2.1.1. Loosely Coupled

Loosely coupled [22] processing, during the state prediction process, relies solely on the sensor’s output data as observation values to update the predicted values. This approach is logically straightforward and practical, allowing for the fusion of multiple sensors to enhance accuracy. For instance, using an IMU as the source of raw data for prediction computation, while utilizing the GNSS positioning results as observation values for error correction updates. The mainstream practice usually involves employing the IMU as the prediction data sensor and other sensors as observation sensors.

Loosely coupled systems are generally divided into open-loop and closed-loop systems. Due to the large errors in the open-loop system where the attitude of the IMU is not corrected by the Kalman filter, this experiment adopts a closed-loop system. In the closed-loop system, the attitude of the IMU is corrected by the Kalman filter. The architecture of the loosely coupled closed-loop system is illustrated in Figure 1.

Figure 1. Architecture of loosely coupled closed-loop system.

2.1.2. Tightly Coupled

In contrast, tightly coupled integration [23] requires the utilization of more raw and comprehensive data for computation, such as pseudorange data from GNSS. In tightly coupled integration, it is common to compare the pseudorange and pseudorange rate estimates computed from INS outputs with the pseudorange and pseudorange rate measurements from GNSS receivers. The difference obtained serves as the measurement input for the filter. Through combined navigation filtering, error estimates of the INS are generated, and these estimates can be used to correct the system through measurement updates, thereby enhancing accuracy.

The tightly coupled structure is relatively more complex but can utilize raw data for computation, thereby enhancing system accuracy. Its architecture is depicted in Figure 2.

Figure 2. Architecture of tightly coupled system.

2.2. Mathematical Model of GNSS/INS Fusion Navigation

Constructing the mathematical model of GNSS/INS fusion navigation using the Kalman filter tightly coupled algorithm as an example [24].

2.2.1. System Equations

In the tightly coupled mode, the state variables consist of two parts [25]: One part is the error state of the INS, including attitude, velocity, position, and sensor biases, totaling 15 dimensions. Its state equations are as follows:

$$X_1=F_1\left(t\right)X_1\left(t\right)+\Gamma \left(t\right)W\left(t\right)$$

(3)

In the equation provided, this equation

$$X_1={\left[{\phi }_E,{\phi }_N,{\phi }_U,\delta {\upsilon }_E,\delta {\upsilon }_N,\delta {\upsilon }_U,\delta L,\delta \lambda ,\delta h,{\epsilon }_x,{\epsilon }_y,{\epsilon }_z,{\nabla }_x,{\nabla }_y,{\nabla }_z\right]}^T$$

is established based on the strapdown INS error equation. The state transition matrix is given by

$$F_1={\left[\begin{array}{cc}{\left(F_N\right)}_{9\times 9}& {\left(F_S\right)}_{9\times 9}\\ 0& {\left(F_M\right)}_{6\times 6}\end{array}\right]}_{15\times 15}$$

(4)

In the equation provided, $F_N$ is the 9 × 9 error matrix of the INS, corresponding to the basic error equation of the INS. Within the transition matrix, $F_S$ is represented as:

$$F_S=\left(\begin{array}{cc}{C}_b^n& O_{3\times 3}\\ O_{3\times 3}& C_b^n\\ O_{3\times 3}& O_{3\times 3}\end{array}\right)$$

(5)

$$F_M=Diag\left[-\frac{1}{T_{rx}},-\frac{1}{T_{ry}},-\frac{1}{T_{rz}},-\frac{1}{T_{ax}},-\frac{1}{T_{ay}},-\frac{1}{T_{az}}\right]$$

(6)

The other part of the error state comprises errors from the GNSS. In tightly coupled integration, two time-dependent errors are usually removed: one is the distance error $\delta t_{ru}$ equivalent to the error in Equation (1), and the other is the distance error $\delta t_u$ equivalent to the clock frequency error, $\delta t_u$ typically modeled as a first-order Markov process. As this system involves two satellite navigation systems, the error states of the GNSS are represented by the distance errors equivalent to the clock errors of the GPS and BeiDou systems, denoted as $\delta t_{u1}$ and $\delta t_{u2}$, respectively, and the distance rate errors equivalent to the clock frequency errors, denoted as $\delta t_{ru1}$ and $\delta t_{ru2}$, respectively.

Therefore, the error state of GNSS is given by

$$X_G\left(t\right)={\left[\delta t_{u1},\delta t_{u2},\delta t_{ru1},\delta t_{ru2}\right]}^T$$

(7)

The corresponding differential equation is

$$\begin{array}{l}\delta t_u=\delta t_{ru}+{\omega }_t\\ \delta t_{ru}=-\beta \delta t_{ru}+{\omega }_{ru}\end{array}$$

(8)

where $\beta$ is the correlation time. Expressing the equation in matrix form yields:

$$X_G\left(t\right)=F_G\left(t\right)X_G\left(t\right)+{\Gamma }_G\left(t\right)W_G\left(t\right)$$

(9)

Hence,

$$\left[\begin{array}{c}\delta t_{u1}\\ \delta t_{u2}\\ \delta t_{ru1}\\ \delta t_{ru2}\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -{\beta }_{t_{ru1}}& 0\\ 0& 0& 0& -{\beta }_{t_{ru2}}\end{array}\right]\left[\begin{array}{c}\delta t_{u1}\\ \delta t_{u2}\\ \delta t_{ru1}\\ \delta t_{ru2}\end{array}\right]+\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\omega }_{u1}\\ {\omega }_{u2}\\ {\omega }_{ru1}\\ {\omega }_{ru2}\end{array}\right]$$

(10)

Combining the error state equations of the INS and the GPS, the state equation of the pseudorange and pseudorange rate combination system is obtained as follows:

$$\left[\begin{array}{c}{X}_1\left(t\right)\\ X_G\left(t\right)\end{array}\right]=\left[\begin{array}{cc}{F}_1\left(t\right)& 0\\ 0& F_G\left(t\right)\end{array}\right]\left[\begin{array}{c}{X}_1\left(t\right)\\ X_G\left(t\right)\end{array}\right]+\left[\begin{array}{cc}{\Gamma }_1\left(t\right)& 0\\ 0& {\Gamma }_G\left(t\right)\end{array}\right]\left[\begin{array}{c}{W}_1\left(t\right)\\ W_G\left(t\right)\end{array}\right]$$

(11)

2.2.2. Observation Equations

(1)

Observation Equation of the System Pseudorange Composition

Since the position information output by the strapdown inertial navigation solution is typically represented in the Earth-centered Earth-fixed (ECEF) coordinate system, which is the longitude, latitude, and altitude coordinate system, it needs to be converted to the ECEF coordinate system. The conversion relationship is as follows:

$$\begin{array}{l}{x}_I=\left(R_n+h\right)\cos L\cos \lambda \\ y_I=\left(R_n+h\right)\cos L\cos \lambda \\ z_I=\left[R_n\left(1-e^2\right)+h\right]\sin L\end{array}$$

(12)

Assuming the position of the j-th satellite in the ECEF coordinate system is $\left(x_s^j,y_s^j,z_s^j\right)$, then the pseudorange from the vehicle to the j-th satellite can be obtained using the position of the vehicle $\left(x_I,y_I,z_I\right)$ calculated by the inertial navigation solution:

$${\rho }_I^j=\sqrt{{\left(x_I-x_s^j\right)}^2+{\left(y_I-y_s^j\right)}^2+{\left(z_I-z_s^j\right)}^2}$$

(13)

Expanding Equation (14) in a Taylor series around the true position of the vehicle in the ECEF coordinate system (x, y, z) and retaining terms up to the first order, it can be obtained as follows:

$${\rho }_I^j={\left[{\left(x_I-x_s^j\right)}^2+{\left(y_I-y_s^j\right)}^2+{\left(z_I-z_s^j\right)}^2\right]}^{\frac{1}{2}}+\frac{\partial {\rho }_I^j}{\partial x}\delta x+\frac{\partial {\rho }_I^j}{\partial y}\delta y+\frac{\partial {\rho }_I^j}{\partial z}\delta z$$

(14)

Then, it has the following relationship:

$$\begin{array}{l}\frac{\partial {\rho }_I^j}{\partial x}=\frac{x-x_s^j}{{\left[{\left(x-x_s^j\right)}^2+{\left(y-y_s^j\right)}^2+{\left(z-z_s^j\right)}^2\right]}^{\frac{1}{2}}}=e_{j1}\\ \frac{\partial {\rho }_I^j}{\partial y}=\frac{y-y_s^j}{{\left[{\left(x-x_s^j\right)}^2+{\left(y-y_s^j\right)}^2+{\left(z-z_s^j\right)}^2\right]}^{\frac{1}{2}}}=e_{j2}\\ \frac{\partial {\rho }_I^j}{\partial z}=\frac{z-z_s^j}{{\left[{\left(x-x_s^j\right)}^2+{\left(y-y_s^j\right)}^2+{\left(z-z_s^j\right)}^2\right]}^{\frac{1}{2}}}=e_{j3}\end{array}$$

(15)

The expression for the pseudorange measured by the GNSS receiver between the vehicle and the j-th GNSS satellite is given by

$${\rho }_G^j={\left[{\left(x_I-x_s^j\right)}^2+{\left(y_I-y_s^j\right)}^2+{\left(z_I-z_s^j\right)}^2\right]}^{\frac{1}{2}}-\delta t_u-{\upsilon }_{\rho }^j$$

(16)

where $\delta t_u$ represents the distance corresponding to the equivalent clock error, and ${\upsilon }_{\rho }^j$ denotes the pseudorange measurement noise, primarily stemming from effects such as multipath, tropospheric delay errors, and ionospheric errors.

Thus, it can be obtained the observation equation for pseudorange error as follows:

$$\delta {\rho }_j={\rho }_I^j-{\rho }_G^j=e_{j1}\delta x+e_{j2}\delta y+e_{j3}\delta z+\delta t_u+{\upsilon }_{\rho }^j$$

(17)

In general, the observation equation for pseudorange is established by selecting the best four satellites as observation satellites.

$$\delta \rho =\left[\begin{array}{c}\delta {\rho }_1\\ \delta {\rho }_2\\ \delta {\rho }_3\\ \delta {\rho }_4\end{array}\right]=\left[\begin{array}{cccc}{e}_{11}& e_{12}& e_{13}& 1\\ e_{21}& e_{22}& e_{23}& 1\\ e_{31}& e_{32}& e_{33}& 1\\ e_{41}& e_{42}& e_{43}& 1\end{array}\right]\left[\begin{array}{c}\delta x\\ \delta y\\ \delta z\\ \delta t_u\end{array}\right]+\left[\begin{array}{c}{\upsilon }_{\rho }^1\\ {\upsilon }_{\rho }^2\\ {\upsilon }_{\rho }^3\\ {\upsilon }_{\rho }^4\end{array}\right]$$

(18)

Now, differentiating both sides of the coordinate transformation formula yields the following transformation relationship:

$$\begin{array}{l}\delta x=\cos L\cos \lambda \delta h-\left(R_n+h\right)\sin L\cos \lambda \delta L-\left(R_n+h\right)\cos L\sin \lambda \delta \lambda \\ \delta y=\cos L\sin \lambda \delta h-\left(R_n+h\right)\sin L\sin \lambda \delta L+\left(R_n+h\right)\cos L\cos \lambda \delta \lambda \\ \delta z=\sin L\delta h+\left[R_n\left(1-e^2\right)+h\right]\delta L\end{array}$$

(19)

Hence, the following observation equation can be derived:

$$Z_{\rho }\left(t\right)=H_{\rho }\left(t\right)X\left(t\right)+V_{\rho }\left(t\right)$$

(20)

where

$$\begin{array}{l}{H}_{\rho }=\left[O_{4\times 6}⋮H_{\rho 1}⋮O_{4\times 6}⋮H_{\rho 2}\right]\\ H_{\rho 1}=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\\ a_{41}& a_{42}& a_{43}\end{array}\right],H_{\rho 2}=\left[\begin{array}{cc}1& 0\\ 1& 0\\ 1& 0\\ 1& 0\end{array}\right]\end{array}$$

(21)

The coefficient calculation formula is as follows:

$$Z_{\rho }\left(t\right)=H_{\rho }\left(t\right)X\left(t\right)+V_{\rho }\left(t\right)$$

(22)

(2)

Observation Equation for the System Pseudorange Rate Composition

The pseudorange rate between the vehicle output by the INS and the j-th satellite can be expressed as follows:

$$\stackrel{•}{{\rho }_{1j}}=e_{j1}\left(\stackrel{•}{x_1}-\stackrel{•}{x_{sj}}\right)+e_{j2}\left(\stackrel{•}{y_1}-\stackrel{•}{y_{sj}}\right)+e_{j3}\left(\stackrel{•}{z_1}-\stackrel{•}{z_{sj}}\right)+e_{j1}\delta \stackrel{•}{x}+e_{j1}\delta \stackrel{•}{y}+e_{j1}\delta \stackrel{•}{z}$$

(23)

The pseudorange rate measured by the GNSS receiver is given by

$$\stackrel{•}{{\rho }_{Gj}}=e_{j1}\left(\stackrel{•}{x_1}-\stackrel{•}{x_{sj}}\right)+e_{j2}\left(\stackrel{•}{y_1}-\stackrel{•}{y_{sj}}\right)+e_{j3}\left(\stackrel{•}{z_1}-\stackrel{•}{z_{sj}}\right)+\delta t_{ru}+{\upsilon }_{pj}$$

(24)

Therefore, the observation equation for pseudorange rate error can be derived.

$$\stackrel{•}{{\rho }_{1j}}-\stackrel{•}{{\rho }_{Gj}}=e_{j1}\delta \stackrel{•}{x}+e_{j2}\delta \stackrel{•}{y}+e_{j3}\delta \stackrel{•}{z}-\delta t_{ru}-{\upsilon }_{pj}$$

(25)

In the case of four observed satellites, it has

$$\delta \stackrel{•}{\rho }=\left[\begin{array}{cccc}{e}_{11}& e_{12}& e_{13}& -1\\ e_{21}& e_{22}& e_{23}& -1\\ e_{31}& e_{32}& e_{33}& -1\\ e_{41}& e_{42}& e_{43}& -1\end{array}\right]\left[\begin{array}{c}\delta \stackrel{•}{x}\\ \delta \stackrel{•}{y}\\ \delta \stackrel{•}{z}\\ \delta t_{ru}\end{array}\right]-\left[\begin{array}{c}{\upsilon }_{\stackrel{•}{\rho }1}\\ {\upsilon }_{\stackrel{•}{\rho }2}\\ {\upsilon }_{\stackrel{•}{\rho }3}\\ {\upsilon }_{\stackrel{•}{\rho }4}\end{array}\right]$$

(26)

As the velocity information outputted by the INS is represented in the geodetic coordinate system (i.e., the East–North–Up coordinate system), it is necessary to convert it through the coordinate transformation matrix from the geodetic coordinate system to the ECEF coordinate system, as follows:

$$\begin{array}{l}\delta \stackrel{•}{x}=-\delta V_{\epsilon }\sin \lambda -\delta V_n\sin L\cos \lambda +\delta V_u\cos L\cos \lambda \\ \delta \stackrel{•}{y}=\delta V_{\epsilon }\cos \lambda -\delta V_n\sin L\sin \lambda +\delta V_u\cos L\sin \lambda \\ \delta \stackrel{•}{z}=\delta V_n\cos L+\delta V_n\sin L\end{array}$$

(27)

Through the above analysis, the observation equation for the pseudorange rate is derived as follows:

$$Z_{\stackrel{•}{\rho }}\left(t\right)=H_{\stackrel{•}{\rho }}\left(t\right)X\left(t\right)+V_{\stackrel{•}{\rho }}\left(t\right)$$

(28)

where

$$\begin{array}{l}{H}_{\stackrel{•}{\rho }}=\left[O_{4\times 3}⋮H_{\stackrel{•}{\rho }1}⋮O_{4\times 9}⋮H_{\stackrel{•}{\rho }2}\right]\\ H_{\stackrel{•}{\rho }1}=\left[\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{22}& b_{23}\\ b_{31}& b_{32}& b_{33}\\ b_{41}& b_{42}& b_{43}\end{array}\right],H_{\stackrel{•}{\rho }2}=\left[\begin{array}{cc}0& 1\\ 0& 1\\ 0& 1\\ 0& 1\end{array}\right]\end{array}$$

(29)

The coefficient calculation formula is as follows:

$$\begin{array}{l}{b}_{j1}=-e_{j1}\sin \lambda +e_{j2}\cos \lambda \\ b_{j2}=-e_{j1}\sin L\cos \lambda -e_{j2}\sin L\sin \lambda +e_{j3}\cos L\\ b_{j3}=e_{j1}\cos L\cos \lambda +e_{j2}\cos L\sin \lambda +e_{j3}\sin L\end{array}$$

(30)

The observation equation for the combined pseudorange and pseudorange rate system is as follows:

$$Z\left(t\right)=\left[\begin{array}{c}{H}_{\rho }\left(t\right)\\ H_{\stackrel{•}{\rho }}\left(t\right)\end{array}\right]X\left(t\right)+\left[\begin{array}{c}{V}_{\rho }\left(t\right)\\ V_{\stackrel{•}{\rho }}\left(t\right)\end{array}\right]$$

(31)

3. Constructing the Framework for CNN and LSTM Assisted GNSS/INS Navigation System

During the study of the Kalman filter algorithm, when severe interference exists in the navigation environment, regardless of whether the loosely coupled or tightly coupled approach is employed, it can lead to significant errors in the final fusion navigation positioning. Therefore, it is necessary to utilize neural network architectures to assist in correcting the signals before fusion.

The algorithm of the Kalman filter assisted by neural networks [26] demonstrates outstanding performance in various application scenarios. The main advantages are as follows:

• Complementarity: Kalman filters are primarily suitable for linear systems and environments with Gaussian noise, while neural networks excel in handling nonlinear, non-Gaussian, or complex systems. Therefore, the combination of the two can fully utilize their respective strengths, complementing each other’s shortcomings, and thereby more accurately describing and predicting the dynamic behavior of the system.
• Improved prediction accuracy: Through the learning and modeling capabilities of neural networks, nonlinear characteristics of the system can be captured, thereby providing more accurate models and predictions for the Kalman filter. This helps reduce errors during the filtering process and improves prediction accuracy.
• Strong adaptability: Due to the powerful learning and adaptation capabilities of neural networks, they can adapt to changes and uncertainties in system parameters. Therefore, even if the dynamic characteristics of the system change, neural-network-assisted Kalman filters can quickly adjust and adapt to the new environment.
• Enhanced robustness: When facing noise interference, missing data, or outliers, the combination of neural networks and Kalman filters can enhance the robustness of the system. Neural networks can learn and handle these exceptional situations, while Kalman filters can smooth and correct estimation results to some extent.
• Expanded application scope: By integrating neural networks and Kalman filters, the application scope of Kalman filters can be expanded to more complex systems and scenarios. For example, in fields such as autonomous driving, robot navigation, and financial forecasting, this fusion method can help achieve more accurate and reliable state estimation and prediction.

Therefore, researching techniques that can improve the performance of navigation systems by constructing neural network architectures to correct signal errors has become one of the current focuses of research work.

3.1. Neural Network Structure and Function

With the advancement of Artificial Intelligence (AI) and deep learning, the application of neural networks in fusion navigation primarily focuses on the integration and processing of multisource navigation information. By constructing appropriate neural network models, data from different navigation systems can be effectively integrated to enhance navigation accuracy and stability.

Specifically, there are various ways in which neural networks are applied in fusion navigation [27]. One common approach is to leverage the self-learning and feature extraction capabilities of neural networks to process data from different navigation sensors, extract useful feature information, and fuse them. This enables the full utilization of the advantages of each sensor, compensating for the limitations of individual sensors, and improving the overall performance of the navigation system. Another approach is to utilize the predictive capabilities of neural networks to forecast the future state of the navigation system. By learning and analyzing historical data, neural networks can capture the motion patterns and trends of the navigation system, thereby accurately predicting future states. This facilitates early detection of navigation errors and corrections, thereby enhancing navigation accuracy and reliability. Additionally, neural networks can be combined with other algorithms and technologies to form more robust fusion navigation solutions. For example, neural networks can be combined with Kalman filter algorithms to filter navigation data, further reducing the impact of noise and errors. Alternatively, neural networks can be combined with map-matching techniques to constrain and optimize navigation results using map information.

The neural network is a mathematical model algorithm that mimics the behavior characteristics of animal neural networks. It achieves information processing by adjusting the relationships between a large number of interconnected nodes internally. It possesses adaptive self-learning capabilities, automatically grasps environmental features, achieves automatic target recognition, and exhibits advantages such as good fault tolerance and strong anti-interference ability.

Structurally, neural networks are composed of a large number of neurons interconnected with each other. These neurons receive input signals, process them through activation functions, and then output signals to the next layer. Different neural network models have different structures, such as perceptrons, feedforward networks, residual networks, and RNNs, among others.

Specifically, the perceptron [28] is the most basic of all neural networks and serves as the fundamental component of more complex neural networks. It connects only one input neuron and one output neuron. Feedforward networks [29] are collections of perceptrons, consisting of input layers, hidden layers, and output layers, with signals propagating unidirectionally between these layers. Residual networks [30] achieve signal propagation across layers by skipping connections, thereby reducing the problem of gradient vanishing. RNNs [31] contain loops and self-repetition, enabling them to handle data with temporal dependencies.

3.1.1. Artificial Neurons

Artificial neurons [32] generate an output value representing their activity by applying a nonlinear activation function. In this process, this study assumes that the neuron receives n input signals $X=\left(X_1,X_2,\cdots ,X_n\right)$. These input signals are weighted and summed up, represented by a state variable z. Finally, the output value of this neuron, namely its activity a, is calculated based on the state z through an activation function. Figure 3 illustrates the model of an artificial neuron.

Figure 3. Model of an artificial neuron.

The most commonly used activation function in traditional neural networks is the sigmoid function. The sigmoid function refers to a class of S-shaped curve functions, with commonly used sigmoid functions including the logistic function $\sigma \left(x\right)$ and the $\tanh$ function.

$$\sigma \left(x\right)=\frac{1}{1+e^{-x}}$$

(32)

$$\tanh \left(x\right)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

(33)

3.1.2. Multilayer Feedforward Neural Network

The multilayer feedforward neural network [33], also known as the multilayer perceptron (MLP), introduces hidden layers between the input and output layers to enhance the performance of single-layer perceptrons. The number of these hidden layers can be one or more, and they function as the “internal representation” of input patterns. With this improvement, the original single-layer perceptrons transform into multilayer perceptrons, thereby enhancing their ability to handle complex patterns. The training of multilayer feedforward neural networks often utilizes the error backpropagation algorithm, hence they are also commonly referred to as Back Propagation (BP) networks [34].

The structure of multilayer feedforward neural networks is hierarchically rich, consisting of an input layer, several hidden layers, and an output layer. Each layer can be viewed as an independent single-layer feedforward neural network, with each one linearly classifying input patterns. However, it is the combination and superposition of these layers that enables multilayer feedforward neural networks to perform more complex and refined classification tasks on input patterns.

Multilayer feedforward neural networks are renowned for their excellent nonlinear processing capabilities. Despite their relatively simple structure, they have an extremely wide range of applications. These networks can approximate any continuous function and square-integrable function with arbitrary precision. Moreover, they can accurately represent any finite training sample set, making them of significant value in various fields. Figure 4 illustrates the model of a multilayer feedforward neural network.

Figure 4. Model of a multilayer feedforward neural network.

3.1.3. Convolutional Neural Network

The CNN [35] is a type of neural network specifically designed to handle data with grid-like structures. This network architecture excels in image processing tasks, capable of identifying two-dimensional patterns with shift, scale, and other forms of distortion invariance. The basic structure of a CNN includes convolutional layers, pooling layers, and fully connected layers.

Convolutional Layer [36]: The convolutional layer is the core of a CNN, consisting of multiple convolutional kernels (or filters). These kernels slide over the input data and perform convolution operations to generate feature maps. Each convolutional kernel can learn specific features from the input data.

Pooling Layer [37]: The pooling layer typically follows the convolutional layer and is used to reduce the spatial size of the data (i.e., downsampling), decrease the number of parameters in the network to prevent overfitting, and enhance the model’s robustness. Common pooling operations include max pooling and average pooling.

Fully Connected Layer [38]: The fully connected layer is usually located in the last few layers of the CNN, responsible for receiving the features extracted from the preceding layers and outputting the final prediction results. In classification tasks, a softmax layer is often appended after the fully connected layer to convert the outputs into probability distributions. Throughout the training process, the CNN continuously updates the weights of the convolutional kernels and fully connected layers using the backpropagation algorithm to minimize the error between the predicted values and the actual values.

3.1.4. Recurrent Neural Network

The RNN [39] is a type of neural network specialized in handling sequential data. Its core idea is to use the previous output as part of the current input to capture dependencies in time series. The basic structure of an RNN includes a hidden layer and an output layer. In RNNs, each unit in the hidden layer receives a weighted sum of the output from the previous time step and the input at the current time step, undergoes a nonlinear transformation through an activation function, and passes the result to the next time step. This structure enables RNNs to handle variable-length sequence data and perform recursive operations along the sequence evolution direction.

RNNs have wide-ranging applications in various fields such as text classification, machine translation, speech recognition, image/video captioning, time series prediction, and recommendation systems. In these applications, RNNs can model dependencies between sentences and phrases and temporal dependencies between speech and language, as well as spatial relationships between frames.

Despite its strong performance in certain domains, RNNs also have some notable drawbacks. During training, RNNs often encounter the problems of exploding or vanishing gradients, leading to unstable training or difficulties in convergence. Additionally, compared with other types of neural networks, RNNs typically require more memory space, limiting their application in large-scale datasets. Moreover, when using certain activation functions, RNNs may struggle to effectively handle excessively long sequences, which can adversely affect their performance.

To address these issues, researchers actively explore and propose various improvement strategies. Among them, LSTM networks [40] undoubtedly stand out as the most prominent and representative solution. LSTM introduces gate mechanisms and memory units, enabling more effective processing of long sequence data and alleviating the problems of vanishing and exploding gradients. This has led to significant performance improvements for LSTM in many sequence processing tasks.

3.2. Constructing the Framework for CNN- and LSTM-Assisted GNSS/INS Navigation System

Because the fusion navigation data is a series of time series, there is this obvious spatiotemporal correlation between them. Therefore, a CNN and LSTM are combined to extract more high-dimensional features from the long-term dataset using the CNN and are combined with LSTM to synthesize the series of high-dimensional features for time series prediction.

The combination of a CNN and LSTM [41,42,43] forms a powerful deep learning architecture, leveraging the CNN’s feature extraction capabilities and LSTM’s ability to handle sequence data and capture long-term dependencies. The key steps in constructing a CNN-LSTM-based network model are feature extraction in the CNN layer and model training in the LSTM layer.

Advantages of this combination include the following:

• Powerful Feature Extraction: The CNN automatically extracts useful features from raw data, reducing the need for manual feature engineering.
• Handling Sequence Data: LSTM can process variable-length sequence data and capture long-term dependencies, which is crucial for many practical applications.

Flexibility: The combination of a CNN and LSTM can be adjusted and optimized based on the specific requirements of the task, such as adjusting the number of CNN layers, convolutional kernel sizes, and LSTM hidden units.

Based on the characteristics of GNSS/INS navigation systems data, the specific steps to construct the corresponding neural network architecture are as follows:

3.2.1. CNN Feature Extraction

The CNN structure consists of an input layer, convolutional layers, pooling layers, a fully connected layer, and an output layer. Among them,

Input Layer: Takes preprocessed GNSS and INS data as input.

Convolutional Layer: Utilizes multiple convolutional kernels to perform convolution operations on input data, extracting local features.

Pooling Layer: Conducts pooling operations on the feature maps output from the convolutional layer, further compressing features and reducing computational complexity.

Fully Connected Layer: Flattens the output of the pooling layer and integrates and transforms features through fully connected layers.

The mathematical model expression for the CNN is

$$y_i^n=f\left(x^{n-1}\ast C_i^n+d_i^n\right)$$

(34)

where $y_i^n$ is the output of the ith convolution in the nth convolutional layer; $x^{n-1}$ is the input of the nth convolutional layer; $\ast$ is the convolution operation; $C_i^n$ is the weight of the ith convolutional kernel in the nth convolutional layer; and $d_i^n$ is the bias parameter of the ith convolutional layer in the nth convolutional layer.

In order to increase the diversity of the learned features, CNN layer feature extraction is performed for 4 convolutional computation layers, where the 1st convolutional layer is 64 layers, the 2nd convolutional layer is 126 layers, the 3rd convolutional layer is 256 layers, and the 4th convolutional layer is 256 layers. After the convolutional computation layer, the output of the convolutional layer is made nonlinearly mapped by the activation function. Here, the ReLU function is used. The expression is

$$f\left(x\right)=\max \left(0,x\right)$$

(35)

It is characterized by fast convergence and simplicity in finding the gradient. Its function image is shown in Figure 5.

Figure 5. ReLU function.

The pooling layer is sandwiched between successive convolutional layers and is used to compress the amount of data and parameters and reduce overfitting. The fully connected layer is at the tail of the convolutional neural network and is connected in the same way as traditional neural network neurons.

3.2.2. LSTM Model Training

The GNSS/INS data processed in the CNN layer are fed into the LSTM layer for further feature learning of the GNSS/INS data, while the GNSS/INS sequence data are processed and memorized using gating and long- and short-term memory modules, and model training and prediction is performed.

The main mechanisms for capturing long-term dependencies in LSTM networks are as follows:

Forget Gate [44]: The forget gate determines which information should be retained in the memory cell. It takes the input at the current time step and the hidden state from the previous time step as inputs and outputs a value between 0 and 1, controlling the degree of information retention in the memory cell. When the output of the forget gate is close to 1, it indicates the retention of most information, while an output close to 0 indicates the forgetting of most information.

Input Gate [45]: The input gate decides which new information should be added to the memory cell. Similarly, it takes the input at the current time step and the hidden state from the previous time step as inputs and outputs two values: one for controlling the amount of new information to be added and another for generating the new candidate cell state.

Cell State [46]: The cell state is the core component of the LSTM network, responsible for storing and transmitting information in long time sequences. At each time step, the cell state is updated based on the outputs of the forget gate and input gate. Specifically, the cell state is determined by the previous time step’s cell state, the output of the forget gate, and the output of the input gate.

Output Gate [47]: The output gate determines the output value at the current time step. It takes the input at the current time step, the hidden state from the previous time step, and the current cell state as inputs, and outputs a value used to compute the current time step’s hidden state. The hidden state is the output of the LSTM network at each time step, which can be used for subsequent layer processing or as a representation of the entire sequence.

Through these mechanisms, LSTM networks can selectively retain and update information, effectively handling dependencies in long time sequences. This capability makes LSTM networks perform excellently in tasks involving long-term dependencies, such as speech recognition, machine translation, and time series prediction.

Figure 6 depicts the structure of an LSTM neural network.

Figure 6. LSTM neural network structure.

The update process of LSTM at time step t is as follows:

$$\left\{\begin{array}{l}{i}_t=\sigma \left(W_i{x}_t+U_i{h}_{t-1}+V_i{c}_{t-1}\right)\\ f_t=\sigma \left(W_f{x}_t+U_f{h}_{t-1}+V_f{c}_{t-1}\right)\\ o_t=\sigma \left(W_o{x}_t+U_o{h}_{t-1}+V_o{c}_{t-1}\right)\\ {\tilde{c}}_t=\tanh \left(W_c{x}_t+U_c{h}_{t-1}\right)\\ c_t=f_t\otimes c_{t-1}+i_t\otimes {\tilde{c}}_t\\ h_t=o_t\otimes \tanh \left(c_t\right)\end{array}\right.$$

(36)

where $x_t$ is the input at the current time step, $\sigma$ represents the logistic sigmoid function, and $V_i$, $V_f$, $V_o$ denote element-wise multiplication. The forget gate $f_t$ controls how much information each memory cell should forget, the input gate $i_t$ controls how much new information should be added to each memory cell, and the output gate $o_t$ controls how much information each memory cell should output.

3.2.3. Constructing the CNN-LSTM Network Model

Based on the above steps, the CNN-LSTM network model is constructed. The specific architecture is illustrated in Figure 7.

Figure 7. Neural network framework combining CNN and LSTM.

4. Experimental Comparison

Objective: The experiment aims to validate the optimization effect of integrating CNN with LSTM to assist Kalman filtering for fused navigation. Therefore, during the experimental process, scenarios are set up for both undisturbed and disturbed conditions. In the undisturbed scenario, the effectiveness of loosely coupled and tightly coupled Kalman filtering methods is primarily compared. In the disturbed scenario, the focus is on comparing the errors between using a conventional CNN and a neural network combining a CNN and LSTM, as well as the differences in navigation effectiveness before and after using neural network assistance.

Experimental Equipment: Ublox M8N for receiving GNSS signals. WHEELTEC N100N as the inertial navigation module. UM980 as RTK ground truth.

Data Collection: Base station coordinates (x, y, z). Measurement distance. Signal strength of the first path for transmitted signals. Signal strength of the first path for received signals.

4.1. Undisturbed Scenario

4.1.1. Experimental Results of Loosely Coupled and Tightly Coupled Systems

Experimental results of the loosely coupled closed-loop system and tightly coupled system were obtained under the same experimental conditions, as shown in Figure 8.

Figure 8. Experimental results of the loosely coupled closed-loop system and tightly coupled system.

4.1.2. Comparative Analysis of Experiments

The experimental results are analyzed for 2D and Z-direction errors, and correlation error analysis plots and CDF plots are constructed. As shown in Figure 9. Their specific data are shown in Table 1 and Table 2.

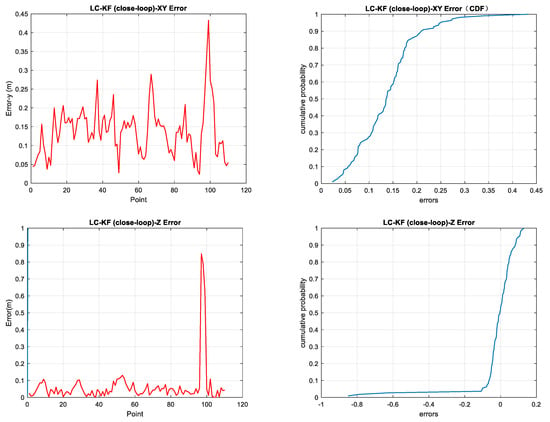
Figure 9. Two-dimensional and Z-direction error analysis plots for loosely coupled closed-loop system vs. tightly coupled system.

Table 1. Table of 2D and Z-direction errors for loosely coupled closed-loop systems.

	Average Value	Variance	Standard Deviation
Statistics of 2D error	0.138227	0.004441	0.066644
The statistics of the Z-direction error	0.017386	0.018335	0.135407

Table 2. Table of 2D and Z-direction errors for tightly coupled systems.

	Average Value	Variance	Standard Deviation
Statistics of 2D error	0.133644	0.004515	0.067196
The statistics of the Z-direction error	0.010795	0.010478	0.102362

Tightly coupled Kalman filtering improves localization performance by (0.133644 − 0.138227)/0.138227 = 0.0332 compared with loosely coupled Kalman filtering.

Based on the experimental results, it can be observed that the tightly coupled system exhibits a noticeable improvement in fusion navigation effectiveness after utilizing raw observation information. Combining the network architectures of loosely coupled and tightly coupled systems, their advantages and disadvantages can be summarized as follows:

The main advantage of the loosely coupled approach lies in its simple and easy-to-implement structure. In a loosely coupled system, each sensor (such as IMU and GNSS) works independently and outputs navigation information, which is then used to correct errors in the Kalman filter by taking the difference of this information as input. This approach preserves the original GNSS results without requiring modifications to GNSS hardware. However, the drawback of the loosely coupled approach is that when the number of visible satellites in the environment is small, GNSS navigation information cannot be obtained, leading to a decrease in the performance of the Kalman filter and thus affecting the positioning accuracy of the entire system.

In contrast, the tightly coupled approach is relatively more complex than the loosely coupled approach. It requires the processing of raw GNSS data (such as pseudorange and pseudorange rate) and comparing them with the corresponding data outputted by INS, with the difference being used as input for the Kalman filter. The main advantage of this approach is that it addresses the problems associated with observation input in a combined system with only one Kalman filter. However, the drawback of the tightly coupled approach lies in its relatively complex implementation structure and inability to independently output GNSS navigation results.

4.2. Disturbed Scenario

In the presence of interference, the process of correcting the Kalman filter with a neural network can be divided into the following steps:

Data Collection and Processing: Initially, data required for training the neural network need to be collected. This includes measurement data from INS, observation data from GNSS, etc. These data undergo appropriate preprocessing, such as noise removal and normalization, to facilitate the training of the neural network.

Definition of Neural Network Structure: Based on specific application scenarios and requirements, an appropriate neural network structure is defined. Here, the networks used for comparison are a conventional CNN and a combination of a CNN and LSTM. The input to the network comprises observation data and state data, while the output is measurement error.

Training of the Neural Network: The collected data are utilized to train the neural network. The training objective is to enable the neural network to learn the mapping relationship between the Kalman filter parameters and the INS state estimation and actual GNSS observation data. During training, the network’s performance is optimized by adjusting parameters such as weights and biases.

Neural Network Correction: In the Kalman filter process, the trained neural network is employed to adjust the covariance matrix and other parameters of the Kalman filter.

4.2.1. Conventional Convolutional Neural Network Architecture

The navigation dataset serves as input information, and the training process is depicted in Figure 10.

Figure 10. CNN training process.

The measurement error obtained through training is shown in Figure 11.

Figure 11. Training process LOSS RMSE error graph.

The final training outcome indicates a loss error of RMSE_error = 1.2106.

4.2.2. Neural Network Architecture Combining CNN and LSTM

The navigation dataset serves as input information, and the training process is depicted in Figure 12.

Figure 12. Training process of the neural network architecture combining CNN and LSTM.

The measurement error obtained through training is shown in Figure 13.

Figure 13. Training process LOSS RMSE error graph.

The final training outcome indicates a loss error of RMSE_error = 0.7395.

4.2.3. Comparison before and after Signal Correction

It is evident that the neural network combining a CNN and LSTM outperforms the general CNN in terms of training effectiveness. Therefore, the noise predicted by the neural network combining a CNN and LSTM is incorporated into the covariance matrix of the tightly coupled Kalman filter, and the navigation performance is compared with the navigation performance before signal correction.

In the case of strong signal interference, a comparison of the effect before and after navigation using neural-network-assisted tightly coupled Kalman filtering is depicted in Figure 14.

Figure 14. Comparison of the effect before and after navigation using neural-network-assisted tightly coupled Kalman filtering.

The experimental results are analyzed for 2D and Z-direction errors, and error analysis plots and CDF plots are constructed. As shown in Figure 15. Their specific data are shown in Table 3 and Table 4.

Figure 15. Two-dimensional and Z-direction error analysis plots before and after signal correction.

Table 3. Table of 2D and Z-direction errors for CNN-LSTM unassisted Kalman filtering.

	Average Value	Variance	Standard Deviation
Statistics of 2D error	1.082632	0.198008	0.444981
The statistics of the Z-direction error	0.654914	0.138698	0.372422

Table 4. Table of 2D and Z-direction errors for CNN-LSTM-assisted Kalman Filtering.

	Average Value	Variance	Standard Deviation
Statistics of 2D error	0.559872	0.063042	0.251082
The statistics of the Z-direction error	0.234357	0.052803	0.229790

After neural network processing, the localization performance was significantly improved, with a performance improvement of (0.559872 − 1.082632)/1.082632 = 0.4829.

From this, it can be concluded that in scenarios where the signal encounters strong interference, relying solely on the Kalman filter algorithm for GNSS/INS fusion navigation will fail to meet the task requirements. However, by incorporating the noise predicted by the neural network into the covariance matrix of the tightly coupled Kalman filter, there is a significant improvement in navigation performance compared with when errors are not corrected.

5. Conclusions

In conclusion, this study focuses on the key technologies of the Kalman filter fusion navigation algorithm assisted by neural networks. By combining the powerful learning capabilities of neural networks with the precise estimation capabilities of the Kalman filter, a novel solution is provided for UAV navigation technology. This algorithm not only significantly improves navigation accuracy and stability but also demonstrates outstanding adaptability in dealing with complex environments and variable noise interference.

During UAV missions, the neural-network-based Kalman filter fusion navigation algorithm can dynamically adjust and optimize the navigation model based on sensor data in real time, effectively overcoming many limitations of traditional navigation methods. Whether facing complex natural environments or deliberate interference, this algorithm can provide precise and reliable navigation services for UAVs due to its excellent performance.

In the construction of neural network architecture, this study combines existing research results and proposes a neural network architecture that combines a CNN with LSTM to assist the Kalman filter optimization algorithm. By leveraging the advantages of both, the proposed architecture significantly outperforms traditional neural network architectures, reducing training result errors by nearly 50% through simulation experiments. Moreover, it verifies the effective improvement of navigation performance under strong interference conditions by the optimization algorithm.

Currently, interference in UAV navigation systems includes not only jamming but also deception techniques, which are widely used. Therefore, in future research, further exploration of interference techniques will be conducted to consider deception techniques in the task environment. The neural network architecture will be further optimized to adapt to even more complex task scenarios.

In summary, the Kalman filter fusion navigation algorithm assisted by neural networks, with its unique advantages and strong potential, has become an important development direction in modern UAV navigation technology. The optimization algorithm will play an increasingly important role in areas such as autonomous driving, UAV cruising, and intelligent robotics.