Order-Preserving Multiple Pattern Matching in Parallel

Abstract

The order-preserving multiple pattern matching problem is to find all substrings of T whose relative orders are the same for any pattern in a set of patterns. Various sequential algorithms have been studied for the order-preserving multiple pattern matching problems. In this paper, we propose two parallel algorithms, each of which uses Aho–Corasick automata and fingerprint tables, respectively. We also present experimental results of comparing the execution times of each parallel algorithm on various types of time-series data.

1. Introduction

Two strings $x,y$$\left(\right|x|=|y\left|\right)$ from an integer alphabet are order-isomorphic if the relative orders of characters are the same. For example, given two strings $x=(17,30,10)$ and $y=(4,9,1)$, they are order-isomorphic because their relative orders of characters are the same as $(2,3,1)$. Given text $T\left(\right|T|=n)$ and pattern $P\left(\right|P|=m)$, finding all substrings of T, which are order-isomorphic to P, is called the order-preserving pattern matching (OPPM for short) problem [1,2,3,4,5]. Given text $T\left(\right|T|=n)$ and a set of patterns $\mathbb{P}=\left\{P_1,\dots ,P_k\right\}$, the order-preserving multiple pattern matching (OPMPM for short) problem is to find all substrings of T that are order-isomorphic to any $P_a(1\le a\le k)$ in $\mathbb{P}$ [1,2,3,4,5]. The order-preserving pattern matching problem and order-preserving multiple pattern matching problem can be used to analyze various time-series data such as stock price indices, music melodies, and biomedical data [1,2,3,4,5].

Most existing OPMPM algorithms are performed in two phases: a preprocessing phase and a search phase. Let m, $\overline{m}$, and M denote the shortest pattern length, the longest pattern length, and the sum of the lengths of all patterns in $\mathbb{P}$, respectively. Kim et al. [1] proposed an algorithm that performs the preprocessing phase in $O(Mlog\overline{m})$ time and the search phase in $O(nlog\overline{m})$ time using Aho–Corasick automata [6]. Han et al. [7] proposed two algorithms for the order-preserving multiple pattern matching problem. In the first algorithm, the preprocessing and search phases run in $O(kmq+Mlog\overline{m})$ time and $O\left(\right(n/m)logM)$ time, on average, and in the second algorithm, the preprocessing and search phases run in $O(Mlog\overline{m})$ time and $O\left(n\right)$ time, on average. Park et al. [8] proposed an algorithm that improved the space complexity of the first algorithm proposed in [7] from $O(q!+k+M)$ to $O(k+M)$ using fingerprint tables. Park et al. [9] parallelized the second algorithm proposed in [7]. The preprocessing phase runs in $O\left(\overline{m}\right)$ time using $O\left(M\right)$ threads and the search phase runs in $O\left(m\right)$ time, on average, using $O\left(n\right)$ threads in [9].

In this paper, we present two parallel algorithms for the OPMPM problem. First, we parallelize the algorithm proposed in [1]. The preprocessing phase of the first algorithm runs in $O\left(\overline{m}\right)$ time using $O\left(M\right)$ threads and the search phase runs in $O(\overline{m}log\overline{m})$ time using $O(n/\overline{m})$ threads. Second, we parallelize the algorithm proposed in [8]. The preprocessing phase of the second algorithm runs in $O\left(\overline{m}\right)$ time using $O\left(M\right)$ threads and the search phase runs in $O\left(M\right)$ time using $O\left(n\right)$ threads. Then, we present experimental results that compare the execution times of each parallel algorithm for various types of time-series data. The experimental results showed that for randomly generated strings, when $n=$ 100,000, $m=9$, and $k=100$, the execution time of the first parallel algorithm was approximately 2.12 times faster than the sequential algorithm, and the second parallel algorithm was approximately 1.6 times faster than the sequential algorithm. For all time-series data used in our experiments, the execution time of our second parallel algorithm was comparable to that of a fast parallel algorithm proposed in [9].

This paper is organized as follows. In Section 2, we introduce the definitions of terms and related studies. In Section 3, we explain our parallel algorithms for the OPMPM problem. In Section 4, the execution times of parallel algorithms are compared through experiments. In Section 5, we conclude.

2. Related Works

Given string x, the length of x is denoted by $\left|x\right|$ and the i-th character of x$(1\le i\le |x\left|\right)$ is denoted by $x\left[i\right]$. The substring from $x\left[i\right]$ to $x\left[j\right]$ is denoted by $x[i..j]$ $(1\le i\le j\le |x\left|\right)$. $x[1..i]$ is called a prefix of x and $x[i..|x\left|\right]$ is called a suffix of x for $1\le i\le \left|x\right|$. For convenience, we assume that all the characters in the string are different. Given two strings $x,y$$\left(\right|x|=|y\left|\right)$, if $x\left[i\right]<x\left[j\right]\iff y\left[i\right]<y\left[j\right](1\le i,j\le |x\left|\right)$ is satisfied, and x and y are order-isomorphic and denoted by $x\approx y$ [1,4,10].

Let $x^{\prime }$ be the string constructed by sorting all the characters of x in ascending order. Then, the position table $PO{S}_x$ of x is defined as follows:

$$PO{S}_x\left[i\right]=j(x^{\prime }\left[i\right]=x\left[j\right],1\le i\le \left|x\right|).$$

That is, $PO{S}_x\left[i\right]$ is the index of the i-th smallest character in x. Given two strings $x,y$$\left(\right|x|=|y\left|\right)$, for all $i(1\le i<n)$, if $y\left[PO{S}_x\left[i\right]\right]\le y\left[PO{S}_x[i+1]\right]$ is satisfied, $x\approx y$ [8]. A prefix table ${\mu }_x$ of string x is defined as follows:

$${\mu }_x\left[i\right]=\left|\{j:x\left[j\right]<x\left[i\right],1\le j<i\}\right|+1.$$

That is, ${\mu }_x\left[i\right]$ represents the number of characters that are smaller than $x\left[i\right]$ in $x[1..i]$. If the prefix tables of two strings x and y are the same, that is, ${\mu }_x={\mu }_y$, $x\approx y$ [1]. Note that when there exist the same characters in the given string, order-isomorphism can still be determined using the extended prefix representation proposed in [2]. Table 1 presents the prefix table ${\mu }_x$ and position table $PO{S}_x$ when $x=(23,29,20,57,59)$.

Table 1. Prefix table and position table of $x=(23,29,20,57,59)$.

x	23	29	20	57	59
${\mu }_x\left[i\right]$	1	2	1	4	5
$PO{S}_x\left[i\right]$	3	1	2	4	5

In [7], an OPMPM algorithm was proposed using fingerprints of q-grams. The fingerprint converts a q-gram (a string of length q) into an integer within the range of $[1,q!]$ using the factorial number system [11,12]. The fingerprints are used to find candidate substrings of text T that may be order-isomorphic to pattern P. Given a q-gram x, fingerprint $f\left(x\right)$ is defined as follows [3,7]:

$$f\left(x\right)={\sum }_{k=1}^q[({\mu }_x\left[k\right]-1)\times (k-1)!]+1.$$

For example, if q-gram $x=(8,10,6)$, $f\left(x\right)=2$.

In [1], the Aho–Corasick automaton [6] is used to solve the order-preserving multiple pattern matching problem. In the preprocessing phase, the Aho–Corasick automaton is created in $O(Mlog\overline{m})$ time using a set of prefix tables of patterns. In each Step $i(1\le i\le n)$ of the search phase, the state for $T\left[i\right]$ is computed and $P_a(1\le a\le k)$ is searched in the automaton using the transition function, the failure function, and the output function of the automaton. Figure 1 shows the Aho–Corasick automaton when $P_1=(17,25,15,30)$, $P_2=(30,44,25,40)$, and $P_3=(40,50,61)$.

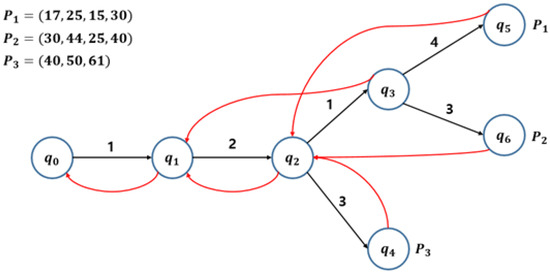
Figure 1. Example of the Aho–Corasick automaton for OPMPM.

Let $\widetilde{P_a}(1\le a\le k)$ be the prefix of length m for each pattern $P_a$ and let $\tilde{\mathbb{P}}=\left\{\widetilde{P_1},\widetilde{P_2},\dots ,\widetilde{P_k}\right\}$. Park et al. [8] proposed an OPMPM algorithm that generates the position table $PO{S}_{P_a}$ for each $P_a(1\le a\le k)$ and the fingerprint table $F{P}_a$ that stores the rightmost q-gram’s fingerprint of $\widetilde{P_a}(1\le a\le k)$ in the preprocessing phase, to find candidate patterns that may be order-isomorphic to substrings of T. In the search phase, all substrings of T, which are order-isomorphic to any $P_a(1\le a\le k)$, are searched using $F{P}_a$ and $PO{S}_{P_a}$.

3. Parallel Algorithms for the OPMPM Problem

In this section, we propose two parallel algorithms for the OPMPM problem. The first algorithm uses the Aho–Corasick automaton, while the second algorithm utilizes the position tables and fingerprint tables.

3.1. Parallel OPMPM Algorithm Using the Aho–Corasick Automaton

Our parallel algorithm for the OPMPM problem using the Aho–Corasick automaton consists of the following steps: In the preprocessing phase, we create prefix tables using $O\left(M\right)$ threads in $O\left(\overline{m}\right)$ time. That is, the prefix table of each pattern is calculated in parallel by assigning $|P_a|$ threads for each pattern $P_a(1\le a\le k)$. In the prefix table ${\mu }_{P_a}$ of pattern $P_a$, each thread $t(1\le t\le |P_a\left|\right)$ linearly searches $P_a[1..t-1]$ to calculate ${\mu }_{P_a}\left[t\right]$. See Algorithm 1. Thus, a set of prefix tables for all patterns can be calculated in $O\left(\overline{m}\right)$ time using $O\left(M\right)$ threads. To create an automaton using ${\mu }_{P_a}$, the existing algorithm [1] method is employed.

Algorithm 1 Preprocessing phase (parallel calculation of prefix tables for a pattern set).

Input: A set of strings $\left\{P_1,P_2,\dots ,P_k\right\}$ Output: A set of prefix tables $\left\{{\mu }_{P_1},{\mu }_{P_2},\dots ,{\mu }_{P_k}\right\}$ 1 parallel for $a\leftarrow 1$ to k do 2        parallel for $t\leftarrow 1$ to $|P_a|$ do 3               ${\mu }_{P_a}\left[t\right]\leftarrow 1$ 4                for $i\leftarrow 1$ to $t-1$ do 5                                if $P_a\left[i\right]<P_a\left[t\right]$ then 6                                  ${\mu }_{P_a}\left[t\right]\leftarrow {\mu }_{P_a\left[t\right]+1}$

In the search phase, T is divided into b blocks and each block is searched in parallel using b threads (Figure 2). Thread $t(1\le t\le b)$ searches each block of T for the location of the substring that is order-isomorphic to $P_a$ using the automaton created in the preprocessing phase. See Algorithm 2. Since the substring of T that is order-isomorphic to $P_a$ can occur across two adjacent blocks, all threads except the last one set the block size to $\lceil n/b\rceil +\overline{m}-1$ (Figure 2). Since the insertion, deletion, and rank calculation operations in the order-statistics tree require $O(log\overline{m})$ time during the search phase, they are conducted in $O((n/b+\overline{m})log\overline{m})$ time. If we set $b=\lceil n/\overline{m}\rceil$, the search phase can be conducted in $O(\overline{m}log\overline{m})$ time. Thus, this parallel algorithm can be solved as an OPMPM problem in $O(M+\overline{m}log\overline{m})$ time using $O\left(max(M,\lceil n/\overline{m}\rceil )\right)$ threads.

Algorithm 2 Search phase.

Input: Aho–Corasick automaton, string T Output: Positions i of substrings of T which is order-isomorphic to $P_a$ 1 $q_s\leftarrow q_0$, OST $\tau$, int r 2 parallel for $t\leftarrow 1$ to b do 3        for $i\leftarrow 1$ to $⌈n/b⌉+\overline{m}-1$ do 4                 if $(t-1)⌈n/b⌉+i>n$ then 5                         break 6                 $\tau$.insert$\left(T[(t-1)⌈n/b⌉+i)\right])$ 7                 $r\leftarrow \tau$.rank$\left(T[(t-1)⌈n/b⌉+i]\right)$ 8                 while $g(q_s,r)=fail$ 9                         $\tau$.delete$\left(T[i-d\left(q_s\right)..i-d\left(\pi \left(q_s\right)\right)-1]\right)$ 10                         $q_s\leftarrow \pi \left(q_s\right)$ 11                         $r\leftarrow \tau$.rank$\left(T[(t-1)⌈n/b⌉+i]\right)$ 12                 $q_s\leftarrow g(q_s,r)$ 13                 if $P_a\in out\left(q_s\right)$ and $i-|P_a|+1\le t⌈n/b⌉$ then 14                           print $(i-|P_a|+1,a)$

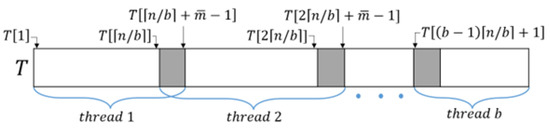
Figure 2. Search phase of the parallel OPMPM algorithm using the Aho–Corasick automaton.

3.2. Parallel OPMPM Algorithm Using the Fingerprint Table

The algorithm that solves the OPMPM problem using a fingerprint table in parallel is as follows: In the preprocessing phase, position table $PO{S}_{P_a}$ and fingerprint table $F{P}_a$ are created in parallel for each pattern of $P_a(1\le a\le k)$. The $PO{S}_{P_a}$ calculation is performed in parallel using $|P_a|$ threads. Each thread $t(1\le t\le |P_a\left|\right)$ linearly searches $P_a$ to calculate the order r of $P_a\left[t\right]$. By the definition of $PO{S}_{P_a}$, it satisfies $PO{S}_{P_a}\left[r\right]=t$, and the position tables for all patterns can be calculated in parallel in $O\left(\overline{m}\right)$ time using $O\left(M\right)$ threads. $F{P}_a$ is created in parallel using q threads (Algorithm 3). Each thread $t(1\le t\le q)$ calculates the fingerprint of $\widetilde{P_a}[m-q+1..m]$ in parallel. Here, atomic operations are used to prevent multiple threads from accessing $F{P}_a$ concurrently (Line 8 in Algorithm 3). Thus, the fingerprint table can be calculated in $O\left(q\right)$ time using $O\left(kq\right)$ threads, and the preprocessing phase is conducted in $O\left(\overline{m}\right)$ time using $O\left(M\right)$ threads.

In the search phase, all substrings of T are checked in parallel using $n-m+1$ threads (Algorithm 4). Each thread $i(1\le i\le n-m+1)$ first calculates $f\left(T\right[i+m-q..i+m-1\left]\right)$. $f\left(T\right[i+m-q..i+m-1\left]\right)$ and each of $F{P}_a(1\le a\le k)$ are sequentially compared, and if they are the same, it is verified whether $P_a$ and $T[i..i+\left|P_a\right|-1]$ are order-isomorphic using $PO{S}_{P_a}$ (from Lines 2 to 5 in Algorithm 4) [13]. If $P_a\approx T[i..i+\left|P_a\right|-1]$, then $(i,a)$ is printed. In the worst case, it verifies whether all substrings of T are order-isomorphic to all patterns. Thus, the search phase can be performed in $O\left(M\right)$ time using $O\left(n\right)$ threads. This parallel algorithm can be solved as an OPMPM problem in $O(\overline{m}+M)$ time using $O\left(max\right(M,n\left)\right)$ threads.

Algorithm 3 Parallel calculation of the fingerprint table. $FP$

Input: A set of strings $\left\{P_1,P_2,\dots ,P_k\right\}$, int m, int q Output: $F{P}_1,F{P}_2,\dots ,F{P}_k$ 1 parallel for $a\leftarrow 1$ to k do 2        parallel for $t\leftarrow 1$ to q do 3                $F{P}_a\leftarrow 1$ 4                $c\leftarrow 0$ 5                for $i\leftarrow 1$ to $t-1$ do 6                        if $P_a[m-q+i]<P_a[m-q+t]$ then 7                                 $c\leftarrow c+1$ 8                atomicAdd$(F{P}_a\leftarrow F{P}_a+c\times (t-1)!)$

Algorithm 4 The search phase of the algorithm using a fingerprint table.

Input: A string $T,F{P}_1,F{P}_2,\dots ,F{P}_k$, int m Output: Positions i of substrings of T which is order-isomorphic to $P_a$ 1 parallel for $i\leftarrow 1$ to $n-m+1$ do 2        for $a\leftarrow 1$ to k do 3                if $f\left(T[i+m-q..i+m-1]\right)=F{P}_a$ then 4                         if $P_a\approx T[i..i+\left|P_a\right|-1]$ then 5                                  print $(i,a)$

4. Experimental Results

The experiment was conducted on the following environment: Windows 10 (64-bit) operating system, AMD Ryzen9 3950X CPU, 64 GB RAM, NVIDIA GeForce RTX 3080 Ti GPU, C++ and CUDA programming language, and Visual Studio 2019 (CUDA SDK 11.0).

The algorithms experimented with in the present paper are denoted as follows: The OPMPM algorithm using the Aho–Corasick automaton proposed in [1] is denoted by $AC$, and the OPMPM algorithm using the fingerprint table proposed in [8] is denoted by $FT$. The parallel OPMPM algorithm proposed in [9] is denoted by $pKR$, the parallel OPMPM algorithm using the Aho–Corasick automaton proposed in this paper is denoted by $pAC$, and the parallel OPMPM algorithm using the fingerprint table is denoted by $pFT$, respectively.

The data used in the experiment are randomly generated strings and two types of time-series data: the Dow Jones Index and electrocardiogram data.

• Randomly generated strings: Texts and patterns consisting of $\sum =\left\{1,2,\dots ,2^{30}\right\}$ were randomly generated. Text T was generated by increasing length n from 10,000 by 10,000 to 100,000. A set of patterns P was generated by increasing the number of patterns k from 100 by 100 to 1000 and increasing the pattern length m from 5 by 1 to 15.
• Dow Jones Index: Texts and patterns were extracted at random for each experiment from the daily closing price of the Dow Jones Industrial Average between 2 May 1885 and 12 April 2019 [14]. The text length n was increased from 1000 by 1000 to 10,000. The number of patterns k and their length m were set to the same values used for the randomly generated strings.
• Electrocardiogram data: The electrocardiogram (ECG) data used in the experiment were obtained from the MIT-BIH ECG biosignal database provided by Physionet [15]. An electrocardiogram records the electrical impulses from the heart. Texts were randomly extracted from the total records, while patterns were extracted evenly from abnormal symptom data and normal data. It should be noted that the texts and patterns were extracted from electrocardiogram data of different individuals. The text length n and the number of patterns k were set equal to those of the randomly generated strings, and the pattern length m increased from 10 by 1 to 15 during the generation process.

The parameter setup of the algorithm and measurement of execution time were conducted as follows: In $FT$ and $pFT$, q was set to 5. In each of the parallel algorithms, $pAC$ employed 1000 threads, and $pKR$ and $pFT$ employed n threads. The execution time of each algorithm was the mean of 100 execution times, which was measured in milliseconds (ms) and rounded to three decimal places. The execution time of parallel algorithms includes the execution time of the cudaMemcpy() function that copies data between host memory and device (GPU) memory.

Experiment (1). Comparison of execution times of $AC$ and $pAC$, and $FT$ and $pFT$ for randomly generated strings: Figure 3 shows the execution times of $AC$ and $pAC$ for randomly generated strings according to n when $m=9$ and $k=100$. When n = 10,000, $pAC$ was slower than $AC$ due to the additional execution time required by the cudaMemcpy() function in $pAC$. Most of the execution time for $pAC$ was spent on the cudaMemcpy() function. However, for $n\ge$ 20,000, $pAC$ performed faster than $AC$. When $n=$ 100,000, $m=9$, and $k=100$, the execution time of $AC$ was around 41.22 ms and that of $pAC$ was around 19.49 ms, indicating that $pAC$ was approximately 2.12 times faster than $AC$. The execution time of $pAC$ increased as n increased due to the limitation of the number of available GPU cores. Figure 4 shows the execution times of $AC$ and $pAC$ for randomly generated strings according to k when $n=$ 100,000 and $m=9$. In this case, $pAC$ was faster than $AC$ in all cases.

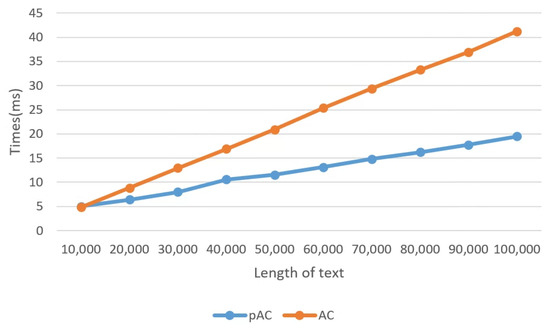
Figure 3. Comparison of execution times of $AC$ and $pAC$ varying n for randomly generated strings when $m=9$ and $k=100$.

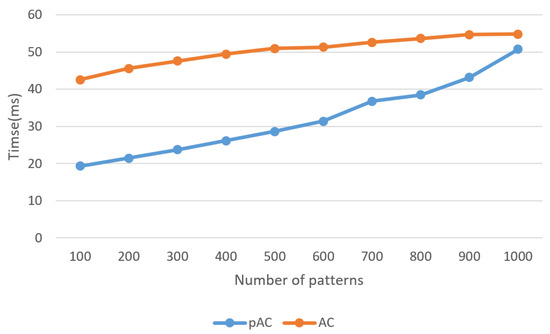
Figure 4. Comparison of execution times of $AC$ and $pAC$ varying k for randomly generated strings when $n=$ 100,000 and $m=9$.

Figure 5 shows the execution times of $FT$ and $pFT$ for randomly generated strings according to n when $m=9$ and $k=100$. $pFT$ was faster than $FT$ in all cases. For instance, when $n=$ 100,000, $m=9$, and $k=100$, the execution time of $FT$ was around 8.6 ms, while that of $pFT$ was around 5.39 ms, indicating that $pFT$ was approximately 1.6 times faster than $FT$. However, as with $pAC$, the execution time of $pFT$ also increased as n increased due to the limitation of the number of available GPU cores. Figure 6 shows the execution times of $FT$ and $pFT$ for randomly generated strings according to k when $n=$ 100,000 and $m=9$. In this case, as in the previous case, $pFT$ was faster than $FT$ in all cases.

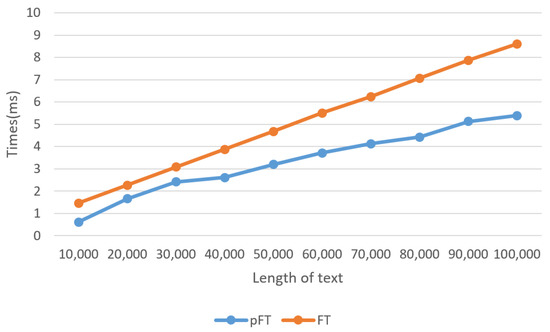
Figure 5. Comparison of execution times of $FT$ and $pFT$ according to n for randomly generated strings when $m=9$ and $k=100$.

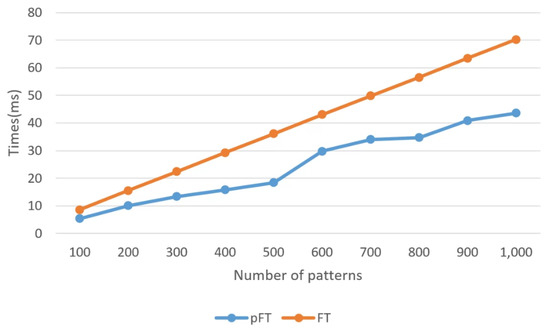
Figure 6. Comparison of execution times of $FT$ and $pFT$ according to k for randomly generated strings when $n=$ 100,000 and $m=9$.

Experiment (2). Comparison of execution times of $pKR$, $pAC$, and $pFT$ for randomly generated strings: Table 2 presents the execution times of $pKR$, $pAC$, and $pFT$ for randomly generated strings with varying parameter settings. In all cases, $pKR$ and $pFT$ performed faster than $pAC$, and $pKR$ and $pFT$ exhibited comparable execution times. When $n=$ 100,000, $m=9$, and $k=1000$, the execution times of $pKR$ and $pFT$ were approximately 1.98 and 2.03 times faster, respectively, than those of pAC.

Table 2. Comparison of execution times of $pAC$, $pKR$, and $pFT$ for random strings.

(a) Comparison of execution times varying m when $n=$ 100,000, $k=1000$
	Execution times of the algorithms (unit: ms)
m	$pAC$	$pKR$	$pFT$
6	41.31	21.58	22.62
9	44.83	22.64	21.98
12	49.07	22.18	22.51
15	52.49	22.16	22.52
(b) Comparison of execution times varying k when $n=$ 100,000, $m=9$
	Execution times of the algorithms (unit: ms)
k	$pAC$	$pKR$	$pFT$
100	19.35	2.22	2.24
500	31.07	11.25	11.47
1000	44.83	22.64	21.98

Table 2a presents the execution times of $pKR$, $pAC$, and $pFT$ according to m when $n=$ 100,000 and $k=1000$. As the length of patterns m increased, the creation time of the Aho–Corasick automaton increased, leading to an increase in the total execution time of $pAC$. The length of patterns m did not significantly affect the execution times of $pFT$ and $pKR$. Table 2b presents the execution times of $pKR$, $pAC$, and $pFT$ according to k when $n=$ 100,000 and $m=9$. The execution times of all algorithms increased as k increased.

Experiment (3). Comparison of execution times of $pKR$, $pAC$, and $pFT$ for Dow Jones Index data: Table 3 presents the execution times of $pKR$, $pAC$, and $pFT$ according to the parameters for Dow Jones Index data. In all conditions, $pKR$ and $pFT$ performed faster than $pAC$, and $pKR$ and $pFT$ exhibited comparable execution times. When $n=$ 10,000, $m=9$, and $k=1000$, the execution times of $pKR$ and $pFT$ were around 5.61 times and 5.71 times faster than that of $pAC$. Overall, it showed a similar trend to that of Experiment 2.

Table 3. Comparison of execution times of $pAC$, $pKR$, and $pFT$ for Dow Jones Index data.

(a) Comparison of execution times varying m when $n=$ 10,000, $k=1000$
	Execution times of the algorithms (unit: ms)
m	$pAC$	$pKR$	$pFT$
6	9.58	2.29	2.55
9	12.84	2.29	2.25
12	16.35	2.22	2.25
15	20.33	2.34	2.45
(b) Comparison of execution times varying k when $n=$ 10,000, $m=9$
	Execution times of the algorithms (unit: ms)
k	$pAC$	$pKR$	$pFT$
100	5.03	0.49	0.47
500	8.52	1.35	1.38
1000	12.84	2.29	2.25

Experiment (4). Comparison of execution times of $pKR$, $pAC$, and $pFT$ for ECG data: Table 4 presents the execution times of $pKR$, $pAC$, and $pFT$ according to the parameters for electrocardiogram data. In all cases, $pKR$ and $pFT$ performed faster than $pAC$, and $pKR$ and $pFT$ exhibited comparable execution times. When $n=$ 100,000, $m=10$, and $k=1000$, the execution times of $pKR$ and $pFT$ were around 2.13 times and 2.16 times faster than that of $pAC$. Overall, it showed a similar result to that of Experiments 2 and 3.

Table 4. Comparison of execution times of $pAC$, $pKR$, and $pFT$ for ECG data.

(a) Comparison of execution times varying m when $n=$ 100,000, $k=1000$
	Execution times of the algorithms (unit: ms)
m	$pAC$	$pKR$	$pFT$
10	41.18	19.32	19.08
12	42.6	18.68	19.03
15	44.83	18.82	18.31
(b) Comparison of execution times varying k when $n=$ 100,000, $m=10$
	Execution times of the algorithms (unit: ms)
k	$pAC$	$pKR$	$pFT$
100	18.57	2.32	2.29
500	28.23	9.89	9.46
1000	41.18	19.32	19.08

5. Conclusions

In this paper, a parallel OPMPM algorithm using the Aho–Corasick automaton and a parallel OPMPM algorithm using a fingerprint table were proposed. In addition, comparison experiments were conducted for randomly generated strings, Dow Jones Index data, and electrocardiogram data to evaluate the performance of the proposed parallel algorithms. The experimental results showed that the execution times of the algorithms had a similar trend regardless of the data type when data-related parameters such as the length of the text, lengths of the patterns, and the number of patterns, as well as algorithm-related parameters such as the q-gram length, were kept the same. This suggests that the performance of the algorithms is dependent on these parameters rather than the specific characteristics of the data type. The performance of the verification of order-isomorphism may vary depending on the order representation method of strings used [16]. Therefore, further studies are necessary to compare the execution times and number of verifications required for different-order representation methods.