Dynamic Characteristics of a Composite Beam with Viscoelastic Layers under Uncertain-But-Bounded Design Parameters
Abstract
1. Introduction
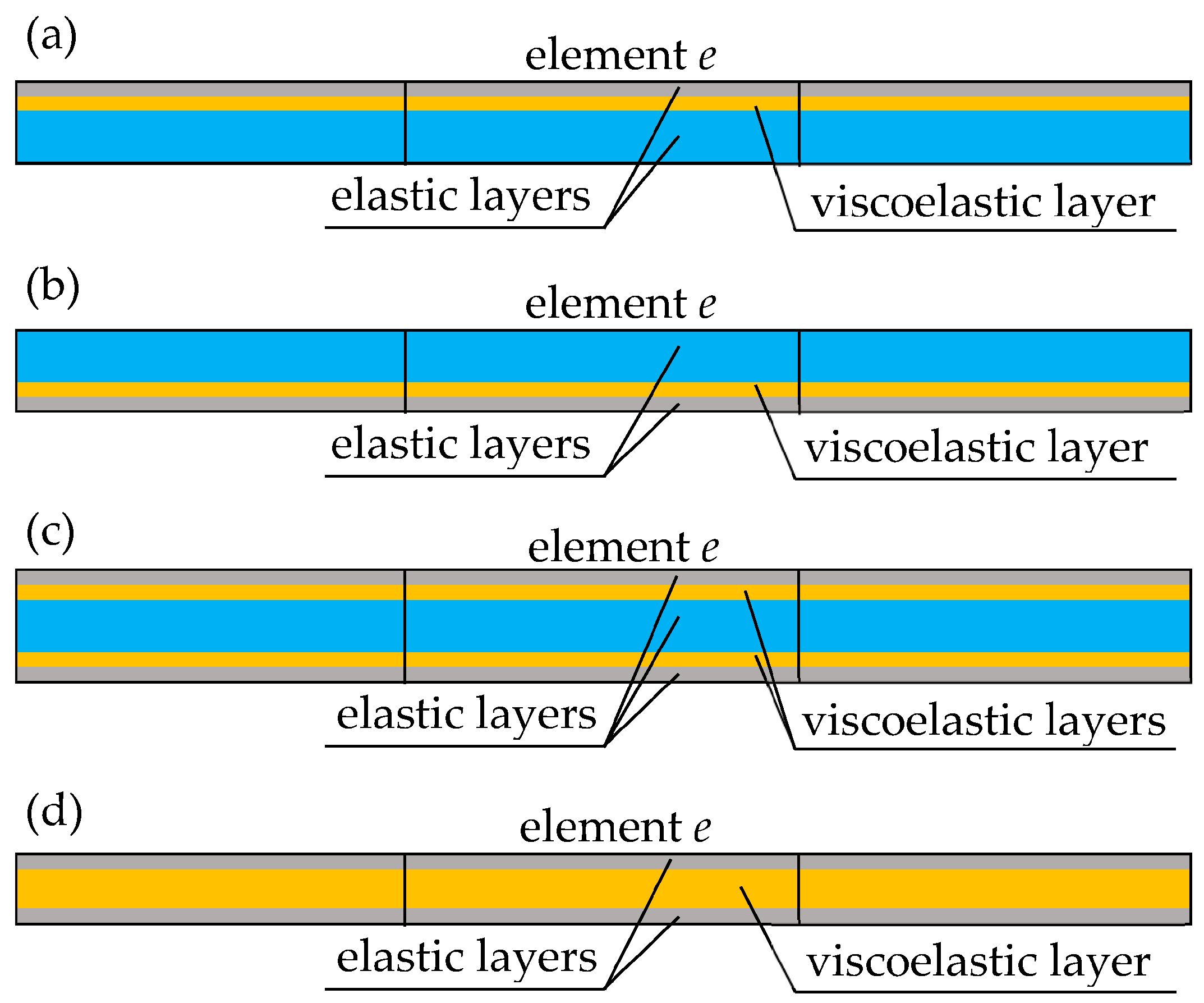
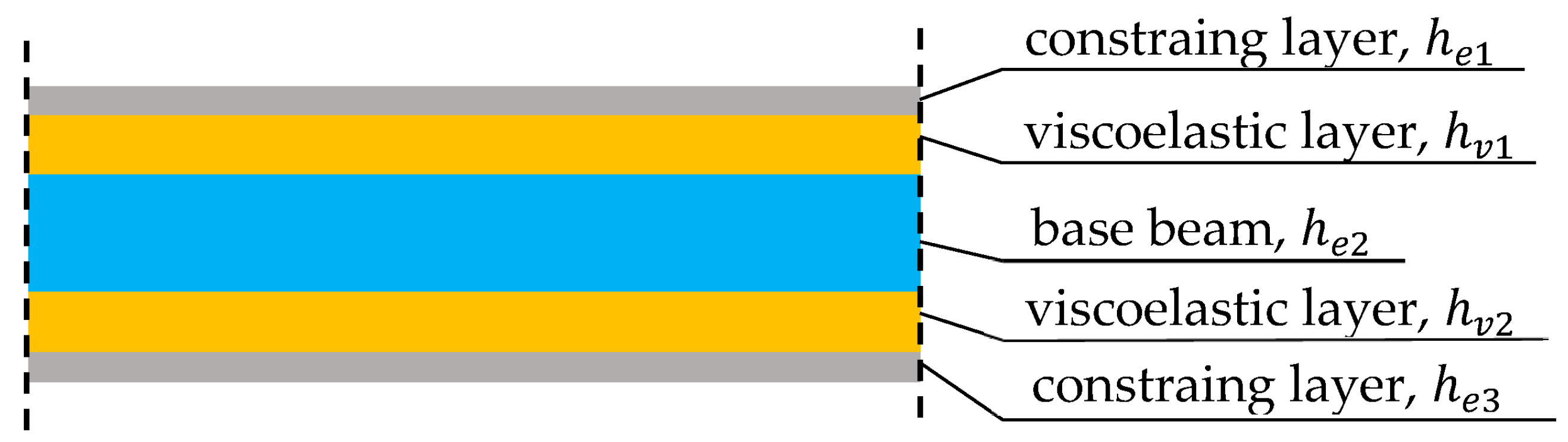
2. Finite Element Formulation of Composite Beam with Viscoelastic Layers
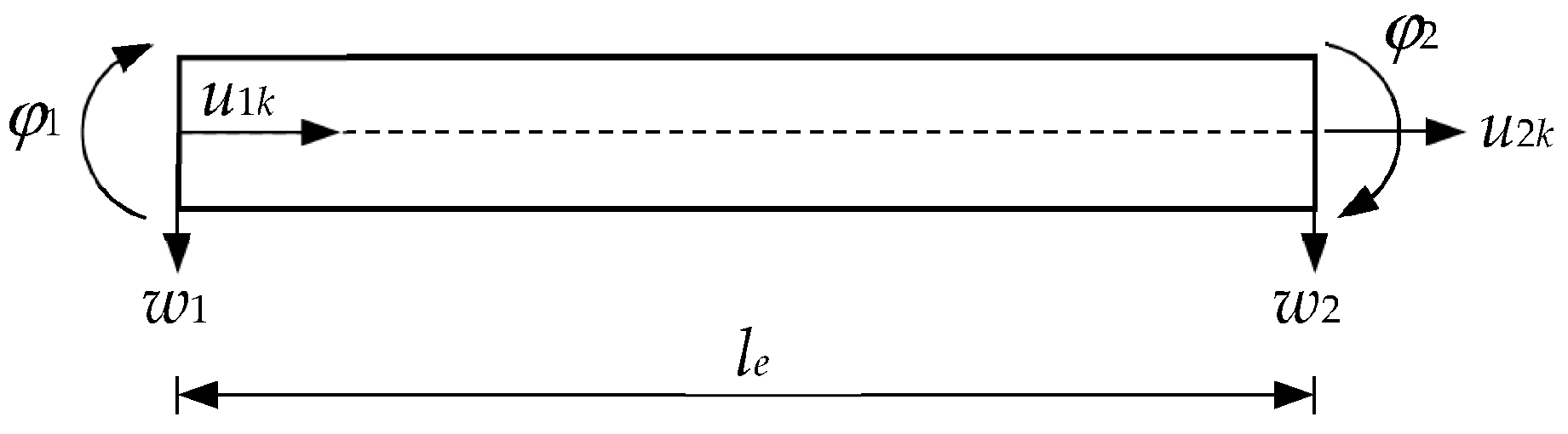
2.1. Elastic Layers
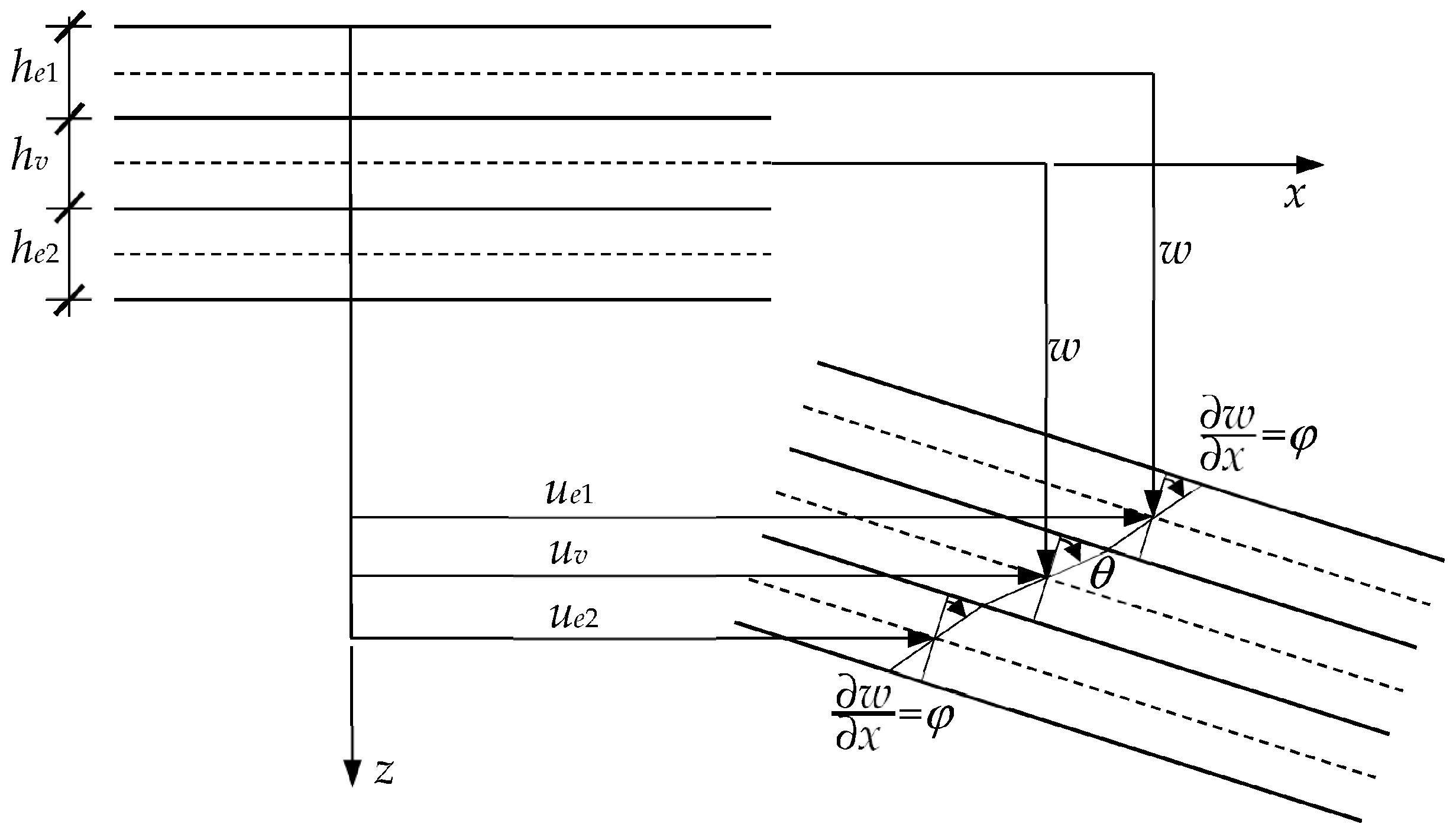
2.2. Viscoelastic Layer
2.3. Matrix Formulation of Equation of Motion for Composite Beam
2.4. Dynamic Characteristics of Composite Beam
3. Uncertain Design Parameters
3.1. Interval Analysis
3.2. Approximation of the Lower and Upper Bounds of Objective Function Based on Taylor Series Expansion
3.3. Vertex Method
4. Algorithm for Determining Critical Combinations of Parameters
| Algorithm 1: Determining the critical combination of parameters. |
| 1° Input data: r—number of uncertain parameters —vector of lower bounds of uncertain parameters —vector of upper bounds of uncertain parameters —vector of middle values of uncertain parameters 2° set n:= r set ( denotes parameter vector for the critical combination) 3° for i = 1,2,…,n calculate sensitivities of the response function with respect to change in parameter (sensitivities of the first order) and (sensitivities of the second order) 4° for i = 1,2,…,n calculate the increment in response function according to Equation (37) for and 5° select the maximum value of and corresponding parameter 6° substitute 7° exclude parameter and its lower and upper bounds from futher calculations 8° update n:=n − 1 9° repeat steps 3° to 8° until n = 0 10° calculate the maximum value of the response function for the critical combination of parameters . |
5. Examples
5.1. Veryfication Example
5.2. The Influence of the Layer Height Uncertainty
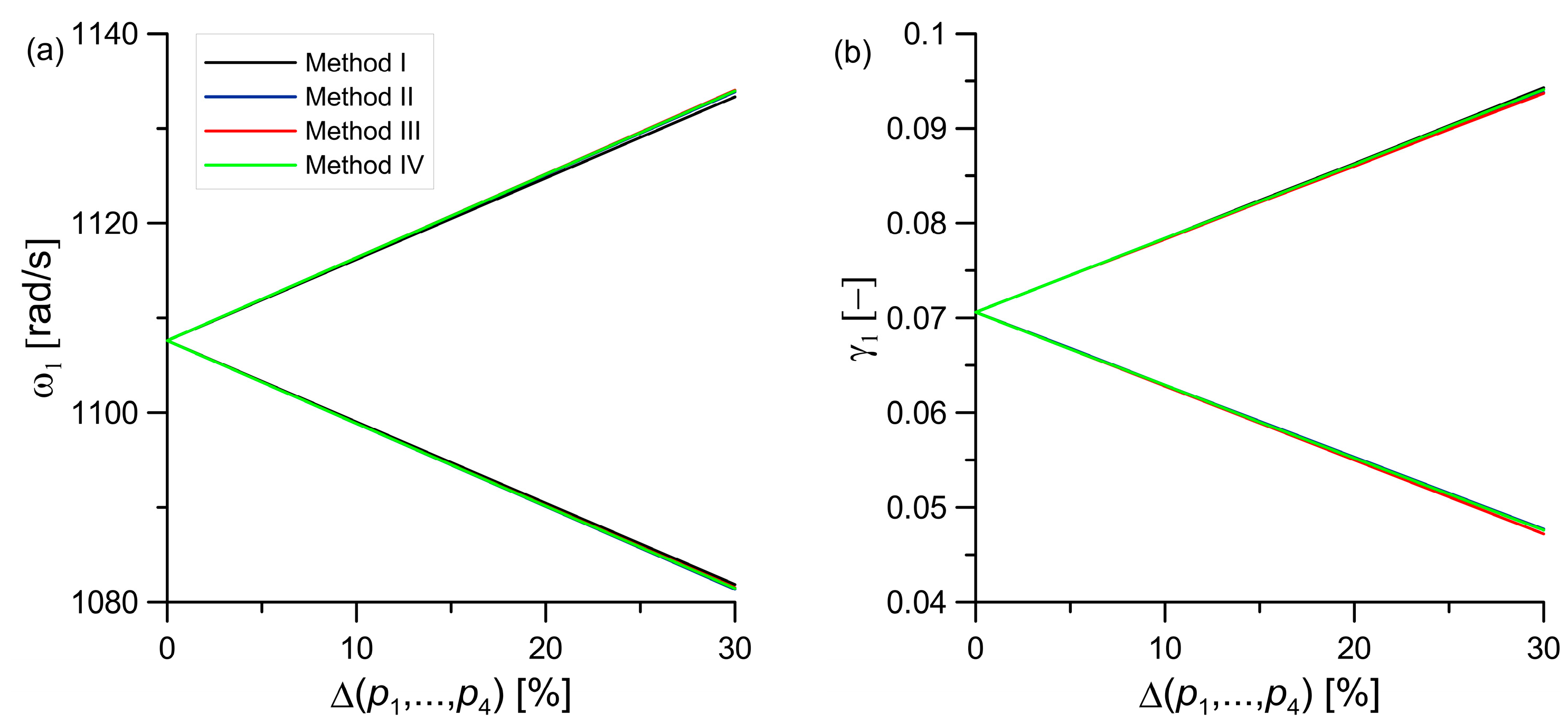
5.3. The Influence of the Parameters and of the Viscoelastic Layers
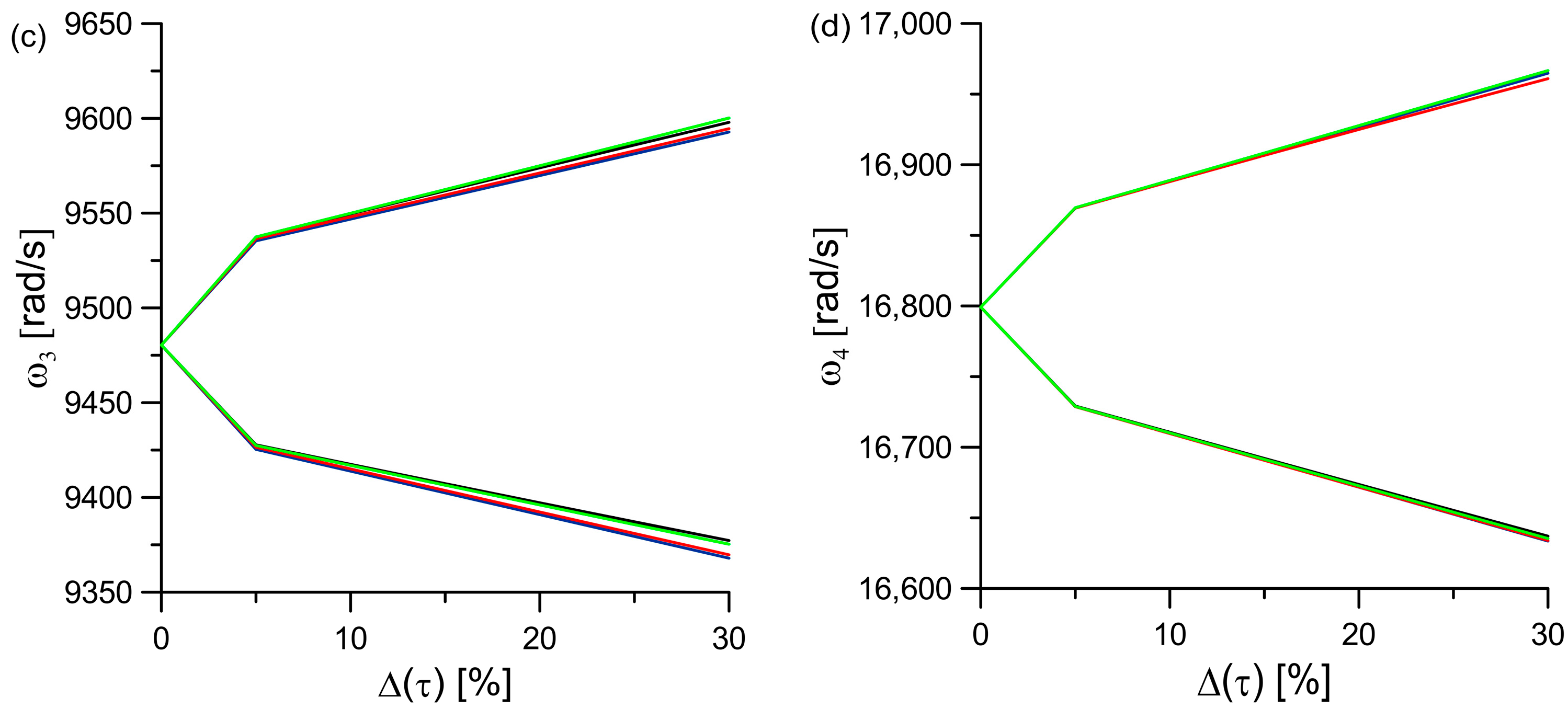
5.4. The Influence of the Parameters α and τ of the Viscoelastic Layers
5.5. Comparison of Methods
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fishman, G.S. Monte Carlo: Concepts, Algorithms and Applications; Springer-Verlag: Berlin, Germany, 1996. [Google Scholar]
- Kleiber, M.; Hien, H.D. The Stochastic Finite Element Method: Basic Perturbation Technique and Computer Implementation; John-Wiley & Sons: Chichester, UK, 1992. [Google Scholar]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer: New York, NY, USA, 1991. [Google Scholar]
- Elishakoff, I.; Ohsaki, M. Optimization and Anti-Optimization of Structures under Uncertainties; Imperial College Press: London, UK, 2010. [Google Scholar]
- Moore, R.E. Methods and Applications of Interval Analysis; Prentice Hall: London, UK, 1979. [Google Scholar]
- Dimarogonas, A.D. Interval analysis of vibrating systems. J. Sound Vib. 1995, 183, 739–749. [Google Scholar] [CrossRef]
- Yang, X. Interval finite element based on the element for eigenvalue analysis of structures with interval parameters. Struct. Eng. Mech. 2001, 12, 669–684. [Google Scholar] [CrossRef]
- Chen, S.H.; Lian, H.D.; Yang, W.Y. Interval eigenvalue analysis for structures with interval parameters. Finite Elem. Anal. Des. 2003, 39, 419–431. [Google Scholar] [CrossRef]
- Chen, S.H.; Lian, H.D. Dynamic response analysis for structures with interval parameters. Struct. Eng. Mech. 2002, 13, 299–312. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, X. Parameter perturbation method for dynamic responses of structures with uncertain-but-bounded parameters based on interval analysis. Int. J. Solids Struct. 2005, 42, 4958–4970. [Google Scholar] [CrossRef]
- Sim, J.; Qiu, Z.; Wang, X. Modal analysis of structures with uncertain-but-bounded parameters via interval analysis. J. Sound Vib. 2007, 303, 29–45. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, X. Vertex solution theorem for the upper and lower bounds on the dynamic response of structures with uncertain-but-bounded parameters. Acta Mech. Sin. 2009, 25, 367–379. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, P. Parameter vertex method and its parallel solution for evaluating the dynamic response bounds of structures with interval parameters. Sci. China Phys. Mech. Astron. 2018, 61, 064612. [Google Scholar] [CrossRef]
- Madares, M.; Asce, M.; Mullen, R.L.; Asce, F.; Muhanna, R.L.; Asce, M. Natural frequencies of a structure with bounded uncertainty. J. Eng. Mech. 2006, 132, 1363–1371. [Google Scholar] [CrossRef]
- Yaowen, Y.; Zhenhan, C.; Yu, L. Interval analysis of frequency response functions of structures with uncertain parameters. Mech. Res. Commun. 2013, 47, 24–31. [Google Scholar] [CrossRef]
- Yaowen, Y.; Zhenhan, C.; Yu, L. Interval analysis of dynamic response of structures using Laplace transform. Probabilistic Eng. Mech. 2012, 29, 32–39. [Google Scholar]
- Muscolino, G.; Santoro, R.; Sofi, A. Explicit frequency response functions of discretized structures with uncertain parameters. Comput. Struct. 2014, 133, 64–78. [Google Scholar] [CrossRef]
- Feng, X.; Wu, J.; Zhang, Y. Time response of structure with interval and random parameters using a new hybrid uncertain analysis method. Appl. Math. Model. 2018, 64, 426–452. [Google Scholar] [CrossRef]
- Li, Q.; Han, J.; Yang, J.; Guo, X. The exact extreme response and the confidence extreme response analysis of structures subjected to uncertain-but-bounded excitations. Appl. Math. Model. 2020, 77, 1742–1761. [Google Scholar] [CrossRef]
- Qiu, Z.; Ni, Z. Interval modal superposition method for impulsive response of structures with uncertain-but-bounded external loads. Appl. Math. Model. 2011, 35, 1538–1550. [Google Scholar] [CrossRef]
- Wei, T.; Li, F.; Meng, G. A bivariate Chebyshev polynomials method for nonlinear dynamic systems with interval uncertainties. Nonlinear Dyn. 2022, 107, 793–811. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, L.; Wang, X. Non-probabilistic interval analysis method for dynamic response analysis of nonlinear systems with uncertainty. J. Sound Vib. 2009, 319, 531–540. [Google Scholar] [CrossRef]
- Chen, S.H.; Ma, L.; Meng, G.W.; Guo, R. An efficient method for evaluating the natural frequencies of structures with uncertain-but-bounded parameters. Comput. Struct. 2009, 87, 582–590. [Google Scholar] [CrossRef]
- Fujita, K.; Takewaki, I. An efficient methodology for robustness evaluation by advanced interval analysis using updated second-order Taylor series expansion. Eng. Struct. 2011, 33, 3299–3310. [Google Scholar] [CrossRef]
- Łasecka-Plura, M.; Lewandowski, R. Dynamic characteristics and frequency response function for frame with dampers with uncertain design parameters. Mech. Based Des. Struct. Mach. 2017, 45, 296–312. [Google Scholar] [CrossRef]
- Kamiński, M.; Lenartowicz, A.; Guminiak, M.; Przychodzki, M. Selected problems of random free vibrations of rectangular thin plates with viscoelastic dampres. Materials 2022, 15, 6811. [Google Scholar] [CrossRef]
- Muscolino, G.; Sofi, A. Stochastic analysis of structures with uncertain-but-bounded parameters via improved interval analysis. Probabilistic Eng. Mech. 2012, 28, 152–163. [Google Scholar] [CrossRef]
- Wang, C.; Gao, W.; Song, C.; Zhang, N. Stochastic interval analysis of natural frequency and mode shape of structures with uncertainties. J. Sound Vib. 2014, 333, 2483–2503. [Google Scholar] [CrossRef]
- Tian, W.; Chen, W.; Ni, B.; Jiang, C. A single-loop method for reliability-based design optimization with interval distribution parameters. Comput. Methods Appl. Mech. Eng. 2022, 391, 114372. [Google Scholar] [CrossRef]
- Jiang, C.; Han, X.; Guan, F.J.; Li, Y.H. An uncertain structural optimization method based on nonlinear interval number programming and interval analysis method. Eng. Struct. 2007, 29, 3168–3177. [Google Scholar] [CrossRef]
- Meggitt, J.W.R. Interval-based identification of response-critical joints: A tool for model refinement. J. Sound Vib. 2022, 529, 116850. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Li, Y.; Lin, G.; Qiu, Z. Structural time-dependent reliability assessment of the vibration active control system with unknown-but-bounded uncertainties. Struct. Control. Health Monit. 2017, 24, e1965. [Google Scholar] [CrossRef]
- Hernandez, W.P.; Castello, D.A.; Ritto, T.G. Uncertainty propagation analysis in laminated structures with viscoelastic core. Comput. Struct. 2016, 164, 23–37. [Google Scholar] [CrossRef]
- Galucio, A.C.; Deu, J.F.; Ohayon, R. Finite element formulation of viscoelastic sandwich beams using fractional derivative operators. Comput. Mech. 2004, 33, 282–291. [Google Scholar] [CrossRef]
- Lewandowski, R.; Baum, M. Dynamic characteristics of multilayered beams with viscoelastic layers described by the fractional Zener model. Arch. Appl. Mech. 2015, 85, 1793–1814. [Google Scholar] [CrossRef]
- Pawlak, Z.; Lewandowski, R. The continuation method for the eigenvalue problem of structures with viscoelastic dampers. Comput. Struct. 2013, 125, 53–61. [Google Scholar] [CrossRef]
- Łasecka-Plura, M.; Lewandowski, R. The subspace iteration method for nonlinear eigenvalue problems occurring in the dynamics of structures with viscoelastic elements. Comput. Struct. 2021, 254, 106571. [Google Scholar] [CrossRef]
- Lewandowski, R.; Łasecka-Plura, M. Design sensitivity analysis of structures with viscoelastic dampers. Comput. Struct. 2016, 164, 95–107. [Google Scholar] [CrossRef]
- Łasecka-Plura, M.; Lewandowski, R. Sensitivity analysis of dynamic characteristics of composite beams with viscoelastic layers. Procedia Eng. 2017, 199, 366–371. [Google Scholar] [CrossRef]
- Łasecka-Plura, M. A comparative study of the sensitivity analysis for systems with viscoelastic elements. Arch. Mech. Eng. 2023, 70, 5–25. [Google Scholar]


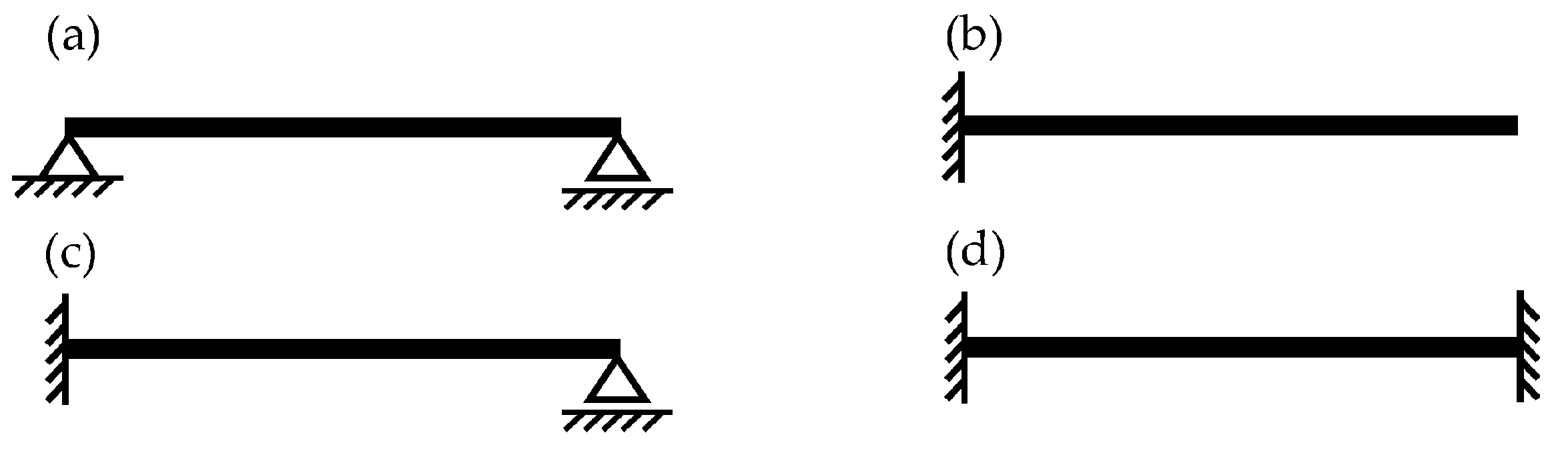




| Method | Characteristics/Advantages and Disadvantages |
|---|---|
| Probabilistic methods [1,2,3] | Parameters are assumed as random variables, and their probability distributions are estimated based on available data. Advantage:
|
| Fuzzy theory methods [4] | Parameters are described as fuzzy sets. Advantage:
|
| Methods based on interval analysis [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,29,30,31,32] | Parameters are modeled as intervals with uncertain-but-bounded values. Advantages:
|
| Hybrid methods [27,28] | A combination of different methods, such as probabilistic, fuzzy, or interval-based. |
| Dynamic Characteristics | Mode | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Natural frequency (present paper) [rad/s] | 404.875 | 1336.507 | 2860.876 | 4990.735 |
| Natural frequency [35] [rad/s] | 404.879 | 1336.560 | 2861.150 | 4991.590 |
| Nondimensional damping ratio (present paper) [-] | 0.1378 | 0.1343 | 0.1184 | 0.1042 |
| Nondimensional damping ratio [35] [-] | 0.1378 | 0.1343 | 0.1184 | 0.1042 |
| Static Scheme | Natural Frequency ω1 [rad/s] | Nondimensional Damping Ratio γ1 [-] |
|---|---|---|
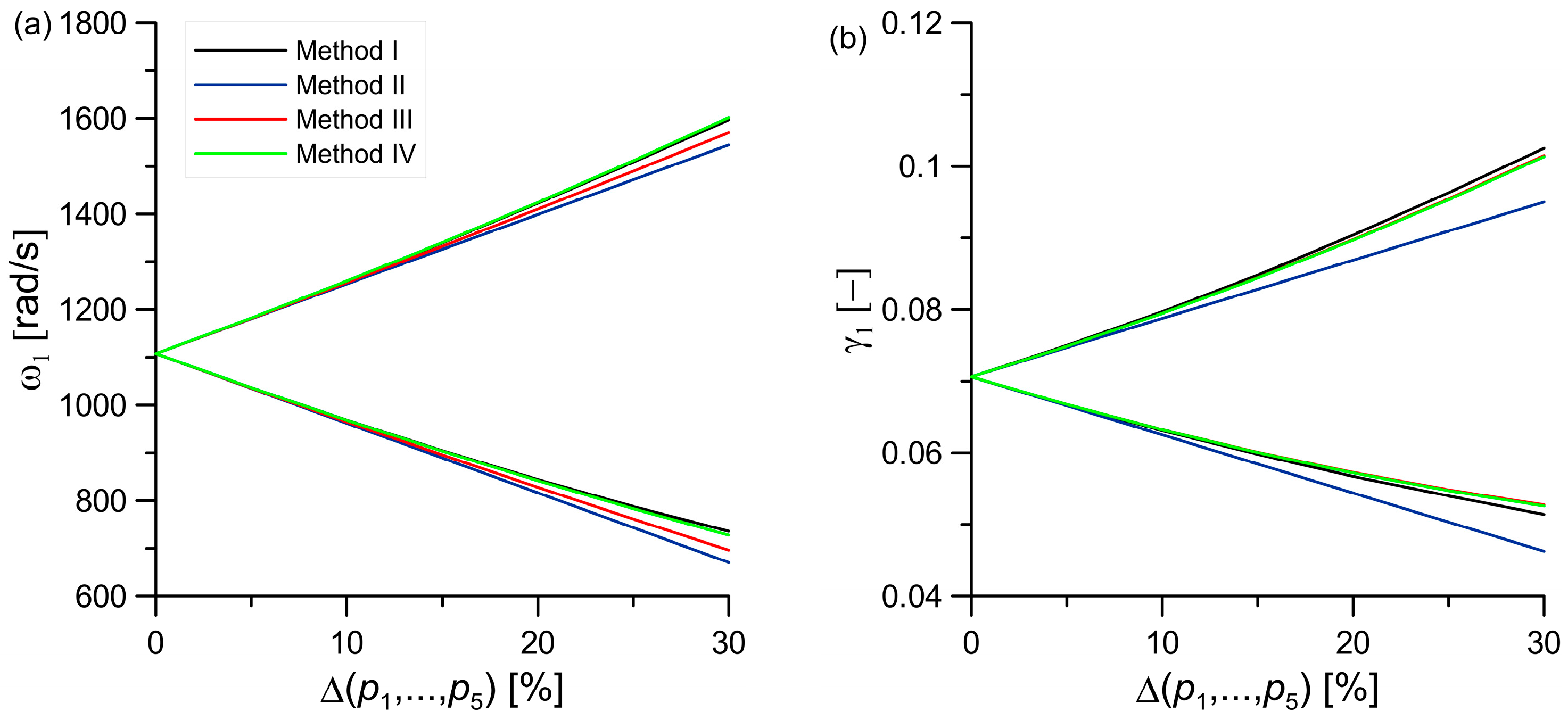
| (a) Simply supported | 1107.60 | 0.0706 |
| (b) Cantilever | 443.36 | 0.0879 |
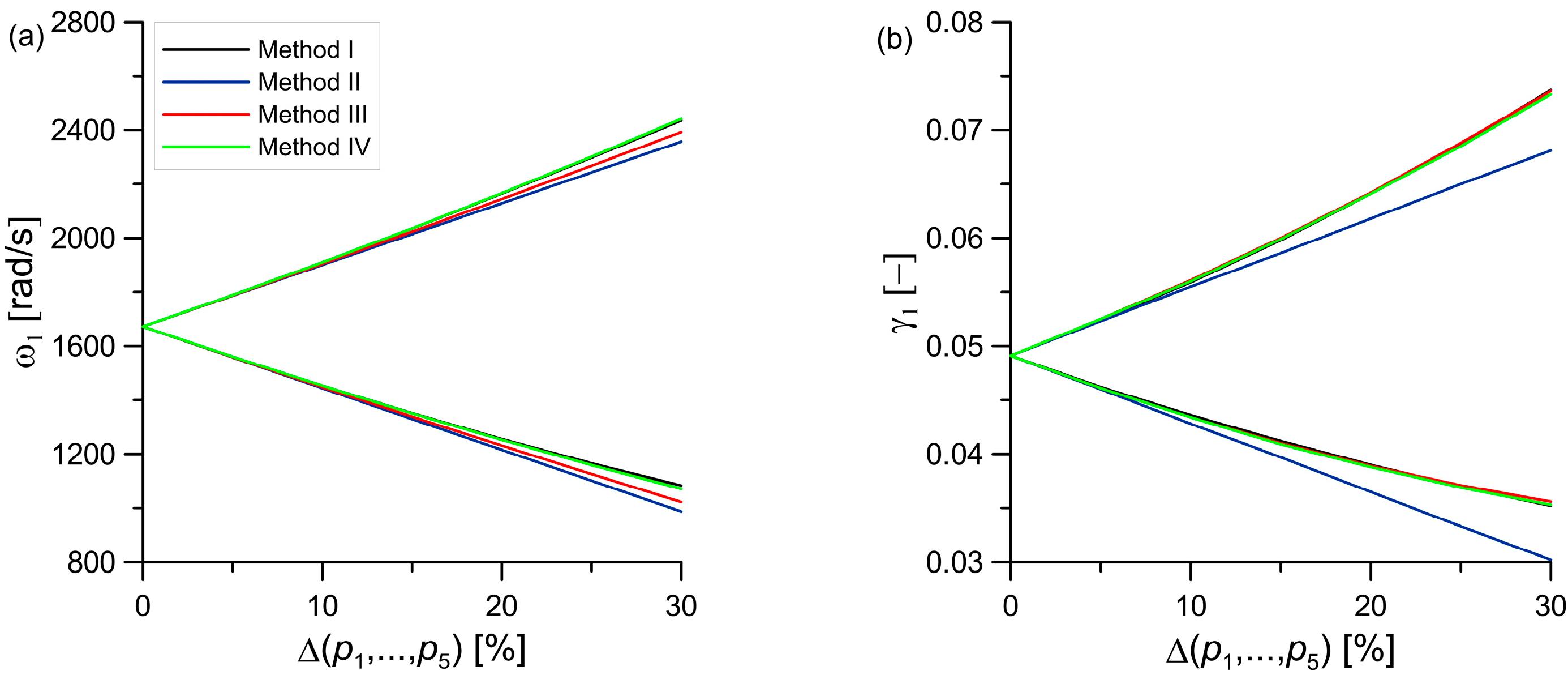
| (c) Fixed-pinned | 1672.05 | 0.0491 |
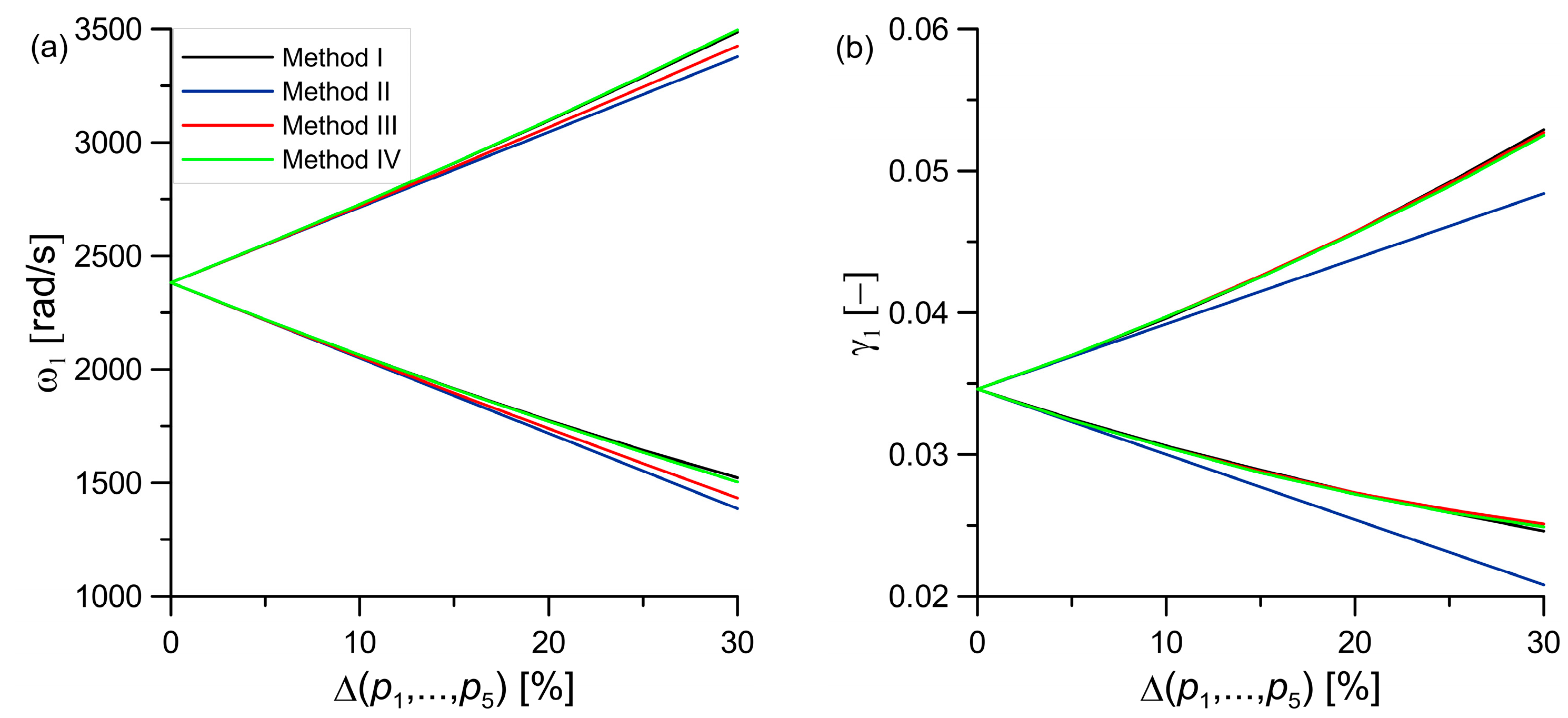
| (d) Fixed-fixed | 2381.97 | 0.0346 |
| Uncertainties of Parameters | Layer Height [m] |
|---|---|
| 5% | |
| 30% |
| Bounds | Methods | Natural Frequency [rad/s] | Error [%] | Combination of Parameters |
|---|---|---|---|---|
| lower upper | 968.63 1259.25 | Comparative method | ||
| lower upper | II | 962.53 1252.67 | 0.63 0.52 | |
| lower upper | III | 965.42 1255.55 | 0.33 0.29 | |
| lower upper | IV | 968.83 1258.96 | 0.02 0.02 | |
| lower upper | V | 968.63 1259.25 | 0.00 0.00 |
| Bounds | Methods | Natural Frequency [rad/s] | Error [%] | Combination of Parameters |
|---|---|---|---|---|
| lower upper | 735.89 1597.05 | Comparative method | ||
| lower upper | II | 672.40 1542.80 | 8.63 3.40 | |
| lower upper | III | 698.38 1568.77 | 5.10 1.77 | |
| lower upper | IV | 729.02 1599.42 | 0.93 0.15 | |
| lower upper | V | 735.89 1597.05 | 0.00 0.00 |
| Uncertainties of Parameters | Design Parameters [Pa] |
|---|---|
| 5% | |
| 30% |
| Uncertainties of Parameters | Design Parameters |
|---|---|
| 5% | |
| 30% |
| Bounds | Methods | Natural Frequency [rad/s] | Error [%] | Combination of Parameters |
|---|---|---|---|---|
| Lower Upper | 1096.63 1122.06 | Comparative method | ||
| Lower Upper | II | 1094.99 1120.21 | 0.15 0.16 | |
| Lower Upper | III | 1096.26 1121.49 | 0.03 0.05 | |
| Lower Upper | IV | 1096.69 1121.91 | 0.01 0.01 | |
| Lower Upper | V | 1096.63 1122.06 | 0.00 0.00 |
| Bounds | Methods | Natural Frequency [rad/s] | Error [%] | Combination of Parameters |
|---|---|---|---|---|
| Lower Upper | 1082.70 1163.71 | Comparative method | ||
| Lower Upper | II | 1069.76 1145.44 | 1.19 1.57 | |
| Lower Upper | III | 1081.24 1156.91 | 0.13 0.58 | |
| Lower Upper | IV | 1085.08 1160.76 | 0.22 0.25 | |
| Lower Upper | V | 1082.70 1163.71 | 0.00 0.00 |
| Bounds | Methods | Natural Frequency [rad/s] | Error [%] | Combination of Parameters |
|---|---|---|---|---|
| Lower Upper | 1075.97 1124.08 | Comparative method | ||
| Lower Upper | II | 1044.54 1170.66 | 2.92 4.36 | |
| Lower Upper | III | 1076.42 1202.54 | 0.04 1.76 | |
| Lower Upper | IV | 1080.85 1213.22 | 0.45 0.89 | |
| Lower Upper | V | 1075.97 1124.08 | 0.00 0.00 |
| Bounds | Methods | Natural Frequency [rad/s] | Error [%] | Combination of Parameters |
|---|---|---|---|---|
| Lower Upper | 1075.87 1227.85 | Comparative method | ||
| Lower Upper | II | 1043.03 1172.17 | 3.05 4.53 | |
| Lower Upper | III | 1074.90 1204.05 | 0.09 1.94 | |
| Lower Upper | IV | 1080.22 1216.86 | 0.40 0.89 | |
| Lower Upper | V | 1075.87 1227.85 | 0.00 0.00 |
| Methods | Number of Combinations | Number of Eigenproblems to Be Solved for the New Parameter Values |
|---|---|---|
| II | 2r | 1 |
| III | 2r | 1 |
| IV | 1 | |
| V | r(r + 1) | r + 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łasecka-Plura, M. Dynamic Characteristics of a Composite Beam with Viscoelastic Layers under Uncertain-But-Bounded Design Parameters. Appl. Sci. 2023, 13, 6473. https://doi.org/10.3390/app13116473
Łasecka-Plura M. Dynamic Characteristics of a Composite Beam with Viscoelastic Layers under Uncertain-But-Bounded Design Parameters. Applied Sciences. 2023; 13(11):6473. https://doi.org/10.3390/app13116473
Chicago/Turabian StyleŁasecka-Plura, Magdalena. 2023. "Dynamic Characteristics of a Composite Beam with Viscoelastic Layers under Uncertain-But-Bounded Design Parameters" Applied Sciences 13, no. 11: 6473. https://doi.org/10.3390/app13116473
APA StyleŁasecka-Plura, M. (2023). Dynamic Characteristics of a Composite Beam with Viscoelastic Layers under Uncertain-But-Bounded Design Parameters. Applied Sciences, 13(11), 6473. https://doi.org/10.3390/app13116473






