Aquila Optimizer with Bayesian Neural Network for Breast Cancer Detection on Ultrasound Images

Abstract

Breast cancer is the second most dominant kind of cancer among women. Breast Ultrasound images (BUI) are commonly employed for the detection and classification of abnormalities that exist in the breast. The ultrasound images are necessary to develop artificial intelligence (AI) enabled diagnostic support technologies. For improving the detection performance, Computer Aided Diagnosis (CAD) models are useful for breast cancer detection and classification. The current advancement of the deep learning (DL) model enables the detection and classification of breast cancer with the use of biomedical images. With this motivation, this article presents an Aquila Optimizer with Bayesian Neural Network for Breast Cancer Detection (AOBNN-BDNN) model on BUI. The presented AOBNN-BDNN model follows a series of processes to detect and classify breast cancer on BUI. To accomplish this, the AOBNN-BDNN model initially employs Wiener filtering (WF) related noise removal and U-Net segmentation as a pre-processing step. Besides, the SqueezeNet model derives a collection of feature vectors from the pre-processed image. Next, the BNN algorithm will be utilized to allocate appropriate class labels to the input images. Finally, the AO technique was exploited to fine-tune the parameters related to the BNN method so that the classification performance is improved. To validate the enhanced performance of the AOBNN-BDNN method, a wide experimental study is executed on benchmark datasets. A wide-ranging experimental analysis specified the enhancements of the AOBNN-BDNN method in recent techniques.

1. Introduction

Despite substantial technological advancements, cancer detection at an initial stage remains a challenging one, and present cancer detection methods are time-consuming, expensive, complex, and uncomfortable [1]. Growths in organic electronic materials with optical imaging modalities, improvised models of different optical properties, optical biosensors, and biocompatibility are auspicious approaches for initial cancer detection and that of other diseases. Latest imaging techniques are compiled with the progression of ultrasound, positron emission tomography (PET), computed tomography (CT), and magnetic resonance imaging (MRI) for enhanced diagnosis of cancer and treatment which will help screen patients more accurately [2]. Developments in optical biosensors or organic electronics help in the segregation between healthy and cancer cells and the remodeling point-of-care gadgets can be used in cancer diagnosis [3]. Presently, utilizing ultrasound approaches for cancer detection depends on the experience of the clinician, particularly for the measurements and marks of cancers. To be specific, a clinician generally makes use of ultrasound instruments for cancer recognition by identifying a good angle for a clear vision of cancer displayed on the screen, and after continuing investigation fixing this for a longer period by utilizing one hand, with the other hand marking and measuring the cancers on the screen [4,5]. It becomes a tough task, because slight shaking of the hand which holds the probe may have a significant influence on the quality of breast ultrasound imagery; depending on this, computer-aided automated detection technologies are in high demand to locate regions of interest (ROIs), i.e., cancers, in breast ultrasound images [6].

Many researchers have involved computer-aided diagnosis (CAD) methods for breast cancer detection; such methods invoke the usage of Bayesian networks, artificial neural networks (ANN), k-means clustering, decision trees (DT), and fuzzy logic (FL) [7,8]. However, some of the authors have applied CAD techniques with DOT for diagnosing breast cancer. In recent times, convolutional neural networks (CNNs) have proved to be effective in distinguishing between malignant and benign breast lesions [9]. In comparison with classical techniques, CNNs eliminate the stages involved in feature extracting of an image; on the other hand, they provide images straight to the network which could automatically study discriminatory features [10]. CNN architecture was specifically adapted to have the benefit of 2D structures for input images.

This article introduces an Aquila Optimizer with Bayesian Neural Network for Breast Cancer Detection (AOBNN-BDNN) model on BUI. The presented AOBNN-BDNN model follows a series of processes to detect and classify breast cancer on BUI. To accomplish this, the AOBNN-BDNN model initially employs Wiener filtering (WF) related noise removal and U-Net segmentation as a pre-processing step. Besides, the SqueezeNet model derives a collection of feature vectors from the pre-processed image. Next, the BNN method was utilized for allocating suitable class labels to the input images. Finally, the AO technique can be employed to fine-tune the parameters relevant to the BNN method so that the classification performance will be enhanced, showing the novelty of our work. To validate the enriched performance of the AOBNN-BDNN algorithm, a wide experimental study is executed on a benchmark dataset.

The rest of the paper is organized as follows. Section 2 offers a brief survey of breast cancer classification using ultrasound images. Section 3 elaborates on the proposed model and Section 4 validates the performance of the proposed model. Lastly, Section 5 concludes the study.

2. Related Works

Hijab et al. [11] present a DL technique for managing this issue. The trained data, which has numerous images of malignant and benign cases, has been employed for training a deep CNN. Three training techniques were devised: a baseline technique in which the CNN structure can be well-trained from scratch, a TL method in which the pretrained VGG16 CNN structure can be additionally well-trained with the ultrasound imagery, and a finely tuned learning method in which the DL variables were optimally tuned to overcome overfitting. Kalafi et al. [12] introduce a novel structure for classifying breast cancer (BC) lesions with an attention module in an adapted VGG16 structure. The implemented attention system will enhance the feature discrimination among the target and background lesions in ultrasound. The author devises a novel ensemble loss function, which can be a grouping of the logarithm and binary cross-entropy of hyperbolic cosine loss, to enhance the method discrepancy among labels and classified lesions.

Lee et al. [13] devised a channel attention module including multiscale grid average pooling (MSGRAP) for segmenting BC sections accurately in ultrasound imagery. The author establishes the efficiency of the channel attention elements by adding MSGRAP for semantic segmentation and advances a new semantic segmentation network including the presented attention modules for segmenting BC regions accurately in ultrasound images. Whereas a standard convolutional function does not use global spatial data on input and just uses small local data in a kernel belonging to a convolution filter, the presented attention component permits utilization of global as well as local spatial data. Xie et al. [14] develop a technique called Domain Guided-CNN (DG-CNN) for incorporating margin data, a feature defined in the consensus for radiotherapists for diagnosing tumors in breast ultrasound (BUS) imagery. In DG-CNN, attention maps which emphasize marginal regions of cancers were initially produced and combined through various techniques into the networks.

Zhu et al. [15] attempted to advance an automated technique for distinguishing thyroid and breast lesions in ultrasound images with the help of deep CNNs (DCNN). To be specific, the author modeled a generic DCNN structure including TL and similar architectural variable settings for training methods for thyroid and BC (BNet and TNet) correspondingly, and to test the feasibility of these GA with an ultrasound image accumulated from medical practice. In [16], an RDAU-NET (Residual-Dilated-Attention-Gate-UNet) method was introduced and used for segmenting the cancers in BUS imagery. The method depends on the classical U-Net, but plain neural components were substituted by residual elements to enhance edge data and overcome the network performance deprivation issue linked with the deep network system. To raise the receptive domain and obtain more characteristic data, dilated convolutions can be utilized for processing the feature maps acquired from the encoder phases.

3. The Proposed Model

In this study, a new AOBNN-BDNN algorithm was modelled for the recognition and classification of breast cancer on BUI. The suggested AOBNN-BDNN model follows a series of processes to detect and classify breast cancer on BUI. At the initial stage, the WF-based noise removal and U-Net segmentation is a pre-processing step. In addition, the SqueezeNet model derives a collection of feature vectors from the pre-processed image. Finally, the AO with the BNN method can be utilized to allocate suitable class labels to the input images. Figure 1 depicts the overall process of the AOBNN-BDNN approach.

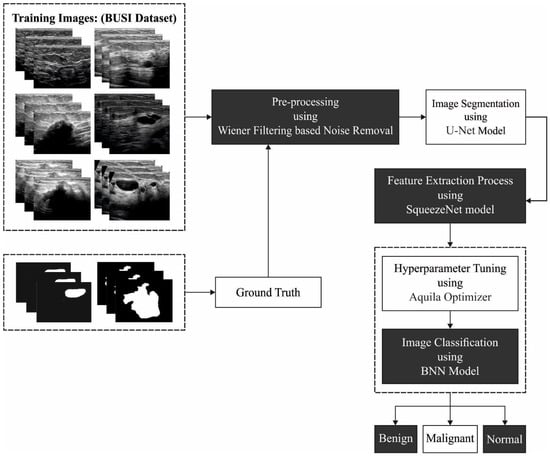
Figure 1. Overall process of AOBNN-BDNN algorithm.

3.1. Image Pre-Processing

At the initial stage, the AOBNN-BDNN algorithm applies WF-based noise removal and U-Net segmentation as a pre-processing step. The WF technique carries out 2D adaptive noise removal filtering using a window size of $3\times 3$ that eliminates the blur generated in Gaussian smoothing [17]. As a result, images are restored without noise. The local mean ($\mu$) and variance (${\sigma }^2)$ of every pixel can be defined as follows.

$$\mu =\frac{1}{NM}{\displaystyle \sum }_{n_1,n_2ϵ\theta }\alpha \left(n_1,n_2\right)$$

(1)

$${\sigma }^2=\frac{1}{NM}{\displaystyle \sum }_{n_1,n_2ϵ\theta }{\alpha }^2\left(n_1,n_2\right)-{\mu }^2$$

(2)

Next, the WF can be defined as follows:

$$b\left(n_1,n_2\right)=\mu +\frac{\left({\sigma }^2-{\beta }^2\right)}{{\sigma }^2}\left(\alpha \left(n_1,n_2\right)-\mu \right)$$

(3)

where $b\left(n_1,n_2\right)$ refers to a recovered image, $\theta$ refers to the $N\times M$ local neighborhood of every pixel in a scaled input image and ${\beta }^2$ stands for the noise variance.

Next, the preprocessed images are passed onto the U-Net architecture to perform the segmentation process. This is a fundamental structure in the medical imaging automation society and has massive applications in the domain. The network structure consists of contractive and expansive paths [18]. The contracting path involves numerous patches of convolution with a filter size of 3 × 33 × 3 and unity strides in both directions, after the ReLU layer. Next, it draws data from the feature vector through up-convolution, and generates, through a consecutive operation, an output segmenting map, and from the contractive path, through cropping and copying. The building block of this architecture is the operation connecting both paths. This connection enables the network to accomplish a precise dataset from the contractive path, therefore producing the segmentation mask for the output.

3.2. Feature Extraction Using SqueezeNet

After pre-processing, the SqueezeNet model derives a collection of feature vectors from the pre-processed image. SqueezeNet is a lightweight and efficient CNN mechanism [19]. Using this model, we accomplish a 50× reduction in module size in comparison with AlexNet, while exceeding or meeting the top-1 and -5 accurateness of AlexNet. The SqueezetNet module accomplishes remarkable outcomes with a small number of variables. There are two significant portions of CNN: classification and feature extraction. The extracted feature was employed for the precise image classification. Especially, these two portions of CNN accomplish the primary operation of CNN. The feature extraction of CNN encompasses convolution and sampling layers. The filtering of convolution layers is applied to diminish the noise in an image; later, the features of the image were enhanced. The convolution process was completed between the presentation layer convolutional kernel layer and the upper layer feature vector. Lastly, the activation function of CNN decides the computation of the convolution process. The effectiveness of training a NN was noticeable while applying the cost function $(Z$), which indicates the proportion between the reached output and trained instance [20].

$$Z=\frac{-1}{m}{\displaystyle \sum }\left[x ln a\left(1-x\right)\ln \left(1-\beta \right)\right]$$

(4)

In Equation (4), $m$ characterizes the trainable dataset amount, $x$ denotes the foreseeable value, and $\beta$ indicates the original values in the resulting layer.

The activation function role is a major portion of the classification technique with weighting the result of the CNN method and transmission kernel size. The ReLU activation function is in the middle of the commonly applied activation function. It is exploited from almost every CNN method for setting each negative value corresponding to zero. The zero setting inhibits several nodes contributed by the learning algorithm. An additional function, called ELU and LReLU, offers a slightly negative value and was hardly employed in the classification technique. ReLU activation function shows optimal results when compared to the LReLU activation function from the classification that is applied in this technique [21]. The ReLU activation function can be arithmetically formulated in the subsequent equation.

$$ReLU\left(x\right)=max\left(0; x\right)$$

(5)

This is more commonly applied in embedded settings; it involves distinct models of compression techniques. For example, $3\times 3$ convolution kernels in the proposed technique are replaced by $1\times 1$ convolution kernels. By using these techniques, the variable number for the individual convolution function is minimalized through a factor of 9. Furthermore, the $3\times 3$ convolution kernel is reduced and down-sampling is hindered in the network. As a result, the suggested technique reduces the computation efforts and the number of trained variables. For that reason, it is practicable to establish SqueezeNet in memory constraint hardware devices. In contrast with the contemporary AI model, we perceived that SqueezeNet has a minimal variable amount; consequently, it is the better choice for robot vacuum applications. Inappropriately, the model size (viz., 6.1 MB) was higher in comparison with the memory space existing in the robot vacuum.

3.3. Image Classification Using BNN

During the classification process, the BNN model is utilized to allocate proper class labels to the input images. The BNN is a kind of probability distribution through network weight, immediate advantages being the fully probabilistic treatment, therefore the approximation of uncertainty in prediction [22]. Here, we consider previous knowledge or $p_0\left(\mathcal{W}\right)$ distribution of the weight and evaluate the posterior weight distribution $p\left(\mathcal{W}|D\right)$ afterward regarding the $D$ dataset and it can be assessed by

$$p\left(\mathcal{W}|D\right)=\frac{p\left(D|\mathcal{W}\right)p_0\left(\mathcal{W}\right)}{p\left(D\right)}$$

(6)

In Equation (6), $p_0\left(\mathcal{W}\right)$ refers to prior weight distribution, generally an isotropic Gaussian, and $p\left(D\right)$ represents the normalized distribution constant. In these settings, prediction is performed by the posterior from Equation (6):

$$p\left(Y^{*}|X^{*},D\right)={\displaystyle \int }p\left(Y^{*}|,X^{*},\mathcal{W}\right)p\left(\mathcal{W}|D\right)d\mathcal{W}$$

(7)

In this study, the uncertainty arises because of sampling the batch normalization (BN) and dropout weight, and prediction can be performed through averaging $T$ forwarded passes through the network:

$$p\left(Y^{*}|X^{*},D\right)=\frac{1}{T}{\displaystyle \sum }_{t=1}^{T}p\left(Y^{*}|X^{*},D,{\mathcal{W}}_t\right)$$

(8)

The network layer (max pool, BN) is presented as follows [23].

• Batch Normalization is a process to accelerate network training via decreasing the internal covariate shift (which defines the variations in the distribution of activation unit because of parameter changes) performed by normalizing the hidden layer activation through an evaluated ${\mu }_{\beta }$ and ${\sigma }_{\beta }$ from every mini-batch.
• Dropout is a regularization method, also regarded as a Bayesian methodology: the process eliminates part of the network in a random fashion which makes the weight stochastic quantity: $\widehat{\mathcal{W}}=\mathcal{W}\otimes \alpha$, where $\alpha \sim Bernoulli\left(p\right),$ $\mathcal{W}$ refers to the first weight of the network, and $\otimes$ denotes the direct product using binary vector randomly.

The network can be trained by the $\mathcal{W}$ dropout and it has a stochastic gradient descent, resulting in robustness and uncertainty.

3.4. Parameter Optimization

Finally, the AO technique is utilized to fine-tune the parameters related to the BNN method so that the classification performance will be improved [24]. The AO technique simulates AO’s social activity for catching their prey. AO is a population-based optimized approach, related to other meta-heuristic systems, which start with establishing a primary population $X$ with $N$ agents. The subsequent formula is utilized for executing this process. Figure 2 demonstrates the flowchart of the AO technique.

$$X_{ij}=r_1\times \left(U{B}_j-L{B}_j\right)+L{B}_j,i=1,2,Nj=1,2,\dots ,Dim$$

(9)

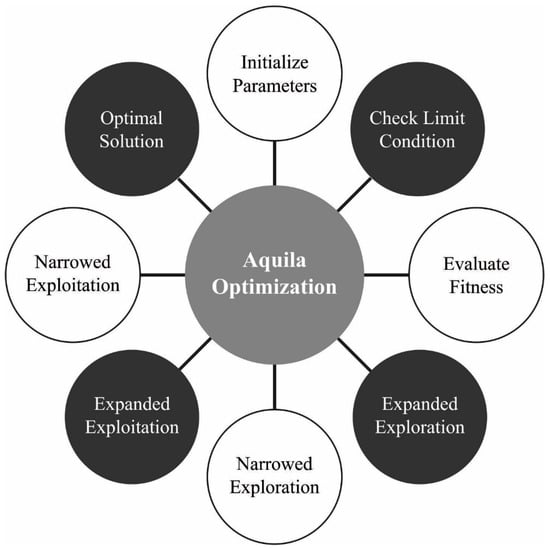
Figure 2. Flowchart of AO technique.

In Equation (9), $U{B}_j$ and $L{B}_j$ demonstrate the restrictions of searching space. $r_1\in \left[0,1\right]$ implies the arbitrary value and $Dim$ denotes the dimensional of agents. In the AO approach, the following step is to perform exploration and exploitation until the optimal solution is established [25]. Two stages exist in exploitation and exploration. The $X_b$ optimal agent and (X) the average of agents are applied in the exploration, and it is mathematically expressed in the following:

$$X_i\left(t+1\right)=X_b\left(t\right)\times \left(\frac{1-t}{T}\right)+\left(X_M\left(t\right)-X_b\left(t\right)\ast rand\right),$$

(10)

$$X_M\left(t\right)=\frac{1}{N}{\displaystyle \sum }_{i=1}^{N}X\left(t\right),\forall j=1,2,\dots ,Dim$$

(11)

The exploration stage can be controlled using $(\frac{1-t}{T})$ in Equation (10). The maximal amount of generations is represented as $T$. The exploration stage applies the Levy flight (Levy(D)) distribution as well as $X_b$ to upgrade the solution as follows:

$$X_i\left(t+1\right)=X_b\left(t\right)\times Levy\left(D\right)+X_R\left(t\right)+\left(y-x\right)\ast rand,$$

(12)

$$Levy \left(D\right)=s\times \frac{u\times \sigma }{|v{|}^{\frac{1}{\beta }}},\sigma =\left(\frac{\Gamma \left(1+\beta \right)\times sine\left(\frac{\pi \beta }{2}\right)}{\Gamma \left(\frac{1+\beta }{2}\right)\times \beta \times 2^{\left(\frac{\beta -1}{2}\right)}}\right)$$

(13)

In Equation (13), $s=0.01$ and $\beta =1.5$. $u$ and $v$ indicate the arbitrary values. $X_R$ refers to arbitrarily selected agents. Additionally, $y$ and $x$ refer to two variables utilized for stimulating the spiral shape:

$$y=r\times cos\left(\theta \right),x=r\times sin\left(\theta \right)$$

(14)

$$r=r_1+U\times D_1,\theta =-\omega \times D_1+{\theta }_1,\theta 1=\frac{3\times \pi }{2}$$

(15)

In Equation (15), $\omega =0.005$ and $U=0.00565$. $r_1\in \left[0,20\right]$ stands for an arbitrary value. The initial method utilized to improve the agent in the exploitation stage depends on $X_b$ and $X_M$, comparable to exploration as follows:

$$X_i\left(t+1\right)=\left(X_b\left(t\right)-X_M\left(t\right)\right)\times \alpha -rnd+\left(UB\times rnd+LB\right)\times \delta$$

(16)

In Equation (16), $UB=\left(UB-LB\right),$ $\alpha ,$ and $\delta$ refer to the exploitation adjustment parameter. $rnd\in \left[0,1\right]$ denotes a random number. The agent is upgraded by $X_b$, Levy, and the quality function $QF$ in the next exploitation phase:

$$X_i\left(t+1\right)=QP\times X_b\left(t\right)-GX-G_2\times Levy\left(D\right)+rnd\times G_1$$

(17)

$$GX=\left(G_1\times X\left(t\right)\times rnd\right)$$

$$QP\left(t\right)=t^{\frac{2\times rnd( )-1}{{(1-T)}^2}}$$

(18)

Moreover, $G_1$ denotes the motion applied to track the optimum individual solution, as follows:

$$G_1=2\times rnd\left(\right)-1,G_2=2\times \left(1-\frac{t}{T}\right)$$

(19)

In Equation (19), $rnd$ refers to a random number. Furthermore, $G_2$ indicates a variable decreased from two to zero as follow:

$$G_2=2\times \left(1-\frac{t}{T}\right)$$

(20)

The AO method derives a fitness function (FF) to exhibit the better performance of the classification. It defines a positive integer to characterize the improved performance of the solution candidate. In this study, the reduction of classification error rate was regarded as the FF, as follows.

$$\begin{array}{ll}fitness\left(x_i\right)& =ClassifierErrorRate\left(x_i\right)\\ & =\frac{number of misclassified samples}{Total number of samples}\ast 100 \end{array}$$

(21)

4. Results and Discussion

The experimental validation of the AOBNN-BDNN method is tested using the breast ultrasound image dataset [26]. It contains a total of 780 images with three class labels, as shown in Table 1.

Table 1. Dataset details.

Class	No. of Images
Benign	437
Malignant	210
Normal	133
Total Number of Images	780

Figure 3 exhibits the confusion matrices created by the AOBNN-BDNN algorithm on the applied data. On the entire dataset, the AOBNN-BDNN method has recognized 429 samples as benign, 210 samples as malignant, and 132 samples as normal. Simultaneously, on 70% of training (TR) data, the AOBNN-BDNN technique has recognized 311 samples as benign, 135 samples as malignant, and 92 samples as normal. Concurrently, on 30% of testing (TS) data, the AOBNN-BDNN method has recognized 118 samples as benign, 75 samples as malignant, and 40 samples as normal.

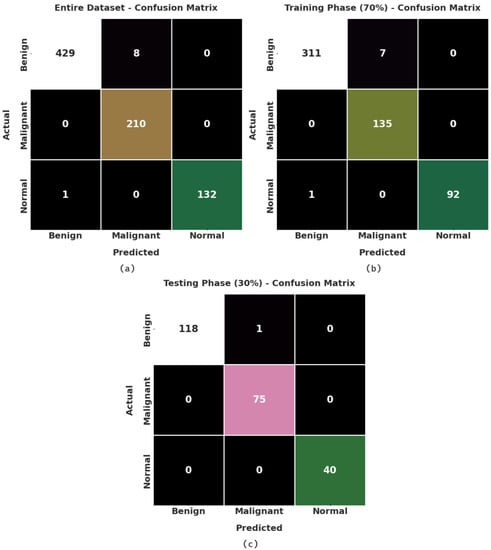
Figure 3. Confusion matrices of AOBNN-BDNN approach: (a) entire dataset, (b) 70% of TR data, and (c) 30% of TS data.

Table 2 and Figure 4 portray a brief classification outcome of the AOBNN-BDNN method on the entire dataset. The results implied that the AOBNN-BDNN method has effectually recognized all three classes. For instance, the AOBNN-BDNN model has identified benign class samples with $acc{u}_y$ of 98.85%, $pre{c}_n$ of 99.77%, $rec{a}_l$ of 98.17%, $F_{score}$ of 98.96%, and MCC of 97.68%. Moreover, the AOBNN-BDNN algorithm has identified Malignant class samples with $acc{u}_y$ of 98.97%, $pre{c}_n$ of 96.33%, $rec{a}_l$ of 100%, $F_{score}$ of 98.13%, and MCC of 97.46%. Furthermore, the AOBNN-BDNN technique has identified normal class samples with $acc{u}_y$ of 99.87%, $pre{c}_n$ of 100%, $rec{a}_l$ of 99.25%, $F_{score}$ of 99.62%, and MCC of 99.55%.

Table 2. Result analysis of the AOBNN-BDNN approach with different measures under the entire dataset.

Entire Dataset
Class Labels	Accuracy	Precision	Recall	F-Score	MCC
Benign	98.85	99.77	98.17	98.96	97.68
Malignant	98.97	96.33	100.00	98.13	97.46
Normal	99.87	100.00	99.25	99.62	99.55
Average	99.23	98.70	99.14	98.91	98.23

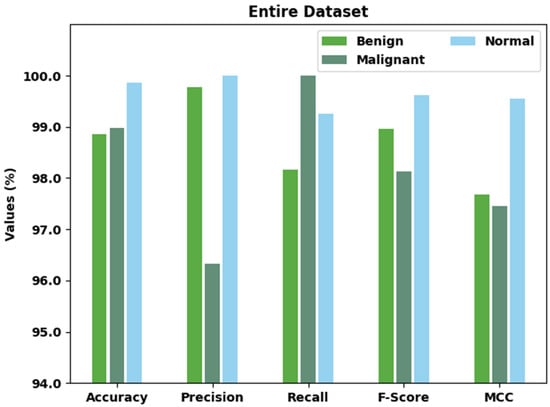
Figure 4. Result analysis of AOBNN-BDNN approach under entire dataset.

Table 3 and Figure 5 display a detailed classification outcome of the AOBNN-BDNN algorithm on 70% of TR data. The results denoted the AOBNN-BDNN methodology has effectually recognized all three classes. For example, the AOBNN-BDNN technique has identified benign class samples with $acc{u}_y$ of 98.53%, $pre{c}_n$ of 99.68%, $rec{a}_l$ of 97.80%, $F_{score}$ of 98.73%, and MCC of 97.02%. Additionally, the AOBNN-BDNN approach has identified Malignant class samples with $acc{u}_y$ of 98.72%, $pre{c}_n$ of 95.07%, $rec{a}_l$ of 100%, $F_{score}$ of 97.47%, and MCC of 96.67%. Besides, the AOBNN-BDNN technique has identified normal class samples with $acc{u}_y$ of 99.82%, $pre{c}_n$ of 100%, $rec{a}_l$ of 98.92%, $F_{score}$ of 99.46%, and MCC of 99.35%.

Table 3. Result analysis of the AOBNN-BDNN approach with various measures under 70% of TR data.

Training Phase (70%)
Class Labels	Accuracy	Precision	Recall	F-Score	MCC
Benign	98.53	99.68	97.80	98.73	97.02
Malignant	98.72	95.07	100.00	97.47	96.67
Normal	99.82	100.00	98.92	99.46	99.35
Average	99.02	98.25	98.91	98.55	97.68

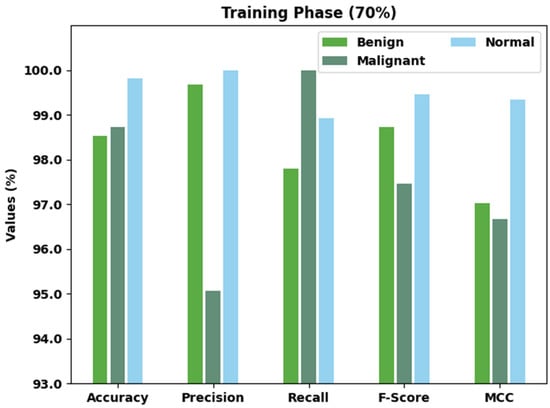
Figure 5. Result analysis of AOBNN-BDNN approach under 70% of TR data.

Table 4 and Figure 6 exhibit brief classification results of the AOBNN-BDNN technique on 30% of the TS dataset. The outcomes implied that the AOBNN-BDNN approach has effectually recognized all three classes. For example, the AOBNN-BDNN methodology has identified benign class samples with $acc{u}_y$ of 99.57%, $pre{c}_n$ of 100%, $rec{a}_l$ of 99.16%, $F_{score}$ of 99.58%, and MCC of 99.15%. along with that, the AOBNN-BDNN algorithm has identified Malignant class samples with $acc{u}_y$ of 99.57%, $pre{c}_n$ of 98.68%, $rec{a}_l$ of 100%, $F_{score}$ of 99.34%, and MCC of 99.03%. In addition, the AOBNN-BDNN methodology has identified normal class samples with $acc{u}_y$ of 100%, $pre{c}_n$ of 100%, $rec{a}_l$ of 100%, $F_{score}$ of 100%, and MCC of 100%.

Table 4. Result analysis of the AOBNN-BDNN approach with various measures under 30% of TS data.

Testing Phase (30%)
Class Labels	Accuracy	Precision	Recall	F-Score	MCC
Benign	99.57	100.00	99.16	99.58	99.15
Malignant	99.57	98.68	100.00	99.34	99.03
Normal	100.00	100.00	100.00	100.00	100.00
Average	99.72	99.56	99.72	99.64	99.39

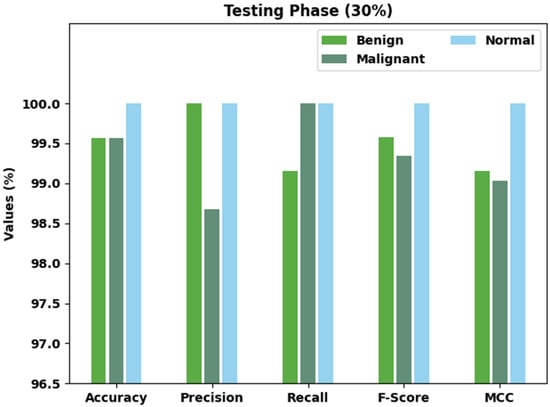
Figure 6. Result analysis of AOBNN-BDNN approach under 30% of TS data.

The training accuracy (TA) and validation accuracy (VA) obtained by the AOBNN-BDNN methodology on the test dataset is established in Figure 7. The experimental result denoted the AOBNN-BDNN algorithm has reached higher values of TA and VA. In Particular, the VA is greater than TA.

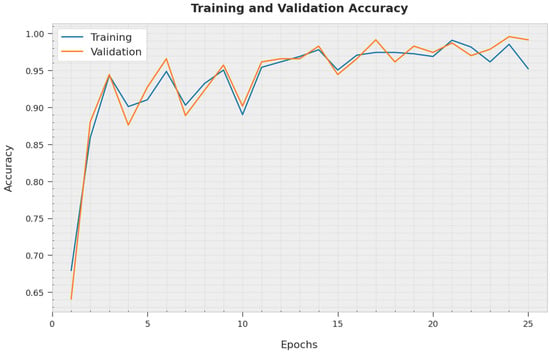
Figure 7. TA and VA analysis of AOBNN-BDNN methodology.

The training loss (TL) and validation loss (VL) obtained by the AOBNN-BDNN approach on the test dataset are displayed in Figure 8. The experimental outcome represented that the AOBNN-BDNN method has exhibited minimal values of TL and VL. To be specific, the VL is lesser than the TL.

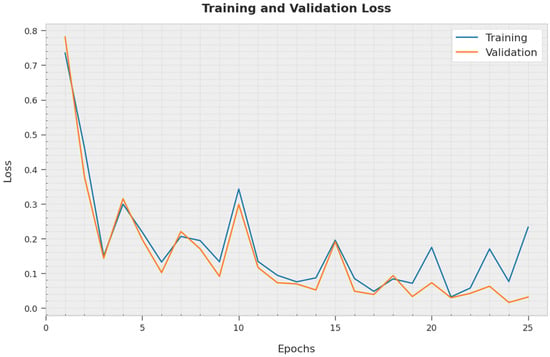
Figure 8. TL and VL analysis of AOBNN-BDNN methodology.

A clear precision-recall analysis of the AOBNN-BDNN technique on the test dataset is represented in Figure 9. The figure inferred the AOBNN-BDNN technique has resulted in enhanced values of precision-recall values in every class label.

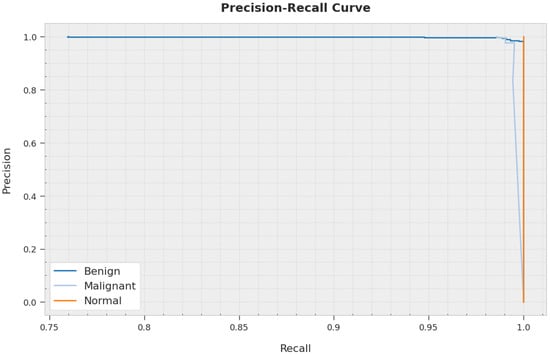
Figure 9. Precision-recall curve analysis of AOBNN-BDNN methodology.

A brief ROC study of the AOBNN-BDNN method on the test dataset is shown in Figure 10. The outcomes signified that the AOBNN-BDNN methodology has displayed its capability in classifying distinct classes on the test dataset.

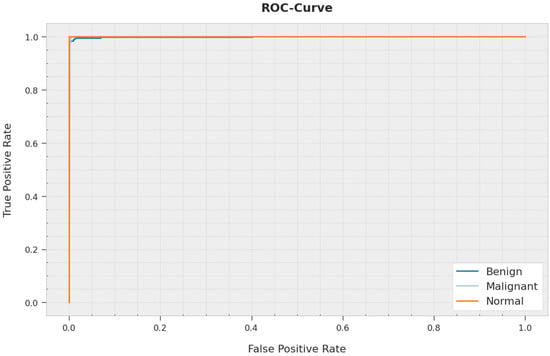
Figure 10. ROC curve analysis of AOBNN-BDNN methodology.

Table 5 provides an overall comparative inspection of the AOBNN-BDNN method with recent approaches [11]. Figure 11 renders a brief study of the AOBNN-BDNN method with existing models in terms of $pre{c}_n$ and $rec{a}_l$. The experimental outcomes reported the betterment of the AOBNN-BDNN model. With respect to $pre{c}_n$, the AOBNN-BDNN model has attained increased $pre{c}_n$ of 99.56% whereas the SEODTL-BDC, ESD, LSVM, ESKNN, FKNN, and LD methods have obtained reduced $pre{c}_n$ of 99.18%, 98.89%, 98.41%, 97.55%, 96.93%, and 97.41% respectively. In addition, with regard to $rec{a}_l$, the AOBNN-BDNN method has achieved increased $rec{a}_l$ of 99.72% whereas the SEODTL-BDC, ESD, LSVM, ESKNN, FKNN, and LD algorithms have gained reduced $rec{a}_l$ of 98.18%, 98.11%, 97.87%, 98.27%, 97%, and 98.05% correspondingly.

Table 5. Comparative analysis of AOBNN-BDNN approach with existing methodologies.

Methods	Precision	Recall	Accuracy	F-Score
AOBNN-BDNN	99.56	99.72	99.72	99.64
SEODTL-BDC	99.18	98.18	99.12	98.14
ESD model	98.89	98.11	99.07	98.88
LSVM model	98.41	97.87	98.73	98.29
ESKNN model	97.55	98.27	97.70	98.61
FKNN algorithm	96.93	97.00	97.42	96.93
LD algorithm	97.41	98.05	97.92	96.99

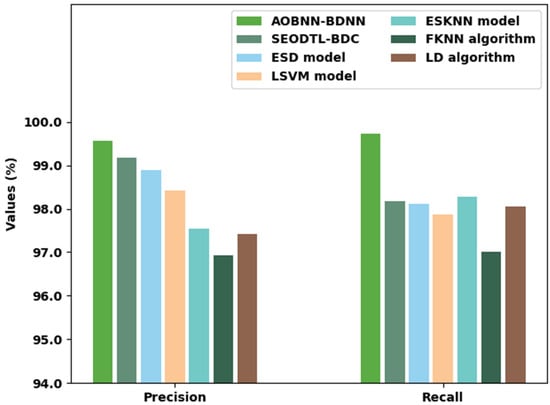
Figure 11. $Pre{c}_n$ and $Rec{a}_l$ analysis of the AOBNN-BDNN approach with existing methodologies.

Figure 12 offers a comparative examination of the AOBNN-BDNN method with existing models with $acc{u}_y$ and $F_{score}$. The experimental outcomes reported the betterment of the AOBNN-BDNN method. With $acc{u}_y$, the AOBNN-BDNN algorithm has gained increased $acc{u}_y$ of 99.72% whereas the SEODTL-BDC, ESD, LSVM, ESKNN, FKNN, and LD methodologies have reached reduced $acc{u}_y$ of 99.12%, 99.07%, 98.73%, 97.70%, 97.42%, and 97.92%, correspondingly. Additionally, concerning $F_{score}$, the AOBNN-BDNN method has received increased $F_{score}$ of 99.64% whereas the SEODTL-BDC, ESD, LSVM, ESKNN, FKNN, and LD methodologies have gained reduced $F_{score}$ of 98.14%, 98.88%, 98.29%, 98.61%, 96.93%, and 96.99%, correspondingly.

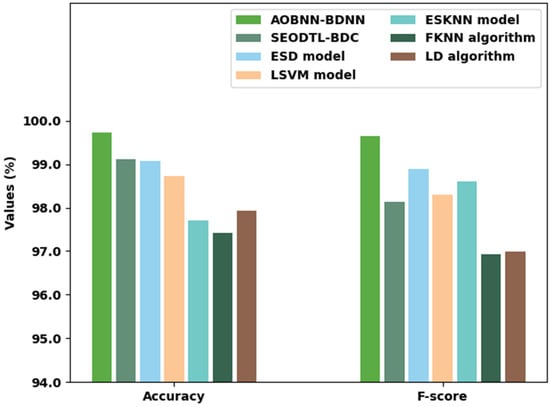
Figure 12. $Acc{u}_y$ and $F_{score}$ analysis of the AOBNN-BDNN approach with existing methodologies.

Finally, a classification time (CT) inspection of the AOBNN-BDNN model with recent models is carried out in Table 6 and Figure 13. The attained values implied the ESKNN method has shown poor results with a higher CT of 2.28 min. In the meantime, the ESD and FKNN methods have obtained slightly reduced outcomes with closer CT of 2.28 min and 2.24 min, respectively.

Table 6. Classification time analysis of AOBNN-BDNN approach with recent algorithms.

Methods	Classifification Time (min)
AOBNN-BDNN	1.01
SEODTL-BDC	1.18
ESD model	2.28
LSVM model	1.95
ESKNN model	2.80
FKNN algorithm	2.24
LD algorithm	1.75

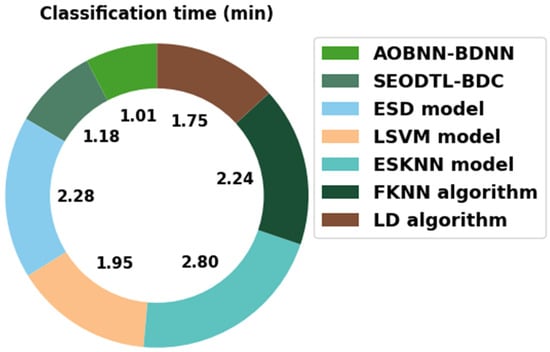
Figure 13. CT analysis of AOBNN-BDNN approach with recent algorithms.

In addition, the LSVM and LD models have accomplished moderately reduced CT of 1.95 min and 1.75 min, respectively. However, the AOBNN-BDNN model has gained maximum outcome with minimal CT of 1.01 min. Therefore, the experimental values guaranteed that the AOBNN-BDNN method was found to be an effective tool compared to other approaches.

5. Conclusions

In this study, a new AOBNN-BDNN method was developed for the recognition and classification of breast cancer on BUI. The suggested AOBNN-BDNN method follows a series of processes to detect and classify breast cancer on BUI, primarily the WF-based noise removal and U-Net segmentation as a pre-processing steps. Besides, the SqueezeNet model derives a collection of feature vectors from the pre-processed image. Next, the BNN method is utilized to allocate suitable class labels to the input images. Finally, the AO technique is utilized to fine-tune the parameters related to the BNN algorithm so that the classification performance will be improved. To validate the enhanced performance of the AOBNN-BDNN method, a wide-ranging experimental analysis has been conducted on the benchmark dataset. An extensive experimental analysis stated the enhancements of the AOBNN-BDNN method over recent approaches with maximum accuracy of 99.72%. In the future, advanced DL models can be designed to enhance breast cancer classification performance. Besides, the proposed model can be tested on a real-time large-scale dataset in the future.