Numerical Analysis Exterior RC Beam-Column Joints with CFRP Bars as Beam’s Tensional Reinforcement under Cyclic Reversal Deformations

Abstract

In this paper the cyclic lateral response of reinforced concrete (RC) beam-column joints with composite carbon fiber-reinforced polymer (CFRP) bars as a longitudinal reinforcement in the beam is simulated with finite element (FE) modeling using software Abaqus. An experimental project of two full-scale joint specimens subjected to cyclic loading with supplementary accompanying pull-out tests of CFRP bars is also included in this study. These test results are used to calibrate the developed FE model, the constitutive laws of the materials and the bond response between CFRP bars and concrete. Comparisons between test data and numerical results indicate that the calibrated model accurately predicts the cyclic response of RC beam-column joint specimens with CFRP longitudinal bars as the beam’s tensional reinforcement. A parametric analysis is also performed to provide useful concluding remarks concerning the design of concrete joints with composite bars and the ability of CFRP bars to substitute for conventional steel bars in RC structural members under seismic excitations.

1. Introduction

Fiber-reinforced polymer (FRP) materials are widely accepted as an important aspect of modern civil infrastructure. The advantages of FRP materials over traditional building materials such as conventional steel and steel-reinforced concrete (RC) rest in their enhanced structural performance in regard of stability, stiffness, strength and durability [1,2,3]. FRP materials are available in a variety of forms, including cables, sheets, plates and more. The use of FRP materials is now widespread throughout the world. As a result, the importance of cost-effective and reliable FRP structures increases. The majority of early research efforts [4,5] concerning FRP reinforcement (strips, sheets and other textiles) focused on rehabilitation and strengthening applications of masonry and concrete structures [6,7,8,9]. Extensive experimental and theoretical research has also been conducted on the strengthening and retrofitting of deficient or/and damaged concrete structures [10,11,12,13]. Nevertheless, the application of FRP rebars in concrete structures continues to be a popular topic of research, as all the design aspects and implementation drawbacks have not been thoroughly investigated and discussed, especially concerning RC joints [14]. In particular, the joint behavior and the framework of design standards have not been thoroughly examined. It is evident from a review of the prior studies that considerable research has been performed in the field of FRP beam-column joint wrappings for repairing and rehabilitation purposes [15,16,17,18], whereas research on using nonmetallic rebars for beam-column joint implementations is limited. In recent years, nonmetallic reinforcements have gained prominence in international structural applications [19,20,21,22]. Even though they have been used successfully in construction, nonmetallic reinforcements will only be widely used in engineering if design specifications and guidelines are developed promptly [23].

The typical method for designing an earthquake-resistant RC structure relies on the plastic deformation (ductility) of the components, which is primarily caused by the yielding of reinforcing steel [24,25]. However, the FRP materials display a linear elastic stress–strain relationship up to failure (no yielding), which has prompted some concerns over their use in prone to earthquakes areas. However, fundamental research in this field reveals that concrete structures reinforced with FRP may sustain substantial lateral displacements without collapsing [26,27,28,29]. This was attributable to the high tensile strength and low modulus of elasticity of FRPs, which permits the structures to tolerate significant deformations before exceeding their ultimate bearing capacity [30].

The characteristics impacting the performance of RC with FRP reinforcement (FRP-RC) moment-resisting frames must be thoroughly investigated in light of the encouraging findings of early research on the potential of utilizing FRPs in RC structures located in seismic zones. To attain this objective, it is vital to comprehend the behavior of beam-column joints as a critical factor in the lateral stability of frames [31,32]. Several researchers have examined the seismic performance of externally applied glass FRP reinforcement in existing RC beam-column joints, focusing on aspects such as joint shear stress, reinforcement details, the existence of lateral beams and the compressive strength of concrete [33,34,35,36,37,38,39]. However, several known characteristics that impact the seismic performance of FRP-RC beam-column joints have not yet been addressed. Current regulations and design recommendations for FRP-RC structures lack complete seismic protections due to a lack of research and data. The implementation of FRP-RC frames in seismic zones is not feasible without a thorough understanding of the properties influencing the behavior of beam-column joints.

Recent research has demonstrated that carbon FRP (CFRP) bars may efficiently replace steel reinforcing bars in concrete members. The bonding strength of FRP reinforcing bars (rebars) in concrete is significantly lower than that of standard steel rebars, despite the evident benefits of FRPs [40,41,42,43]. The bond between concrete and reinforcing bars affects the transmission of stress among them, and thus debonding has become one of the most challenging aspects of the investigation of concrete structures [44]. The bond between FRP reinforcing bars and the concrete matrix is complex, and a number of variables can affect the bonding properties of FRP reinforcements to concrete [45,46,47,48,49]. The geometry and surface characteristics of FRP rebars, concrete compressive strength, confinement pressure, rebar diameter and location in the cast and specimen, embedment length, temperature variations and environmental factors all impact bonding between FRP rebars and concrete [50,51].

Numerous experimental investigations have been performed to examine the bond strength of FRP rebars in concrete and the effects of factors such as fiber type, surface treatment, bar diameter and temperature on the bond properties of FRP rebars [52,53,54,55,56]. In addition, these studies demonstrated that the needed embedment lengths of these rebars must be carefully considered. In contrast to steel rebars, there is little information in the literature about the bonding behavior of CFRP rebars in normal and high-strength concrete members, particularly under cyclic loading circumstances [57].

To explore the seismic behavior of RC external beam-column joints with CFRP longitudinal bars in the beam, experimental testing followed by finite element (FE) model analysis were performed in this study. The influence of CFRP bar bond slip on joint hysteretic performance was also examined. An FE model was developed to simulate the behavior of the CFRP-RC joints. The accuracy of the FE simulation was accomplished by accounting for the nonlinear behavior of concrete, the decrease in concrete’s compressive strength caused by crack initiation, the confinement given by the internal reinforcement and the bond slip relation between the reinforcement and concrete. For the purpose of accurately simulating the bond strength of the CFRP bars, further pull-out tests were conducted to determine the bond stress versus slip behavior. Finally, further FE analyses were performed to compare the performance of the CFRP-RC joints to conventionally steel-reinforced RC joints and to evaluate the potential of replacing conventional reinforcement with CFRP bars.

2. Experimental Test Program

The experimental program of this study was carried out to investigate the ability of FRP bars to substitute conventional steel bars in RC structural members during seismic excitations. Two (2) external T-shaped beam-column RC joints at full size (scale 1:1) were subjected to cyclic reversal loading with increasing imposed displacement. The beams were reinforced with CFRP longitudinal bars, whereas the columns were commonly reinforced with deformed steel bars.

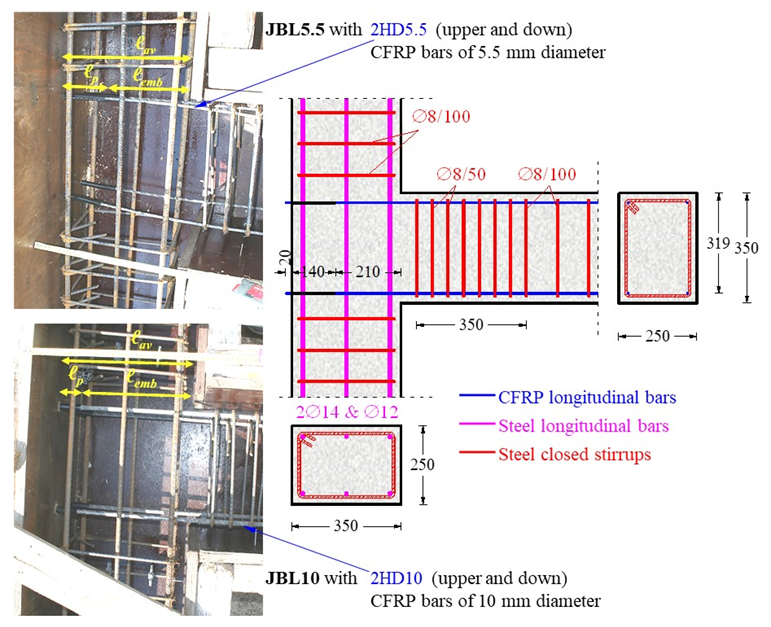
2.1. Geometry and Reinforcement Characteristics of the Specimens

The specimens shared the same geometrical characteristics. The column’s overall length was 2950 mm with a cross-section of 350/250 mm, and the beam’s overall length (net span) was 1875 mm with a cross-section of 250/350 mm. The clear concrete cover was 20 mm. Figure 1 and Figure 2 depict the geometry, cross-sectional dimensions and reinforcing features of the tested beam-column joint specimens. The columns of both specimens contained four longitudinal bars with a 14 mm diameter, placed at each angle, and two longitudinal bars with a 12 mm diameter positioned in the middle of the sides. As transverse reinforcement in the column area, stirrups with an 8 mm diameter were arranged per 100 mm. No shear reinforcement was installed in the joint area in either of the specimens as shown in Figure 2.

The specimens differed in the longitudinal reinforcement of the beam. JBL5.5 contained four CFRP longitudinal bars of a 5.5 mm diameter positioned on the top and bottom sides of the beam, and JBL10 contained four CFRP bars of a 10 mm diameter as top (2 bars) and bottom (2 bars) longitudinal reinforcing bars, respectively. The beams were designed as under-reinforced in accordance with ACI 440.1R-15 [58] design criteria. In particular, the beams of the beam-column joint specimens were designed in order for their longitudinal CFRP reinforcing bars to fail under pull-out bond failure between the bar and concrete instead of fiber rupture at CFRP bar ultimate tension capacity. The reinforcement ratio of the longitudinal CFRP bars was 0.06% and 0.20% for specimens JBL5.5 and JBL10, respectively. Furthermore, the anchorage length of the longitudinal CFRP bars utilized in the beams was specified in accordance with the design requirements of ACI 440.1R-15 [58]. Based on these provisions, or the specimens, straight anchoring lengths of ℓ_emb = 38Ø_f and 30Ø_f were calculated and adopted for the specimens JBL5.5 and JBL10, respectively. This way, pull-out bond failure of the longitudinal CFRP bars during the cyclic loading procedure was anticipated. To ensure that the tested specimen had the desired anchorage length ℓ_emb, a stiff polyvinyl chloride (PVC) pipe with a diameter of 10 mm was placed around the remaining part of the bars near the outside end of the column to form noncontact (de-bonded) zones between the bars and the surrounding concrete, as shown in Figure 2. The overall length of this PVC pipe was ℓ_p = ℓ_av − ℓ_emb = 350 − 210 = 140 mm, where ℓ_av is the available anchorage length for the longitudinal bars of the beams, which is equal to the column’s width.

Both specimens’ shear transverse reinforcement comprised of closed deformed steel stirrups of an 8 mm diameter spaced uniformly at 50 mm (8/50 mm) along the critical region of the beams that equals to 350 mm, and at 100 mm (8/100 mm) outside this area.

For the JBL10 specimen, the anchorage length of the CFRP bars was determined to be ℓ_emb = 30Ø_f = 300 mm. For the HD10 CFRP bars, a rigid PVC pipe with an external diameter of 16 mm and a total length of ℓ_p = ℓ_av − ℓ_emb = 350 − 300 = 50 mm was selected and applied around the remaining portion of the bars near the exterior end of the columns.

2.2. Mechanical Properties of Materials

2.2.1. Concrete

Supplementary compression tests of six standard 150/300 mm cylinders were also performed to measure the concrete’s compressive strength with grade C20/25. On the day that the tests were conducted, three cylinders were subjected to axial compression, while three others were tested under splitting tension. The average compressive and splitting tensile strengths of the employed concrete were f_c = 28.0 Mpa and f_ct,spl = 2.05 Mpa, respectively, for all specimens.

2.2.2. Steel and CFRP Reinforcement

The HD5.5 and HD10 longitudinal CFRP bars of the beams were supplied by Sintecno Company. They were produced using the pultrusion method and were comprised of continuous longitudinal carbon fibers with a high tensile strength joined together with an epoxy resin. The HD5.5 and HD10 bars contained approximately 57% and 60% carbon fiber, respectively. These carbon fibers have nominal tensile strengths and elastic moduli in excess of 4 Gpa and 230 Gpa, respectively. Due to a particular surface treatment with quartz sand, the outer layer of the utilized CFRP bars had a rough external surface. The nominal ultimate tensile strength and elastic modulus of the used CFRP bars were f_fu = 1.8 Gpa and E_f = 130 Gpa, respectively.

The experimentally determined yield tensile strength, f_y, of the deformed steel bars was 550 Mpa for the Ø14 and Ø12 longitudinal bars of the columns, respectively, and 550 Mpa for the Ø8 utilized stirrups.

2.3. Experimental Setup and Instrumentation

The experimental setup and instrumentation are presented in Figure 3a,b. After performing a 90-degree counterclockwise rotation, the specimens of each beam-column joint were positioned so that the column was in the horizontal position and the beam was in the vertical position. In order to replicate the inflection points of the columns in the center, the specimen was supported with equipment that allowed rotation.

During the testing, a constant N_c = 0.05A_c f_c column compressive axial load was applied (where A_c is the area of the column cross-section). All of the specimens were subjected to full cycle deformations that were applied by a swivel connector that was attached to the actuator near the free end of the beam. Throughout the whole loading procedure, the column axial load was maintained at a constant amount of 122.5 kN (=N_c = 0.05A_c f_c = 0.05 × 250 × 350 × 28.0 × 10⁻³) for all specimens.

The cyclic displacement-controlled loading history at the beam end began after applying the constant axial load to the column. The specimens were subjected to increasing cyclic reversal deformation across an eight-step loading history, with maximum displacement, d = ±8.50 mm, ±12.75 mm, ±17.00 mm, ±25.50 mm, ±34.00 mm, ±51.00 mm, ±68.00 mm and ±85.00 mm.

As indicated in Figure 4, each loading step contained three complete loading cycles for each story drift (SD) level. It is noted that d = 17 mm corresponds to SD = 1%. The loading pace was 0.05 mm/s for the initial four loading phases and then raised to 1 mm/s for the last four loading steps.

The load was measured with an accuracy of 0.05 kN by a load cell. The displacements of the beams were measured using two string position transducers placed 0.75 m and 1.84 m from the end of the column (see also Figure 1), while the slip of the longitudinal FRP bars of the beams was measured using two linear variable differential transducers (LVDT) with 0.01 mm accuracy (see Figure 3b).

In addition, two SPTs were inserted on the front side of the joint core to assess the shear deformation until specimen failure. Moreover, one LVDT was installed at the left end of the specimen column to monitor the support during the test. The photographs of Figure 3a,b provide additional information on test rig instrumentation.

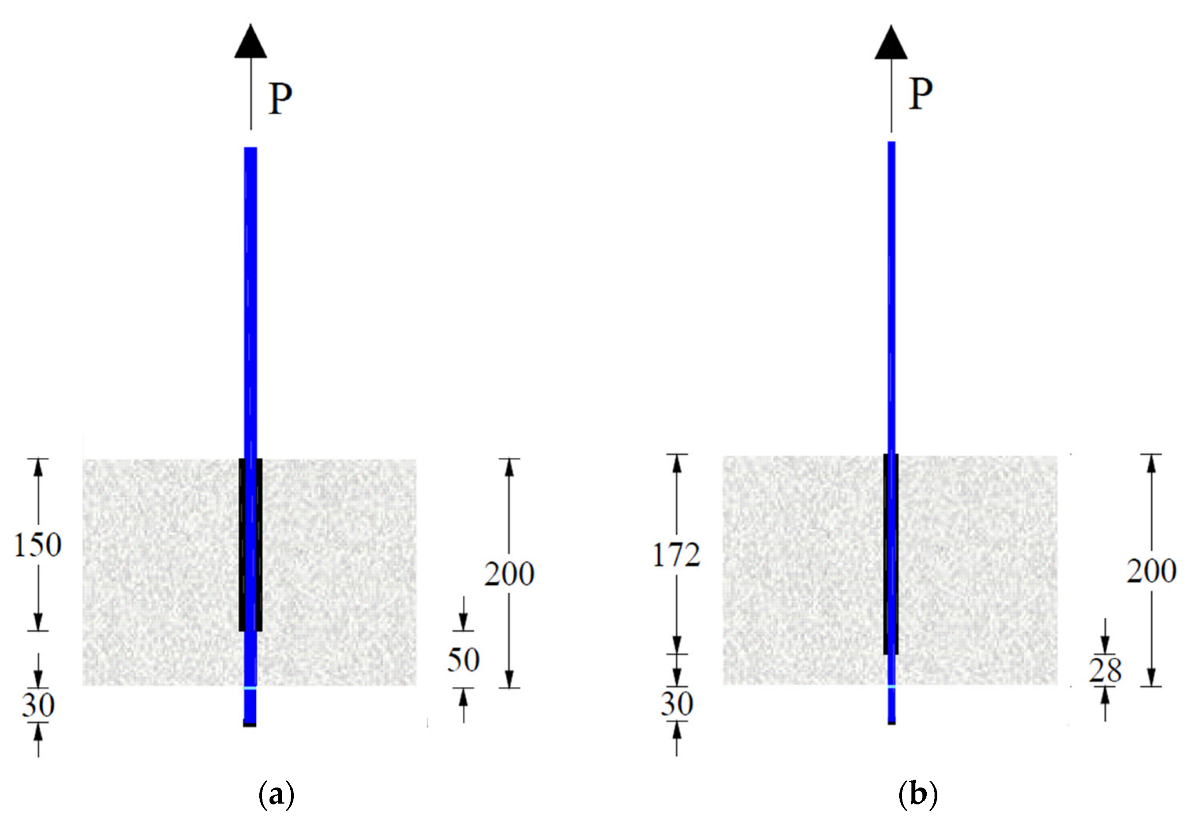
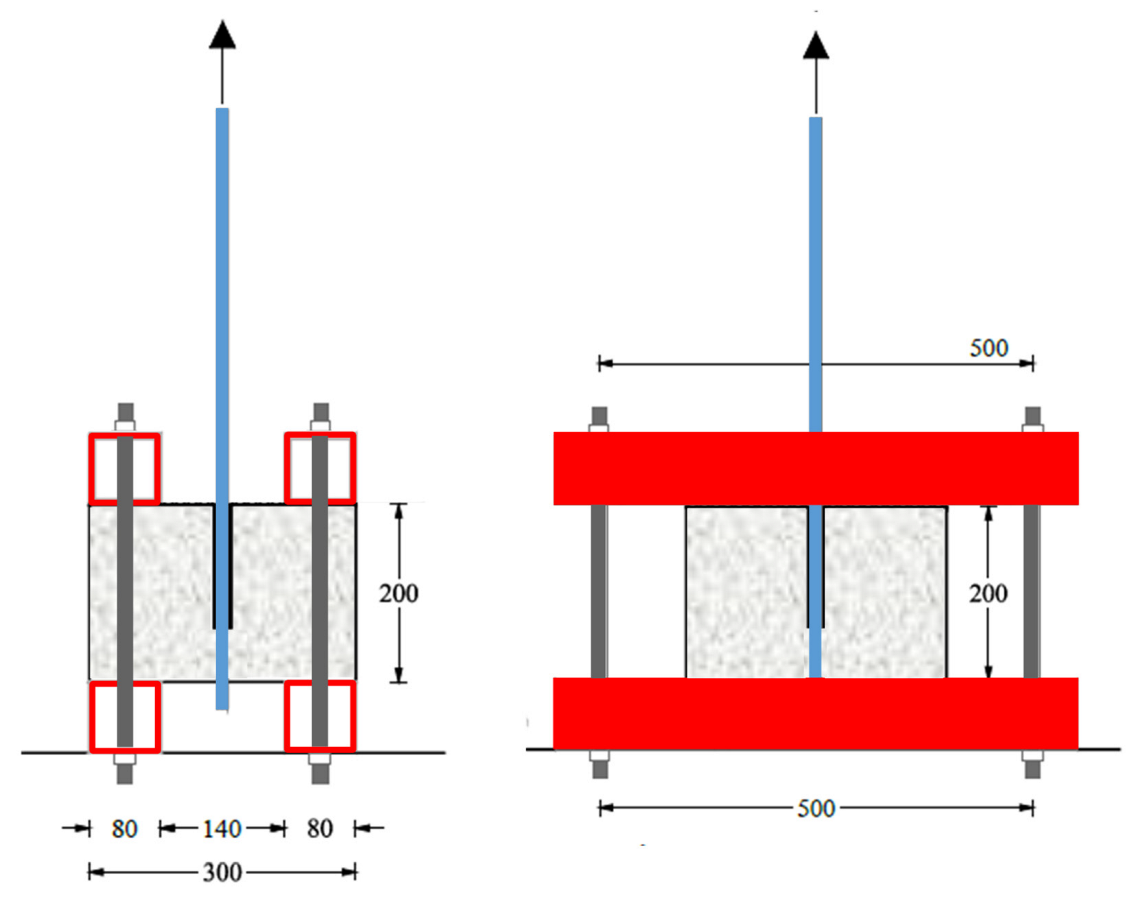
2.4. Bond Strength Evaluation—Pull-Out Tests

Pull-out tests were conducted to determine the bond slip behavior of the bars embedded in concrete in order to accurately simulate the contact law in the subsequent FE analysis. Pull-out specimens with a central rebar arrangement were used.

Each bar was embedded in a 300 × 300 × 200 mm concrete cube. Test specimens comprised of 1.20 m length bars embedded in concrete cubes over a length of five times their diameter (5Ø in Figure 5). In order to accomplish the specified embedment length, contact between the concrete and the bar was avoided using PVC tubing during the casting of concrete, as depicted in Figure 5. A steel tube was bonded to the loading end of the FRP bar using adhesive to form the loading end grip for the adjustment to the test setup.

Figure 6 shows a schematic of the pull-out specimen. For each rebar, four identical specimens were tested to ensure the test setup’s reliability and the test findings’ scatter (Figure 7).

The test setup of the pull-out experiments is illustrated in Figure 8. The load was applied at a rate of 0.5 mm/min to the CFRP reinforcing bar. In order to determine the post peak behavior, all tests were conducted in displacement control mode. During the test, three laser sensors, as depicted in Figure 8, measured the slip of the loaded end of the bar. Typical test results of the performed pull-out tests are presented in Figure 8 in terms of average bond stress versus slip behavioral curves.

3. FE Model

In this section, the FE software, Abaqus, was used to study the behavior of full-scale beam-column joints under lateral imposed cyclic reversal deformations [59]. A 3D FE model was created to account for both the material and geometric nonlinearity, as well as the bond interaction of the longitudinal CFRP reinforcement and the surrounding concrete.

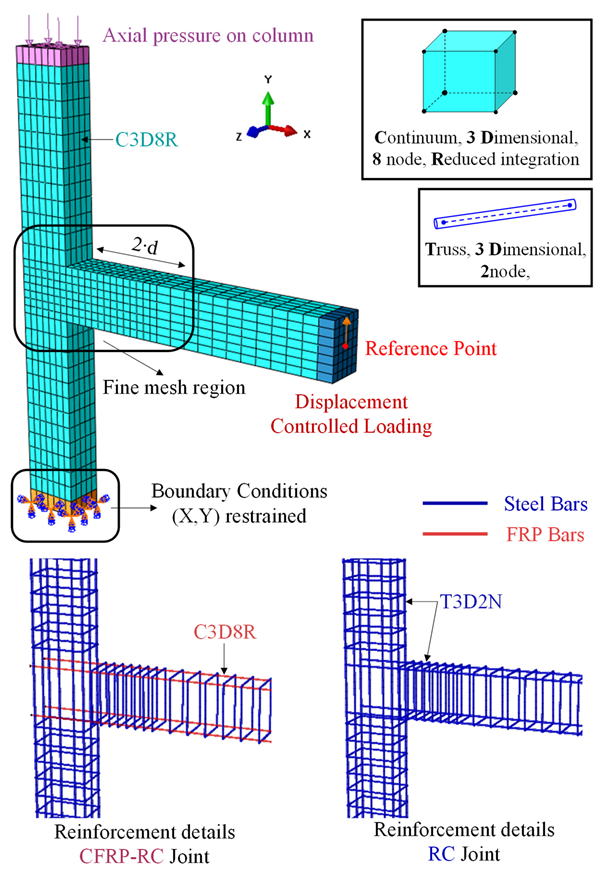
3.1. Meshing

All parts of the beam-column joints were simulated using 3D elements; the concrete and the CFRP bars were modelled using eight-node linear brick elements (C3D8R), while the longitudinal and transversal reinforcement was simulated with two-node linear 3D truss elements (T3D2) in the developed FE model. The mesh arrangement that was adopted in the numerical model was nonuniform to reduce simulation time and avoid convergence issues at the expected regions of substantial inelastic deformations, while a finer mesh was applied in areas of importance and at regions where stress concentration was expected to appear (Figure 9). In the areas of a fine mesh, the maximum mesh element size was set to 25 mm, while it was 50 mm in the rest.

3.2. Material Constitutive Relationship

In order to appropriately simulate the CFRP-RC and RC joints’ behavior, the FE simulation took into account the nonlinearity of concrete under compression and tensile cracking, the elastic–plastic behavior of steel reinforcement, and the elastic–brittle performance of the CFRP reinforcement.

3.2.1. Concrete

In the current FE model, the concrete damaged plasticity (CDP) model available in Abaqus [53] is used to simulate concrete behavior. The CDP model is designed to analyze RC structures imposed to monotonic, cyclic or dynamic stresses. The CDP model enables the definition of both the elastic and plastic properties of concrete. In previous studies, the authors provide further information about the constitutive laws and parameters used [60,61,62].

3.2.2. Steel

The conventional steel reinforcement (longitudinal bars and stirrups) was described as an elastic–plastic material with a strain-hardening behavior. The material demonstrates an elastic linear behavior, following the modulus of elasticity, up to yielding point. After the yielding point is reached, the strain hardening effect begins with an incline of 0.01E_s [63] and reaches its maximum at a strain value of 0.05. Furthermore, the FE analysis required the steel’s poison’s ratio, which was assumed to be 0.3.

Concerning the interaction of steel reinforcement with concrete (column longitudinal bars and stirrups of the beam and column), a full bond was adopted by the use of the embedded region method.

3.2.3. CFRP Reinforcing Bars

The stress–strain curve for CFRP rebars was described as a linear elastic material up to the point of ultimate tensile strength and, afterwards, the brittle failure of the material was considered. The characteristics of CFRP bars varied in the transverse direction because of their fibrous nature, and it would be more appropriate to simulate them as anisotropic materials. However, for the sake of computational simplicity, an isotropic material assumption is used. The model’s accuracy in the current case is unaffected by this supposition as the beam-column joints investigated in the present study are designed not to fail in shear; the contribution of the CFRP reinforcement’s shear dowel action is presumed to be minimal. Consequently, the shear failure of the CFRP bars is not included in this work. The longitudinal beam reinforcement mostly contributes by transmitting axial tensile forces, and, hence, CFRP bars contribute in the fiber direction. The modulus of elasticity and ultimate strength are the mechanical properties necessary to define the CFRP material within the FE model.

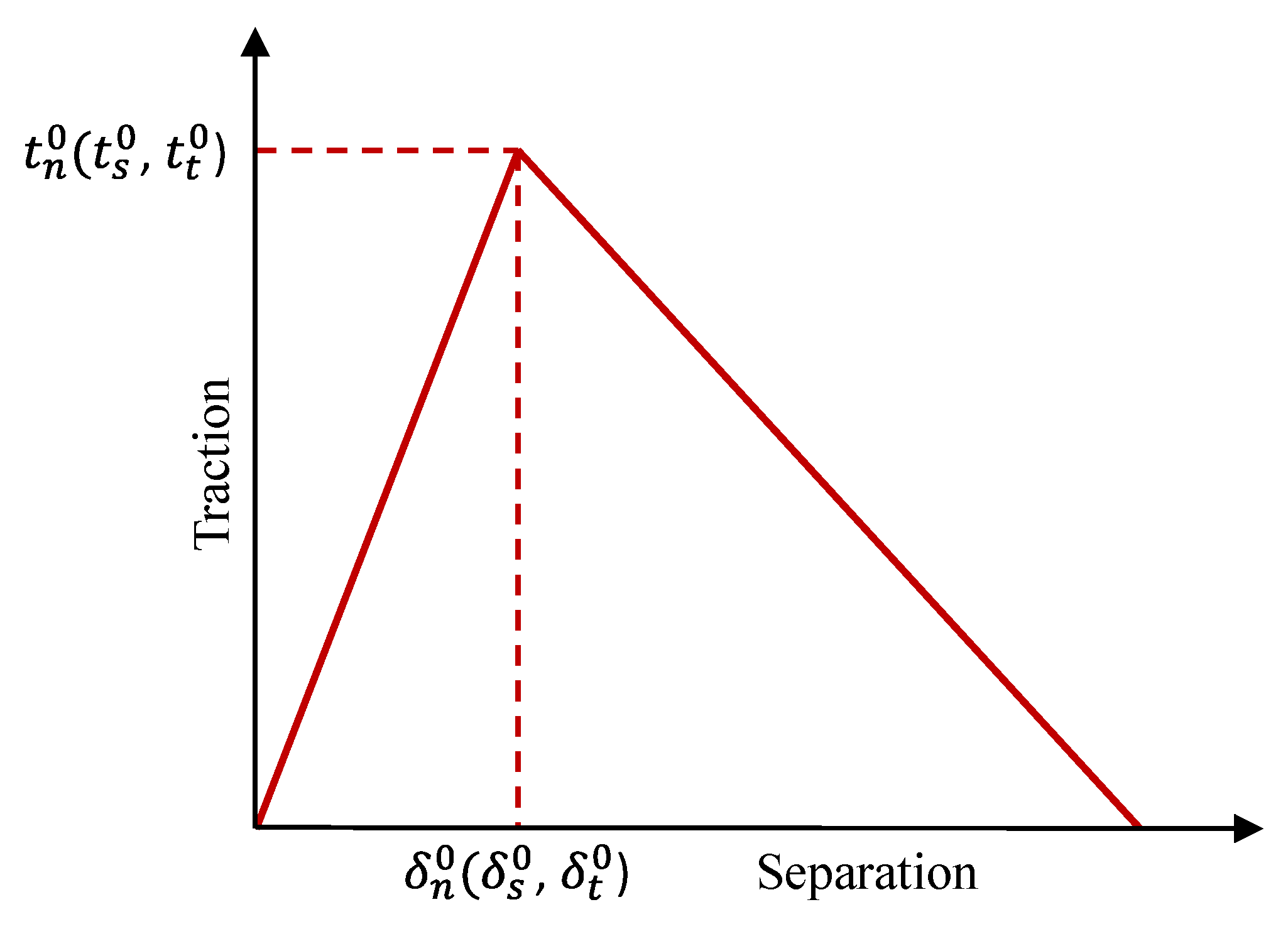
3.3. Bond Slip Interaction—Cohesive Method

In this model, the surface-based cohesive behavior was employed to represent the bond stress versus slip behavior between CFRP bars and concrete, utilizing the Abaqus cohesive approach. This approach, referred to as the surface-to-surface method, can be used to determine the contact parameters of two surfaces in contact. In comparison to the node-to-surface approach, this method was selected because it generates more trustworthy results [64]. Moreover, the surface-to-surface technique applies contact criteria in an average sense over the regions that surround the slave nodes, suggesting that each restriction will not only consider one slave node but also nearby slave nodes [65].

To assign surface-to-surface contact, the user must identify two surfaces that are in touch. The surface that has a coarse mesh is defined as the master surface, while the surface that contains a fine mesh is defined as the slave surface.

Abaqus calculates the bond behavior for this contact model using the linear elastic traction–separation model, as illustrated in Figure 10. This model begins by making the assumption of elastic behavior, then proceeds on to consider the initiation and progression of damage. The elastic behavior is expressed in terms of an elastic constitutive matrix that connects normal and shear stresses to normal and shear interface separations. Considering uncoupled normal and tangential stiffness components, the traction–separation behavior matrix is as follows

$$T=\left\{\begin{array}{c}{t}_n\\ t_s\\ t_t\end{array}\right\}=\left[\begin{array}{ccc}{k}_{nn}& 0& 0\\ 0& k_{ss}& 0\\ 0& 0& k_{tt}\end{array}\right]\left\{\begin{array}{c}{\delta }_n\\ {\delta }_s\\ {\delta }_t\end{array}\right\}={\rm K}\delta ,$$

(1)

where t_n = nominal traction in the normal direction; t_s and t_t = nominal stresses in two local shear directions; δ_n, δ_s and δ_t = corresponding displacements. k_ss, k_tt, and k_nn are derived as follows [66]

$$k_{ss}=k_{tt}=\raisebox{1ex}{${\tau }_m$}\!\left/ \!\raisebox{-1ex}{$s_m$}\right.,$$

(2)

$$k_{nn}=100·k_{ss}=100·k_{tt},$$

(3)

The pull-out tests that were conducted in the current research provided the specifications for maximum bond strength (τ_m) and slip at maximum bond strength (s_m) (see also Figure 8).

3.4. Boundary Conditions and Load Application

To achieve convergence, the boundary conditions were modelled equivalently to the experimental test’s supports. To simulate the boundary conditions for the beam-column joints in the experimental testing, the top face of the column was restricted in the X-direction resulting in a roller support, while at the bottom of the column, a hinge support was formed by constraining against the X and Y movement.

As indicated in Figure 9, the column’s axial load was applied to the surface of the column, while the displacement control load was applied to the reference point on the beam profile. The load was applied steadily and gradually in accordance with the loading sequence of the experimental procedure.

4. Results and Discussion

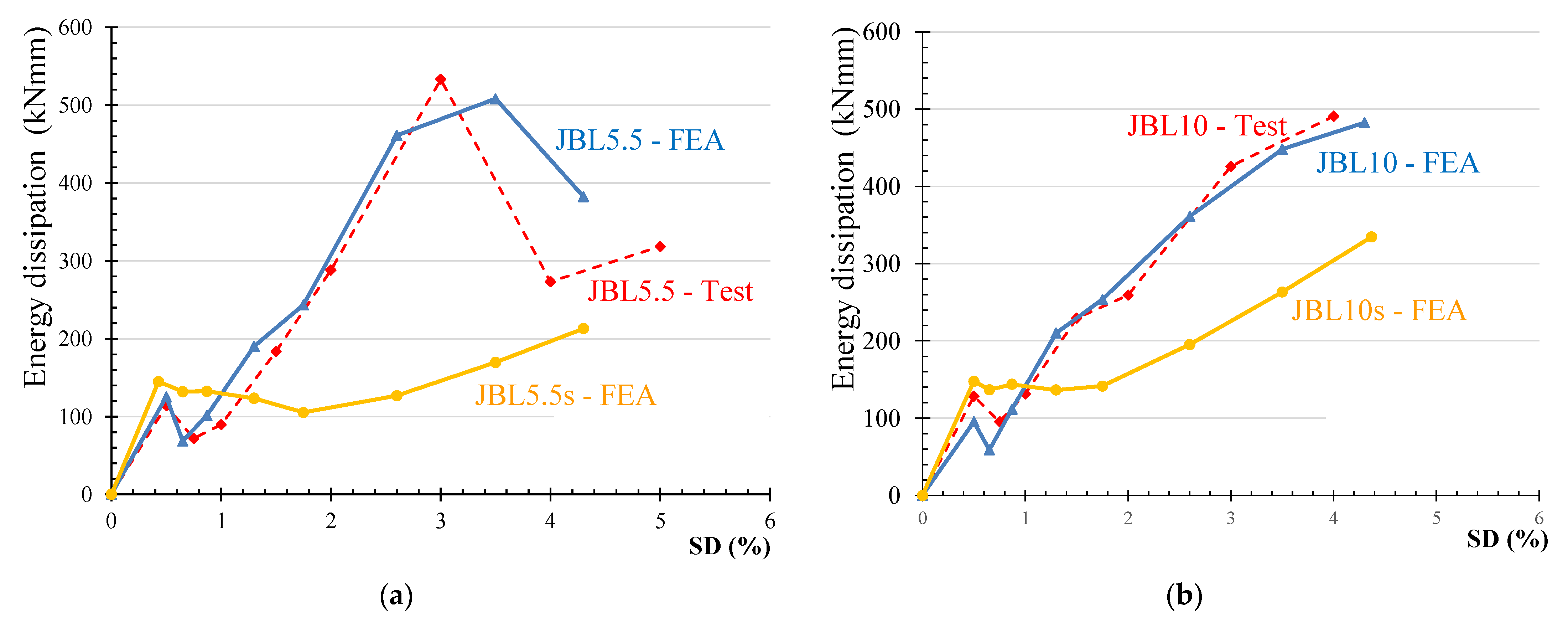
4.1. Verification of the FE Model

To evaluate the ability of the developed FE simulation to estimate the lateral response of beam-column joints using CFRP bars as a longitudinal reinforcement in the beam, a comparison was made between the predicted and experimental CFRP-RC beam-column joint specimens. The next section provides specific comparative results. Figure 11 shows a comparison between the applied load versus SD curves predicted using the FE analysis (noted as “FEA”) and the experimental one (noted as “Test”). In both investigated joints the model predicts the maximum load at a satisfactory level as well as the post cracking behavior.

Figure 12 presents a comparison between the predicted area of damage occurrence and the experimental results. Clearly, the model was capable of accurately predicting the failure of the specimens. For the specimen JBL10 a large crack opened in the beam area close to the joint connection, while no cracking occurred in the joint body. The corresponding mode of failure predicted by the FE analysis also illustrates damage close to this area, while in the joint core no damage is represented as in the experimental specimen. Only low strain concentration around the CFRP bars is illustrated, which is attributed to the slippage of the CFRP bars.

Figure 13 illustrates that the developed model can also successfully capture the CFRP bar slippage. In particular, for the specimen JBL10, the predicted slip is almost identical to the corresponding slip calculated in the experimental test. In the case of the JBL5.5 specimen, the FE analysis predicted a smaller slip than that experimentally measured but this still remains within acceptable limits. The observed differences between the experimental results and FE model predictions of slip of JBL5.5 could be attributed to the protentional discrepancies and uncertainties of the CFRP bar and concrete bond slip simulation adopted in the cohesive approach described in Section 3.3.

Figure 14 represents the energy dissipation calculated from the experimental results simply summing up the amount of energy that was lost over the course of several load-displacement cycles and the energy dissipation extracted from the FE analysis. In terms of energy dissipation, the FE simulation is satisfyingly close to the experimental results.

According to the validation results, the developed FE simulation can accurately estimate the lateral response of CFRC beam-column joints.

4.2. Use of CFRP Bars versus Conventional Steel Rebars as Beam Longitudinal Reinforcement

Since the experimental program did not contain steel RC joints with conventional steel rebars in the beam, the authors were not able to validate the developed FE simulation against such experimental results of RC joints. Nonetheless, the previously developed FE models by the authors [52,53], which were validated for the monotonic and cyclic response of RC beams against shear and flexure, are equally applicable for predicting the behavior of RC joints. Notably, no significant alterations to the established FE analysis for the CFRP-RC joints were performed aside from employing longitudinal steel reinforcing bars in the beam region shown in Figure 9.

Compared to the CFRP-RC specimens (JBL10, JBL5.5), the steel-reinforced specimens (JBL10s, JBL5.5s) demonstrated a quicker decline in load bearing capacity (Figure 11). The steel RC specimens exhibited linear behavior up to an SD = 0.6%. Due to the yielding of the steel reinforcement, the rate of growth in the specimens’ lateral capacity reduced and stayed practically constant up to an SD = 4%.

At greater SD ratios, the CFRP-RC maintained a higher load. This suggests that CFRP-RC beam-column joints may withstand a seismic event with minimal residual damage. This function decreases the post event cost of repairing the framed structure and permits the complete restoration of the original CFRP-RC section performance by replacing the damaged concrete. However, this is not applicable for steel RC sections, which are intended to yield at such a point of ultimate loading. Even by repairing the damaged concrete, the original section’s strength and stiffness (prior to yielding) cannot be recovered.

After attaining their design capacity, specimens JBL10 and JBL5.5 revealed a decrease in lateral load resistance at an SD = 1%. This decrease is attributable to the slip of the beam longitudinal bars that were anchored in the joint as a result of bar anchoring failure. As seen in Figure 11a,b, despite the anchorage’s failure, both specimens were still able to withstand about 35.0% of their initial capacity through their final loading cycles until the completion of the test at an SD = 4%. Despite the fact that the slip of the bar is a brittle form of failure, it must be emphasized that specimens JBL10 and JBL5.5 were initially intended to attain the desired shear stress in the joint body when the beam achieves its flexural capacity. The failure due to slip of the bars occurred after the joint achieved the intended load level, as illustrated in Figure 13a,b, and that has no effect on the study’s analysis or findings given the study’s scope. In addition, earthquake occurrences are regarded as extreme–ultimate limit state situations; hence, the performance of both specimens after the failure occurrence is significant since it exhibited a residual strength greater than 35% of the maximum load after the slip of the bars.

The envelope of the specimens’ total dissipated energy at each loading versus SD is depicted in Figure 14. It is evident that both CFRP-RC specimens had a comparable degree of dissipated energy up to an SD = 3%, but the energy dissipated at failure slightly differed for each specimen. In addition, the figure indicates a substantial association between the energy lost due to hysteretic activity and the extent of damage detected during the test. As the specimens fail, the inclination of the curve of cumulative energy dissipation versus SD rises, indicating the concrete deterioration rate owing to the development of plastic hinges. Nevertheless, the increase in energy dissipation during the final steps of loading for specimens JBL10 and JBL5.5 is mostly attributable to the slippage of the longitudinal reinforcement of the beam, as previously noted. Figure 14 also demonstrates that specimens with conventional reinforcement dissipated less energy than those with CFRP. While reduced energy dissipation is regarded as a disadvantage, it also implies that the joint recovers its previous form when the stresses are eliminated, needing only a minimal degree of restoration after undergoing such loading action.

5. Conclusions

This paper deals with the application of CFRP bars as a beam’s longitudinal reinforcement in RC beam-column joint full-scale specimens under cyclic lateral deformations. An experimental investigation that involved two full-scale CFRP-RC joints was conducted and accompanied with eight CFRP bar pull-out tests in order to obtain the bond stress versus slip behavior for the bars. Furthermore, a numerical study was performed. An FE model was developed that could successfully predict the behavior of CFRP-RC joints. Additionally, a comparative study of steel RC joints and CFRP-RC joints was conducted to investigate the potential replacement of the conventional steel reinforcement with CFRP bars. On the basis of the study’s findings and discussion, the following conclusions may be drawn:

• The experimentally evaluated specimens’ load-carrying capacity and load-deflection response could be accurately predicted using the nonlinear FE model provided in this work. The failure mechanism, bond slip of CFRP bars and energy dissipation comparison data demonstrated that the model can properly predict the behavior of CFRP-RC joints.
• The slippage of the CFRP bars occurs after the reach of the ultimate load and thus does not significantly affect the post failure behavior and the hysteretic performance of the joint. The investigated CFRP-RC joints exhibited a residual strength higher than 35% of the flexural capacity after the occurrence of slippage. However, more investigation must be conducted in order to ensure the post failure mode and overall response of joints with CFRP longitudinal reinforcement bars.
• The dissipated energy of the CFRP-RC joints increased gradually following the specimen’s mode of failure. However, after a certain point the continuous increase up to failure is possibly attributed to the bar slippage. After the reach of an approximate SD = 0.5%, the dissipated energy of the steel-reinforced joints was significantly lower than that of the CFRP-RC joints.

Overall, the behavior of RC joints with beams’ CFRP longitudinal reinforcements indicated promising results and the favorable contribution of the CFRP bars in the seismic performance of RC joints. CFRP bars have great potential of partially or even fully replacing conventional steel bars in RC structural elements. More research must be conducted though in order to form regulations and design specifications so that CFRP bars become widely applicable in the construction industry.