Investigations on Interface Shear Fatigue of Semi-Precast Slabs with Lattice Girders
Featured Application
Abstract
1. Introduction
2. Lattice Girders for Use in Cyclically Loaded Structures
2.1. General
2.2. Fatigue Tests from Literature
2.3. Fatigue Design of Semi-Precast Slabs with Lattice Girders in Germany
- vRdi design (d) shear resistance (R) of interface (i)
- c coefficient of adhesion
- fctd design value of concrete (c) tensile (t) strength of the weaker concrete layer
- μ coefficient of friction
- σn external normal (n) stress perpendicular to the interface acting simultaneously with the shear stress
- compressive stress: 0 ≤ σn ≤ 0.6·fcd
- tensile stress: σn < 0 with c·fctd = 0
- ρ interface reinforcement ratio ρ = Asi/Ai
- with
- Asi the area (A) of steel (s) reinforcement crossing the interface including shear reinforcement from shear design with sufficient anchorage at both sides of the interface
- Ai the area of the interface
- fyd design yield (y) strength of the interface reinforcement
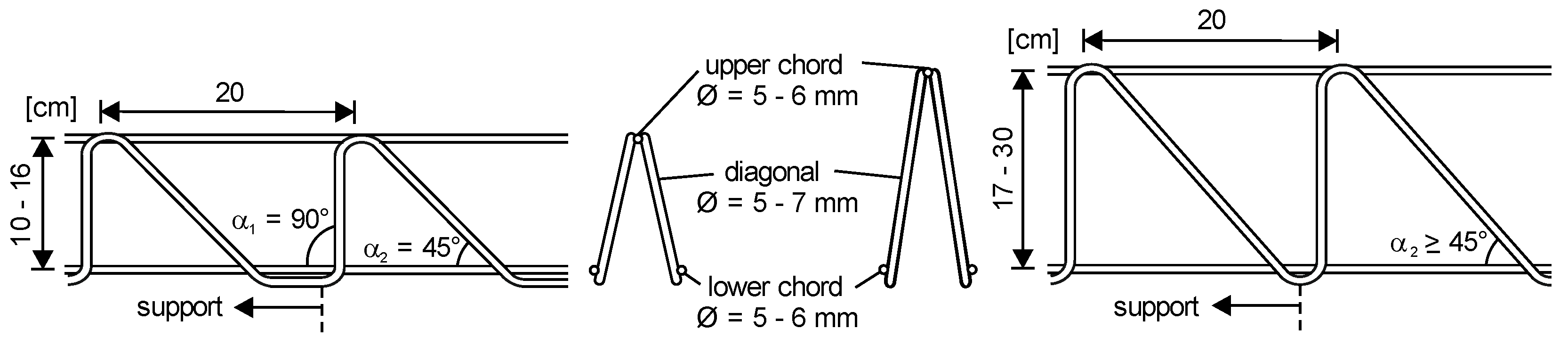
- α inclination of interface reinforcement 45° ≤ α ≤ 90°
- ν strength reduction factor for concrete cracked in shear
- fcd design concrete cylinder compressive strength.
- ΔvRdi,fat,LG range of fatigue (fat) design (d) shear resistance (R) of interface (i) using lattice girders (LG)
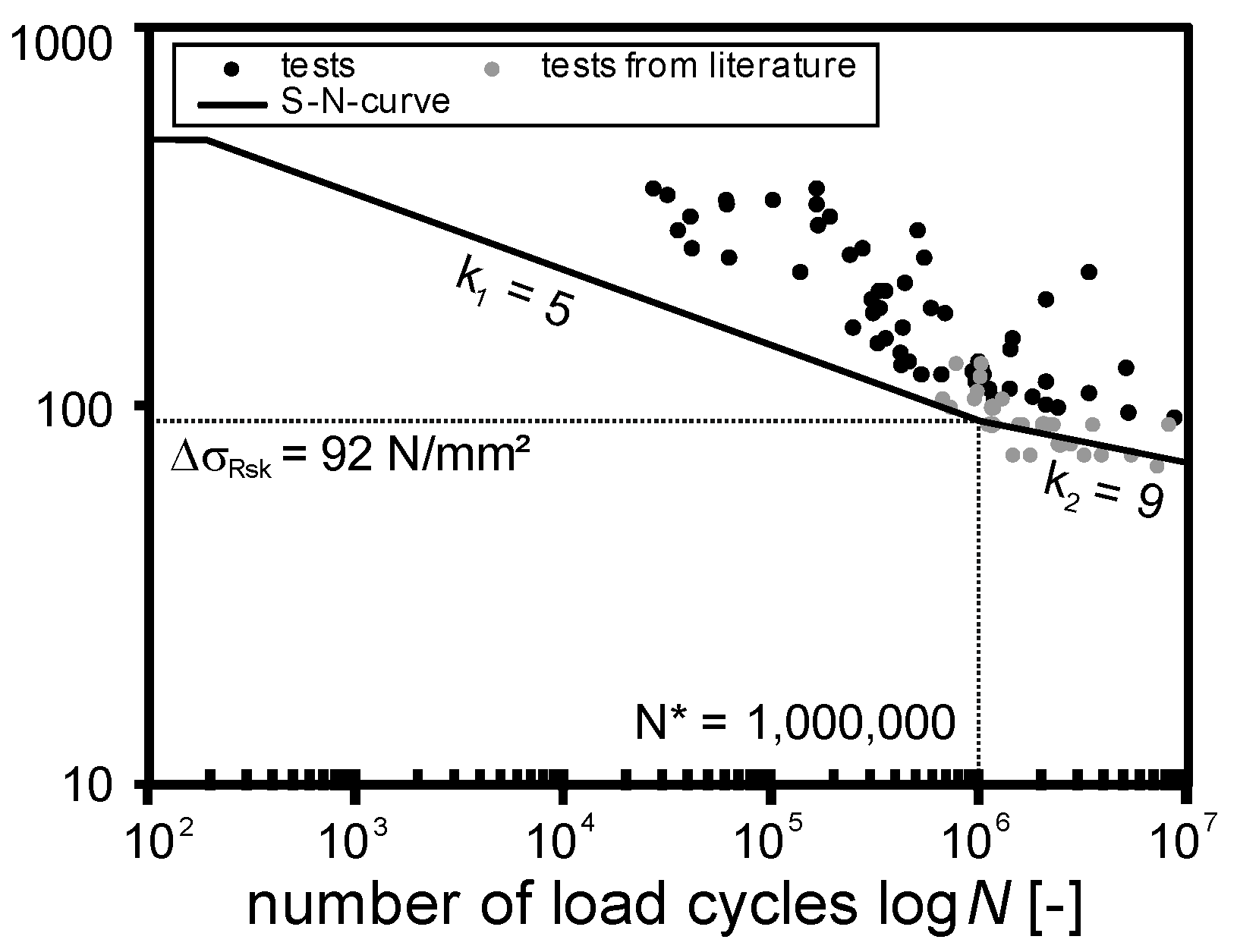
- ΔσRsk approved characteristic stress range with ΔσRsk = 92 N/mm2 for N = 2.0 million load cycles
- γs,fat partial safety factor of reinforcement under fatigue γs,fat = 1.15
- α2 inclination of inclined diagonal in accordance to Figure 2.
- vRdi,max,fat maximum fatigue shear resistance
- vRdi,max maximum static shear resistance according to Table 2.
3. Small Size Fatigue Tests to Determine S–N Curves for Lattice Girders
3.1. Introduction
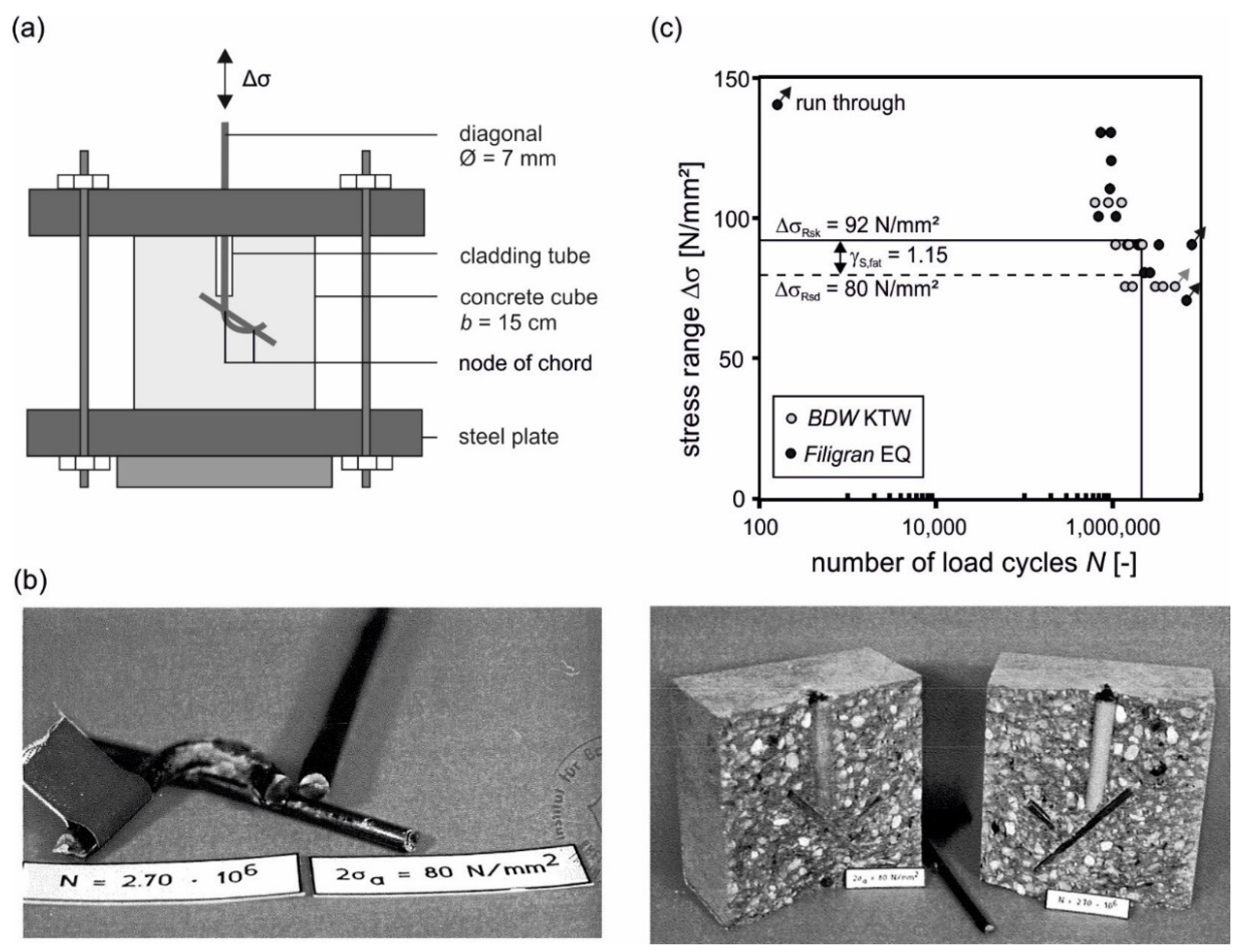
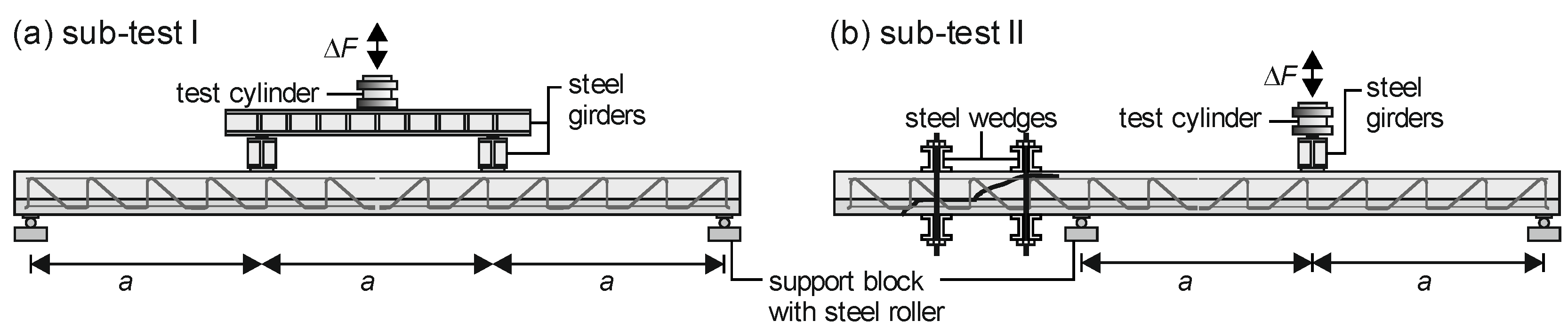
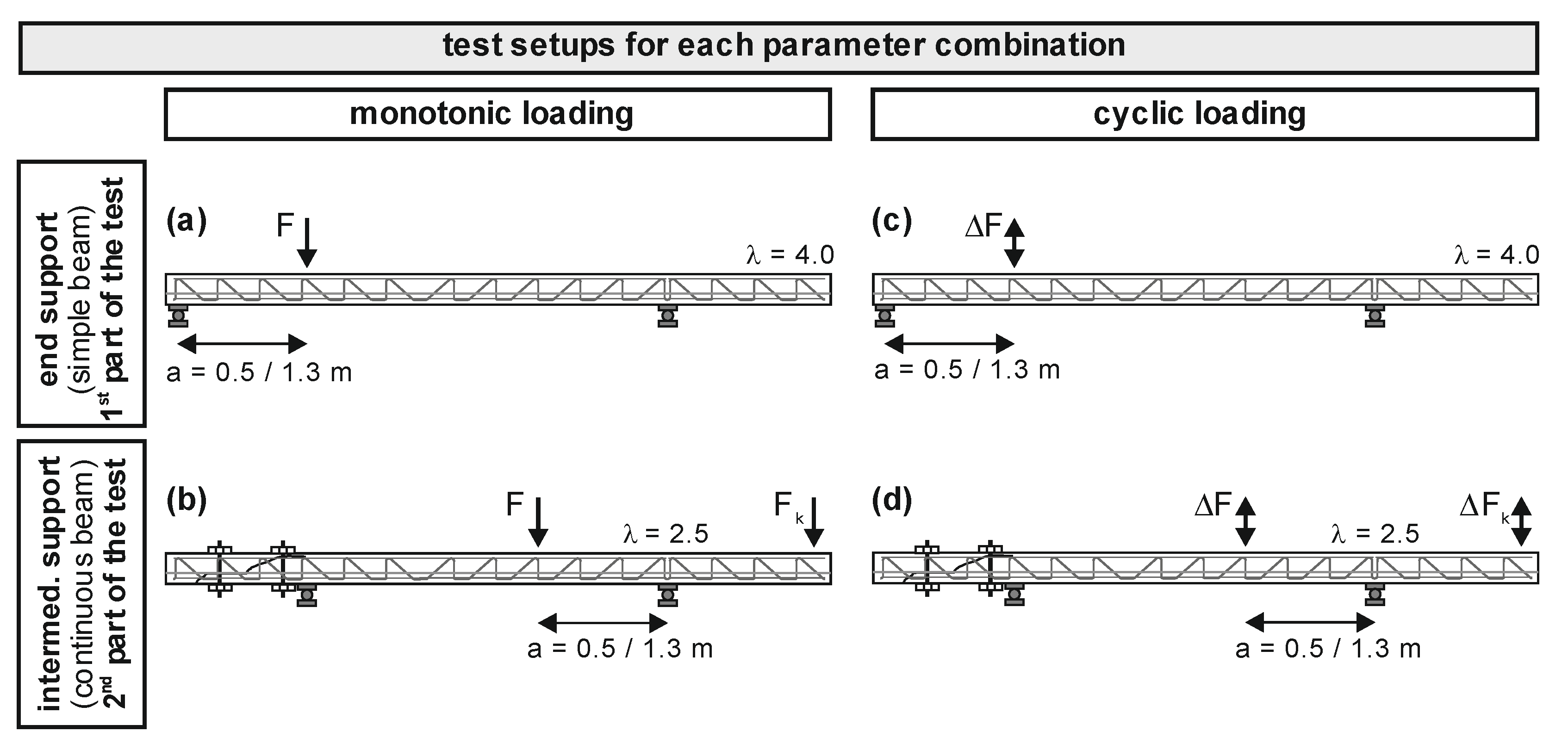
3.2. Description of Test Specimens and Test Setup
3.3. Test Procedure
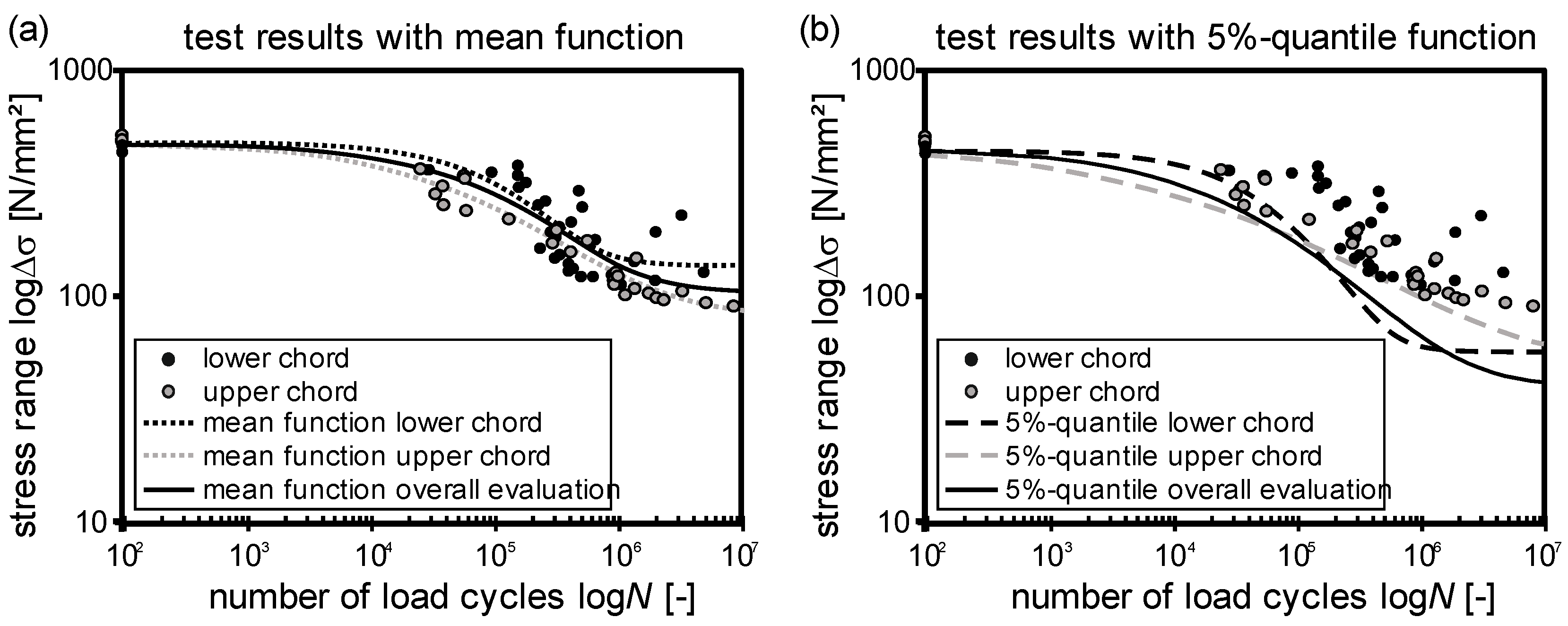
3.4. Results of Small-Size Fatigue Tests
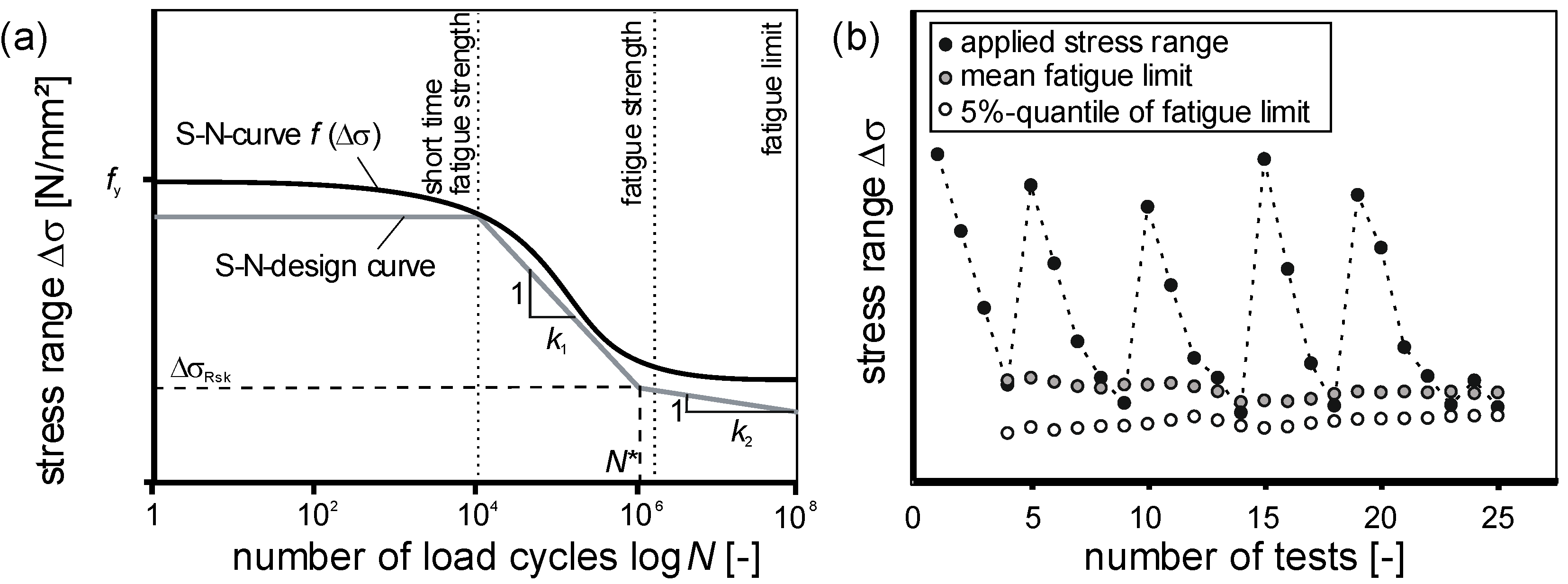
3.5. Evaluation of S–N curves for Lattice Girders
- ΔσRsk expected stress range
- ΔσRsk(N*) stress range at N* load cycles
- N* number of load cycles at break of slope
- N expected number of load cycles
- k stress exponents
- with
- k = k1 stress exponent for N < N*
- k = k2 stress exponent for N > N* with k2 = 2·k1—1
- fyk characteristic yield strength.
4. Fatigue Tests on Semi-Precast Slabs with Lattice Girders
4.1. Introduction
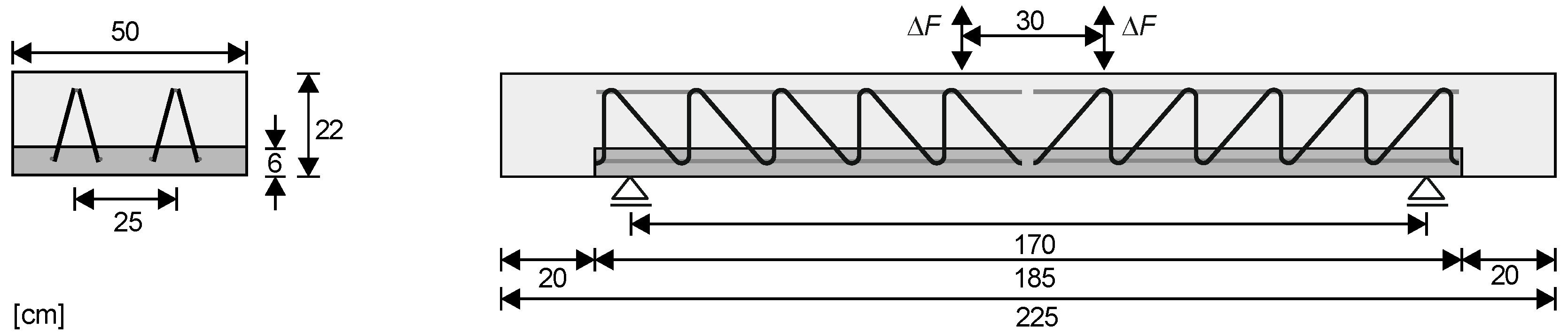
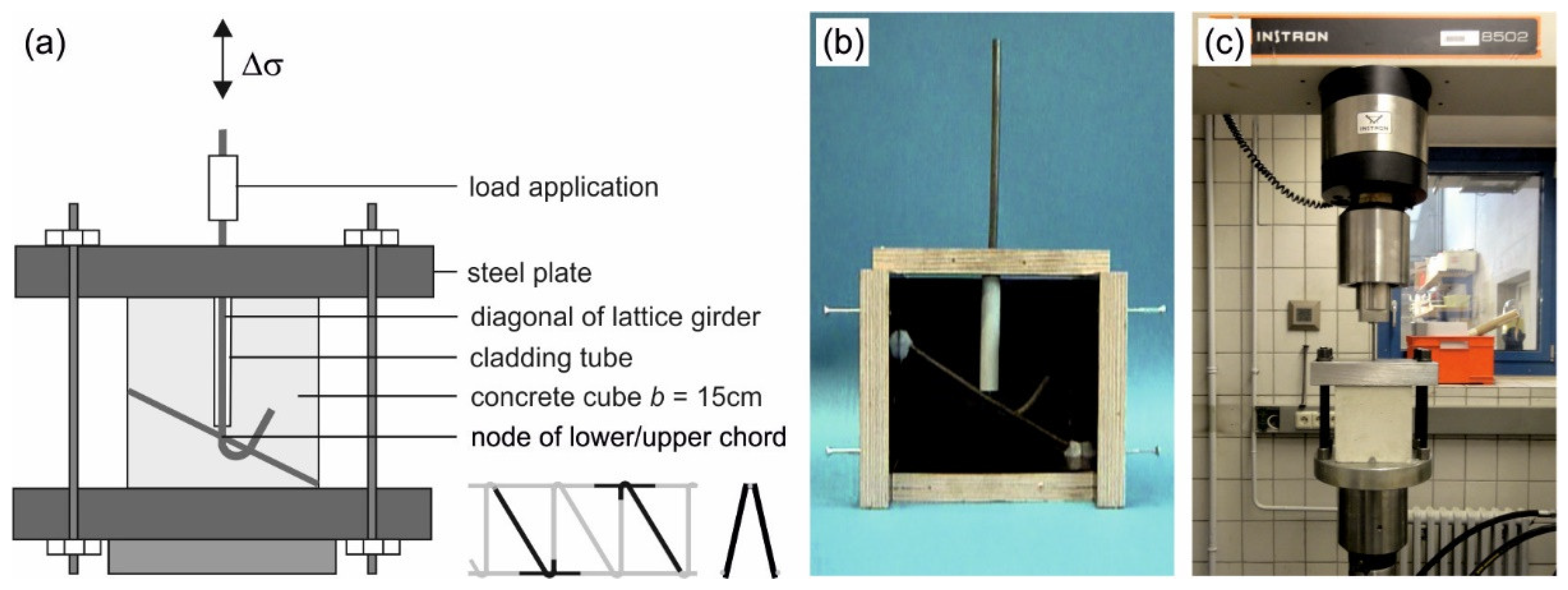
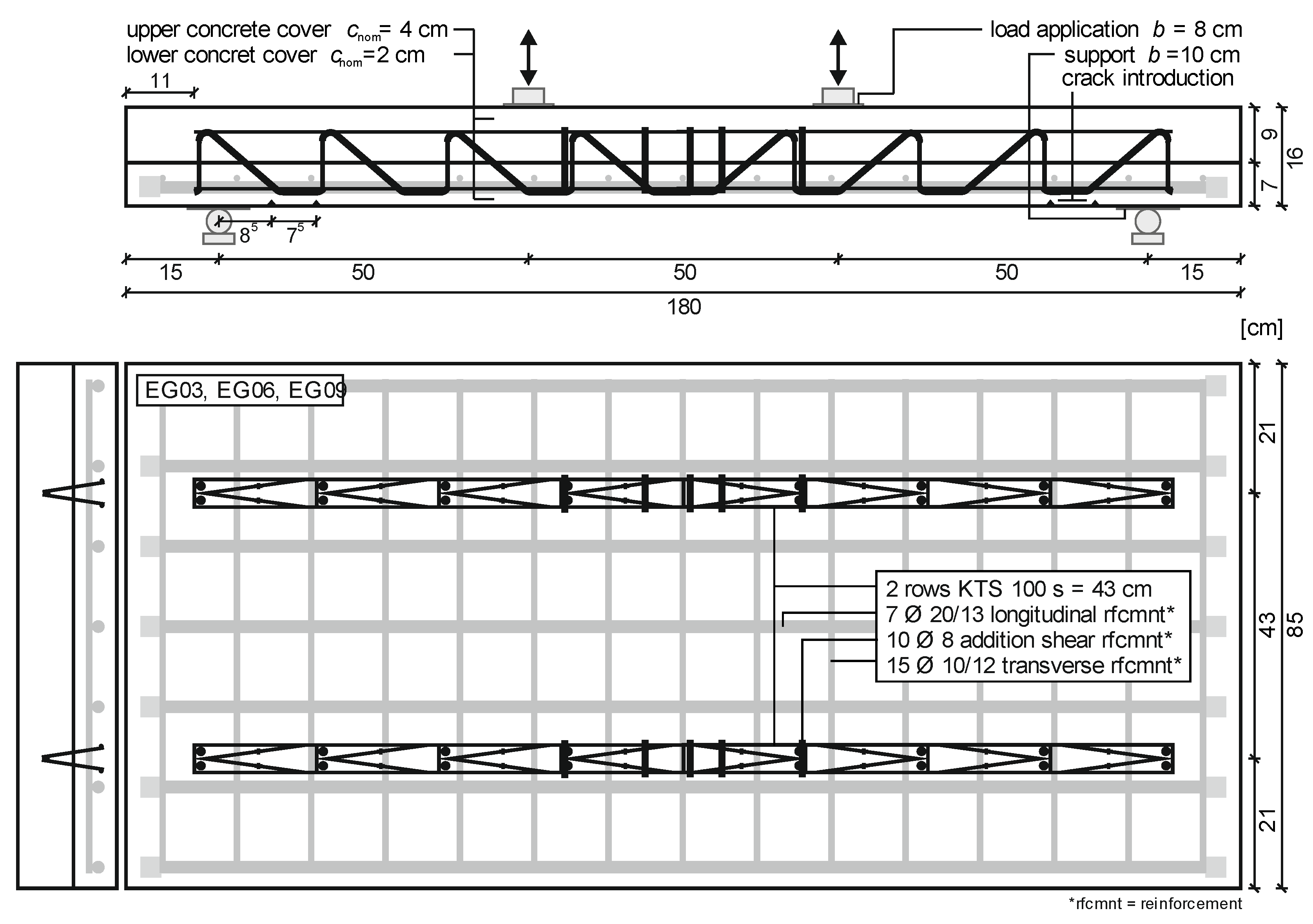
4.2. Description of Test Specimens
4.3. Fabrication of Test Specimens
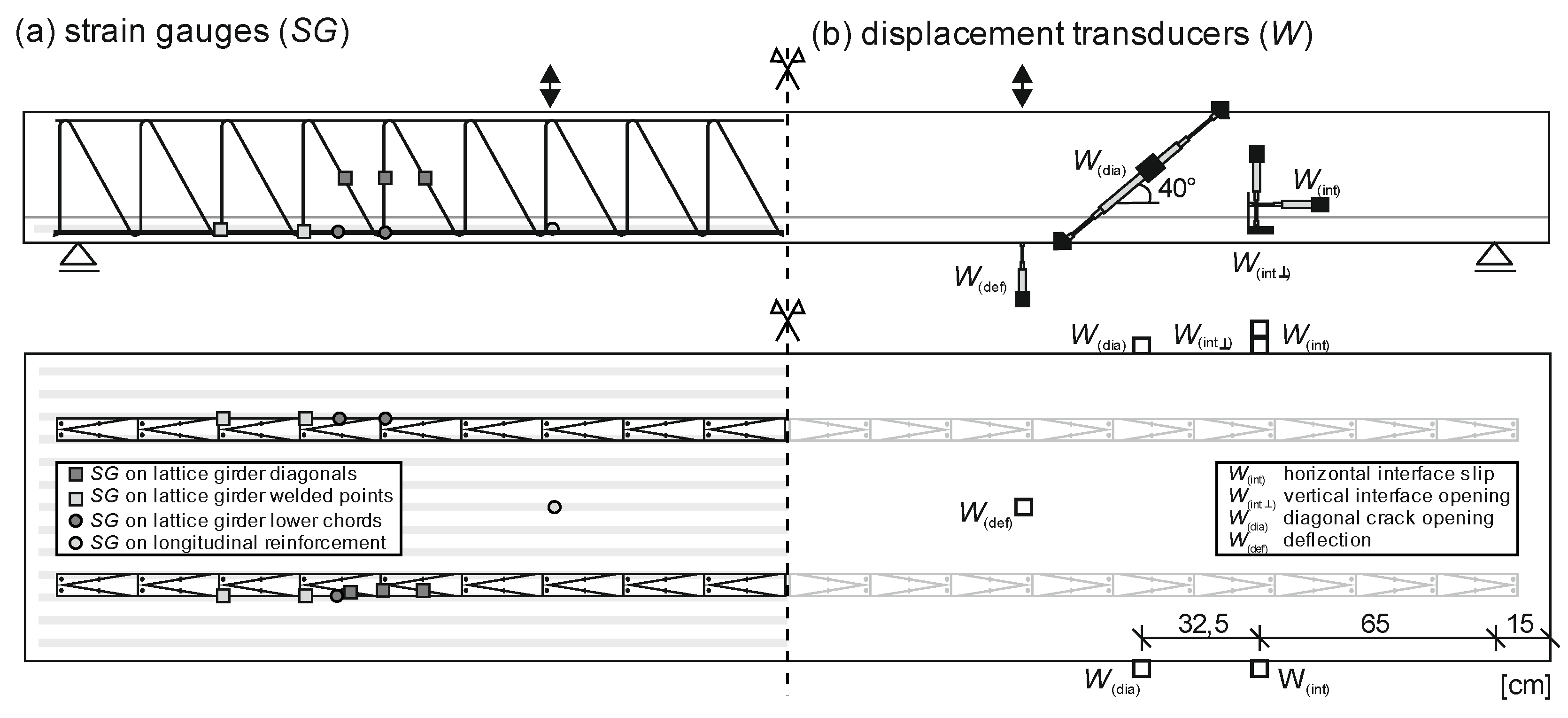
4.4. Test Setup and Test Execution
4.5. Test Results
4.5.1. General
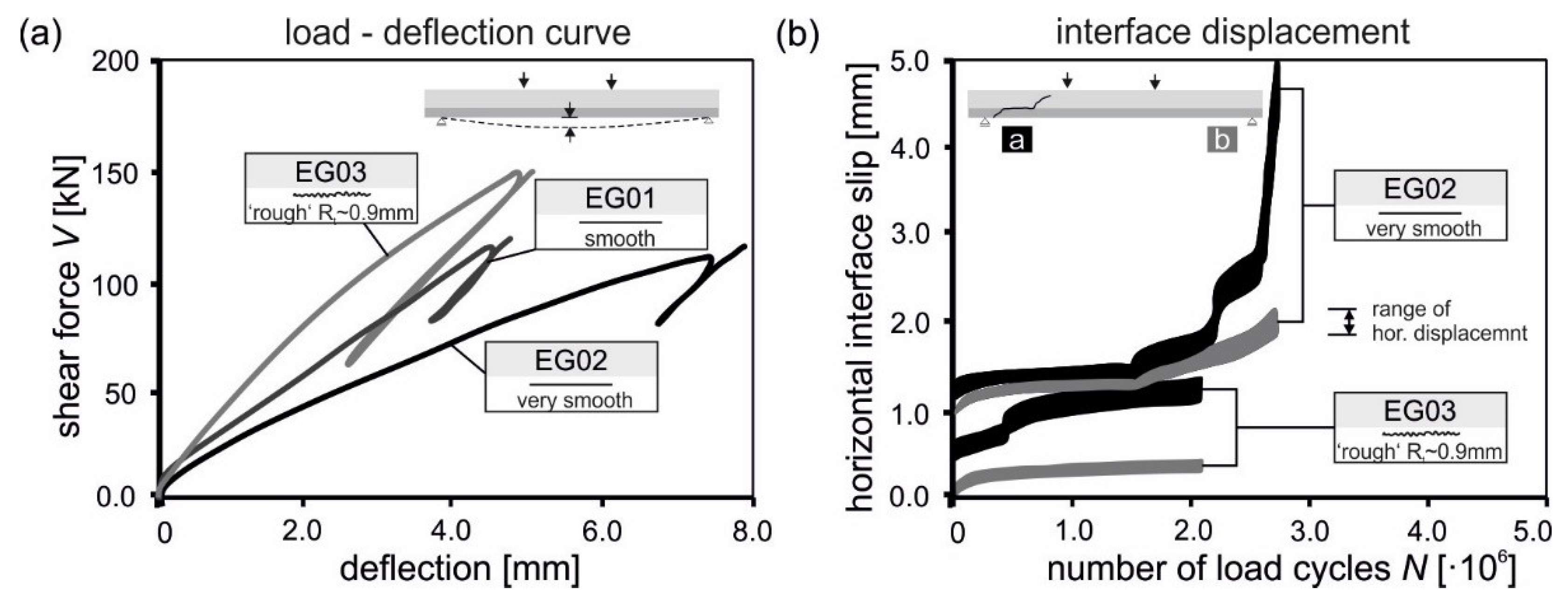
4.5.2. Influence of Interface Roughness
- left as cast with bond breaker (very smooth, EG02)
- left as cast with a roughness depth of Rt = 0.24 mm determined by the sand-patch method (smooth, EG01)
- left as cast with an aspired roughness depth of Rt ≈ 0.9 mm (‘rough’, EG03)
- left as cast with slightly roughening to Rt ≈ 2.0 mm after casting (rough, EG09)
4.5.3. Influence of Interface Reinforcement Ratio
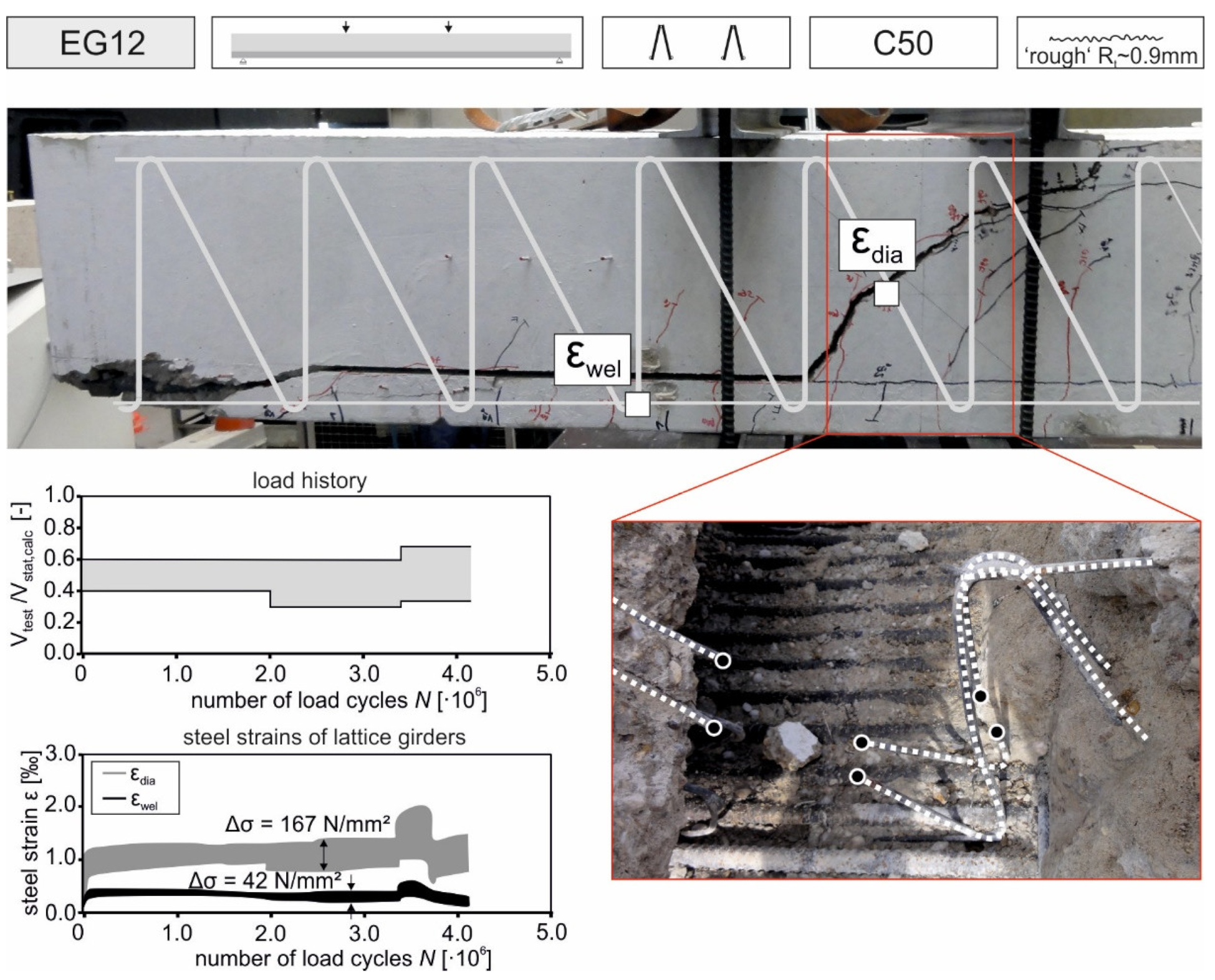
4.5.4. Influence of Steel Strains
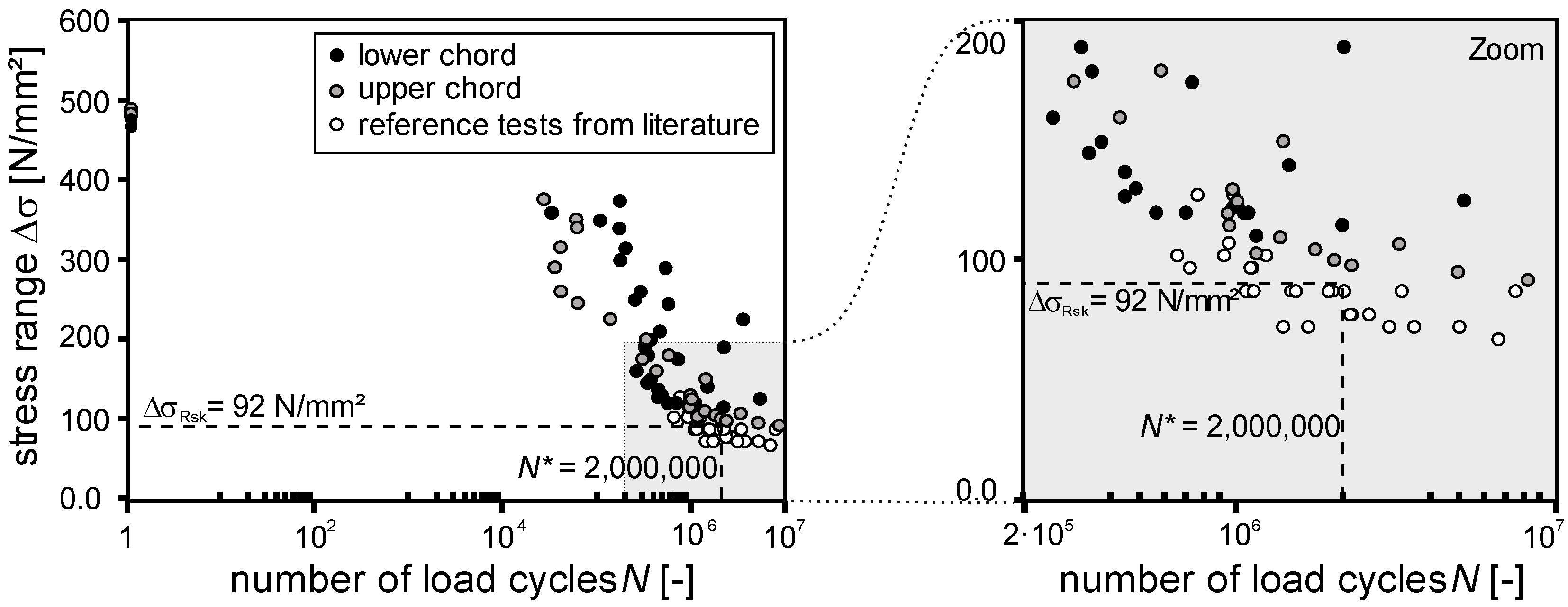
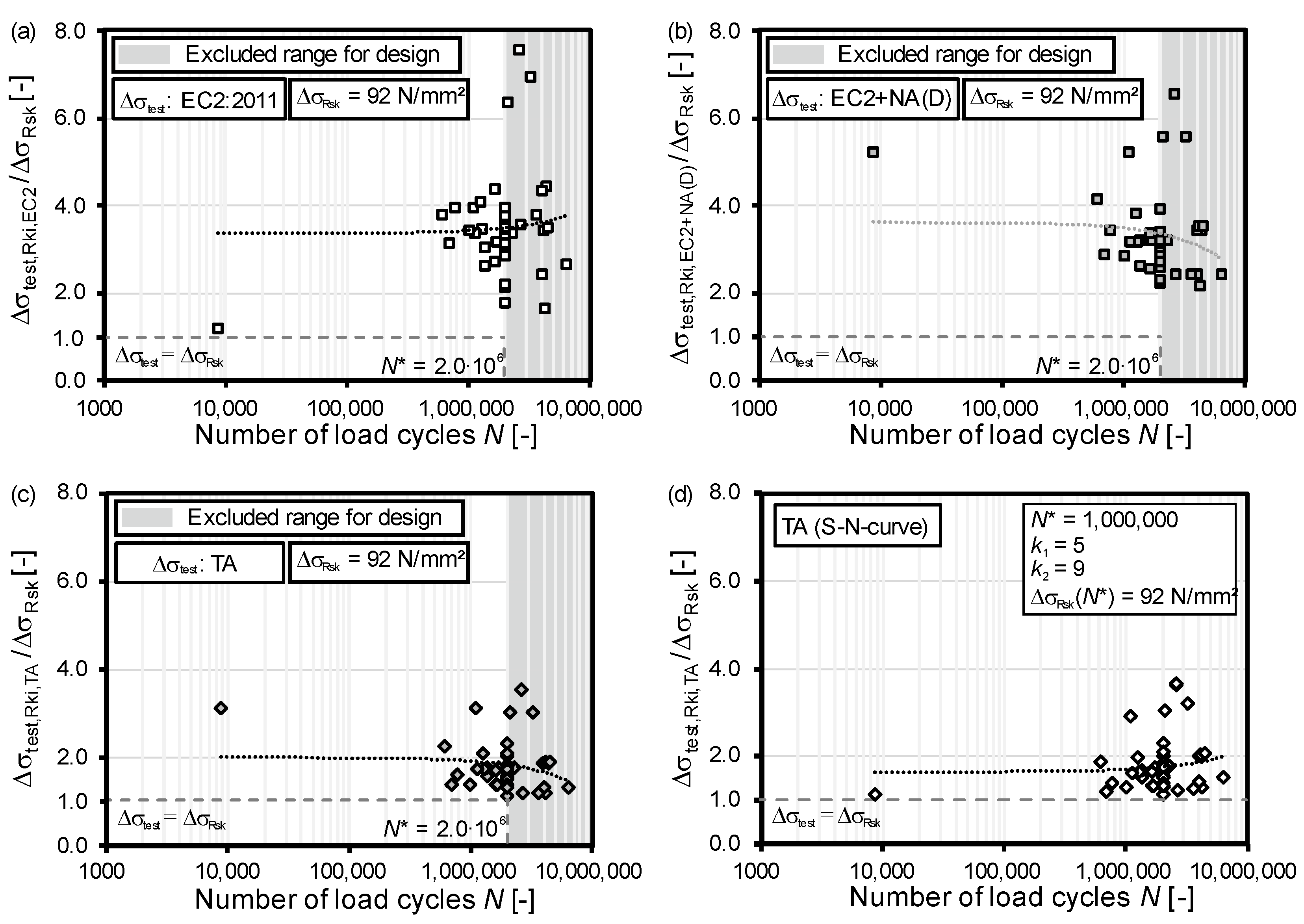
4.6. Test Evaluation and Comparison to Design Regulations
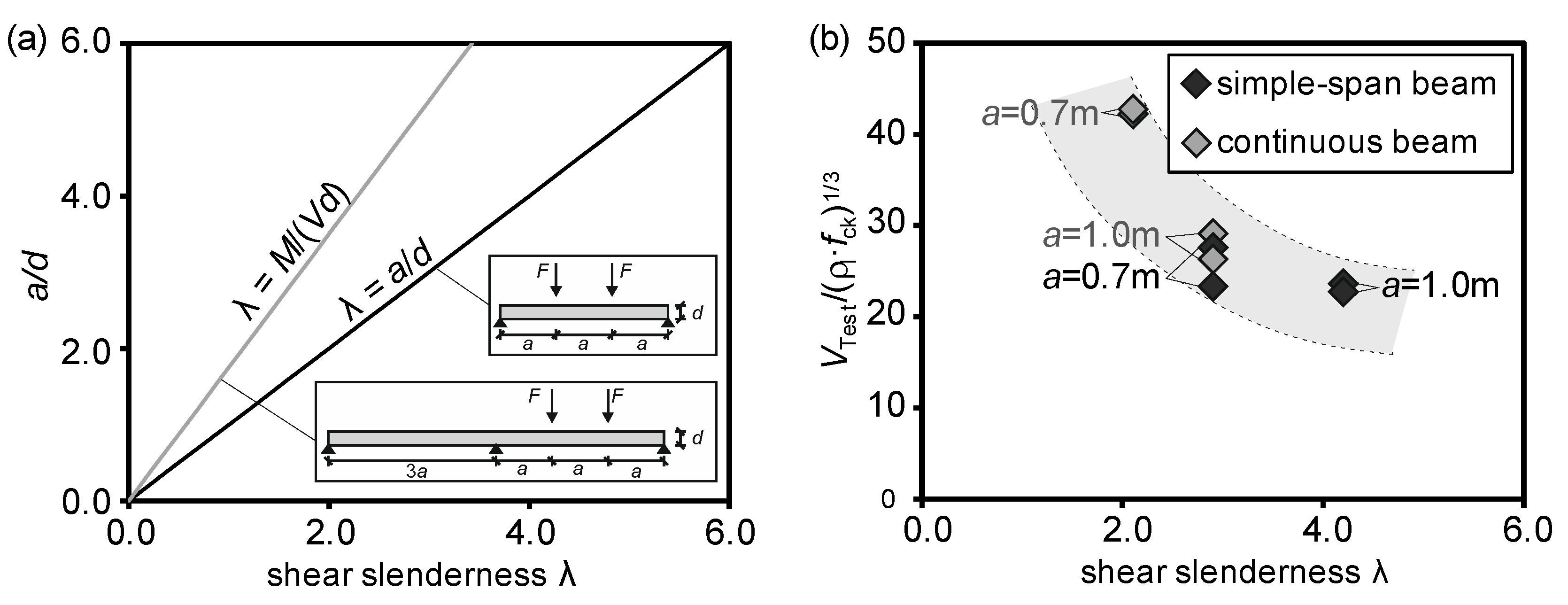
5. Tests on Continuous Semi-Precast Slabs with Lattice Girders
6. Summary and Conclusions
- For the fatigue tests, higher scatter occurred compared to static tests. The scatter concerns the failure mode, interface delamination, strain of lattice girders, and achieved number of load cycles.
- The failure of specimens with low degrees of interface reinforcement was generally induced by interface failure after high numbers of load cycles with N > 2.0 million. Therefore, the bearable fatigue load level generally increases with increasing roughness. Only one specimen with a rough interface had an unexpected premature failure, which needs further investigation.
- Specimens with medium interface reinforcement ratios failed predominantly by vertical shear with only small interface delamination.
- The failure of specimens with high interface reinforcement ratios was generally introduced by anchorage failure of the lattice girder in the compression zone or by anchorage failure of the longitudinal reinforcement.
- The stress ranges in the lattice girders determined by test results were considerably higher compared to the approved stress range according to the technical approvals.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Furche, J.; Bauermeister, U. Flachdecken in Elementbauweise mit Gitterträgern. Beton-Stahlbetonbau 2014, 109, 783–792. [Google Scholar] [CrossRef]
- Chang, T.S.; Kesler, C.E. Fatigue Behavior of Reinforced Concrete Beams. J. Am. Concr. Inst. 1958, 55, 245–254. [Google Scholar]
- Price, K.M.; Edwards, A.D. Fatigue Strength in Shear of Prestressed Concrete I-Beams. ACI J. 1971, 68, 282–292. [Google Scholar]
- Frey, R.P. Fatigue design concept considering the indefinite state of stress in the reinforcement of RC-beams. IABSE Rep. 1982, 37, 409–414. [Google Scholar]
- Ueda, T.; Okamura, H. Behavior in shear of reinforced concrete beams under fatigue loading. Concr. Libr. JSCE 1983, 37, 37–69. [Google Scholar]
- Kwak, K.-H.; Park, J.-G. Shear-fatigue behavior of high-strength reinforced concrete beams under repeated loading. Struct. Eng. Mech. 2001, 11, 301–314. [Google Scholar] [CrossRef]
- Gallego, J.M.; Zanuy, C.; Albajar, L. Shear fatigue behaviour of reinforced concrete elements without shear reinforcement. Eng. Struct. 2014, 79, 45–57. [Google Scholar] [CrossRef]
- Rombach, G.A.; Kohl, M. Fatigue Strength of Reinforced Concrete Beams without Links under Shear Loads. ACI Struct. J. 2016, 113, 941–950. [Google Scholar] [CrossRef]
- Hillebrand, M.; Teworte, F.; Hegger, J. Shear fatigue of prestressed I-beams with shear reinforcement. Struct. Concr. 2021, 22, 1085–1099. [Google Scholar] [CrossRef]
- Hillebrand, M.; Hegger, J. Fatigue testing of shear reinforcement in prestressed concrete T-beams of bridges. Appl. Sci. 2020, 10, 5560. [Google Scholar] [CrossRef]
- Schläfli, M.; Brühwiler, E. Fatigue of existing reinforced concrete bridge deck slabs. Eng. Struct. 1998, 20, 991–998. [Google Scholar] [CrossRef]
- Natário, F.; Fernández Ruiz, M.; Muttoni, A. Experimental investigation on fatigue of concrete cantilever bridge deck slabs subjected to concentrated loads. Eng. Struct. 2015, 89, 191–203. [Google Scholar] [CrossRef][Green Version]
- Lantsoght, E.O.L.; van der Veen, C.; Koekkoek, R.; Sliedrecht, H. Fatigue Testing of Transversely Prestressed Concrete Decks. ACI Struct. J. 2019, 116, 143–154. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; Koekkoek, R.; van der Veen, C.; Sliedrecht, H. Fatigue Assessment of Prestressed Concrete Slab-Between-Girder Bridges. Appl. Sci. 2019, 9, 2312. [Google Scholar] [CrossRef]
- Löfgren, I. Lattice Girder Elements_Investigation of structural behaviour and performance enhancements. Nord. Concr. Res. 2003, 29, 85–104. [Google Scholar]
- Figueiredo Filho, J.R.; Shiramizu, A.K.H. Design, manufacture and construction of buildings with precast lattice-reinforced concrete slabs. IBRACON Struct. Mater. J. 2011, 4, 123–146. [Google Scholar] [CrossRef]
- Mahmutovic, A.; Zuna, S. Trends in the improvement of lattice girders production technology in steelwork zenica. In Trends in the Development of Machinery and Associated Technology, Proceedings of the 15th International Research/Expert Conference, Prague, Czech Republic, 12–18 September 2011; Ekinović, S., Calvet, J.V., Tacer, E., Eds.; Faculty of Mechanical Engineering: Zenica, Bosnia and Herzegovina; pp. 185–188.
- Youn, S.-G.; Cho, G.-D. Experimental Study on the Cracking Loads of LB-DECKs with Varied Cross-Section Details. J. Korea Concr. Inst. 2011, 23, 657–665. [Google Scholar] [CrossRef]
- Newell, S.; Goggins, J. Experimental study of hybrid precast concrete lattice girder floor at construction stage. Structures 2019, 20, 866–885. [Google Scholar] [CrossRef]
- Qi, J.; Yang, H.-C. Improvement of a Truss-Reinforced, Half-Concrete Slab Floor System for Construction Sustainability. Sustainability 2021, 13, 3731. [Google Scholar] [CrossRef]
- Eum, K.-Y.; Lee, J.-H.; Park, Y.-K.; Yun, J.; Jeong, S. Analysis of Spiral Lattice Girder Shape in preparation for HSR Speed Increase. Int. J. Railw. 2013, 6, 160–168. [Google Scholar] [CrossRef]
- Newell, S.; Goggins, J.; Hajdukiewicz, M. Real-time monitoring to investigate structural performance of hybrid precast concrete educational buildings. J. Struct. Integr. Maint. 2016, 1, 147–155. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Liang, S.; Zhang, H. Experimental and Numerical Study of Lattice Girder Composite Slabs with Monolithic Joint. Crystals 2021, 11, 219. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, X.; Xie, Z.; Yang, Y.; Liang, S. On-Site Experimental and Numerical Investigations of Latticed Girder Composite Slabs. Sustainability 2021, 13, 3775. [Google Scholar] [CrossRef]
- Eligehausen, R.; Vocke, H.; Clauss, A.; Furche, J.; Bauermeister, U. Neue Durchstanzbewehrung für Elementdecken. Beton- Stahlbetonbau 2003, 98, 334–344. [Google Scholar] [CrossRef]
- Held, M.; Welsch, T. Besondere Aspekte bei der Verwendung von Gitterträger-Elementdecken zur Herstellung punktgestützter Flachdecken. Bautechnik 2011, 88, 233–236. [Google Scholar] [CrossRef]
- Junker, F.; Holschemacher, K.; Müller, T. Shear-friction behavior of traditional and self-consolidating concrete in reinforced precast elements with in-situ concrete overlay. In Proceedings of the 10th Central European Congress on Concrete Engineering “Concrete Offers for The Period of Economic Recovery”, Liberec, Czech Republic, 1–2 October 2014; pp. 1–7. [Google Scholar] [CrossRef]
- DIN Deutsches Institut für Normung e.V. Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken—Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau: Deutsche Fassung EN 1992-1-1:2004 + AC:2010; ICS 91.010.30, 91.080.40 (DIN EN 1992-1-1:2011-01); Beuth: Berlin, Germany, 2011. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. Nationaler Anhang—National Festgelegte Parameter—Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken—Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau; ICS 91.010.30, 91.080.40 (DIN EN 1992-1-1/NA:2013-04); Beuth: Berlin, Germany, 2013. [Google Scholar]
- Beutel, R.; Hegger, J. The Effect of Anchorage on the Effectiveness of the Shear Reinforcement in the Punching Zone. Cem. Concr. Compos. 2002, 24, 539–549. [Google Scholar] [CrossRef]
- Park, H.-G.; Kim, Y.-N.; Song, J.-G.; Kang, S.-M. Lattice Shear Reinforcement for Enhancement of Slab-Column Connections. J. Struct. Eng. 2012, 138, 425–437. [Google Scholar] [CrossRef]
- Kueres, D.; Siburg, C.; Hegger, J.; Furche, J.; Sippel, T. Zur konstruktiven Durchbildung des Decke-Stütze-Knotens in Flachdecken aus Elementplatten. Bautechnik 2016, 93, 356–365. [Google Scholar] [CrossRef]
- Eom, T.-S.; Song, J.-W.; Song, J.-K.; Kang, G.-S.; Yoon, J.-K.; Kang, S.-M. Punching-shear behavior of slabs with bar truss shear reinforcement on rectangular columns. Eng. Struct. 2017, 134, 390–399. [Google Scholar] [CrossRef]
- Hegger, J.; Sherif, A.G.; Kueres, D.; Siburg, C. Efficiency of Various Punching Shear Reinforcement Systems for Flat Slabs. ACI Struct. J. 2017, 114, 631–642. [Google Scholar] [CrossRef]
- Furche, J.; Schmidt, P. Orthogonal Arrangement of Effective Lattice Punching Shear Reinforcement. In Concrete-Innovations in Materials, Design and Structures, Proceedings of the 2019 fib Symposium, Krakow, Poland, 27–29 May 2019; Derkowski, W., Gwozdziewicz, P., Hojdys, L., Krajewski, P., Pantak, M., Eds.; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2019; pp. 2209–2217. ISBN 978-2-940643-00-4. [Google Scholar]
- Furche, J.; Bauermeister, U.; Kummerow, A.; Hillebrand, M. Durchstanzen bei Ermüdungsbeanspruchung. Beton-Stahlbetonbau 2019, 87, 216. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Pereira Filho, M.J.M.; Freitas, M.V.P.; Lima Neto, A.F.; Melo, G.S.S.A. Experimental resistance of slab-column connections with prefabricated truss bars as punching shear reinforcement. Eng. Struct. 2021, 233, 1–14. [Google Scholar] [CrossRef]
- Badische Drahtwerke GmbH. Allgemeine Bauaufsichtliche Zulassung Z-15.1-38: Kaiser-Omnia-Träger KTS für Fertigplatten mit Statisch Mitwirkender Ortbetonschicht; DIBt: Berlin, Germany, 2015. [Google Scholar]
- Filigran Trägersysteme GmbH & Co., KG. Allgemeine Bauaufsichtliche Zulassung Z-15.1-93: Filigran-EQ-Gitterträger für Fertigplatten mit Statisch Mitwirkender Ortbetonschicht; DIBt: Berlin, Germany, 2014. [Google Scholar]
- Weber, J.W.; Schmidt, R. Zulassungsversuche für den Filigran EQ-Träger unter Dynamischer Beanspruchung: Prüfbericht A2064; Institut für Bauforschung: Aachen, Germany, 1989. [Google Scholar]
- Baustahlgewebe Gmbh. Allgemeine Bauaufsichtliche Zulassung Z-15.1-38: Gitterträger KTS für Fertigplatten mit Statisch Mitwirkender Ortbetonschicht; DIBt: Berlin, Germany, 2020. [Google Scholar]
- Filigran Trägersysteme GmbH & Co., KG. Allgemeine Bauaufsichtliche Zulassung Z-15.1-93: Filigran-EQ-Gitterträger für Fertigplatten mit Statisch Mitwirkender Ortbetonschicht; DIBt: Berlin, Germany, 2019. [Google Scholar]
- Hegger, J.; Wieneke, K. Ermüdung von Elementdecken mit Gitterträgern: Abschlussbericht zum IGF-Forschungsvorhaben 18407 N/1; Institutsbericht 383/2017 (Test Report); Institut für Massivbau: Aachen, Germany, 2017. [Google Scholar]
- Baustahlgewebe GmbH. Allgemeine Bauaufsichtliche Zulassung Z-15.2-100: Gittertraeger KT 800, KT900 oder KTE und Anwendungsbestimmungen für Wandartige Bauwerksstrukturen bei Verwendung Dieser Bewehrung; DIBt: Berlin, Germany, 2020. [Google Scholar]
- Baustahlgewebe GmbH. Allgemeine Bauaufsichtliche Zulassung Z-15.2-9 Gitterträger KTW 200 oder KTW 300 und Anwendungsbestimmungen für Wandartige Bauwerksstrukturen bei Verwendung Dieser Bewehrung; DIBt: Berlin, Germany, 2020. [Google Scholar]
- Baustahlgewebe GmbH. Allgemeine Bauaufsichtliche Zulassung Z-15.1-136 Gittertraeger KT 100 fuer Fertigplatten mit Statisch Mitwirkender Ortbetonschicht (Montaquick-Fertigplatten); DIBt: Berlin, Germany, 2020. [Google Scholar]
- Filigran Trägersysteme GmbH & Co., KG. European Technical Assessment ETA-13/0521: Filigran FDB: Filigran Lattice Girders as Punching Reinforcement; DIBt: Berlin, Germany, 2018. [Google Scholar]
- Filigran Trägersysteme GmbH & Co., KG. Allgemeine Bauaufsichtliche Zulassung Z-15.2-40: Filigran-D- und/oder Filigran-E- und/oder Filigran-EW- und/oder Filigran-SE/SE2- und/oder Filigran-SWE- und Filigran-EQ-Gitterträger und Anwendungsbestimmungen für Wandartige Bauwerksstrukturen aus Elementwänden bei Verwendung Dieser Bewehrung; DIBt: Berlin, Germany, 2020. [Google Scholar]
- Intersig NV. Allgemeine Bauaufsichtliche Zulassung Z-15.1-143: Intersig-EQ-Gitterträger; DIBt: Berlin, Germany, 2020. [Google Scholar]
- Schießl, P.; Schwarzkopf, M. Kaiser Omnia-Träger KTS für Fertigplatten mit Statisch Mitwirkender Ortbetonschicht bei Dynamischer Beanspruchung; Institut für Betonstahl und Stahlbetonbau: Munich, Germany, 1985. [Google Scholar]
- Schießl, P.; Schwarzkopf, M. Montaquick Teilfertigdecken mit Statischer Ortbetonschicht bei Dynamischer Beanspruchung: Versuchsbericht; Serie 1; Institut für Betonstahl und Stahlbetonbau: Munich, Germany, 1981. [Google Scholar]
- Weber, J.W. Zulassungsversuche für die Kaiser-Omnia-Plattenwand mit Gitterträgern KTW 200 oder KTW 300 bei Dynamischer Belastung, Prüfbericht A 2889; Institut für Bauforschung: Aachen, Germany, 1995. [Google Scholar]
- Wieneke, K.M. Horizontal Shear Design of Concrete Interfaces in Beam and Slab Structures. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2019. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. Beton und Stahlbeton, Bemessung und Ausführung (Zurückgezogen); (DIN 1045:1988-07); Beuth: Berlin, Germany, 1988. [Google Scholar]
- Deutscher Ausschuss für Stahlbeton; Bertram, D.; Bunke, N. Erläuterungen zu DIN 1045, Beton- und Stahlbeton, Ausgabe 07.88—Hinweise für die Verwendung von Zement zu Beton, Grundlagen für die Neuregelung zur Beschränlung der Rißbreite Erläuterungen zur Richtlinie für Beton mit Fließmitteln für Fließbeton; Beuth: Berlin, Germany, 1989; pp. 3–144. ISBN 9783410658009. [Google Scholar]
- Wieneke, K.; van Elten, L.; Claßen, M.; Hegger, J. Ermüdung von Elementdecken mit Gitterträgern. Beton-Stahlbetonbau 2017, 112, 723–733. [Google Scholar] [CrossRef]
- Maurer, R.; Block, K.; Dreier, F. Ermüdungsfestigkeit von Betonstahl-Bestimmung mit dem Interaktiven Verfahren. Bauingenieur 2010, 85, 17–28. [Google Scholar]
- Block, K. The Interactive Method—Reliable and Reproducible S-N-Curves for Materials. In Mechanical Fatigue of Metals; Correia, J.A.F.O., Jesus, A.M.P., de Fernandes, A.A., Calçada, R., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 197–204. ISBN 978-3-030-13979-7. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. Stähle für die Bewehrung und das Vorspannen von Beton–Prüfverfahren–Teil 1: Bewehrungsstäbe, Walzdraht und Draht; ICS 77.140.15 (DIN EN ISO 15630-1:2019-05); Beuth: Berlin, Germany, 2019. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. Betonstahl-Teil 1: Stahlsorten, Eigenschaften, Kennzeichnung; (DIN 488-1:2009-08); Beuth: Berlin, Germany, 2009. [Google Scholar]
- Wieneke, K.; Claßen, M.; Hegger, J. Elementdecken mit Gitterträgern unter zyklischer Belastung. Beton-Stahlbetonbau 2017, 112, 579–588. [Google Scholar] [CrossRef]
- Wieneke, K.; Hegger, J. Fatigue of Semi-precast Slabs with Lattice Girders. In High Tech Concrete: Where Technology and Engineering Meet, Proceedings of the 2017 fib Symposium, Maastricht, The Netherlands, 12–14 June 2017; Hordijk, D.A., Luković, M., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 921–928. ISBN 3319594710. [Google Scholar]
- DIN Deutsches Institut für Normung e.V. Tragwerke aus Beton, Stahlbeton und Spannbeton–Teil 1: Bemessung und Konstruktion; ICS 91.080.40 (DIN 1045-1:2008-08); Beuth: Berlin, Germany, 2008. [Google Scholar]
- Kaufmann, N. Das Sandflächenverfahren. Strassenbau Tech. 1971, 24, 131–135. [Google Scholar]
- Vogler, N.; Gluth, G.; Oppat, K.; Kühne, H.-C. Charakterisierung von Bauteiloberflächen-Rautiefebestimmung mittels konventioneller und laserbasierter Verfahren. Bauingenieur 2017, 92, 97–104. [Google Scholar] [CrossRef]
- Wieneke, K.; Herbrand, M.; Vogler, N.; Schwermann, R.; Blankenbach, J. Messverfahren zur Bestimmung der Rautiefe von Betonoberflächen. Bauingenieur 2018, 93, 365–373. [Google Scholar] [CrossRef]
- Ungermann, J.; Adam, V.; Classen, M. Fictitious Rough Crack Model (FRCM): A Smeared Crack Modelling Approach to Account for Aggregate Interlock and Mixed Mode Fracture of Plain Concrete. Materials 2020, 13, 2774. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Pam, H.J.; Kwan, A.K.H. Shear capacity of high strength concrete beams with their point of inflection within the shear span. Proc. Inst. Civ. Eng. Struct. Build. 1998, 128, 91–99. [Google Scholar] [CrossRef]
- Tue, N.V.; Ehmann, R.; Tung, N.D. Schubversuche an Stahlbetonbalken unterschiedlicher M/V-Kombinationen. BuSt 2015, 110, 446–457. [Google Scholar] [CrossRef]
- Leonhardt, F.; Walther, R. Schubversuche an Einfeldrigen Stahlbetonbalken Mit und Ohne Schubbewehrung zur Ermittlung der Schubtragfähigkeit und der Oberen Schubspannungsgrenze: DAfStb-Heft 151; Ernst & Sohn: Berlin, Germany, 1962. [Google Scholar]
- Yang, Y.; Walraven, J.C.; Uijl, J.D. Shear Behavior of Reinforced Concrete Beams without Transverse Reinforcement Based on Critical Shear Displacement. J. Struct. Eng. 2017, 143, 1–13. [Google Scholar] [CrossRef]
- Reissen, K.; Classen, M.; Hegger, J. Shear in reinforced concrete slabs—Experimental investigations in the effective shear width of one-way slabs under concentrated loads and with different degrees of rotational restraint. Struct. Concr. 2018, 19, 36–48. [Google Scholar] [CrossRef]
- Bielak, J.; Adam, V.; Hegger, J.; Classen, M. Shear Capacity of Textile-Reinforced Concrete Slabs without Shear Reinforcement. Appl. Sci. 2019, 9, 1382. [Google Scholar] [CrossRef]
- Classen, M. Shear Crack Propagation Theory (SCPT)—The mechanical solution to the riddle of shear in RC members without shear reinforcement. Eng. Struct. 2020, 210, 110207. [Google Scholar] [CrossRef]
- Schmidt, M.; Schmidt, P.; Wanka, S.; Classen, M. Shear Response of Members without Shear Reinforcement—Experiments and Analysis Using Shear Crack Propagation Theory (SCPT). Appl. Sci. 2021, 11, 3078. [Google Scholar] [CrossRef]
- Adam, V. Shear in Reinforced Concrete Structures without Shear Reinforcement—Analysis and Design. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2021. [Google Scholar]
- Adam, V.; Herbrand, M.; Claßen, M. Experimentelle Untersuchungen zum Einfluss der Bauteilbreite und der Schubschlankheit auf die Querkrafttragfähigkeit von Stahlbetonplatten ohne Querkraftbewehrung. Bauingenieur 2018, 93, 37–45. [Google Scholar] [CrossRef]
- Adam, V.; Classen, M.; Hillebrand, M.; Hegger, J. Shear in Continuous Slab Segments without Shear Reinforcement under Distributed Loads. In Concrete-Innovations in Materials, Design and Structures, Proceedings of the 2019 fib Symposium 2019, Krakow, Poland, 27–29 May 2019; Derkowski, W., Gwozdziewicz, P., Hojdys, L., Krajewski, P., Pantak, M., Eds.; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2019; pp. 1771–1778. ISBN 978-2-940643-00-4. [Google Scholar]
- Leonhardt, F.; Walther, R.; Dilger, W. Schubversuche an Durchlaufträgern (Zweifeldrige Stahlbetonbalken mit und ohne Schubbewehrung): DAfStb-Heft 163; Ernst & Sohn: Berlin, Germany, 1964. [Google Scholar]
- Herbrand, M.; Hegger, J. Experimentelle Untersuchungen zum Einfluss einer externen Vorspannung auf die Querkrafttragfähigkeit vorgespannter Durchlaufträger. Bauingenieur 2013, 88, 428–437. [Google Scholar]
- Maurer, R.; Gleich, P.; Zilch, K.; Dunkelberg, D. Querkraftversuch an einem Durchlaufträger aus Spannbeton. Beton-Stahlbetonbau 2014, 109, 654–665. [Google Scholar] [CrossRef]
- Teworte, F.; Herbrand, M.; Hegger, J. Structural Assessment of Concrete Bridges in Germany—Shear Resistance under Static and Fatigue Loading. Struct. Eng. Int. 2015, 25, 266–274. [Google Scholar] [CrossRef]
- Herbrand, M.; Classen, M. Shear tests on continuous prestressed concrete beams with external prestressing. Struct. Concr. 2015, 16, 428–437. [Google Scholar] [CrossRef]
- Gleich, P.; Kattenstedt, S.; Maurer, R. Erweitertes Druckbogenmodell für die Bestimmung der Querkrafttragfähigkeit von Stahl- und Spannbetonbalken. Beton-Stahlbetonbau 2016, 111, 268–277. [Google Scholar] [CrossRef]
- Herbrand, M.; Classen, M.; Adam, V. Querkraftversuche an Spannbetondurchlaufträgern mit Rechteck-und I-Querschnitt. Bauingenieur 2017, 92, 465–473. [Google Scholar] [CrossRef]
- Hegger, J.; Sherif, A.; Görtz, S. Investigation of Pre- and Postcracking Shear Behavior of Prestressed Concrete Beams Using Innovative Measuring Techniques. ACI Struct. J. 2004, 101, 183–192. [Google Scholar]
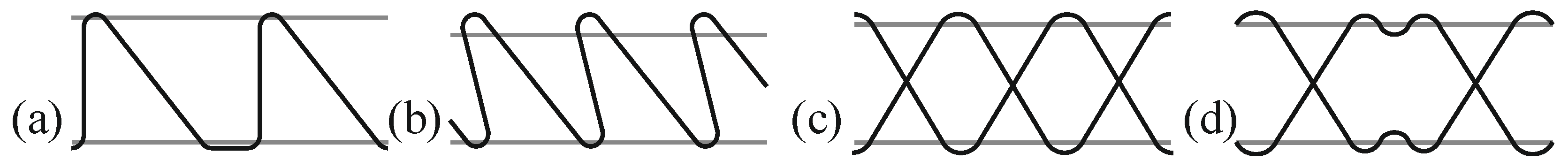





| Geometry | Lattice Girder | Test Setup | ||
|---|---|---|---|---|
| Baustahlgewebe | Filigran | |||
| slabs |  | KTS n = 10 | EQ n = 2 |  |
| KT100 n = 14 | ||||
| walls |  | KTW n = 3 |  | |
| Series 0 | Series 1 | Series 2 | |
|---|---|---|---|
| dimensions (l/b/h) (cm) | 190/85/16 | 180/85/16 | 420/85/36 (EG10–13)390/85/33 (EG14) |
| height precast slab/ in situ concrete (cm) | 7/9 | 7/9 | 7/29 (EG10–13) 7/26 (EG14) |
| effective depth d (cm) | 13 | 13 | 33 (EG10–13) 30 (EG14) |
| distance load-support a (cm) | 50 | 50 | 130 |
| lattice girder type | KTS 100 | KTS 100 | EQ 30 |
| shear slenderness a/d | 4.0 | 4.0 | 4.0 |
| long. reinforcement ρl (%) | 2.0 | 2.0 | 2.0 |
| Test | hges | a | nLG | fym,LG | nl | fym,l | fcm,pre | fcm,in situ | Roughness | Rt,sand | Rt,laser |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (cm) | (cm) | (-) | (N/mm2) | (-) | (N/mm2) | (N/mm2) | (N/mm2) | (-) | (mm) | (mm) | |
| EG01 | 16 | 50 | 2 | 546 | 7 | 954 | 25.3 | 35.6 | smooth | 0.24 | 0.42 |
| EG02 | 16 | 50 | 2 | 546 | 7 | 954 | 25.6 | 33.9 | very smooth 1 | 0.26 | 0.43 |
| EG03 | 16 | 50 | 2 | 546 | 7 | 939 | 27.7 | 33.2 | ‘rough’ (Rt ≈ 0.9mm) | 0.64 | - |
| EG04 | 16 | 50 | 3 | 546 | 7 | 939 | 27.9 | 34.0 | ‘rough’ (Rt ≈ 0.9 mm) | 0.93 | - |
| EG05 | 16 | 50 | 4 | 546 | 7 | 939 | 28.2 | 35.2 | ‘rough’ (Rt ≈ 0.9 mm) | 0.78 | - |
| EG06 | 16 | 50 | 2 | 546 | 7 | 939 | 51.1 | 61.3 | ‘rough’ (Rt ≈ 0.9 mm) | 0.97 | 1.33 |
| EG07 | 16 | 50 | 3 | 546 | 7 | 939 | 51.1 | 61.3 | ‘rough’ (Rt ≈ 0.9 mm) | 1.01 | 1.19 |
| EG08 | 16 | 50 | 4 | 546 | 7 | 939 | 51.4 | 61.3 | ‘rough’ (Rt ≈ 0.9 mm) | 1.07 | 1.04 |
| EG09 | 16 | 50 | 2 | 546 | 7 | 939 | 32.9 | 34.4 | rough (Rt > 1.5 mm) | 2.02 | - |
| EG10 | 36 | 130 | 2 | 554 | 18 | 939 | 36.0 | 32.0 | ‘rough’ (Rt ≈ 0,9 mm) | 0.82 | 1.01 |
| EG11 | 36 | 130 | 4 | 554 | 18 | 939 | 37.2 | 36.0 | ‘rough’ (Rt ≈ 0,9 mm) | 0.78 | 0.85 |
| EG12 | 36 | 130 | 2 | 554 | 18 | 939 | 48.6 | 55.6 | ‘rough’ (Rt ≈ 0.9 mm) | 1.02 | 0.63 |
| EG13 | 36 | 130 | 4 | 554 | 18 | 939 | 49.0 | 56.8 | ‘rough’ (Rt ≈ 0.9 mm) | 1.19 | 1.67 |
| EG14 | 33 | 120 | 4 | 554 | 17 | 939 | 31.5 | 34.8 | ‘rough’ (Rt ≈ 0.9 mm) | 0.96 | - |
| Series | Test | Vmax,1 | ∆V1 | N1 | Vmax,f | ∆Vf | Nf | Nov | ∆σcalc,1 | ∆σmax,test | Failure |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (kN) | (kN) | (-) | (kN) | (kN) | (-) | (-) | (N/mm2) | (N/mm2) | |||
| Series 0 | EG01a | 116 | 35 | 1.50 × 106 | 162 | 58 | 0.18 × 106 | 4.18 × 106 | 109 | 270 | I/V |
| EG01b | 162 | 58 | 350 | 4.18 × 106 | V | ||||||
| EG02a | 116 | 35 | 1.50 × 106 | 116 | 58 | 1.16 × 106 | 2.66 × 106 | 109 | 215 * | I | |
| EG02b | 116 | 58 | 0.93 × 106 | 3.59 × 106 | I/V | ||||||
| Series 1 | EG03a | 152 | 90 | 2.07 × 106 | 2.07 × 106 | 279 | 230 * | I/V | |||
| EG03b | 152 | 90 | 1.17 × 106 | 3.24 × 106 | V | ||||||
| EG04a | 165 | 83 | 3.00 × 106 | 165 | 112.5 | 1.36 × 106 | 4.36 × 106 | 171 | 215 * | V | |
| EG04b | 260 1 | V | |||||||||
| EG05a | 226 | 133 | 2.70 × 104 | 2.70 × 104 | 176 | 125 | VDZ | ||||
| EG05b | 271 1 | V | |||||||||
| EG06a | 172 | 105 | 2.25 × 106 | 197 | 120 | 0.35 × 106 | 2.60 × 106 | 326 | 195 | I/V | |
| EG06b | 197 | 120 | 1.12 × 104 | 2.62 × 106 | I/V | ||||||
| EG07a | 172 | 88 | 2.00 × 106 | 197 | 120 | 3.32 × 104 | 4.03 × 106 | 121 | 55 | V | |
| EG07b | 197 | 120 | 2.25 × 106 | 6.28 × 106 | V | ||||||
| EG08a | 215 | 110 | 2.0 × 106 | 215 | 152.5 | 1.95 × 106 | 3.95 × 106 | 171 | 115 * | V | |
| EG08b | − 2 | ||||||||||
| EG09a | 155 | 93 | 8677 | 8677 | 187 | 175 * | I/V | ||||
| EG09b | 155 | 61 | 1.09 × 106 | 1.09 × 106 | I/V | ||||||
| Series 2 | EG10a | 282 | 150 | 2.00 × 106 | 372 | 225 | 1000 | 2.00 × 106 | 193 | 100* | I/V |
| EG10b | −2 | ||||||||||
| EG11a | 537 | 195 | 0.31 × 106 | 0.31 × 106 | 125 | 115 | VDZ/VL | ||||
| EG11b | 537 | 195 | 0.90 × 106 | 1.21 × 106 | VL | ||||||
| EG12a | 359 | 135 | 2.00 × 106 | 420 | 233 | 0.74 × 106 | 4.12 × 106 | 173 | 255 * | I/V | |
| EG12b | 420 | 233 | 0.35 × 106 | 4.47 × 106 | V/VL | ||||||
| EG13a | 519 | 165 | 435 | 435 | 105 | 115 | VDZ/VL | ||||
| EG13b | 519 | 165 | 9129 | 9564 | VL | ||||||
| EG14a | 487 | 178 | 1.63 × 106 | 1.63 × 106 | 125 | 175 | VDZ/VL | ||||
| EG14b | 487 | 178 | 2.87 × 104 | 1.66 × 106 | V/VL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hillebrand, M.; Schmidt, M.; Wieneke, K.; Classen, M.; Hegger, J. Investigations on Interface Shear Fatigue of Semi-Precast Slabs with Lattice Girders. Appl. Sci. 2021, 11, 11196. https://doi.org/10.3390/app112311196
Hillebrand M, Schmidt M, Wieneke K, Classen M, Hegger J. Investigations on Interface Shear Fatigue of Semi-Precast Slabs with Lattice Girders. Applied Sciences. 2021; 11(23):11196. https://doi.org/10.3390/app112311196
Chicago/Turabian StyleHillebrand, Matthias, Maximilian Schmidt, Katrin Wieneke, Martin Classen, and Josef Hegger. 2021. "Investigations on Interface Shear Fatigue of Semi-Precast Slabs with Lattice Girders" Applied Sciences 11, no. 23: 11196. https://doi.org/10.3390/app112311196
APA StyleHillebrand, M., Schmidt, M., Wieneke, K., Classen, M., & Hegger, J. (2021). Investigations on Interface Shear Fatigue of Semi-Precast Slabs with Lattice Girders. Applied Sciences, 11(23), 11196. https://doi.org/10.3390/app112311196