Saddle Point Approximation of Mutual Information for Finite-Alphabet Inputs over Doubly Correlated MIMO Rayleigh Fading Channels

Abstract

Given the mutual information of finite-alphabet inputs cannot be calculated concisely and accurately over fading channels, this paper proposes a new method to calculate the mutual information. First, the applicability of the saddle point method is studied, and then the mutual information is estimated by the saddle point approximation method with known channel state information. Furthermore, we induce the expectation of mutual information over doubly correlated multiple-input multiple-output (MIMO) Rayleigh fading channels. The validity of the saddle point approximation method is verified by comparing the numerical results of the Monte Carlo method and the saddle point approximation method under different doubly correlated MIMO fading channel scenarios.

1. Introduction

Mutual information plays an irreplaceable role in the theoretical analysis of communication system performance, including analysis, evaluation and optimization of transceiver structure [1], encoding and decoding schemes [2], and communication system bit error rate (BER) performance [3], etc., so it attracts increasing research interest. Channel capacity, defined as the upper bound of mutual information, is realized under Gaussian inputs over additive white Gaussian noise (AWGN) channels [4]. A large number of theoretical analyses and research are also based on this concept [5,6,7]. By means of Minkowski’s inequality [1], two lower bounds of system capacity are obtained and are used as selection indexes to discuss the selection of antenna subsets in spatial multiplexing systems. Under the condition of Gaussian inputs, the hybrid encoder and combiners are designed by maximizing the achievable SE [2].

However, Gaussian inputs are rarely realized in practice because the unbounded amplitude of Gaussian distribution may lead to infinite transmitting power, and the continuity of Gaussian distribution will make it difficult to detect and decode the signal at the receiver. In practical communication systems, inputs are usually taken from finite-alphabet constellation sets with average distribution, rather than Gaussian inputs [8]. Considerable gaps in terms of transmitting performance exist [9,10,11] due to the differences between Gaussian and finite-alphabet inputs and then lead to deviations from optimal strategies. For example, it is believed that the traditionally optimal strategy to achieve capacity for Gaussian inputs is to allocate higher power to the sub-channels with a larger signal-to-noise ratio (SNR). In [10], it is demonstrated that such strategy may be quite suboptimal for the reason that the mutual information with finite-alphabet inputs is upper bounded, and there is little incentive to allocate more power to the sub-channels already close to saturation. At the same time, channel capacity reflects the upper bound of communication system performance, so the performance of digital communication systems can be accurately evaluated by mutual information under the condition of finite alphabet sets inputs and actual transmission environment [12,13].

Due to the great complexity of the direct calculation of mutual information, it is almost impossible to obtain a closed-form solution. Monte Carlo trials are usually used for direct and accurate calculation [14]. In order to reduce the computational complexity, a bit-level algorithm using PDF of a log-likelihood ratio (LLR) to calculate mutual information is proposed [15]. However, each modulation mode of the algorithm requires a lot of prior simulations, and it is only suitable for specific scenarios without universality. To optimize linear precoding with finite-alphabet inputs, the authors in [16,17] deduced the closed-form lower and upper bounds of mutual information as alternatives, which reduce the computational effort by several orders of magnitude compared to calculating the average mutual information directly. Then the bounds of mutual information are applied to multiple antennas, secure cognitive radio networks [18], and relay networks [19]. The study in [20] utilized the cutoff rate (CR) as the alternative of mutual information (MI) to design the linear precoders. Mutual information was also used to develop a two-step algorithm to enhance the achievable secrecy rate of cooperative jamming for secure communication with finite-alphabet inputs in [11]. However, the gaps between approximation and accurate mutual information are still ambiguous, which limits the range where mutual information can be applied. Recently, the authors of [21] approximated ergodic mutual information based on multi-exponential decay curve fitting under M-ary quadrature amplitude modulation (M-QAM) signaling, but other modulation modes were neglected.

This study takes a step toward evaluating accurate mutual information for finite-alphabet-based transmissions over doubly correlated MIMO fading channels. After discussing the applicability of the saddle point method, we obtain the approximate solution of mutual information for any known CSI and modulation mode by using this method, which is universal. On this basis, the mutual information expectation of doubly-correlated MIMO Rayleigh fading channels is further derived. This proposition highlights the considerable accuracy with radically reduced complexity.

The outline of this paper is as follows. The second section introduces the MIMO transmission model and its preliminary research. In the third section, the saddle point approximation method is used to estimate the mutual information, and then we calculate the mutual information expectation over doubly correlated MIMO Rayleigh fading channels. Then the validity and accuracy of the proposed method are verified under different doubly correlated MIMO fading channels scenarios in the fourth section. Finally, the fifth section gives conclusions.

2. Problem Formulation

2.1. Model of MIMO Transmission

Consider MIMO system with ${\mathit{N}}_T$ transmitting antennas and ${\mathit{N}}_{\mathrm{R}}$ receiving antennas. Let $\widetilde{\tilde{\mathit{x}}}\in {ℂ}^{{\mathit{N}}_{\mathrm{T}}\times 1}$ (${ℂ}^{\mathit{N}\times m}$ denotes the $\mathit{N}\times m$ complex spaces) be a transmitting signal vector, satisfying ${\mathbb{E}}_{\widetilde{\tilde{\mathit{x}}}}\left\{\widetilde{\tilde{\mathit{x}}}\right\}=0$ and ${\mathbb{E}}_{\widetilde{\tilde{\mathit{x}}}}\left\{\widetilde{\tilde{\mathit{x}}}{\widetilde{\tilde{\mathit{w}}}}^{\mathrm{H}}\right\}=\mathit{I}$, where ${\mathbb{E}}_{(•)}\{\ast \}$ stands for the statistical expectation of random $\ast$ with respect to its variable $·$; $\mathit{I}$ and $0$ denote an unit and zero matrix of appropriate dimensions, respectively. ${(•)}^{\mathrm{H}}$ is the conjugate transpose of matrix $·$. MIMO transmission is generally modeled by

$$\widetilde{\tilde{\mathit{y}}}=\widetilde{\tilde{\mathit{H}}}\widetilde{\tilde{\mathit{x}}}+\widetilde{\tilde{\mathit{w}}}$$

(1)

where preliminaries are made as below.

1.

$\widetilde{\tilde{\mathit{H}}}\in {ℂ}^{{\mathit{N}}_{\mathrm{R}}\times {\mathit{N}}_{\mathrm{T}}}$ is a complex fading channel matrix between transmitting antenna and receiving antenna arrays. The doubly correlated MIMO Rayleigh fading channel is modeled by ${\mathit{\Psi }}_{\mathrm{R}}{}^{1/2}{\widetilde{\tilde{\mathit{H}}}}_{\mathrm{WG}}{\mathit{\Psi }}_{\mathrm{T}}{}^{1/2}\in {ℂ}^{{\mathit{N}}_{\mathrm{R}}\times {\mathit{N}}_{\mathrm{T}}}$ [1], where ${\widetilde{\tilde{\mathit{H}}}}_{\mathrm{WG}}\in {ℂ}^{{\mathit{N}}_{\mathrm{R}}\times {\mathit{N}}_{\mathrm{T}}}$ is a matrix consisted of independent and identically distributed $\mathcal{C}\mathcal{N}(0,1)$ complex Gaussian entries; ${\mathit{\Psi }}_{\mathrm{T}}$ and ${\mathit{\Psi }}_{\mathrm{R}}$ are transmitting and receiving correlation matrices, respectively. ${\mathit{\Psi }}_{\mathrm{T}}$ and ${\mathit{\Psi }}_{\mathrm{R}}$ can be expressed as

$${\mathit{\Psi }}_{\mathrm{T}}={\mathit{U}}_{\mathrm{T}}{\mathit{\Sigma }}_{\mathrm{T}}{\mathit{U}}_{\mathrm{T}}{}^{\mathrm{H}}\mathrm{and}{\mathit{\Psi }}_{\mathrm{R}}={\mathit{U}}_{\mathrm{R}}{\mathit{\Sigma }}_{\mathrm{R}}{\mathit{U}}_{\mathrm{R}}{}^{\mathrm{H}}$$

(2)

where ${\mathit{U}}_{\mathrm{T}}$ and ${\mathit{U}}_{\mathrm{R}}$ are unitary matrices whose columns are eigenvectors of ${\mathit{\Psi }}_{\mathrm{T}}$ and ${\mathit{\Psi }}_{\mathrm{R}}$; ${\mathit{\Sigma }}_{\mathrm{T}}$ and ${\mathit{\Sigma }}_{\mathrm{R}}$ represent diagonal matrices whose diagonal entries are the eigenvalues of ${\mathit{\Psi }}_{\mathrm{T}}$ and ${\mathit{\Psi }}_{\mathrm{R}}$, respectively.

2.

$\widetilde{\tilde{\mathit{w}}}\in {ℂ}^{{\mathit{N}}_{\mathrm{R}}\times 1}$ stands for AWGN corresponding to N_R receiving antennas, where each element is independent and identically complex Gaussian distributed, satisfying ${\mathbb{E}}_{\widetilde{\tilde{\mathit{w}}}}\left\{\widetilde{\tilde{\mathit{w}}}\right\}=0$ and ${\mathbb{E}}_{\widetilde{\tilde{\mathit{w}}}}\left\{\widetilde{\tilde{\mathit{w}}}{\widetilde{\tilde{\mathit{w}}}}^{\mathrm{H}}\right\}={\sigma }^2\mathit{I}$.

2.2. Mutual Information for Finite-Alphabet Inputs

When a linear unitary transform ${\mathit{U}}_R^{\mathit{H}}$ is applied on the receiving signal $\tilde{\tilde{y}}$, the MIMO model in (1) is equivalent to a model with channel matrix ${\mathit{U}}_R^{\mathit{H}}\widetilde{\tilde{\mathit{H}}}$ and noise ${\mathit{U}}_R^{\mathit{H}}\widetilde{\tilde{\mathit{w}}}$ [16], which is written as

$$y={\mathit{U}}_{\mathrm{R}}{}^{\mathrm{H}}\tilde{\tilde{y}}={\mathit{\Sigma }}_{\mathrm{R}}{}^{1/2}{\mathit{H}}_{\mathrm{WG}}{\mathit{\Sigma }}_{\mathrm{T}}{}^{1/2}{\mathit{U}}_{\mathrm{T}}{}^{\mathrm{H}}\widetilde{\tilde{\mathit{x}}}+\mathit{w}$$

(3)

where ${\mathit{H}}_{\mathrm{WG}}={\mathit{U}}_{\mathrm{R}}{}^{\mathrm{H}}{\widetilde{\tilde{\mathit{H}}}}_{\mathrm{WG}}{\mathit{U}}_{\mathrm{T}}$ and $\mathit{w}={\mathit{U}}_R^{\mathit{H}}\widetilde{\tilde{\mathit{w}}}$. $\widetilde{\tilde{\mathit{x}}}$ is selected equiprobably from $N_T$-dimension constellation consisted of $N={\displaystyle {\prod }_{I=1}^{N_T}{N}_I}$ vectors, where ${\mathit{N}}_{\mathit{I}}$ denotes the number of symbols in the i-th discrete constellation ${\mathsf{\Omega }}_I$. The mutual Information for Finite-Alphabet inputs between $\mathit{x}$ and $y$ is given by [22]

$$\begin{array}{l}\mathcal{I}(\widetilde{\tilde{\mathit{x}}};\tilde{\tilde{y}})=\mathcal{I}({\mathit{U}}_T{}^{\mathrm{H}}\widetilde{\tilde{\mathit{x}}};y)\\ ={\log }_2\mathit{N}+\frac{1}{\mathit{N}}{\displaystyle \sum _{m=1}^{\mathit{N}}{\mathbb{E}}_{{\mathit{H}}_{\mathrm{WG}},\mathit{w}}\left\{{\log }_2\left[\exp \left(-\frac{||\mathit{w}|{|}^2}{{\sigma }^2}\right)/{\displaystyle \sum _{k=1}^{\mathit{N}}\exp \left(-\frac{||{\mathit{c}}_{m,k}+\mathit{w}|{|}^2}{{\sigma }^2}\right)}\right]\right\}}\end{array}$$

(4)

where ${\mathit{c}}_{m,k}={\mathit{\Sigma }}_{\mathrm{R}}{}^{1/2}{\mathit{H}}_{\mathrm{WG}}{\mathit{\Sigma }}_{\mathrm{T}}{}^{1/2}{\mathit{U}}_{\mathrm{T}}{}^{\mathrm{H}}{\mathit{d}}_{m,k}$ and ${\mathit{d}}_{m,k}=q_m-q_k$. $q_m$ and $q_k$ are the m-th and k-th points in the constellation of $\widetilde{\tilde{\mathit{x}}}$, and $||•||$ stands for the Euclidean norm of the variable $•$.

Since the statistical Channel State Information (CSI) is varying much slower than instantaneous $\widetilde{\tilde{\mathit{H}}}$, and can be obtained by channel estimation, this work assumed the statistical CSI was a perfectly-known constant. Consequently, the problem was to calculate the average mutual information with given statistical CSI.

3. Saddle Point Approximation for Mutual Information

Mutual information by (4) needs multiple integrals to compute expectation over ${\mathit{H}}_{\mathrm{WG}}$ and $\mathit{w}$. As N increases, it leads to prohibitive complexity and becomes the most significant obstacle in achieving accurate mutual information. Therefore, we used the idea of the mean value theorem of integrals to simplify multiple integrals by finding an appropriate point. In this section, we explore the saddle point approximation method and highlight the convenient calculation with a weighted mean over constellation set of $\mathit{x}$, instead of expectation over all possible samples of random ${\mathit{H}}_{\mathrm{WG}}$ and $\mathit{w}$.

3.1. Saddle Point Approximation

We first considered the expectation over the AWGN vector $\mathit{w}$. The Taylor series of (4) is expanded to

$$ℐ(\mathit{x};\mathit{y}|\mathit{H})={\log }_{2}N-\frac{1}{N\ln 2}{\displaystyle \sum _{m=1}^N{\displaystyle \sum _{\sigma =1}^{+\infty }\frac{1}{\sigma }{\displaystyle \sum _{q=0}^{\sigma }\frac{\sigma !{(-1)}^q}{q!(\sigma -q)!}\frac{1}{{\mathsf{\pi }}^{{\mathit{N}}_{\mathrm{R}}}{\sigma }^{2N_R}}{\displaystyle {\int }_{\mathit{w}}{\left({\displaystyle \sum _{k=1}^N{\sigma }_{m,k}(\mathit{w})}\right)}^{-q}\mathrm{d}\mathit{w}}}}}$$

(5)

where

$$p_{m,k}(\mathit{w})=\exp \left(\frac{||\mathit{w}-q{\mathit{c}}_{m,k}|{|}^2}{q{\sigma }^2}-\frac{(q+1)||{\mathit{c}}_{m,k}|{|}^2}{{\sigma }^2}\right)\mathrm{and}\mathit{H}={\mathit{\Sigma }}_{\mathrm{R}}{}^{1/2}{\mathit{H}}_{\mathrm{WG}}{\mathit{\Sigma }}_{\mathrm{T}}{}^{1/2}$$

(6)

Before proceeding to the saddle point approximation, we needed to establish the following lemma, which guarantees the existence of the saddle point.

Lemma 1.

For non-zero natural number$q$, the maximum of${\left({\displaystyle {\sum }_{k=1}^{\mathit{N}}{\sigma }_{m,k}(\mathit{w})}\right)}^{-q}$exists and is achieved at$\mathit{w}={\mathit{w}}_0$, where${\mathit{w}}_0$is the weighted average vector of${\mathit{c}}_{m,1}$,${\mathit{c}}_{m,2}$, …, and${\mathit{c}}_{m,\mathit{N}}$.

$${\mathit{w}}_0={\displaystyle \sum _{k=1}^{\mathit{N}}q{\rho }_{m,k}{\mathit{c}}_{m,k}}\triangleq q{\overline{\mathit{c}}}_m$$

(7)

where${\rho }_{m,k}={\sigma }_{m,k}({\mathit{w}}_0)/{\displaystyle {\sum }_{k=1}^{\mathit{N}}{\sigma }_{m,k}({\mathit{w}}_0)}={\sigma }_{m,k}({\mathit{w}}_0)/{\sigma }_m({\mathit{w}}_0)$is a positive real number over an open interval (0, 1) and satisfies${\displaystyle {\sum }_{k=1}^{\mathit{N}}{\rho }_{m,k}}=1$.

The proof of Theorem 1 is shown in Appendix A.

We are now at $\mathit{w}={\mathit{w}}_0$ to perform saddle point approximation.

Proposition 1.

For non-zero natural number$q$, integral over complex AWGN vector$\mathit{w}$is approximated by

$${\displaystyle {\int }_{\mathit{w}}\frac{1}{{\mathsf{\pi }}^{N_{\mathrm{R}}}{\sigma }^{2N_{\mathrm{R}}}}{\left({\displaystyle \sum _{k=1}^N{\sigma }_{m,k}(\mathit{w})}\right)}^{-q}\mathrm{d}\mathit{w}}\approx {\left[{\displaystyle \sum _{k=1}^N\exp \left(-\frac{{\alpha }_{m,k}||c_{m,k}|{|}^2}{{\sigma }^2}\right)}\right]}^{-q}$$

(8)

where

$${\alpha }_{m,k}=\left[1-q\frac{||{\overline{\mathit{c}}}_m|{|}^2}{||{\mathit{c}}_{m,k}|{|}^2}+q\frac{{\mathit{c}}_{m,k}{}^{\mathrm{H}}{\overline{\mathit{c}}}_m+{\overline{\mathit{c}}}_m{}^{\mathrm{H}}{\mathit{c}}_{m,k}}{||{\mathit{c}}_{m,k}|{|}^2}-{\left(\frac{||{\mathit{c}}_{m,k}|{|}^2}{{\sigma }^2}\right)}^{-1}\ln \left({\displaystyle \sum _{k=1}^{\mathit{N}}\frac{{\rho }_{m,}{}_k||{\mathit{c}}_{m,k}|{|}^2}{{\sigma }^2}}-\frac{||{\overline{\mathit{c}}}_m|{|}^2}{{\sigma }^2}\right)\right]$$

(9)

The proof of Proposition 1 is shown in Appendix B.

Mutual information is approximated by (5) and (8) as

$$ℐ(\mathit{x};y|\mathit{H})\approx ℐ({\alpha }_{m,k},\mathit{H})={\log }_2\mathit{N}-\frac{1}{N}{\displaystyle \sum _{m=1}^N{\log }_2\left[{\displaystyle \sum _{k=1}^N\exp \left(-\frac{{\alpha }_{m,k}||{\mathit{c}}_{m,k}|{|}^2}{{\sigma }^2}\right)}\right]}$$

(10)

Generally speaking, the close-form solution is hardly obtained. That is to say, we cannot write down the exact expression of ${\alpha }_{m,k}$. Optionally, we adopt a numerical method to obtain approximated ${\alpha }_{m,k}$,

$$\underset{{\alpha }_{m,k}:k=1,2}{\arg \min }\{|ℐ(\mathit{x};y|1)-ℐ({\alpha }_{m,k},1)\}\approx {\{3-\exp [-||{\mathit{c}}_{m,k}|{|}^2/(4{\sigma }^2)]\}}^{-1}$$

(11)

where $ℐ(\mathit{x};y|1)$ is computed by Monte Carlo method by taking BPSK over single-input and single-output (SISO) over AWGN channel (that is $\mathit{H}=1$) as an example, and ${\alpha }_{m,k}$ is fixed at each signal to noise ratio (SNR). Thus, (10) can be written as

$$\begin{array}{l}ℐ(\mathit{x};y|\mathit{H})\approx {\log }_{2}N-\frac{1}{N}{\displaystyle \sum _{m=1}^N{\log }_2\left[{\displaystyle \sum _{k=1}^N\exp \left(-\frac{||{\mathit{c}}_{m,k}|{|}^2}{{\sigma }^2}\frac{1}{3-\exp [-||{\mathit{c}}_{m,k}|{|}^2/(4{\sigma }^2)]}\right)}\right]}\\ ={\log }_{2}N-\frac{1}{N}{\displaystyle \sum _{m=1}^N{\log }_2\left[{\displaystyle \sum _{k=1}^N\exp \left(-\frac{||\mathit{H}{\mathit{d}}_{m,k}|{|}^2}{{\sigma }^2}\frac{1}{3-\exp [-||\mathit{H}{\mathit{d}}_{m,k}|{|}^2/(4{\sigma }^2)]}\right)}\right]}\end{array}$$

(12)

3.2. Average Mutual Information over Doubly Correlated MIMO Rayleigh Fading Channels

The average mutual information over doubly correlated MIMO Rayleigh fading channels is computed as below,

$$\mathcal{I}(\mathit{x};y)\approx {\log }_2\mathit{N}-\frac{1}{\mathit{N}}{\displaystyle \sum _{m=1}^{\mathit{N}}{\mathbb{E}}_{{\mathit{H}}_{\mathrm{WG}}}\left\{{\log }_2\left[{\displaystyle \sum _{k=1}^{\mathit{N}}\exp \left(-\frac{||{\mathit{c}}_{m,k}|{|}^2}{{\sigma }^2}{\alpha }_{m,k}\right)}\right]\right\}}$$

(13)

Since ${\mathit{c}}_{m,k}={\mathit{\Sigma }}_{\mathrm{R}}{}^{1/2}{\mathit{H}}_{\mathrm{WG}}{\mathit{\Sigma }}_{\mathrm{T}}{}^{1/2}{\mathit{U}}_{\mathrm{T}}{}^{\mathrm{H}}{\mathit{d}}_{m,k}$, it is still quite hard to compute the expectation of ${\mathit{H}}_{\mathrm{WG}}$. Consequently, (13) remains unsuitable for theoretical applications. Obviously, when SNR varies from $-\infty$ to $+\infty$, ${\alpha }_{m,k}$ satisfies $1/3<{\alpha }_{m,k}<1/2$ by (11), so average mutual information is approximated by

$$\begin{array}{l}\mathcal{I}(\mathit{x};y)\approx {\log }_{2}N-\frac{1}{2N}{\displaystyle \sum _{m=1}^N{\mathbb{E}}_{{\mathit{H}}_{\mathrm{WG}}}\left\{{\log }_2\left[{\displaystyle \sum _{k=1}^{\mathit{N}}\exp \left(-\frac{||{\mathit{c}}_{m,k}|{|}^2}{2{\sigma }^2}\right)}\right]\right\}}\\ -\frac{1}{2N}{\displaystyle \sum _{m=1}^N{\mathbb{E}}_{{\mathit{H}}_{\mathrm{WG}}}\left\{{\log }_2\left[{\displaystyle \sum _{k=1}^N\exp \left(-\frac{||{\mathit{c}}_{m,k}|{|}^2}{3{\sigma }^2}\right)}\right]\right\}}\end{array}$$

(14)

For the simplified calculation, the following proposition provides approximate solution:

Proposition 2.

Average mutual information integral over${\mathit{H}}_{\mathrm{WG}}$is lower bounded by

$$\begin{array}{l}ℐ(\mathit{x};y)\ge {\log }_{2}N-\frac{1}{2N}{\displaystyle \sum _{m=1}^N{\log }_2\left[{\displaystyle \sum _{k=1}^N{\displaystyle \prod _{l=1}^{N_{\mathrm{R}}}{\left(1+\frac{{[{\mathit{\Sigma }}_{\mathrm{R}}]}_{l,l}}{2{\sigma }^2}{\mathit{d}}_{m,k}{}^{\mathrm{H}}{\sigma }^{\mathrm{H}}{\mathit{\Sigma }}_{\mathrm{T}}\sigma {\mathit{d}}_{m,k}\right)}^{-1}}}\right]}\\ -\frac{1}{2N}{\displaystyle \sum _{m=1}^N{\log }_2\left[{\displaystyle \sum _{k=1}^N{\displaystyle \prod _{l=1}^{N_{\mathrm{R}}}{\left(1+\frac{{[{\mathit{\Sigma }}_{\mathrm{R}}]}_{l,l}}{3{\sigma }^2}{\mathit{d}}_{m,k}{}^{\mathrm{H}}{\sigma }^{\mathrm{H}}{\mathit{\Sigma }}_{\mathrm{T}}\sigma {\mathit{d}}_{m,k}\right)}^{-1}}}\right]}\end{array}$$

(15)

where$\mathit{P}={\mathit{U}}_{\mathrm{T}}{}^{\mathrm{H}}$.

The proof of Proposition 2 is shown in Appendix C.

4. Simulation Verification and Result Analysis

This section presents examples to illustrate that the saddle point approximation method is very accurate. We considered an exponential correlation model. According to [23], the correlation matrix elements of transmitting and receiving antennas can be expressed as:

$$\left\{\begin{array}{l}[{\mathit{\Psi }}_{\mathrm{T}}({\rho }_{\mathrm{T}})]{\mathit{I}}_{\mathrm{T}},j_{\mathrm{T}}={\rho }_{\mathrm{T}}{}^{|{\mathit{I}}_{\mathrm{T}}-j_{\mathrm{T}}|}\\ [{\mathit{\Psi }}_{\mathrm{R}}({\rho }_{\mathrm{R}})]{\mathit{I}}_{\mathrm{R}},j_{\mathrm{R}}={\rho }_{\mathrm{R}}{}^{|{\mathit{I}}_{\mathrm{R}}-j_{\mathrm{R}}|}\end{array}\right.\mathrm{and}\left\{\begin{array}{l}{\mathit{I}}_{\mathrm{T}},j_{\mathrm{T}}=1,2,\dots ,{\mathit{N}}_{\mathrm{T}}\\ {\mathit{I}}_{\mathrm{R}},j_{\mathrm{R}}=1,2,\dots ,{\mathit{N}}_{\mathrm{R}}\end{array}\right.$$

(16)

where ${\rho }_{\mathrm{T}},{\rho }_R\in \left[0,1\right)$.

4.1. Accuracy of Saddle Point Approximation

In Figure 1 and Figure 2, doubly correlated Rayleigh fading and Rice fading channel models were considered, respectively. We compared the average mutual information by the Monte Carlo method and saddle point approximation method by (12). Different input types (BPSK, QPSK, QAM, 8PSK, and 16QAM) were assigned to transmitting antennas to ensure generality. Obviously, with the increase in SNR, mutual information presented an upward trend. When the SNR was greater than 15dB, mutual information tended to be stable. In these cases, (12) offered a very good approximation to the average mutual information for known channel state information.

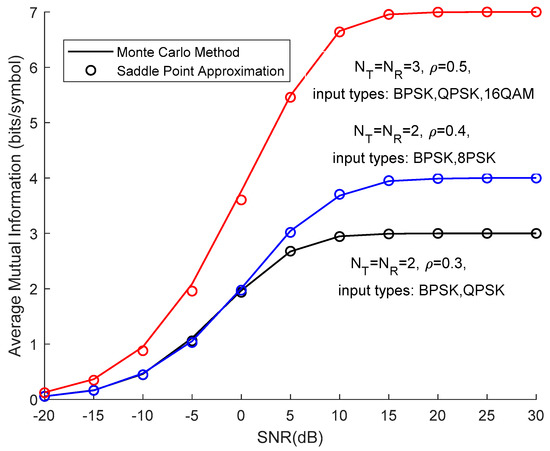
Figure 1. Comparison on MI calculated by Monte Carlo and saddle point approximation under different input types and correction parameters (${\rho }_{\mathrm{T}}={\rho }_R=\rho$) over doubly correlated Rayleigh fading channel model.

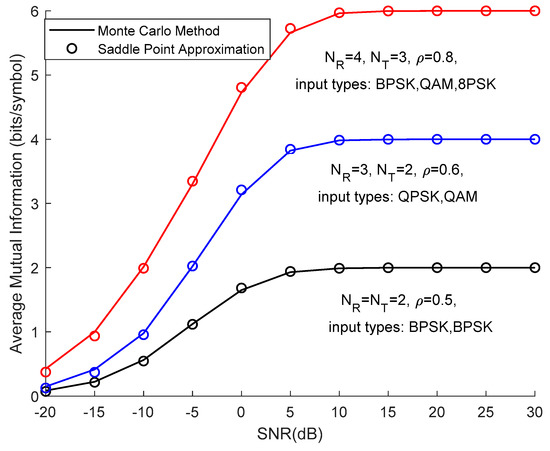
Figure 2. Comparison on MI calculated by Monte Carlo and saddle point approximation under different input types and correction parameters (${\rho }_{\mathrm{T}}={\rho }_R=\rho$) over doubly correlated Rice fading channel model.

Figure 3 compares normalized MI calculated by Monte Carlo and saddle point approximation according to upper and lower bounds of ${\alpha }_{m,k}$ by (14) over doubly correlated Rayleigh fading channels. At low SNR, the normalized average mutual information of different modulation signals had little difference. With the increase in SNR, the normalized average mutual information of different input types tended to 1, and the growth rate of BPSK was the fastest. All simulation values were very close to the approximation values.

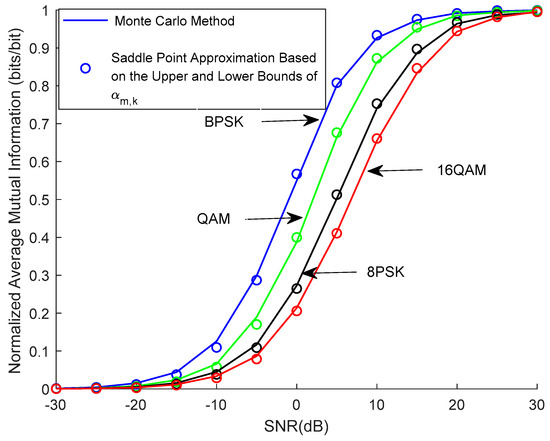
Figure 3. Comparison on normalized MI calculated by Monte Carlo and saddle point approximation according to upper and lower bounds of ${\alpha }_{m,k}$ by (14) under different input types, correction parameters (${\rho }_{\mathrm{T}}={\rho }_R=\rho =0.5$) over doubly correlated Rayleigh fading channel model (N_T = N_R = 2).

Comparison of MI calculated by Monte Carlo and the lower bound of saddle point approximation methods by (15) over doubly correlated Rayleigh fading channel are shown in Figure 4. With the increase in SNR, the mutual information increased, and the accuracy of saddle point approximation became higher. It was also clear that the lower bound of saddle point approximation achieved considerable accuracy for different doubly correlated MIMO fading channel scenarios.

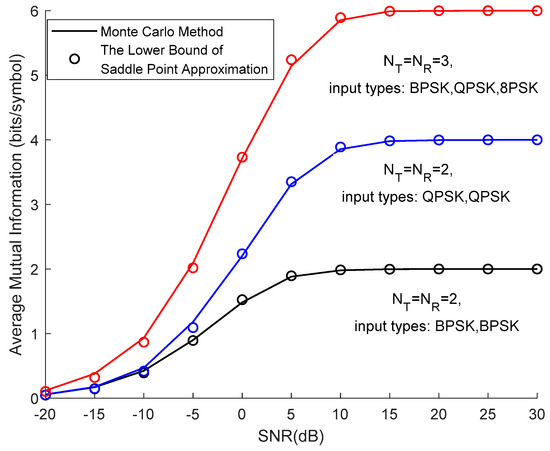
Figure 4. Comparison on MI calculated by Monte Carlo and the lower bound of saddle point approximation method under different input types and correction parameters (${\rho }_{\mathrm{T}}={\rho }_R=0.5$) over doubly correlated Rayleigh fading channel model.

4.2. Conciseness of Saddle Point Approximation

The average mutual information has no closed-form expression, so it is usually calculated by the Monte Carlo method. The more sample points, the more accurate the calculation result is. We denoted the sample points as N_W. In order to obtain a relatively accurate value of mutual information, N_W was at least 10⁴. Table 1 and Table 2 compare the computational complexity of the Monte Carlo method and the saddle point approximation method according to the number of operations and CPU time under the condition that N_W was 10⁴. The codes of mutual information calculation based on the Monte Carlo method and the saddle point approximation method were executed on an Intel Core i5-5200U 2.20 GHz processor. The results showed that the computational complexity of the proposed saddle point approximation method was much lower than that of the traditional Monte Carlo method. For example, as shown in Table 2, when N_T and N_R were equal to 2 and the input type of the two transmitting antennas was 16QAM, the CPU time of saddle point approximation methods by (15) was several orders of magnitude less than that of Monte Carlo method.

Table 1. Comparison of computational complexity between Monte Carlo method and saddle point approximation method according to the number of operations.

Number of Operations	Monte Carlo Method	Formula (15)
Exponential operation	NW * (N2 + 1)	0
Logarithm operation	NW * N	2N + 1

Table 2. Comparison of computational complexity between Monte Carlo method and saddle point approximation method according to CPU time (seconds) under different input types and correction parameters (${\rho }_{\mathrm{T}}={\rho }_R=0.4$). The symbol/indicates the CPU time is more than half an hour.

Cases	Input Type	Monte Carlo Method	Formula (15)
NT = NR = 2	BPSK	3.043959	0.001049
NT = NR = 3	BPSK	4.444435	0.019326
NT = NR = 4	BPSK	8.427808	0.029586
NT = NR = 2	QPSK	7.457080	0.027120
NT = NR = 3	QPSK	69.558626	0.081062
NT = NR = 4	QPSK	/	0.558082
NT = NR = 2	8PSK	58.627341	0.070549
NT = NR = 3	8PSK	/	1.573137
NT = NR = 4	8PSK	/	/
NT = NR = 2	16QAM	1281.853	0.612448
NT = NR = 3	16QAM	/	255.736633
NT = NR = 4	16QAM	/	/

5. Conclusions

This paper studied the numerical calculation of mutual information for finite-alphabet-based transmissions over doubly correlated MIMO fading channels. The average mutual information was dominated by statistical CSI, and the obstacle of computation was complexity. We examined the appropriateness of the saddle point method first. Then mutual information over any known channel model was calculated by saddle point approximation. Furthermore, we induced the expectation of mutual information over doubly correlated MIMO Rayleigh-fading channels. Numerical results for various MIMO scenarios showed the efficacy of the proposed method. Compared to existing conclusions, the proposed approximation is of considerable accuracy in estimating the average mutual information with radically reduced complexity. It is promising that its accuracy and convenience will facilitate the practical application of mutual information.