Multi-Objective Optimization of Atrium Form Variables for Daylighting, Energy Consumption and Thermal Comfort of Teaching Buildings at the Early Design Stage in Cold Climates

Abstract

Atrium spaces are widely applied in university buildings. However, achieving effective energy reduction while maintaining adequate daylighting and indoor comfort remains a major challenge at the early design stage. This study identifies key building form design variables significantly influencing atrium daylighting, energy use, and thermal comfort, including building orientation, atrium width-to-depth ratio, atrium aspect ratio, atrium bottom area ratio, and skylight–roof ratio. A multi-objective optimization (MOO) framework is proposed to balance daylight performance, energy consumption, and thermal comfort under fixed envelope parameters. Using typical single- and double-atrium teaching buildings in cold regions as case studies, this research adopts Useful Daylight Illuminance (UDI), Energy Use Intensity (EUI), and Discomfort Time Percentage (DTP) as key indicators to evaluate the interactions between design parameters and building performance. Based on the Pareto-optimal results for the studied prototypes, a south-by-west orientation, moderately slender atrium proportions, relatively compact atrium bottom areas, and medium skylight–roof ratios together yield a balanced performance. Compared with the reference to the initial solution, the optimized solutions reduce EUI by up to 5.66% while also improving UDI and DTP. These results are intended as quantitative references and optimization for early-stage geometric forms design of atrium teaching buildings in cold regions.

1. Introduction

The rapid growth of the global population, environmental pollution, and increasing energy consumption have become major obstacles to sustainable development since the mid-20th century [1]. With the advancement of technology and the improvement of economic standards, buildings increasingly rely on mechanical systems to meet the growing demand for spatial comfort, particularly thermal comfort, along with total building energy consumption is expected to increase accordingly.

In China, public buildings accounted for only 20% of the total building floor area in 2020, ranking third among all building categories [2]. However, their energy consumption and carbon emissions were the highest. Among public buildings, from 2001 to 2020, the main types of newly completed projects were offices, commercial buildings, and schools. In 2020, school buildings accounted for approximately 19% of the newly completed public building area and about 16% of the total public building floor area [3]. Within the category of educational public buildings, university buildings represent about 85% of the total and consistently exhibit high energy consumption [2]. As an important category of public architecture, teaching buildings require a relatively high level of indoor visual and thermal comfort [4].

As an effective solution to problems such as insufficient daylighting and poor ventilation in educational buildings, atriums have become a common spatial form in university architecture. In cold regions characterized by severe winters and hot summers, spacious indoor public areas provide a more comfortable environment for occupants compared with outdoor public spaces [5].

The diverse forms and interface scales of atriums exert varying impacts on building energy consumption. Compared with other interior spaces, the atrium temperature tends to be excessively high in summer and too low in winter, thereby requiring active cooling and heating strategies to maintain a comfortable physical environment [5]. Therefore, atriums possess considerable potential for energy conservation [2].

1.1. Architectural Form

Humans modify and regulate their environment to achieve safety and comfort, and this constitutes the original driving force of architecture. In the pursuit of climate-responsive and environmentally regulated building design, conflicts and challenges are inevitable. In this study, architectural form encompasses both the external configuration of the building and its internal spatial organization, which directly affect heat gain, natural ventilation, and daylighting. Previous studies have demonstrated that early form decisions determine the basic building volume, proportions, and atrium layout, thereby influencing solar radiation, natural ventilation, and daylight penetration. Architectural form is thus regarded as the most critical mechanism linking climate and energy performance [6], and it consequently affects heating and cooling costs [7]. By contrast, the thermal and optical properties of the envelope and the HVAC system are typically optimized at subsequent design stages. Based on these assumptions, a well-designed architectural form can ensure indoor comfort with minimal energy use [8,9]. For instance, can bring daylight deep into the building core and establish efficient routes for natural ventilation, which in turn reduces reliance on artificial lighting and HVAC systems and lowers energy use for building services [10,11].

According to the Annual Report on China Building Energy Efficiency Development 2023, lighting and thermal loads account for the majority of total energy use in the case of large public buildings. Consequently, studies on the improvement of architectural form have investigated the relationships between form-related parameters and specific performance indicators, with most focusing on optimizing atrium design for improved daylighting and thermal performance—particularly in cold regions characterized by pronounced temperature fluctuations [12].

However, achieving optimal daylighting and thermal performance simultaneously remains challenging. For instance, while an atrium skylight can enhance daylight penetration and thereby reduce the need for artificial lighting, natural illumination is often accompanied by solar radiation. The greater the amount of incoming light, the higher the associated radiation, which can diminish indoor thermal comfort. In hot summer conditions, this effect leads to increased cooling energy consumption [13]. Therefore, the optical and thermal performances of an atrium can conflict under certain conditions, yet achieving an appropriate balance between them is essential [14].

1.2. Architectural Form Optimization Method

Architectural geometric form is generally determined at the early stage of the building design process, where rational form decisions can achieve energy-saving effects far superior to those attained through post-design technological interventions [9,15]. Traditionally, architects have relied on experiential intuition and case-based reasoning to shape building forms, while performance simulation and evaluation are often conducted at later design stages—an approach that limits the overall performance potential of buildings. Therefore, it is essential to propose an atrium design method for teaching buildings with a focus on optimizing and predicting performance, aiming to achieve optimal outcomes in thermal comfort, daylighting performance and energy use.

With the rapid advancement of digital technology, new methods and tools have become available for object-oriented green design [16]. Architects can employ various approaches to enhance the performance of architectural forms, such as scenario-based analysis, performance simulation and analysis, passive optimization strategies, and algorithmic optimization methods [17]. Among these methods, performance simulation and analysis, scenario-based analysis, and passive optimization each have inherent limitations in practical application, whereas optimization algorithms have been widely adopted because they can handle complex nonlinear problems effectively. Parametric optimization algorithms allow architects to utilize computational methods to adjust building parameters, generate multiple energy-efficient retrofit schemes, and identify the optimal one, thereby fully tapping into the energy-saving potential of university educational buildings.

Among the optimization algorithms commonly used in the design process, the accuracy of results generated by the simulated annealing algorithm is slightly lower than that of other algorithms; both the PSO and direct search approaches exhibit relatively slow convergence rates, while surrogate model optimization algorithms tend to have limited model precision. In contrast, the genetic algorithm (GA) is a stochastic search method that simulates the natural processes of biological evolution and inheritance, preserving optimal solutions through selection mechanisms. Its main advantages include: (1) the ability to generate a global optimum by maintaining population diversity and avoiding premature convergence; (2) strong adaptability and scalability; (3) the capacity to evaluate all individuals in the population simultaneously, thereby enhancing computational flexibility and efficiency; (4) the capability to operate continuously in dynamically changing environments, obtaining and utilizing the best current solution at any given time [18].

1.3. Literature Review

1.3.1. Study on the Relationship Between Architectural Form and Lighting–Thermal Performance

The selection of optimization techniques for atrium form design is determined by the characteristics of optimization parameters and objectives. The optimizable architectural form parameters are inherently uncertain, multi-factor complexity, and discreteness. The inherently multi-objective and nonlinear response of buildings confronts architects with the challenge of balancing energy efficiency and indoor lighting–thermal comfort from the very early stages of design. Given the diversity and non-singularity of optimization goals, some relationships are hard to assess and certain factors are difficult to reconcile.

A considerable body of research has therefore focused on geometric form variables and their relationship with specific performance indicators, while treating envelope constructions, glazing properties and HVAC systems as fixed boundary conditions rather than optimization variables. Abdelsalam Aldawoud et al. [19] analyzed the impact of geometric form on the energy performance of atrium building models and found that rectangular atriums with higher aspect ratios exhibit greater total energy consumption than square atriums. Nasrollahi et al. [19] examined different atrium plan configurations and found that elongated, corridor-like atria consume more energy than atria with a roughly square plan. Wang et al. [20] quantitatively analyzed the energy performance of atriums with different sectional aspect ratios and skylight area ratios, and identified the optimal atrium dimensions that minimize annual energy use. Jeong-Tak Jin et al. [21] investigated the thermal load characteristics of free-form architectural designs and employed a genetic algorithm to rapidly predict and optimize variations in thermal load performance resulting from changes in building form. Zheng Caidan [22] conducted on-site measurements and numerical simulations using a core daylight atrium in Guangzhou as a case study to verify the applicability of the FLUENT model in indoor thermal environment analysis. Subsequently, daylighting simulations with ECOTECT and indoor thermal environment analyses with CFD were employed to investigate the effects of factors such as building area ratio, skylight height-to-width ratio, and skylight inclination angle. Freewan [23] examined the thermal performance and energy consumption of building south and north façades with various inward and outward inclination angles and compared the results with those of vertical façades.

1.3.2. Study on the Optimization Scheme of Building Light–Thermal Performance

In addition to examining the correlations between building form parameters and performance outcomes, some studies have also conducted comprehensive evaluations of the objective values in optimization schemes. Research on performance-oriented multi-objective optimization in architecture has been extensively developed.

Research on the relationship between atrium building form variables and performance parameters is often conducted through multi-objective optimization. Many studies have analyzed building form parameters to obtain the optimal atrium configuration according to different optimization objectives. For example, Guan et al. [5] verified and evaluated the geometric design variables of atriums at the architectural design stage with various objectives such as energy use, cost, and proposed a method for optimizing atrium energy consumption. The most suitable design scheme was then selected based on different design requirements. The study showed that the influence of atrium design variables on building energy use decreases in the following order: atrium shape coefficient, atrium height-to-span ratio (DSR), atrium volume ratio (VR), skylight area ratio (SAR), and atrium width-to-depth ratio (FDR). Through the analysis of parameter combinations, a new atrium design variable—the atrium shape coefficient—was identified.

Wu et al. [24] analyzed the effects of the skylight-to-roof area ratio (AR) and sectional aspect ratio (SAR) of atriums on daylighting and thermal environment, and identified the optimal dimensionless combination for atrium configuration. The optimal nondimensional combination of the atrium configuration was AR = 1/5 and SAR = 4. Ji et al. [25] introduced a multi-objective optimization strategy about daylighting, energy, and thermal comfort performance of open atrium geometries and verified its effectiveness through practical case studies. The results showed that the optimization framework can significantly improve all three building performance objectives. Xiao et al. [7] proposed a set of atrium form parameters and conducted multi-objective optimization to establish an optimization framework that balances daylighting, energy consumption, and thermal performance. Liang et al. [1] studied the daylight–thermal environment and energy consumption levels of university buildings with atriums in cold regions, using skylight area ratio, window-to-wall ratio of side windows, glass type, shading panel rotation angle, and spacing width as optimization variables for multi-objective optimization, thereby providing strategies for the optimization and renovation of existing university atrium buildings in cold regions. Xu et al. [26] developed a rapid strategy that integrates multi-objective optimization with machine learning algorithms, providing guidance for policymakers to conduct performance-based design of university atriums. Chen et al. [27] established four different atrium models and conducted multi-objective optimization following performance simulations, resulting in significant improvements in both energy-saving rates and daylight comfort for all four atrium types.

According to recent studies (

Table 1. Representative research into architectural geometric form optimization.

Researchers	Climate Zone	Design Independent Parameters	Optimization Objective	Research Objectives
Liang et al. [1]	Cold climate	Skylight, side window area ratio, glass type and sunshade plate rotation angle and interval width	Thermal and Energy performance	Performance simulation analysis
Guan et al. [5]	Cold, HSCW and HSWW zones	Skylight–roof ratio (SRR); section aspect ratio of the atrium (SAR); Atrium building volume ratio (VR); Atrium width-to-depth ratio (FDR)	Energy consumption; Correlation analysis and multiple linear regression	Multi-objective optimization
Xiao et al. [7]	HSCW climate zone	Orientation, south facade inclination, roof inclination, south/north section aspect ratio of the atrium, east/west section aspect ratio of the atrium, and top-to-floor area ratio of the atrium	Useful daylight illuminance (UDI); Energy use intensity (EUI); Thermal discomfort percentage (TDP)	Multi-objective optimization
Nasrollahi et al. [19]	Hot-dry & humid, cold, mild	Atrium width-to-depth ratio; Skylight glass type (SGT); Skylight–roof area (SRR)	Energy consumption	Performance simulation analysis
Wang et al. [20]	Cold climate	Atrium section aspect ratio (ASAR), atrium top surface area (TA)	Temperature distribution, EUI	Performance simulation analysis
Wu et al. [24]	HSCW climate zone	Skylight–roof ratio (SRR); Atrium section aspect ratio (ASAR)	Temperature distribution, illumination	Performance simulation analysis
Freewan, 2022, [23]	Hot, arid climate	South and north facade inclination	Energy consumption	Performance simulation analysis
Ji et al., 2023 [25]	Cold climate	Shape ratio; well index; volume ratio; inner window-to-wall ratio; position index	UDI; EUI; DTP	Multi-objective optimization
Xu et al. [26]	HSCW climate zone	Height-to-Width ratio (HWR), the skylight solar heat gain coefficient (SHGCs), and the sidewall window-to-wall ratio (SWWR)	Building energy efficiency (BEE); indoor environmental quality (IEQ)	Multi-objective optimization
Chen et al. [27]	Cold climate	Window-to-wall ratio (WWR); skylight–roof ratio (SRR); skylight aspect ratio (SAR)	Energy consumption, light and thermal comfort	Multi-objective optimization

), the design variables and performance indicators of architectural form are diverse and complex, making it difficult to incorporate them all into a single study. It is evident that although numerous researchers have concentrated on optimizing architectural form, several research limitations and gaps remain: (1) In cold regions, the improvement of educational building form remains insufficient. The geometric form of buildings in these locations tends to focus more on winter light and thermal conditions. Since building performance in this climate zone is intricately related to environmental factors, balancing relevant performance indicators through optimization techniques is essential. (2) According to survey results, university educational buildings in cold regions are mostly characterized by four-sided atrium layouts. The majority of existing research has concentrated on the simulation and optimization of single four-sided atrium configurations, while research on multi-atrium configurations, which also account for a considerable proportion in practical applications, remains limited. (3) Most studies have not verified the reliability of simulated data using field observations, which may lead to deviations in subsequent multi-objective optimization and model prediction accuracy.

In response to the limitations and deficiencies identified in previous studies, this research applies a genetic algorithm to refine the atrium form design of teaching buildings in cold regions. Using a university educational building in Xi’an as a case example, field measurements were conducted to examine the complexity of the atrium’s light and thermal environment and to validate the accuracy of simulation results against measured data. On this basis, the study evaluates the effectiveness of building performance simulation and genetic algorithm–based optimization in improving daylighting performance, energy use, and thermal comfort of atriums. The findings provide a valuable reference for future research on related topics and contribute to advancing the development of sustainable architectural design.

1.4. Research Content

Architectural form is not only an important aspect of architectural design but also exerts a significant influence on building performance. Multi-objective optimization of architectural form can greatly promote building design at the early stage. Therefore, this study focuses on architectural form design, comprehensively considering both external form and internal spatial configuration, establishing relevant form design variables, and determining performance optimization objectives. An overall framework for architectural form design optimization is developed to balance daylighting, energy consumption, and comfort in the atrium spaces of teaching buildings through form optimization. Accordingly, the optimization objectives of this study are the Useful Daylight Illuminance (UDI), Energy Use Intensity (EUI), and Discomfort Time Percentage (DTP) of the atrium. Numerous variables related to architectural form design are considered throughout the optimization process. The interactions between different variables and optimization objectives are analyzed during the optimization procedure. Subsequently, both the optimal and trade-off solutions generated in the optimization process are comprehensively evaluated to determine the recommended design combinations. This optimization study makes the following main contributions:

• This study primarily centers on architectural form of university teaching buildings. By comprehensively considering variables related to both external form and internal spatial configuration, design parameters with significant impacts on building performance in cold regions were identified through literature analysis and field investigation. On one hand, the study conducts an integrated exploration and evaluation of architectural form; meanwhile, it determines the main parameters that need to be considered in the early stage of performance-oriented design.
• Taking a typical atrium educational building in a cold climate as the study object, this study collected extensive fundamental data through simulations of daylighting, energy consumption, and thermal comfort. It expands the existing research on the relationship between cold-region climate and the performance parameters of teaching buildings, thereby enriching the empirical basis for studies on atrium form and performance in such regions.
• The best combination of design parameters identified in this study can be directly applied to the architectural design of educational buildings in cold climate. It provides a reference for the selection, design, renovation, and improvement of architectural forms at the early design stage, and ultimately enriches the empirical research on the relationship between atrium form and performance in cold-region buildings. These aspects enhance the practical significance of this study.

2. Materials and Methods

2.1. Research Framework

This research investigates the optimization design of atrium form parameters in teaching buildings sited in cold climate of China. The process of simulating and optimizing daylighting, energy consumption, and thermal comfort is carried out in three main steps, as illustrated in Figure 1.

• Establishment of a parametric base design model: Field surveys were conducted on the atriums of 25 university teaching buildings in Xi’an to collect and analyze relevant data. Based on these findings, a representative parametric atrium model was developed. Design variables were extracted from parameters found to exert substantial effects on atrium space performance.
• Simulation of the physical environment of the atrium: Environmental performance simulations of the base model were performed in terms of daylighting, energy consumption, and thermal comfort. The simulation results include the Useful Daylight Illuminance (UDI), Energy Use Intensity (EUI), and Discomfort Time Percentage (DTP).
• Multi-objective optimization (MOO) and data analysis: A genetic algorithm was applied to perform multi-objective optimization of the atrium design. The architectural form design parameters were treated as independent variables, while the physical environmental performance indicators served as dependent variables. Through an iterative process, a set of optimal Pareto front solutions was generated, from which the optimal combination was determined by balancing the performance of all target objectives.

Figure 1. Optimization framework of this study.

Figure 1. Optimization framework of this study.

In this study, parametric modeling was conducted using Rhinoceros [28] and its plugin Grasshopper [29]. The Ladybug plugin [30] integrated within Grasshopper was employed to link the simulation engines EnergyPlus [31] and Radiance [32] with the geometric model. The optimization was implemented with the aid of the multi-objective optimization plugin Octopus.

2.2. Baseline Architectural Model

According to the building climate zoning standards, China is divided into five major climate zones: Severe Cold (SC), Cold, Hot Summer and Cold Winter (HSCW), Hot Summer and Warm Winter (HSWW), and Mild [33].

Cold regions are characterized by long, cold, and dry winters, hot and humid summers, and relatively short transitional seasons with large temperature fluctuations. Xi’an (108.93° E, 34.27° N) was selected as the study area. The city experiences extreme temperatures ranging from nearly 40 °C in summer to −10 °C or lower in winter. Given the high concentration of universities in Xi’an, studying teaching buildings in this region holds significant practical importance. The climatic information of Xi’an is shown in Figure 2.

To investigate the physical environment of atriums in university educational buildings located in cold regions, it is first necessary to establish a representative base model. In this study, on-site and online surveys were conducted on the atrium forms of 25 university teaching buildings in Xi’an, providing data and energy simulation support for the development of the base model. The survey was carried out from March to April 2025, focusing on the types, quantities, and forms of atriums in 25 university teaching buildings across Xi’an. Buildings were first identified from campus master plans and online information, and then included in the sample if they were multi-storey teaching buildings located on university campuses and contained at least one enclosed atrium that could be clearly documented. The objective of the survey was to collect data for constructing a representative model to support ensuing analysis. The detailed dataset gathered include atrium type, number of atriums (C), floor height (H), building length and width (L1 and W1), atrium length and width (L2 and W2), as well as skylight–roof ratio (R).

Table 2. Summary of atrium dimensions for each field-surveyed building.

Name of Research University	Atrium Layouts	C	H/m	L1/m	W1/m	L2/m	W2/m	R/%	Atrium Illustration
Shaanxi University of Science and Technology	Tetra-directional	1	3.9	68	20	15	11	0.65
Shaanxi University of Science and Technology	Tetra-directional	1	4.5	90	26	52	15	0.70
Xi’an Shiyou University	Tetra-directional	1	4.5	100	45	15	18	0.52
Shaanxi Normal University	Tetra-directional	2	4.5	80	35	18	8	0.45
Xi’an Polytechnic University	Tetra-directional	2	4.5	88	28	20	8	0.86
Xi’an University	Tetra-directional	1	3.6	45	45	20	20	0.65
Xi’an University	Bidirectional	1	4.5	45	18	18	8	0.95
Xizang Minzu University	Tetra-directional	1	3.6	76	30	13	16	0.82
Xidian University	Tetra-directional	1	3.6	73	47	20	24	0.73
Xidian University	Tridirectional atrium	3	3.9	137	30	34	8	0.55
Xidian University	Tetra-directional	2	3.6	60	26	18	7	0.75
Xi’an Jiaotong University	Tetra-directional	1	3.6	34	43	12	12	0.80
Xi’an Jiaotong University	Tetra-directional	1	4.5	40	40	15	15	0.65
Xi’an Jiaotong University	Tridirectional	1	3.9	37	43	8	16	0.92
Xi’an Jiaotong University City College	Tetra-directional	1	3.9	90	47	40	18	0.76
Chang’an University	Tetra-directional	1	3.9	60	48	22	12	0.42
Chang’an University’s Wei Shui Campus	Tetra-directional	1	4.5	65	40	43	18	0.35
Chang’an University’s Wei Shui Campus	Tetra-directional	1	3.9	75	50	26	24	0.85
Northwest A&F University	Tetra-directional	2	4.5	145	35	25	15	0.74
Shaanxi University of Chinese Medicine	Tetra-directional	1	3.9	88	40	21	14	0.32
Baoji(Shaanxi) University of Arts and Sciences	Tetra-directional	2	3.9	94	23	15	5	0.85
Weinan Normal University	Tetra-directional	1	4.8	88	46	30	15	0.53
Xi’an University of Finance and Economics	Tetra-directional	2	5.4	80	28	18	11	0.90
Shaanxi Xueqian Normal University	Tetra-directional	1	3.9	85	50	22	8	0.82
Shaanxi Xueqian Normal University	Tridirectional	1	4.2	52	18	21	9	0.85

presents selected morphological information of the surveyed university atriums.

Based on the climatic characteristics of cold regions and the results of on-site investigations, the atrium layouts were categorized into four types: single-sided atrium, double-sided atrium, three-sided atrium, and four-sided atrium, as shown in Figure 3. The survey revealed that the floor plans tend to adopt simple geometric shapes, with rectangular layouts being the most common—17 cases, accounting for 68% of the 25 surveyed buildings. Among them, four-sided atriums were the most prevalent, appearing in 22 cases, representing 88% of the total. The number of atriums in four-sided configurations was generally one or two, with 15 buildings (60%) having a single atrium and 6 buildings (24%) having two. Atrium lengths were mainly between 12 and 30 m, widths between 8 and 24 m, and floor heights between 3.6 and 4.8 m, with the primary plan dimensions generally under 100 m. Most skylights were rectangular and designed for top lighting, and in most cases the skylight–roof ratio ranges between 30% and 90%.

Based on the architectural characteristics of the study area, this research established a typical rectangular-plan, four-sided atrium teaching building as the base model for simulation. Two base models were constructed, respectively, for the single- and double-atrium configurations of the four-sided type, as shown in Figure 4. The constant parameters of the model include building length, building width, number of floors, number of classrooms per side, floor height, external window-to-wall ratio, internal window-to-wall ratio, and windowsill height. The fixed parameters are listed in

Table 3. Fixed parameters of the baseline building.

Fixed Parameters	Model Parameters Value
Building length	100 m
Building width	30 m
Number of Floors	6 floors
Floor-to-ceiling Height	4.5
Exterior window-wall ratio	0.5
Openable exterior window area ratio	0.5
Openable interior window area ratio	0.3
Sill height	1.1
Door width	2.7
Door height	2.2
Number of doors	4

.

The occupancy schedules of the teaching spaces in the baseline model follow a typical university timetable (

Table 4. Occupancy schedules of the baseline building.

Space Type	Weekday Occupied Hours	Weekend Occupied Hours	Occupancy Level (Relative)
Classrooms	08:00–12:00, 14:00–18:00, 19:00–22:00	Unoccupied	0.95 during class time
Offices	08:00–19:00	Unoccupied	0.8
Corridors & atrium	Follow adjacent spaces	Follow adjacent spaces	0.3

). The annual schedule is divided into term time and winter/summer vacation periods. According to the academic calendars of universities in Xi’an, the winter vacation is from 20 January to 20 February, and the summer vacation is from 20 July to 31 August. On teaching days during the semester (Monday to Friday), the classroom occupancy rate is set to 0.95 during regular class hours (08:00–12:00, 14:00–18:00, 19:00–22:00), and reduced to 0.80 during the remaining daytime periods (12:00–14:00 and 18:00–19:00). During night-time (22:00–08:00 of the following day), the classroom occupancy rate is set to 0. The office occupancy rate is set to 0.8 during working hours (08:00–19:00), and zero at other times. Corridor and atrium spaces are assumed to follow the same usage schedule as the adjacent functional spaces, with an occupancy rate of 0.3. On weekends and public holidays, the building is assumed to be unoccupied (occupancy rate = 0). The metabolic rate of occupants is set to 120 W/person, representing a sedentary activity level corresponding to seated learning and lecture attendance.

Architectural form serves as the most important mechanism of environmental regulation and feedback, playing a crucial role in the process of building adaptation to climate. Therefore, in this study, all considered variables are related to architectural form, while variables associated with building envelope, materials, and operational conditions (such as heating and cooling settings) are kept constant [34]. Variables related to architectural form design encompass aspects such as plan layout, overall shape, and spatial organization. In this study, the form of university teaching buildings with atriums differs from that of other urban building types, exerting distinct impacts on both energy use and the indoor thermal environment. The geometric configuration of the atrium and its spatial relationship with other building components can be regarded as the fundamental unit of architectural form. Accordingly, this study identifies variables associated with the atrium form of teaching buildings as the design variables for optimization, based on their significance to environmental performance.

Previous studies on architectural form have demonstrated that orientation significantly influences heat gain, natural daylighting, and ventilation [35]. The layout, number, size, and proportions of atriums affect building ventilation and, consequently, indoor thermal comfort. Similarly, variations in skylight area influence both the daylighting performance and thermal comfort of the atrium interior, thereby impacting the building’s overall energy consumption [12,24]. Therefore, based on the literature and field investigation results, the design variables considered in the optimization process include: building orientation (V1), atrium width-to-depth ratio (V2), atrium aspect ratio (V3), atrium bottom area ratio (V4), and skylight–roof ratio (V5). The ranges of these design variables are set relatively wide to provide greater flexibility in the combination of optimization schemes. The value ranges of the design parameters are illustrated in Figure 5 and

Table 5. Building form design variables.

Form Design Variables	Definition	Initial Value	Range
V1: Orientation	The orientation changes from southeast (<0) to southwest (>0)	0	[−45°, 45°]
V2: Atrium width-to-depth ratio	The width-to-depth ratio of the atrium	0.52	[0.24, 1.2]
V3: Atrium aspect ratio	The aspect ratio of the atrium	2.5	[1.875, 3.75]
V4: Atrium bottom area ratio	The ratio of the atrium bottom area to the building area	4%	[1.5%, 7.5%]
V5: Skylight–roof ratio	The area ratios for skylights	0.6	[0.3, 0.9]

.

2.3. Building Performance Simulation

2.3.1. Energy Consumption Simulation

Based on the national standards of the People’s Republic of China [36,37], the fundamental parameters of the energy consumption model for university teaching buildings, including structural parameters, temperature settings, and occupant density were summarized. The energy model was created using the template “ASHRAE 90.1–2019 [38]: College”.

Table 6. Construction element parameters for the baseline energy model.

Construction Element	Type	Input Value
		R-Value (m2·K/W)	Roughness	Thermal Absorptance	Solar Absorptance	Visible Absorptance	U-Value (W/m2·K)	SHGC	Visible Transmittance
External wall	Outdoor wall	1.668	Medium	0.9	0.5	0.7	-	-	-
Roof	Outdoor roof	2.35	Medium	0.9	0.74	0.7	-	-	-
Internal wall	Wall	0.517	-	-	-	-	-	-	-
Floor	Adiabatic floor	0.517	-	-	-	-	-	-	-
Ceiling	Adiabatic ceiling	0.517	-	-	-	-	-	-	-
Window	6Low-E + 12A + 6C	-	-	-	-	-	2.0	0.4	0.62

and

Table 7. Building operation settings for the baseline energy model.

Building Operation Settings	Type	Input Value
Infiltration rate (per area of facade)	-	0.00023 m3/s·m2
Lighting density (per area of floor)	-	7.9653 W/m2
People density (per area of floor)	-	0.33 ppl/m2
Equipment load	-	6.89 W/m2
HVAC system	Ideal air load system	-
Cooling setpoint	-	28 °C
Heating setpoint	-	18 °C

summarizes the specific parameters of the enclosed teaching building in the energy consumption model. In the energy simulation of this study, the HVAC system was set as an ideal loads air system, with temperature setpoints of 18 °C for heating and 28 °C for cooling, which are considered relatively energy-efficient values [39,40]. In the energy model, natural ventilation is primarily driven by two mechanisms: (1) cross-ventilation driven by pressure differences between indoor and outdoor openings, and (2) stack-driven ventilation induced by variations in the dimensions of the atrium. The use of natural ventilation helps reduce indoor temperatures during summer and conserve energy, without conflicting with the operation of mechanical cooling systems. The model assumes that natural ventilation is adopted when the outdoor mean dry-bulb temperature ($T_{a,out}$) and the indoor mean dry-bulb temperature ($T_{a,in}$) satisfy the following conditions:

$$12\le T_{a,out}\le 28 °\mathrm{C}$$

$$23\le T_{a,in}\le 28 °\mathrm{C}$$

$$T_{a,out}-T_{a,\dot{in}}\ge 0.5 °\mathrm{C}$$

In this study, Energy Use Intensity (EUI) (kWh/m²·y) is adopted as one of the optimization objectives. It represents the annual total energy load per unit area, including cooling, heating, lighting, and equipment energy loads [41], and is calculated using the EnergyPlus engine [31] integrated within Grasshopper [25,29].

2.3.2. Daylighting Performance Simulation

For the daylighting model, the sensor points are arranged on a grid at a height of 0.8 m above the floor on the first level of the atrium. The number of sensor points varies according to the atrium’s form design variables. According to the Chinese Standard [42], artificial lighting in buildings is modelled as a supplementary system to daylight, and the indoor natural illuminance in standard classrooms of educational buildings should not be lower than 450 lx, while that in corridors, stairwells and similar spaces should not be lower than 150 lx. During occupied hours, a daylight-linked lighting control strategy is adopted: when daylight is sufficient, the power of artificial lighting is reduced, and when daylight alone cannot achieve the prescribed illuminance levels, the artificial lighting power is increased; during unoccupied periods, all lighting is switched off. The electricity use of this lighting system was fully accounted for in the simulated EUI. At the same time, the sensible heat released by lighting contributed to the internal heat gains of the zones, thereby affecting both heating and cooling loads. The final EUI therefore includes the energy for space conditioning (heating and cooling), ventilation fans and electric lighting. The detailed optical properties of the building materials are presented in

Table 8. Optical performance parameters of construction materials.

Construction Element	Material Type	Input Value
		Roughness	Reflectance
Exterior wall	Radiance opaque material	0.05	0.8
Interior wall	Radiance opaque material	0.05	0.75
Roof	Radiance opaque material	0.05	0.32
Ceiling	Radiance opaque material	0.05	0.75
Floor	Radiance opaque material	0.05	0.58
Door	Radiance opaque material	0.05	0.1
Window	Radiance glass material	Visible transmittance: 0.86

.

In this research, UDI is adopted as one of the optimization objectives. UDI is a dynamic metric used to evaluate the suitability of indoor natural lighting. It represents the proportion of time during an assessment period (typically one year) when indoor illuminance levels fall within a useful range. The concept was first introduced by Nabil and Mardaljevic (2005) as an alternative to the traditional Daylight Factor (DF) method [43].

UDI is divided into three standard ranges corresponding to the proportion of time that illuminance levels reach: 0–100 lx, 100–2000 lx, and over 2000 lx. In this study, UDI refers to the proportion of time that the average illuminance of all test points within the atrium falls within the range of 100–2000 lx, denoted as UDI_100–2000, hereafter referred to simply as UDI [44].

2.3.3. Thermal Comfort Simulation

The design and construction of buildings should achieve a comfortable indoor thermal environment while keeping energy use to a minimum; therefore, it is necessary to consider thermal comfort in conjunction with building energy performance and daylighting quality. According to the definition provided by ASHRAE, thermal comfort is “the condition of mind that expresses satisfaction with the thermal environment and is assessed by subjective evaluation.” The thermal environment is influenced by factors such as air temperature, humidity, air velocity, and mean radiant temperature, as well as human factors including metabolic rate and clothing insulation, in addition to regional climatic differences and seasonal variations. Subjective evaluations also involve physiological, psychological, social, and cultural aspects, as well as geographical context [45,46].

In this study, the PMV–PPD model was employed to assess the thermal comfort conditions of occupants in university teaching buildings. The Predicted Mean Vote (PMV) is one of the most widely used indices for evaluating indoor thermal environments [47].

Another indicator, the Predicted Percentage of Dissatisfied (PPD), represents the percentage of occupants likely to feel thermally dissatisfied based on the PMV value. It is calculated from the energy simulation results of air temperature, mean radiant temperature (MRT), and relative humidity. In this study, the thermal comfort model was established in accordance with the ASHRAE Standard 55, which suggests that a PPD value below 20% within a given period indicates that the thermal comfort requirements of occupants are generally satisfied [25,48].

To better characterize thermal comfort conditions, the percentage of time during which the PPD value exceeds 20% was recorded and used as an evaluation indicator, referred to as the Discomfort Time Percentage (DTP).

2.4. Multi-Objective Optimization

In many cases, there exist certain coupling relationships among various physical performance parameters of buildings, which are difficult to identify through theoretical analysis alone. Multi-objective optimization algorithms are primarily designed to address such problems [49]. The Genetic Algorithm (GA), a search method inspired by the principle of survival of the fittest in biological evolution, is widely regarded as the most accurate and efficient method for multi-objective optimization [50].

Several factors contribute to the widespread application of GA in multi-objective optimization studies of building design [51,52]. First, it is well-suited for complex nonlinear design problems, particularly those involving both discrete and continuous variables with nonlinear relationships among performance indicators [53]. Second, GA supports the simultaneous optimization of multiple conflicting objectives, generating a set of trade-off solutions (Pareto-optimal solutions) that provide designers with diverse decision options [54]. Third, it possesses strong global exploration capabilities, enabling efficient identification of high-quality regions within large design spaces and reducing the likelihood of being trapped in local optima compared with gradient-based or local search methods [55]. Fourth, GA can be seamlessly integrated with simulation tools such as EnergyPlus and Radiance, allowing automated iterative calculations of energy use, daylighting, and thermal performance, thereby achieving efficient design space exploration while maintaining physical accuracy [54,56]. In summary, GA provides a stable, flexible, and general framework for the multi-objective optimization of complex building systems.

Therefore, this study adopts the Genetic Algorithm (GA) as the core method to address the multi-objective optimization problem, implemented through the Octopus plugin. Octopus is a genetic optimization engine that enables users to run and evolve simulations within the parametric modeling platform Grasshopper, and it has seen widespread application in the area of building performance optimization [57]. Octopus employs the Strength Pareto Evolutionary Algorithm 2 (SPEA-2) and the Hypervolume Estimation (HypE) algorithm to generate a set of Pareto-optimal solutions, the distribution of which in the objective space constitutes the Pareto front [58]. In this study, the parametric factors were introduced into Octopus as genetic variables, while EUI, UDI, and DTP were defined as the optimization objectives. The Pareto front was used to identify trade-off solutions among these objectives. The parameters set for Octopus include a crossover rate of 0.8, a mutation rate of 0.9, a mutation probability of 0.2, and an elitism level of 0.5. The population size was set to 50, and the optimization terminated after 40 generations, as shown in

Table 9. Octopus optimized parameter settings.

Optimization Parameters	Value
Elitism	0.5
Mutation Probability	0.2
Mutation Rate	0.9
Crossover Rate	0.8
Population Size	50
Max Generation	40

.

The trade-off solution that minimizes EUI and DTP while maximizing UDI was considered the ideal solution in this research. Accordingly, a fitness function (Equation (1)) was employed to rank all Pareto-optimal solutions. This type of linear weighted-sum function is a standard and transparent multi-criteria decision-making tool for selecting preferred solutions from a Pareto front.

$$y=\left(EU{I}_i-EU{I}_{min}\right)C_1+\left(UD{I}_i-U{DI}_{min}\right)C_2+\left({PPD}_i-{PPD}_{min}\right)C_3$$

(1)

maximize(y)

where

$i$ = result of the iteration;

min = minimum value in the optimization set;

max = maximum value in the optimization set.

$$C_1={\displaystyle \frac{100}{EU{I}_{max}-EU{I}_{min}}}$$

$$C_2={\displaystyle \frac{100}{UD{I}_{max}-UD{I}_{min}}}$$

$$C_3={\displaystyle \frac{100}{{PPD}_{max}-{PPD}_{min}}}$$

With this definition, each term in Equation (1) corresponds to a normalized score that varies approximately between 0 and 100 within the Pareto set. This normalization removes the effects of different physical units and numerical scales among EUI, UDI and DTP, and ensures that each objective contributes with equal potential weight to the composite fitness value. The factor 100 is used only to express the normalized values on a per-centage-like scale and does not affect the ranking of solutions.

3. Results

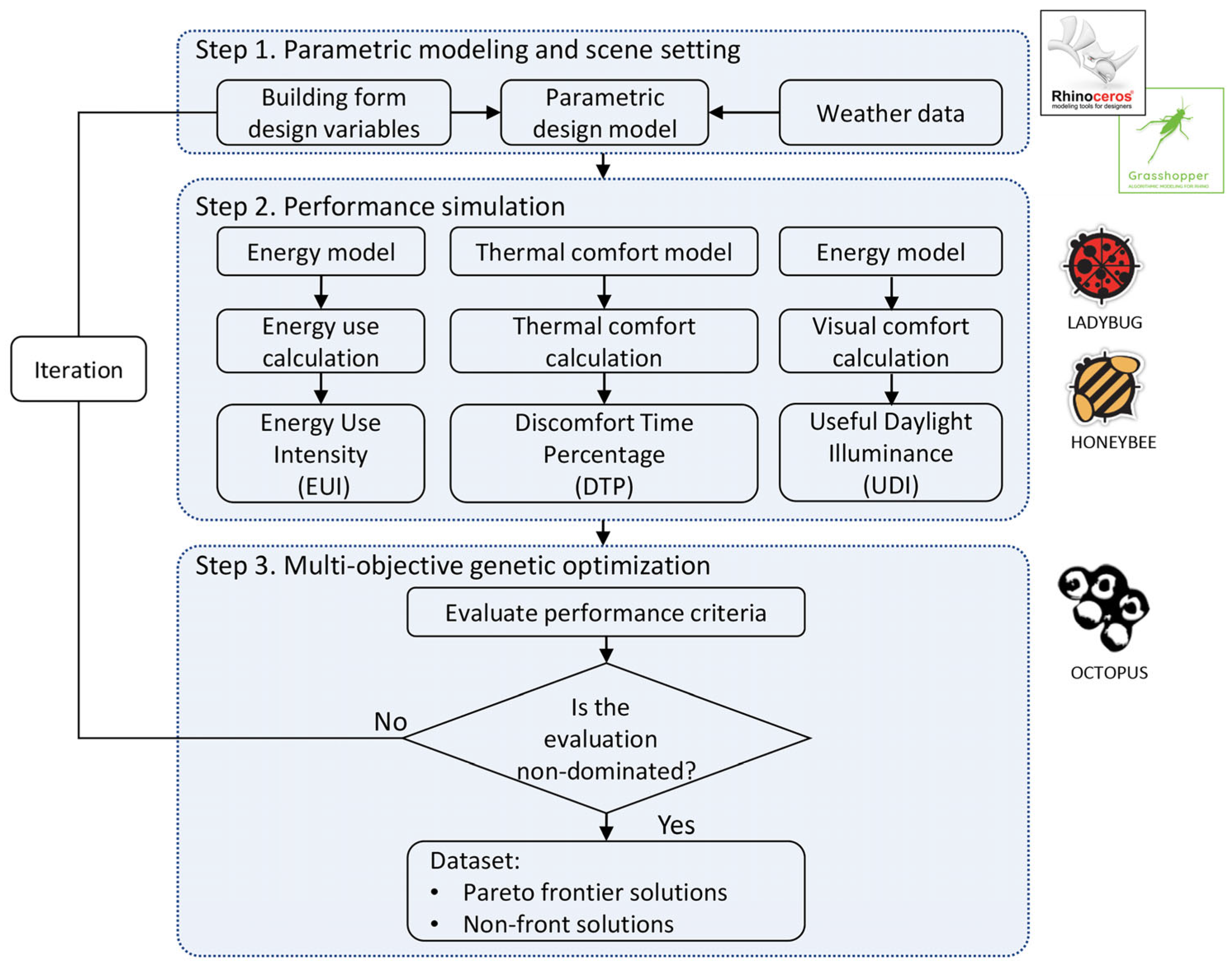
3.1. Model Validation

In this study, on-site measurements were conducted on a university teaching building to check the validity of the simulation model. Since the simulated building was built upon a representative a typical teaching building with a four-sided atrium configuration, an actual university building with a similar architectural form was selected to ensure the reliability of the model (Figure 6). Temperature and illuminance are key parameters that characterize the light and thermal environmental responses of a building, reflecting the accuracy of the physical model in simulating indoor thermal dynamics and daylighting performance. Therefore, the field measurements in this study focused on illuminance and time-dependent temperature variations throughout a single day. The first-floor atrium was selected as the measurement area for daylighting. Illuminance was measured at a height of 0.8 m above the floor within the designated zones. Each atrium was divided into measurement areas (Zones 1–2), with 12–15 test points in each zone used to calculate average temperature values.

Illuminance was measured using a MASTECH MS6300 Environment Multimeter (dynamic range: 0–50,000 lx; accuracy: ±(5.0% + 10) lx; resolution: 1 lx). Temperature was measured using a HOBO MX2301A Temperature and Humidity Data Logger (temperature range: −40 °C to +70 °C; temperature resolution: 0.02 °C; humidity range: 0 %RH to 100 %RH; humidity resolution: 0.01 %RH; response time: approximately 17 min for temperature and 30 s for humidity).

Illuminance measurements were conducted on 30 August 2025, at five time points: 8:00, 10:00, 12:00, 14:00, and 16:00, with each measurement completed within ten minutes. Temperature measurements were carried out on the same day from 7:00 to 19:00 at one-hour intervals in two designated zones. Over the course of the measurements, both the artificial lighting and air-conditioning systems in the teaching building were turned off. The weather on the measurement day was clear and cloudless. The meteorological data used for the building simulation experiment were obtained from the National Meteorological Science Data Center [59], and a corresponding sky model was established based on the observed climatic and sky conditions.

In addition to on-site measurements of air temperature and illuminance, this study also investigated and calculated the annual dynamic energy use of the building. Complete monthly electricity consumption data for the year 2024 were obtained from the campus energy management office for the case-study building. The building relies on natural ventilation and is not equipped with a mechanical cooling system; in summer, indoor air movement is assisted by electric fans, while in winter space heating is pro-vided by a central district heating system. Therefore, the recorded electricity consumption primarily covers lighting, plug loads, and auxiliary equipment, and does not include electricity for air-conditioning systems. To enable a meaningful comparison between the measured data and the simulation results, the monthly electricity consumption (kWh) was normalized by the total gross floor area of the teaching building (10,829.16 m²) to derive the monthly electricity use intensity (kWh/m²·month). In the simulation experiments, the same operating schedules as those of the real building were adopted, and the simulated monthly electricity consumption was post-processed using the same method. Figure 7b presents a comparison between the simulated and measured monthly electricity use intensities.

For the studied teaching building, the occupancy and operation schedule is as follows: the building is closed throughout the winter vacation (15 January to 15 February) and the summer vacation (15 July to 30 August), with no electricity use assumed during these periods. Outside the vacation periods, the building is assumed to be in use daily from 07:00 to 23:00.

According to ASHRAE Guideline 14–2014, the Mean Bias Error (MBE) and the Coefficient of Variation of the Root Mean Square Error (CV-RMSE) are explicitly recommended for evaluating the agreement between simulation results and measured data. MBE (Equation (2)) represents the systematic deviation between simulated and measured values, used to determine whether the model consistently overestimates or underestimates the results. CV-RMSE (Equation (3)) measures the overall dispersion between simulated and measured values, assessing whether the model’s fluctuations align with actual observations. A common validation criterion for temperature or illuminance simulations is MBE ≤ ±10% and CV-RMSE ≤ 30% [60,61].

$$\mathrm{M}\mathrm{B}\mathrm{E}={\displaystyle \frac{{\sum }_{i=1}^n \left(X_i-Y_i\right)}{{\sum }_{i=1}^n X_i}}$$

(2)

$$CV\left(RMSE\right)={\displaystyle \frac{1}{M}}\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n {\left(X_i-Y_i\right)}^2}{n}}}$$

(3)

where $X_i$ denotes the measured value for model $i$, $Y_i$ denotes the simulated value for model $i$, $n$ is the total number of data pairs, and $M$ is the mean of the measured value.

As shown in Figure 7a, the simulated and measured illuminance data exhibit similar distribution patterns, indicating that the model is capable of generating realistic results. Illuminance was measured and simulated at 5 time points throughout the day: 8:00, 10:00, 12:00, 14:00, and 16:00. Under idealized model conditions, the simulated illuminance values were consistently higher than the measured ones, leading to a more conservative optimum in the later optimization process. Based on the measured and simulated illuminance values at each point, the MBE was calculated to be 0.10742%, and the CV(RMSE) was 0.15594%.

Figure 7b presents the monthly electricity use intensity of the teaching building over the entire year. The calibration results indicate that the mean bias error (MBE) is 1.8% and the coefficient of variation of the root mean square error (CV-RMSE) is 6.5%, both falling within commonly accepted threshold values.

Figure 7c presents a comparison between the measured and simulated temperatures in the two test zones at one-hour intervals on the measurement day. The MBE and CV(RMSE) were calculated as 0.735% and 5.815%, respectively. Therefore, the deviation between the simulated and measured temperature data in this validation falls within the acceptable range.

Although the validation of the baseline near-zero energy model in this study is not yet fully complete, its energy consumption results are still according to the verified daylighting and thermal environment models. Given that the primary objective of this research is to optimize the atrium form design of teaching buildings, the energy use results are analyzed mainly as relative indicators to compare the performance differences among various design schemes, rather than to assess absolute energy levels. Therefore, when analyzing the optimal and trade-off solutions, the focus is placed on the trends and relative improvements in energy performance. In summary, the adopted model has been validated in terms of thermal and daylighting performance simulations, providing a reliable basis for relative evaluation in energy consumption analysis and multi-objective optimization.

3.2. Objective Analysis Based on Different Design Parameters

Based on more than 2000 simulation runs of the single- and double-atrium base models, the resulting scatter plots were used to identify the correlations between each design variable and the selected optimization objectives. Each scatter point generated by Octopus represents a building design scheme composed of a specific combination of design variables. The relationships among the design variables, building orientation (V1), atrium width-to-depth ratio (V2), atrium height-to-width ratio (V3), atrium bottom area ratio (V4), and skylight–roof ratio (V5), and the optimization objectives, including EUI, UDI, and DTP, are illustrated in Figure 8. Scatter plots exhibiting clear trends indicate the interactions between design variables and optimization objectives, as well as the distribution of the optimal design variable configurations.

3.2.1. Simulation Results of Building Orientation

For the single-atrium building, all three performance indicators vary significantly with orientation in Figure 8a. As the building orientation shifts from southwest (+45°) to southeast (−45°), the EUI decreases from approximately 192 kWh/m² to 178 kWh/m². When the orientation approaches −30° to −45°, the DTP drops from 37% to 34%, while the UDI reaches its highest and most stable level within this range (approximately 85–88%). These results indicate that a southeast orientation achieves the best balance among energy use, daylighting, and thermal comfort, demonstrating strong multi-objective synergy and representing the optimal orientation range for single-atrium teaching buildings. In contrast, the double-atrium building shows a much lower sensitivity to orientation changes, as shown in Figure 8b. The EUI remains relatively stable within the range of 186–190 kWh/m², suggesting that the double-atrium configuration substantially mitigates the impact of orientation on energy use. The DTP values are generally higher (36–39%) and show no clear relationship with orientation, while the UDI remains consistently stable. This indicates that although the double-atrium structure exhibits more stable overall performance, its optimization potential is limited, and its overall thermal comfort is inferior to that of the single-atrium configuration, which demonstrates a more pronounced response to orientation optimization.

3.2.2. Simulation Results of Building Width-to-Depth Ratio

Different atrium design configurations influence the overall energy performance of a building. Among them, the atrium width-to-depth ratio (FDR) determines the slenderness or compactness of the atrium’s plan form, shaping the cross-sectional spatial configuration and reflecting the openness and light–thermal exchange characteristics of the atrium. For the single-atrium building, the FDR exhibits a clear relationship with both energy consumption and thermal performance, as shown in Figure 8a. As the FDR increases from 0.2 to 0.8, the EUI first decreases slightly and then rises again after 0.6, indicating that a moderate increase in atrium width improves daylighting and reduces lighting load, whereas an overly wide atrium increases solar radiation gains, leading to higher cooling loads. The DTP also shows nonlinear variation: when FDR < 0.3, poor ventilation and uneven temperature distribution occur; when FDR > 0.8, overheating becomes likely. The optimal range appears between 0.4 and 0.6, corresponding to the lowest DTP values (around 33–34%), suggesting the most balanced thermal environment. When the atrium is narrow (FDR < 0.3), the UDI remains relatively low; as the FDR increases to 0.6–0.8, the UDI rises significantly, exceeding 85%, indicating that a moderately open atrium can substantially enhance daylighting performance. Therefore, for single-atrium buildings, an FDR between 0.4 and 0.6 achieves an optimal balance of minimum energy consumption, optimal thermal comfort, and adequate daylighting performance. For the double-atrium building, the influence of FDR on performance indicators is notably weaker, as shown in Figure 8b. The EUI increases slightly with larger FDR values but remains within a narrow range (186–190 kWh/m²), suggesting a limited effect of atrium geometry on energy consumption. The DTP fluctuates between 36% and 39%, showing no significant correlation with FDR, implying that thermal effects are evenly distributed between the two atriums. The UDI remains stable (82–88%) and is almost unaffected by FDR variation, indicating that the double-atrium configuration achieves high daylight uniformity through bilateral lighting.

3.2.3. Simulation Results of Atrium Height-to-Width Ratio

The atrium height-to-width ratio is another key aspect of atrium design form, as it defines the spatial configuration of the vertical cross-section and influences the extent of solar radiation entering the atrium. For the single-atrium building, the height-to-width ratio exerts a pronounced nonlinear effect on energy consumption, thermal comfort, and daylighting performance, as shown in Figure 8a. As the ratio increases from 2.0 to 3.5, the EUI shows a slight upward trend. A taller and narrower atrium reduces the horizontal daylighting area but increases the exposed façade area, thereby raising the cooling load. Within this same range (2.0–2.5), the DTP reaches its minimum (about 34–35%), but when the ratio exceeds 3.0, it rises significantly, suggesting that overly tall atriums intensify air stratification—causing overheating in the upper zones and cooler temperatures below, leading to reduced comfort. As the height-to-width ratio increases, the UDI continuously declines. When the ratio is below 2.5, the UDI exceeds 85%, whereas when it exceeds 3.5, it drops below 80%, indicating that tall, narrow atriums hinder daylight penetration and require more artificial lighting. Overall, a height-to-width ratio of 2.0–2.5 provides the optimal balance between daylighting, thermal performance, and energy efficiency for single-atrium buildings; beyond this range, vertical stratification and shading effects lead to a decline in both daylighting and comfort performance. For the double-atrium building, the influence of the height-to-width ratio on overall performance is notably weaker, as shown in Figure 8b. The EUI varies only slightly, suggesting that dual-side daylighting and ventilation pathways help offset the impact of vertical height. The DTP fluctuates between 37% and 39% without a clear trend, indicating that air circulation within the double atrium helps mitigate vertical temperature stratification. The UDI shows no significant correlation with the height-to-width ratio, suggesting that multi-directional daylighting within the double atrium already provides sufficient illumination with minimal dependence on height.

3.2.4. Simulation Results of Atrium Bottom Area Ratio

The atrium bottom area ratio represents the relationship between the atrium space and the overall building layout. It influences how much solar radiation enters the atrium and spreads into the adjacent spaces., thereby affecting both the building’s energy use and the thermal comfort of the atrium. For single-atrium building, a clear trade-off relationship is observed among energy consumption, thermal comfort, and daylighting performance, as shown in Figure 8a. When the bottom area ratio is below 3%, the EUI remains relatively stable; however, once it exceeds 3.5%, a slight increase is observed. This indicates that moderately enlarging the atrium floor area improves daylighting performance, whereas an excessively large opening increases solar heat gain and cooling load. The DTP remains low (approximately 34–35%) when the bottom area ratio is within 1.5–2.5%, but rises gradually beyond 3.0%, which can be attributed to intensified air stratification and heat accumulation effects resulting from the increased atrium volume. As the bottom area ratio increases, the UDI continues to improve from approximately 75% to 90%, indicating that a larger atrium opening significantly enhances light distribution and visual comfort. Overall, for single-atrium buildings, an atrium bottom area ratio of 2–3% achieves an optimal trade-off between daylighting availability and thermal performance; beyond this range, the benefits of improved daylighting become marginal, while energy consumption and discomfort risks increase markedly. For the double-atrium building, the influence of the bottom area ratio on performance indicators is substantially weaker, and the overall performance remains more stable, as shown in Figure 8b. The EUI shows no significant correlation with the bottom area ratio, suggesting that the spatial distribution effect of the double-atrium layout mitigates the adverse impact of increased opening area on energy consumption. Due to the combined solar heat gains from both atriums, the DTP increases slightly with a higher bottom area ratio. The UDI exhibits a positive correlation with a clear upward trend. Owing to its bilateral daylighting paths, the double-atrium configuration ensures sufficient indoor light uniformity even when the bottom area ratio is relatively small.

3.2.5. Simulation Results of Skylight–Roof Area Ratio

The skylight area governs how much solar radiation enters the atrium through the roof openings. In summer, high solar radiation increases the indoor temperature of the atrium, while in winter, the high heat transfer coefficient of skylights may lead to heat loss, thereby affecting both atrium comfort and overall building energy consumption. Therefore, it is necessary to examine the impact of different skylight ratios on building energy use and thermal comfort. For the single-atrium building, the skylight ratio strongly affects both energy use and thermal comfort in Figure 8a. As the skylight ratio increases from approximately 30% to 60%, the EUI remains stable initially but rises slightly beyond 45%, indicating that a moderate skylight area facilitates the use of natural daylight, whereas excessive skylight openings lead to higher solar heat gains and increased cooling loads. The DTP exhibits a similar pattern: when the skylight ratio is below 40%, the proportion of discomfort time remains low (around 33–34%), but it increases noticeably beyond 45%, suggesting that a high skylight ratio raises the frequency of overheating events. Meanwhile, the UDI increases significantly with the skylight ratio, reaching 85–88% when the ratio exceeds 45%, indicating that larger skylight areas greatly enhance daylighting performance but also intensify energy consumption and thermal comfort risks. For the double-atrium building, the influence of skylight ratio on overall performance becomes much less pronounced, as shown in Figure 8b. The EUI remains largely stable within 186–190 kWh/m², implying that the distributed internal volume of the double atrium mitigates solar heat gains. The DTP shows no clear correlation with skylight ratio, suggesting that internal airflow and thermal buffering effects weaken the impact of skylight size on comfort. The UDI remains within 82–88%, indicating that the double-atrium configuration can maintain good daylighting performance even with relatively small skylight areas.

3.3. Analysis of Pareto Front Solutions Among Optimization Objectives

The main optimization objectives of this study are to minimize EUI and DTP while maximizing UDI. Figure 9 illustrates the Pareto front relationships among all simulation results for EUI–DTP, EUI–UDI, and UDI–DTP in the multi-objective optimization (MOO), where the red points represent Pareto-optimal solutions.

Figure 9a shows the relationships among the three optimization objectives in the single-atrium educational building. The entire set of EUI–DTP solutions indicates a negative correlation between EUI and DTP. The scatter points exhibit a shallow U-shaped distribution, showing that when EUI is approximately 186–188 kWh/m²·y, DTP reaches its lowest value. The Pareto front solutions demonstrate that as EUI increases, DTP decreases slightly, suggesting that a small increase in energy consumption can bring limited improvement in thermal comfort. Specifically, when EUI increases by about 10 kWh/m²·y, DTP decreases by only 0.5–1.0%. This weak trade-off relationship indicates that the passive effect of building geometry on reducing indoor thermal discomfort is limited. Therefore, the interaction between energy use and thermal comfort is relatively indirect and exhibits nonlinear characteristics. A weak positive correlation exists between EUI and UDI. Although the overall sample does not show a clear linear relationship, the Pareto front indicates that when UDI increases, EUI also rises slightly, suggesting that the improvement of daylighting performance is often accompanied by higher energy consumption. This trend is mainly affected by the combined influence of skylight ratio and atrium geometry. A positive correlation is found between UDI and DTP, indicating that the enhancement of daylighting performance tends to reduce thermal comfort. Schemes with higher UDI values generally have larger skylight ratios, which improve the uniformity of indoor lighting but also intensify solar radiation entering the space. This leads to increased air temperature and more pronounced vertical stratification, extending the duration of thermal discomfort. When UDI exceeds 86%, DTP rises significantly to over 35%, suggesting that excessive daylighting can severely worsen the indoor thermal environment. These findings verify the inherent contradiction between visual comfort and thermal comfort in single-atrium buildings.

Figure 9b shows the relationships among the three optimization objectives in the double-atrium educational building. The relationship between EUI and DTP overall exhibits a negative correlation, but the scatter distribution is more dispersed. Most Pareto front solutions are concentrated in the range of EUI = 187–188 kWh/m²·y and DTP ≈ 37%. Regarding the relationship between UDI and EUI, the double-atrium configuration shows a slight positive correlation. When energy consumption is relatively low, UDI is approximately 85–86%; as EUI increases to 189–190 kWh/m²·y, UDI rises to 87–88%. This indicates that the enhancement of daylighting performance is often accompanied by increased energy consumption. In particular, in double-atrium configurations, large skylight areas and transparent enclosures improve daylighting but simultaneously increase cooling and heat transfer loads. A clear positive correlation is also observed between UDI and DTP. When DTP increases from about 37.0% to 39.0%, UDI simultaneously rises from about 82% to 87–88%, indicating that improving daylighting performance also increases the proportion of thermal discomfort.

3.4. Analysis of Optimal Solutions

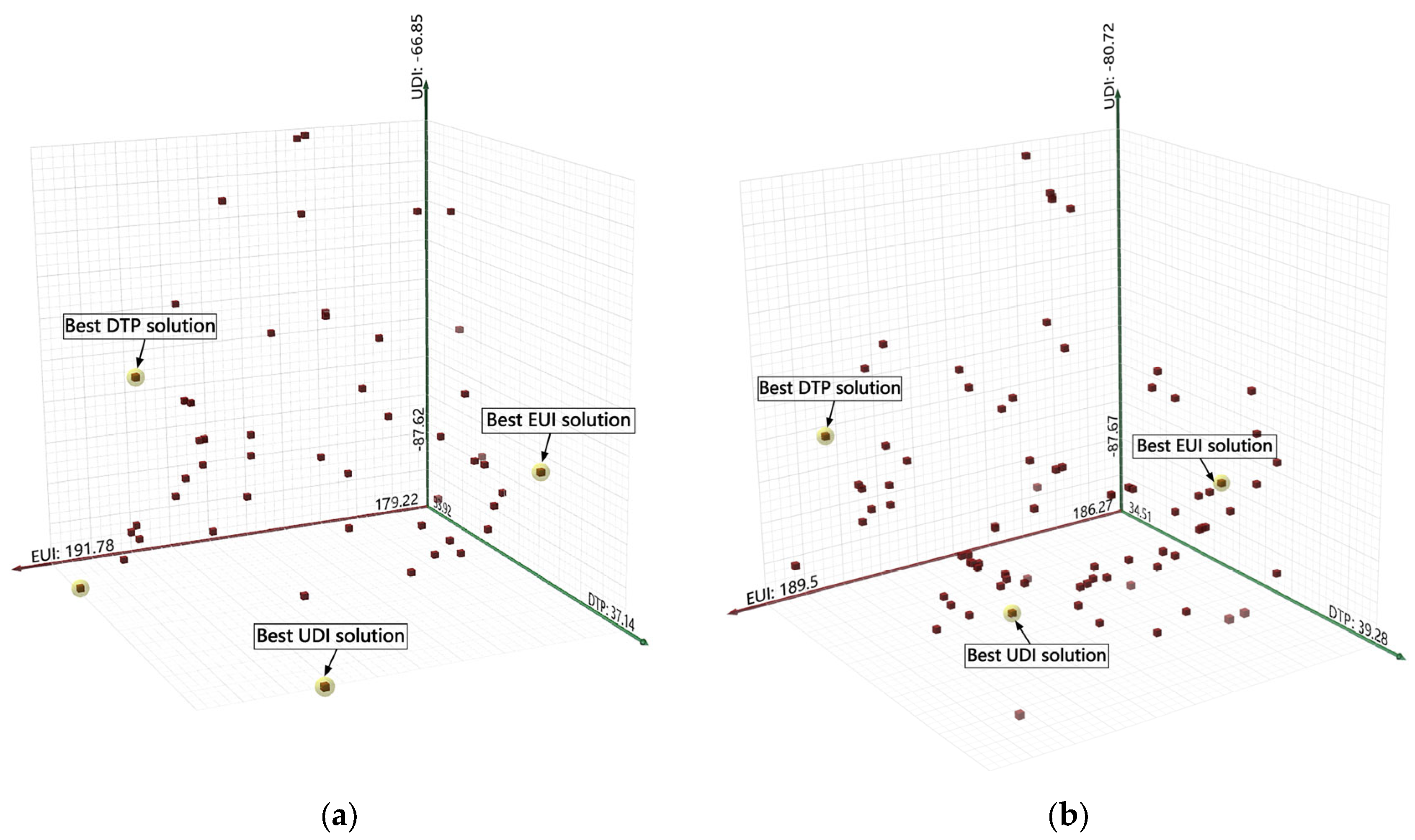
Figure 10 presents the Pareto front and the UDI, EUI, and DTP scatter plots obtained from the final generation. Based on Equation (1), the optimal and trade-off values of UDI, EUI, and DTP were calculated. Architects can select the most appropriate solution according to specific design objectives and project requirements.

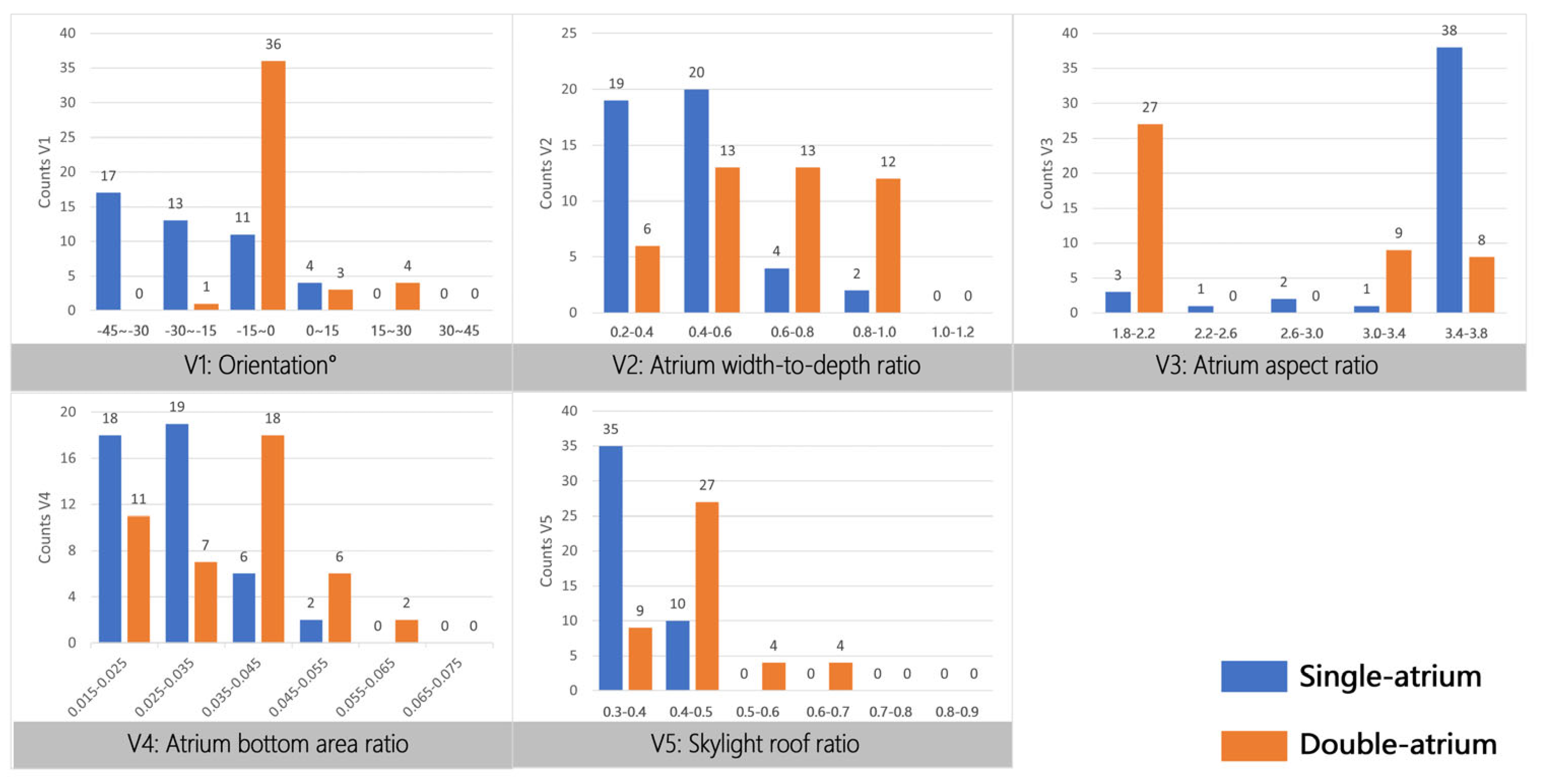
Figure 11 presents the distribution of atrium design variable values within the Pareto-optimal solutions. As shown in the figure, the optimal orientation solutions for the single-atrium building are relatively dispersed, primarily concentrated within the range of −45° to −15° (southeast-oriented). This indicates that single-atrium configurations are more sensitive to orientation, as a southeast-facing layout provides more stable daylighting and thermal balance during the morning while avoiding overheating caused by afternoon west solar exposure. In contrast, the double-atrium building shows optimal solutions that are highly concentrated within the −15° to 0° range (near-south orientation), suggesting that when two atriums are located symmetrically on both sides of the building’s central axis, maintaining an overall south-facing orientation ensures balanced daylight distribution and a more stable internal thermal environment. Therefore, single-atrium configurations rely more on a southeast orientation to regulate light and heat performance, whereas double-atrium configurations perform best near the south-facing direction.

Regarding the atrium width-to-depth ratio, the optimal solutions for single-atrium buildings are primarily distributed within the 0.2–0.6 range, indicating that relatively “elongated” atrium spaces achieve a better balance between daylighting and thermal comfort. In contrast, the optimal solutions for double-atrium buildings are concentrated within the 0.6–1.0 range, suggesting that “nearly square” atriums contribute to balanced light and thermal distribution between the two atriums. The single-atrium configuration tends to adopt a more elongated layout to mitigate heat accumulation, while the double-atrium configuration favors a more square plan to achieve uniform light distribution.

For the atrium height-to-width ratio, the optimal solutions for single-atrium buildings are concentrated within the 3.4–3.8 range, representing a tall and narrow vertical space. This configuration enhances the stack effect, promotes the upward movement and discharge of warm air, and utilizes reflected light from the upper portion to improve illuminance at the lower level. In contrast, the optimal solutions for double-atrium buildings are concentrated within the 1.8–2.2 range, corresponding to a lower and wider space, which helps avoid excessive vertical temperature stratification and maintains balanced ventilation between the two atriums.

Regarding the atrium bottom area ratio, the optimal solutions for single-atrium buildings are concentrated within the 2–3% range, while in double-atrium buildings, the optimal bottom area ratio for each individual atrium is concentrated within 1.8–2.2%. The optimal area ratios for individual atriums in both cases are therefore comparable. This suggests that double-atrium configurations do not rely on a larger single atrium but instead achieve spatial distribution of daylighting and redundant ventilation through two medium-sized atriums. This approach maintains high UDI values while reducing the sensitivity of EUI and DTP to variations in bottom area ratio, resulting in more stable performance.

With regard to the skylight–roof ratio, the optimal solutions for single-atrium buildings are concentrated within the 0.3–0.4 range, while those for double-atrium buildings are concentrated within the 0.4–0.5 range. This indicates that double-atrium configurations require a higher skylight opening ratio to maintain sufficient daylight penetration depth and airflow, whereas for single-atrium configurations, an excessively high skylight ratio can easily lead to overheating in the upper zone and increased energy consumption, thus resulting in a relatively lower optimal value.

By comparing the three Pareto-optimal designs and the balanced trade-off design with the reference scheme, the performance improvements achieved through optimization can be clearly identified, as shown in

Table 10. Optimized design variables and corresponding performance outcomes for UDI, EUI, DTP, and trade-off solutions of the single-atrium building.

		Single-Atrium Building
		Reference Solution	Best EUI	Best DTP	Best UDI	Trade-Off
Design variables	V1: Orientation (°)	0	−1.404	−44.676	0.640	−3.396
	V2: Width-to-Depth Ratio	0.48	0.26	0.472	0.842	0.3052
	V3: Aspect Ratio	2.85	3.617	3.529	2.042	3.7041
	V4: Bottom Area Ratio	5.25%	3.71%	2.15%	3.61%	3.02%
	V5: Skylight–Roof Ratio	45.5%	30.8%	30.46%	47.19%	30.46%
Performance metrics	EUI (kWh/m2/y)	188.532	179.28	187.845	185.12	179.46
	DTP (%)	35.721	35.257	33.921	36.318	35.04
	UDI (%)	82.735	84.410	75.100	87.191	83.225
y value		-	34.097	−35.855	−46.481	35.208

and

Table 11. Optimized design variables and corresponding performance outcomes for UDI, EUI, DTP, and trade-off solutions of the double-atrium building.

		Double-Atrium Building
		Reference Solution	Best EUI	Best DTP	Best UDI	Trade-Off
Design variables	V1: Orientation (°)	0	−4.228	−6.144	−4.547	−4.400
	V2: Width-to-Depth Ratio	0.55	0.350	0.484	0.751	0.353
	V3: Aspect Ratio	3.15	3.230	3.586	1.928	3.215
	V4: Bottom Area Ratio	6.15%	3.47%	2.03%	4.54%	3.47%
	V5: Skylight–Roof Ratio	42.3%	43.45%	33.41%	48.12%	43.28%
Performance metrics	EUI (kWh/m2/y)	190.325	187.035	188.365	188.775	187.035
	DTP (%)	37.236	37.722	36.684	38.609	36.722
	UDI (%)	83.352	85.312	76.280	87.679	85.324
y value		-	39.305	−19.731	−1.949	39.37

. The reference solution is constructed from the survey data of 25 atrium teaching buildings in Xi’an, by assigning the key geometric variables to the median values of the sample and selecting a configuration that closely represents a typical code-compliant case.

For the single-atrium configuration, the optimization results reveal distinct performance improvements compared with the reference scheme. The best EUI solution achieves a substantial 4.9% reduction in energy use intensity, accompanied by a slight 1.3% improvement in thermal comfort and increasing UDI by about 2.0%. This reduction results primarily from a narrower and taller atrium geometry combined with a moderate skylight ratio and a near-south-east orientation. Such a configuration enhances buoyancy-driven ventilation and reduces envelope heat gain while maintaining sufficient daylight via vertical reflections. The best DTP solution further minimizes thermal discomfort by reducing the bottom area ratio and skylight opening, combined with an eastward orientation that limits solar exposure. However, these changes lead to a UDI decrease about 9.2%, implying that thermal comfort is achieved at the cost of daylight quality and lighting energy demand. In contrast, the best UDI case improves daylight performance by 5.2% through a wider and shallower atrium and a large skylight opening, but causes an increase in DTP due to indoor overheating. The trade-off solution (y = 35.21) closely aligns with the best EUI configuration, balancing EUI = 179.46 kWh/m²·y, DTP = 35.04%, and UDI = 83.23%. Overall, the single-atrium model achieves the best comprehensive efficiency under a tall and slender form with a moderate skylight ratio, effectively reducing energy use while keeping comfort and daylight performance at acceptable levels.

For the double-atrium configuration, the overall optimization performance is more balanced but less sensitive to geometry changes. Compared with its reference case, the best EUI solution yields a 1.7% reduction in energy consumption, a 2.4% increase in daylight performance, but a 1.3% deterioration in thermal comfort. This outcome corresponds to relatively tall atrium, and a large skylight ratio. The larger skylight enhances daylight and reduces lighting demand, but also increases solar heat gain, causing a rise in discomfort hours. The best DTP solution attempts to mitigate thermal stress by reducing the skylight and bottom area ratio, yet the DTP decreased by 2.75% compared to the reference value. Conversely, the best UDI case achieves the highest daylight performance through a wide and low atrium and a large skylight opening, but at the cost of increased overheating. The trade-off solution (y = 39.37) coincides with the best EUI configuration, featuring EUI = 187.04 kWh/m²·y, DTP = 37.72%, and UDI = 85.32%, suggesting that in double-atrium designs, further energy reduction or daylight improvement inevitably sacrifices thermal comfort.

Overall, the optimization results highlight a clear distinction between the two typologies. The single-atrium configuration exhibits a stronger optimization potential, achieving significant energy savings with minimal daylight or comfort losses under a slender vertical form and moderate skylight opening. In contrast, the double-atrium configuration provides more balanced daylight distribution and visual comfort, but its dual-lightwell structure increases the internal heat load, limiting further improvement in thermal comfort. Hence, while the double-atrium design favors daylight utilization, the optimized single-atrium layouts in this study tend to achieve lower simulated energy use with acceptable thermal comfort under the specific modeling assumptions for cold-region educational buildings.

4. Discussion

4.1. The Relationship Between Design Variables and Optimization Objectives

The interactions among different architectural form design variables collectively influence the environmental performance of buildings. As discussed previously, altering a single variable while keeping other parameters constant often fails to achieve the desired outcome. The multi-objective optimization (MOO) method can effectively identify and quantify the coupling effects among these variables, as different combinations of design parameters lead to significant variations in building performance levels. The improvement of one performance indicator is often accompanied by the decline of another, reflecting the inherent trade-offs among energy consumption, daylighting, and thermal comfort.

As shown in Figure 9, a strong linear correlation exists between UDI and DTP, indicating that improvements in daylighting are often achieved at the expense of thermal comfort. This trend remains consistent across all Pareto-optimal solutions and in the final iteration of the optimal solutions, for both the single-atrium and double-atrium configurations. Meanwhile, the enhancement of thermal comfort is often accompanied by an increase in energy consumption, a phenomenon more pronounced in single-atrium buildings. The conflicting relationships among building energy use, thermal comfort, and daylighting performance further emphasize the critical role of architectural form design in regulating the indoor environmental performance of buildings.

4.2. The Recommended Range of Values for Design Variables

By integrating the findings from the single-factor analysis and the multi-objective optimization, the recommended value ranges for each design variable are as follows: (1) the building orientation should primarily face southeast (−30° to −45°), which can effectively balance daylighting performance, thermal comfort, and energy efficiency; (2) the atrium width-to-depth ratio should be within the range of 0.4 to 0.6, ensuring adequate daylighting while avoiding excessive solar heat gain; (3) a moderate height-to-width ratio of 2.0 to 2.5 provides a better balance between vertical daylighting and temperature stratification effects; (4) the atrium bottom area ratio should range from 2% to 3%, which allows for proper ventilation and moderate solar exposure; (5) the skylight–roof ratio should be maintained between 40% and 50%, improving natural daylighting while avoiding overheating and excessive cooling loads. Overall, the single-atrium configuration exhibits higher optimization potential but also greater variability, making it more suitable for performance-oriented design requiring detailed fine-tuning. In contrast, the double-atrium configuration shows stronger geometric coupling and more stable performance, making it more appropriate for building types that emphasize environmental balance and operational reliability.

4.3. Sensitivity of Optimized Atrium Designs to Skylight Glazing Properties

To examine the robustness of the above design recommendations and to clarify the role of glazing properties in the UDI–DTP trade-off, a supplementary sensitivity analysis was conducted for typical skylight glass types. Based on the optical and thermal performance data of typical glazing in Code for thermal design of civil building GB 50176-2016 [36], three representative skylight configurations were defined: clear double insulating glazing (G1: U = 2.6 W/m²·K, SHGC = 0.75, VT = 0.81), double-silver Low-E insulating glazing (G2: U = 1.72 W/m²·K, SHGC = 0.46, VT = 0.62), and triple-silver Low-E insulating glazing (G3: U = 1.27 W/m²·K, SHGC = 0.42, VT = 0.56). Among them, G2 is the fixed glazing parameter configuration adopted in this study. For both the single-atrium and double-atrium buildings, three representative geometries were selected from the Pareto-optimal solutions (Best UDI, Best EUI and Best DTP), and annual simulations were performed for all combinations of geometry and glazing type (

Table 12. Performance of different skylight glazing types for representative optimal solutions in single- and double-atrium buildings.

		Single-Atrium Building			Double-Atrium Building
	Skylight Glass Type	UDI (%)	EUI (kWh/m2·y)	DTP (%)	UDI (%)	EUI (kWh/m2·y)	DTP (%)
Best EUI solution	G1	84.344	192.143	45.495	85.306	200.790	41.947
	G2	84.41	179.28	35.257	85.312	187.035	37.722
	G3	84.334	178.400	34.487	85.299	186.009	37.485
Best DTP solution	G1	75.125	201.708	44.025	76.160	201.914	41.150
	G2	75.1	187.845	33.977	76.28	188.365	36.684
	G3	75.092	186.860	33.921	76.435	187.415	36.448
Best UDI solution	G1	87.141	198.198	44.107	87.706	202.614	42.277
	G2	87.191	185.12	36.318	87.679	188.775	38.609
	G3	87.176	184.151	35.621	87.654	187.663	38.410

).

The results indicate that improving the skylight glazing from G1 to G2–G3 leads to a pronounced reduction in energy use and thermal discomfort, whereas daylight performance is only marginally affected. For the single-atrium building, replacing clear double glazing with triple-silver Low-E glazing reduces EUI by approximately 13–15 kWh/m²·y and lowers DTP by about 8–11 percentage points, while UDI changes by less than 0.2%. Similar reductions in EUI and DTP are observed for the double-atrium building. These findings confirm that skylight thermal–optical properties and solar control measures strongly modulate the absolute levels of energy use and thermal discomfort, and partly mediate the observed conflict between UDI and DTP.

However, the relative influence and ranking of the atrium geometry remain consistent across all glazing scenarios: the daylight-oriented geometry (Best UDI) always achieves the highest UDI but also exhibits higher DTP, the energy-oriented geometry (Best EUI) consistently yields the lowest EUI, and the comfort-oriented geometry (Best DTP) attains the lowest DTP in most cases. This indicates that, although glazing properties significantly influence the magnitude of performance indicators, they do not overturn the main design tendencies and the relative influence of atrium geometric parameters identified in the multi-objective optimization. Consequently, the recommended ranges of orientation, atrium width-to-depth ratio, aspect ratio, bottom area ratio and skylight–roof ratio should be interpreted as valid under typical code-compliant glazing configurations, and can be further refined in practice through detailed envelope and shading design.

4.4. Limitations and Future Work

Although this research developed a multi-objective optimization framework for atrium design in university educational buildings located in cold climate and verified its capability in balancing energy use, daylighting, and thermal comfort, several limitations remain:

First, the optimization framework proposed in this study primarily focuses on the optimization of building form and geometric parameters and serves as a preliminary exploration conducted prior to the formulation of other design strategies. Therefore, this study does not fully account for the potential constraints that may arise in later design stages, such as the thermal performance of the building envelope, shading configurations, façade material reflectivity, glazing properties, HVAC system efficiency, and occupant behavior patterns. These factors can significantly influence energy consumption and indoor environmental performance during the building’s operational phase.

Second, this study selected five key morphological variables as the main optimization parameters, emphasizing their dominant influence on overall building performance. However, this parameter set is still insufficient to comprehensively capture the complexity of atrium morphology. Other geometric or physical parameters—such as roof geometry, opening position, roof inclination, and spatial relationships with surrounding areas—may also affect energy balance and daylighting performance.

Third, the field investigations and simulations in this study were conducted on teaching building atriums located in cold regions, whose thermal and daylighting characteristics differ significantly from those in other climatic zones. Therefore, the conclusions and recommended parameter ranges presented in this paper are not yet applicable to buildings located in other climate regions or to other building types.

This study provides a feasible data-driven multi-objective optimization approach for atrium design. Future research can further evolve this framework into a multidisciplinary design model integrating form, material, and climate adaptability, thereby supporting performance-oriented design decision-making across a wider range of architectural contexts.

5. Conclusions

This study focuses on the atriums of university teaching buildings in cold regions and establishes a multi-objective optimization framework for atrium form design based on three key performance objectives: energy consumption, thermal comfort, and daylighting. This framework is applicable to tetra-directional atrium configurations in cold climate regions. Under the condition of fixed envelope and glazing performance parameters, key design variables are identified and optimized to obtain an optimal set of atrium design parameters for teaching buildings. The results support early-stage decision-making for atrium geometric design and provide a scientific reference for green and high-performance design of educational buildings in cold regions.

• The single-atrium model achieved the best overall performance under a tall and slender configuration (H/W ≈ 3.7, W/D ≈ 0.3) with a moderate skylight ratio, effectively reducing energy consumption while maintaining thermal comfort and daylighting performance at acceptable levels. The double-atrium layout provided a more uniform distribution of daylight and improved visual comfort but exhibited lower sensitivity to geometric variations. Overall, the results indicate that single-atrium buildings have greater optimization potential and morphological sensitivity, whereas double-atrium buildings demonstrate higher stability and robustness. These comparative results should be interpreted on the basis of the current modeling assumptions; introducing high-performance glazing, external shading, or advanced control strategies may alter the relative performance of single- and double-atrium layouts and therefore requires further investigation.
• In cold regions, daylighting performance shows a negative correlation with energy and thermal performance, with UDI and DTP exhibiting the most pronounced contradiction; moreover, UDI and EUI are also conflicting within a certain range. Compared with the baseline configuration, the optimal single-atrium scheme achieved improvements of 4.9% in EUI, 1.3% in DTP, and 2.0% in UDI; for the double-atrium scheme, the corresponding improvements were 1.7%, 1.3%, and 2.4%, respectively. These results indicate that, under the investigated conditions, atrium form optimization can simultaneously enhance all three performance dimensions; however, the magnitude of improvement and the balance among the objectives largely depend on the selected atrium configuration.
• The recommended parameter ranges obtained through multi-objective optimization: building orientation toward the southeast (−30° to −45°), width-to-depth ratio between 0.4 and 0.6, height-to-width ratio between 2.0 and 2.5, atrium bottom area ratio between 2% and 3%, and skylight ratio between 40% and 50%. These can provide quantitative guidance for achieving a balanced integration of energy efficiency, daylighting, and thermal comfort in university buildings located in cold regions. Within these ranges, architects can further select specific parameter values according to their design priorities. For energy-saving schemes, an orientation close to −45°, a relatively narrow atrium with a width-to-depth ratio of about 0.4, a smaller skylight ratio of approximately 40%, and a bottom area ratio near the lower bound are recommended. For daylight-oriented schemes, an orientation close to −30°, a larger width-to-depth ratio near 0.6, and a higher skylight ratio close to 50% can be adopted to enhance daylight availability. For thermal comfort-oriented schemes, an orientation between −35° and −45°, a moderate width-to-depth ratio of 0.4–0.5, a height-to-width ratio close to the lower limit of the investigated range, and a relatively small skylight ratio of about 40% are suggested. These recommendations are intended as quantitative guidance within the specified modelling ranges, rather than universally applicable design codes.

In the early design stage of teaching buildings with atriums, architects’ decisions on building form are crucial to overall performance. For different atrium configurations and optimization objectives, the proposed framework in this study can be effectively applied to the early-stage morphological design of university teaching buildings in cold regions, enabling rapid prediction and optimization of design alternatives. This approach addresses the limitations of traditional design methods that rely solely on experience and simulation by providing a more systematic, diversified, and scientifically grounded decision-making process. Future research may establish a more comprehensive index system encompassing morphological and physical characteristics, further integrating envelope design, material properties, and operational strategies into the form optimization framework. This will enable holistic performance evaluation from geometric to physical dimensions and facilitate the application and validation of the proposed optimization method and framework across different climatic zones and building types, ensuring regional adaptability and model refinement.