Discrete Element Simulation Study of Soil–Rock Mixture Under High-Frequency Vibration Loading

Abstract

Research on the dynamic characteristics of roadbeds has primarily focused on traffic loads and foundation treatment responses during the operation and maintenance phase. However, there remains a lack of in-depth exploration into vibration compaction during the construction phase, particularly the differences in stress paths under roller dynamic loading. Laboratory dynamic triaxial tests are limited by low-frequency loading, making it difficult to simulate real-world roadbed compaction conditions. Therefore, this study employs discrete element numerical simulation technology to construct a numerical model for subgrade compaction under roller dynamic loading. It aims to reveal the macro- and micro-scale evolution patterns of soil under compaction conditions, thoroughly analyze the influence of factors such as roller frequency and vibratory force on subgrades with varying rock content in soil–stone mixed fill, and provide a theoretical foundation for intelligent compaction (IC) of soil–stone mixed subgrades in subsequent research.

1. Introduction

In response to the national strategy promoting intelligent construction and the digital transformation of infrastructure, highway engineering construction is entering a critical phase of intelligent transformation [1,2]. Against this backdrop, the concepts of smart construction and new infrastructure development are being powerfully propelled toward deep integration throughout the entire lifecycle of highway engineering projects. In highway engineering, soil–rock mixtures are frequently used as subgrade fill materials due to their widespread availability and favorable engineering mechanical properties [3,4]. However, their inherent characteristics of “non-uniformity, high porosity, and difficult compaction,” primarily governed by complex particle gradation and fluctuating rock content, pose significant challenges for compaction quality control [5]. Insufficient compaction directly compromises the long-term stability and bearing capacity of subgrades [6,7]. While current specifications recommend using porosity or settlement differential as on-site compaction quality control indicators, traditional water/sand filling methods suffer from inherent flaws such as low testing accuracy, poor efficiency, destructive nature, and insufficient representativeness [8]. Meanwhile, the settlement differential indicator faces inconsistencies due to test section dependency, making its uniform application challenging in practice [9]. This testing lag has become a significant bottleneck in enhancing subgrade compaction quality. This lag in testing methods has become a significant bottleneck in improving subgrade compaction quality [10].

Notably, the convergence of sensing technology, digital twins, and artificial intelligence is driving a profound transformation in compaction technology [11]. As a representative of this trend, IC technology centers on real-time sensing and feedback of “machine-soil” interaction status through multi-source sensors integrated into compaction equipment [12]. Based on this data, the system dynamically evaluates soil mechanical properties and adaptively optimizes construction parameters, achieving precision and intelligence in the compaction process [13]. Numerous scholars have actively explored this field. For instance, Zhang et al. developed a real-time classification system for compaction quality based on machine learning [14]; Zhu et al. revealed the energy transfer mechanism in the vibratory roller-subgrade system through numerical simulation [15]; other studies have also examined the application effectiveness of different sensing technologies in IC [16,17]. However, the effectiveness of such intelligent systems fundamentally depends on an accurate understanding of soil response under real-world roller-loading conditions. Modern heavy vibratory rollers can impose significant dynamic loads; laboratory dynamic triaxial tests are typically limited to low frequencies, making it difficult to replicate these field conditions and creating a critical gap between field practice and laboratory-based models [18].

To address these challenges, the industry has turned its attention to IC technology. By integrating intelligent sensing and control systems onto rollers, this technology enables real-time monitoring of the dynamic response between machinery and soil. It then evaluates soil mechanical properties and dynamically adjusts compaction parameters, aiming to achieve precise and intelligent control over the compaction process. However, the mature application of this technology is far from straightforward. Its fundamental bottleneck lies in the current incomplete understanding of the dynamic mechanisms governing the vibration compaction process. Whether it involves accurately identifying the compaction state of the subgrade or making intelligent decisions regarding the vibratory parameters of the roller, both tasks require a profound understanding of the macro–micro dynamic evolution laws between the vibrating wheel and the soil–rock mixture. Therefore, revealing the macro–micro mechanical responses and structural evolution mechanisms of soil–rock mixed filler under varying aggregate content and excitation modes (e.g., strong/weak vibration) has become a critical theoretical task for advancing IC technology—and the core objective of this research. In summary, the primary innovations of this study are as follows:

(1)

A discrete element model for soil–rock mixtures suitable for high-frequency vibratory compaction was established, addressing the limitation of laboratory tests in simulating high-frequency loading.

(2)

A multi-scale particle modeling approach was proposed, combining realistically shaped aggregates, lumpy soil, and spherical fine particles to more accurately replicate field gradations.

(3)

Systematically revealed the influence mechanisms of stone content and vibration modes on porosity, cumulative strain, and structural evolution, providing theoretical foundations for optimizing IC process parameters.

2. An Introduction to the Discrete Element Method for Particle Flow

2.1. An Introduction to the Theory of Numerical Simulation of Particle Flows

2.1.1. Principles of Computation

The research subjects in geotechnical engineering are all granular media, which are discontinuous aggregates of particles. These aggregates can be regarded as particles exhibiting identical mechanical behavior. Complex interactions exist between these particles, and analytical solutions based on continuum mechanics theory cannot capture the intricate interactions between particles or their highly nonlinear characteristics. Given the nature of the research subjects, Cundall first proposed the discrete element theory and applied it to geotechnical engineering research [19].

In discrete elements, each particle is treated as an individual computational entity. Interactions between particles vary dynamically with changes in external loading conditions [20]. The force–displacement equation and the equation of motion form the foundation of discrete element calculations. The equation of motion determines the displacement of each particle. Based on this displacement, the force–displacement equation calculates the contact forces acting on the particle, which in turn determine the particle’s displacement. Within a sufficiently small time step (equivalent to a minuscule differential variable Δ in the integration), particle acceleration remains constant, enabling computation without iteration. The force–displacement equation and the equation of motion update in real-time, mutually constraining each other until the specified computational state is satisfied. Particle motion exhibits two modes: rotational and translational.

During uniform motion, the acceleration a and contact force F of a particle of mass m satisfy the relationship:

$$\mathit{a}={\displaystyle \frac{\mathit{F}}{\mathit{m}}}$$

(1)

The angular acceleration ω during rotation satisfies the relationship with the torque M and the moment of inertia I:

$$\mathit{\omega }={\displaystyle \frac{\mathit{M}}{\mathit{I}}}$$

(2)

And exhibits variations depending on the contact type, but can generally be normalized into a generalized Hooke’s law, where the contact force F relates to the contact stiffness k and the displacement u [21]:

$$\mathit{F}=\mathit{k}\mathit{u}$$

(3)

From the equations of motion and force–displacement relations, it is evident that particles are treated as point masses in discrete element analysis. inter-particle contacts resemble a system of point masses connected by springs. Therefore, the following assumptions hold for particles in discrete elements:

(1)

Particles are rigid bodies without deformation, consistent with the assumption in soil mechanics that solid-phase particles are incompressible and non-deformable.

(2)

The contact area between particles is very small.

(3)

Particle-to-particle contact is flexible, allowing particles to overlap, with the overlap amount being significantly smaller than the particle size.

2.1.2. Particle Flow Program Model

Particle Flow Code (PFC) is a computational program based on discrete element theory, primarily designed to simulate the motion and internal interactions of rigid particles at the microscopic scale. The PFC model contains three types: ball, clump, and wall. These three types can be regarded as the program’s three distinct computational entities.

A sphere is the smallest computational unit in the program. A cluster is formed by binding a series of spheres together through set cohesion parameters. Clusters formed by combining different types of spheres can simulate particles of any shape. The motion of spheres and clusters follows Newton’s laws of motion and possesses mass properties.

Walls are objects in PFC used to apply boundary conditions. They possess no mass properties, meaning there are no contact forces or moments acting on the wall itself, nor any externally applied forces or moments. Instead, the wall’s motion is converted into loads applied to particles through a servo mechanism.

Particle flow programs are applied to analyze the mechanical behavior of bulk materials under specific boundary conditions. In this model, measurements of strain, stress, and other parameters are approximated by averaging values from selected measurement entities. Boundary conditions are applied by using servo mechanisms to impart specific velocities to the walls, simulating the loading conditions encountered in experimental testing.

2.2. Contact Constitutive Model for Particle Flow Programs

In the PFC model, particles interact through generalized internal forces at contact points. Contact mechanics is embodied in the particle interaction laws employing soft contact, where all deformations occur at the contact points between rigid bodies. These particle interaction laws are termed contact models, with the software providing three types: contact stiffness models, sliding models, and bonding models. This paper primarily employs the linear model, hence focusing on its description; other contact constitutive models are not elaborated upon.

The linear model incorporates parallel linear and damping components. The linear component exhibits linear elastic (tension-free) friction behavior, while the damper component provides viscous behavior, as shown in Figure 1. Both components act within an extremely small area, thus transmitting only a single force. The linear force is generated by a linear spring with constant normal stiffness and shear stiffness. The damping force is produced by the damper, whose viscosity is determined by the normal and tangential critical damping ratios. The linear spring and damper operate in parallel.

Linear models are defined by normal stiffness (Kⁿ) and tangential stiffness (K^s), assuming two contacting bodies are connected in series. The contact normal tangent stiffness is

$${\mathit{k}}^{\mathit{n}}={\displaystyle \frac{{\mathit{k}}_{\mathit{n}}^{\left[\mathit{A}\right]}{\mathit{k}}_{\mathit{n}}^{\left[\mathit{B}\right]}}{{\mathit{k}}_{\mathit{n}}^{\left[\mathit{A}\right]}+{\mathit{k}}_{\mathit{n}}^{\left[\mathit{B}\right]}}}$$

(4)

$${\mathit{k}}^{\mathit{s}}={\displaystyle \frac{{\mathit{k}}_{\mathit{s}}^{\left[\mathit{A}\right]}{\mathit{k}}_{\mathit{s}}^{\left[\mathit{B}\right]}}{{\mathit{k}}_{\mathit{s}}^{\left[\mathit{A}\right]}+{\mathit{k}}_{\mathit{s}}^{\left[\mathit{B}\right]}}}$$

(5)

In the equation, ${\mathit{k}}_{\mathit{n}}^{\left[\mathit{A}\right]}$ and ${\mathit{k}}_{\mathit{n}}^{\left[\mathit{B}\right]}$ represent the normal contact stiffnesses of the two contacting particles A and B, respectively; ${\mathit{k}}_{\mathit{n}}^{\left[\mathit{A}\right]}$ and ${\mathit{k}}_{\mathit{n}}^{\left[\mathit{B}\right]}$ denote the tangential contact stiffnesses of the two contacting particles A and B, respectively.

The parameters for linear stiffness are inherited. Parameters assigned using k_n and k_s can be converted between effective modulus (E^*) and 15-stiffness ratio (k^*):

$${\mathit{k}}_{\mathit{n}}=\mathit{A}{\mathit{E}}^{\mathbf{*}}\mathbf{/}\mathit{L}$$

(6)

$${\mathit{k}}^{\mathbf{*}}={\mathit{k}}_{\mathit{n}}\mathbf{/}{\mathit{k}}_{\mathit{s}}$$

(7)

In the formula, A represents the contact area, and L denotes the center distance when the contact distance between the two bodies is zero; it can be calculated using the following formula:

$$\left.\mathit{A}=\left\{\begin{array}{c}\mathbf{2}\mathit{\pi }\mathit{t},\mathbf{2}\mathit{D}(\mathit{t}=\mathbf{1})\\ \mathit{\pi }{\mathit{r}}^{\mathbf{2}},\mathbf{3}\mathit{D}\end{array}\right.\right\}$$

(8)

$$\left.\mathit{L}=\left\{\begin{array}{c}{\mathit{R}}^{\left(\mathbf{1}\right)}+{\mathit{R}}^{\left(\mathbf{2}\right)},\mathit{b}\mathit{a}\mathit{l}\mathit{l}\mathit{\text{-}}\mathit{b}\mathit{a}\mathit{l}\mathit{l}\\ {\mathit{R}}^{\left(\mathbf{1}\right)},\mathit{b}\mathit{a}\mathit{l}\mathit{l}\text{-}\mathit{f}\mathit{a}\mathit{c}\mathit{e}\mathit{t}\end{array}\right.\right\}$$

(9)

Among these, the value of r is

$$\left.\mathit{r}=\left\{\begin{array}{c}\mathit{m}\mathit{i}\mathit{n}\left({\mathit{R}}^{\left(\mathbf{1}\right)}+{\mathit{R}}^{\left(\mathbf{2}\right)}\right),\mathit{b}\mathit{a}\mathit{l}\mathit{l}\text{-}\mathit{b}\mathit{a}\mathit{l}\mathit{l}\\ {\mathit{R}}^{\left(\mathbf{1}\right)},\mathit{b}\mathit{a}\mathit{l}\mathit{l}\text{-}\mathit{f}\mathit{a}\mathit{c}\mathit{e}\mathit{t}\end{array}\right.\right\}$$

(10)

2.3. Principles and Implementation of Three-Axis Servo Mechanisms

In discrete element simulations, the initially generated specimen assembly is often in an unbalanced stress state and lacks tight inter-particle contacts. To achieve a stable initial state and accurately simulate laboratory testing conditions, a servo mechanism is employed to apply and maintain a constant confining pressure.

In this model, the rubber membrane from the laboratory test is represented by rigid walls. As illustrated in Figure 2, four smooth walls (top, bottom, left, and right) confine the granular specimen. The top and bottom walls serve as loading plates, moving at a constant velocity to apply axial deviatoric stress. Simultaneously, the lateral walls (left and right) function as confining boundaries.

The servo mechanism operates as a closed-loop feedback control system. It continuously calculates the average stress exerted by the lateral walls on the particle assembly and compares this measured stress with the required confining pressure. Based on the difference between these values, the normal velocity of the lateral walls is dynamically adjusted. This process ensures that the measured confining stress converges and remains stable at the target value throughout the simulation [22], thereby replicating the constant confining pressure condition essential for triaxial testing.

3. Profile of Dynamic Triaxial Test

3.1. Test Apparatus

The test was carried out in the provincial key laboratory of key technology and system of intelligent building equipment in Shandong Province, and the MTS810 electro-hydraulic servo universal testing machine was used. This testing machine primarily consists of a load frame, hydraulic power unit, cooling system, digital controller, and remote station controller, as shown in Figure 3. When performing compaction operations at construction sites, rollers typically conduct multiple passes over specific areas within a short timeframe. To simulate this rapid and repetitive compaction process, loading was completed when the cycle count reached 50.

3.2. Soil Sample Properties and Specimen Preparation

The rock–soil mixture tested in this study was sourced from a highway construction site near Jinan Airport in Shandong Province, China. The “rock” component primarily consists of granite, diorite, and crushed stone, while the “soil” (fine grain soil) component is mainly low-liquid-limit silt. Test specimens were collected from the construction site. The maximum particle size of the original soil sample was less than 60.0 mm, with a coefficient of uniformity (C_u) of 40.56 (greater than 5) and a coefficient of curvature (C_c) of 0.099, which is less than 1, indicating poorly graded soil. The soil exhibits a wide particle-size distribution, but fine particles (0.075–0.25 mm) constitute a large proportion. These particles have high roundness, uniform grain size, low surface strength, and poor interlocking properties, making the subgrade difficult to compact and resulting in poor engineering characteristics. The sieve analysis results and gradation curve of the soil sample are shown in Figure 4.

Compaction tests were conducted to determine the maximum dry density and optimum moisture content of the soil–rock mixture. Tests were performed in accordance with Chinese Standards (JTG 3430-2020) [23]. Compaction specimens were prepared using the dry soil method. Prior to specimen preparation, the required soil samples were dried or reduced to a moisture content below the minimum compaction moisture content. Different moisture levels were added to each sample, thoroughly mixed, and left to cure overnight for later use. The heavy compaction test was conducted in three layers to obtain the moisture content versus dry density curve for the soil sample, as shown in Figure 5. The maximum dry density and optimum moisture content were determined to be 2.17 g/cm³ and 7.1%, respectively.

The standard specimen dimensions for the dynamic triaxial testing equipment are 100.0 mm in diameter and 200.0 mm in height, as per reference procedure [23]. To minimize the impact of equipment limitations, particles exceeding the instrument’s permissible size (20.0 mm for this testing apparatus) are removed. When oversized particles exceed 5% by volume, the mass substitution method is applied. This involves proportionally substituting oversized particles with all coarse materials permitted by the instrument (ranging from 5.0mm to the maximum particle size). The new gradation composition can be calculated using the following formula:

$${\mathit{p}}_{\mathit{i}}={\displaystyle \frac{\mathbf{100}-{\mathit{p}}_{\mathit{m}}}{{\mathit{p}}_{\mathit{m}}-{\mathit{p}}_{\mathbf{5}}}}({\mathit{p}}_{\mathbf{0}\mathit{i}}-{\mathit{p}}_{\mathbf{5}})+{\mathit{p}}_{\mathbf{0}\mathit{i}}$$

(11)

In the formula: P_i denotes the percentage (%) of particles of a certain size passing after substitution; P₅ denotes the percentage (%) of particles with a size of 5 mm passing in the original gradation; P_m denotes the percentage (%) of particles with a size of 20 mm passing in the original gradation; P_0i denotes the percentage (%) of particles of a certain size passing in the original gradation.

The effectiveness of this method has been validated. Figure 6 shows a comparison of the particle size distribution curves before and after replacement. Figure 7 illustrates the process for preparing replacement soil samples and test specimens. After molding, specimens are wrapped in plastic wrap to maintain a constant moisture content.

3.3. Test Loading Scheme

As the number of compaction passes increases under the vibratory compaction of a roller, the stiffness and compaction degree of the subgrade correspondingly increase. The relationship between subgrade compaction degree and stiffness at different compaction pass counts was obtained through field tests, and the test design was based on the data obtained from these field tests.

Road rollers operate in two modes: strong vibration and weak vibration. In a strong vibration mode, the eccentric weights align with the eccentric shaft, producing maximum vibratory force. In a weak vibration mode, the eccentric weights oppose the eccentric shaft, yielding a minimum vibratory force. Under vibratory compaction, the effective confining pressure is determined according to the research [24]. To replicate the field stress condition in the laboratory triaxial test, the stress applied by the roller must be converted into an equivalent confining pressure for the specimen. The confining pressure within the soil equals the principal stress multiplied by the lateral pressure coefficient. The principal stress primarily comprises the additional stress σ_p generated by the vibrating wheel and the self-weight stress σ_z of the soil mass. The latter is negligible relative to the former. Since the vibratory force in vibratory compaction varies sinusoidally, considering the average stress throughout the compaction process, the force exerted by the vibratory wheel on the soil can be taken as half the amplitude of the vibratory force plus the weight of the vibratory wheel itself. The contact area between the vibratory wheel and the soil can be considered a rectangle, with its long side being the width of the vibratory wheel, and its short side contact width empirically assumed to be 15 cm. The roller parameters are shown in

Table 1. Vibratory roller parameters.

Parameter	Symbols	Size	Unit
vibration wheel mass	md	6500	kg
frame quality	mf	10,500	kg
excitation frequency	f	29/35	Hz
nominal amplitude	H	1.8/0.9	mm
vibratory force	P	410/300	kN
vibration wheel width	L	2.14	M
vibration wheel radius	R	0.775	m
driving speed	v	2.8/5.6/9.1	m/s2

. The additional stress exerted by the vibrating wheel on the soil can be calculated using Formula (12). The resulting soil confining pressure and principal stress levels are presented in

Table 2. Strong vibration, weak vibration parameters.

Parameter	Strong Vibration	Weak Vibration
vibratory force (kN)	410	300
frequency (Hz)	29	35
principal stress (kPa)	781	615
confining pressure (kPa)	260	205

. Since the vibratory force F₀ varies sinusoidally, its average value over a complete cycle is zero. However, for estimating the average compaction stress transmitted to the soil, the sustained load is more relevant than the oscillatory component. Therefore, half of the amplitude (0.5F₀) is adopted as a rational representation of the effective dynamic force contributing to soil compaction, a method consistent with established practices in the literature [24].

It is important to note that the mechanical response of soil–rock mixtures under static and dynamic loading conditions is fundamentally different. While static triaxial tests characterize strength and deformation under monotonous loading, dynamic tests capture the accumulation of permanent strain and the evolution of stiffness under cyclic loading, which is crucial for simulating roller compaction. For evaluating compaction behavior, dynamic parameters such as the dynamic modulus and damping ratio are the focus of this study, as they are more sensitive indicators of the material’s state and structural stability under vibratory loading than static strength parameters. Therefore, the dynamic triaxial tests conducted in this study aim to obtain these key dynamic properties and analyze their evolution, providing a reliable experimental basis for the subsequent development of a discrete element model capable of simulating high-frequency vibratory compaction.

$${\mathit{\sigma }}_{\mathit{p}}={\displaystyle \frac{\left(\mathbf{0.5}{\mathit{F}}_{\mathbf{0}}+{\mathit{m}}_{\mathit{d}}\mathit{g}\right)}{\mathit{L}\mathit{b}}}$$

(12)

For the forced vibration mode at 29 Hz,

$${\mathit{\sigma }}_{\mathit{p},\mathbf{29}\mathbf{Hz}}={\displaystyle \frac{(\mathbf{0.5}\times \mathbf{300}\mathbf{,}\mathbf{000}+\mathbf{5500}\times \mathbf{9.8})}{\mathbf{2.14}\times \mathbf{0.155}}}\approx \mathbf{615}\mathbf{kPa}$$

(13)

When in weak vibration mode, the frequency is 35 Hz,

$${\mathit{\sigma }}_{\mathit{p},\mathbf{35}\mathbf{Hz}}={\displaystyle \frac{(\mathbf{0.5}\times \mathbf{410}\mathbf{,}\mathbf{000}+\mathbf{5500}\times \mathbf{9.8})}{\mathbf{2.14}\times \mathbf{0.155}}}\approx \mathbf{781}\mathbf{kPa}$$

(14)

The ultimate earth pressure can be determined using Formula (12).

$${\mathit{\sigma }}_{\mathbf{0}}=\mathit{k}({\mathit{\sigma }}_{\mathit{p}}+{\mathit{\sigma }}_{\mathit{z}})$$

(15)

In the formula: σ_p—additional stress generated by the vibrating wheel; σ_z—self-weight stress of the soil; F₀—amplitude of vibratory force; m_d—mass of the vibrating wheel; L—width of the vibrating wheel; b—contact width of the vibrating wheel on the soil; K—the lateral pressure coefficient at rest, typically taken as 1/3 for normally consolidated soils.

Due to the on-site roller vibration frequency being around 30 Hz, low-frequency loading was the only feasible option under instrument limitations. To ensure experimental rigor, a discrete element dynamic triaxial model was established to simulate dynamic triaxial tests under identical conditions. The obtained test data calibrated the model parameters. The feasibility of the discrete element model was validated using indoor test data at 1 Hz, 5 Hz, and 10 Hz frequencies, thereby enabling high-frequency loading. The designed indoor test plan is shown in

Table 3. Indoor test scheme.

Frequency (Hz)	Confining Pressure (kPa)	Load (kN)
1	200	600
5
10

.

The results of the indoor triaxial tests on soil–rock mixtures are shown in Figure 8. Figure 8a presents the vertical cumulative strain curves for specimens with a 30% aggregate content under loading frequencies of 1 Hz, 5 Hz, and 10 Hz. Figure 8b depicts the failed specimens after loading.

The figure shows that at lower loading frequencies (e.g., 1 Hz), the vertical cumulative strain of the specimen increases; whereas at higher loading frequencies (e.g., 10 Hz), the vertical cumulative strain decreases. This occurs because under low-frequency loading conditions, particles experience longer contact times, facilitating greater rearrangement and displacement between particles, which leads to larger accumulations of plastic deformation. In contrast, high-frequency loading results in shorter contact times, suppressing the extent of particle rearrangement and thus exhibiting smaller cumulative strain.

Vertical cumulative strain exhibits an upward trend with increasing number of loading cycles N. During the initial loading phase (first 10 cycles), cumulative strain increases rapidly, indicating that specimens are prone to significant plastic deformation in the early stages. As the number of loading cycles increases, the strain growth rate gradually slows down, the specimens tend toward stability, and strain accumulation gradually approaches saturation. This indicates that soil–rock mixtures possess high porosity prior to loading. Under external force, pores rapidly compress, with smaller particles filling voids between larger ones, thereby increasing inter-particle contact area. This compression effect induces significant plastic deformation. As loading cycles increase, these initial adjustments gradually complete, leading the specimen toward a more compact arrangement. The deformation rate consequently slows, ultimately manifesting as a progressive stabilization of the deformation state.

4. Dynamic Triaxial Discrete Element Numerical Simulation of Soil–Rock Mixture

To transcend the frequency limitations of the laboratory apparatus, this study pivots to discrete element simulation, using the low-frequency triaxial tests as a benchmark for model calibration. Particle flow discrete element software PFC6.0 is a command-driven program that requires adherence to a specific sequence during model construction. The command flow compilation process is illustrated in Figure 9.

4.1. The Composition of the Numerical Model

4.1.1. Coordinate System and Unit System

All stress directions in PFC 6.0 are defined as follows: For stresses acting on positive coordinate planes, the positive direction is along the positive axis; for stresses acting on negative coordinate planes, the positive direction is along the negative axis; all others are negative. PFC 6.0 does not specify a particular unit system and does not perform any unit conversions itself. However, it accepts any consistent unit system. Therefore, when creating command sequences and assigning model parameters, the unit system must be defined in advance according to your own specifications. The unit system for mechanical parameters used in this paper is shown in

Table 4. Unit system of mechanical parameters.

Physical Values	Symbol	Unit
mass	M	kg
length	L	m
time	T	s
density	ρ	kg/m3
force	F	N
stress	σ	kPa
stiffness	kn, ks	N/m

.

4.1.2. Calculation Area and Wall Boundary

The computational domain is a bounding box within which all model components in PFC 6.0 reside. This computational domain remains fixed regardless of changes to model components, and its boundaries can be configured with different boundary conditions. Spatial searches and contact detection can be performed within the computational domain. Using the domain command, the model computational domain is constructed as a rectangular prism with a length and width of 200 mm and a height of 600 mm, as shown in Figure 10a. The boundary condition is set to destroy, meaning any model components extending beyond the boundary will be destroyed.

In PFC3D 6.0, walls are composed of a series of triangular planes. The side surfaces of cylindrical walls are generated using the wall generate cylinder command, while the top and bottom surfaces are created with the wall generate plane command, as shown in Figure 10b. The simulated wall dimensions should match those of the indoor test, set at 100 mm diameter × 200 mm height. Each top and bottom surface comprises 2 triangular facets, while the lateral wall consists of 46 triangular facets. In dynamic triaxial numerical simulations, the lateral wall simulates the rubber diaphragm and the lateral confinement of indoor dynamic triaxial tests. The top and bottom wall surfaces simulate the axial actuator and axial confinement in dynamic triaxial tests.

4.1.3. Construction of Particle System

In PFC3D numerical experiments, materials such as sand and rock can be simulated using large particles with relatively uniform grain sizes without special treatment. However, soil–rock mixtures possess distinct gradations, and particle grading significantly influences the material’s mechanical behavior. This study breaks away from traditional models using simplified spherical particles by proposing a novel multi-scale modeling strategy to more accurately capture the complex structure of crushed stone aggregates. Based on a 5 mm soil–rock threshold and a 2.5 mm morphological transition point, this method classifies particles into three categories: true-shaped aggregates (modeled as convex polyhedrons via 3D-scanned STL templates), clumpy soil particles (represented as aggregates), and spherical soil particles. This approach ensures more accurate representation of particle interlocking and gradation characteristics, which are critical for precisely simulating compaction processes. Therefore, when scaling particles, it is essential to preserve the gradation characteristics of the soil–rock mixture as much as possible. Ma et al. [25] proposed and demonstrated the validity and reliability of the “melt small stones, retain large stones” multi-scale analysis method. Building upon the soil–rock threshold concept, Lucianno Defaveri et al. [26] introduced a locally coarse-grained equivalent approach, classifying the particle system into three components: field stones with true shapes, spherical field stones, and fine soil particles. Since the dynamic triaxial test employs uniformly sized, similarly shaped graded crushed stone, ten randomly selected crushed stones were subjected to three-dimensional reconstruction of their morphological features, generating STL files as modeling templates. Subsequently, convex polyhedral elements in PFC 6.0 were employed to characterize the crushed stone particle morphology. The imported template was used to generate convex polyhedral elements, with the schematic of convex polyhedron generation shown in Figure 11. As illustrated, the convex polyhedral elements exhibit distinct angular features, largely reproducing the shape of real particles and reflecting the morphological characteristics of actual crushed stone.

Yongshuai and Sun et al. [27,28,29,30] adopted 5 mm as the boundary value between soil and field stones in soil–rock mixtures. This study also employs 5 mm as the soil–rock boundary value. For the experimental subjects in this study, since soil particles with a gravel-like morphology also exist within the 1–5 mm range, the particle system is categorized into three types: field stones with true morphology, lumpy soil particles, and spherical soil particles. A value of 2.5 mm is adopted as the morphological boundary between discrete element spherical particles and Clumb-shaped gravel particles. The final key particle sizes are shown in Figure 12. Therefore, during specimen formation, spherical soil particles are first generated based on the porosity of crushed stone. These are then replaced with true-shape crushed stone particles. Spherical soil particles are generated according to the porosity of soil particles. Finally, spherical soil particles between 2.5 mm and 5 mm are replaced with lumpy soil particles.

The number of particles is also a critical factor in selecting the soil–rock threshold. A higher particle count reduces computational efficiency. Therefore, considering both particle count and computational capacity, if generating soil particles with true gradation results in an excessive number exceeding computational limits, particles smaller than 0.5 mm are equivalently replaced by particles from the 1~5 mm size group to better simulate soil particle morphology and enhance computational efficiency. For particles larger than 5 mm, to align with laboratory tests and ensure consistent rock content between laboratory and numerical simulations during subsequent parameter calibration and numerical modeling, the numerical model’s particle size distribution corresponds to the actual soil particle size distribution, as shown in Figure 13. It is noteworthy that the boundary conditions were set as fixed geometric constraints and did not influence the selection of rock content, which was solely governed by the research objectives and particle gradation control.

This particle scaling is a recognized simplification, but the controlled rock content ensures that the primary macro-mechanical behavior is preserved.

4.1.4. Modeling

Set sample models with rock content ratios R of 30%, 50%, and 70%. By controlling the R value using the clump porosity command, sample models with different rock content ratios were obtained, as shown in Figure 14. Taking the 30% rock content ratio as an example, the model generated according to the specified gradation is shown in Figure 15.

4.2. Contact Model Setting

PFC 5.0 incorporates multiple built-in contact models, including the Linear model, Linear contact bond model, and Linear parallel bond model. Different models must be selected when simulating granular assemblies under varying conditions, requiring case-specific analysis. Choosing a contact model that accurately reflects the physical and mechanical properties of the granular assembly is critical to the success of the granular flow discrete element method.

For soil–rock mixed fill subgrades, soil particles primarily interact through interlocking forces and friction, with cohesive forces being relatively minor. Furthermore, the fine soil studied here is a low-liquid-limit silt with low viscosity. Therefore, the linear model is selected as the contact model between soil–soil and soil–rock interfaces. The linear model was chosen as it sufficiently captures the key frictional behavior governing compaction, avoiding unnecessary complexity from bonds or rolling resistance not critical to this study.

4.3. Numerical Experimentation Scheme

To investigate the dynamic behavior and micro-evolution mechanisms of subgrade soils under high-frequency loading, the same confining pressure, principal stress levels, and number of loading cycles as those in the dynamic triaxial laboratory tests described in Section 3 of this chapter were employed to ensure the accuracy and comparability of experimental results. Following the calibration strategy outlined above, to validate the accuracy of numerical simulation data under high-frequency loading, parameters were calibrated and verified using the 1 Hz, 5 Hz, and 10 Hz laboratory triaxial tests as a benchmark.

Based on the on-site roller parameters, two vibration modes are employed during subgrade compaction: strong vibration and weak vibration, each corresponding to distinct frequencies and vibratory forces. To simulate real-world subgrade compaction conditions, this chapter’s numerical experiments will analyze the variation patterns of soil–rock mixture compaction characteristics under strong vibration (29 Hz, 410 kN), weak vibration (35 Hz, 300 kN), and aggregate content (30%, 50%, 70%) conditions. This will yield the geotechnical parameters of the compacted soil.

The number of particles in this study is controlled by the porosity of each component. In PFC3D, the average porosities corresponding to the loosest and densest packing states of particles with identical diameters are 48.33% and 20.45%, respectively. Field tests by Junfeng Qian et al. [29] indicate that at a rock content of 30% and a loading frequency of 29 Hz, the compaction degrees after the zeroth and sixth passes of compaction are 80% and 96%, respectively. And at a loading frequency of 35 Hz, the compaction degrees after the zeroth and sixth passes were 80% and 94%, respectively. Higher compaction corresponds to lower porosity. By correlating different compaction levels with their respective porosities, we analyzed the dynamic properties of soil specimens at varying compaction degrees under different loading frequencies. The porosities corresponding to crushed stone particles and soil particles at different compaction levels are listed in

Table 5. The corresponding porosity of gravel particles and soil particles at different compaction degrees.

Rock Content R/%	30
Original porosity n0	0.35	0.27	0.22	0.20
Broken-stone particles occupied by volume particles $b=S(1-n_0){/}_{100}$	0.195	0.219	0.234	0.240
Soil grain occupied by volume particles $a=1-n_0-b$	0.455	0.511	0.546	0.560
Corresponding porosity of broken-stone particles $n_0=1-b$	0.805	0.781	0.766	0.760
Corresponding porosity of soil grain particles $n_0=1-a$	0.545	0.489	0.454	0.440
Compaction degree C/%	87	91	93	94

. To investigate the effects of strong vibration, weak vibration, and rock content on compaction efficiency, an initial average porosity of n₀ = 35% was adopted. The influence patterns of different vibration settings on compaction efficiency were observed, yielding the corresponding porosities for crushed stone particles and soil particles at various vibration settings, as listed in

Table 6. The corresponding porosity of gravel particles and soil particles at different stone content.

Rock Content R/%	30	50	70
Original porosity n0	0.25	0.25	0.25
Broken-stone particles occupied by volume particles $b=S(1-n_0){/}_{100}$	0.25	0.375	0.525
Soil grain occupied by volume particles $a=1-n_0-b$	0.5	0.375	0.225
Corresponding porosity of broken-stone particles $n_0=1-b$	0.75	0.625	0.475
Corresponding porosity of soil grain particles $n_0=1-a$	0.5	0.625	0.775

. With an initial average porosity of n₀ = 25%, the compaction effects under identical loading conditions but varying rock content were examined. The corresponding porosities for crushed stone particles and soil particles in the specimens at different rock contents are presented in

Table 7. The corresponding porosity of gravel particles and soil particles at different vibration gears.

Rock Content R/%	30
Original porosity n0	0.35
Broken-stone particles occupied by volume particles $b=S(1-n_0){/}_{100}$	0.195
Soil grain occupied by volume particles $a=1-n_0-b$	0.455
Corresponding porosity of broken-stone particles $n_0=1-b$	0.805
Corresponding porosity of soil grain particles $n_0=1-a$	0.545

.

5. Mesoscopic Parameter Calibration

As introduced in Section 4, the low-frequency laboratory tests served as the benchmark for model calibration. Parameters in

Table 8. Mesoscopic parameters of the numerical model.

Contact Type	Effective Modulus E* (MPa)	Stiffness Ratio k*	Stiffness Ratio μ
soil–soil	6	0.65	0.65
soil–field stone	10	3.0	0.55
field stone–field stone	20	3.5	0.4
soil–wall	6	0.5	0.45
field stone–wall	10	3.0	0.3

* represents the equivalent parameters derived from the corresponding parameters of the two objects in the contact pair.

were iteratively calibrated by manually matching the simulated vertical cumulative strain curves to the experimental data across all calibrated frequencies. The calibration at low frequencies (1–10 Hz) aims to determine the rate-independent meso-parameters (e.g., contact stiffness, friction) that define the intrinsic mechanical behavior of the material. The validated model then inherently captures the dynamic response at higher frequencies within the DEM framework. This discrete element model simulates the macroscopic dynamic response of specimens by adjusting the mechanical parameters of the linear contact model between particles, thereby altering the mesoscopic dynamic evolution mechanism at the granular scale. However, the mesoscopic parameters of the contact constitutive model cannot generally be directly obtained from experiments. It is commonly accepted that these mesoscopic parameters are considered reasonable when the mechanical response of the discrete element model aligns with actual experimental results. By iteratively adjusting the values of the mesoscopic parameters, the simulation results were made to exhibit the same mechanical response as the laboratory test results. The final mesoscopic parameters obtained are shown in Table 8.

The results of discrete element simulations at different frequencies were compared with those from MTS triaxial tests. As shown in Figure 16, the numerical test results generally agreed well with the laboratory test results, with the maximum discrepancy in vertical cumulative strain not exceeding 10%. This close agreement validates that the discrete element model can effectively simulate dynamic triaxial tests under roller compaction conditions. The discrepancies between simulations and actual tests may stem from size effects caused by particle scaling, modifications to the simulated gradation relative to the actual gradation, and the contact constitutive model’s inability to fully capture soil properties. The mesoscopic parameters were calibrated through an iterative process to match the macroscopic vertical cumulative strain curves obtained from laboratory dynamic triaxial tests at 1, 5, and 10 Hz, ensuring that the numerical model accurately reflects the mechanical behavior of the physical specimens.

6. Typical Law of the Dynamic Triaxial Test of Soil–Rock Mixture

6.1. Porosity

In investigating the evolution of soil particle microstructure under strong and weak vibration at different rock content levels, porosity emerges as a critical research subject. Its dynamic variation patterns characterize the local particle arrangement distribution within the specimen. Analyzing the specimen’s porosity curve indirectly reveals particle motion behavior and reflects the overall stress–strain characteristics of the specimen [31]. The measurement sphere arrangement is shown in Figure 17, with a measurement circle radius of 9 mm. With a specimen aggregate content of 30% and an average porosity of 0.35, porosity was monitored at the end of the 0th, 30th, and 50th vibration cycles. The porosity variation plots for specimens under strong and weak vibration are presented in Figure 18 and Figure 19.

It can be seen from Figure 18 and Figure 19 that when N = 0 times, that is, when the loading has not started, the porosity distribution of the soil sample is relatively uniform; with the increase in number of loading cycles, the low value area of porosity in the strong vibration mode expands faster than that in the weak vibration mode, indicating that the compaction effect is more significant [32], while the porosity distribution in the weak vibration mode is relatively dispersed, and the high porosity area (red area) is more dispersed. This is because in the strong vibration mode, due to the large vibratory force and low frequency, the soil particles are more closely arranged, reducing the pores, and thereby improving the compaction degree. In the weak vibration mode, although the frequency is higher, the compaction effect on the soil is weaker due to the smaller vibratory force, and the change in porosity is not as obvious as that in the strong vibration mode. For the specimen with 30% rock content under strong vibration, the average porosity decreased from 0.35 to 0.29 and further to 0.22 after 0, 30, and 50 cycles, respectively. This represents a reduction of approximately 37%, which is significantly higher than the 26% reduction observed under weak vibration (from 0.35 to 0.26).

Figure 20, Figure 21 and Figure 22, respectively, compared the rock content in 30%, 50%, 70%, the initial porosity in the case of 0.25, and the porosity with the change in number of loading cycles. It can be seen from the diagram that when N = 0 times, that is, when the loading is not started, the porosity distribution is relatively uniform, and the porosity in the local area is low due to the good filling of soil particles and gravel. With the increase in number of loading cycles, the change range of porosity shows a trend of “first increase and then decrease” with the increase in rock content. The porosity change is the largest when the rock content is 50%, the porosity change is the second-largest when the rock content is 30%, and the porosity change is the smallest when the rock content is 70%. This is because when the rock content is small (about 30%), more fine particles make the coarse particles separate from each other, and there is basically no contact between the coarse particles, and the compression properties of the soil–rock mixture sample are mainly controlled by the soil. When the rock content gradually increases from 30% to about 50%, the fine particles decrease in number, and the coarse particles are in contact with each other after compaction and gradually play a skeleton role. The compression properties are affected by the soil and rock. Under this gradation, the coarse and fine particles of the soil–rock mixture can be filled with each other to obtain a denser structure; when the rock content rate reaches about 70%, the skeleton is fully formed between the blocks, and the fine particles cannot completely fill the pores between the coarse particles. The compression properties are mainly controlled by the blocks, resulting in a large porosity.

6.2. Vertical Cumulative Strain and Particle Displacement

Figure 23 compares the curves of plastic cumulative strain ε_p versus number of loading cycles N for dynamic triaxial specimens under strong and weak vibration at a rock content of 30%. The figure shows that both plastic cumulative strains under strong and weak vibrations exhibit an increasing trend with a rising number of loading cycles N, while the rate of increase gradually slows down. The plastic cumulative strain under strong and weak vibration exhibits distinct differences, with the former yielding a larger cumulative plastic strain. This occurs because under strong vibration, the vertical loading force is greater and the frequency is lower [33]. Consequently, the specimen remains in contact with the instrument for a longer duration, allowing sufficient time for force application. This results in more pronounced particle slippage and rearrangement. However, lower frequencies prolong loading time and may induce over-compaction and bounce during the later stages of compaction. Therefore, selecting an appropriate rolling process is crucial for optimizing subgrade construction and enhancing subgrade compaction quality.

Figure 24 and Figure 25 compare the displacement contour plots of specimen particles under strong and weak vibrations. It can be observed that during loading, the colors around the specimen periphery are darker than those at the center, indicating relatively larger displacements at the periphery. As the number of loading cycles N increases, the color at the ends progressively darkens. This occurs because under confining pressure and vertical loading conditions, particle displacements at the specimen periphery are more pronounced and larger than those at the center. The cumulative deformation in the central region develops more slowly compared to other areas, and particle displacements in the central region predominantly occur horizontally outward. Under an identical number of loading cycles, the stronger vibration cycle—characterized by higher confining pressure, greater vertical loading force, and lower frequency—exposes the specimen periphery to prolonged force contact. This results in increased energy transfer. Prolonged stress accumulation causes particles at the periphery to compact and densify, subsequently transferring stress to the central region. This induces particle displacement within the central zone, leading to greater cumulative strain.

Figure 26 compares the curves of plastic cumulative strain ε_p versus number of loading cycles N for dynamic triaxial specimens with varying rock content during weak vibration loading, after the first and last 50 loading cycles. The figure shows that under the first 50 loading cycles, specimens with 50% aggregate content exhibit the highest cumulative plastic strain, followed by those with 30% aggregate content, while specimens with 70% aggregate content show the lowest cumulative strain. During the subsequent 50 loading cycles, the cumulative strain of the 50% aggregate content specimen gradually slowed its growth rate around the 20th loading cycle and approached a stable state. The 30% aggregate content specimen gradually reached strain equilibrium between the 40th and 50th number of loading cycles. The 70% aggregate content specimen exhibited a stable trend of strain increase. This nonlinear variation indicates that aggregate content does not monotonically influence cumulative strain. At low aggregate contents, the higher proportion of fine particles facilitate plastic deformation; as the proportion of crushed stone particles increases, the greater stiffness of the crushed stone facilitates the formation of a skeletal structure. Soil particles and crushed stone can interlock, creating a relatively dense composite system, thus achieving strain equilibrium in a relatively short time. At high aggregate content, the interlocking structure between crushed stone particles effectively constrains plastic deformation. As the number of load cycles increases, the contact and collision between aggregate particles cause irreversible structural rearrangement and yielding of the granular skeleton, leading to gradual plastic deformation in the soil–rock mixture specimens. Therefore, selecting an appropriate compaction process for different soil-aggregate ratios is crucial for enhancing subgrade performance.

Figure 27, Figure 28 and Figure 29 compare the displacement contour plots of specimen particles at different loading stages for varying rock content ratios. It can be observed that at a rock content of 50%, the proportion of red areas around the specimen increases significantly while the blue areas decrease markedly. This indicates relatively uniform particle distribution within the specimen, facilitating stress transfer and dispersion. Consequently, greater displacement and plastic deformation occur at the specimen ends and surrounding regions, enabling the specimen to reach strain equilibrium in a shorter time. At a 30% aggregate content, although the increase in the red proportion is less pronounced than at 50%, the blue area still decreases significantly, indicating that cumulative deformation has also developed in these regions of the specimen. Compared to the 50% aggregate content, specimens with 30% aggregate content may exhibit relatively lower plastic deformation due to less uniform particle distribution, which limits stress transfer and dispersion. Conversely, when aggregate content reaches 70%, specimens show almost no red regions, with only a slight reduction in blue areas. This indicates that displacement and plastic deformation are significantly suppressed at high aggregate content. This may be attributed to the dense distribution of crushed stone particles at high aggregate content, which impedes effective stress transfer and dispersion. Consequently, significant stress concentration and deformation resistance develop within the specimen, prolonging the time required to reach strain equilibrium [34].

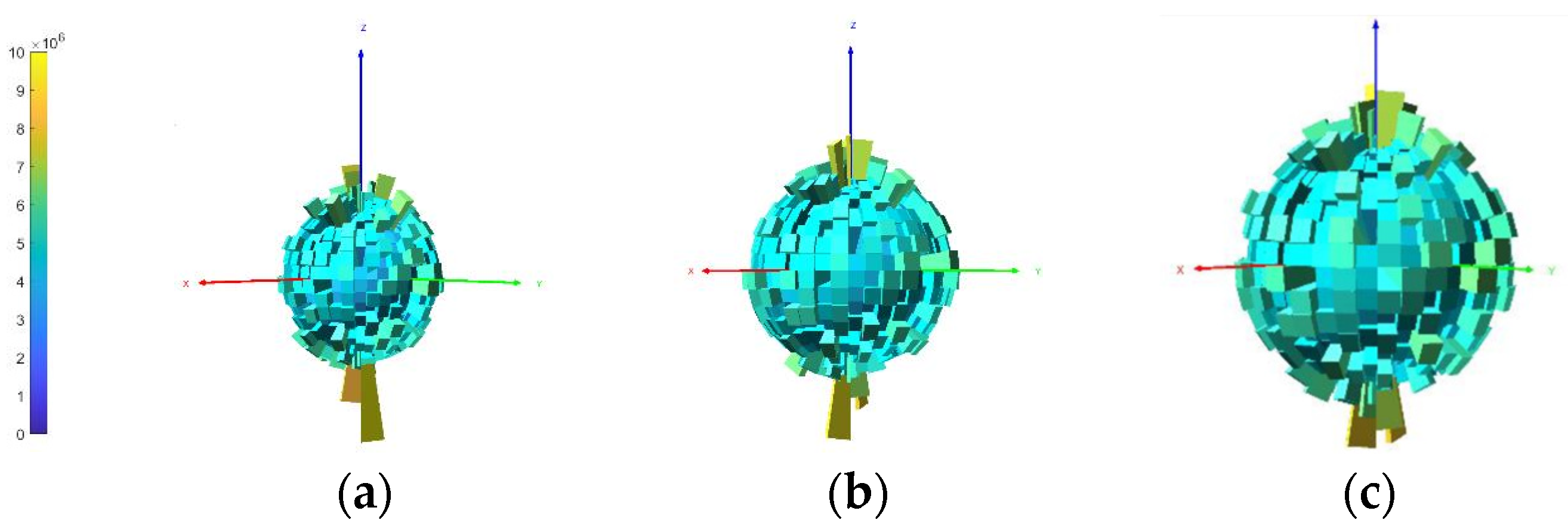
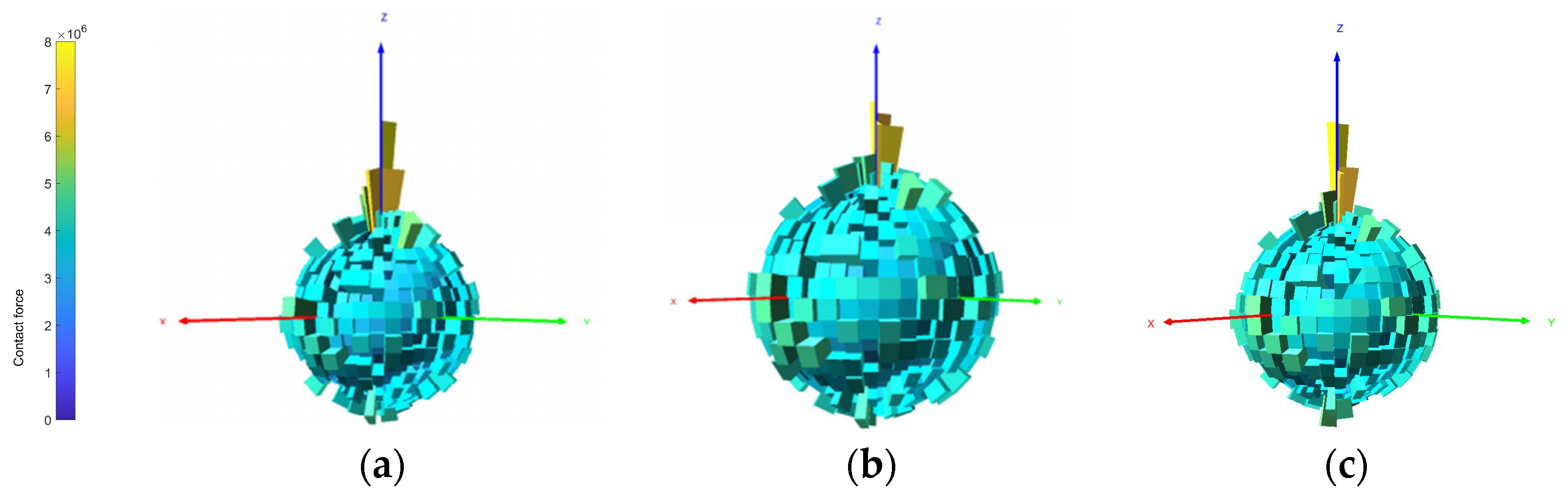
6.3. Fabric Evolution

Soil, as a granular material, transmits forces through mutual contact between soil particles. When subjected to external loads, its internal microstructure undergoes changes, simultaneously altering the macroscopic properties of the soil. Under anisotropic stress, soil exhibits characteristics such as anisotropy and non-coaxiality, a phenomenon that becomes more pronounced under the effect of stress axis rotation. Coordinate number, as a key indicator for investigating soil micro-evolution, clearly characterizes local contact and structural stability within soil. However, analyzing the overall contact conditions and directions across a sample remains challenging. To address this, Oda et al. [35,36] introduced and explored the concept of the “fabric tensor.” By incorporating the fabric tensor concept, Lade et al. [37] established strength criteria and constitutive relationships for anisotropic soils. Their research indicates that the stress–fabric tensor relationship in granular materials mirrors the stress–strain relationship, serving as a bridge between force and deformation. Thus, fabric, as a parameter characterizing the overall microscopic structure of soil, holds significant research value for establishing anisotropic strength criteria and constitutive relationships for materials. Satake et al. [38] proposed the soil particle contact direction fabric defined by Formula (16) to characterize contact distribution in arbitrary directions.

$$\mathit{\phi }={\displaystyle \frac{\mathbf{1}}{\mathit{N}}}\mathsf{\sum }_{\mathit{c}=\mathbf{1}}^{\mathit{N}}{\mathit{n}}_{\mathit{i}}{\mathit{n}}_{\mathit{j}}{\mathit{n}}_{\mathit{k}}$$

(16)

The sum of the principal values of the fabric tensor equals 1; φ represents the contact orientation between particles; n denotes the unit normal vector of the particle contact surface; n_i, n_j and n_k are the components in three spatial directions; N represents the total number of particle contacts.

In three-dimensional space, the specimen’s texture tensor can be expressed using Formula (17):

$$\left.{\mathit{\phi }}_y=\left[\begin{array}{ccc}{\mathit{\phi }}_{\mathbf{11}}& {\mathit{\phi }}_{\mathbf{12}}& {\mathit{\phi }}_{\mathbf{13}}\\ {\mathit{\phi }}_{\mathbf{21}}& {\mathit{\phi }}_{\mathbf{22}}& {\mathit{\phi }}_{\mathbf{23}}\\ {\mathit{\phi }}_{\mathbf{31}}& {\mathit{\phi }}_{\mathbf{32}}& {\mathit{\phi }}_{\mathbf{33}}\end{array}\right.\right]=\left[\begin{array}{ccc}{\mathit{\phi }}_{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{\phi }}_{\mathbf{2}}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathit{\phi }}_{\mathbf{3}}\end{array}\right]$$

(17)

The components of the fabric tensor characterize the strength of soil microstructure along that direction. More particle contacts in a given direction indicate tighter compaction and higher strength in that direction. Greater contact forces in a direction signify that particles bear more stress in that direction.

Figure 30 and Figure 31 indicate that during the initial loading phase, the average contact force of the soil exhibits a tendency to diverge in all directions, suggesting relatively poor stability of the soil structure prior to loading. As the number of loading cycles increases, this divergent trend gradually diminishes, with divergence concentrating at the upper and lower ends. This indicates that the average contact force of the specimen primarily concentrates in the vertical direction to counteract the vertical stress induced by the vertical load. Compared to strong vibration, weak vibration exhibits more pronounced divergence in the vertical average contact force. This occurs because weak vibration involves smaller vertical loading forces and higher frequencies, resulting in shorter and faster contact times between the specimen ends and the load. Consequently, the compaction effect is relatively weaker than that achieved with strong vibration.

As shown in Figure 32, Figure 33 and Figure 34, the contact configuration characteristics of specimens with different rock contents also demonstrate significant differences after 50 cyclic loadings. The specimen with 50% rock content exhibits reduced divergence trends in all directions after loading, indicating well-packed soil–stone particles that rapidly achieve a dense structure. In contrast, the 30% rock content specimen contains a higher proportion of soil particles, where the ends bear a more pronounced cyclic loading effect. Consequently, the divergence trend at the ends is more pronounced, and the contact configuration diagram shows darker colors, indicating larger average contact forces. The 70% rock content specimen contained a higher proportion of coarse gravel with greater stiffness, hindering effective stress transfer and dispersion. Consequently, the average contact force transmitted between particles was lower, resulting in a lighter-colored contact graph. Simultaneously, due to the potential concentration of fine particles at the base, stress transfer was more efficient, leading to a more pronounced divergence trend at the bottom. The proportion of contact forces in the vertical direction increased from an initial isotropic state of approximately 33% to over 60% after 50 cycles under strong vibration.

6.4. Implications for Intelligent Compaction

The meso-scale evolution patterns revealed in this study provide a mechanistic foundation for optimizing and controlling IC processes. The identification of 50% rock content as the optimal range for the most significant porosity reduction and rapid strain stabilization offers a critical guideline for the real-time evaluation of compaction quality in IC systems. Furthermore, the distinct compaction efficiencies observed under strong and weak vibration modes, along with their corresponding fabric evolution characteristics, can directly inform the adaptive selection of roller excitation parameters. Specifically, the concentrated contact force distribution under strong vibration, as captured by the fabric tensor, serves as a potential mesoscopic indicator for achieving uniform density. These findings bridge the gap between macroscopic field responses and underlying particle-scale mechanisms, enabling more intelligent decision-making for achieving desired compaction states in soil–rock mixture subgrades.

7. Conclusions

This study employs high-frequency vibration discrete element simulation to fill the gap in macro–micro behavior research of soil–rock mixtures under high-frequency compaction conditions. The proposed multi-scale modeling approach enhances the authenticity of numerical models. The findings hold clear theoretical and engineering value for parameter optimization and decision support in IC technology. The specific findings that underpin this overall contribution are as follows, which also correspond to the primary innovations of this research:

(1)

A validated high-frequency DEM model: The established discrete element model successfully overcomes the low-frequency limitations of laboratory tests, enabling the simulation of field-like vibratory compaction. This addresses the first innovation point and reveals that the evolution of specimen porosity is significantly more pronounced under strong vibration than under weak vibration. Furthermore, the relationship between porosity reduction and rock content is nonlinear, with the most significant compaction occurring at a rock content of 50%.

(2)

Macro-response explained by multi-scale modeling: The multi-scale modeling strategy, which combines true-shaped aggregates, clumpy soil, and spherical fine particles, provides a credible micromechanical basis for macroscopic observations. It elucidates that the macroscopic cumulative strain increases with loading cycles at a decelerating rate, a direct result of particle rearrangement and void filling. Strong vibration generates greater cumulative strain due to longer inter-particle contact duration. The nonlinear impact of rock content on strain—peaking at 50%—is attributed to the formation of an optimal skeleton–soil structure at this content.

(3)

Influence mechanisms of vibration mode and rock content: The systematic analysis reveals the underlying mechanisms through which vibration modes and rock content influence compaction. Fabric tensor analysis demonstrates that the internal force chain network evolves from an initial isotropic state to a vertically concentrated distribution to resist external stress. This fabric anisotropy is more developed under strong vibration, forming a denser and more stable structure. The rock content dictates the efficiency of this fabric evolution: 50% content facilitates a uniform and efficient force distribution; 30% content leads to a more dispersed pattern in a soil-dominated matrix; and 70% content results in a rigid skeleton with weaker inter-particle contacts.

(4)

The meso-scale mechanisms quantified in this study—the systematic reduction in porosity and the reorientation of contact forces—provide a physical interpretation for the macro-scale indicators used in IC. The documented densification and force chain formation are the fundamental reasons for the increase in soil stiffness, which is the key parameter that IC systems aim to evaluate indirectly. Thus, this work links the evolution of the internal soil structure to the engineering practice of compaction quality control.

Accordingly, high-frequency compaction demonstrates superior efficiency in achieving target density, particularly during the initial compaction phases; however, corresponding compaction techniques should be selected for different soil–rock mixtures based on specific project requirements that consider both construction efficiency and long-term performance implications.

Future research should investigate how the microstructural features resulting from different compaction methods, particularly those formed under high-frequency vibration, influence the long-term service performance of subgrades, such as their resistance to permanent deformation and fatigue.