Influence of Tilt Angle and Sag-to-Span Ratio on the Wind-Induced Interference Effects on Structural Response in a Cable-Supported Photovoltaic Array

Abstract

As a common large-scale civil engineering structure, cable-supported photovoltaic (PV) arrays are typically designed with a 25-year service life, with their primary structural system composed of beam-column frames, pre-tensioned cables and modules. Cable-supported photovoltaic arrays are susceptible to large-amplitude wind-induced vibrations (WIV), threatening structural safety and serviceability. This study investigates interference effects on an eight-row array that employs aeroelastic wind tunnel tests, focusing on how tilt angle and sag-to-span ratio influence vibration characteristics and interference mechanisms. Results show coupled vertical–torsional vibrations with amplitudes increasing with wind speed and that are more intense under wind suction than under wind pressure. Reducing tilt angle and sag-to-span ratio effectively suppresses vibrations and raises critical flutter speed. For interference effects, mean response demonstrates clear shielding with amplitudes decreasing leeward. In contrast, fluctuating response behavior depends on tilt angle: 5° tilt angle produces a shielding effect, while 25° tilt angle causes an amplification effect with periodic fluctuations. The 25° tilt angle shows greater sensitivity to wind speed, evidenced by decreasing interference coefficients from the second to eighth windward rows with increasing wind speed. Although reducing the sag-to-span ratio most effectively suppresses vibrations in the first windward row and consequently affects downstream interference coefficients, it does not alter the fundamental trends governed by tilt angle.

1. Introduction

Against the backdrop of the global energy crisis, the photovoltaic industry has experienced rapid development. Due to the shortage of land for PV power plant construction and the demands of specific application scenarios, cable-supported PV systems [1] have been widely adopted in engineering projects. Traditional fixed supports not only consume substantial amounts of steel but also struggle to adapt to complex environments and terrains. In contrast, cable-supported PV systems, which support the photovoltaic modules via cables fixed between end columns, offer exceptional terrain adaptability. This configuration enables large-span arrangements while significantly reducing the required number of supporting components such as columns. However, these systems are characterized by large module dimensions, long spans, and low structural stiffness. Furthermore, as they are typically deployed in array configurations, they are highly susceptible to WIV, which can lead to extensive damage across the PV array. Figure 1 shows field documentation of wind-induced damage to the cable-supported PV array, collected by the author during an investigation following the landfall of Typhoon Yagi in Hainan, China, in 2024.

Scholars worldwide have conducted extensive research on the wind loads affecting PV arrays. These studies have consistently identified significant interference effects between PV supports, which are influenced by factors such as module tilt angle, wind direction, ground clearance, and row spacing. Bitsuamlak [2] employed numerical simulations to investigate the wind loads on both isolated and tandem PV modules, finding distinct differences between the two configurations. The significant interference effects generated in tandem arrangements substantially reduced the wind loads on adjacent panels. Abiola-Ogedengbe [3] performed wind tunnel tests on a PV module comprising 24 components, revealing that the tilt angle, wind direction, and inter-panel gaps significantly affect the magnitude and distribution of surface pressures on PV modules. Shademan [4] utilized numerical simulations to analyze the influence of longitudinal spacing, lateral gap spacing, ground clearance, and wind direction on the overall wind loads acting on PV panels. Jubayer [5], using three-dimensional numerical simulations, found that the maximum wind loads typically occur near the leading edge of the modules. He also observed that the mean pressure distribution and wake structure exhibited symmetry characteristics along the flow centerline. Studies focusing solely on the wind loads of isolated modules or single-row supports are insufficient. Numerous researchers have investigated the interference effects on wind loads within PV arrays using rigid model pressure measurement tests and Computational Fluid Dynamics (CFD) simulations. These studies demonstrate that tilt angle, wind direction, array spacing, and structural configuration are all significant factors influencing the interference effects. Through rigid model pressure tests, Ginger [6], Browne [7], and Yemenici [8] studied the interference effects on PV array wind loads. They concluded that the shielding effect becomes more pronounced with larger tilt angles, and the wind load stabilizes after the third row. Based on these interference effects, they provided recommendations for shape factor values, suggesting that different zones be designed according to varying wind load distributions. Warsido [9] investigated the impact of shielding effects on both the wind load and wind-induced vibration of PV arrays, finding that leeward modules consistently experience lower wind loads than windward modules due to shielding, resulting in different wind-induced vibration responses for modules at different positions within the array. Ma [10], conducting rigid pressure-measurement wind tunnel tests on multi-row PV supports, found that the interference effect manifested as a shielding effect on the mean pressure and torque coefficients of the solar tracker array, which was more significant at larger tilt angles. Regarding the fluctuating components, the interference effect showed a shielding effect at small tilt angles but an amplification effect at large tilt angles. Xu [11] used numerical simulations to study the wind loads on multi-row PV supports, finding that support height and row spacing both influence the standard deviations of pressure and torque coefficients. Furthermore, vortex shedding from the PV supports affects the wind load fluctuations on the module surfaces, with pronounced vortex shedding observed at larger tilt angles, consistent with the findings of Suárez [12]. Given that the WIV of cable-supported PV arrays is caused by fluctuating wind loads, it is reasonable to infer that significant interference effects are also present during their WIV response.

Existing research has revealed that cable-supported PV systems can undergo large-amplitude WIV, with forced vibrations caused by fluctuating wind loads at low wind speeds and self-excited vibrations induced by aerodynamic instabilities at high wind speeds being the most common. This phenomenon is influenced by numerous factors. To this end, Feltrin [13] and Kim [14] investigated the effects of sag, wind direction, inflow conditions, and wind speed on the WIV of single-row cable-supported systems through aeroelastic model wind tunnel tests. Their studies found that the fluctuating displacement of PV supports is closely related to factors such as the sag-to-span ratio, wind speed, and wind direction. Under certain conditions, these cable-supported systems experience self-excited vibrations due to fluid–structure interaction effects. Wu [15] studied the effects of wind direction, PV module tilt angle, initial prestress of the stability cable, and flow field on the WIV response characteristics of a single-row cable-supported system. It was found that an increase in the tilt angle leads to a decrease in the critical wind speed; an increase in the initial prestress can raise the critical wind speed, but the effect is not significant; and the critical wind speed in a turbulent flow field is approximately 30% higher than that in a uniform flow field. The instability vibration was identified as a result of multi-mode coupling involving vertical bending and torsion. Xu [16] employed aeroelastic and rigid model wind tunnel tests to study the WIV characteristics of a single-row cable-supported system. The wind-induced vertical vibration of the PV modules increased with a larger tilt angle and decreased with higher pre-tension force; the fluctuating displacement exhibited a quadratic increase with wind speed. Zhu [17] used CFD numerical simulations to study the effect of tilt angle on the WIV of cable-supported systems. The results showed that as the tilt angle increased from 0° to 60°, the displacement wind-induced vibration coefficient ranged from 1.70 to 1.93, indicating that the influence of the tilt angle on the wind vibration coefficient must be considered in practical engineering design. However, cable-supported PV systems are typically deployed in large-scale arrays, where significant differences in wind load exist between rows. Vibration suppression measures are sometimes adopted to enhance the overall stability of the array, but these are not always implemented in mountainous or certain complex terrains. He [18] conducted aeroelastic model wind tunnel tests on a double-layer cable-supported PV system and found that WIV initiates at relatively low wind speeds, with the amplitude increasing with wind speed. The windward modules and those at a 180° wind direction experienced greater vibration, with torsional vibration being stronger than vertical vibration. The study verified that adding inter-row connections effectively reduces the WIV of PV modules. Zhang [19] investigated the WIV characteristics and shielding effects of a double-layer cable-supported PV array through aeroelastic wind tunnel tests. The research demonstrated that the WIV of the first row in the array is significantly greater than that of the downstream rows. The maximum WIV occurs when the wind direction is perpendicular to the supporting cables and the modules are subjected to wind suction. Within a certain range, a larger initial tilt angle of the PV modules leads to greater WIV. Ding [20] studied the effects of shielding and wind direction on the WIV of a cable-supported PV array through wind tunnel tests. The WIV of PV modules in the central and leeward regions was significantly weaker than that in the windward region. Within the array, the windward modules provide a shielding effect for the downstream modules. The wind direction of the incoming flow also significantly affects the WIV of the structure, with crosswind directions (0° and 180°) producing the strongest WIV and being identified as the most critical conditions. The vibration amplitude decreases almost linearly as the wind direction deviates from the perpendicular. Yang [21] studied the interference effects in a cable-supported PV array and conducted a comparative analysis with the vibration of a single-row support. The results indicated that both single-row and multi-row PV modules experience flutter instability as wind speed increases. Vertical vortex-induced vibration was observed in the multi-row array at low wind speeds prior to the onset of flutter instability, with the middle row exhibiting the most significant response. In summary, existing research has primarily focused on the aeroelastic response of individual cable-supported PV supports or simplified arrays. There remains a lack of in-depth understanding of the interference mechanisms governing the overall wind-induced response of multi-row cable-supported PV arrays. Li [22] conducted wind tunnel tests on a sectional model of a cable-supported PV support system to investigate the critical flutter wind speeds at various tilt angles. Their study confirmed that installing a central stabilizer fin does not enhance the critical flutter wind speed. Chen [23] performed aeroelastic model wind tunnel tests on a cable-supported PV support structure. Using a single-row model, they examined the aerodynamic stability under different tilt angles, wind directions, and both uniform and turbulent flow fields. Furthermore, with an array model, they investigated the interference effects resulting from varying wind directions, the number of PV supports, and the interconnections between adjacent PV modules. In summary, no study has yet clearly and systematically revealed how key design parameters, such as tilt angle and sag-to-span ratio, influence the interference effects, particularly their distinct impacts on the mean and fluctuating response components.

To address the unclear mechanisms of interference effects based on wind-induced responses in cable-supported photovoltaic arrays, this study investigates the interference effects on the WIV of an eight-row cable-supported PV array through aeroelastic wind tunnel tests. The research analyzes the influence of tilt angle, sag-to-span ratio, wind direction, and wind speed on the WIV characteristics of the array. An interference factor is defined for both the mean and fluctuating components of the displacement response for each row of the cable-supported PV array, aiming to elucidate the underlying interference mechanisms governing the wind-induced vibrations in such systems.

2. Wind Tunnel Test

2.1. Wind Tunnel and Flow Simulation

The aeroelastic wind tunnel test on the single-layer cable-supported PV array was conducted in the low-speed test section of the Shijiazhuang Tiedao University (STDU-1) atmospheric boundary layer wind tunnel laboratory. This facility is a single-return, series-connected, dual-test-section laboratory. The low-speed test section measures 24 m in length, 4.4 m in width, and 3 m in height. It achieves a maximum wind speed of 30 m/s, with a background turbulence intensity of ≤0.5%, mean velocity non-uniformity of ≤0.5%, and velocity instability of ≤0.6%. The Category B atmospheric boundary layer flow field was simulated using spires and roughness elements, corresponding to a terrain roughness exponent α₁ = 0.15, which satisfies the code-specified requirements for terrain roughness. The wind speed profile, turbulence intensity profile, and fluctuating wind speed spectrum at the center of the turntable are shown in Figure 2, where Z_g represents the height at the top of the test model and U_g denotes the wind speed at the corresponding model top height.

2.2. Test Model

The prototype structure investigated in this study is a single-layer cable-supported PV system with a span of 17.8 m. The cable spacing is 1.4 m, and the ground clearance of the PV modules is 2.5 m. Each support unit consists of eight rows with a row spacing of 3.5 m. Each row features a three-span continuous configuration, resulting in a total length of 53.4 m for the cable-supported PV system. Fourteen PV modules are installed per span, with module dimensions of 2278 mm × 1134 mm × 30 mm and an inter-module gap of 40 mm. Each module has a mass of 35.65 kg, and the system employs steel strands with a diameter of 15.2 mm.

The natural frequencies and mode shapes of cable-supported PV systems are crucial factors influencing their wind-induced vibration behavior. This study analyzes the natural vibration characteristics of the prototype structure through a finite element model of a single-row cable-supported PV system with a tilt angle of 25° and a sag-to-span ratio of l/100. Figure 3 shows the first six mode shapes of the cable-supported PV system. The first three modes are the symmetrical vertical vibrations of the three individual sub-spans, all with a natural frequency of 1.25 Hz. Modes four to six correspond to symmetrical torsional vibrations of the three sub-spans, each exhibiting a natural frequency of 1.35 Hz.

Based on the dimensions of the aforementioned cable-supported PV system prototype and similarity criteria, combined with the cross-sectional dimensions of the wind tunnel, the geometric scale ratio of the aeroelastic model was ultimately determined to be 1:30. The total length of the three-span model is 1780 mm. The scaled PV modules were constructed using wooden boards with dimensions of 76 mm × 37.8 mm × 1 mm. Wooden boards meeting the mass requirements were bonded to two No. 8 fishing lines (simulating the cables) using glue, with an inter-module spacing of 1.3 mm. The model’s end columns were fabricated from 45 mm × 45 mm × 2.5 mm channel steel, while the intermediate columns were constructed from acrylic sheets with a column height of 88.5 mm. The relevant parameters of the model and the prototype structure are listed in

Table 1. Parameters of the prototype structure and the model.

Parameter		Unit	Prototype	Similarity Ratio	Model
column	height	mm	2655	1/30	88.5
PV module	chord	mm	2278	1/30	76
	width	mm	1134	1/30	37.8
	thickness	mm	30	1/30	1
	mass	g	35,650	1/303	1.32
cable	length	mm	17,800	1/30	590
	diameter	mm	15.2	1/30	0.5
wind speed	-	m/s	28.5	$\sqrt{30}:1$	5.2
frequency	-	Hz	1.25	$1:\sqrt{30}$	6.6

.

The vertical natural frequency of the scaled cable-supported PV system model, determined through finite element analysis, is 6.8 Hz. After completion of the aeroelastic model construction, its natural frequency was validated. The measured free vibration decay curve for the model’s vertical vibration is shown in Figure 4, where the vertical coordinate ΔV represents the vibration amplitude. The solid line in the diagram is the vibration time history curve, and the dashed line is the exponential decay envelope fitted based on the free vibration theory. The model’s vertical vibration frequency and damping ratio, obtained via Fourier Transform, are 6.6 Hz and 3.12%, respectively. The designed aeroelastic model accurately represents the vibration characteristics of the actual structure, as demonstrated by the fact that the measured natural frequency and damping ratio of the model satisfy the similarity relationship with the results from the finite element simulation of the prototype.

2.3. Parameter Definition

The installation of testing equipment in the wind tunnel laboratory is shown in Figure 5a. Video-based displacement measurement system, installed on the ceiling via magnetic bases, was employed for displacement measurements. This system is capable of a sampling frequency up to 300 Hz, which was set to 70 Hz in the present tests, with a measurement accuracy of 0.01 mm. Wind speed was measured using a Series 100 Cobra probe, which offers a sampling frequency range of 0~2000 Hz and a wind speed measurement range of 2~100 m/s. The probe was mounted on the sidewall of the wind tunnel at the same height as the model to ensure accurate wind speed measurement at the model height. Figure 5b illustrates the cable-supported PV array and the definition of wind direction. The array consists of 3 spans and 8 rows, with the 3 spans sequentially labeled K1, K2, and K3. The wind direction angle, denoted as α, is defined as the angle between the chord line of the PV modules and the incoming flow direction. During testing, this angle was adjusted by rotating the turntable embedded in the wind tunnel floor. Based on the inflow direction, the eight rows are designated as R1 to R8 from front to back.

The tilt angle of the PV modules, denoted as β, is defined as the angle between the module plane and the horizontal ground. This angle was adjusted during testing by rotating the T-shaped beams, with a schematic representation provided in Figure 5c. In this study, two typical tilt angles, 5° and 25°, were selected for investigation. The sag-to-span ratio, represented by γ, is defined as the ratio of the mid-span sag in the initial state to the single-span length. Two ratios commonly used in engineering practice, l/100 and l/200, were chosen for targeted analysis. The wind-induced displacement response was measured at the mid-span of each of the three spans in the cable-supported PV array through aeroelastic wind tunnel tests. The measurement locations are illustrated in Figure 5b,d. Two measurement points were established at each mid-span: the point closer to the ground is designated as Point 1, and the point farther from the ground as Point 2. The horizontal distance between these two points is denoted as d, enabling the acquisition of two separate displacement time histories, recorded as Z₁ and Z₂. The cable closer to the ground is referred to as C₁, and the cable farther from the ground as C₂. When the wind direction angle α = 0°, the wind first encounters C₁, making it the windward cable, with row R1 serving as the first windward row. Conversely, when α = 180°, the wind first encounters C₂, making it the windward cable, and row R8 becomes the first windward row.

In practical engineering applications, numerous cable-supported photovoltaic (PV) systems have experienced failure due to modules being dislodged or overturned under wind loads. This damage mechanism primarily results from excessive wind-induced displacement responses of the PV modules, leading to failure of the connectors that secure the modules to the load-bearing cables. Consequently, investigating the displacement response of cable-supported systems is essential. It not only provides critical references for the structural design of the supports themselves but also holds significant importance for the strength design of key components, including connectors and module attachments. The displacement response is further decomposed into vertical and torsional components. The vertical displacement (V) and torsional displacement (T) are calculated using Equation (1) and Equation (2), respectively:

$$V(t)={\displaystyle \frac{Z_1(t)+Z_2(t)}{2}},$$

(1)

$$T(t)=\arctan {\displaystyle \frac{Z_1(t)-Z_2(t)}{d}},$$

(2)

where d represents the horizontal distance between the two measurement points at the mid-span of the cable-supported system, which varies with changes in the tilt angle β; Z₁ and Z₂ denote the displacement time histories recorded at the two measurement points, with upward displacement defined as positive. According to the sign convention defined for Z₁ and Z₂, vertical displacement V is positive in the upward direction and negative downward, while torsional displacement T is positive in the counter-clockwise direction. Following the acquisition of displacement time histories at the mid-span, the mean value and standard deviation were calculated separately for the vertical and torsional displacement components, yielding the mean vertical displacement (V_m), fluctuating vertical displacement (V_ḍ), mean torsional displacement (T_m), and fluctuating torsional displacement (T_ḍ).

3. WIV Characteristics of Cable-Supported PV Array

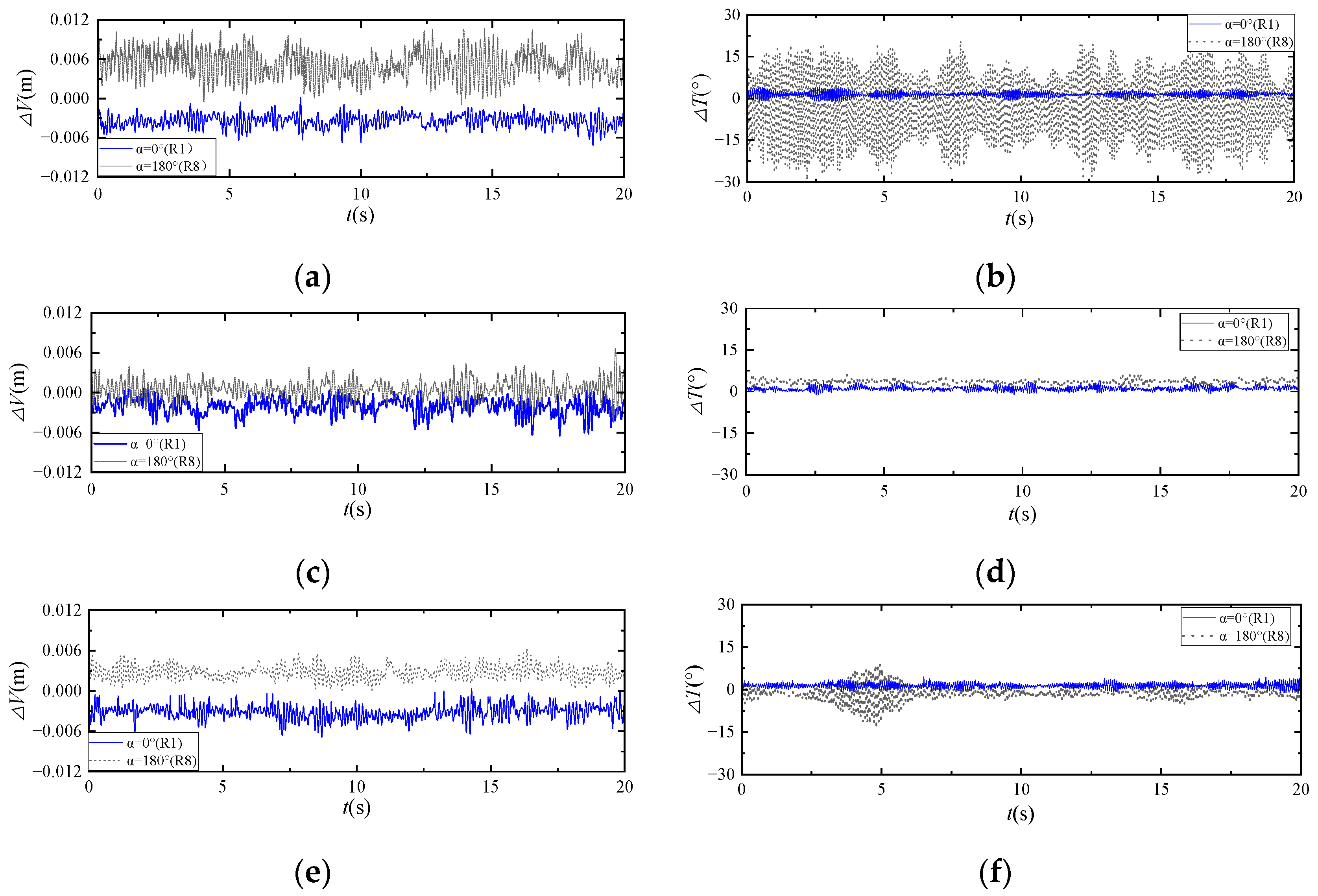
Figure 6 presents the time-history responses of vertical and torsional displacements for each row in three different structural configurations of the cable-supported array at a wind speed of U = 5.2 m/s. Under all tested combinations of wind direction, sag-to-span ratio, and module tilt angle, the cable-supported PV array exhibits coupled vertical and torsional vibrations at this wind speed. The vibrational response is more intense at a wind direction of 180° than at 0°. Moreover, the coupling between vertical and torsional motions is more pronounced under the 180° condition. These directional differences become particularly significant in configurations combining larger tilt angles with greater sag-to-span ratios.

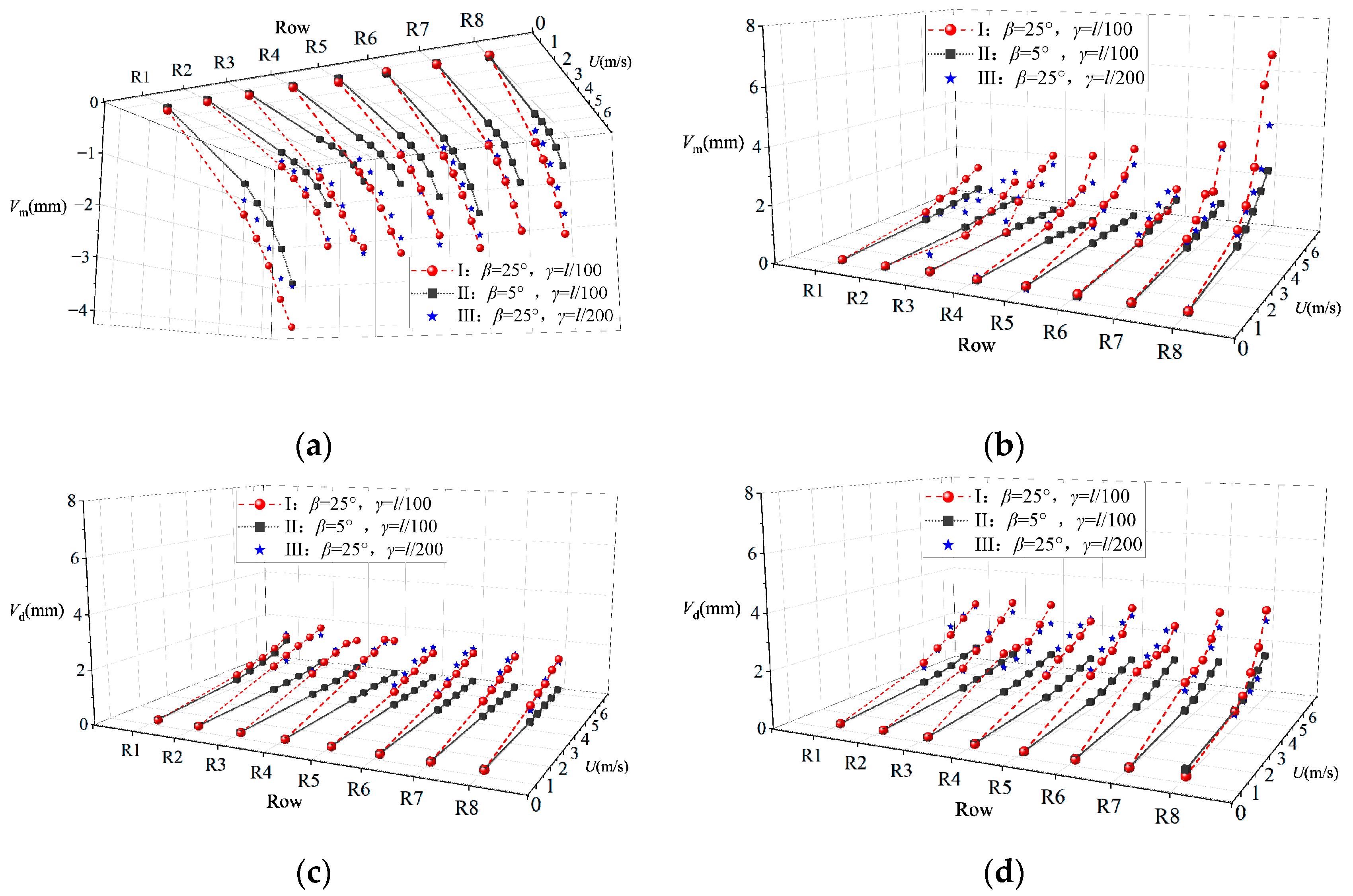
Figure 7 compares the variation in vertical displacement response with wind speed for the cable-supported PV array under different tilt angles and sag-to-span ratios. Under all test conditions, both V_m and V_d for each row exhibit a monotonic increasing trend with rising wind speed. Furthermore, the influence of the sag-to-span ratio on the vertical displacement response becomes progressively more pronounced at higher wind speeds. Reducing the sag-to-span ratio directly enhances the structural stiffness, thereby significantly improving the system’s resistance to deformation under static wind loads and effectively suppressing vertical vibrations across all positions. Regardless of wind direction, the first two windward rows represent the most critical positions in the array, with the maximum V_m typically occurring at the first windward row and the maximum V_d at the second. A reduction in the sag-to-span ratio substantially decreases both maximum V_m and V_d values. At a wind speed of 5.2 m/s, decreasing the sag-to-span ratio from γ = l/100 to γ = l/200 results in maximum reductions of 48.7% in V_m and 54.1% in V_d for the first windward row, while for the second windward row, the maximum reductions reach 30.1% in V_m and 13.7% in V_d.

The cable-supported PV array with β = 5° exhibits a more gradual increase in vertical displacement response with wind speed across all rows. Under varying wind directions, wind speeds, and span configurations, the vertical displacement response remains consistently smaller compared to arrays with greater tilt angles. At a wind speed of 5.2 m/s, for instance, compared to the β = 25° configuration, the array with β = 5° shows reductions of 34.9% in maximum V_m and 36.6% in maximum V_d at α = 0°. Under α = 180° conditions, the maximum V_m and V_d for the β = 5° array are reduced by 64.6% and 43.2%, respectively.

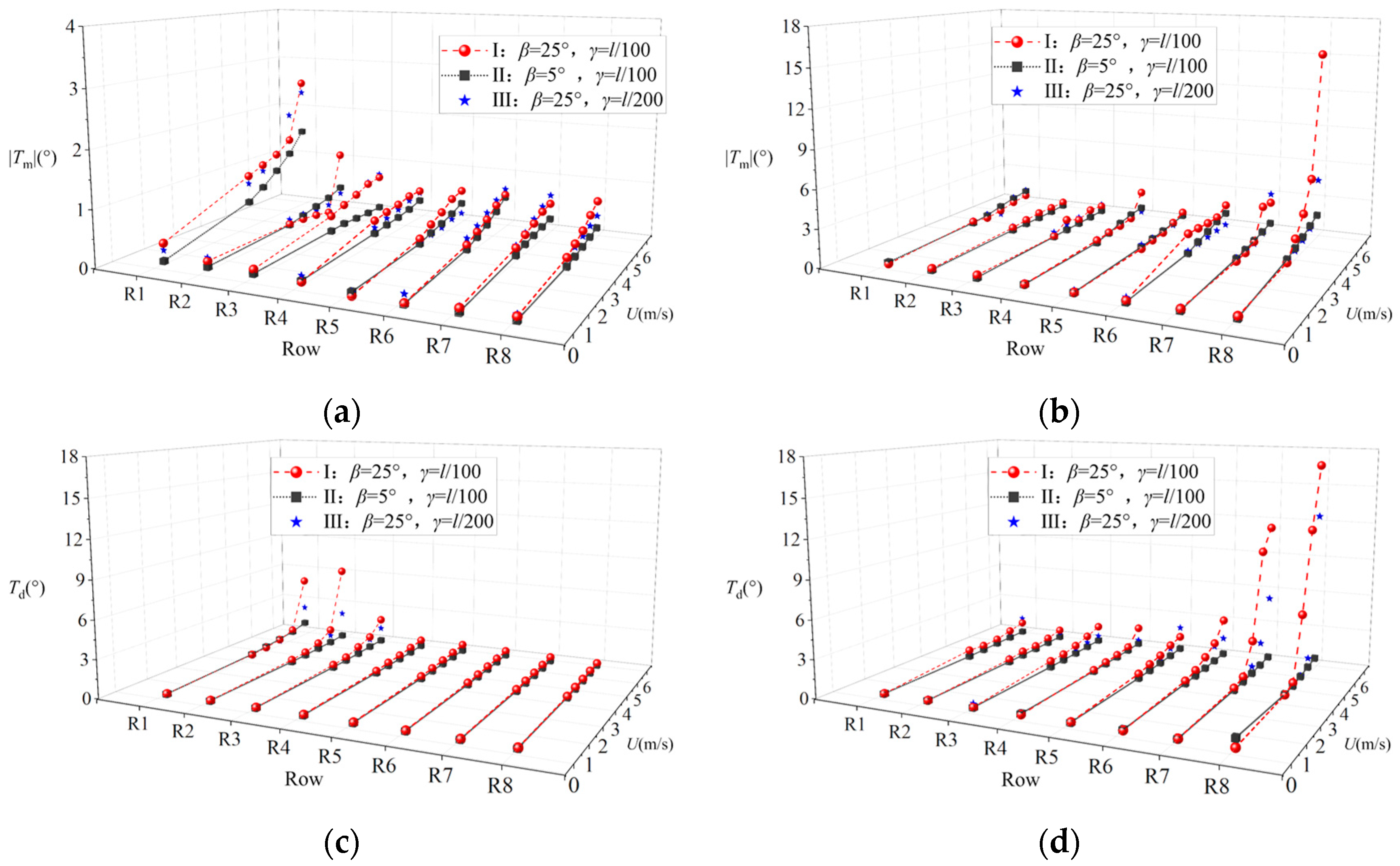
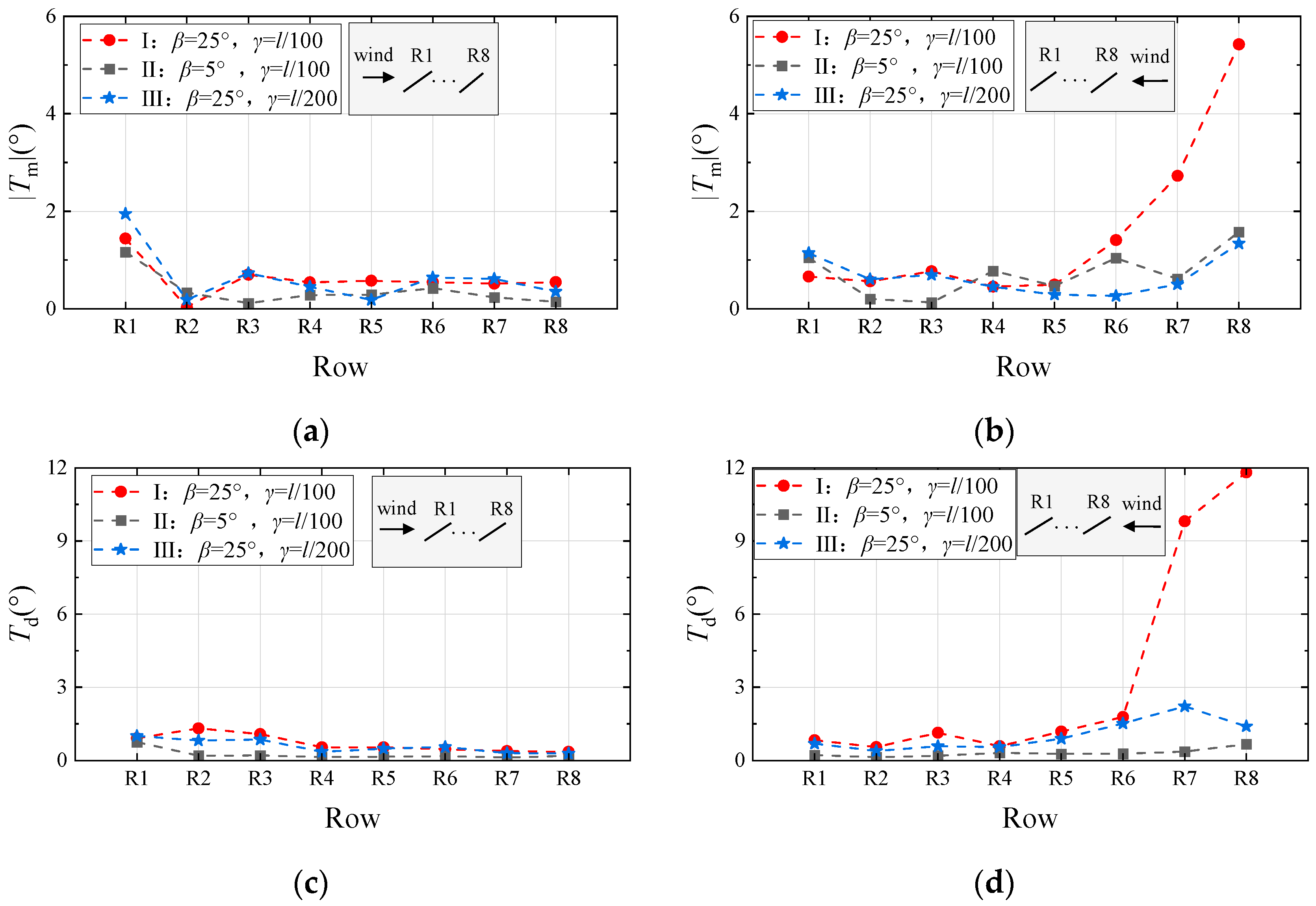
Figure 8 compares the variation in torsional displacement response with wind speed for the cable-supported PV array under different tilt angles and sag-to-span ratios. Under all test conditions, both the mean and fluctuating components of torsional displacement exhibit an increasing trend with rising wind speed across all rows. Figure 8a and Figure 8b show the variations of T_m under wind directions of 0° and 180°, respectively. The results indicate that reducing the sag-to-span ratio has a more pronounced effect on T_m at α = 180°. At a wind speed of 5.8 m/s, the maximum T_m occurs at row R8 for the configuration with γ = l/100, while this maximum value is significantly reduced when γ = l/200. Figure 8c and Figure 8d present the variations of T_d under 0° and 180° wind directions, respectively. For the configuration with γ = l/100, aerodynamic instability occurs to varying degrees in the first two windward rows, exhibiting a sudden increase in T_d with increasing wind speed. At a wind direction of α = 0°, the aerodynamic instability wind speed for both R1 and R2 is 5.8 m/s under the γ = l/100. Reducing the sag-to-span ratio decreases the torsional vibration amplitude during aerodynamic instability by 49% to 61.9% at the same wind speed, with the amplitude reduced to below 3.2°. Under α = 180°, the aerodynamic instability wind speed decreases to 4.0 m/s for the γ = l/100, indicating that the 180° wind direction is more susceptible to aerodynamic instability compared to 0°. Reducing the sag-to-span ratio to l/200 not only increases the critical wind speed for aerodynamic instability but also reduces the torsional amplitude during instability, thereby significantly enhancing structural safety. When the sag-to-span ratio is reduced from γ = l/100 to γ = l/200, the first windward row experiences reductions of 75.3% in T_m and 88.1% in T_d, while the second windward row shows a 79% reduction in T_m and a 77.4% reduction in T_d. The mitigating effect of reducing the sag-to-span ratio on wind-induced torsional vibration is more pronounced at α = 180°.

The cable-supported PV array with β = 5° exhibits a more gradual increase in torsional displacement response with wind speed across all rows. Under different wind directions and wind speeds, the torsional displacement response remains consistently smaller compared to the cable-supported PV array with β = 25°. As shown in Figure 8a,b, under both α = 0° and 180° conditions, reducing the tilt angle demonstrates a more pronounced effect in decreasing T_m at the first windward row of the array. In Figure 8c,d, for the configuration with β = 25° and γ = l/100, aerodynamic instability occurs in both the first and second windward rows under α = 0° and 180° wind directions. The onset wind speeds for this instability are 5.8 m/s and 4.6 m/s, respectively. However, reducing the tilt angle significantly increases the critical wind speed for aerodynamic instability in the cable-supported PV array, with no instability observed even at 5.8 m/s. Taking a wind speed of 5.2 m/s as an example, compared to the β = 25°, the array with β = 5° shows reductions of 19.4% in maximum T_m and 42.4% in maximum T_d at α = 0°. Under α = 180° conditions, the maximum T_m and T_d are reduced by 70.8% and 94.4%, respectively, compared to the β = 25°. The differences in displacement response between β = 25° and 5° are more pronounced at α = 180°.

4. Wind-Induced Interference Effects of Cable-Supported Photovoltaic Array

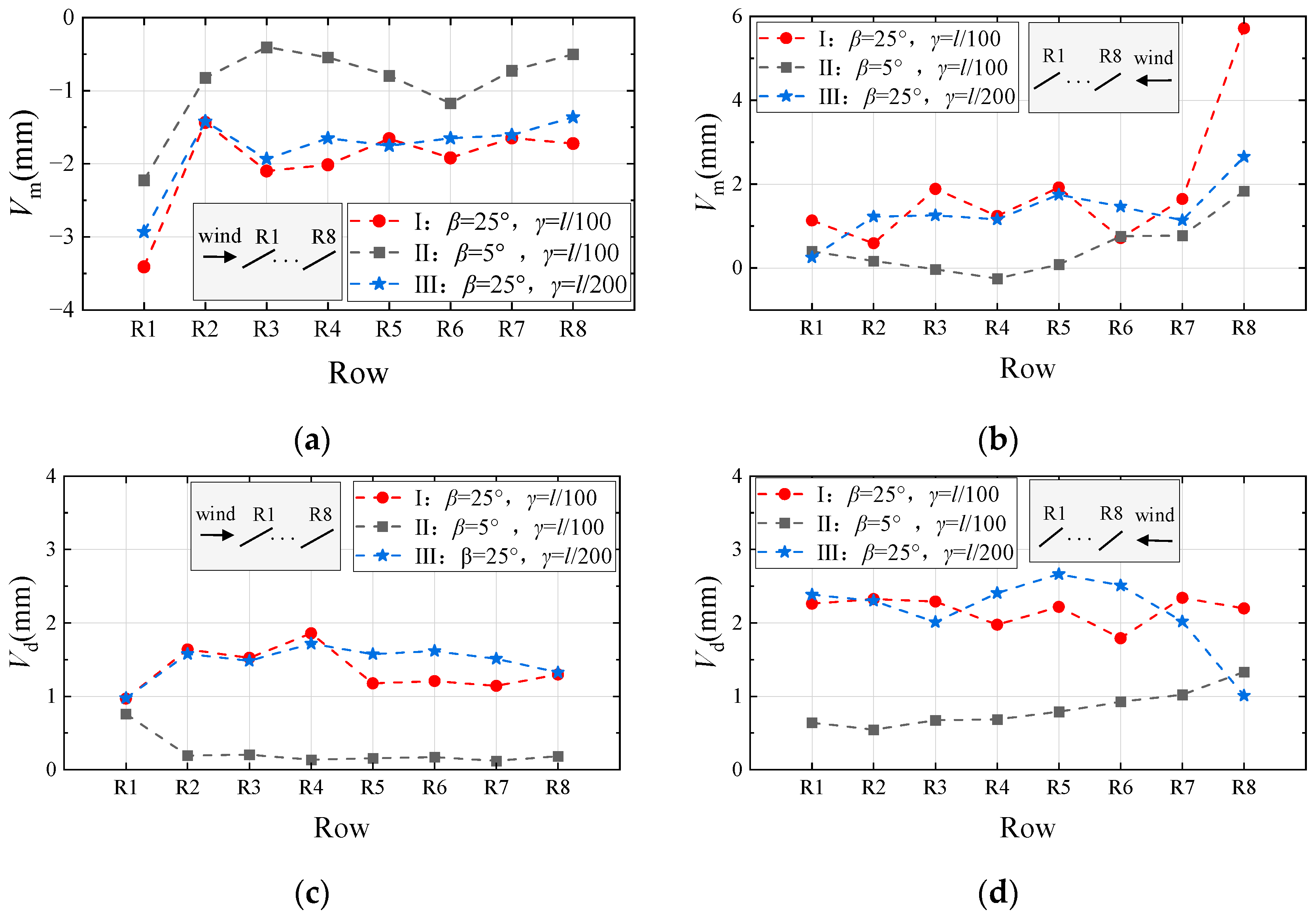
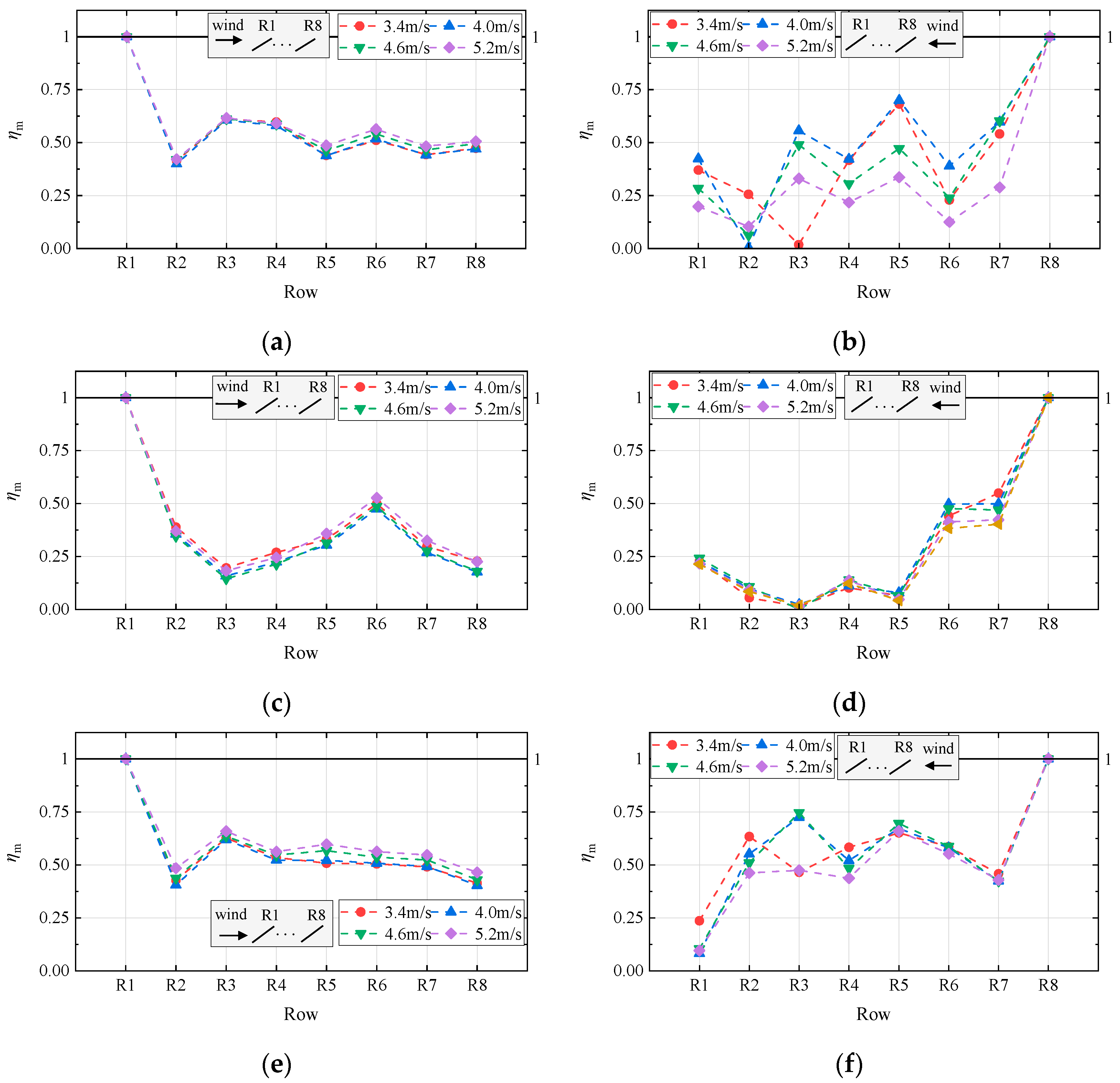
Having identified the wind-induced response characteristics of the cable-supported PV array, the mean and fluctuating components of the wind-induced vibration for each row at a wind speed of 5.2 m/s were extracted to further investigate the interference effects. Figure 9 shows the variation in vertical displacement response with array position under different test conditions. Across all configurations, the maximum V_m consistently occurs at the first windward row, followed by a substantial reduction at the second windward row. Under 0° wind direction, the reduction in V_m reaches 58.8% for Case I, 63.1% for Case II, and 48.5% for Case III. Similarly, under 180° wind direction, the corresponding reductions are 71.3%, 57.9%, and 57.0% for Cases I, II, and III, respectively. Thus, across all tested tilt angles and sag-to-span ratios, the interference effect of the front rows on the rear rows consistently manifests as a pronounced shielding effect on V_m. A comparison between Case I and Case III in Figure 9 reveals that reducing the sag-to-span ratio may lead to increased V_d values in the middle and rear sections of the array. The interference from front rows manifests as a more pronounced amplification of dynamic response in downstream rows. This phenomenon occurs because the reduced sag-to-span ratio, while increasing structural stiffness, subjects rear rows to more complex wake interference patterns. The enhanced structural stiffness may render rear rows more susceptible to excitation by specific frequencies present in the wake, consequently leading to amplified vibrations.

The interference effects in cable-supported PV arrays exhibit significantly different patterns in their influence on V_d depending on the module tilt angle. In Case II, the maximum V_d occurs at the first windward row, with the second windward row showing reductions of 75% and 22.6% under 0° and 180° wind directions, respectively. The rear windward rows consistently demonstrate lower V_d values than the first row. In contrast, Case I shows increases of 69.8% and 6.4% in V_d at the second row under 0° and 180° wind directions, with most rear rows exhibiting higher V_d values than the first windward row, where V_d generally remains the lowest in the array. This indicates that changes in tilt angle significantly alter the flow structures through the PV array, resulting in two distinct interference mechanisms governing the fluctuating response. For β = 5°, the consistent attenuation of both mean and fluctuating displacements along the downstream rows indicates the predominance of shielding effects. The wake generated by the front windward rows acts as a buffer, reducing the wind load intensity on the downstream supports. In contrast, for β = 25°, the significant amplification of fluctuating displacements from the second row onward reveals the dominance of wake excitation effects. The larger tilt angle promotes strong, periodic vortex shedding from the upstream panels. The second windward row, located directly within the impingement zone of these vortices, experiences enhanced forced vibration, creating potential risks for vortex-induced vibrations.

In summary, variations in the sag-to-span ratio exert minimal influence on the overall trend of interference effects within the array, whereas distinct patterns of interference mechanisms emerge across different module tilt angles. Specifically, under all tested configurations of tilt angle and sag-to-span ratio, the interference from front to rear rows consistently manifests as a shielding effect on V_m. However, for V_d, the interference characteristics diverge significantly: arrays with larger tilt angles exhibit an amplification effect from front to rear rows, whereas those with smaller tilt angles maintain a shielding effect on V_d.

Figure 10 presents the variation in torsional displacement response with position in the cable-supported PV array. The torsional displacement follows patterns generally consistent with those observed for vertical displacement. For the mean torsional displacement T_m, the interference from windward to downstream rows demonstrates a clear shielding effect. Changes in the sag-to-span ratio show negligible influence on the overall interference trend across the array. However, distinct mechanisms govern the fluctuating torsional displacement T_d: arrays with β = 25° exhibit an amplification effect from front to rear rows, while those with β = 5° maintain a shielding effect on T_d. In Case I under 180° wind direction, as shown in Figure 10d of this figure, the significantly higher T_d values observed at the first two windward rows R8 and R7 compared to downstream rows result from the occurrence of aerodynamic instability in these front rows.

Analysis of Figure 9 and Figure 10 reveals that the aerodynamic interference effects on the wind-induced response of the cable-supported PV array vary with module tilt angle and sag-to-span ratio. Unlike the consistent shielding effect observed in wind load studies where upstream panels protect downstream ones, the wind-induced vibration interference in cable-supported arrays does not uniformly manifest as shielding. It may also exhibit dynamic amplification effects. To further quantify the interference mechanism in the wind-induced vibration of cable-supported PV arrays, and with reference to the reduction factor defined in the literature [11], this study defines the positional interference coefficient η using Equations (3) and (4):

$${\eta }_{\mathrm{m}i}={\displaystyle \frac{V_{\mathrm{m}i}}{V_{\mathrm{m}1}}},$$

(3)

$${\eta }_{\mathrm{d}i}={\displaystyle \frac{V_{\mathrm{d}i}}{V_{\mathrm{d}1}}},$$

(4)

where V_mi represents the mean vertical displacement of the i-th windward row, V_m1 denotes the mean vertical displacement of the first windward row, η_mi is the positional interference coefficient of the i-th row based on mean vertical displacement; V_di indicates the fluctuating vertical displacement of the i-th windward row, V_d1 represents the fluctuating vertical displacement of the first windward row, and η_di is the positional interference coefficient of the i-th row based on fluctuating vertical displacement. In the wind-induced vibration analysis of cable-supported PV systems, both vertical and torsional displacements offer distinct advantages. This study adopts vertical displacement for defining the interference coefficient. Since the interference coefficient is derived from both mean and fluctuating components, vertical displacement provides a more accurate characterization of wind-induced response trends, while torsional displacement proves more suitable for investigating critical wind speed behavior.

In previous studies, research on interference coefficients has predominantly focused on wind loads, without accounting for the aeroelastic effects of cable-supported systems. The characteristics of wind-induced vibration interference may differ between mean and fluctuating. Studies on single-axis trackers have demonstrated significant shielding effects at the second and third windward rows [11], which aligns with observations for cable-supported systems. Figure 11 shows the variation of η_m with array position across test cases at wind speeds ranging from 3.4 m/s to 5.2 m/s. At the mean, a strong correlation exists between load and response interference effects, leading to consistent conclusions regarding the decreasing trend from windward to leeward rows [9]. The reduction coefficients η_m for the second to eighth windward rows all remain below unity. However, differences emerge in the downstream trend, which exhibits greater instability compared to wind-load-based reduction coefficients, particularly under 180° wind direction. This instability arises from increased flow complexity due to more intense wind-induced vibrations of the cable-supported system at this wind direction. Therefore, investigating load reduction can provide reasonable predictions for the attenuation of mean.

In Figure 11a,c, under 0° wind direction, the array with β = 25° exhibits the minimum reduction coefficient η_m at the second row, ranging between 0.40 and 0.42. For the β = 5° configuration, the minimum η_m occurs at the third row, with values between 0.14 and 0.20 across wind speeds. In Figure 11b,d, under 180° wind direction, the array with β = 25° displays a zigzag variation pattern of η_m along windward rows, indicating that the larger tilt angle induces more complex flow field disturbances. In contrast, the β = 5° array shows η_m values around 0.5 at the second and third windward rows, while downstream rows maintain relatively stable reduction coefficients, all below 0.25.

In Figure 11a,b,e,f, arrays sharing the same tilt angle but different sag-to-span ratios exhibit fundamentally consistent trends in η_m variation. The array with γ = l/200, being stiffer and having higher natural frequencies, demonstrates greater sensitivity to wind speed variations. It also shows improved shielding effects from front to rear rows. Under 0° wind direction, the downstream η_m trend remains more stable, displaying an initial increase followed by a gradual decrease from the second windward row backward. Although considerable variations persist between rows under 180° wind direction, similar to the 0° wind direction, the smallest η_m consistently occurs at the last windward row. This pattern confirms that the overall performance of the shielding effect in the array with γ = l/200 is superior to that of the γ = l/100.

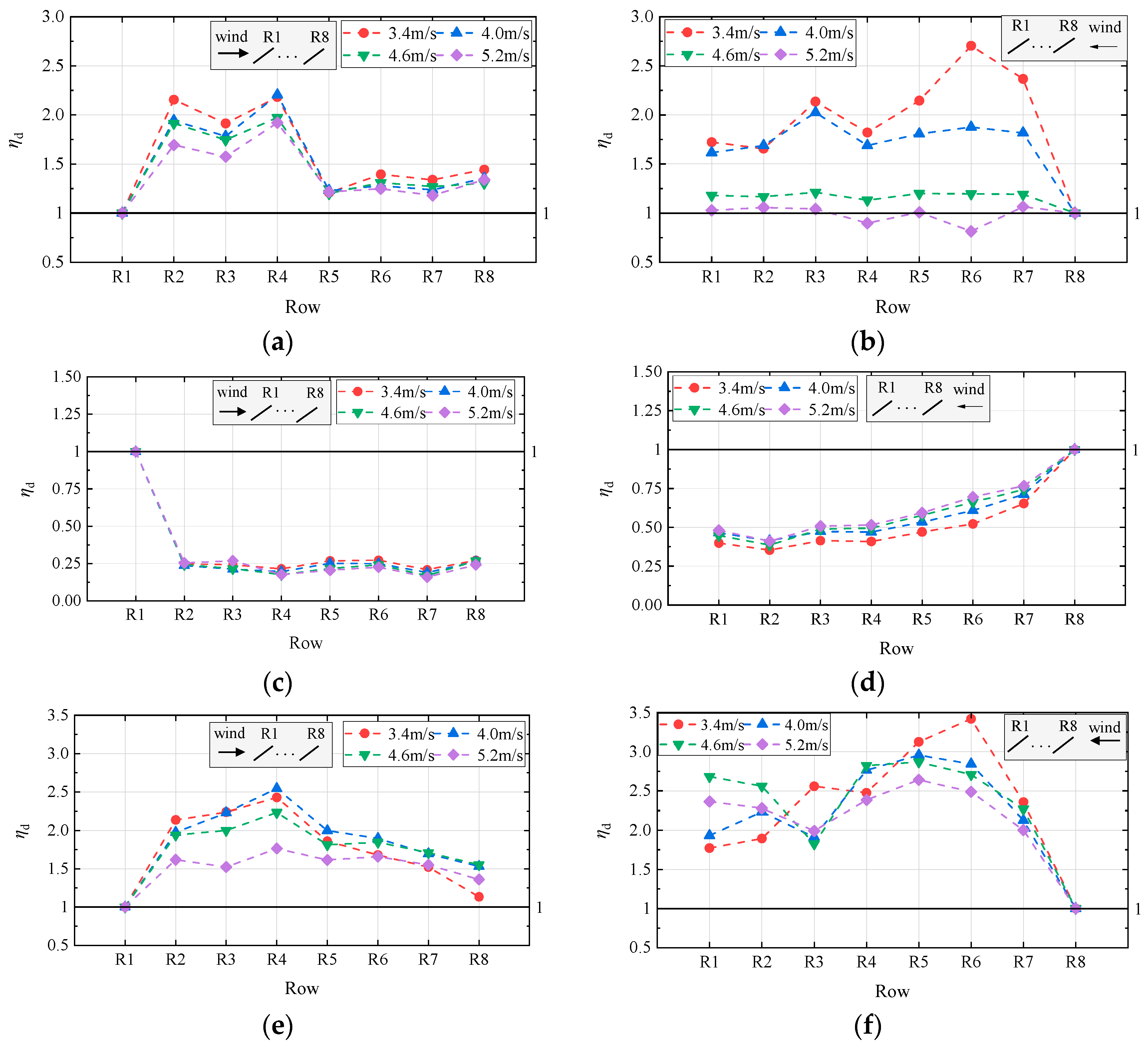
Figure 12 illustrates the variation of η_d with array position under different wind speeds. In Figure 12a,b,e,f, for the large-tilt-angle configuration within the wind speed range of 3.4–5.2 m/s, η_d decreases with increasing wind speed, indicating a weakening interference effect of front rows on the dynamic response of downstream rows. In Figure 12c,d, the arrays with small tilt angles show negligible variation in η_d across different wind speeds.

For the cable-supported PV array with β = 25° and γ = l/100, shown in Figure 12a,b, the interference coefficient η_d exhibits significant fluctuations in downstream rows. At lower wind speeds, the second to fourth windward rows experience strong wake effects from upstream rows, with η_d reaching values as high as 2.7. The spatial evolution of η_d from windward to leeward rows generally stabilizes after two complete cycles of initial increase followed by decrease, suggesting the development of a relatively uniform turbulent wake. In contrast, at higher wind speeds, η_d values decrease substantially and demonstrate a more stable progression along the array.

In Figure 12c,d, the variation trends of η_d differ significantly under different tilt angles. For the cable-supported PV array with β = 5° and γ = l/100, the interference from front to rear rows is pronounced and consistently manifests as a shielding effect. A substantial decrease in η_d is observed at the second windward row across wind speeds, with values ranging between 0.23~0.25 under 0° wind direction and 0.35~0.42 under 180° wind direction. Furthermore, the variation in η_d from the second to the last windward row remains relatively small under both wind directions: differences fall within 0.06~0.13 at 0° and 0.30~0.36 at 180°. In summary, the phenomenon of significant dynamic response in the central region of the array [14,21] occurs in configurations with large tilt angles rather than small ones. This behavior is attributed to vortex shedding from the first windward row, which induces notable fluctuations in the flow field across the central part of the array. Subsequently, the wake gradually stabilizes toward the downstream region of the array.

5. Conclusions

This study employed a full aeroelastic model wind tunnel test to investigate the wind-induced vibration characteristics of an eight-row cable-supported photovoltaic array. The research aimed to examine the wind-induced vibration patterns of cable-supported PV arrays and analyze the influence of tilt angle and sag-to-span ratio on their interference effects. The primary findings are summarized as follows:

• The cable-supported PV array exhibits coupled vertical and torsional vibrations under wind loads, with both vertical and torsional responses increasing with wind speed across all rows. The wind-induced vibration is significantly more intense at 180° wind direction compared to 0°. The most substantial vibration difference within the array occurs between the first and second windward rows. Consequently, if inter-row connections are implemented, particular attention should be paid to reinforcing the strength of connections between these first two rows.
• At both tested wind directions and across the measured wind speed range, the array with a 5° tilt angle exhibits smaller vertical and torsional vibrations, demonstrating a more gradual, monotonic increase with wind speed. In contrast, the 25° tilt angle array shows more pronounced differences in response between wind directions and significantly lowers the critical wind speed for aerodynamic instability, causing the structure to enter a hazardous state at substantially lower wind speeds. Reducing the sag-to-span ratio from γ = l/100 to γ = l/200 increases structural stiffness, resulting in a highly significant reduction in the mean components of both vertical and torsional displacements, with reductions exceeding 75% for the windward rows. Reducing the sag-to-span ratio also raises the critical wind speed for aerodynamic instability and dramatically reduces the vibration amplitude during instability events, decreasing torsional amplitude by more than 60%.
• The wind-induced vibration of cable-supported PV arrays exhibits significant interference effects. For the mean vibration, this manifests as a consistent shielding effect, with vibration amplitudes decreasing progressively from windward to leeward rows. The interference coefficient for the mean vibration remains below unity from the second to the eighth windward rows. Based on the experimental results, a value of 0.8 is recommended for the interference coefficient pertaining to the mean wind-induced vibration.
• For the fluctuating component of wind-induced vibration, the interference effect is predominantly governed by the tilt angle. In cable-supported PV arrays with a 5° tilt angle, the interference manifests as a shielding effect. Conversely, arrays with a 25° tilt angle exhibit an amplification effect. This amplification typically follows a periodic pattern along the array, initially increasing then decreasing from the windward to leeward rows, though these fluctuations tend to stabilize at higher wind speeds. As wind speed increases, the interference coefficient for the 25° tilt configuration decreases and its spatial variation along the array becomes more gradual. In contrast, the interference coefficient for the 5° tilt array shows minimal sensitivity to wind speed variations. While reducing the sag-to-span ratio most effectively suppresses vibrations in the first windward row, resulting in an increased interference coefficient, it does not alter the fundamental trends determined by the tilt angle.