Stability and Design Charts for 3D Rectangular Cavity Crowns with Limited Buried Depth in Rock Masses
Abstract
1. Introduction
2. The Generalized Hoek–Brown (GHB) Strength Criterion
3. Stability Analysis for 3D Shallow-Buried Rectangular Cavities
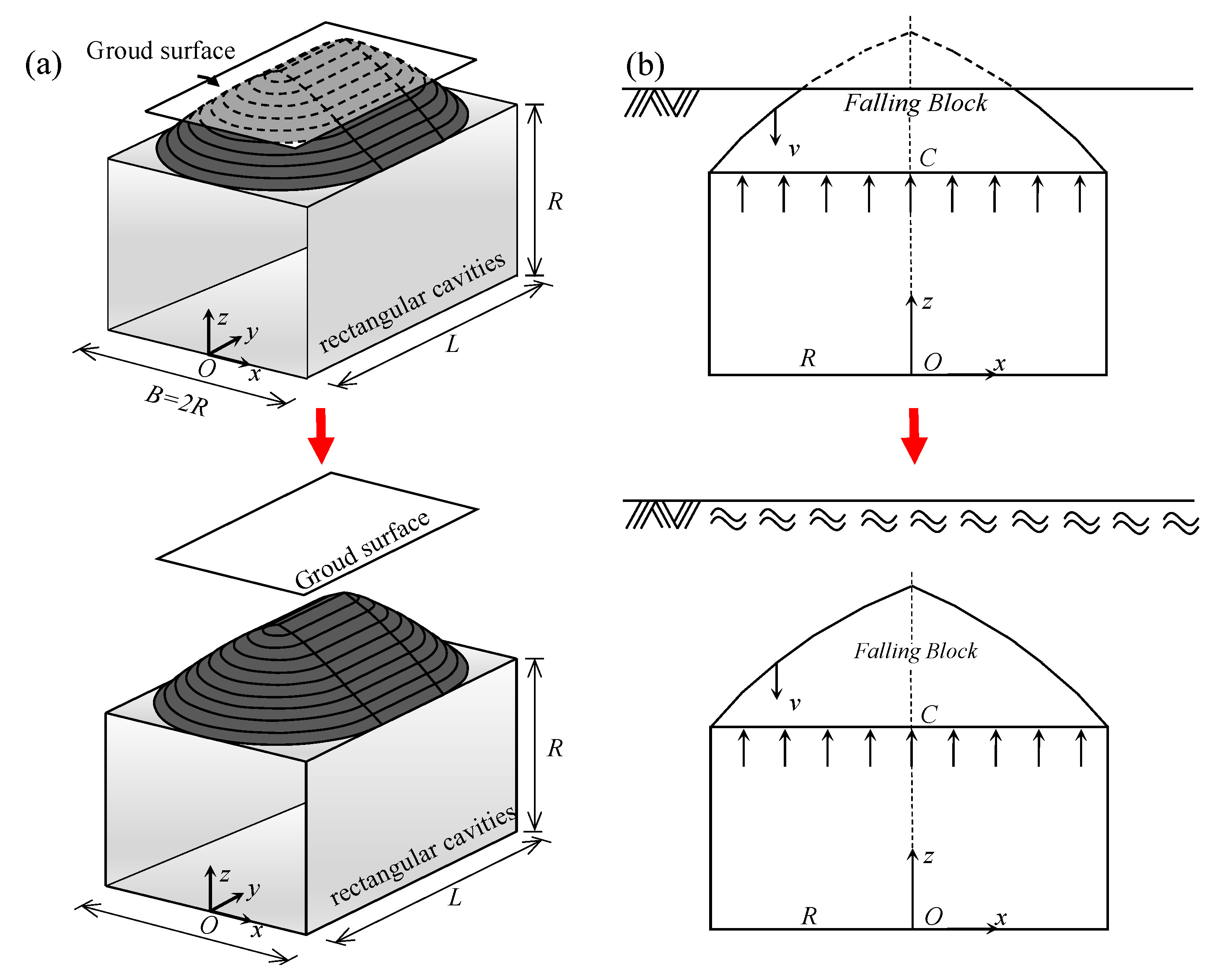
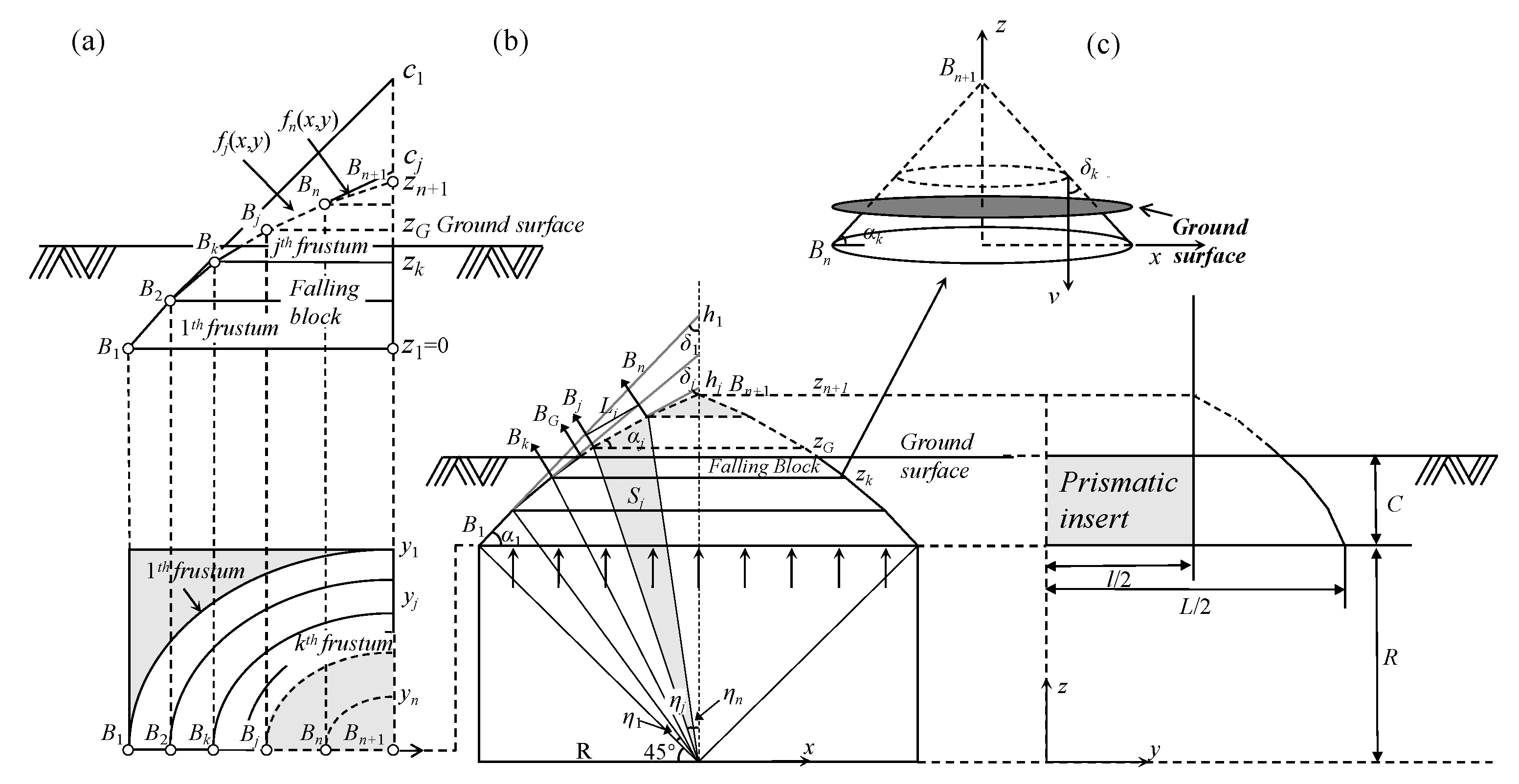
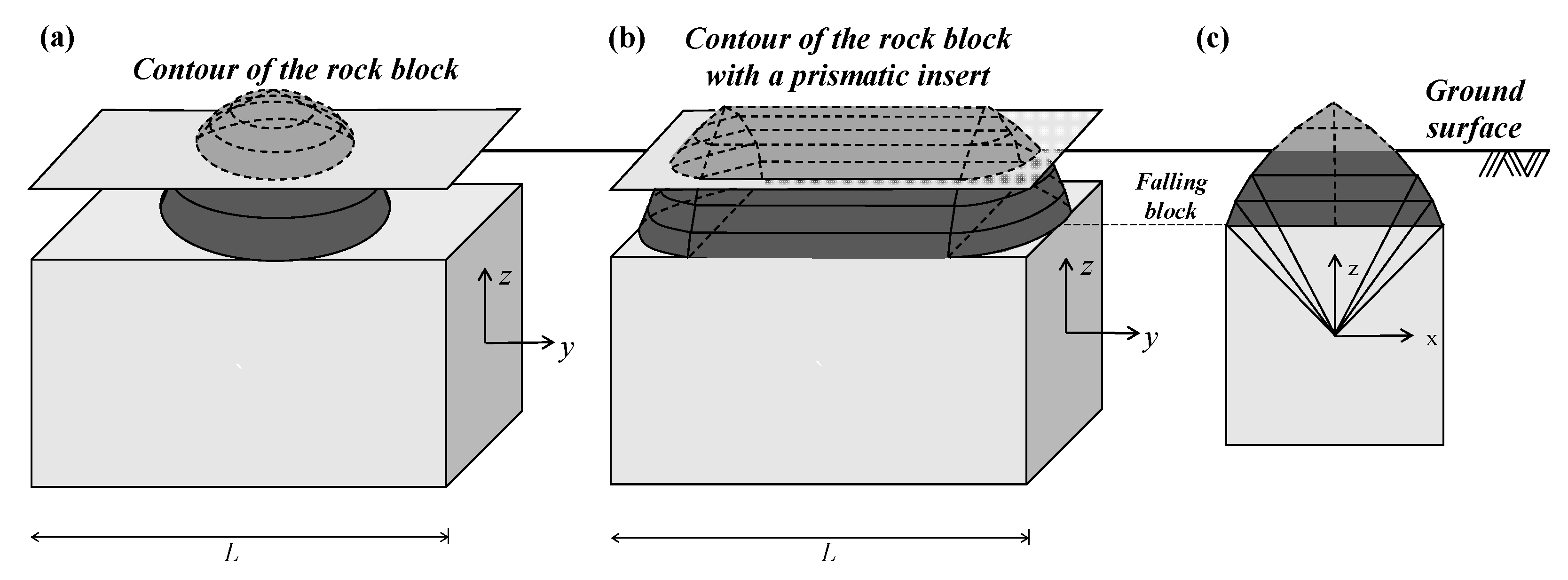
3.1. Collapse Mechanism of 3D Shallow-Buried Rectangular Cavities
3.2. Stability Measures for a Shallow-Buried Cavity Crown
3.2.1. The Stability Number
3.2.2. The FoS Solution
3.2.3. The Required Supporting Pressure
3.3. Objective Optimization
4. Numerical Solutions
5. Parametric Analysis and Design Charts
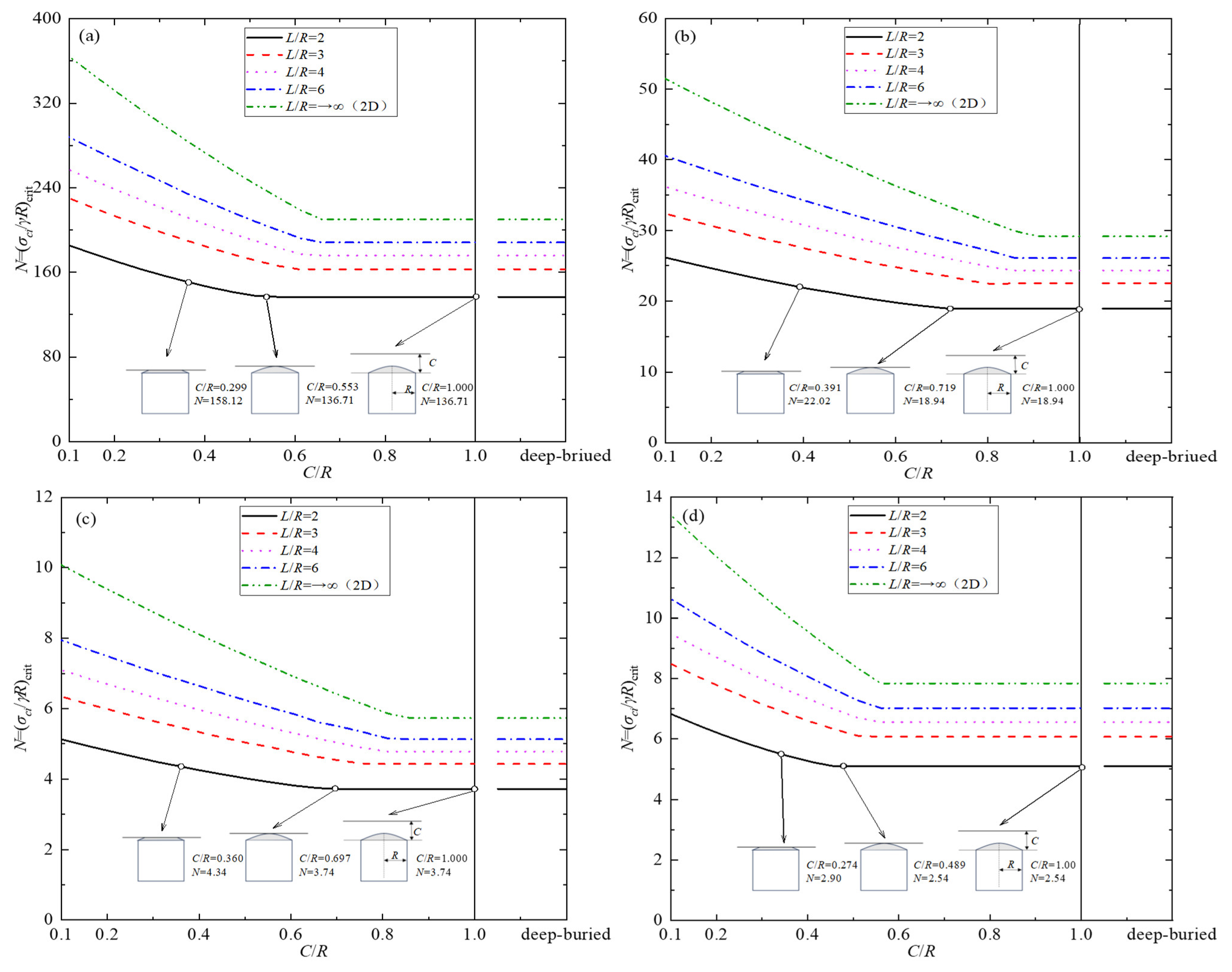
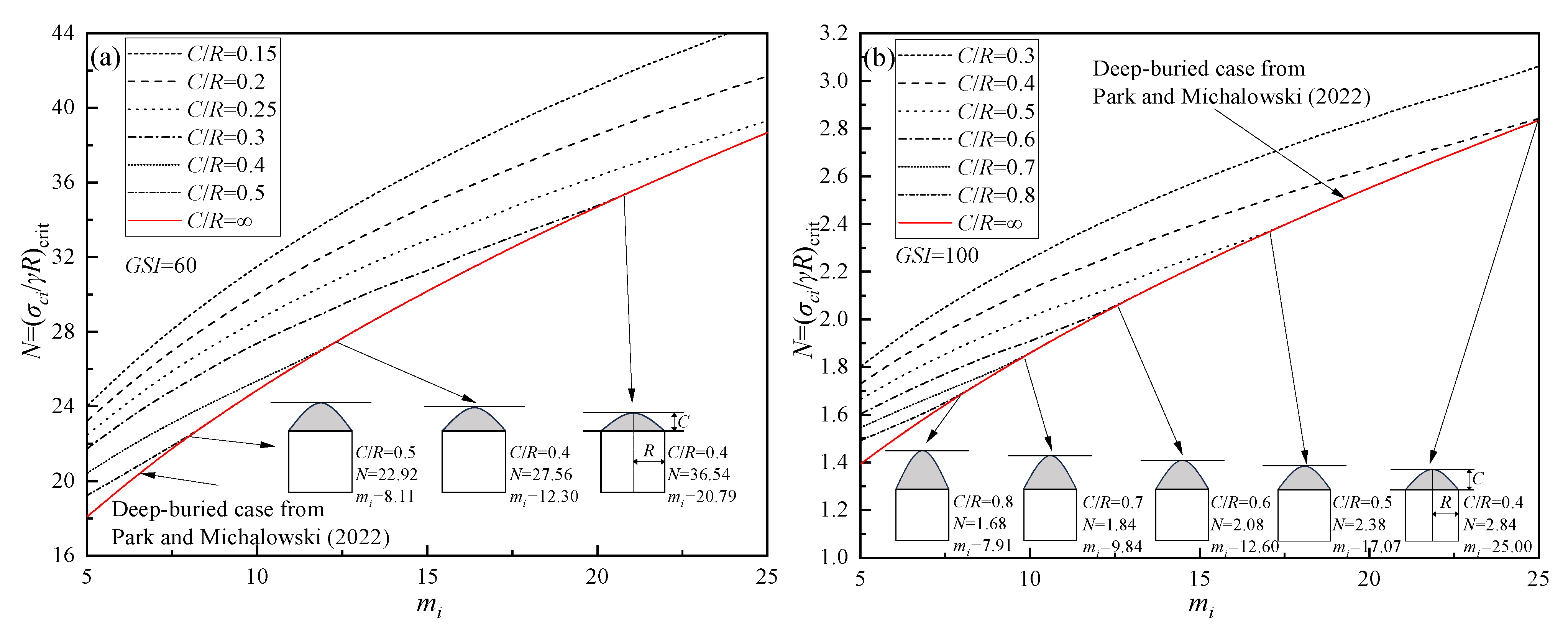
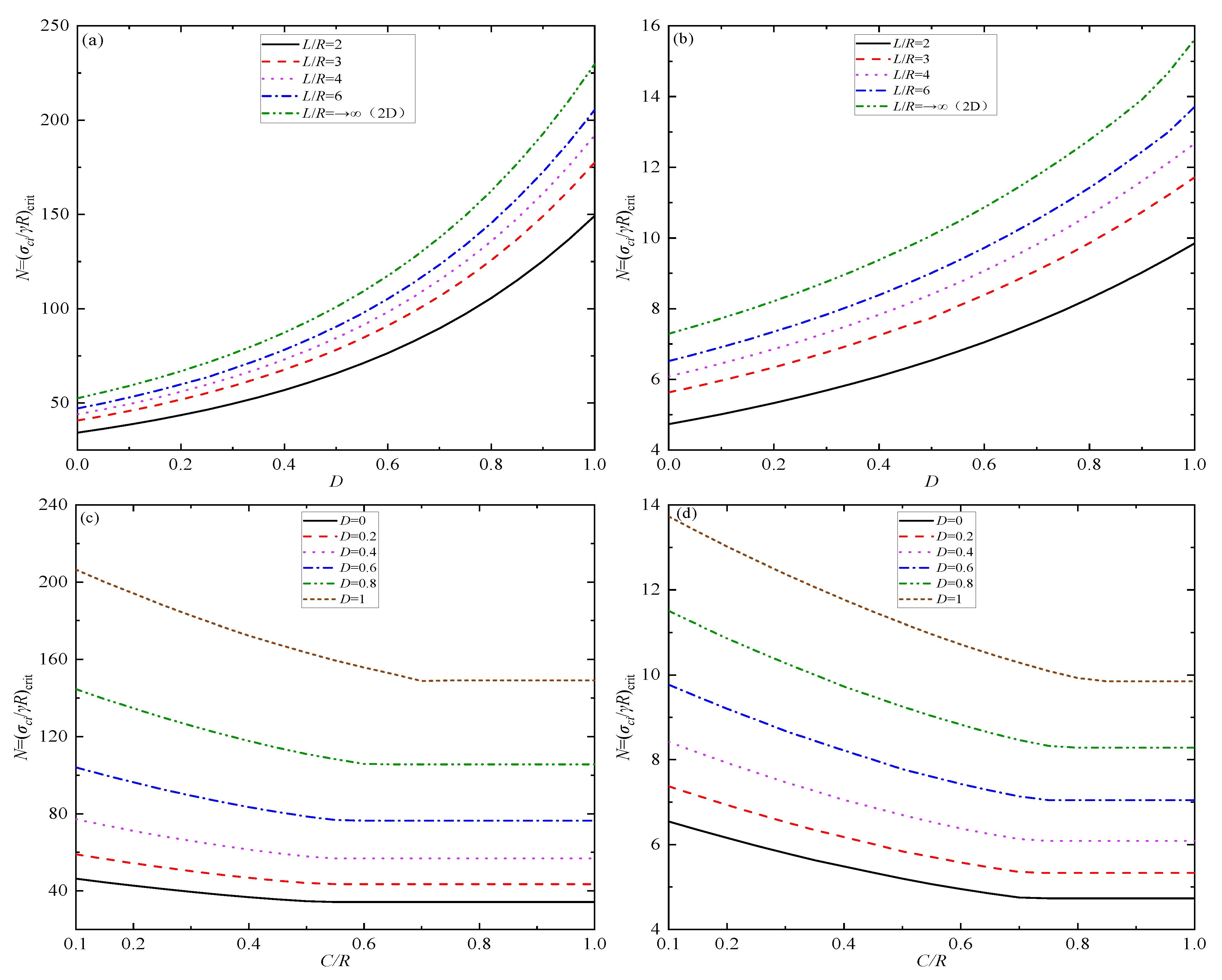
5.1. Stability Number
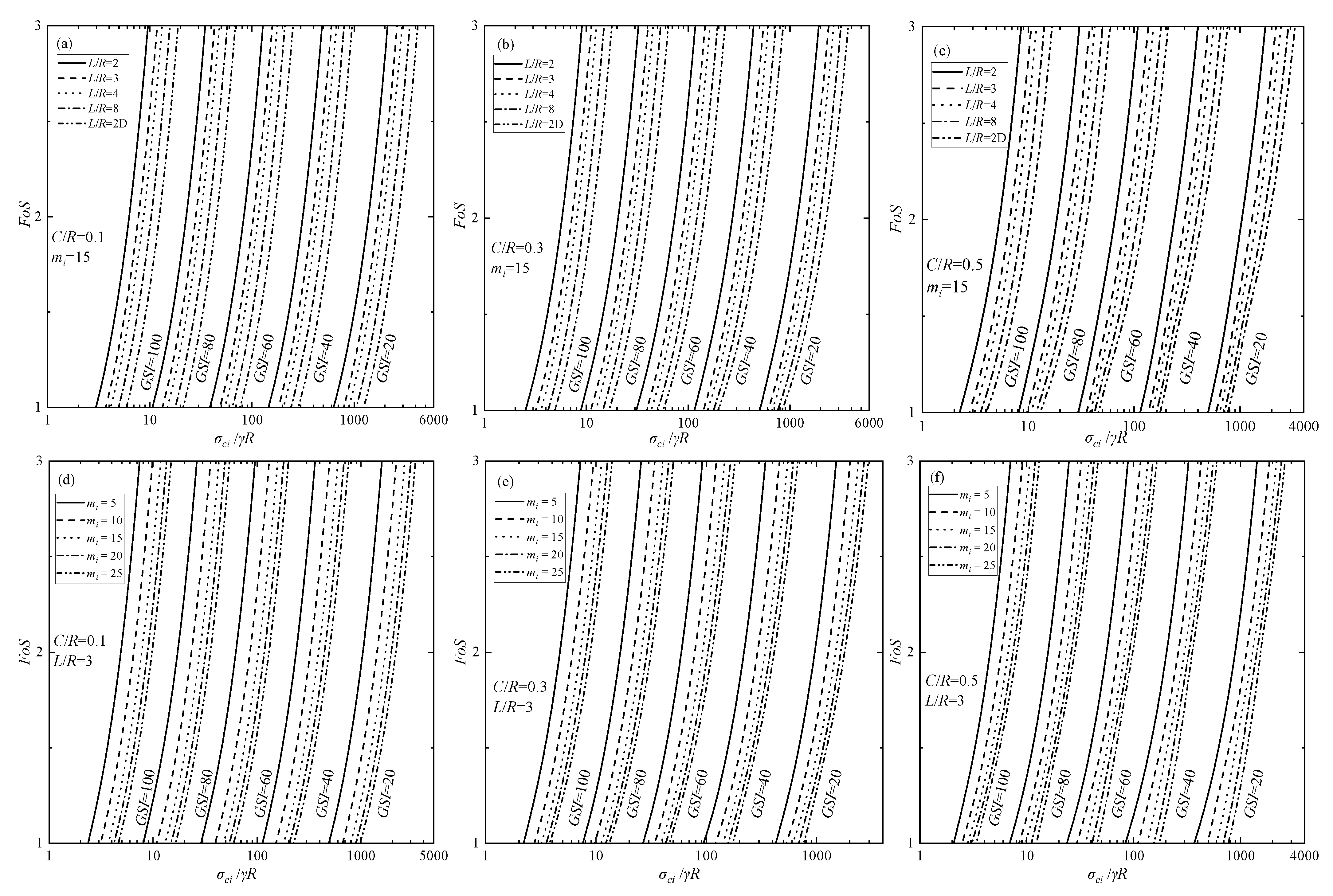
5.2. FoS Solutions
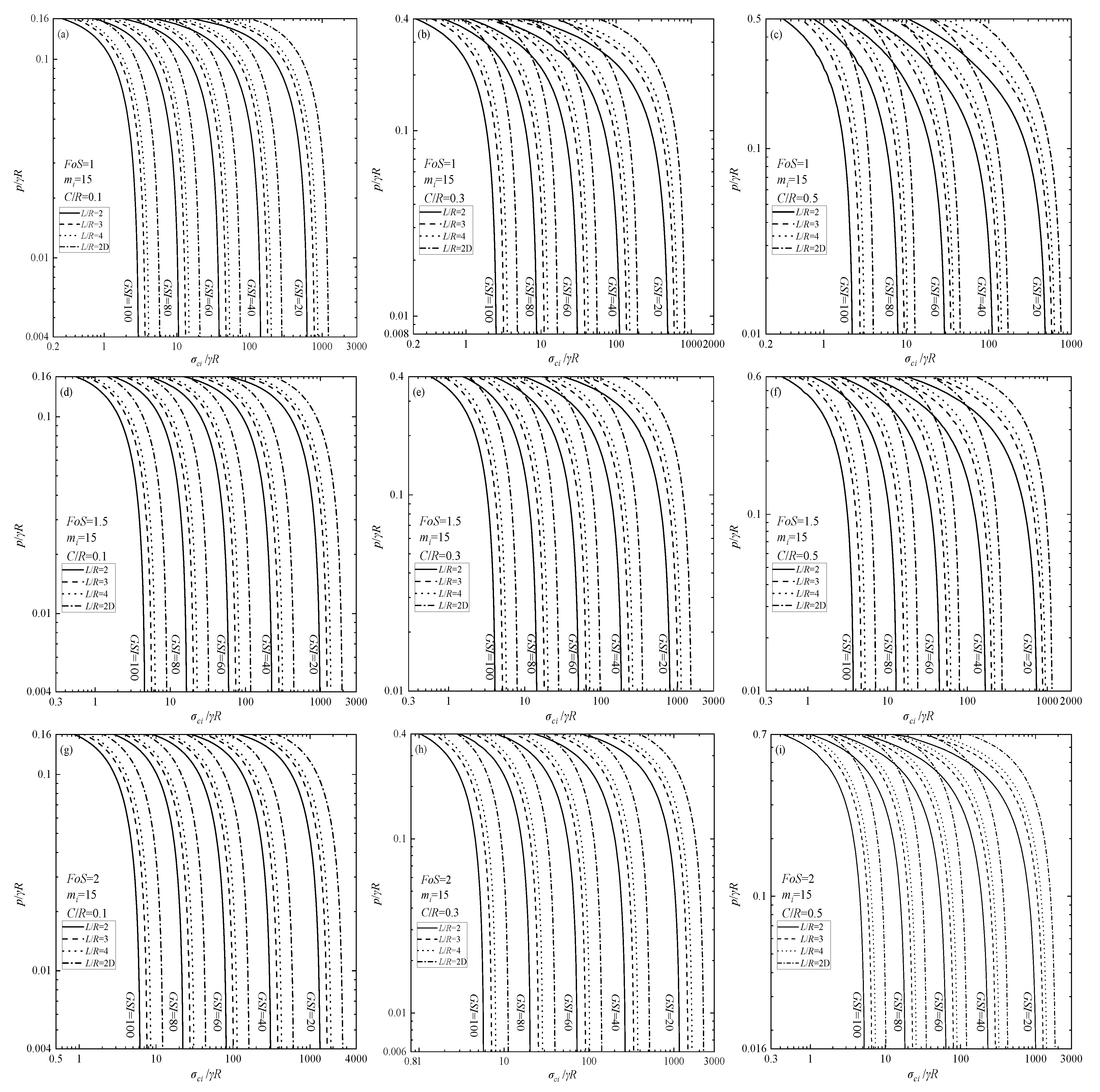
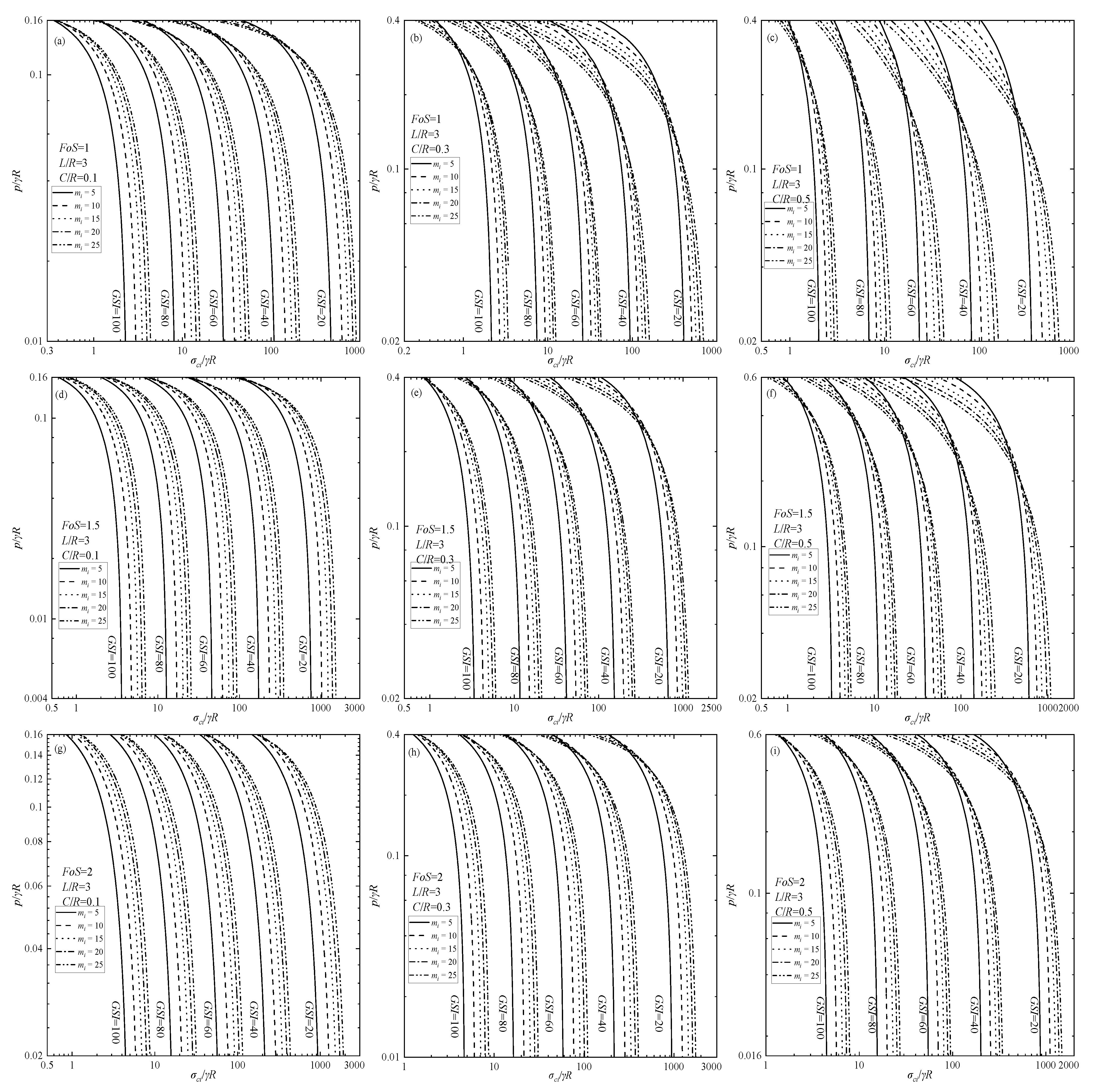
5.3. Required Supporting Pressure
5.4. Application Example
- (1)
- Application Examples for the FoS Design Charts
- (2)
- Application Examples for the Required Supporting Pressure Charts
6. Conclusions
- (1)
- The increases in the buried depth ratio C/R and the strength index GSI have significant beneficial effects on the stability of cavity crowns by reducing the stability number, while increases in mi and L/R weaken this stability by increasing the stability number. Once C/R reaches the critical buried depth, the cavity crown transitions to a deeply buried case; further increases in C/R will no longer impact the stability of the cavity crowns.
- (2)
- From a FoS perspective, increases in mi and L/R are poised to result in a reduction in the FoS for the cavity crowns. Conversely, the increases in C/R and GSI can improve the stability of the cavity crown, indicating that the crown of a shallowly buried cavity exhibits worse stability compared to that of a deeply buried one.
- (3)
- From the required supporting pressure, it can be seen that the increase in L/R will obviously reduce the crown stability by increasing the required supporting pressures. The increase in the dimensionless index σci/γR not only results in an opposite trend in the required supporting pressure, but also affects the mode of influence of mi on the required supporting pressure. The required supporting pressure decreases with the increase of mi under a smaller σci/γR. On the contrary, as σci/γR increases, the required supporting pressure increases with the increase of mi.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of Symbols | |||
| σn | The normal stress | σ1 | Major effective principal stress |
| τ | The shear stress | σ3 | Minor effective principal stress |
| δ | The fracture angle | mb | Hoek–Brown constant for rock mass |
| σci | The uniaxial compressive strength of the rock | a | Hoek–Brown constant for rock mass |
| GSI | The Geological Strength Index | S | Lateral surface area of a right cone |
| mi | Contingent upon the rock type | σt | Isotropic tensile strength |
| D | The disturbance parameter | ft | Reduced tensile strength |
| λ | Ratio of the minor axis to the major axis of an ellipse | d | The energy dissipation per unit area on the collapse surface |
| v | The velocity change vector | Lj | Length of the generatrix of the jth cone |
| αj | Inclination angle of jth generatrix | Wp | The rate of work performed by the supporting pressure |
| η | Independent variable angle | N | The stability number |
| p | Supporting pressure | FoS | Factor of safety |
| W | The external power | τd | Demand on shear strength needed for the limit equilibrium |
| Dint | The internal dissipation power | σnd | The normal stress |
| γ | The unit weight of the rock mass | C | The burial depth |
| K | Symbols for rectangular cavities | L | Cavity excavation width |
| s | Hoek–Brown constant for rock mass | Wγ | Rate of work performed by unit weight of geomaterials |
| The boundary in limit analysis | The strain rate | ||
| The volume in the limit analysis | The stress | ||
Appendix A
References
- Fraldi, M.; Guarracino, F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections. Int. J. Solids Struct. 2010, 47, 216–223. [Google Scholar] [CrossRef]
- Qin, C.; Chian, S.C.; Yang, X. 3D limit analysis of progressive collapse in partly weathered Hoek–Brown rock banks. Int. J. Geomech. 2017, 17, 04017011. [Google Scholar] [CrossRef]
- Qin, C.; Li, Y.; Yu, J.; Chian, S.C.; Liu, H. Closed-form solutions for collapse mechanisms of tunnel crown in saturated non-uniform rock surrounds. Tunn. Undergr. Space Technol. 2022, 126, 104529. [Google Scholar] [CrossRef]
- Yu, L.; Lyu, C.; Wang, M.; Xu, T. Three-dimensional upper bound limit analysis of a deep soil-tunnel subjected to pore pressure based on the nonlinear Mohr-Coulomb criterion. Comput. Geotech. 2019, 112, 293–301. [Google Scholar] [CrossRef]
- Yang, X.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Fraldi, M.; Cavuoto, R.; Cutolo, A.; Guarracino, F. Stability of tunnels according to depth and variability of rock mass parameters. Int. J. Rock Mech. Min. Sci. 2019, 19, 222–229. [Google Scholar] [CrossRef]
- Liang, J.; Cui, J.; Lu, Y.; Li, Y.; Shan, Y. Limit analysis of shallow tunnels collapse problem with optimized solution. Appl. Math. Model. 2022, 109, 98–116. [Google Scholar] [CrossRef]
- Park, D.; Michalowski, R.L. Roof stability in deep rock tunnels. Int. J. Rock Mech. Min. Sci. 2019, 124, 104139. [Google Scholar] [CrossRef]
- Park, D.; Michalowski, R.L. Roof stability in flat-ceiling deep rock cavities and tunnels. Eng. Geol. 2022, 303, 106651. [Google Scholar] [CrossRef]
- Fraldi, M.; Guarracino, F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek–Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2009, 46, 665–673. [Google Scholar] [CrossRef]
- Yang, X.; Huang, F. Three-dimensional failure mechanism of a rectangular cavity in a Hoek–Brown rock medium. Int. J. Rock Mech. Min. Sci. 2013, 61, 189–195. [Google Scholar] [CrossRef]
- Xu, J.S.; Wang, X.R.; Du, X.L. Seismic active earth pressure for 3D earth retaining structure following a nonlinear failure criterion. Comput. Geotech. 2024, 165, 105902. [Google Scholar] [CrossRef]
- Qin, C.; Zhou, J. On the seismic stability of soil slopes containing dual weak layers: True failure load assessment by finite-element limit-analysis. Acta Geotech. 2023, 18, 3153–3175. [Google Scholar] [CrossRef]
- Qin, C.; Li, Y.; Shi, Y.; Dai, C.; Zhang, W. On the dynamic stability of tunnel roof in nonuniform rock/soils characterized by nonlinear Mohr envelope. Tunn. Undergr. Space Technol. 2024, 145, 105490. [Google Scholar] [CrossRef]
- Huang, F.; Yang, X.; Ling, T. Prediction of collapsing region above deep spherical cavity roof under axis-symmetrical conditions. Rock Mech. Rock Eng. 2014, 47, 1511–1516. [Google Scholar] [CrossRef]
- Fraldi, M.; Guarracino, F. Limit analysis of progressive tunnel failure of tunnels in Hoek-Brown rock masses. Int. J. Rock Mech. Min. Sci. 2022, 50, 170–173. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Empirical strength criterion for rock masses. J. Geotech. Eng. Div. 1980, 106, 1013–1035. [Google Scholar] [CrossRef]
- Hoek, E.; Carranza-Torres, C.T.; Corkum, B. Hoek-Brown failure criterion–2002 edition. Geotech. Eng. 2022, 19, 26–38. [Google Scholar]

| L/R | mi | C/R | Solutions | GSI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | Error | 40 | Error | 60 | Error | 80 | Error | 100 | Error | ||||
| 2 | 5 | 0.1 | Present research | 404.74 | 32.7% | 92.66 | 32.7% | 24.86 | 34.2% | 6.92 | 35.7% | 1.96 | 36.1% |
| 0.3 | 341.69 | 12.1% | 78.95 | 13.0% | 21.74 | 17.4% | 6.22 | 22.0% | 1.80 | 25.0% | |||
| 0.5 | 300.00 | 1.6% | 69.22 | 0.1% | 19.22 | 3.8% | 5.62 | 10.2% | 1.66 | 15.3% | |||
| Deep-buried | 299.62 | 1.6% | 68.38 | 2.1% | 18.10 | 2.3% | 4.98 | 2.4% | 1.40 | 2.7% | |||
| Park and Michalowski [9] | 304.80 | 69.84 | 18.52 | 5.10 | 1.44 | ||||||||
| 15 | 0.1 | Present research | 638.86 | 24.3% | 146.38 | 24.3% | 39.24 | 27.3% | 10.86 | 30.0% | 3.02 | 32.4% | |
| 0.3 | 506.27 | 1.5% | 115.26 | 2.1% | 31.26 | 1.4% | 8.97 | 6.5% | 2.58 | 13.2% | |||
| 0.5 | 506.54 | 1.5% | 115.32 | 2.0% | 30.18 | 2.1% | 8.18 | 1.7% | 2.26 | 0.8% | |||
| Deep-buried | 506.54 | 1.5% | 115.32 | 2.0% | 30.18 | 2.1% | 8.18 | 1.7% | 2.24 | 1.7% | |||
| Park and Michalowski [9] | 514.00 | 117.72 | 30.82 | 8.42 | 2.28 | ||||||||
| 25 | 0.1 | Present research | 783.90 | 18.7% | 179.72 | 19.2% | 48.42 | 22.2% | 13.44 | 26.3% | 3.74 | 30.0% | |
| 0.3 | 650.40 | 1.5% | 147.99 | 1.8% | 38.68 | 1.9% | 10.64 | 0.0% | 3.06 | 5.5% | |||
| 0.5 | 650.76 | 1.4% | 148.08 | 1.7% | 38.70 | 1.9% | 10.44 | 1.9% | 2.84 | 2.9% | |||
| Deep-buried | 650.76 | 1.4% | 148.08 | 1.7% | 38.70 | 1.9% | 10.44 | 1.9% | 2.84 | 2.9% | |||
| Park and Michalowski [9] | 660.30 | 150.76 | 39.44 | 10.64 | 2.90 | ||||||||
| 3 | 5 | 0.1 | Present research | 502.78 | 40.5% | 108.94 | 33.0% | 30.78 | 41.6% | 8.56 | 42.7% | 2.42 | 44.6% |
| 0.3 | 430.02 | 20.2% | 99.20 | 21.1% | 27.22 | 25.2% | 7.76 | 29.3% | 2.24 | 33.3% | |||
| 0.5 | 371.46 | 3.8% | 86.28 | 5.3% | 24.22 | 11.4% | 7.06 | 17.7% | 2.08 | 23.8% | |||
| Deep-buried | 356.32 | 0.4% | 81.32 | 0.8% | 21.52 | 1.0% | 5.96 | 0.6% | 1.66 | 1.2% | |||
| Park and Michalowski [9] | 357.76 | 81.94 | 21.74 | 6.00 | 1.68 | ||||||||
| 15 | 0.1 | Present research | 799.62 | 32.3% | 182.88 | 32.7% | 48.92 | 35.4% | 13.50 | 176.1% | 3.76 | 40.3% | |
| 0.3 | 612.43 | 1.3% | 141.72 | 2.9% | 39.30 | 8.7% | 11.28 | 130.7% | 3.25 | 21.3% | |||
| 0.5 | 600.60 | 0.7% | 137.16 | 0.5% | 35.92 | 0.5% | 9.72 | 98.8% | 2.82 | 5.2% | |||
| Deep-buried | 600.60 | 0.7% | 137.16 | 0.5% | 35.92 | 0.5% | 4.87 | 0.4% | 2.66 | 0.7% | |||
| Park and Michalowski [9] | 604.58 | 137.80 | 36.14 | 4.89 | 2.68 | ||||||||
| 25 | 0.1 | Present research | 984.86 | 26.8% | 225.68 | 27.6% | 60.60 | 20.0% | 16.78 | 34.5% | 4.66 | 37.2% | |
| 0.3 | 774.01 | 0.3% | 176.11 | 0.4% | 46.15 | 1.0% | 13.30 | 6.6% | 3.85 | 13.2% | |||
| 0.5 | 774.00 | 0.3% | 176.12 | 0.4% | 45.02 | 3.4% | 12.40 | 0.6% | 3.38 | 0.6% | |||
| Deep-buried | 774.00 | 0.3% | 176.12 | 0.4% | 46.02 | 0.6% | 12.40 | 0.6% | 3.38 | 0.6% | |||
| Park and Michalowski [9] | 776.68 | 176.88 | 46.26 | 12.48 | 3.40 | ||||||||
| 2D | 5 | 0.1 | Present research | 795.66 | 72.6% | 182.08 | 72.3% | 48.84 | 74.2% | 13.62 | 76.0% | 3.86 | 77.1% |
| 0.3 | 650.96 | 41.2% | 150.96 | 42.8% | 42.00 | 49.8% | 12.11 | 56.5% | 3.52 | 62.5% | |||
| 0.5 | 522.06 | 13.3% | 123.30 | 16.7% | 35.78 | 27.6% | 10.72 | 38.6% | 3.22 | 47.7% | |||
| Deep-buried | 458.92 | 0.4% | 105.00 | 0.7% | 27.84 | 0.7% | 7.68 | 0.8% | 2.16 | 0.9% | |||
| Park and Michalowski [9] | 460.88 | 105.70 | 28.04 | 7.74 | 2.18 | ||||||||
| 15 | 0.1 | Present research | 1246.62 | 60.3% | 285.46 | 143.0% | 76.78 | 64.6% | 21.32 | 68.9% | 5.94 | 71.7% | |
| 0.3 | 837.37 | 7.67% | 197.53 | 69.2% | 57.06 | 22.3% | 16.84 | 33.4% | 4.94 | 42.8% | |||
| 0.5 | 774.68 | 0.4% | 176.74 | 0.4% | 46.34 | 0.6% | 13.00 | 3.0% | 4.06 | 17.3% | |||
| Deep-buried | 774.66 | 0.4% | 176.74 | 0.4% | 46.34 | 0.6% | 12.54 | 0.6% | 3.44 | 0.6% | |||
| Park and Michalowski [9] | 777.70 | 177.46 | 46.64 | 12.62 | 3.46 | ||||||||
| 25 | 0.1 | Present research | 1517.06 | 52.5% | 348.54 | 44.8% | 94.34 | 59.0% | 26.26 | 64.1% | 7.34 | 68.3% | |
| 0.3 | 994.89 | 0.1% | 226.85 | 0.4% | 62.61 | 5.5% | 19.07 | 19.2% | 5.71 | 31.0% | |||
| 0.5 | 998.72 | 0.4% | 228.28 | 0.6% | 59.72 | 0.7% | 16.10 | 0.6% | 4.38 | 0.5% | |||
| Deep-buried | 998.72 | 0.4% | 228.28 | 0.6% | 59.72 | 0.7% | 16.10 | 0.6% | 4.38 | 0.5% | |||
| Park and Michalowski [9] | 994.88 | 226.84 | 59.32 | 16.00 | 4.36 | ||||||||
| σci/γR | GSI | mi | C/R | Solutions | L/R | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | Error | 3 | Error | 4 | Error | 2D | Error | |||||
| 1000 | 20 | 5 | 0.1 | Present research | 2.35 | 29.4% | 1.92 | 31.4% | 1.72 | 33.6% | 1.24 | 42.9% |
| 0.3 | 2.51 | 24.6% | 2.06 | 26.4% | 1.86 | 28.2% | 1.40 | 35.5% | ||||
| 0.5 | 2.67 | 19.8% | 2.20 | 21.4% | 2.00 | 22.8% | 1.57 | 27.7% | ||||
| Deep-buried | 3.34 | 0.3% | 2.81 | 0.4% | 2.60 | 0.4% | 2.18 | 0.5% | ||||
| Park and Michalowski [9] | 3.33 | 2.80 | 2.59 | 2.17 | ||||||||
| 15 | 0.1 | Present research | 1.49 | 24.4% | 1.22 | 26.1% | 1.10 | 28.1% | 0.83 | 35.2% | ||
| 0.3 | 1.74 | 11.7% | 1.45 | 12.1% | 1.34 | 12.4% | 1.12 | 12.5% | ||||
| 0.5 | 1.94 | 1.5% | 1.64 | 0.6% | 1.54 | 0.7% | 1.29 | 0.8% | ||||
| Deep-buried | 1.97 | 0.0% | 1.67 | 1.2% | 1.54 | 0.7% | 1.29 | 0.8% | ||||
| Park and Michalowski [9] | 1.97 | 1.65 | 1.53 | 1.28 | ||||||||
| 25 | 0.1 | Present research | 1.23 | 19.6% | 1.01 | 21.7% | 0.92 | 22.7% | 0.72 | 28.0% | ||
| 0.3 | 1.51 | 1.3% | 1.28 | 0.8% | 1.20 | 0.8% | 1.01 | 1.0% | ||||
| 0.5 | 1.54 | 0.7% | 1.29 | 0.0% | 1.20 | 0.8% | 1.01 | 1.0% | ||||
| Deep-buried | 1.54 | 0.7% | 1.29 | 0.0% | 1.20 | 0.8% | 1.01 | 1.0% | ||||
| Park and Michalowski [9] | 1.53 | 1.29 | 1.19 | 1.00 | ||||||||
| 40 | 60 | 5 | 0.1 | Present research | 1.57 | 28.6% | 1.28 | 30.8% | 1.15 | 32.7% | 0.83 | 42.0% |
| 0.3 | 1.70 | 22.7% | 1.40 | 24.3% | 1.26 | 26.3% | 0.96 | 32.9% | ||||
| 0.5 | 1.81 | 17.7 | 1.50 | 18.9% | 1.37 | 19.9% | 1.08 | 24.5% | ||||
| Deep-buried | 2.22 | 0.9% | 1.86 | 0.5% | 1.72 | 0.6% | 1.44 | 0.7% | ||||
| Park and Michalowski [9] | 2.20 | 1.85 | 1.71 | 1.43 | ||||||||
| 15 | 0.1 | Present research | 1.02 | 22.7% | 0.84 | 24.3% | 0.76 | 26.2% | 0.58 | 32.6% | ||
| 0.3 | 1.21 | 8.3% | 1.01 | 9.0% | 0.94 | 8.7% | 0.80 | 7.0% | ||||
| 0.5 | 1.33 | 0.8% | 1.11 | 0.0% | 1.03 | 0.0% | 0.86 | 0.0% | ||||
| Deep-buried | 1.32 | 0.0% | 1.11 | 0.0% | 1.03 | 0.0% | 0.86 | 0.0% | ||||
| Park and Michalowski [9] | 1.32 | 1.11 | 1.03 | 0.86 | ||||||||
| 25 | 0.1 | Present research | 0.85 | 17.5% | 0.70 | 19.5% | 0.64 | 21.0% | 0.51 | 25% | ||
| 0.3 | 1.03 | 0.0% | 0.87 | 0.0% | 0.81 | 0.0% | 0.68 | 0.0% | ||||
| 0.5 | 1.03 | 0.0% | 0.87 | 0.0% | 0.81 | 0.0% | 0.68 | 0.0% | ||||
| Deep-buried | 1.03 | 0.0% | 0.87 | 0.0% | 0.81 | 0.0% | 0.68 | 0.0% | ||||
| Park and Michalowski [9] | 1.03 | 0.87 | 0.80 | 0.67 | ||||||||
| 4 | 100 | 5 | 0.1 | Present research | 2.00 | 30.1% | 1.63 | 31.1% | 1.46 | 34.2% | 1.04 | 43.5% |
| 0.3 | 2.08 | 27.3% | 1.70 | 29.2% | 1.54 | 30.6% | 1.12 | 39.1% | ||||
| 0.5 | 2.16 | 24.5% | 1.77 | 26.3% | 1.60 | 27.9% | 1.20 | 34.8% | ||||
| Deep-buried | 2.87 | 0.3% | 2.41 | 0.4% | 2.23 | 0.5% | 1.86 | 1.1% | ||||
| Park and Michalowski [9] | 2.86 | 2.40 | 2.22 | 1.84 | ||||||||
| 15 | 0.1 | Present research | 1.30 | 27.4% | 1.06 | 29.3% | 0.96 | 30.9% | 0.70 | 39.7% | ||
| 0.3 | 1.44 | 19.6% | 1.19 | 20.7% | 1.09 | 21.6% | 0.85 | 26.7% | ||||
| 0.5 | 1.57 | 12.3% | 1.31 | 12.7% | 1.20 | 13.7% | 0.99 | 14.7% | ||||
| Deep-buried | 1.79 | 0.0% | 1.51 | 0.7% | 1.39 | 0.0% | 1.17 | 0.9% | ||||
| Park and Michalowski [9] | 1.79 | 1.50 | 1.39 | 1.16 | ||||||||
| 25 | 0.1 | Present research | 1.06 | 24.8% | 0.87 | 26.3% | 0.79 | 27.5% | 0.59 | 35.2% | ||
| 0.3 | 1.24 | 12.1% | 1.03 | 12.7% | 0.95 | 12.8% | 0.78 | 14.3% | ||||
| 0.5 | 1.38 | 2.1% | 1.16 | 1.7% | 1.08 | 0.9% | 0.92 | 1.1% | ||||
| Deep-buried | 1.41 | 0.0% | 1.19 | 0.8% | 1.10 | 0.9% | 0.92 | 1.1% | ||||
| Park and Michalowski [9] | 1.41 | 1.18 | 1.09 | 0.91 | ||||||||
| σci/γR | GSI | mi | C/R | Solutions | L/R | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | Error | 3 | Error | 4 | Error | 2D | Error | |||||
| 200 | 20 | 5 | 0.1 | Present research | 42.62 | 40.9% | 52.42 | 53.3% | 56.90 | 57.7% | 68.64 | 65.2% |
| 0.3 | 75.72 | 4.9% | 107.54 | 4.3% | 122.70 | 8.8% | 161.76 | 18.1% | ||||
| 0.5 | 71.63 | 0.7% | 118.93 | 5.9% | 142.73 | 6.0% | 204.89 | 3.8% | ||||
| Deep-buried | 68.06 | 5.7% | 110.88 | 1.2% | 133.26 | 1.0% | 194.88 | 1.3% | ||||
| Park and Michalowski [9] | 72.16 | 112.32 | 134.60 | 197.40 | ||||||||
| 15 | 0.1 | Present research | 51.36 | 34.3% | 59.04 | 43.3% | 62.94 | 47.0% | 72.46 | 54.3% | ||
| 0.3 | 76.86 | 1.7% | 103.34 | 0.8% | 116.42 | 1.9% | 150.06 | 5.3% | ||||
| 0.5 | 75.89 | 3.0% | 103.57 | 0.6% | 117.88 | 0.7% | 156.94 | 1.0% | ||||
| Deep-buried | 75.90 | 3.0% | 103.56 | 0.6% | 117.88 | 0.7% | 156.94 | 1.0% | ||||
| Park and Michalowski [9] | 78.22 | 104.20 | 118.70 | 158.46 | ||||||||
| 25 | 0.1 | Present research | 51.88 | 27.9% | 59.12 | 36.8% | 62.64 | 40.6% | 72.20 | 47.7% | ||
| 0.3 | 70.16 | 35.2% | 93.40 | 0.1% | 105.50 | 0.1% | 136.64 | 1.0% | ||||
| 0.5 | 70.17 | 35.3% | 93.00 | 0.6% | 104.78 | 0.6% | 136.83 | 0.9% | ||||
| deep-buried | 70.18 | 35.3% | 93.00 | 0.6% | 104.78 | 0.6% | 136.84 | 0.9% | ||||
| Park and Michalowski [9] | 71.96 | 93.52 | 105.44 | 138.06 | ||||||||
| 20 | 60 | 5 | 0.1 | Present research | 17.04 | 31.30 | 30.7% | 37.88 | 19.7% | 55.08 | 53.2% | |
| 0.3 | 15.78 | 57.26 | 139.2% | 77.24 | 63.6% | 128.58 | 9.3% | |||||
| 0.5 | - | 50.92 | 112.7% | 80.32 | 10.2% | 159.20 | 35.3% | |||||
| Deep-buried | - | 20.90 | 12.7% | 45.56 | 3.5% | 114.56 | 2.7% | |||||
| Park and Michalowski [9] | - | 23.94 | 47.20 | 117.68 | ||||||||
| 15 | 0.1 | Present research | 38.40 | 25.9% | 48.62 | 39.4% | 53.28 | 44.3% | 65.48 | 53.4% | ||
| 0.3 | 53.42 | 3.0% | 82.82 | 3.3% | 98.52 | 2.9% | 137.56 | 2.1% | ||||
| 0.5 | 48.57 | 6.3% | 78.81 | 1.7% | 94.34 | 1.4% | 142.40 | 1.3% | ||||
| Deep-buried | 48.58 | 6.3% | 78.82 | 1.7% | 94.70 | 1.1% | 138.64 | 1.3% | ||||
| Park and Michalowski [9] | 51.84 | 80.20 | 95.72 | 140.52 | ||||||||
| 25 | 0.1 | Present research | 43.22 | 26.1% | 52.32 | 36.2% | 56.50 | 40.5% | 67.50 | 48.8% | ||
| 0.3 | 56.66 | 3.2% | 83.32 | 1.6% | 96.42 | 1.5% | 131.18 | 0.5% | ||||
| 0.5 | 55.88 | 4.5% | 80.99 | 1.3% | 94.14 | 0.9% | 130.36 | 1.2% | ||||
| Deep-buried | 55.88 | 4.5% | 80.98 | 1.3% | 94.14 | 0.9% | 130.36 | 1.2% | ||||
| Park and Michalowski [9] | 58.52 | 82.02 | 94.96 | 131.88 | ||||||||
| 2 | 100 | 5 | 0.1 | Present research | - | 16.08 | 24.34 | 46.04 | ||||
| 0.3 | - | 26.32 | 50.46 | 114.00 | ||||||||
| 0.5 | - | 14.45 | 51.78 | 152.23 | ||||||||
| Deep-buried | - | - | - | - | ||||||||
| Park and Michalowski [9] | - | - | - | - | ||||||||
| 15 | 0.1 | Present research | 28.86 | 8.3% | 40.92 | 38.1% | 46.50 | 46.7% | 61.16 | 59.4% | ||
| 0.3 | 42.18 | 58.3% | 78.72 | 19.1% | 95.88 | 9.9% | 141.10 | 6.3% | ||||
| 0.5 | 26.41 | 0.9% | 77.90 | 17.9% | 104.00 | 19.2% | 172.92 | 14.8% | ||||
| Deep-buried | 21.68 | 18.6% | 63.52 | 3.9% | 85.76 | 1.7% | 147.84 | 1.8% | ||||
| Park and Michalowski [9] | 26.64 | 66.10 | 87.22 | 150.62 | ||||||||
| 25 | 0.1 | Present research | 37.78 | 27.8% | 48.16 | 43.1% | 52.92 | 48.2% | 65.44 | 57.4% | ||
| 0.3 | 56.44 | 7.8% | 88.32 | 4.3% | 103.78 | 1.6% | 144.02 | 6.2% | ||||
| 0.5 | 48.49 | 7.4% | 85.01 | 0.4% | 105.91 | 3.7% | 163.64 | 6.6% | ||||
| Deep-buried | 48.52 | 7.3% | 82.86 | 2.1% | 101.00 | 1.1% | 151.32 | 1.4% | ||||
| Park and Michalowski [9] | 52.36 | 84.66 | 102.16 | 153.52 | ||||||||
| σci/γR | GSI | mi | C/R | Solutions | L/R | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | Error | 3 | Error | 4 | Error | 2D | Error | |||||
| 200 | 20 | 5 | 0.1 | Present research | 70.18 | 78.8% | 75.46 | 82.6% | 77.96 | 84.1% | 84.32 | 87.1% |
| 0.3 | 175.46 | 47.0% | 196.28 | 54.8% | 205.84 | 58.1% | 230.88 | 64.8% | ||||
| 0.5 | 245.32 | 25.8% | 285.21 | 34.3% | 303.66 | 38.1% | 352.02 | 46.3% | ||||
| Deep-buried | 317.50 | 34.0% | 429.40 | 1.2% | 487.48 | 0.7% | 648.80 | 1.1% | ||||
| Park and Michalowski [9] | 330.82 | 434.64 | 490.76 | 655.84 | ||||||||
| 15 | 0.1 | Present research | 74.24 | 69.4% | 78.76 | 74.4% | 80.82 | 76.5% | 86.22 | 80.6% | ||
| 0.3 | 169.68 | 30.0% | 190.14 | 38.2% | 200.00 | 41.9% | 225.04 | 49.4% | ||||
| 0.5 | 217.70 | 10.2% | 258.16 | 16.1% | 277.02 | 19.5% | 326.49 | 26.6% | ||||
| Deep-buried | 236.62 | 2.4% | 306.00 | 0.5% | 342.06 | 0.6% | 440.86 | 0.9% | ||||
| Park and Michalowski [9] | 242.42 | 307.58 | 344.10 | 444.98 | ||||||||
| 25 | 0.1 | Present research | 74.26 | 63.1% | 78.70 | 69.8% | 80.54 | 72.3% | 86.10 | 76.9% | ||
| 0.3 | 160.54 | 20.3% | 182.04 | 30.1% | 191.98 | 33.9% | 218.32 | 42.4% | ||||
| 0.5 | 196.03 | 2.7% | 236.20 | 9.3% | 256.16 | 11.8% | 305.65 | 17.9% | ||||
| Deep-buried | 202.38 | 0.5% | 259.24 | 0.5% | 288.66 | 0.6% | 369.00 | 0.9% | ||||
| Park and Michalowski [9] | 201.44 | 260.52 | 290.32 | 372.30 | ||||||||
| 20 | 60 | 5 | 0.1 | Present research | 57.14 | 78.7% | 64.80 | 83.2% | 68.32 | 84.8% | 77.54 | 87.9% |
| 0.3 | 144.30 | 46.2% | 170.06 | 56.0% | 182.60 | 59.3% | 214.28 | 66.7% | ||||
| 0.5 | 201.54 | 24.8% | 249.94 | 35.3% | 270.41 | 39.8% | 329.30 | 48.8% | ||||
| Deep-buried | 249.00 | 7.1% | 375.58 | 2.8% | 442.72 | 1.4% | 633.36 | 1.4% | ||||
| Park and Michalowski [9] | 268.04 | 386.32 | 448.86 | 642.62 | ||||||||
| 15 | 0.1 | Present research | 67.50 | 71.3% | 73.30 | 76.3% | 75.90 | 78.3% | 82.74 | 82.3% | ||
| 0.3 | 157.48 | 33.1% | 180.32 | 41.7% | 190.88 | 45.4% | 218.78 | 53.2% | ||||
| 0.5 | 205.85 | 12.6% | 248.35 | 19.8% | 269.01 | 23.0% | 321.85 | 31.1% | ||||
| Deep-buried | 226.88 | 3.7% | 305.30 | 1.4% | 346.84 | 0.7% | 462.42 | 1.1% | ||||
| Park and Michalowski [9] | 235.52 | 309.50 | 349.40 | 467.74 | ||||||||
| 25 | 0.1 | Present research | 69.62 | 66.9% | 74.90 | 72.3% | 77.44 | 74.5% | 83.74 | 79.1% | ||
| 0.3 | 155.00 | 26.2% | 177.64 | 34.4% | 188.42 | 38.0% | 215.58 | 46.1% | ||||
| 0.5 | 193.93 | 7.7% | 235.82 | 12.9% | 255.78 | 15.8% | 309.10 | 22.7% | ||||
| deep-buried | 203.34 | 3.2% | 266.40 | 1.6% | 301.84 | 0.7% | 395.88 | 1.1% | ||||
| Park and Michalowski [9] | 210.04 | 270.76 | 303.90 | 400.12 | ||||||||
| 2 | 100 | 5 | 0.1 | Present research | 48.00 | 82.8% | 57.38 | 87.6% | 61.70 | 89.0% | 73.02 | 91.6% |
| 0.3 | 127.00 | 54.4% | 156.92 | 66.0% | 170.72 | 69.5% | 207.24 | 76.1% | ||||
| 0.5 | 186.60 | 33.0% | 238.64 | 48.2% | 262.74 | 53.0% | 326.90 | 62.2% | ||||
| Deep-buried | 247.90 | 11.0% | 437.02 | 5.2% | 542.26 | 3.0% | 850.34 | 1.8% | ||||
| Park and Michalowski [9] | 278.50 | 461.06 | 558.98 | 865.78 | ||||||||
| 15 | 0.1 | Present research | 63.06 | 77.9% | 69.62 | 82.2% | 72.64 | 83.8% | 80.58 | 87.0% | ||
| 0.3 | 156.92 | 45.1% | 180.12 | 54.0% | 191.74 | 57.2% | 220.56 | 64.5% | ||||
| 0.5 | 217.96 | 23.7% | 260.14 | 33.6% | 282.40 | 46.9% | 336.46 | 45.8% | ||||
| Deep-buried | 271.32 | 5.0% | 382.80 | 2.3% | 442.82 | 1.1% | 612.46 | 1.3% | ||||
| Park and Michalowski [9] | 285.68 | 391.68 | 447.62 | 620.66 | ||||||||
| 25 | 0.1 | Present research | 67.40 | 74.2% | 73.16 | 79.0% | 75.80 | 80.7% | 82.72 | 84.4% | ||
| 0.3 | 161.54 | 38.2% | 184.12 | 47.0% | 194.54 | 50.5% | 222.00 | 58.2% | ||||
| 0.5 | 217.24 | 16.9% | 259.84 | 25.2% | 279.17 | 29.0% | 331.25 | 37.6% | ||||
| Deep-buried | 252.00 | 3.6% | 342.04 | 1.6% | 390.02 | 0.8% | 524.34 | 1.2% | ||||
| Park and Michalowski [9] | 261.48 | 347.68 | 393.00 | 530.66 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yang, Z.; Ren, Q.; Huang, Z.; Xu, J. Stability and Design Charts for 3D Rectangular Cavity Crowns with Limited Buried Depth in Rock Masses. Buildings 2025, 15, 4151. https://doi.org/10.3390/buildings15224151
Wang Z, Yang Z, Ren Q, Huang Z, Xu J. Stability and Design Charts for 3D Rectangular Cavity Crowns with Limited Buried Depth in Rock Masses. Buildings. 2025; 15(22):4151. https://doi.org/10.3390/buildings15224151
Chicago/Turabian StyleWang, Zemian, Zihan Yang, Qiankai Ren, Zhen Huang, and Jingshu Xu. 2025. "Stability and Design Charts for 3D Rectangular Cavity Crowns with Limited Buried Depth in Rock Masses" Buildings 15, no. 22: 4151. https://doi.org/10.3390/buildings15224151
APA StyleWang, Z., Yang, Z., Ren, Q., Huang, Z., & Xu, J. (2025). Stability and Design Charts for 3D Rectangular Cavity Crowns with Limited Buried Depth in Rock Masses. Buildings, 15(22), 4151. https://doi.org/10.3390/buildings15224151







