Local Fracture of a Reinforced Concrete Beam Under High-Velocity Impact on Biaxial Bending and Torsion Deformation
Abstract
1. Introduction
- Analysis of combined torsion and bending requires supplementary research and revision of regulations with a focus on load combinations, including new analytical and numerical approaches.
- Risks of progressive collapse of structures can be effectively reduced by optimizing parameters of joints, using composites to strengthen structures, and developing accurate calculation and prediction methods.
- Dynamic torsional loads, including a combination of torsion and bending, can greatly affect the mechanical safety of structures, which is proved by experimental and theoretical studies.
2. Materials and Methods
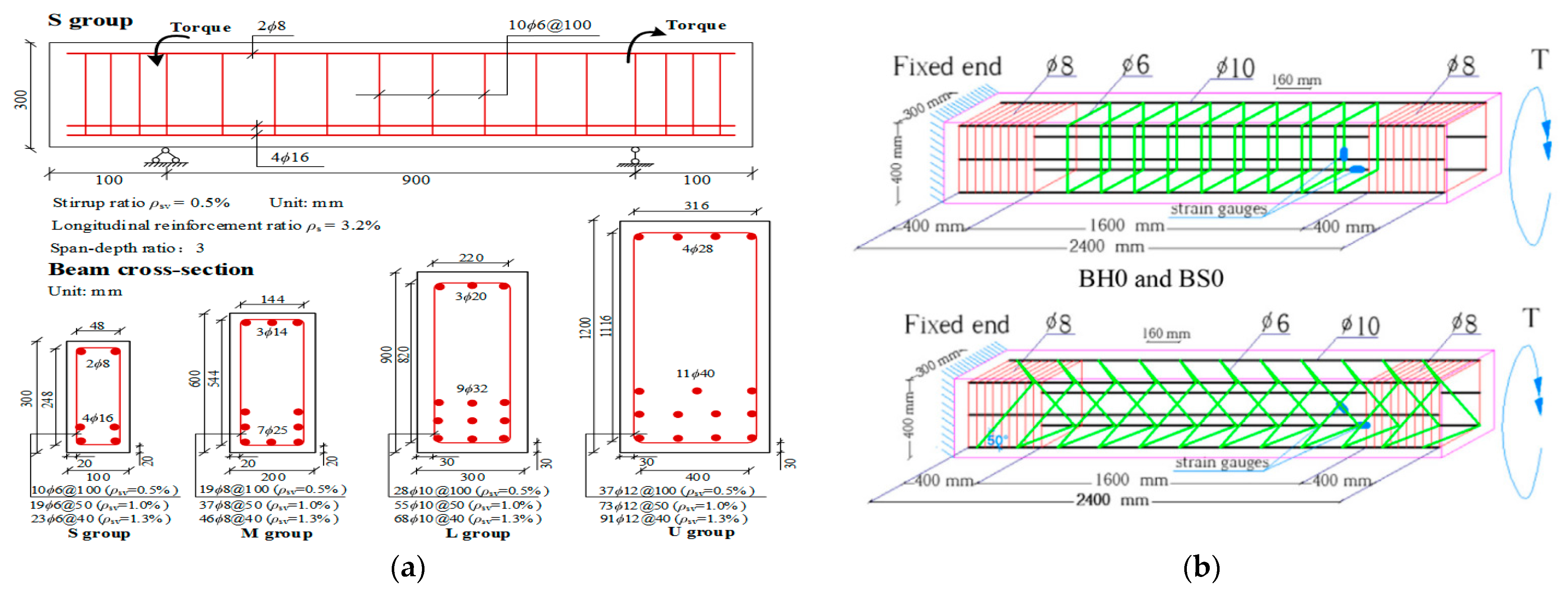
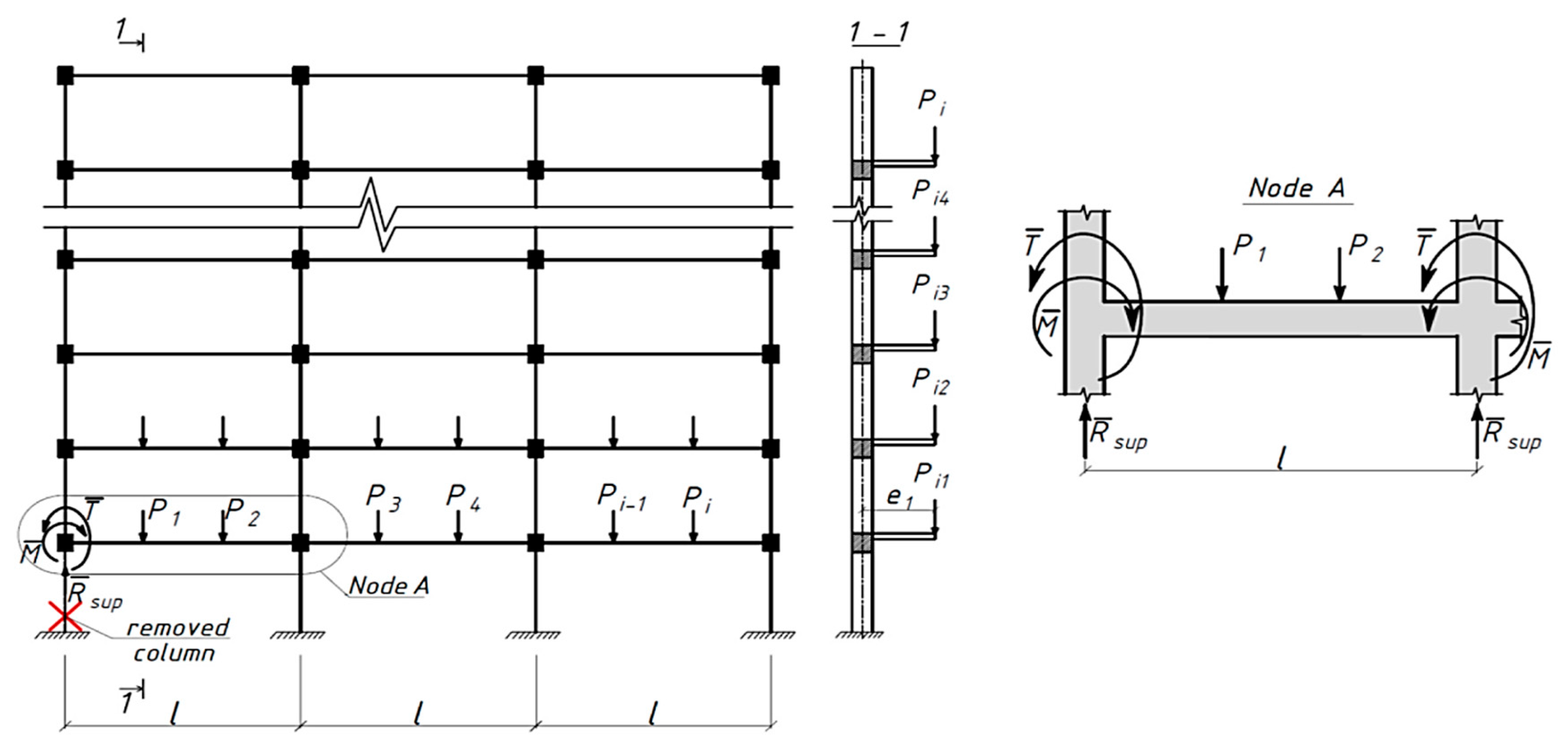
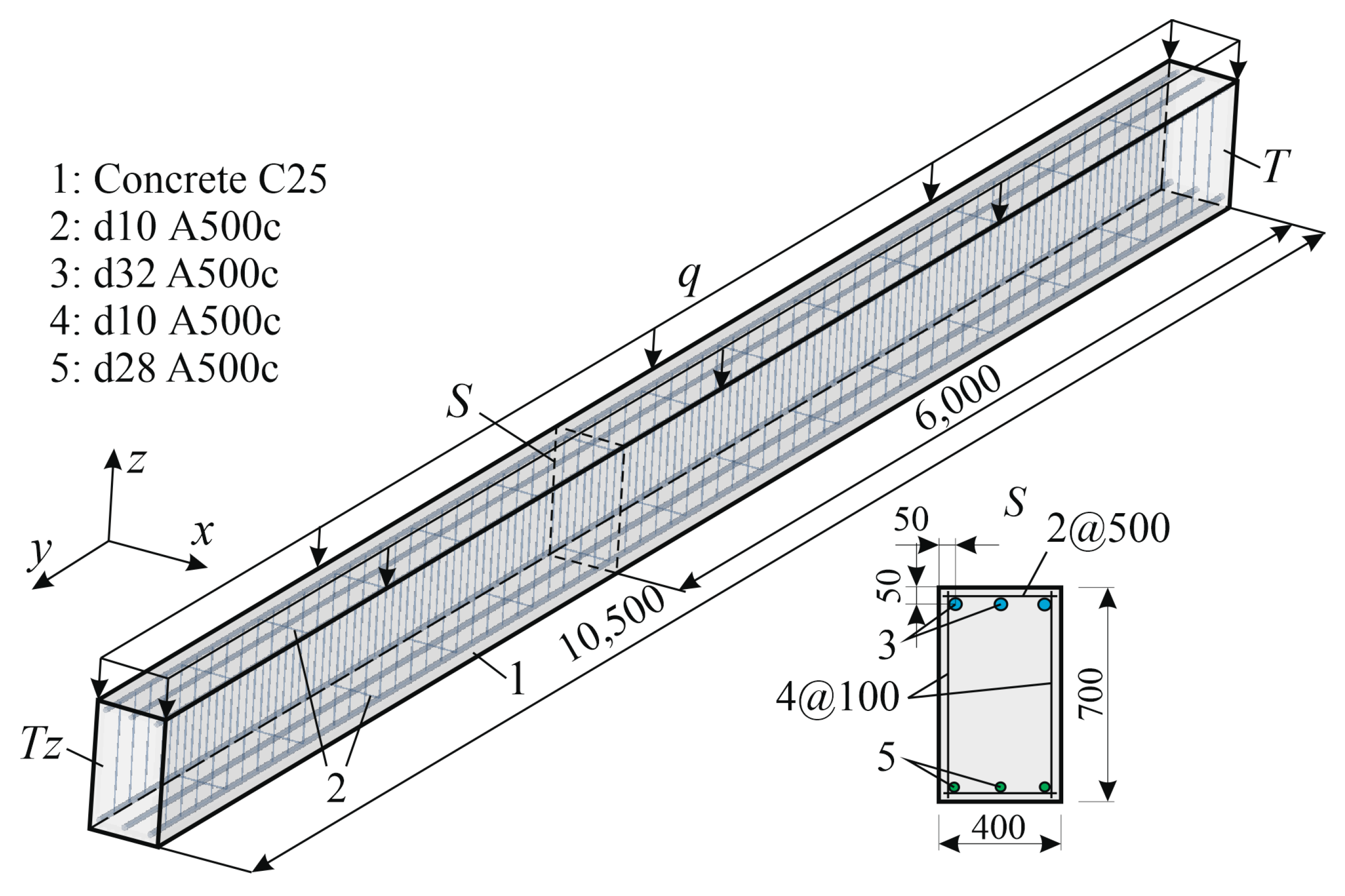
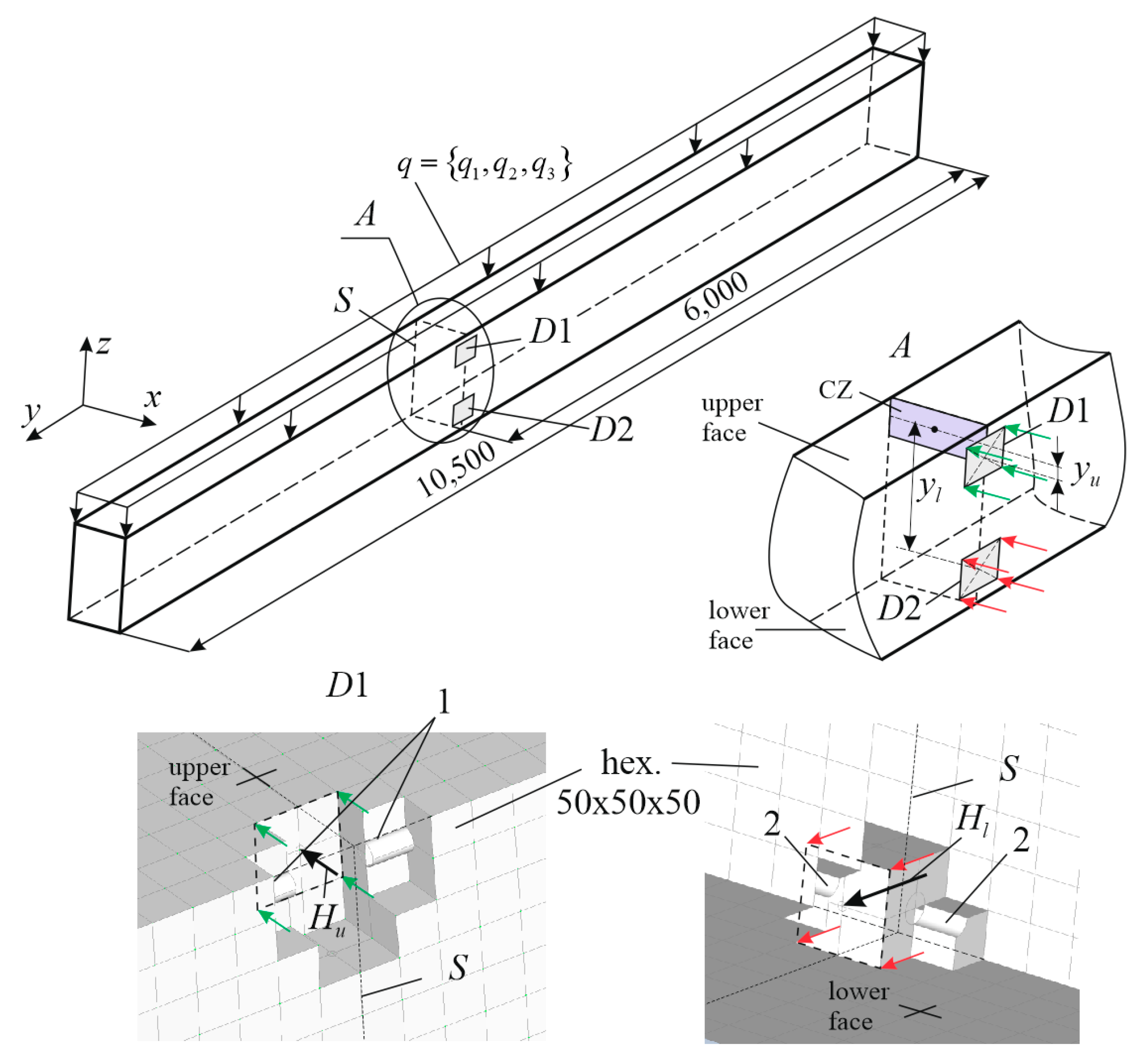
2.1. Problem Statement and Target of Research
2.2. Problem Constraints
2.3. Basic Provisions of the FEM Analysis
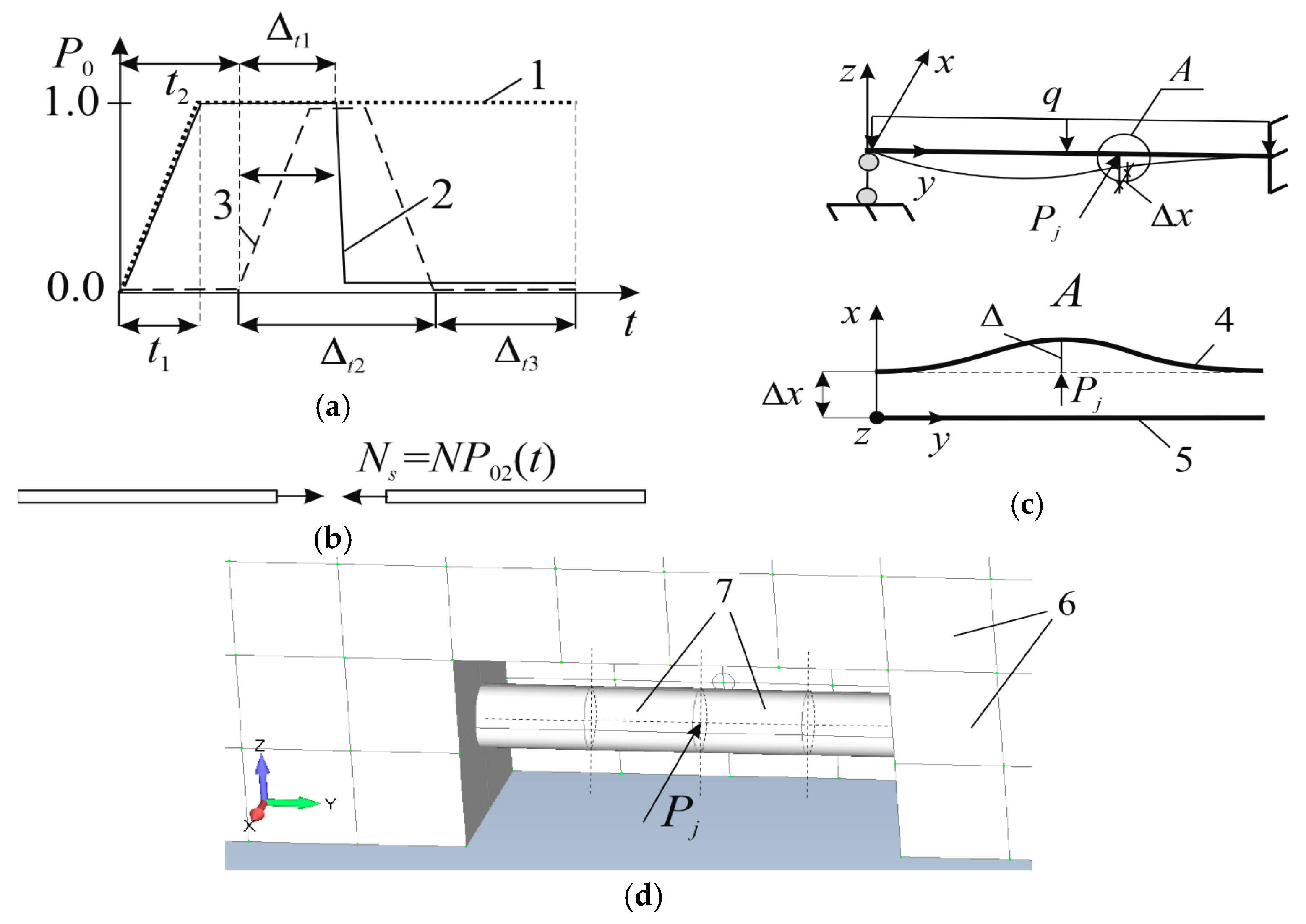
2.3.1. Simulation of Loads
2.3.2. Strain of Materials
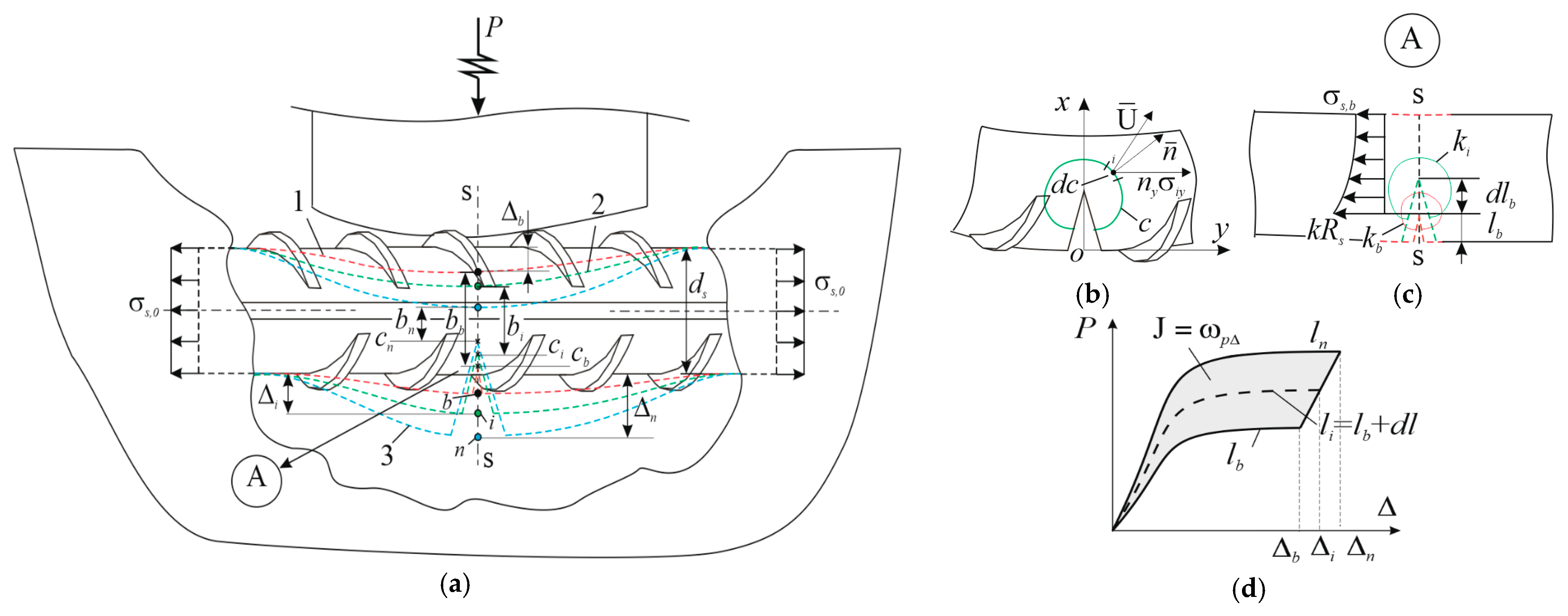
2.3.3. Impact Mechanics
- -
- interaction with the impactor causes brittle failure of concrete in the vicinity of the rebar, and only the rebar takes the kinetic energy at the moment of the impact.
- -
- The potential energy of the rebar strain in the case of the elastic-plastic behavior of the material consists of the impact energy transferred from the impactor and causing the local bending of the rebar and the longitudinal deformation energy from the operation load.
- -
- Since local fracture of the structure is considered here, which in some cases may not lead to complete fracture, it is sufficient to consider the quasi-elastic behavior of the rebar by focusing on one integral (6).
3. Results
3.1. Verification of the Intact Beam Model
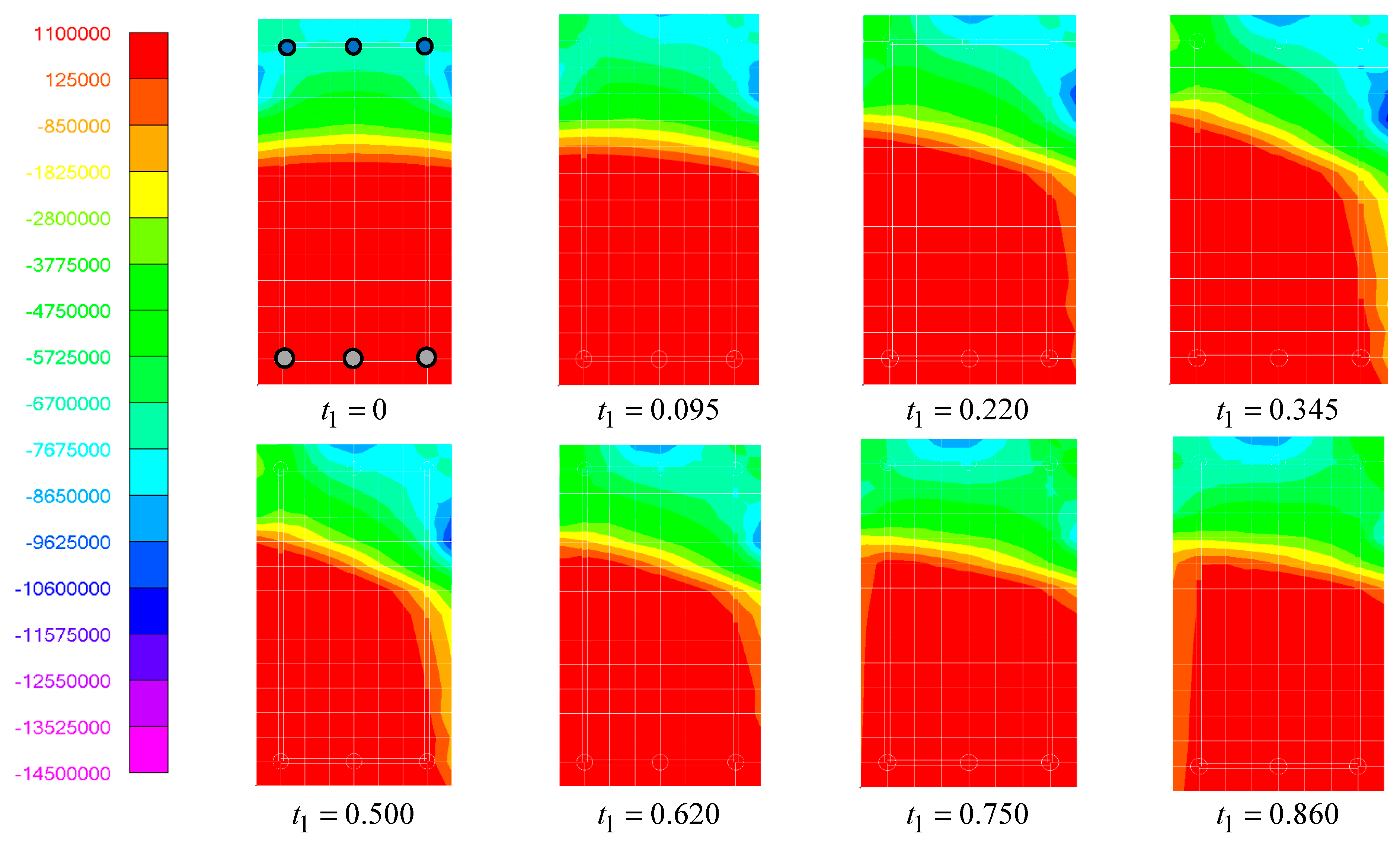
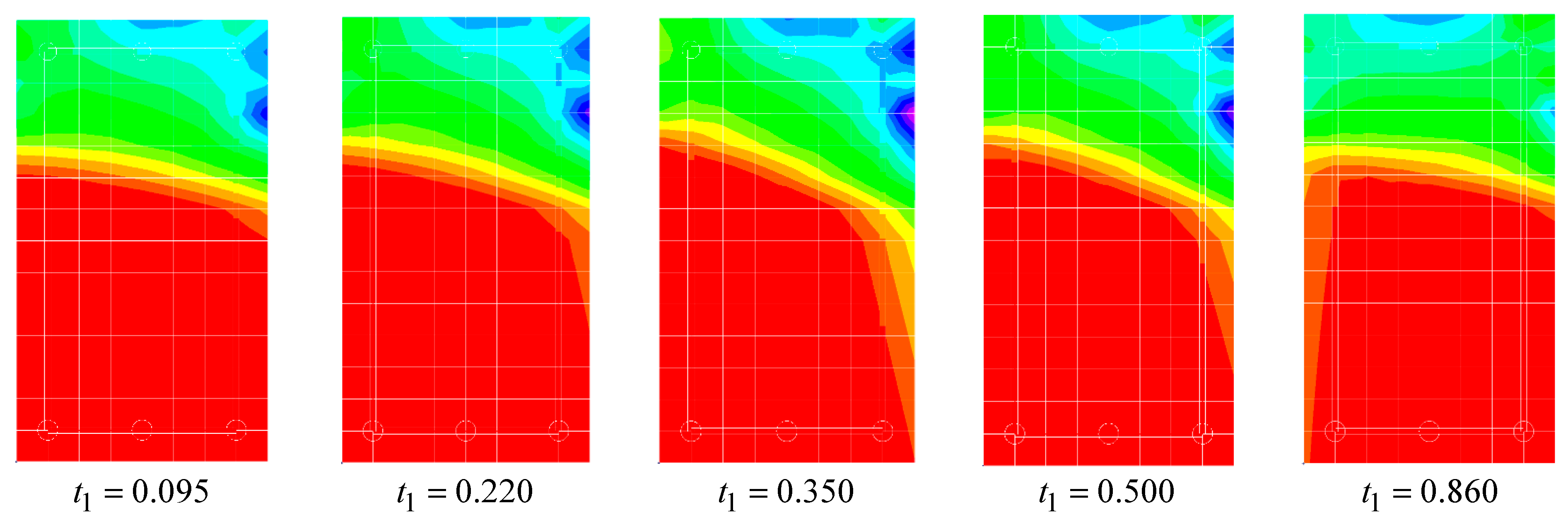
3.2. Resulting Study of the Bearing Capacity of Concrete Without Ruptured Rebars
3.3. Resulting Study of the Bearing Capacity in the Case of Local Mechanical Fracture of Concrete and Facture of Rebars
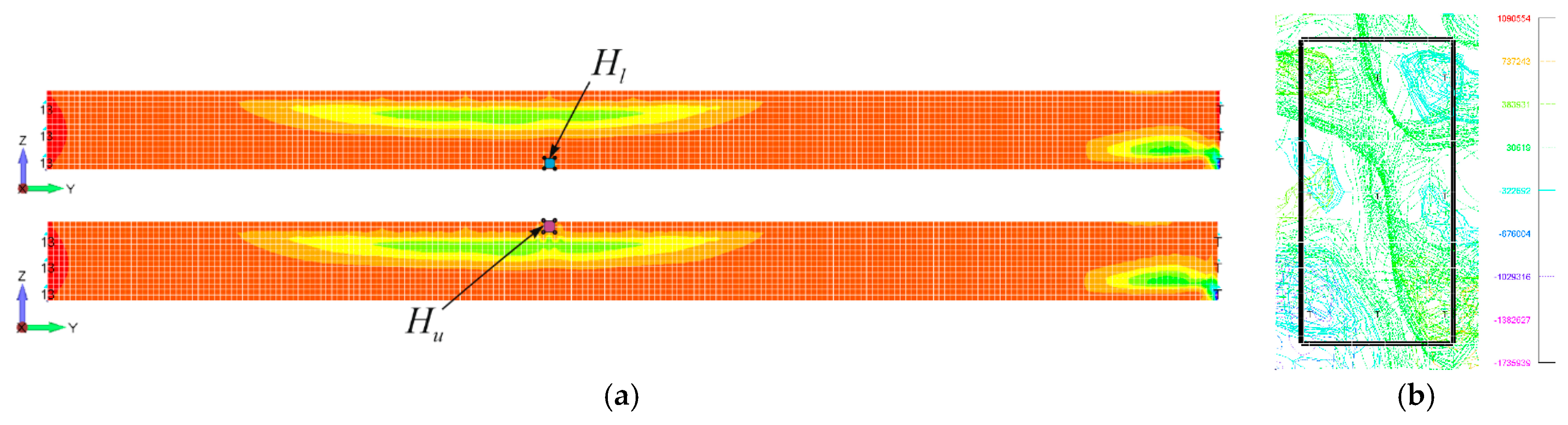
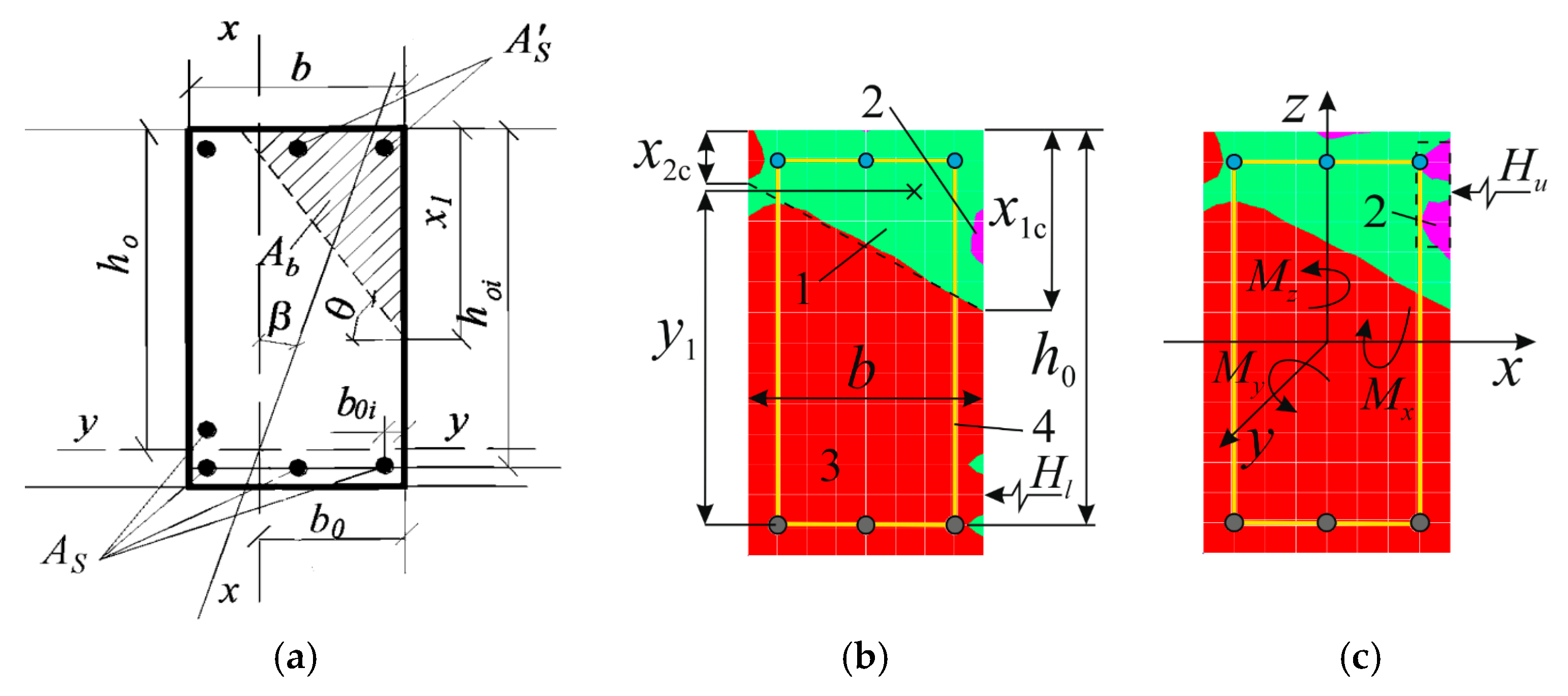
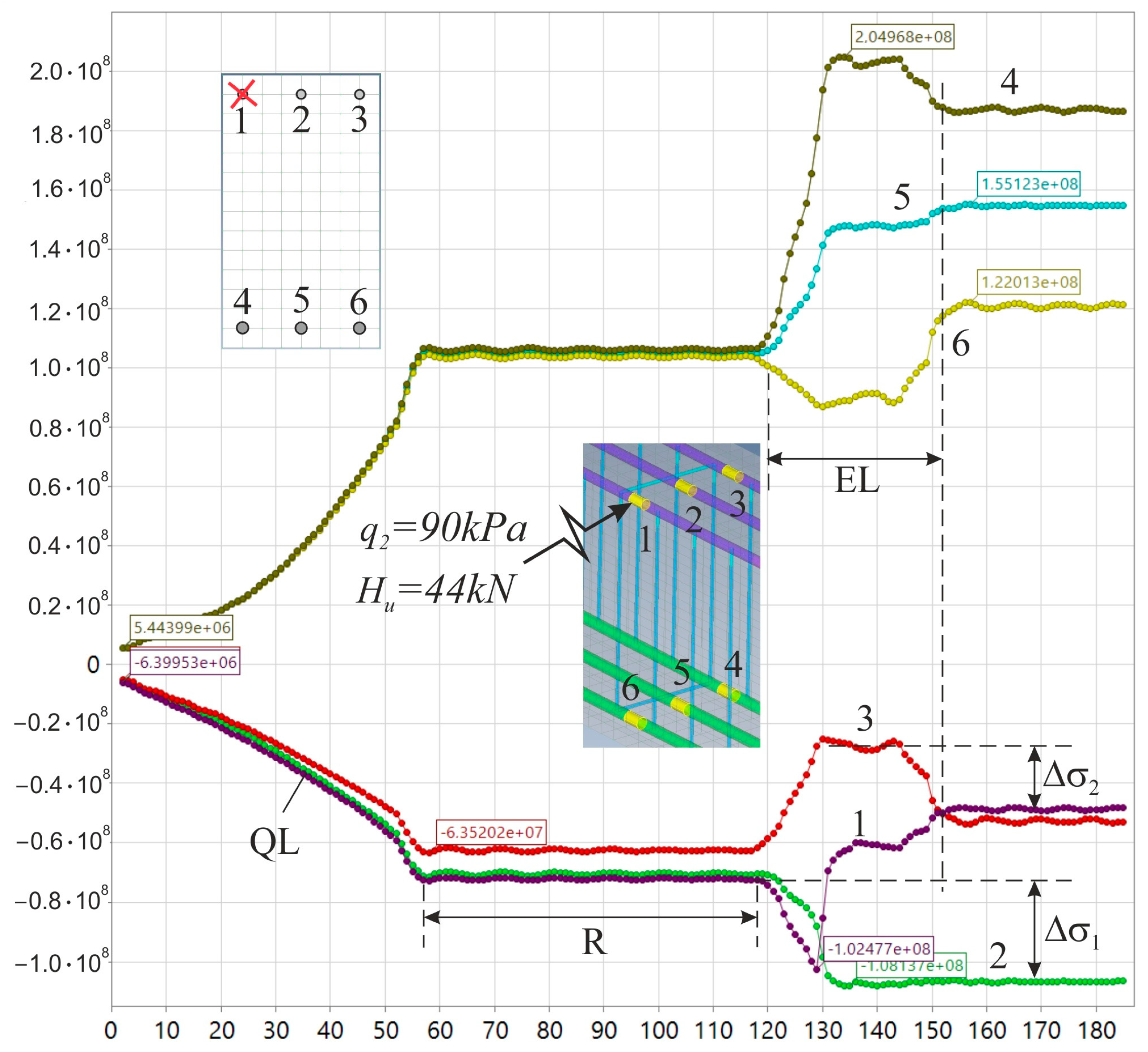
- The computation is made and the initial displacement of the rebar in the horizontal direction is determined, given that this displacement is triggered by initial impact loading, shown in Figure 5c. Actual stress in the rebar is identified.
- The initial opening width of an infinitely small crack is determined by Formula (8).
- The Rice integral (7) is calculated and the condition of crack development to fracture (5) is verified. If the condition is satisfied, the rebar is considered fractured.
- -
- The value of the ultimate force () causing the torsion moment taken by the beam when the value of the vertical load () is below 70% of its ultimate value is greater if the impact focuses on the upper (compressed) zone of concrete;
- -
- If values of vertical load are , rebars do not facture. The fracture process starts from the local loss of stability of the rebar, followed by the fracture of the compressed zone of concrete.
3.4. Studying Changes in the Compressed Zone of Concrete
- -
- Deriving analytical expressions for variables , taking into account their change in time;
- -
- Identifying the zone of crushing in the compressed zone of concrete;
- -
- Determining the condition for the rupture of a rebar (rebars) in the zone of contact with the impactor initiating the impact action;
- -
- Accurately analyzing the resulting force taken by the compressed concrete, taking into account potential microcracking in the concrete zones that became tensile at earlier moments of time;
- -
- Finding the areas of longitudinal rebars on the basis of the condition of plastic fracture of the section;
- -
- Finding (verifying) the area of stirrups capable of supporting the torsion moment with regard for the confined concrete strain within the loop.
3.5. Studying the Strain of Rebars Subjected to Accidental Actions
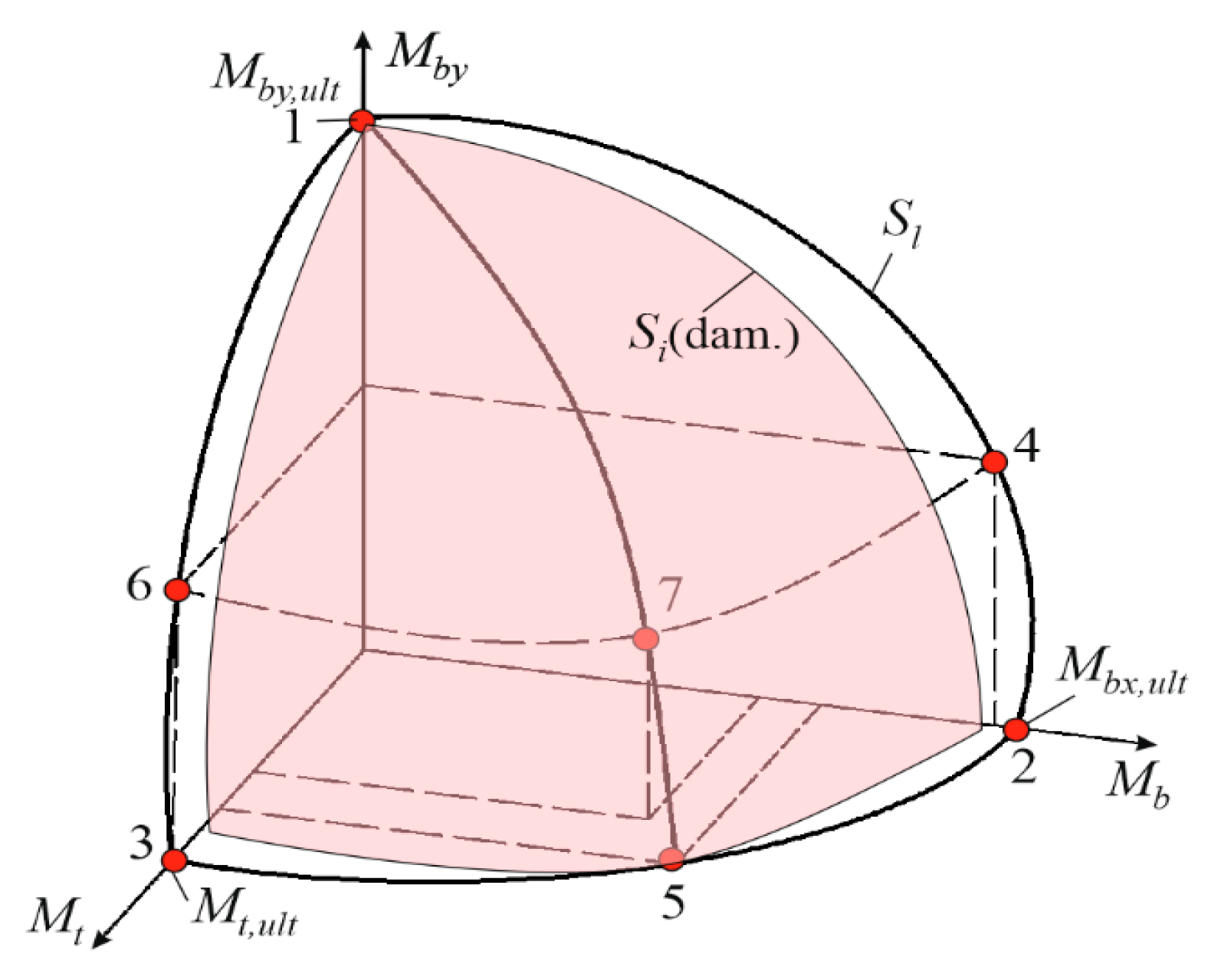
3.6. Development of the Limiting Surface and Conclusion About the Mechanical Safety of the Key Element
4. Discussion
- -
- Support zones of beams in case of lateral impacts, where loss of shear bearing capacity may occur. It will also be necessary to construct limiting envelope surfaces in the axes;
- -
- Columns, if the impact is transverse; the limiting envelope surface will be constructed in the axes.
5. Conclusions
- A method for evaluating the mechanical safety of key elements in structural systems was developed. This method is based on construction of limiting envelope surfaces based on minimum values of prevailing internal forces. This method unambiguously determines the range of emergency load values for pre-set design parameters of a bearing structure (section sizes, material classes, and reinforcement features) that do not cause the element fracture, protecting the structural system from progressive collapse.
- Analysis of the dynamics of reinforced concrete beams in the 3D formulation proved the need to develop a new safety criterion for key load-bearing elements. This criterion is to be formulated in the form of Expression (2). This criterion stems from a differentiated approach to the evaluation of section strength, taking into account the discrete location of rebars and their specific areas.
- The general Rice formula was employed to formulate the analytical dependence for the J integral, which allows a simplified evaluation of the condition of failure of a rebar under the direct action of an impactor. This approach allows detecting the possibility of preventing the local fracture of rebars/concrete parts of the key structure in the process of computation.
- Analysis of a specific reinforced concrete beam without prestressing shows that construction of the limiting envelope surface for the most dangerous sections makes it possible to unambiguously determine the range of values of emergency loading, at which the key element will not collapse and will be able to localize the progressive collapse in the structural system as a whole, even in the case of local damage.
- A limitation of the method is its inability to perform calculations for the purpose of determining design parameters (such as reinforcement layout, concrete grade, etc.). The generation of ultimate load envelopes and the subsequent safety assessment of structures presuppose a fixed design, where these parameters remain unchanged.
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z.; Chen, Y.; Wu, H.; Ye, P. Experimental Investigation on Shear Capacity of Steel Reinforced Concrete Columns under Combined Torque. J. Constr. Steel Res. 2024, 213, 108345. [Google Scholar] [CrossRef]
- Nasser, A.G.; Makhlouf, M.H.; Elsayed, K.M.; Gamal, I.K. Experimental and Numerical Investigation on RC Beams with Web Openings Subjected to Pure Torsion Strengthened by Ferrocement Technique or GFRP Sheets. Structures 2024, 69, 107479. [Google Scholar] [CrossRef]
- Patane, A.; Vesmawala, G. Experimental and Analytical Investigation of the Behaviour of Reinforced Concrete Beam under Pure Torsion. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Hui, L.; López-Almansa, F. New Modifying Truss Model and Numerical Simulation of Steel Fiber Reinforced Concrete under Pure Torsion. Structures 2018, 14, 32–42. [Google Scholar] [CrossRef]
- Selmy, Y.M.; El-Salakawy, E.F. Behaviour of Circular Concrete Bridge Columns Internally Reinforced with GFRP under Reversed-Cyclic Loading Including Torsion. Structures 2024, 59, 105680. [Google Scholar] [CrossRef]
- Qian, K.; Weng, Y.-H.; Fu, F.; Deng, X.-F. Numerical Evaluation of the Reliability of Using Single-Story Substructures to Study Progressive Collapse Behaviour of Multi-Story RC Frames. J. Build. Eng. 2021, 33, 101636. [Google Scholar] [CrossRef]
- Du, F.; Wang, J.A.J.; Tan, T. Using Spiral Notch Torsional Test to Investigate Fracture of Unidirectional Fiber Reinforced Composites. Compr. Struct. Integr. 2023, 10, 349–359. [Google Scholar] [CrossRef]
- Lei, Y.; Jin, L.; Li, D.; Zhu, H.; Du, X. Comparison of Torsional Damage and Size Effects of BFRP- and Steel-Reinforced Concrete Beams with Different Stirrup Ratios. Eng. Struct. 2023, 285, 116042. [Google Scholar] [CrossRef]
- Ibrahim, A.; Askar, H.S.; El-Zoughiby, M.E. Torsional Behavior of Solid and Hollow Concrete Beams Reinforced with Inclined Spirals. J. King Saud Univ. Eng. Sci. 2022, 34, 309–321. [Google Scholar] [CrossRef]
- Mo, Y.L.; Yang, R.Y. Response of Reinforced/Prestressed Concrete Box Structures to Dynamically Applied Torsion. Nucl. Eng. Des. 1996, 165, 25–41. [Google Scholar] [CrossRef]
- Ayaad, N.; Oukaili, N. Impact Torsional Behavior and Strengthening of Reinforced Concrete Spandrel Beams. Case Stud. Constr. Mater. 2023, 19, e02591. [Google Scholar] [CrossRef]
- Xin, Z.; Jianyang, X.; Rui, R.; Linlin, M. Test on Pure Torsion Behavior of Channel Steel Reinforced Concrete Beams. J. Build. Eng. 2021, 44, 102967. [Google Scholar] [CrossRef]
- MohamedSalih, M.M.; Yousif, A.R. Effect of Type, Amount and Configuration of Reinforcement in HSC Box-Girders Reinforced with BFRP Bars and Steel Stirrups under Torsion-Shear-Bending. Ain Shams Eng. J. 2022, 13, 101787. [Google Scholar] [CrossRef]
- Chen, Y.; He, Q.; Chen, Z.; Liang, X. Bending Restoring Force Model of Angle-Steel Reinforced Concrete Columns under Combined Torsion. Structures 2023, 55, 2186–2198. [Google Scholar] [CrossRef]
- Becks, H.; Schmidt, M.; Bosbach, S.; Classen, M. Large-Scale Combined Torsional and Axial Loading System (TorAx)—A New Perspective on Multiaxial Testing of Fracture and Stress Transfer in Plain and Reinforced Concrete. Eng. Struct. 2024, 302, 117391. [Google Scholar] [CrossRef]
- Eltaly, B.; EL_Sayed, M.; Meleka, N.; Kandil, K. Torsion Behavior of Strengthened Reinforced Concrete Box Girders with Openings: Analytical and Experimental Investigation. Structures 2024, 60, 105908. [Google Scholar] [CrossRef]
- Cocchi, G.M.; Cappello, F. Inelastic Analysis of Reinforced Concrete Space Frames Influenced by Axial, Torsional and Bending Interaction. Comput. Struct. 1993, 46, 83–97. [Google Scholar] [CrossRef]
- De-la-Colina, J.; Valdés-González, J.; González-Pérez, C.A. Experiments to Study the Effect of Foundation Rotation on the Seismic Building Torsional, Response of a Reinforced Concrete Space Frame. Eng. Struct. 2013, 56, 1154–1163. [Google Scholar] [CrossRef]
- Valipour, H.R.; Foster, S.J. Nonlinear Reinforced Concrete Frame Element with Torsion. Eng. Struct. 2010, 32, 988–1002. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Morillas, L.; Escolano-Margarit, D. Inelastic Torsional Seismic Response of Nominally Symmetric Reinforced Concrete Frame Structures: Shaking Table Tests. Eng. Struct. 2014, 80, 109–117. [Google Scholar] [CrossRef]
- Kolchunov, V.I.; Moskovtseva, V.S. Robustness of Reinforced Concrete Frames with Elements Experiencing Bending with Torsion. Eng. Struct. 2024, 314, 118309. [Google Scholar] [CrossRef]
- Ding, L.; Chen, J.; Caspeele, R. Determination of Dynamic Collapse Limit States Using the Energy-Based Method for Multi-Story RC Frames Subjected to Column Removal Scenarios. Eng. Struct. 2024, 311, 118170. [Google Scholar] [CrossRef]
- Alshaikh, I.M.H.; Nehdi, M.L.; Abadel, A.A. Numerical Investigations on Progressive Collapse of Rubberized Concrete Frames Strengthened by CFRP Sheets. Structures 2024, 60, 105918. [Google Scholar] [CrossRef]
- Cheng, J.F.; Gu, Q.; Qian, K.; Fu, F.; Deng, X.F. Dynamic Behavior of RC Frames against Progressive Collapse Subjected to Loss of a Corner Column Scenario. J. Build. Eng. 2024, 86, 108872. [Google Scholar] [CrossRef]
- Xiong, Z.; Jia, W.; Chen, X. Progressive Collapse Mechanism of RC Framed Structures Under Earthquake Using Energy Method. KSCE J. Civ. Eng. 2024, 29, 100104. [Google Scholar] [CrossRef]
- Qu, T.; Zeng, B.; Zhou, Z.; Huang, L.; Chang, D. Dynamic and Uncertainty-Based Assessment of the Progressive Collapse Probability of Prestressed Concrete Frame Structures with Infill Walls. Structures 2024, 61, 106105. [Google Scholar] [CrossRef]
- Yi, F.; Yi, W.J.; Sun, J.M.; Ni, J.; He, Q.F.; Zhou, Y. On the Progressive Collapse Performance of RC Frame Structures under Impact Column Removal. Eng. Struct. 2024, 307, 117926. [Google Scholar] [CrossRef]
- Lin, K.; Zheng, J.; Wu, Z.; Lu, X.; Li, Y. Risk-Based Life Cycle Cost–Benefit Analysis for Progressive Collapse Design of RC Frame Structures. Structures 2024, 63, 106468. [Google Scholar] [CrossRef]
- Alshaikh, I.M.H.; Abu Bakar, B.H.; Alwesabi, E.A.H.; Abadel, A.A.; Alghamdi, H.; Altheeb, A.; Tuladhar, R. Progressive Collapse Behavior of Steel Fiber-Reinforced Rubberized Concrete Frames. J. Build. Eng. 2022, 57, 104920. [Google Scholar] [CrossRef]
- Liu, X.Y.; Qin, W.H.; Xu, Z.D.; Xi, Z.; Zhang, Z.C. Investigation on the Progressive Collapse Resistance of Three-Dimensional Concrete Frame Structures Reinforced by Steel-FRP Composite Bar. J. Build. Eng. 2022, 59, 105116. [Google Scholar] [CrossRef]
- Feng, F.F.; Hwang, H.J.; Zhou, Y.; Sun, J.M.; Zhang, H.Z.; Roh, J.H.; Kang, S.M.; Yi, W.J. Effect of Three-Dimensional Space on Progressive Collapse Resistance of Reinforced Concrete Frames under Various Column Removal Scenarios. J. Build. Eng. 2024, 90, 109405. [Google Scholar] [CrossRef]
- Husain, M.; Yu, J.; Osman, B.H.; Ji, J. Progressive Collapse Resistance of Post-Tensioned Concrete Beam-Column Assemblies under a Middle Column Removal Scenario. J. Build. Eng. 2021, 34, 101945. [Google Scholar] [CrossRef]
- Yu, X.-H.; Dai, K.-Y.; Li, Y.-S. Variability in Corrosion Damage Models and Its Effect on Seismic Collapse Fragility of Aging Reinforced Concrete Frames. Constr. Build. Mater. 2021, 295, 123654. [Google Scholar] [CrossRef]
- Wang, S.; Cheng, X.; Li, Y.; Yang, X.; Zhang, H.; Guo, R.; Song, X.; Liang, Z. Assessing Progressive Collapse Regions of Reinforced Concrete Frame Structures Using Graph Convolutional Networks. Eng. Struct. 2025, 322, 119076. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Lim, N.S.; Tan, K.H. Effect of torsion on the mobilisation of alternate load paths in double-span reinforced concrete edge beams subjected to progressive collapse. Structures 2025, 77, 109106. [Google Scholar] [CrossRef]
- Lei, Y.; Jin, L.; Du, X. Experimental investigation of size effects on BFRP-RC beams under combined bending-shear-torsion loading. Eng. Struct. 2025, 336, 120457. [Google Scholar] [CrossRef]
- Fayed, S.; Badawi, M.; Ghalla, M.; Mlybari, E.A.; Iskander, Y.; Yehia, S.A. Effect of reinforcement configurations on behavior of non-straight RC beams under torsion: Optimization for construction safety. Eng. Struct. 2025, 340, 120725. [Google Scholar] [CrossRef]
- Rice, J.R. A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. J. Appl. Mech. Trans. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Chen, A.; Liu, Y.; Ma, R.; Zhou, X. Experimental and Numerical Analysis of Reinforced Concrete Columns under Lateral Impact Loading. Buildings 2023, 13, 708. [Google Scholar] [CrossRef]
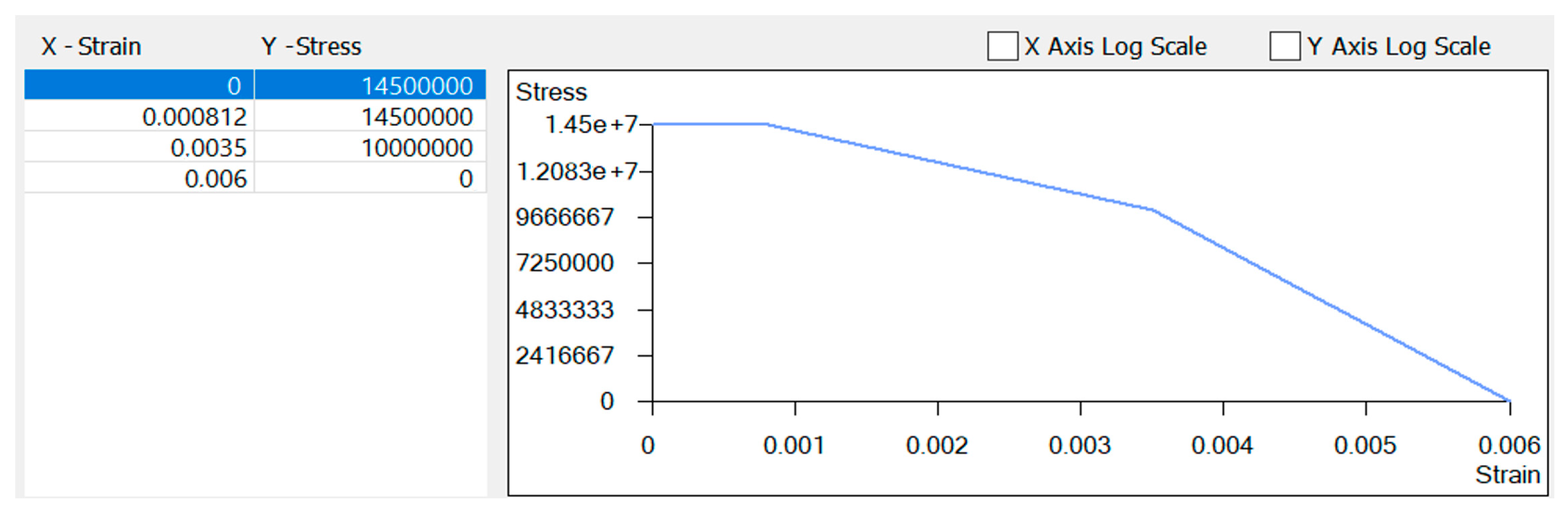


| Compressive Strength, MPa | Tensile Strength, MPa | Angle of Internal Friction , Degrees | Cohesion Stresses C, MPa | Dilation Angle, Degrees | Dilatation Level, |
|---|---|---|---|---|---|
| 14.5 | 1.05 | 34 | 3.5 | 28 | 0.3 |
| Method of Analysis | Maximum Deflection, mm | M/Mult * | Q/Qult * |
|---|---|---|---|
| Collection of Regulations 63.13330.2018 | 16.578 | 0.956 | 0.765 |
| Collection of Regulations 63.13330.2018 (redistribution of forces in a statically indeterminate system) | 16.57 | 0.656 | 0.555 |
| DP-model (3D model) | 16.44 | 0.7013 | 0.559 |
| D1, Lower Zone, at Peak Intensity | Bearing Capacity, Exposure Time | D2, Upper Zone, at Peak Intensity | Bearing Capacity, Exposure Time |
|---|---|---|---|
| Load q2 = 90,000 N/m2 (3.6 t/m) *, if an impact on concrete does not cause any fracture of rebars | |||
| 40 kN | Bearing capacity maintained, t = 0.8 s | 40 kN | Bearing capacity maintained, t = 0.8 s |
| 60 kN | The same | 60 kN | The same |
| 80 kN | The same | 80 kN | Fracture, t = 0.36 s |
| 84 kN | Fracture, t = 0.351 s | 84 kN | Fracture, t = 0.336 s |
| 86 kN | Fracture, t = 0.328 s | 86 kN | Fracture, t = 0.323 s |
| 88 kN | Fracture, t = 0.332 s | 88 kN | Fracture, t = 0.320 s |
| 90 kN | Fracture, t = 0.326 s | 90 kN | Fracture, t = 0.310 s |
| q3 = 120,000 N/m2 (4.8 t/m), if an impact on concrete does not cause any fracture of rebars | |||
| 10 kN | Bearing capacity maintained, t = 0.8 s | 10 kN | Bearing capacity maintained, t = 0.8 s |
| 20 kN | The same | 20 kN | The same |
| 30 kN | -//- | 30 kN | The same |
| 40 kN | Fracture, t = 0.303 s | 40 kN | Fracture, t = 0.287 s |
| 50 kN | Fracture, t = 0.251 s | 50 kN | Fracture, t = 0.231 s |
| 60 kN | Fracture, t = 0.186 s | 60 kN | Fracture, t = 0.172 s |
| 80 kN | Fracture, t = 0.135 s | 80 kN | t = 0.123 s |
| № | P, kN | , MPa | , m | , m | , N/m | Fracture |
|---|---|---|---|---|---|---|
| Operating load q1 = 60,000 (2.4 t/m) | ||||||
| 1 | 44 | 30.5 | 0.02975 | 0.53 | 88,963 | no |
| 2 | 50 | 0.61 | 110,080 | yes | ||
| 3 | 54 | 0.71 | 134,092 | yes | ||
| Operating load q2 = 90,000 (3.6 t/m) | ||||||
| 1 | 35 | 62.2 | 0.02742 | 0.39 | 96,645 | no |
| 2 | 36 | 0.40 | 100,035 | yes | ||
| 3 | 38 | 0.43 | 109,948 | yes | ||
| Operating load q3 = 120,000 (4.8 t/m) | ||||||
| 1 | 28 | 85.5 | 0.02571 | 0.29 | 91,177 | no |
| 2 | 30 | 0.31 | 98,972 | no | ||
| 3 | 32 | 0.34 | 110,203 | yes | ||
| Peak Intensity | Bearing Capacity, Exposure Time | Peak Intensity | Bearing Capacity, Exposure Time | Peak Intensity | Bearing Capacity, Exposure Time |
|---|---|---|---|---|---|
| Load q1 = 60,000 (2.4 t/m), | Load q2 = 90,000 (3.6 t/m), | Load q3 = 120,000 (2.4 t/m), | |||
| 30 kN | Not evaluated because J < Jcr | 48 kN | Rebar fracture J > Jcr The bearing capacity is maintained, t = 0.8 s | 24 kN | Not evaluated because J < Jcr |
| 40 kN | The same | 52 kN | The same | 32 kN | Rebar rupture J > Jcr Fracture, t = 0.356 s |
| 50 kN | Rebar rupture J > Jcr. The bearing capacity is maintained, t = 0.8 s | 56 kN | Fracture, t = 0.354 s | 40 kN | Fracture, t = 0.300 s |
| 60 kN | The same | 60 kN | Fracture, t = 0.323 s | 48 kN | Fracture, t = 0.254 s |
| 72 kN | The same | 68 kN | Fracture, t = 0.307 s | 60 kN | Fracture, t = 0.181 s |
| 76 kN | Fracture, t = 0.285 s | 72 kN | Fracture, t = 0.298 s | 64 kN | Fracture, t = 0.127 s |
| 80 kN | Fracture, t = 0.303 s | 76 kN | Fracture, t = 0.292 s | 70 kN | Fracture, t = 0.083 s |
| № | P, kN | , MPa | , m | , m | , N/m | Rebar Fracture |
|---|---|---|---|---|---|---|
| Operating load q = 60,000 (2.4 t/m) | ||||||
| 1 | 50 | 37 | 0.02561 | 0.41 | 95,304 | no |
| 2 | 56 | 0.46 | 114,624 | yes | ||
| 3 | 60 | 0.49 | 127,566 | yes | ||
| Operating load q = 90,000 (3.6 t/m) | ||||||
| 1 | 20 | 70 | 0.02349 | 0.36 | 91,426 | no |
| 2 | 24 | 0.40 | 106,450 | yes | ||
| 3 | 26 | 0.46 | 125,215 | yes | ||
| Operating load q = 120,000 (4.8 t/m) | ||||||
| 1 | 12 | 130 | 0.01963 | 0.21 | 99,309 | no |
| 2 | 16 | 0.27 | 131,616 | yes | ||
| 3 | 24 | 0.30 | 154,970 | yes | ||
| Peak Intensity | Bearing Capacity, Exposure Time | Peak Intensity | Bearing Capacity, Exposure Time | Peak Intensity | Bearing Capacity, Exposure Time |
|---|---|---|---|---|---|
| Load q1 = 60,000 (2.4 t/m), | Load q2 = 90,000 (3.6 t/m), | Load q3 = 120,000 (4.8 t/m), | |||
| 48 kN | Not evaluated as J < Jcr | 28 kN | Rebar rupture, J > Jcr. Bearing capacity maintained, t = 0.8 s | 14 kN | Rebar rupture, J > Jcr. Bearing capacity maintained, t = 0.8 s |
| 52 kN | The same | 30 kN | The same | 16 kN | The same |
| 56 kN | Rebar rupture, J > Jcr. Bearing capacity maintained, t = 0.8 s | 32 kN | The same | 20 kN | The same |
| 60 kN | The same | 38 kN | The same | 24 kN | The same |
| 68 kN | The same | 44 kN | The same | 28 kN | Fracture, t = 0.287 s |
| 72 kN | Fracture, t = 0.304 s | 48 kN | Fracture, t = 0.285 s | 32 kN | Fracture, t = 0.312 s |
| 76 kN | Fracture, t = 0.359 s | 52 kN | Fracture, t = 0.264 s | 36 kN | Fracture, t = 0.069 s |
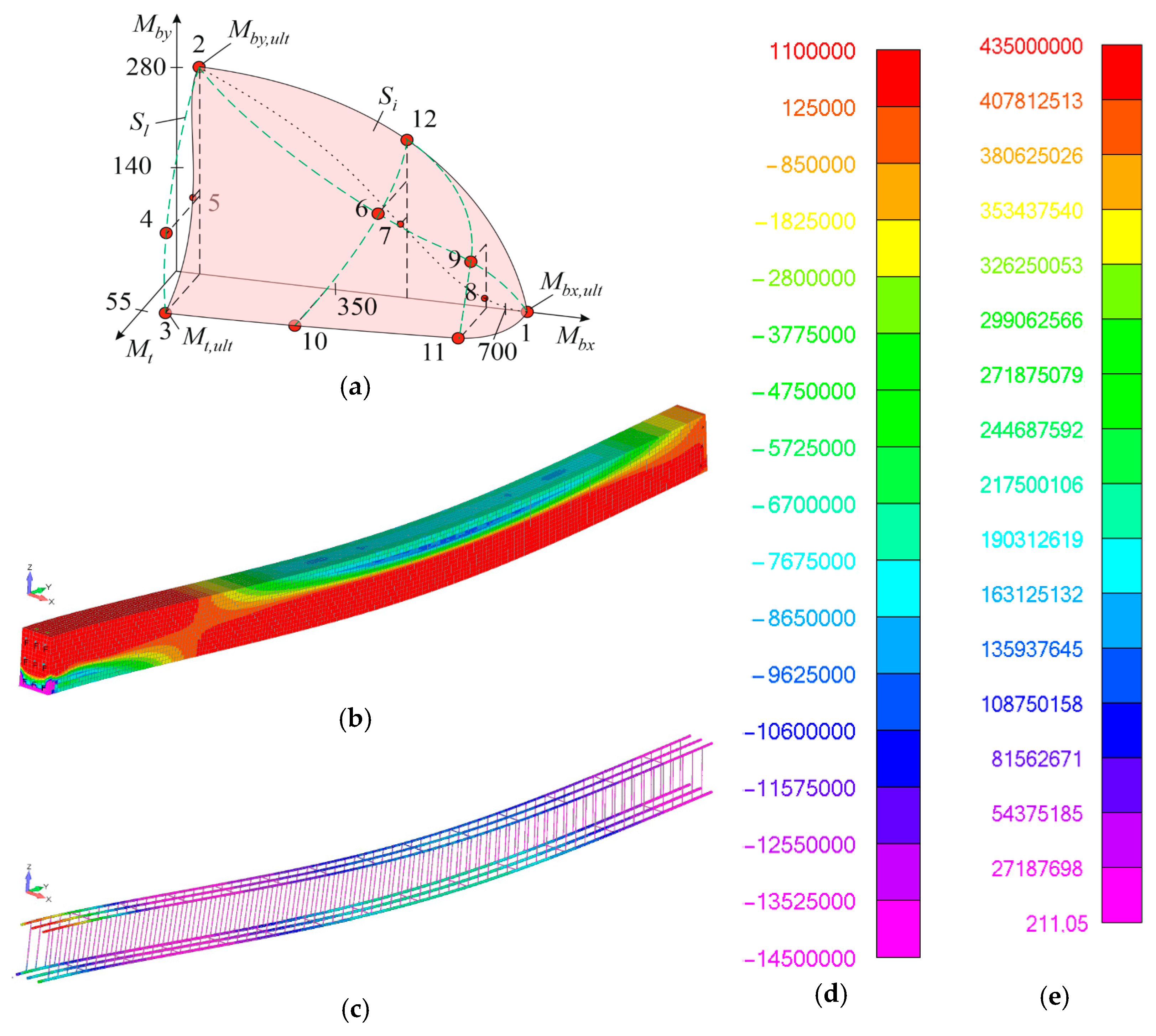
| No. of Points (Figure 16a) | , kN | , kNm | , kNm |
|---|---|---|---|
| 1 | 731.8 | 0 | 0 |
| 2 | 38.58 * | 280.70 | 0 |
| 3 ** | 38.58 | 0 | 54.00 |
| 4 | 38.58 | 126.04 | 50.63 |
| 5 | 38.58 | 120.15 | 4.41 |
| 6 | 496.12 | 115.21 | 46.04 |
| 7 | 496.12 | 86.25 | 3.20 |
| 8 | 661.50 | 21.20 | 1.40 |
| 9 | 661.50 | 72.91 | 28.70 |
| 10 | 330.75 | 0 | 52.54 |
| 11 | 661.50 | 0 | 51.01 |
| 12 | 496.12 | 239.0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alekseytsev, A. Local Fracture of a Reinforced Concrete Beam Under High-Velocity Impact on Biaxial Bending and Torsion Deformation. Buildings 2025, 15, 4153. https://doi.org/10.3390/buildings15224153
Alekseytsev A. Local Fracture of a Reinforced Concrete Beam Under High-Velocity Impact on Biaxial Bending and Torsion Deformation. Buildings. 2025; 15(22):4153. https://doi.org/10.3390/buildings15224153
Chicago/Turabian StyleAlekseytsev, Anatoly. 2025. "Local Fracture of a Reinforced Concrete Beam Under High-Velocity Impact on Biaxial Bending and Torsion Deformation" Buildings 15, no. 22: 4153. https://doi.org/10.3390/buildings15224153
APA StyleAlekseytsev, A. (2025). Local Fracture of a Reinforced Concrete Beam Under High-Velocity Impact on Biaxial Bending and Torsion Deformation. Buildings, 15(22), 4153. https://doi.org/10.3390/buildings15224153






