Mechanical Performance Evaluation and Strengthening of Rectangular RC Columns with Deficient Lap Splices: Monotonic Loading Tests and Equivalent Plastic Hinge Modeling
Abstract
1. Introduction
2. Experiment Program
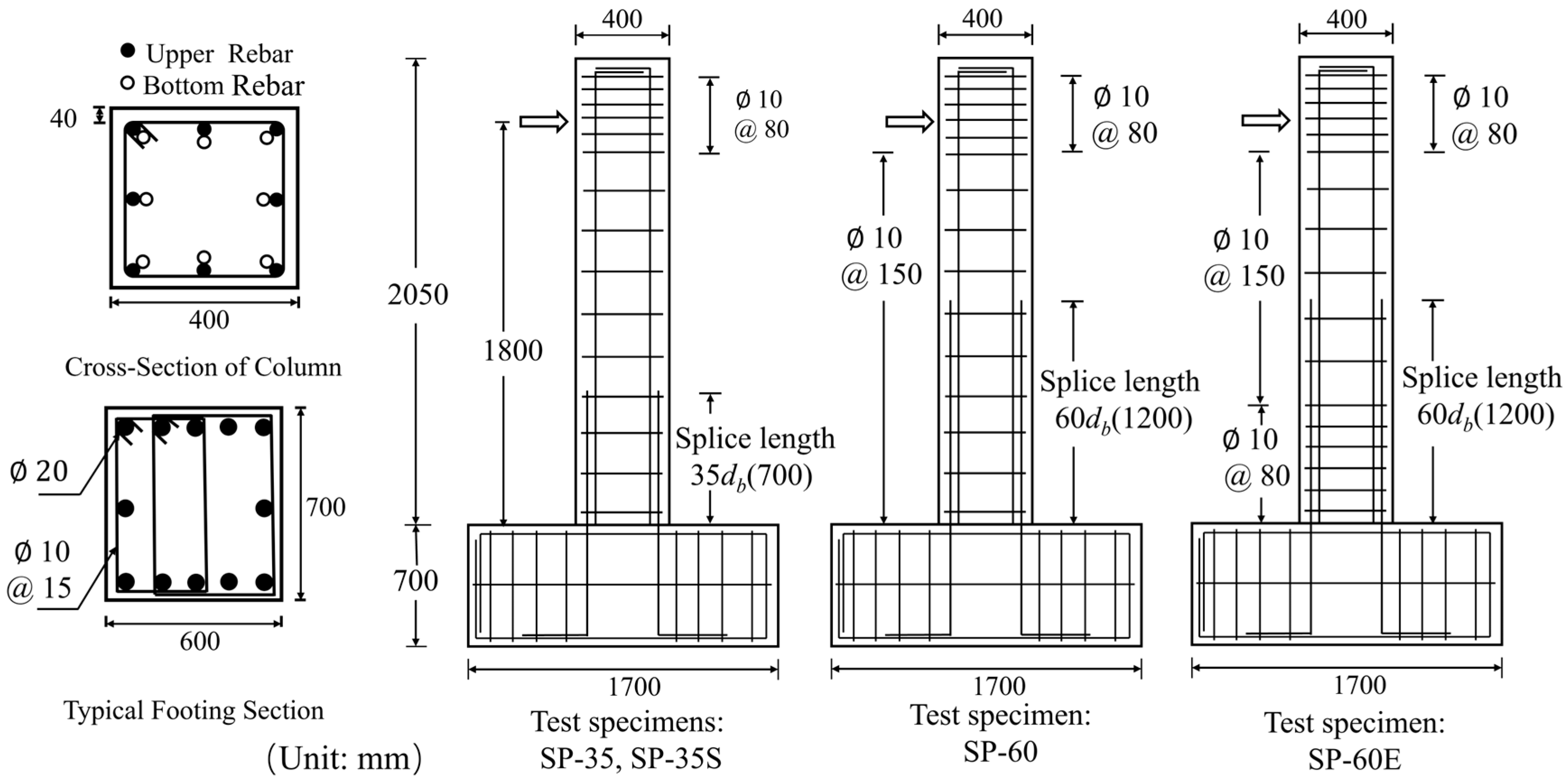
2.1. Specimen Design and Materials
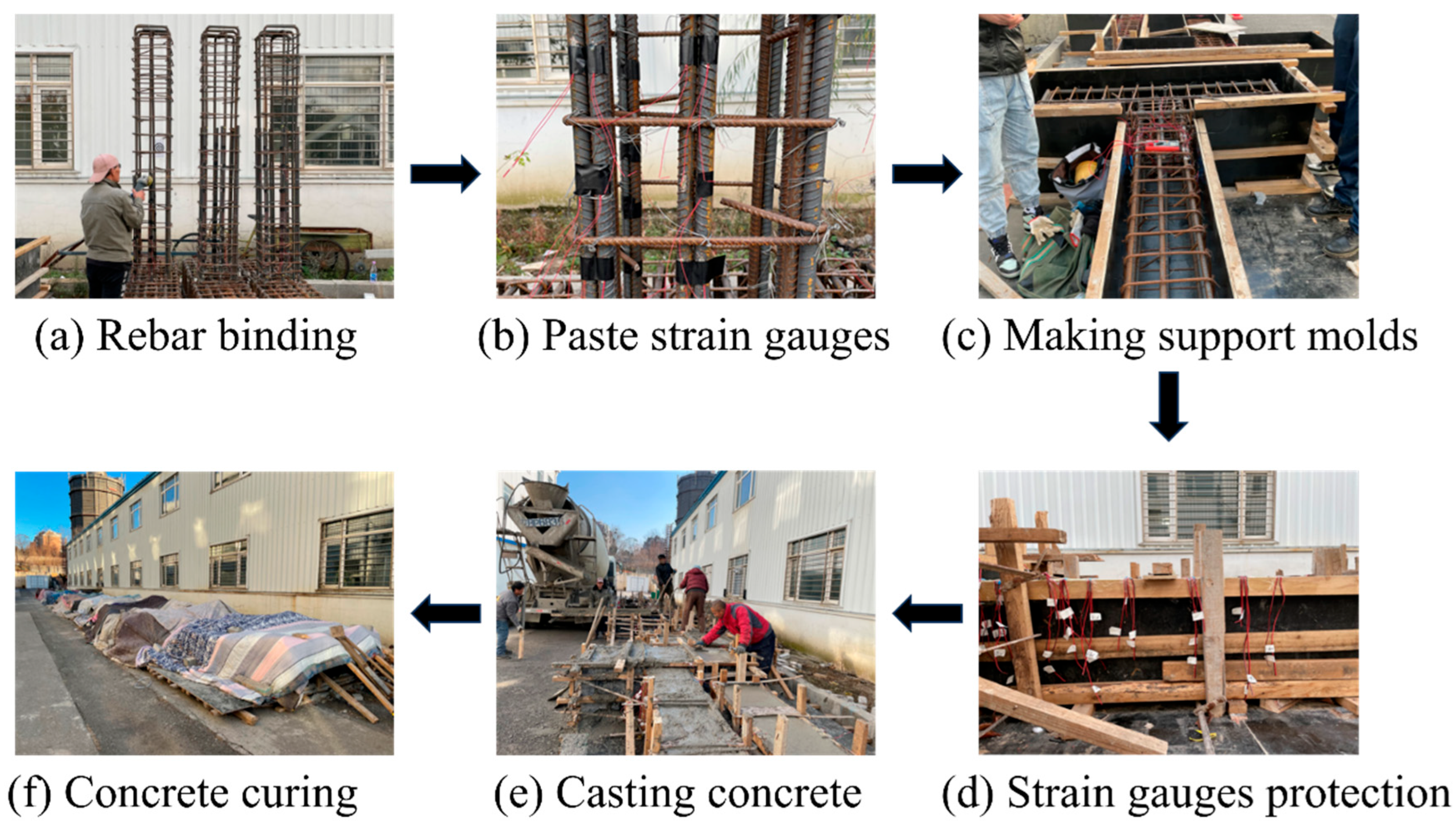
2.2. Construction Process
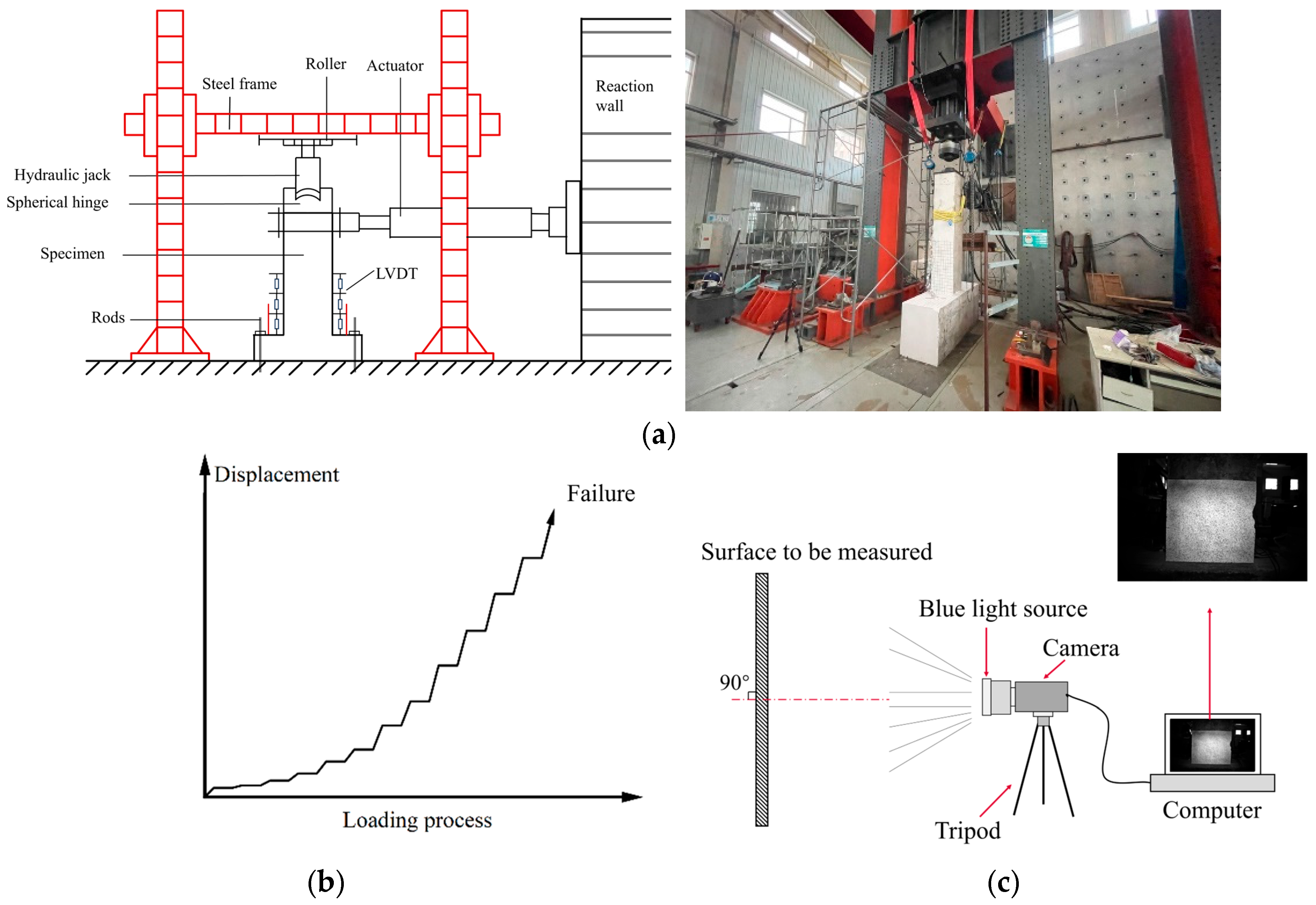
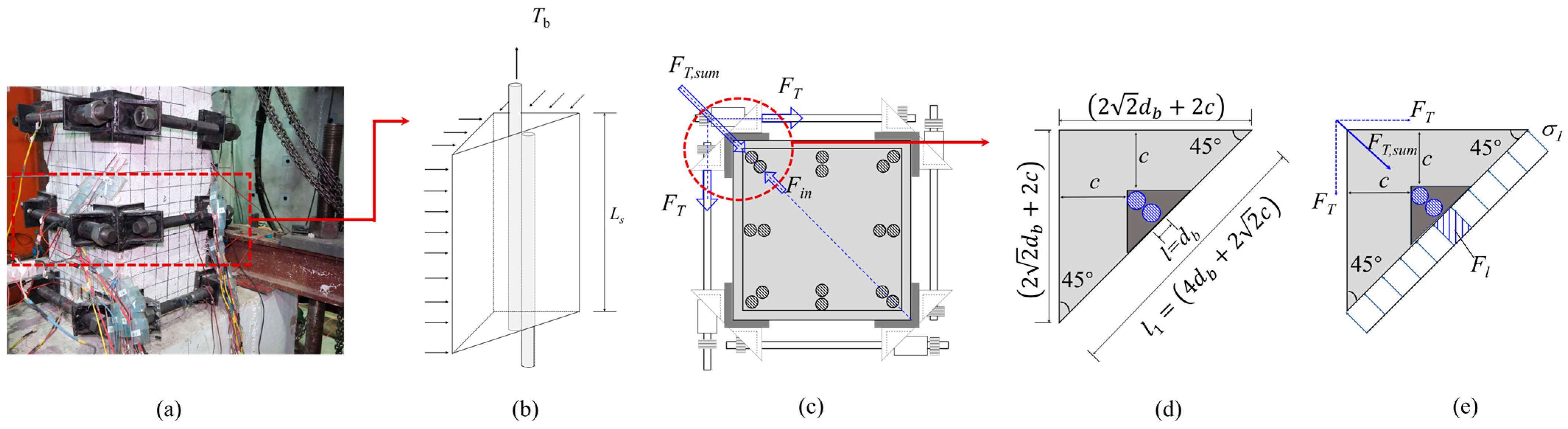
2.3. Loading and Instrumentation
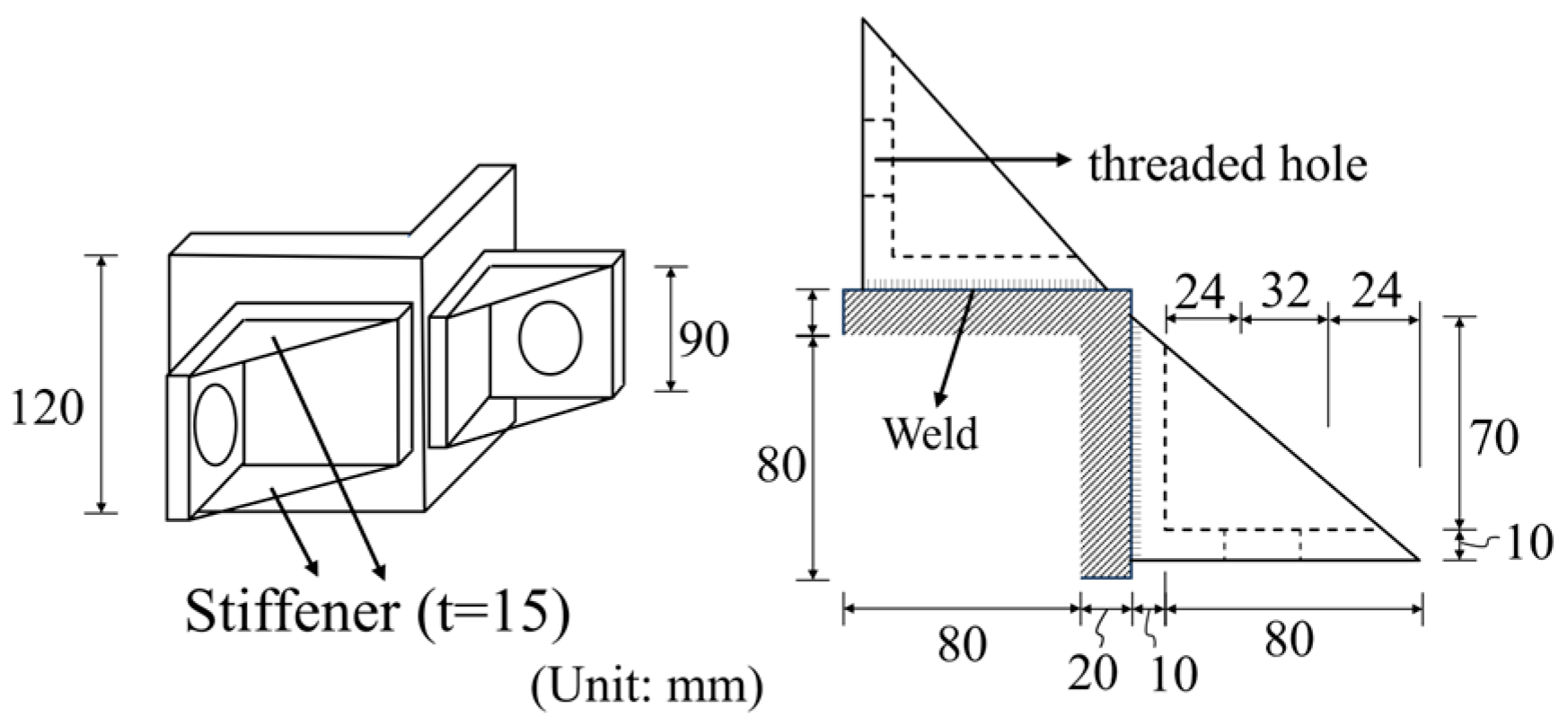
2.4. Strengthening Method
3. Experiment Results and Discussion
3.1. Failure Mode
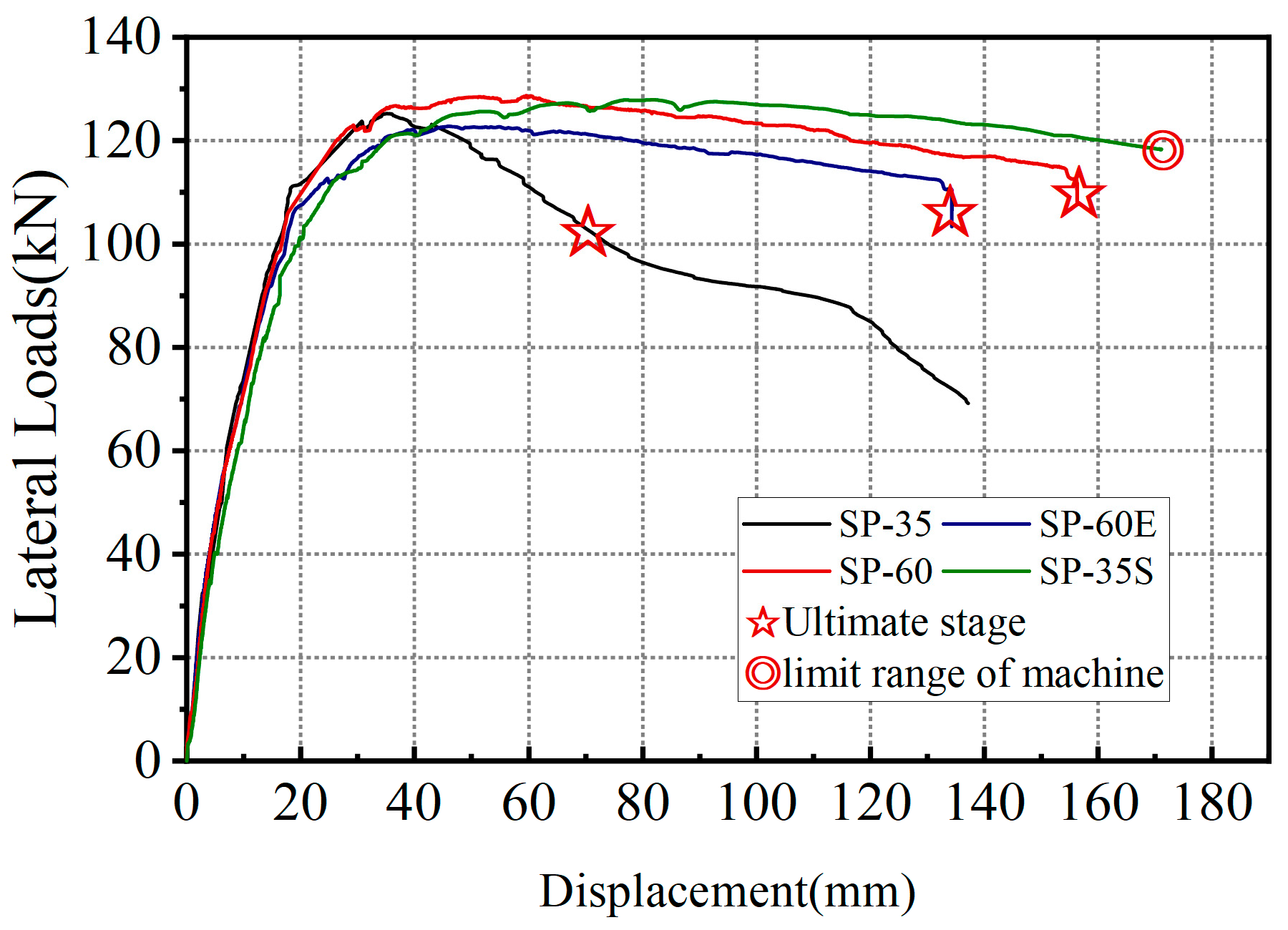
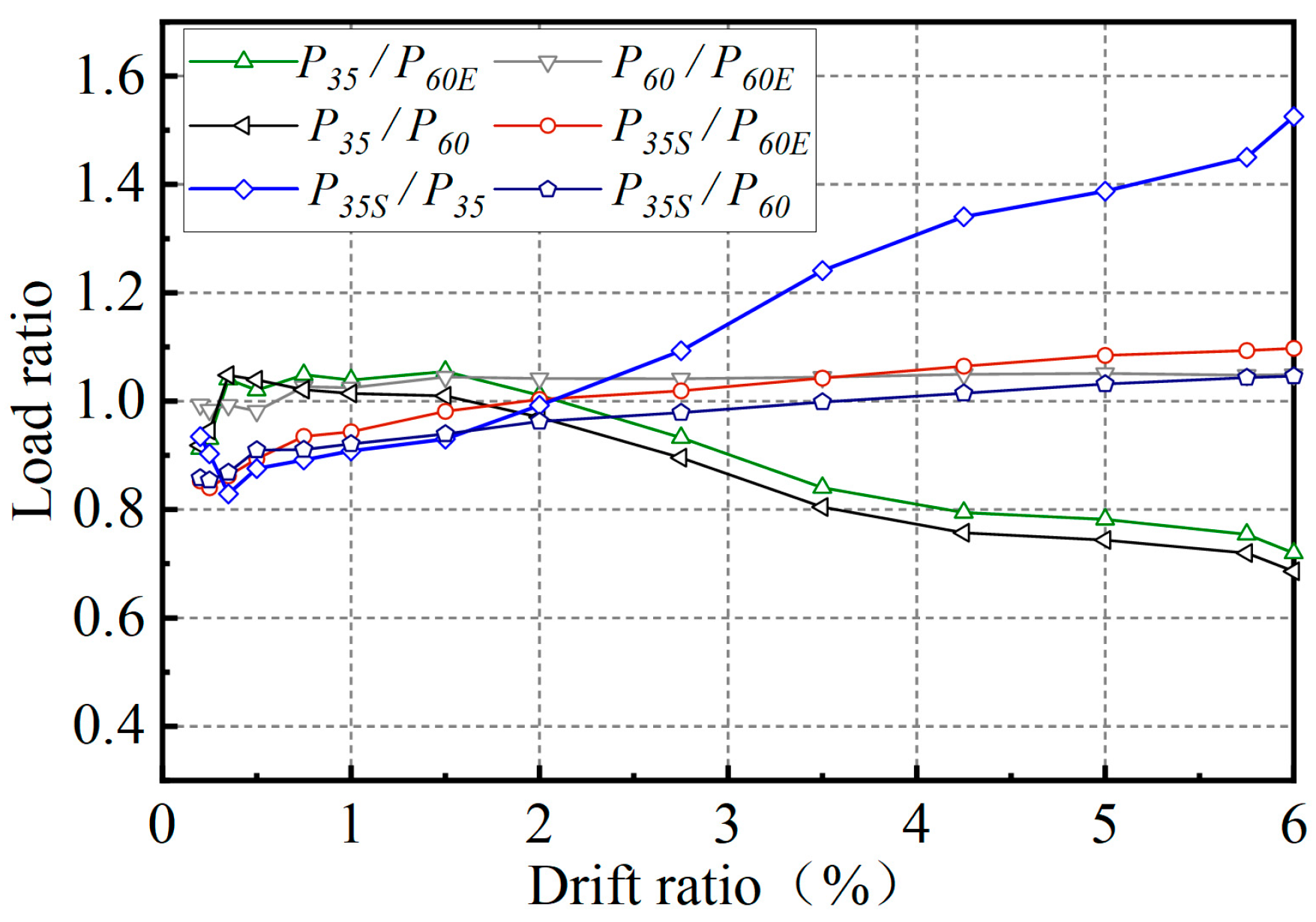
3.2. Load–Displacement Relationship
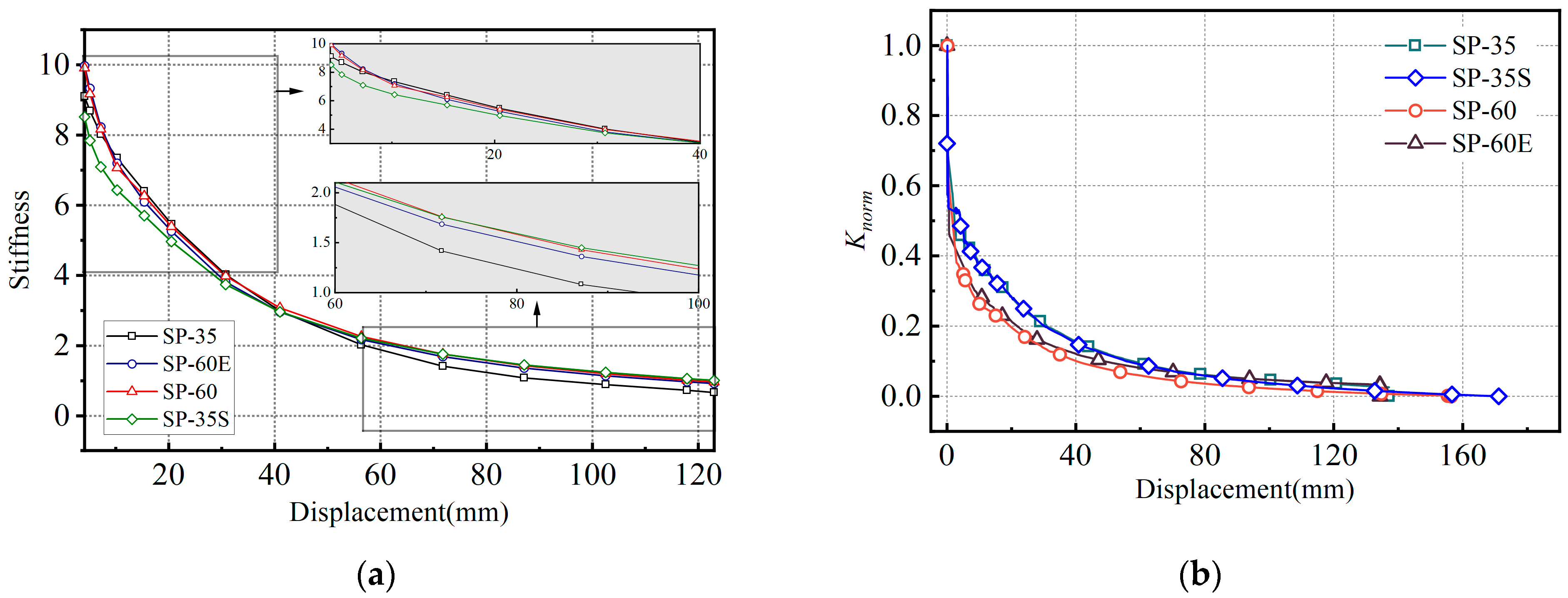
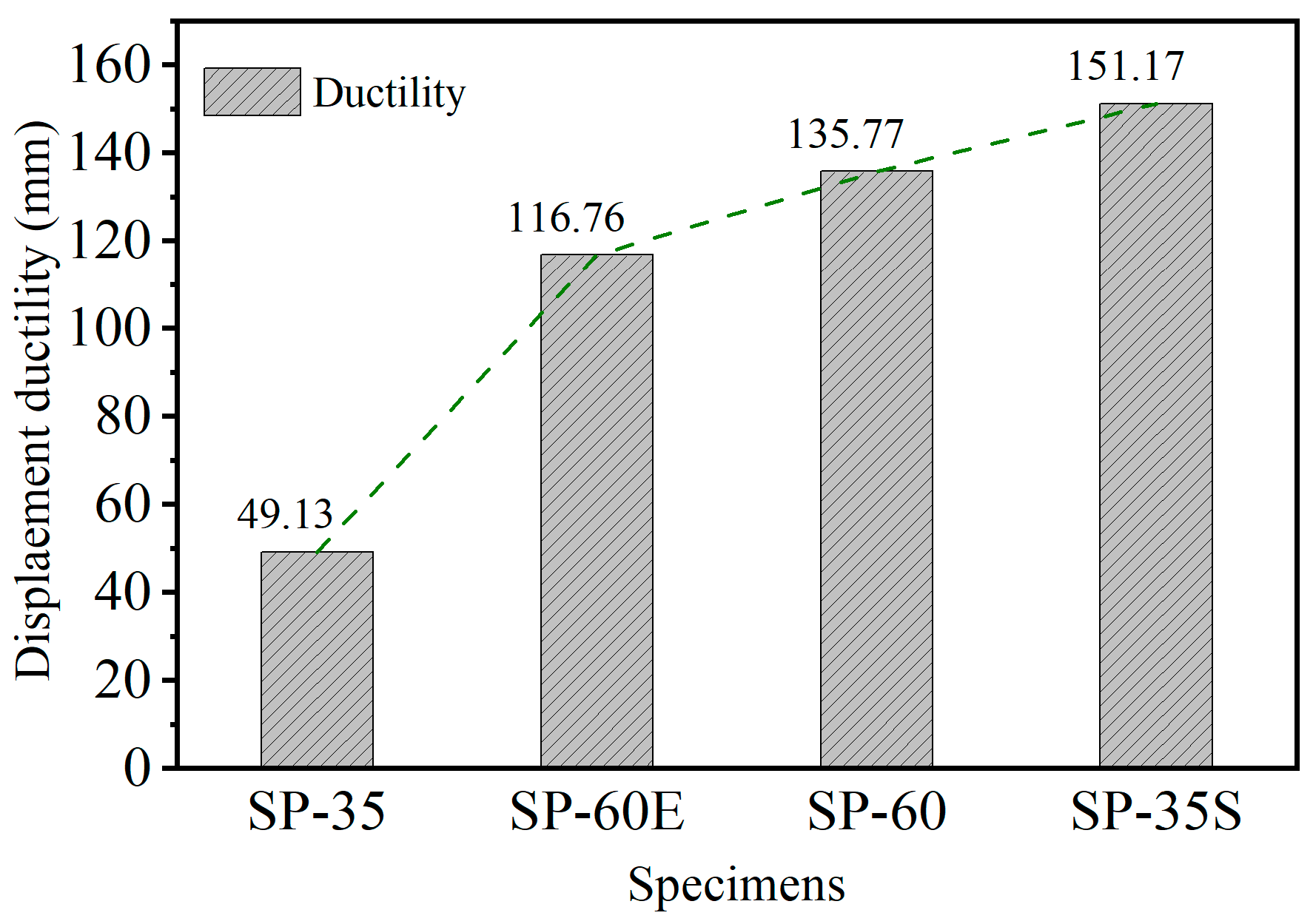
3.3. Stiffness Degradation and Ductility
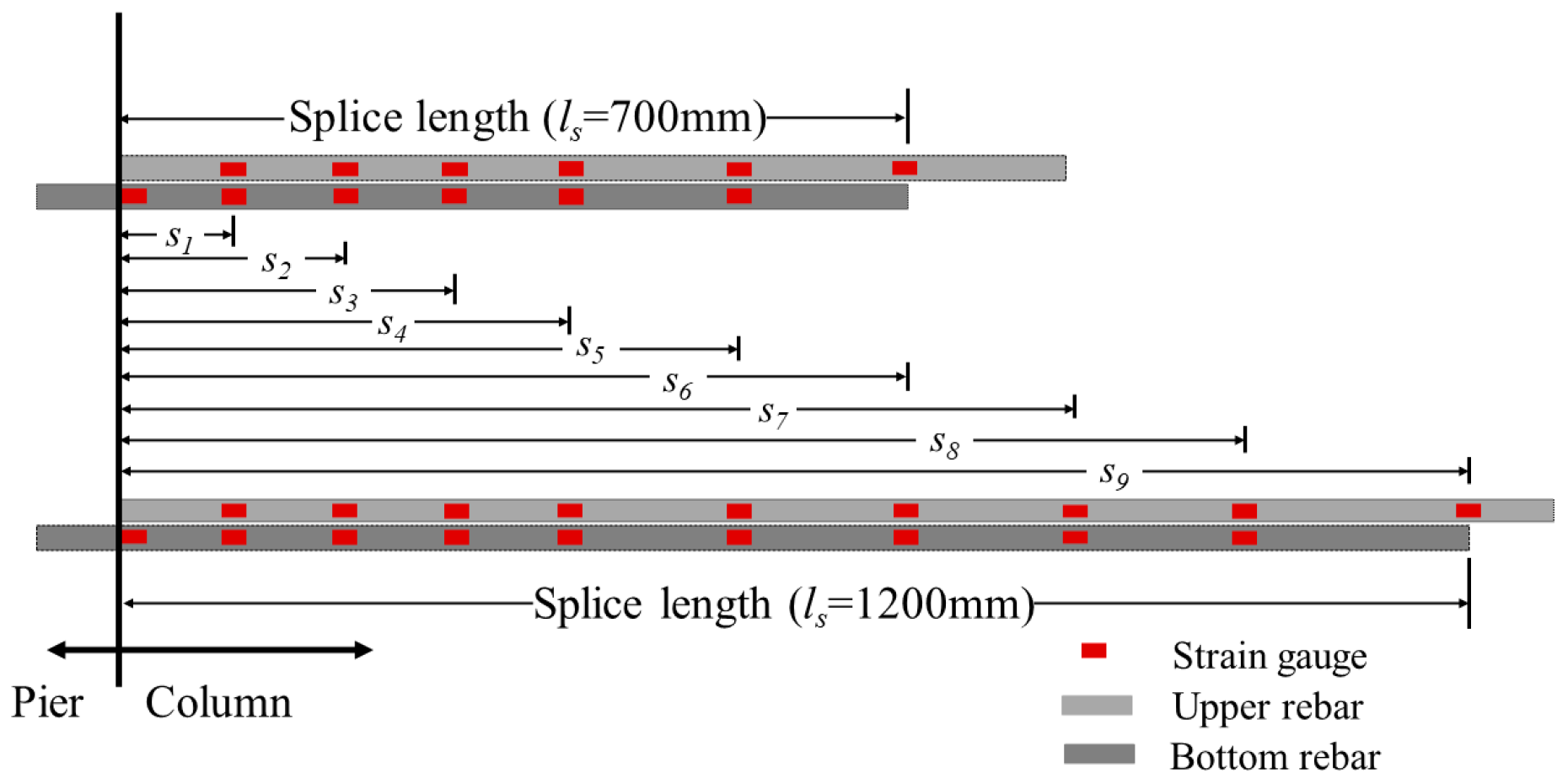
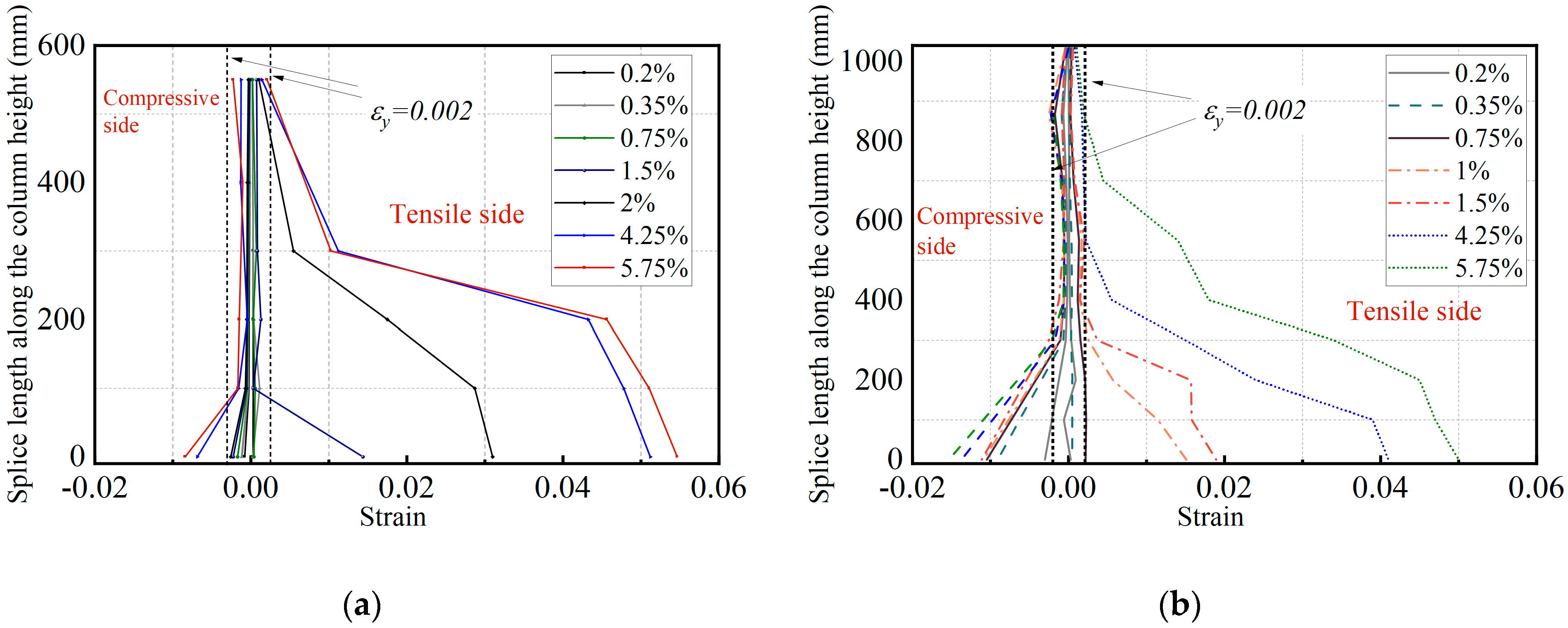
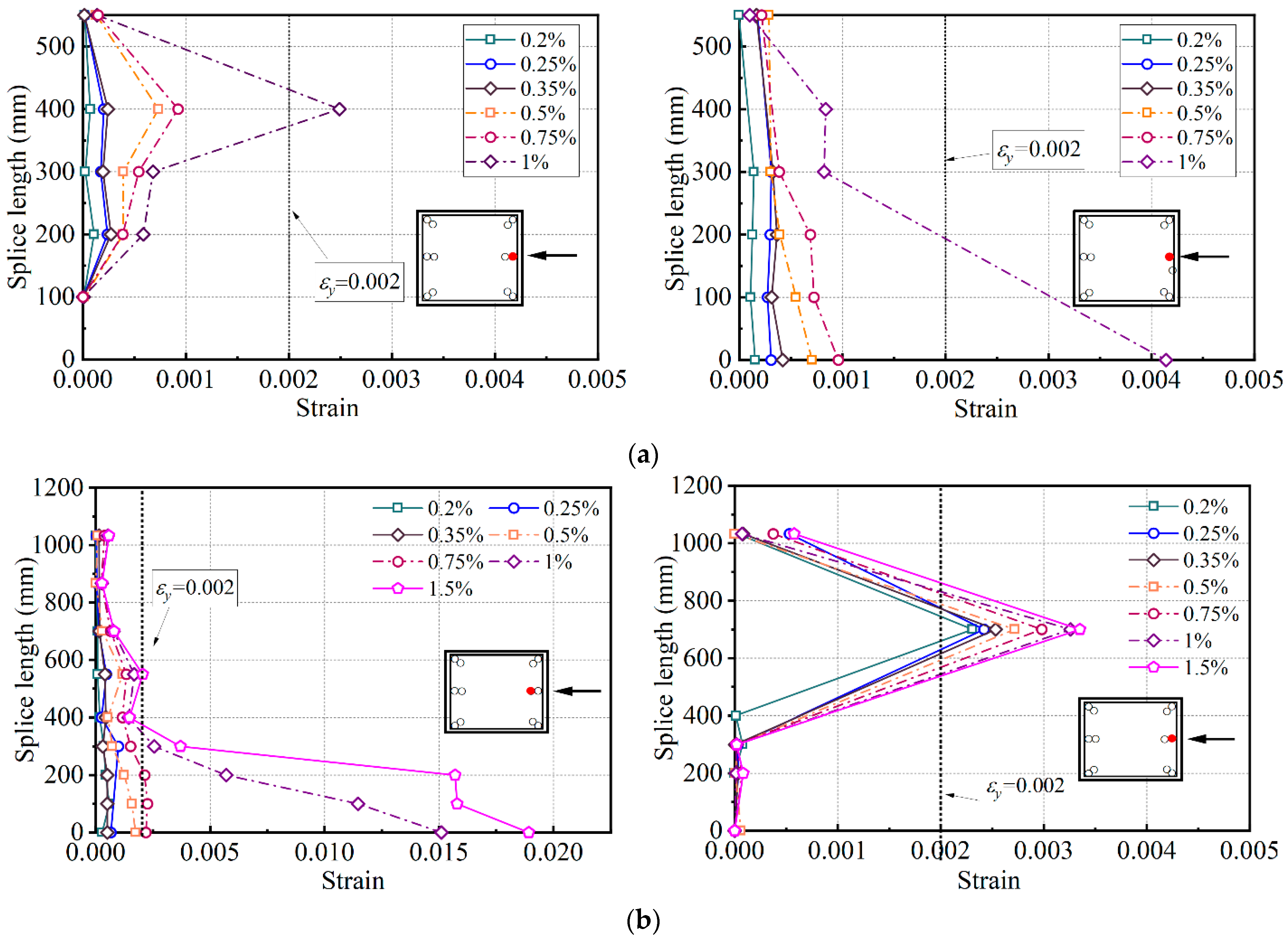
3.4. Strain Distribution
3.5. Stress Transfer
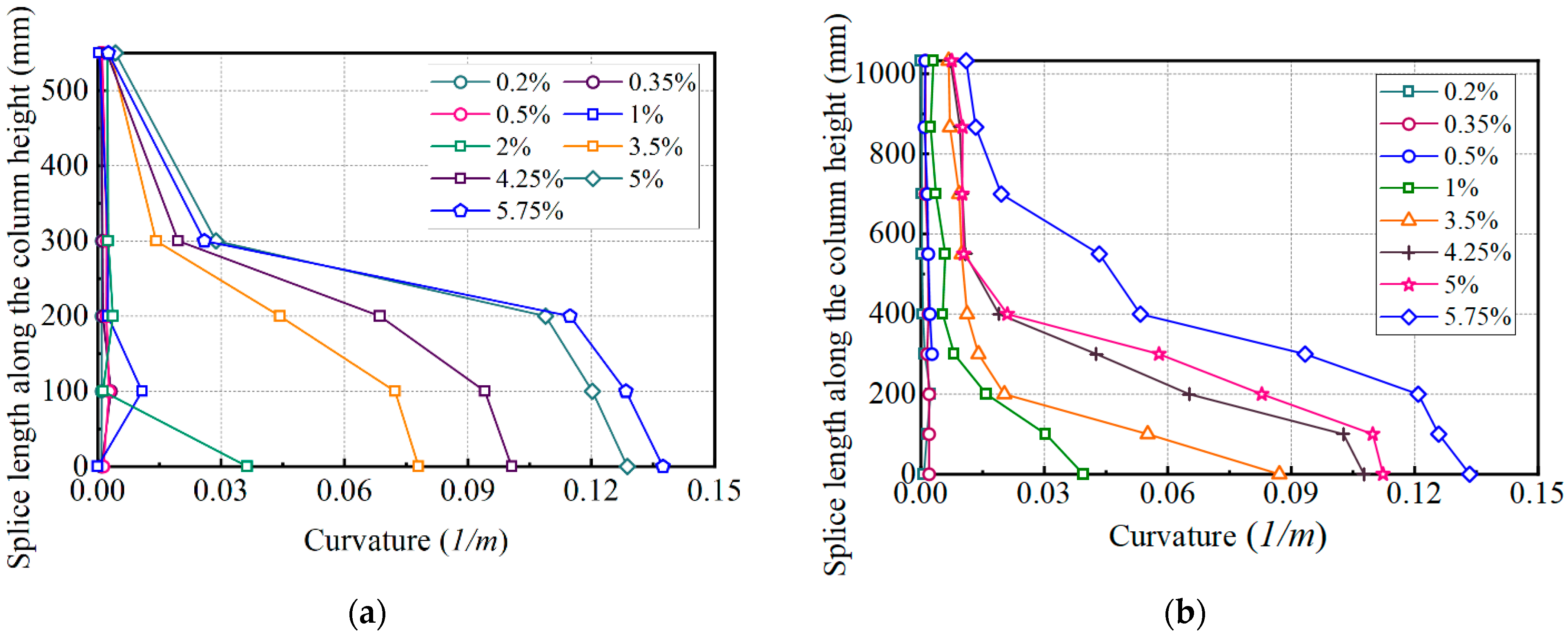
3.6. Curvature Along the Column Height
3.7. Plastic Hinge
4. Equivalent Plastic Hinge Model of Lap-Spliced Columns
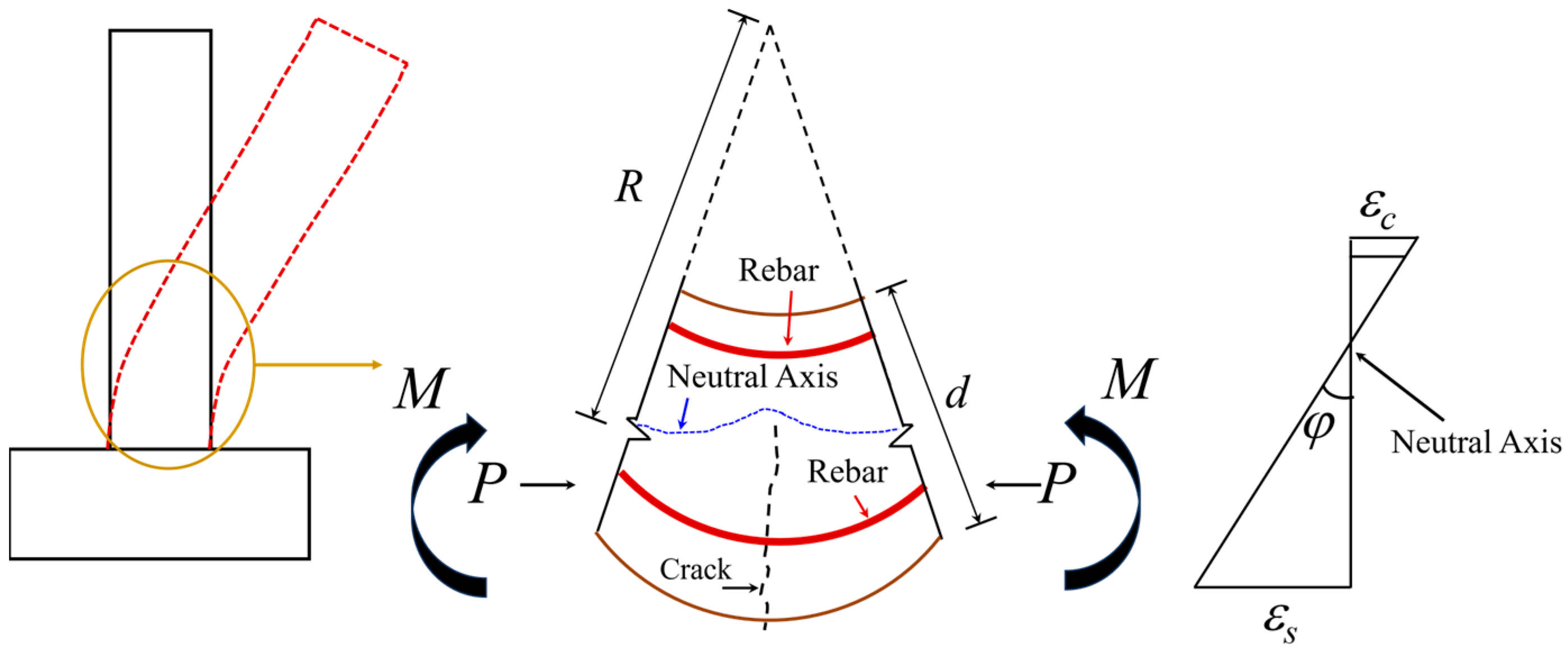
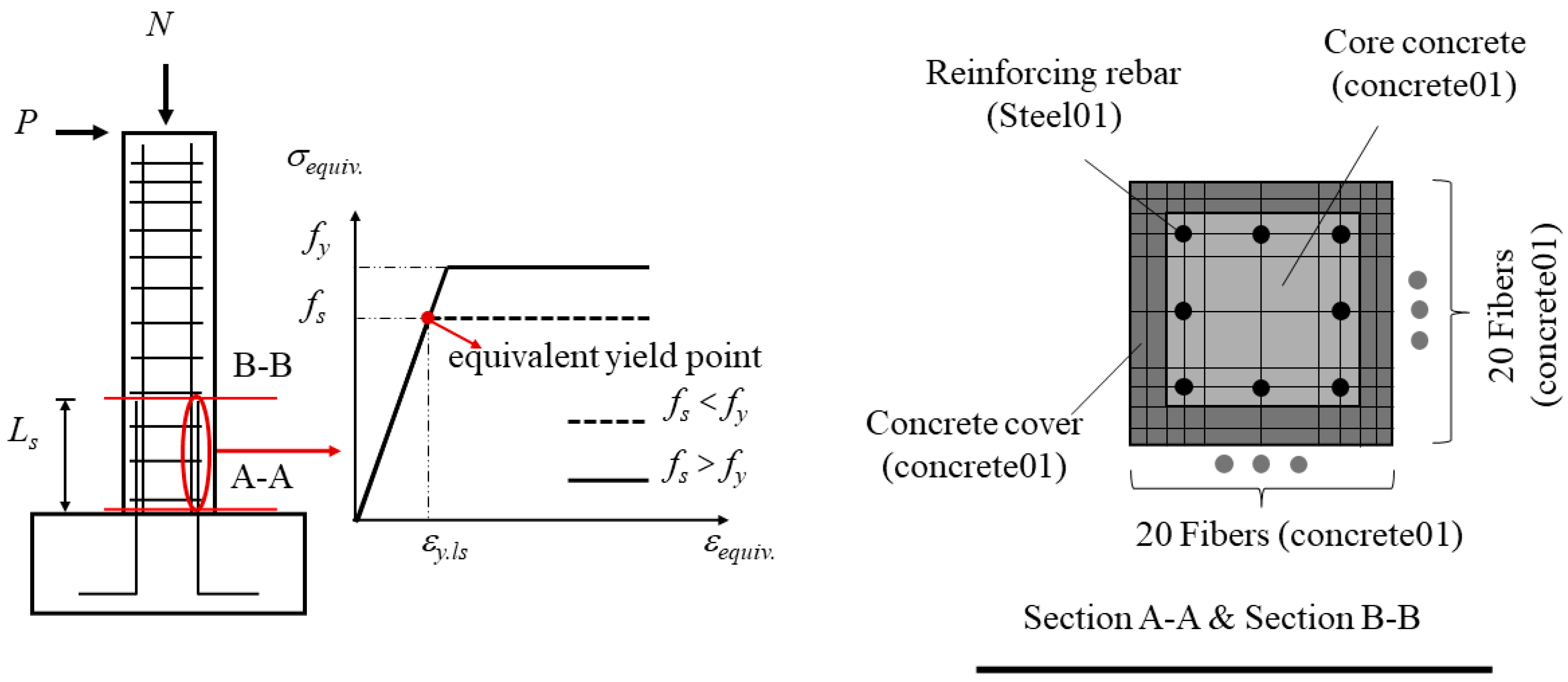
4.1. Cross-Section Analysis
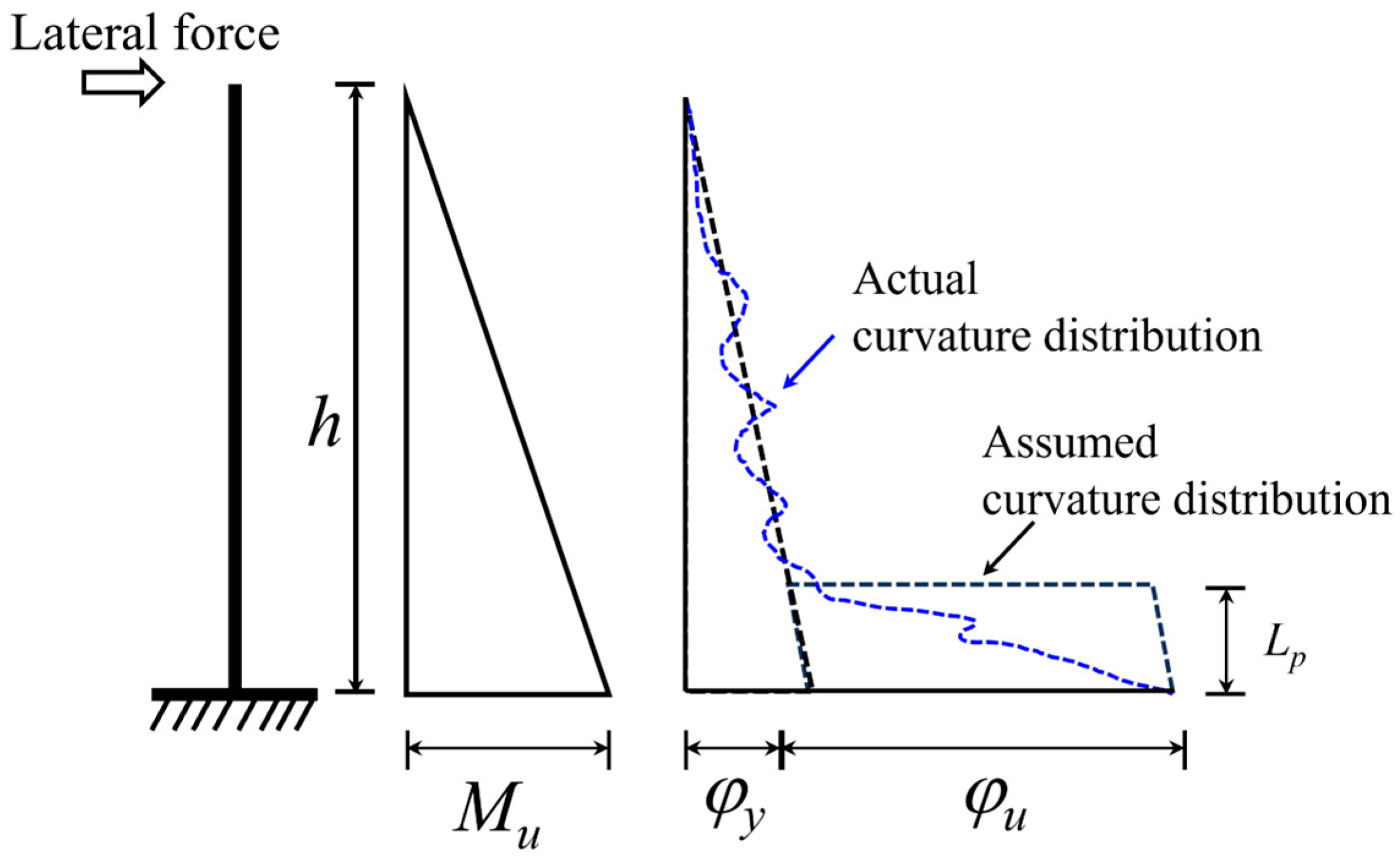
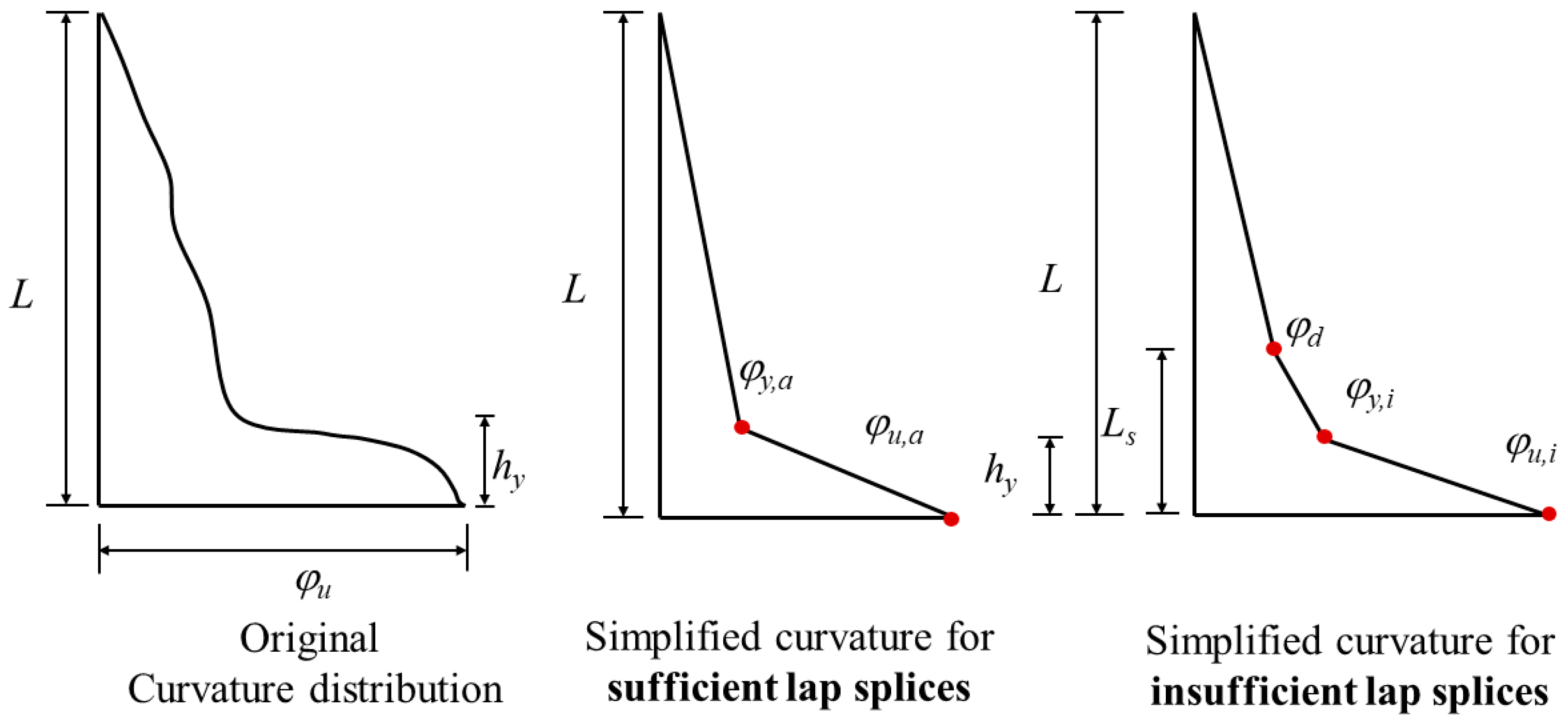
4.2. Equivalent Curvature Distribution
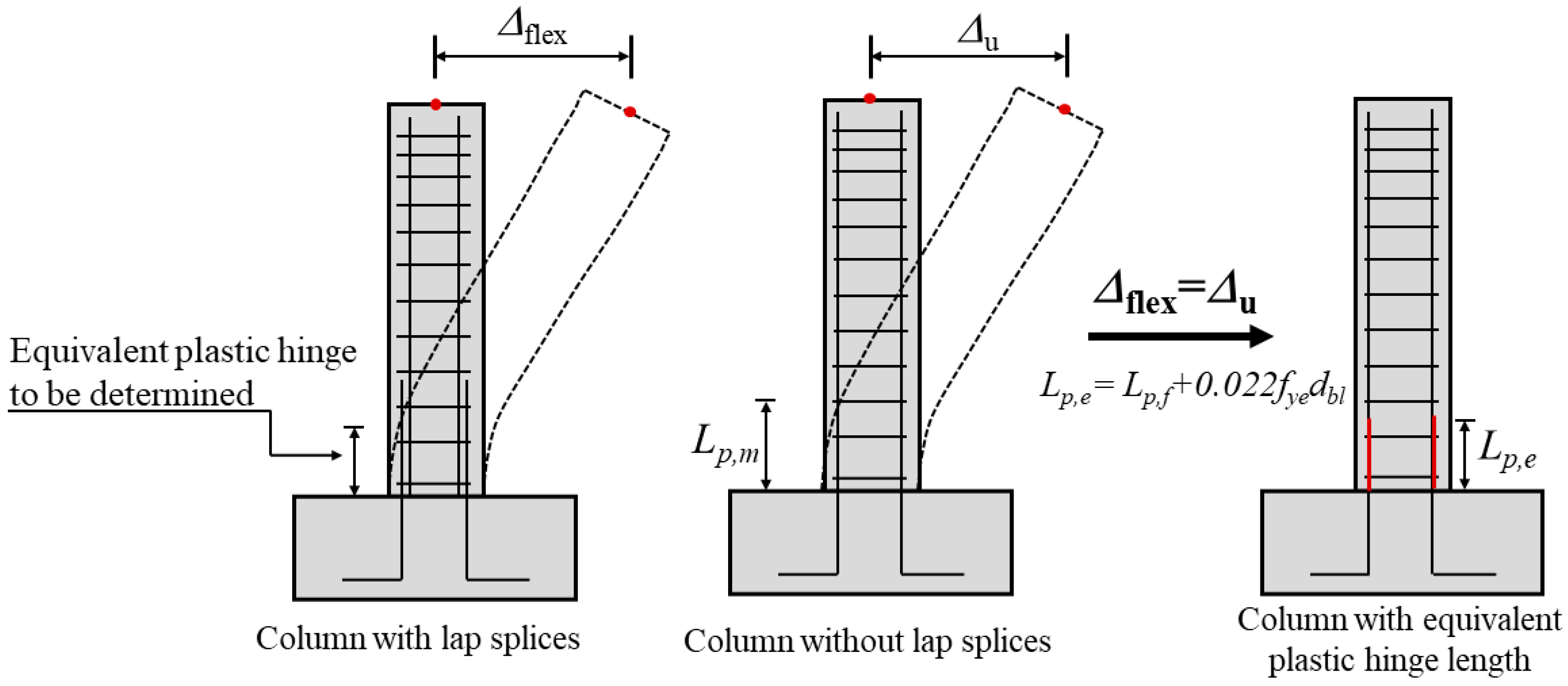
4.3. Equivalent Plastic Hinge Model
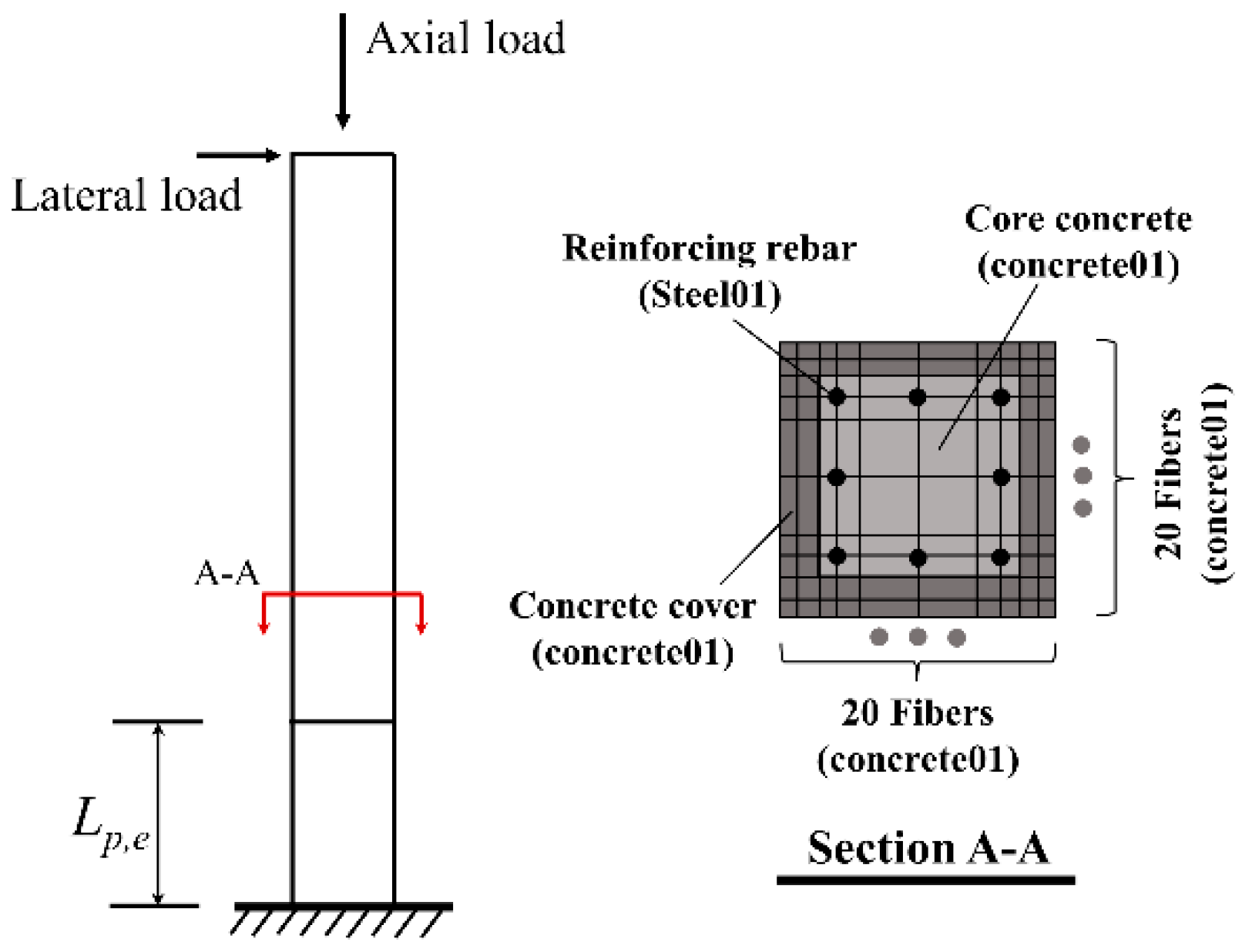
5. Verification of Proposed Modelling Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aboutaha, R.S.; Engelhardt, M.D.; Jirsa, J.O.; Kreger, M.E. Experimental investigation of seismic repair of lap splice failures in damaged concrete columns. ACI Struct. J. 1999, 96, 297–306. [Google Scholar]
- Lucchini, A.; Franchin, P.; Kunnath, S. Failure simulation of shear-critical RC columns with non-ductile detailing under lateral load. Earthq. Eng. Struct. Dyn. 2017, 46, 855–874. [Google Scholar] [CrossRef]
- American Concrete Institute (ACI) Committee 318. Building Code Requirements for Structural Concrete (ACI 318-56) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 1956. [Google Scholar]
- American Concrete Institute (ACI) Committee 318. Building Code Requirements for Structural Concrete (ACI 318-63) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 1963. [Google Scholar]
- American Concrete Institute (ACI) Committee 318. Building Code Requirements for Structural Concrete (ACI 318-77) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 1977. [Google Scholar]
- Jeon, J.-S.; Lowes, L.N.; DesRoches, R.; Brilakis, I. Fragility curves for non-ductile reinforced concrete frames that exhibit different component response mechanisms. Eng. Struct. 2015, 85, 127–143. [Google Scholar] [CrossRef]
- Haavisto, J.; Alho, H.; Laaksonen, A. Behavior of lap splices in reinforced concrete beams after bar yielding. Struct. Concr. 2023, 24, 5245–5264. [Google Scholar] [CrossRef]
- Bousias, S.; Spathis, A.L.; Fardis, M.N. Seismic retrofitting of columns with lap splices through CFRP jackets. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. (No. 765). [Google Scholar]
- Muhammad Gillani, A.S.; Lee, S.-G.; Lee, S.-H.; Lee, H.; Hong, K.J. Local Behavior of Lap-Spliced Deformed Rebars in Reinforced Concrete Beams. Materials 2021, 14, 7186. [Google Scholar] [CrossRef]
- Zhang, Y.; DesRoches, R.; Tien, I. Impact of corrosion on risk assessment of shear-critical and short lap spliced bridges. Eng. Struct. 2019, 189, 260–271. [Google Scholar] [CrossRef]
- Kim, C.-G.; Park, H.-G.; Eom, T.-S. Seismic Performance of Reinforced Concrete Columns with Lap Splices in Plastic Hinge Region. ACI Struct. J. 2018, 115, 235–245. [Google Scholar] [CrossRef]
- Kim, C.-G.; Park, H.-G.; Eom, T.-S. Effects of Type of Bar Lap Splice on Reinforced Concrete Columns Subjected to Cyclic Loading. ACI Struct. J. 2019, 116, 183–194. [Google Scholar] [CrossRef]
- American Concrete Institute (ACI) Committee 318. Building Code Requirements for Structural Concrete (ACI 318-95) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 1995. [Google Scholar]
- CAN/CSA-S6-06; Canadian Highway Bridge Design Code. Canadian Standards Association (CAN/CSA): Mississauga, ON, Canada, 2006.
- American Association of State Highway and Transportation Officials (AASHTO). LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2013. [Google Scholar]
- Melek, M.; Wallace, J.W. Cyclic Behavior of Columns with Short Lap Splices. ACI Struct. J. 2004, 101, 802–811. [Google Scholar]
- Lynn, A.C.; Moehle, J.P.; Mahin, S.A.; Holms, W.T. Seismic Evaluation of Existing Reinforced Concrete Building Columns. Earthq. Spectra 1996, 12, 715–739. [Google Scholar] [CrossRef]
- Haroun, M.A.; Elsanadedy, H.M. Fiber-Reinforced Plastic Jackets for Ductility Enhancement of Reinforced Concrete Bridge Columns with Poor Lap-Splice Detailing. J. Bridge Eng. 2005, 10, 749–757. [Google Scholar] [CrossRef]
- Harries, K.A.; Ricles, J.M.; Pessiki, S.; Sause, R. Seismic Retrofit of Lap Splices in Nonductile Square Columns Using Carbon Fiber-Reinforced Jackets. ACI Struct. J. 2006, 103, 874–884. [Google Scholar]
- Harajli, M. Seismic Behavior of RC Columns with Bond-Critical Regions: Criteria for Bond Strengthening Using External FRP Jackets. J. Compos. Constr. 2008, 12, 69–79. [Google Scholar] [CrossRef]
- Tarquini, D.; Almeida, J.P.; Beyer, K. Influence of Lap Splices on the Deformation Capacity of RC Walls. II: Shell Element Simulation and Equivalent Uniaxial Model. J. Struct. Eng. 2017, 143, 04017157. [Google Scholar] [CrossRef]
- Tariverdilo, S.; Farjadi, A.; Barkhordary, M. Fragility curves for reinforced concrete frames with lap spliced columns. IJE Trans. A Basics 2009, 22, 213–224. [Google Scholar]
- Barkhordary, M.; Tariverdilo, S. Vulnerability of ordinary moment resistant concrete frames. Earthq. Eng. Eng. Vib. 2011, 10, 519–533. [Google Scholar] [CrossRef]
- Choi, E.; Park, S.H.; Chung, Y.S.; Kim, H.S. Seismic fragility analysis of lap spliced reinforced concrete columns retrofitted by SMA wire jackets. Smart Mat. Struct. 2013, 22, 085028. [Google Scholar] [CrossRef]
- Bai, Y.-L.; Bai, S.-C.; Mei, S.-J.; Jia, J.-F. Experimental and numerical study of PEN FRP-strengthened circular RC columns under lateral cyclic loading with high axial compression ratio. Eng. Struct. 2023, 294, 116711. [Google Scholar] [CrossRef]
- Iacobucci, R.D.; Sheikh, S.A.; Bayrak, O. Retrofit of square concrete columns with carbon fiber-reinforced polymer for seismic resistance. ACI Struct. J. 2003, 100, 785–794. [Google Scholar]
- Wang, D.Y.; Wang, Z.Y.; Smith, S.T.; Yu, T. Seismic performance of CFRP-confined circular high-strength concrete columns with high axial compression ratio. Constr. Build. Mater. 2017, 134, 91–103. [Google Scholar] [CrossRef]
- Kharal, Z.; Sheikh, S.A. Seismic behavior of square and circular concrete columns with GFRP reinforcement. J. Compos. Constr. 2020, 24, 04019059. [Google Scholar] [CrossRef]
- Ye, Y.-Y.; Liang, S.-D.; Feng, P.; Zeng, J.-J. Recyclable LRS FRP composites for engineering structures: Current status and future opportunities. Compos. Part. B-Eng. 2021, 212, 108689. [Google Scholar] [CrossRef]
- Anggawidjaja, D.; Ueda, T.; Dai, J.; Nakai, H. Deformation capacity of RC piers wrapped by new fiber-reinforced polymer with large fracture strain. Cem. Concr. Comp. 2006, 28, 914–927. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, L.; Elchalakani, M.; Cai, J. Cyclic loading test for reinforced concrete columns strengthened with high-strength engineered cementitious composite jacket. Eng. Struct. 2023, 278, 115571. [Google Scholar] [CrossRef]
- Hong, S.-G.; Lee, J.-H.; Choi, Y.; Gu, I.-Y. Seismic Strengthening of Concrete Columns by Ultrahigh-Performance Fiber-Reinforced Concrete Jacketing. J. Struct. Eng. 2021, 47, 04021157. [Google Scholar] [CrossRef]
- Mansour, W.; Li, W.; Ghalla, M.; Badawi, M.; El Zareef, M.A. Improving the punching capacity of two-way RC flat slabs via external strengthening using various configurations of aluminum sheets. Constr. Build. Mater. 2024, 420, 135611. [Google Scholar] [CrossRef]
- Saleh, H.; Kalfat, R.; Abdouka, K.; Al-Mahaidi, R. Experimental and numerical study into the punching shear strengthening of RC flat slabs using post-installed steel bolts. Constr. Build. Mater. 2018, 188, 28–39. [Google Scholar] [CrossRef]
- Abas Golham, M.; Al-Ahmed, A.H.A. Behavior of GFRP reinforced concrete slabs with openings strengthened by CFRP strips. Results Eng. 2023, 18, 101033. [Google Scholar] [CrossRef]
- Harajli, M.H.; Hantouche, E.G. Effect of Active versus Passive Confinement on Seismic Response of Wide RC Columns with Lap Splices. J. Struct. Eng. 2014, 141, 04014221. [Google Scholar] [CrossRef]
- FEMA (Federal Emergency Management Agency). Multi-Hazard Loss Estimation Methodology-Earthquake Model (HAZUS-MH MR1); FEMA (Federal Emergency Management Agency): Washington, DC, USA, 2003.
- National Standards Authority of Ireland. Design of Structures for Earthquake Resistance: Part 3: Assessment and Retrofitting of Buildings (Eurocode 8); National Standards Authority of Ireland: Brussels, Belgium, 1998.
- American Concrete Institute (ACI) Committee 318. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- ACI Committee 374. Acceptance Criteria for Moment Frames Based on Structural Testing and Commentary (ACI 374.1-05); American Concrete Institute: Farmington Hills, MI, USA, 2005; pp. 1–9. [Google Scholar]
- Park, R. Valuation of ductility of structures and structural assemblages from laboratory testing. Bull. N. Z. Soc. Earthq. Eng. 1989, 22, 155–166. [Google Scholar]
- Pan, B.; Qian, K.M.; Xie, H.M.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Zhang, X.; Zhuang, X.H. Seismic performance of squared lap-spliced RC columns strengthened by active confinement technique under quasi-static cyclic load. Structures 2025, 74, 108622. [Google Scholar] [CrossRef]
- Orangun, C.O.; Jirsa, J.O.; Breen, J.E. Strength of Anchored Bars: A Reevaluation of Test Data on Development Length and Splices; Research Rep. No. 154-3F1975; Center for Highway Research, University of Texas at Austin: Austin, TX, USA, 1975; p. 78. [Google Scholar]
- Park, R.; Paulay, T. Reinforced Concrete Structures; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Canbay, E.; Frosch, R.J. Bond Strength of Lap-Spliced Bars. ACI Struct. J. 2005, 102, 605–614. [Google Scholar]
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Scott, B.D.; Park, R.; Priestly, M.J.N. Stress-strain Behavior of Concrete Confined by Overlapping Hoops at Low and High Strain Rates. ACI Struct. J. 1982, 79, 13–27. [Google Scholar]
- Lee, C.S.; Han, S.W. Cyclic behaviour of lightly-reinforced concrete columns with short lap splices subjected to unidirectional and bidirectional loadings. Eng. Struct. 2019, 189, 373–384. [Google Scholar] [CrossRef]




| Specimen | Splice Length (mm or Ratio) | Load Capacity (kN or Ratio) | Displacement (mm or Ratio) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ls | ls/db | ls/lsm a | Py | Pm | Δy | Δm | Δu | Δu/Δy | |
| SP-35 | 700 | 35 | 0.71 | 111.20 | 125.23 | 16.37 | 35.17 | 65.5 | 4.00 |
| SP-60 | 1200 | 60 | 1.22 | 110.8 | 128.71 | 20.53 | 60.36 | 156.3 | 7.61 |
| SP-60E | 1200 | 60 | 1.22 | 107.48 | 122.78 | 19.91 | 46.04 | 134.3 | 7.65 |
| SP-35S | 700 | 35 | 0.71 | 10.50 | 127.88 | 19.97 | 81.72 | 171.1 | 8.56 |
| Specimen | Δy (mm) | φy (1/m) | Δu (mm) | φu (1/m) |
|---|---|---|---|---|
| SP-35 | 16.37 | 0.01805 | 65.5 | 0.096 |
| SP-60 | 20.53 | 0.0202 | 156.3 | 0.1302 |
| SP-60E | 17.54 | 0.02038 | 134.3 | 0.133 |
| No. | Source | Section Dimensions (mm or MPa) | Concrete (MPa) | Envelope Curve Response (mm or kN) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m | n | c | ls/db | db | fy | fu | a | fc’ | Δy | Δu | Py | Pm | ||
| 1 | This study | 400 | 400 | 40 | 35 | 20 | 447.61 | 637.29 | 1800 | 20.6 | 16.37 | 35.17 | 111.20 | 125.23 |
| 2 | 400 | 400 | 40 | 60 | 20 | 447.61 | 637.29 | 1800 | 20.6 | 20.53 | 60.36 | 110.8 | 128.71 | |
| 3 | Kim et al. [11] | 400 | 400 | 40 | 30 | 25.4 | 557.5 | 689.5 | 2400 | 25 | 16.2 | 132.0 | 89.41 | 115.83 |
| 4 | 400 | 400 | 40 | 40 | 25.4 | 557.5 | 689.5 | 2400 | 25 | 17.9 | 168 | 92.79 | 117.08 | |
| 5 | Lee et al. [49] | 450 | 450 | 40 | 20 | 25.4 | 524 | / | 1800 | 25 | 7.4 | 31.5 | 121.44 | 161 |
| 6 | 450 | 450 | 40 | 20 | 25.4 | 524 | / | 1800 | 25 | 6.0 | 23.4 | 137.55 | 185 | |
| No. | Source | Predicted Results (mm or kN) | Model Error (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dy | Du | Py | Pm | Dy | Du | Py | Pm | ||
| 1 | This study | 16.36 | 70.77 | 114.73 | 128.91 | −0.06 | +8.05 | +3.17 | +2.72 |
| 2 | 17.87 | 142.5 | 114.02 | 128.68 | −3.56 | −8.83 | +3.11 | −0.02 | |
| 3 | Kim et al. [11] | 16.7 | 128.3 | 92.16 | 109.38 | +3.1 | −2.8 | +0.5 | −5.6 |
| 4 | 14.9 | 165 | 96.58 | 115.95 | −16.8 | +1.7 | +4.1 | −1.0 | |
| 5 | Lee et al. [49] | 6.2 | 30.0 | 131.27 | 156.22 | −16.2 | −4.8 | +8.1 | −3.0 |
| 6 | 6.3 | 19.8 | 156.61 | 188.27 | +5.0 | −15.4 | +13.9 | +1.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Jiang, F.; Zhang, X.; Guo, Y. Mechanical Performance Evaluation and Strengthening of Rectangular RC Columns with Deficient Lap Splices: Monotonic Loading Tests and Equivalent Plastic Hinge Modeling. Buildings 2025, 15, 1964. https://doi.org/10.3390/buildings15121964
Zhao Y, Jiang F, Zhang X, Guo Y. Mechanical Performance Evaluation and Strengthening of Rectangular RC Columns with Deficient Lap Splices: Monotonic Loading Tests and Equivalent Plastic Hinge Modeling. Buildings. 2025; 15(12):1964. https://doi.org/10.3390/buildings15121964
Chicago/Turabian StyleZhao, Yuheng, Fangxin Jiang, Xue Zhang, and Yufeng Guo. 2025. "Mechanical Performance Evaluation and Strengthening of Rectangular RC Columns with Deficient Lap Splices: Monotonic Loading Tests and Equivalent Plastic Hinge Modeling" Buildings 15, no. 12: 1964. https://doi.org/10.3390/buildings15121964
APA StyleZhao, Y., Jiang, F., Zhang, X., & Guo, Y. (2025). Mechanical Performance Evaluation and Strengthening of Rectangular RC Columns with Deficient Lap Splices: Monotonic Loading Tests and Equivalent Plastic Hinge Modeling. Buildings, 15(12), 1964. https://doi.org/10.3390/buildings15121964







