Numerical Study on Heat Transfer, Deformation, and Breakup of Flying Droplets During Gas Atomization of Molten Aluminum
Abstract
1. Introduction
2. Model Descriptions
2.1. Basic Assumptions
2.2. Governing Equations
2.2.1. Turbulence Model
2.2.2. Multiphase Flow
2.2.3. Heat Transfer
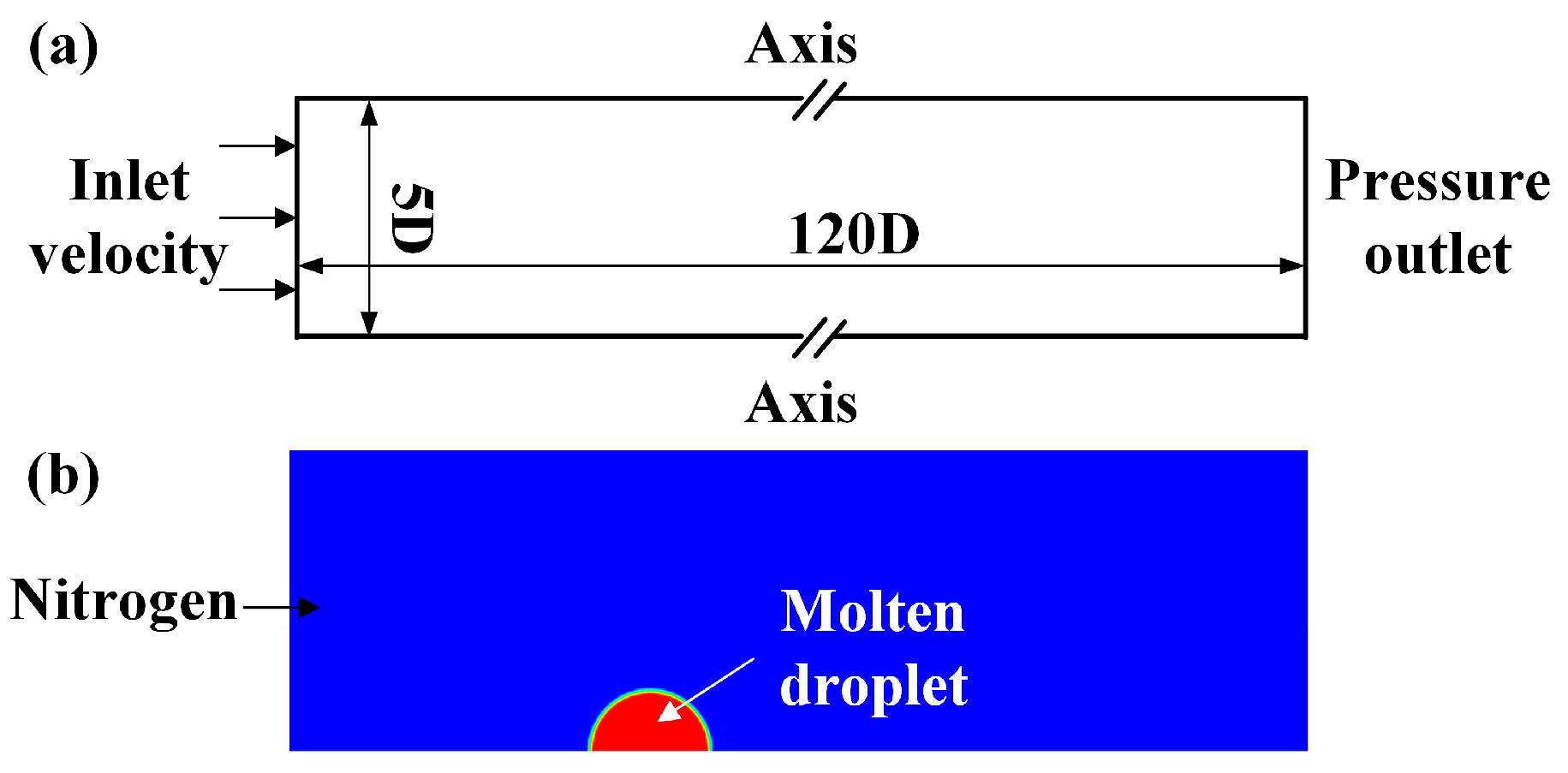
2.3. Model Building and Parameters
2.4. Initial and Boundary Conditions
3. Results and Discussion
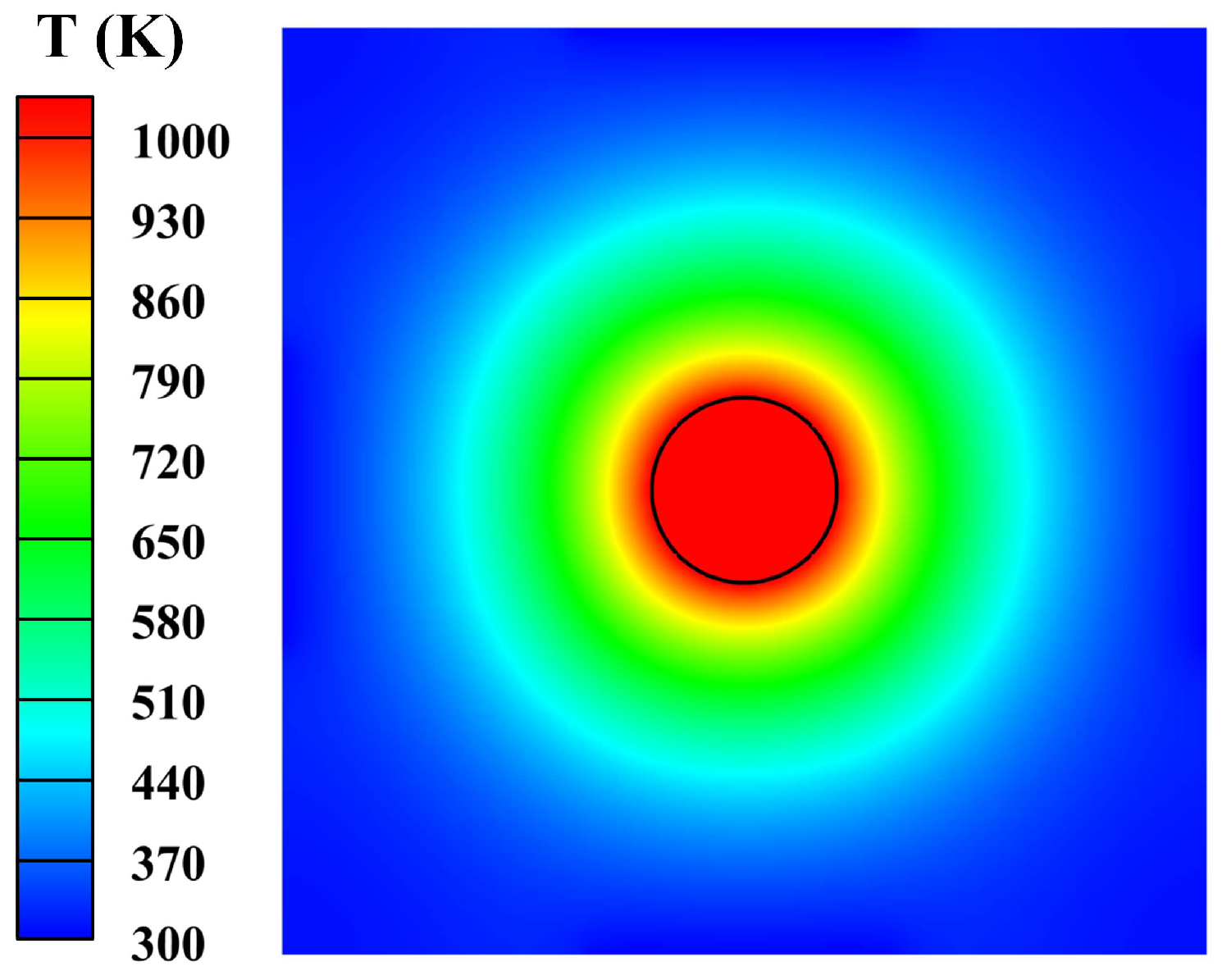
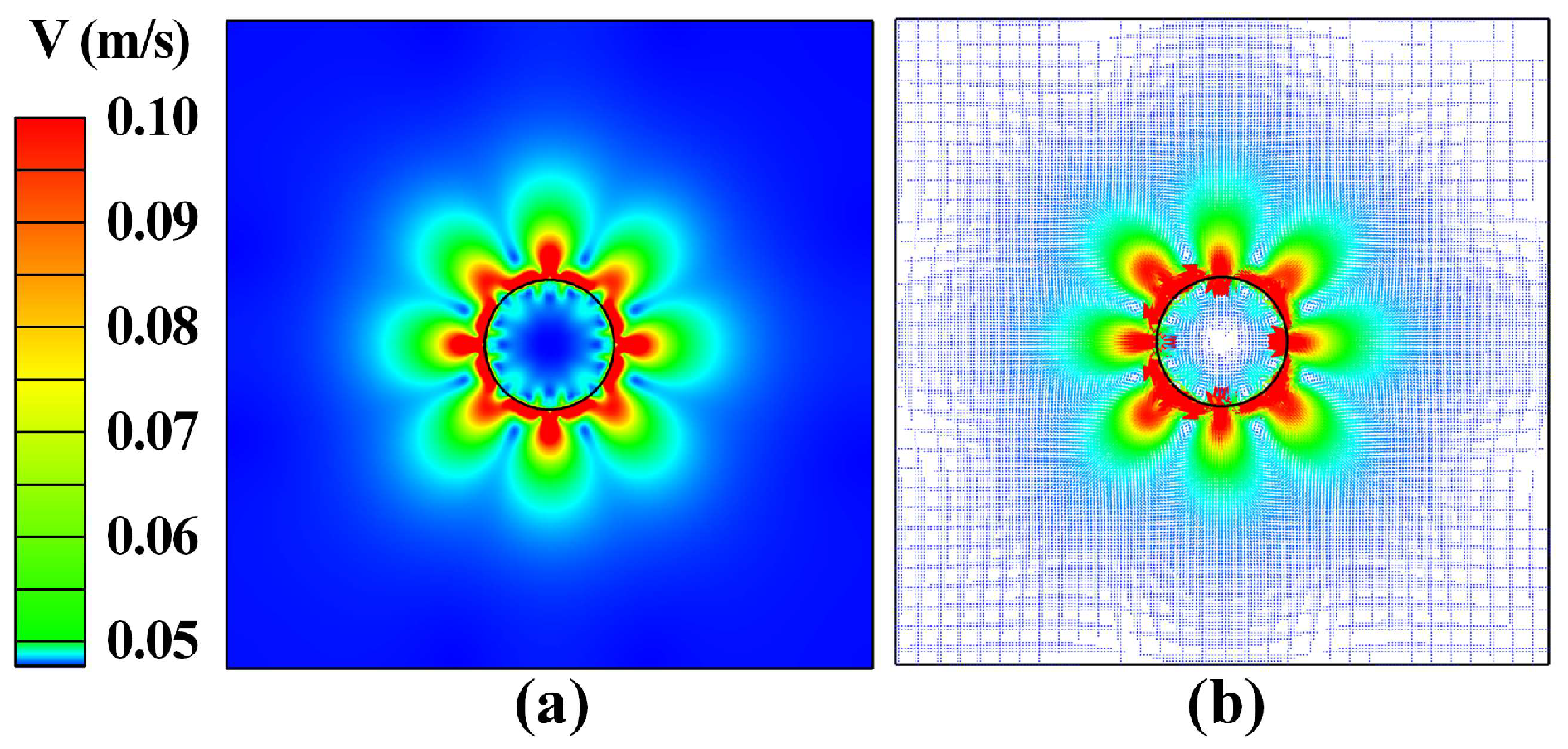
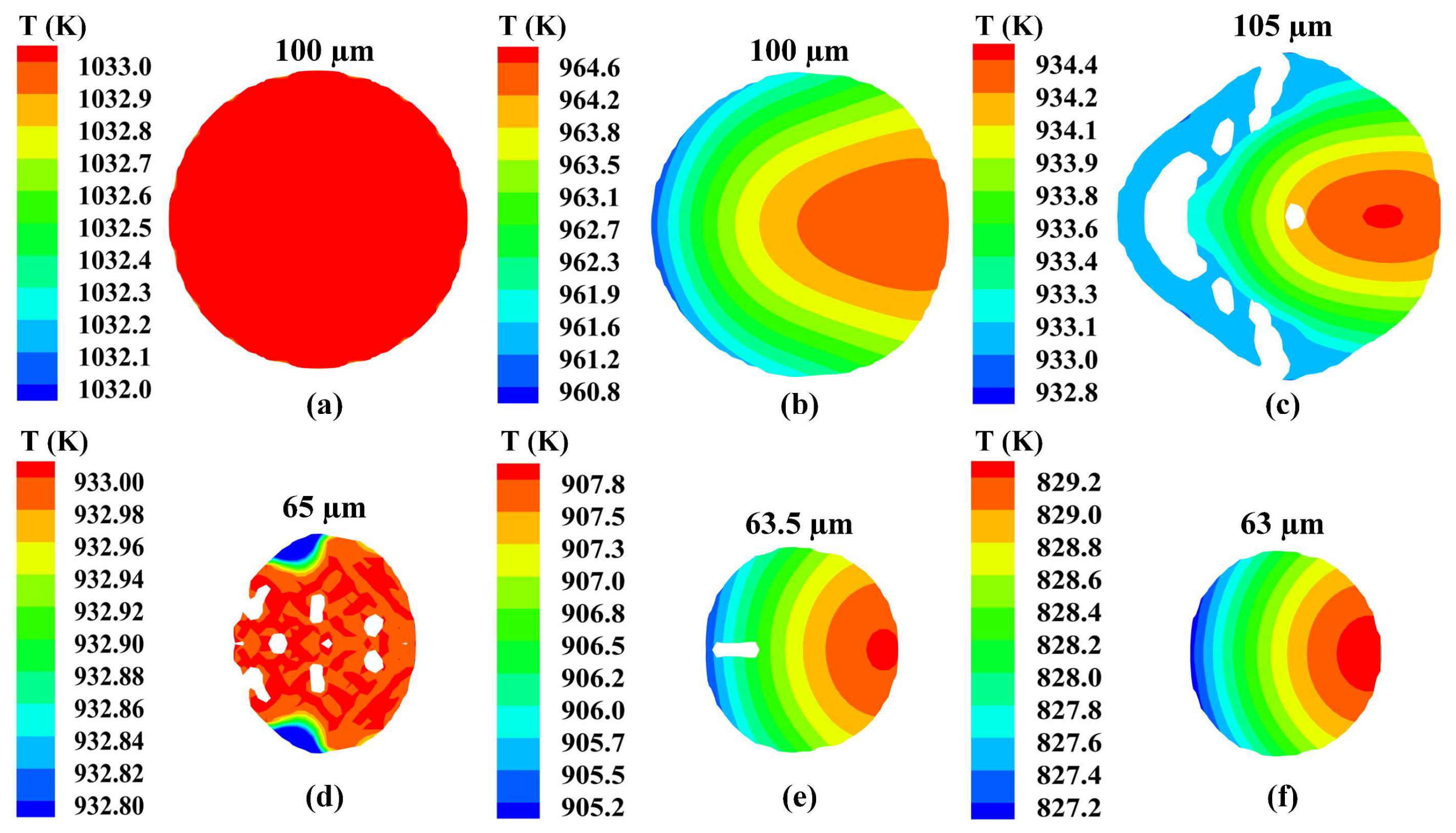
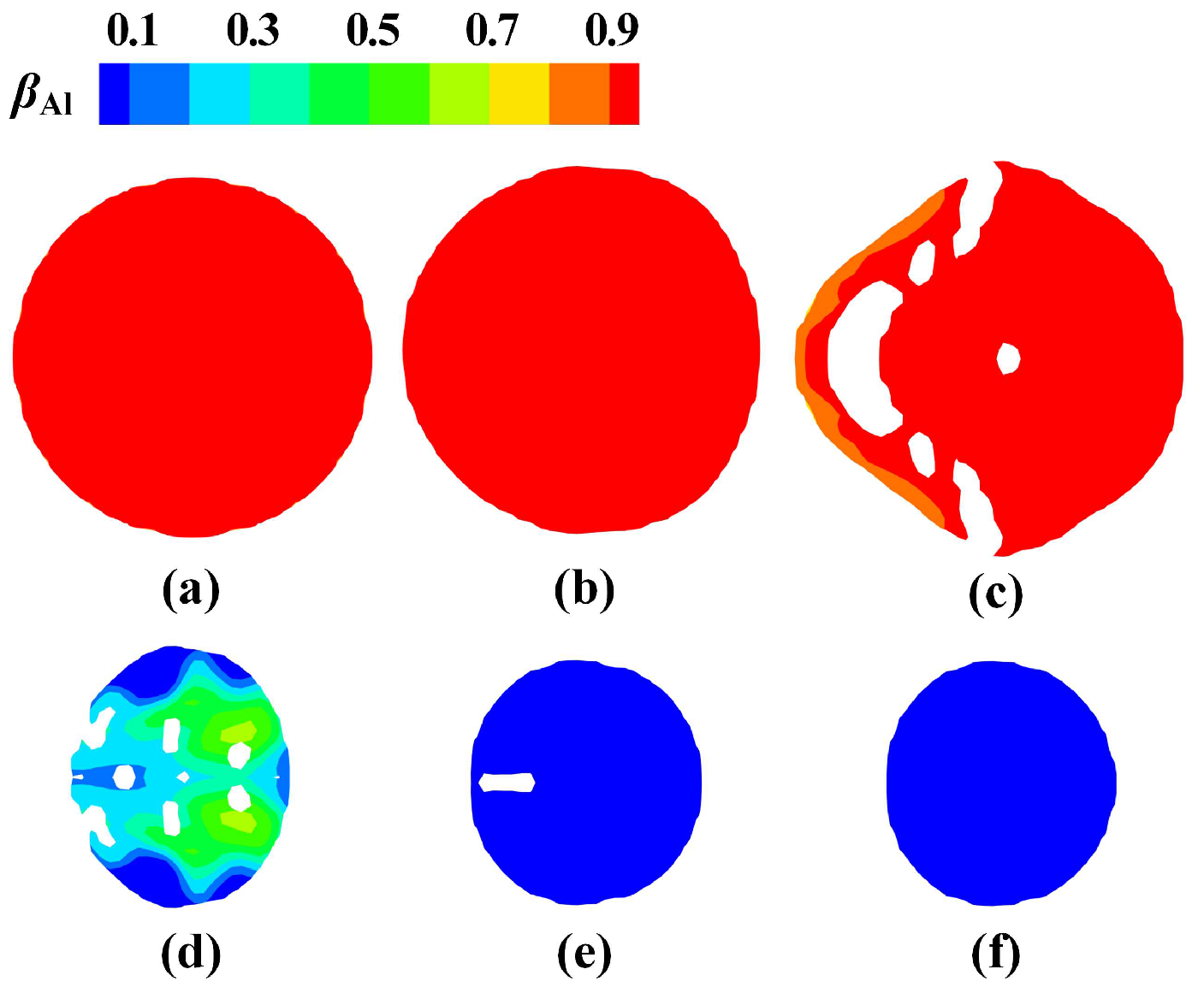
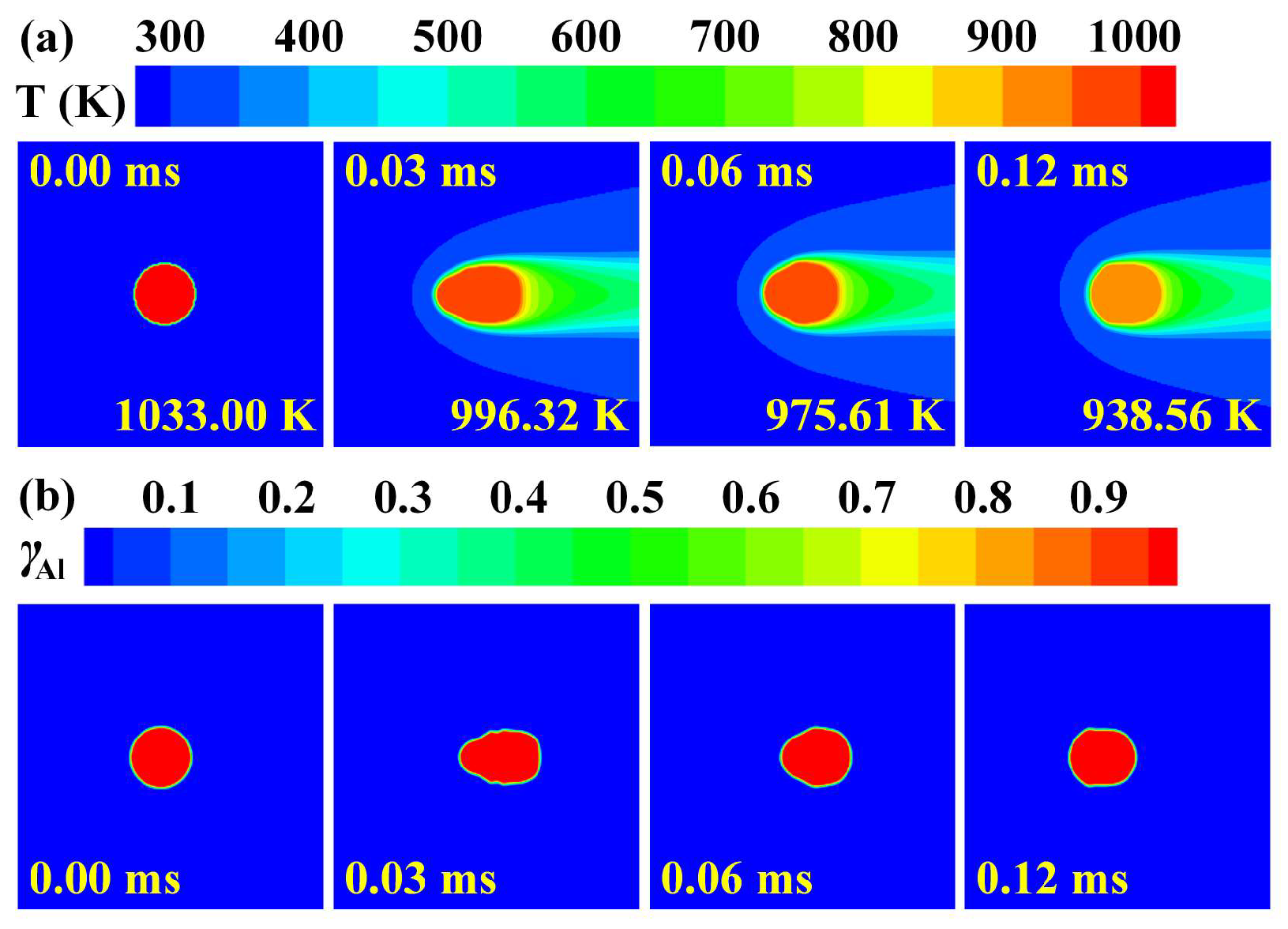
3.1. Heat Transfer Behavior of Static Molten Droplet
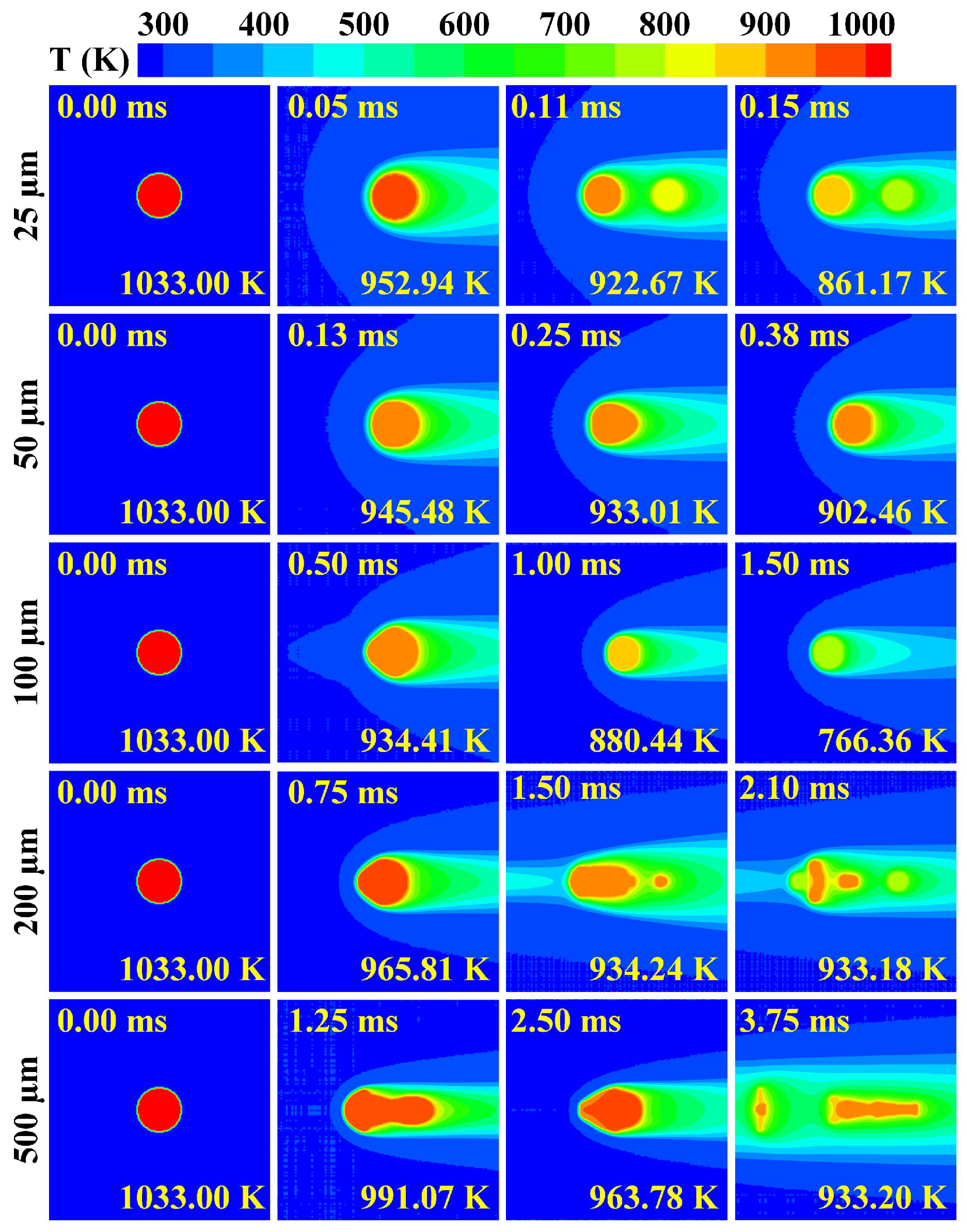
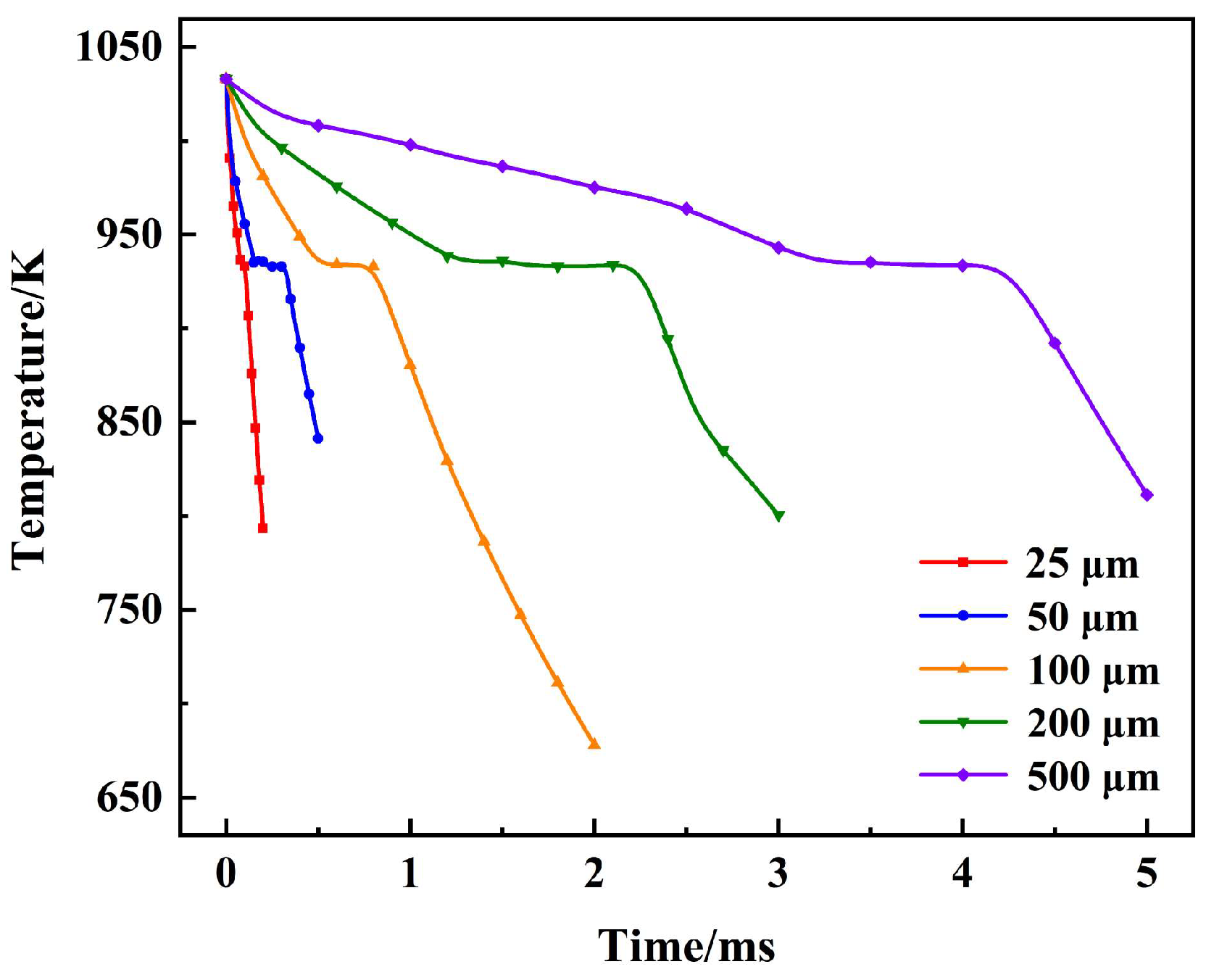
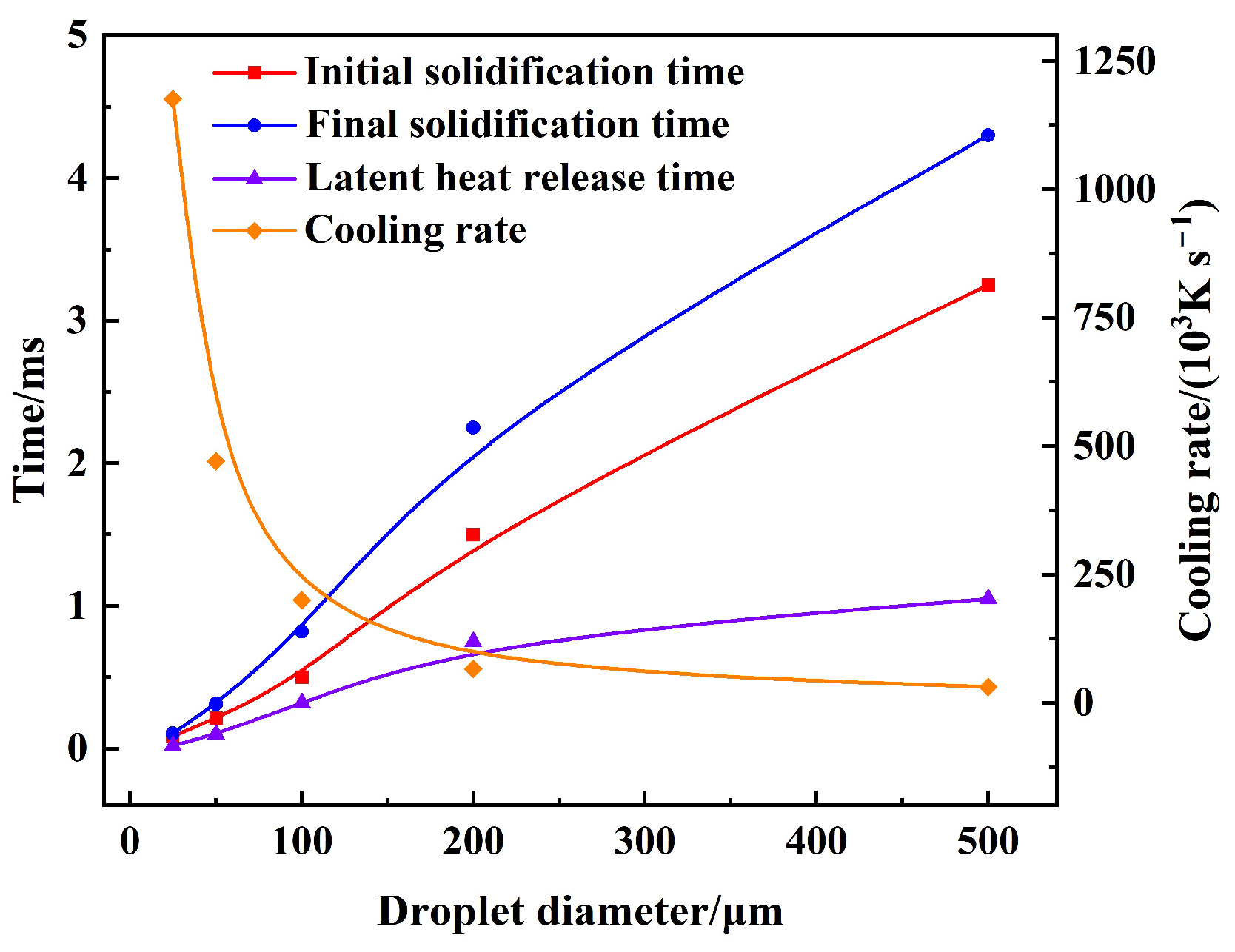
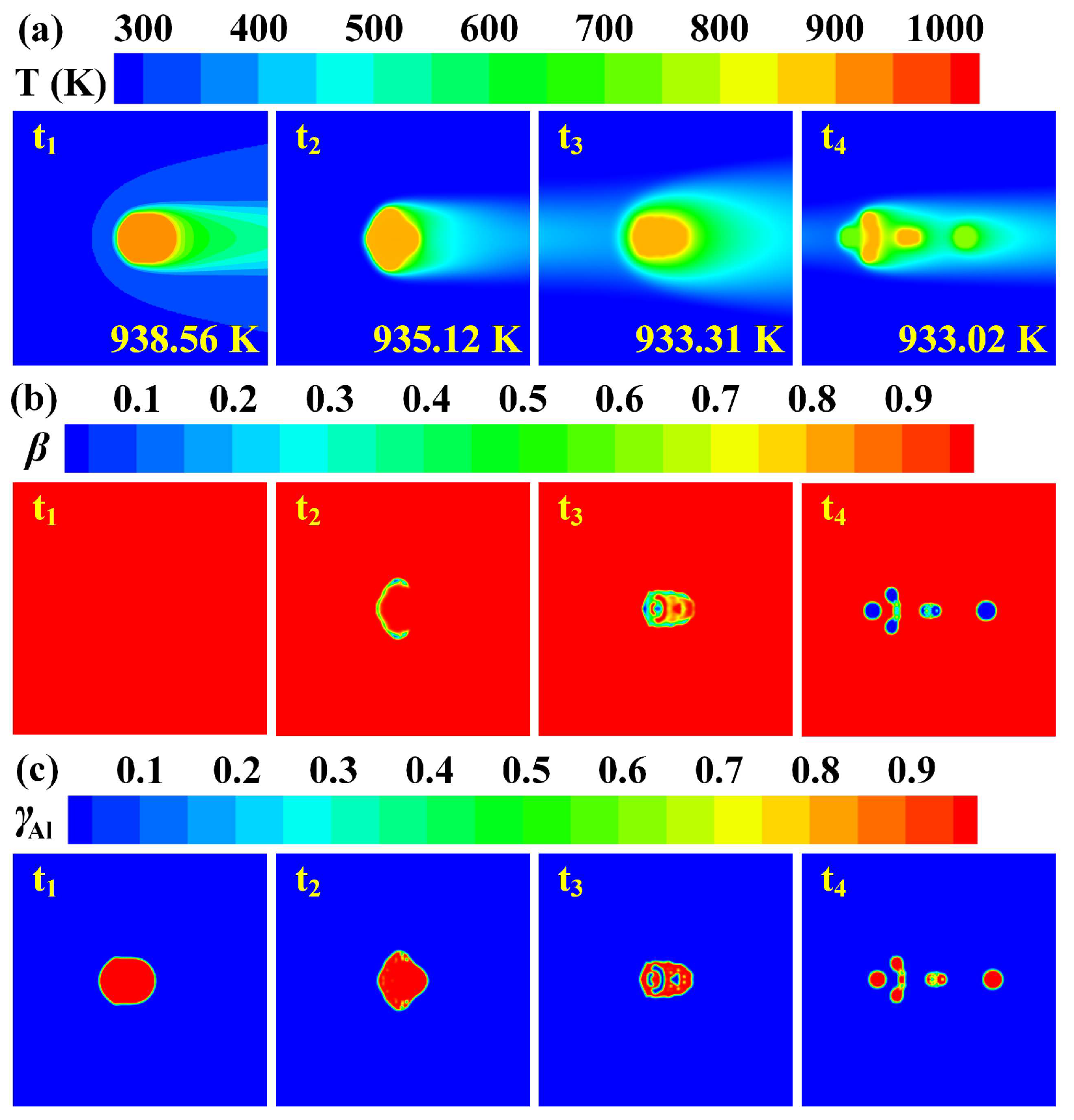
3.2. Cooling and Solidification Characteristics of Flying Molten Droplet
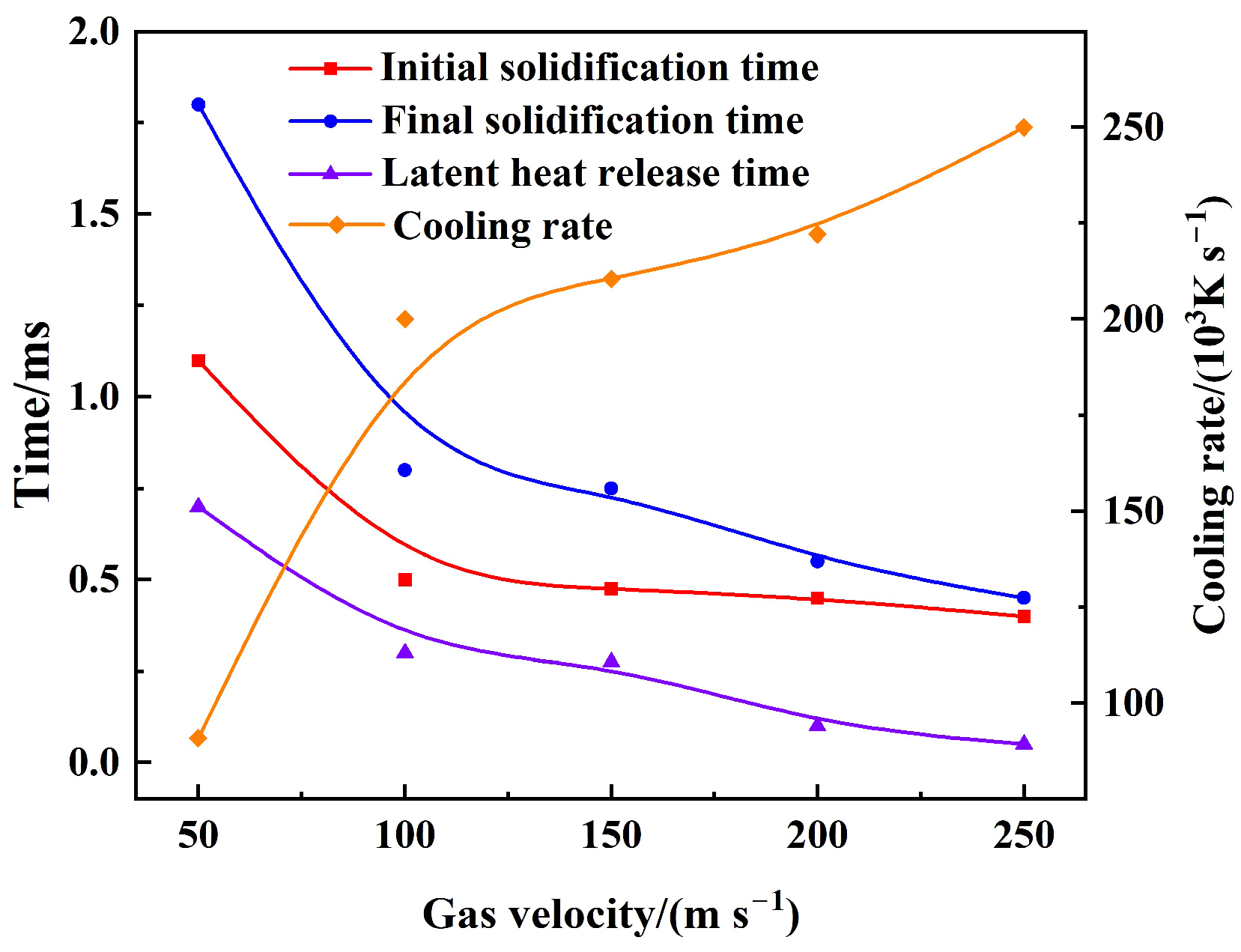
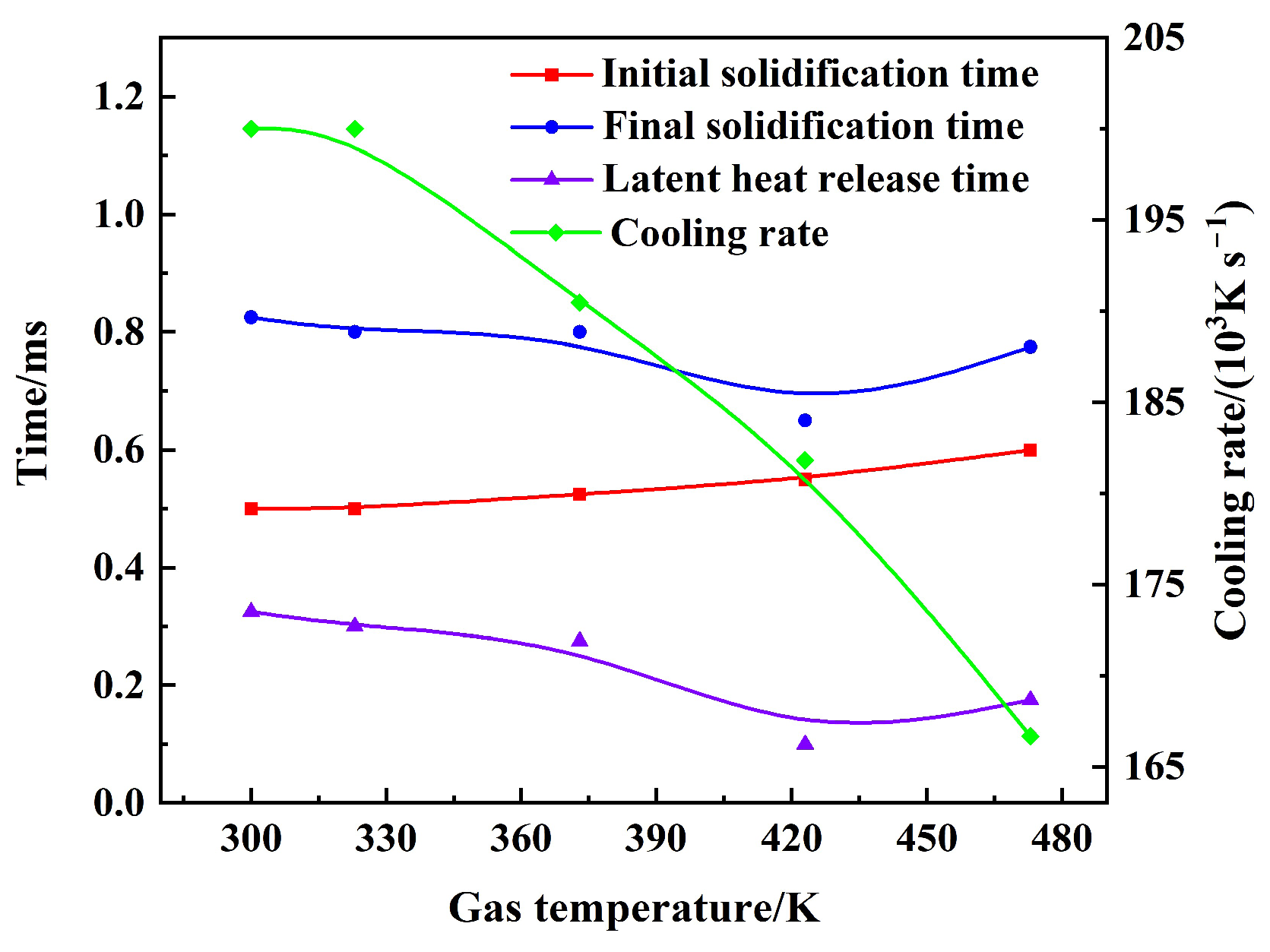
3.3. Effect of Gas–Liquid Parameters on Flight Heat Transfer of Molten Droplet
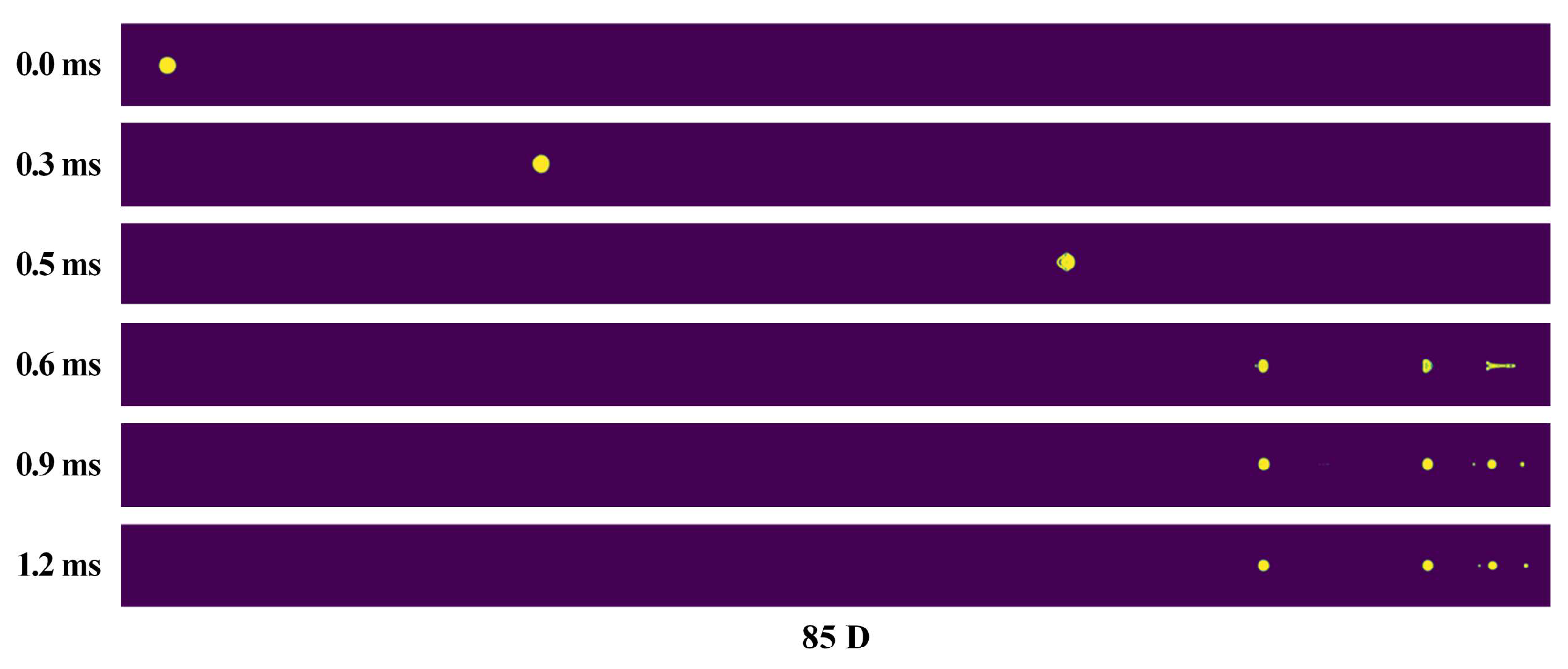
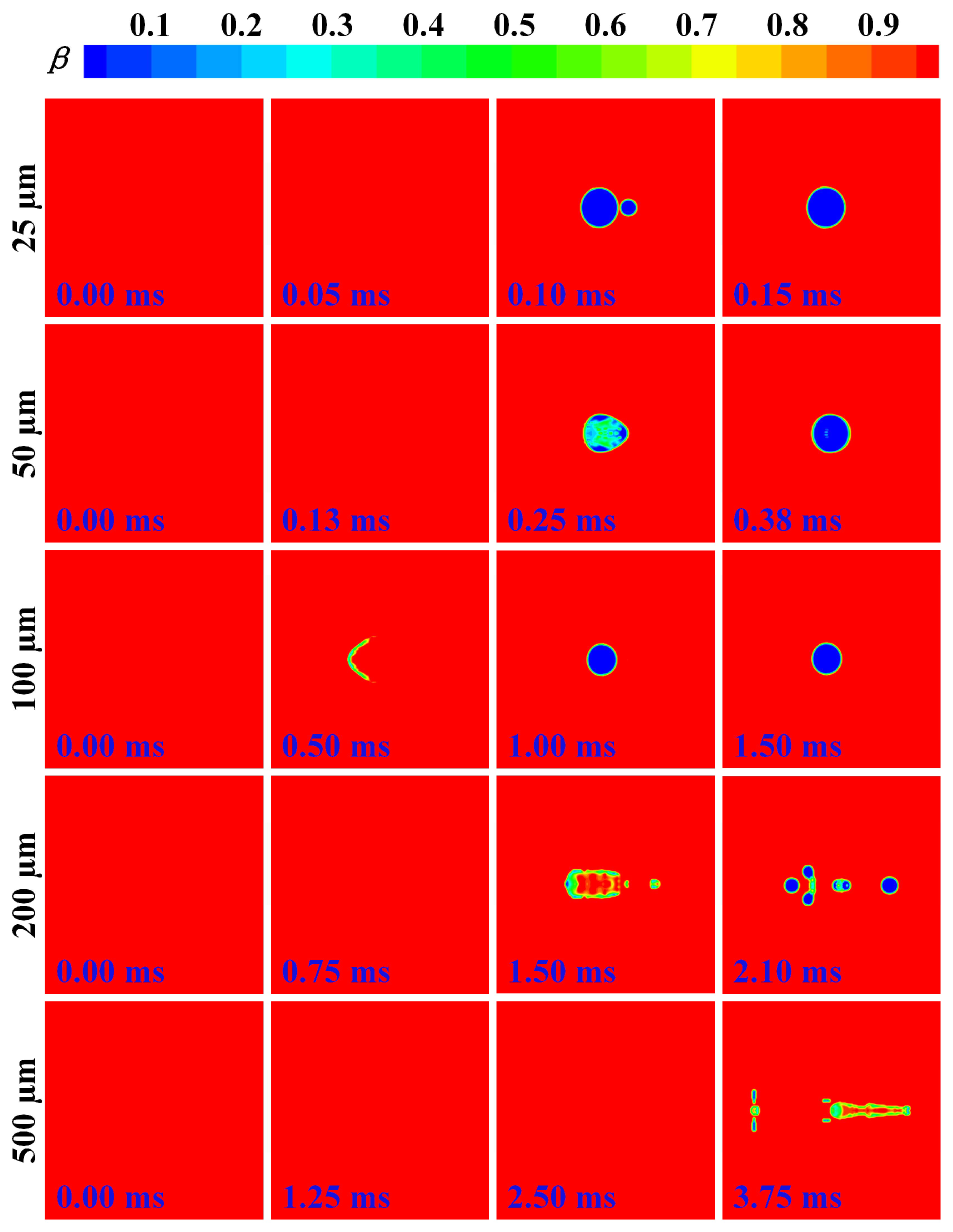
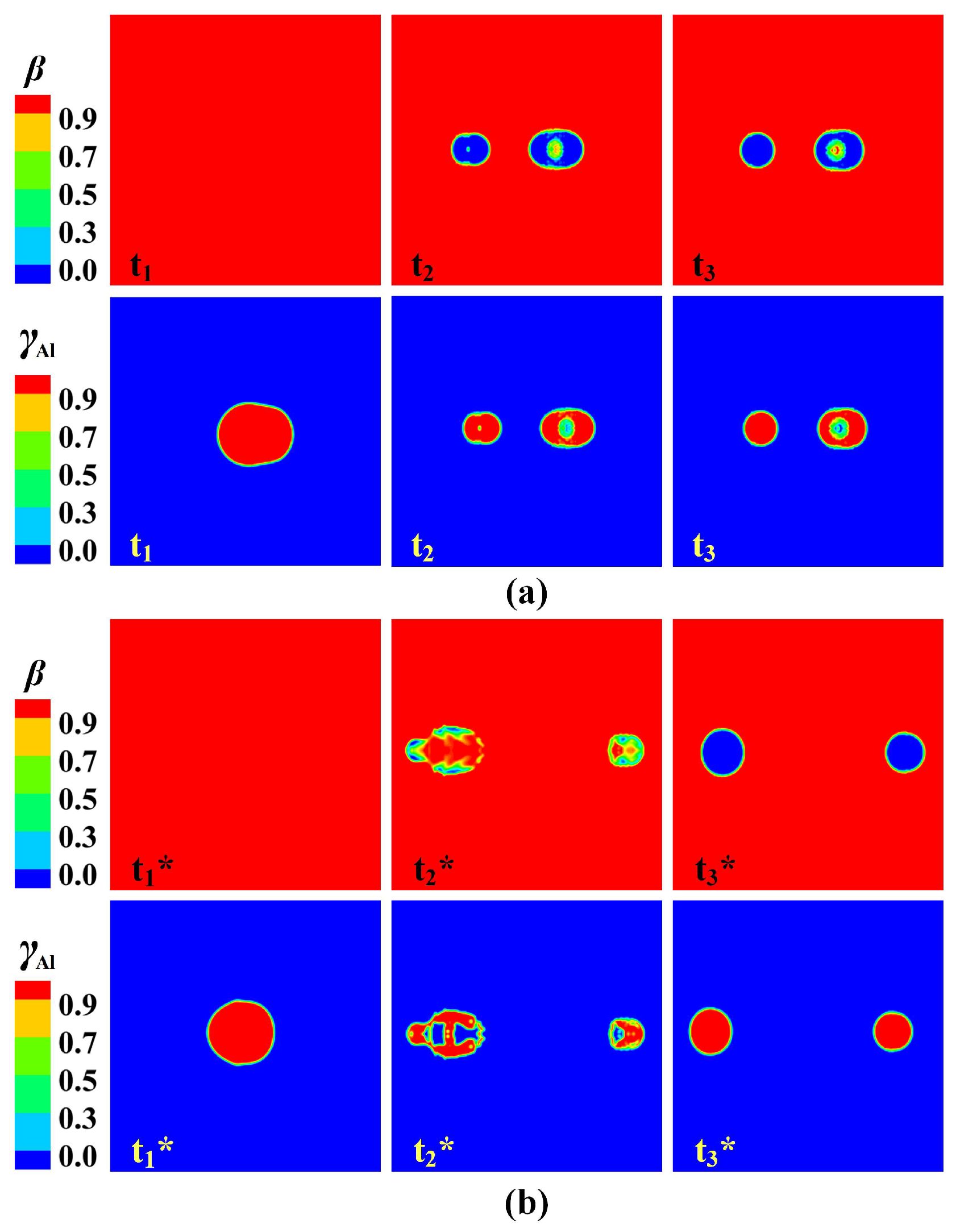
3.4. Deformation and Breakup Behavior of Flying Molten Droplet
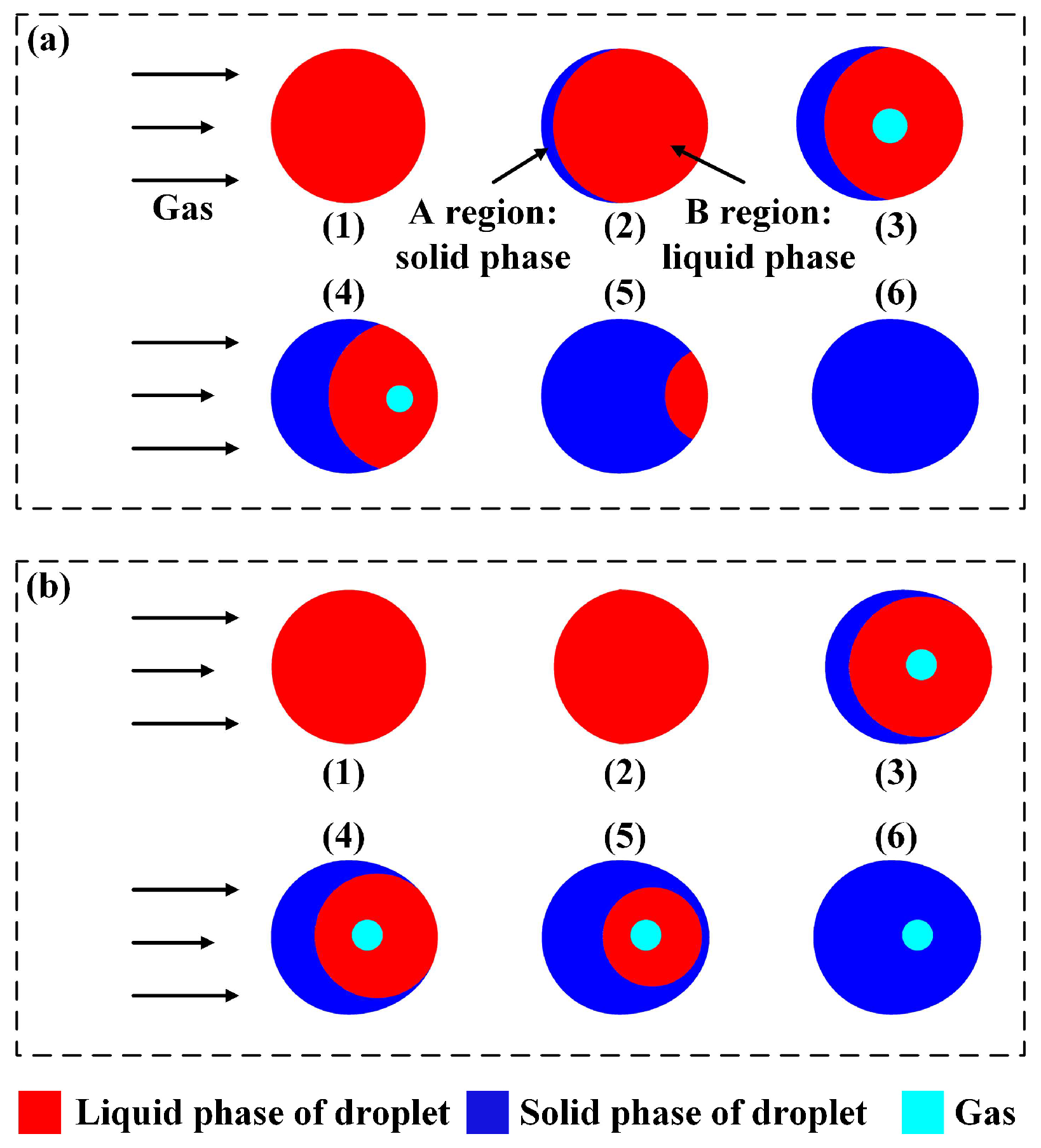
3.5. Formation of Hollow Powder
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VOF | Volume of Fluid |
References
- Khanna, N.; Salvi, H.; Karaş, B.; Fairoz, I.; Shokrani, A. Cost modelling for powder bed fusion and directed energy deposition additive manufacturing. J. Manuf. Mater. Process. 2024, 8, 142. [Google Scholar] [CrossRef]
- Boretti, A. Metal additive manufacturing for internal combustion engine components: A narrative review of applications, materials, processes, challenges, and future directions. Int. J. Adv. Manuf. Technol. 2025, 139, 6355–6397. [Google Scholar] [CrossRef]
- Bhat, C.; Jiang, C.P.; Romario, Y.S.; Paral, S.K.; Toyserkani, E. Critical review of metal-ceramic composites fabricated through additive manufacturing for extreme condition applications. Mech. Adv. Mater. Struct. 2025, 32, 2153–2180. [Google Scholar] [CrossRef]
- Mohd, Y.S.; Cutler, S.; Gao, N. The impact of metal additive manufacturing on the aerospace industry. Metals 2019, 9, 1286. [Google Scholar] [CrossRef]
- Lanzutti, A.; Marin, E. The challenges and advances in recycling/re-using powder for metal 3D printing: A comprehensive review. Metals 2024, 14, 886. [Google Scholar] [CrossRef]
- Sun, X.; Chen, M.; Liu, T.; Zhang, K.; Wei, H.; Zhu, Z.; Liao, W. Characterization, preparation, and reuse of metallic powders for laser powder bed fusion: A review. Int. J. Extreme Manuf. 2023, 6, 012003. [Google Scholar] [CrossRef]
- Soong, S.Z.; Lai, W.L.; Lup, A.N.K. Atomization of metal and alloy powders: Processes, parameters, and properties. AIChE J. 2023, 69, e18217. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.; Zhang, Q.; Zhai, C.; Zheng, H. Computational insights into gas atomization of FeCoNiCrMoBSi high-entropy alloy: From droplet formation to rapid solidification. Int. J. Heat Mass Transfer 2024, 228, 125628. [Google Scholar] [CrossRef]
- Luo, S.; Wang, H.; Gao, Z.; Wu, Y.; Wang, H. Interaction between high-velocity gas and liquid in gas atomization revealed by a new coupled simulation model. Mater. Des. 2021, 212, 110264. [Google Scholar] [CrossRef]
- Hattel, J.H.; Pryds, N.H.; Thorborg, J.; Ottosen, P. A quasi-stationary numerical model of atomized metal droplets. I: Model formulation. Modell. Simul. Mater. Sci. Eng. 1999, 7, 413–430. [Google Scholar] [CrossRef]
- Grant, P.S.; Cantor, B.; Katgerman, L. Modelling of droplet dynamic and thermal histories during spray forming—I. Individual droplet behaviour. Acta Metall. Mater. 1993, 41, 3097–3108. [Google Scholar] [CrossRef]
- Grant, P.S.; Cantor, B.; Katgerman, L. Modelling of droplet dynamic and thermal histories during spray forming—II. Effect of process parameters. Acta Metall. Mater. 1993, 41, 3109–3118. [Google Scholar] [CrossRef]
- Zeoli, N.; Gu, S. Computational simulation of metal droplet break-up, cooling and solidification during gas atomisation. Comput. Mater. Sci. 2008, 43, 268–278. [Google Scholar] [CrossRef]
- Gorokhovski, M.; Herrmann, M. Modeling primary atomization. Annu. Rev. Fluid Mech. 2008, 40, 343–366. [Google Scholar] [CrossRef]
- Fuster, D.; Bagué, A.; Boeck, T.; Moyne, L.L.; Leboissetier, A.; Popinet, S.; Ray, P.; Scardovelli, R.; Zaleski, S. Simulation of primary atomization with an octree adaptive mesh refinement and VOF method. Int. J. Multiphase Flow 2009, 35, 550–565. [Google Scholar] [CrossRef]
- Shao, C.; Luo, K.; Yang, J.; Chen, S. Accurate level set method for simulations of liquid atomization. J. Fan. Chin. J. Chem. Eng. 2015, 23, 597–604. [Google Scholar] [CrossRef]
- Orazzo, A.; Sébastien, T. Direct numerical simulations of droplet condensation. Int. J. Heat Mass Transfer 2019, 129, 432–448. [Google Scholar] [CrossRef]
- Luo, K.; Shao, C.; Chai, M. Level set method for atomization and evaporation simulations. J. Fan. Prog. Energy Combust. Sci. 2019, 73, 65–94. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Liu, J.; Zhang, L.; Gao, L.; Zheng, G.; Shen, H. Microstructure and flight behaviors of droplet and its solidification in twin-wire arc sprayed Ni-Al composite coatings. J. Sun. Mater. Res. 2018, 21, e20170394. [Google Scholar] [CrossRef]
- Reutzsch, J.; Kieffer-Roth, C.; Weigand, B. A consistent method for direct numerical simulation of droplet evaporation. J. Comput. Phys. 2020, 413, 109455. [Google Scholar] [CrossRef]
- Kumar, A.; Ghosh, S.; Dhindaw, B.K. Simulation of cooling of liquid Al–33 wt.% Cu droplet impinging on a metallic substrate and its experimental validation. Acta Mater. 2010, 58, 122–133. [Google Scholar] [CrossRef]
- Alavi, S.; Passandideh-Fard, M. Numerical simulation of droplet impact and solidification including thermal shrinkage in a thermal spray process. Int. Heat Transf. Conf. 2010, 49415, 731–739. [Google Scholar] [CrossRef]
- Peng, H.; Hu, Z.; Shan, X.; Ling, X.; Liu, L. Study on the solidification characteristics of molten slag droplets cooled by mixed cooling medium. Appl. Therm. Eng. 2019, 149, 939–949. [Google Scholar] [CrossRef]
- Assael, M.J.; Kakosimos, K.; Banish, R.M.; Brillo, J.; Egry, I.; Brooks, R.; Quested, P.N.; Mills, K.C.; Nagashima, A.; Sato, Y.; et al. Reference data for the density and viscosity of liquid aluminum and liquid iron. J. Phys. Chem. Ref. Data 2006, 35, 285–300. [Google Scholar] [CrossRef]
- Xia, S.; Hu, C. Review of physical property calculations of liquid aluminum and alumina. J. Propul. Technol. 2019, 40, 961–969. [Google Scholar] [CrossRef]
- Hatch, J.E. Aluminum: Properties and Physical Metallurgy; American Society for Metals: Cleveland, OH, USA, 1984. [Google Scholar]
- Molina, M.; Voytovych, R.; Louis, E.; Eustathopoulos, N. The surface tension of liquid aluminium in high vacuum: The role of surface condition. Int. J. Adhes. Adhes. 2007, 27, 394–401. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Z. Numerical simulation study on cooling of metal droplet in atomizing gas. Mater. Today Commun. 2020, 25, 101423. [Google Scholar] [CrossRef]


| Parameter | Value | |
|---|---|---|
| Molten Aluminum Droplet | Nitrogen | |
| Density (kg/m3) | Equation (15) | 1.205 |
| Viscosity (Pa·s) | Equation (16) | 1.511 × 10−5 |
| Thermal conductivity (W·m−1·K−1) | Equation (17) | 0.0242 |
| Specific heat (J·kg−1·K−1) | 1176.8 | 1040.67 |
| Latent heat of solidification (J/kg) | 3.98 × 105 | - |
| Liquidus temperature (K) | 933 | - |
| Solidus temperature (K) | 933 | - |
| Surface tension (N/m) | Equation (18) | - |
| Factor of Influence | Values |
|---|---|
| Gas velocity (m/s) | 50, 100, 150, 200, 250 |
| Gas temperature (K) | 300, 323, 373, 423, 473 |
| Droplet diameter (μm) | 25, 50, 100, 200, 500 |
| Initial droplet temperature (K) | 983, 1033, 1083, 1133 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Wang, Y.; Huang, S.; Wang, B.; Zhou, J.; Chen, C. Numerical Study on Heat Transfer, Deformation, and Breakup of Flying Droplets During Gas Atomization of Molten Aluminum. Metals 2026, 16, 37. https://doi.org/10.3390/met16010037
Wang Y, Huang S, Wang B, Zhou J, Chen C. Numerical Study on Heat Transfer, Deformation, and Breakup of Flying Droplets During Gas Atomization of Molten Aluminum. Metals. 2026; 16(1):37. https://doi.org/10.3390/met16010037
Chicago/Turabian StyleWang, Yi, Shanzheng Huang, Bao Wang, Jian’an Zhou, and Changyong Chen. 2026. "Numerical Study on Heat Transfer, Deformation, and Breakup of Flying Droplets During Gas Atomization of Molten Aluminum" Metals 16, no. 1: 37. https://doi.org/10.3390/met16010037
APA StyleWang, Y., Huang, S., Wang, B., Zhou, J., & Chen, C. (2026). Numerical Study on Heat Transfer, Deformation, and Breakup of Flying Droplets During Gas Atomization of Molten Aluminum. Metals, 16(1), 37. https://doi.org/10.3390/met16010037







