Some Inequalities for Convex Sets

Abstract

The paper concerns inequalities between fundamental quantities as area, perimeter, diameter and width for convex plane fugures.

1. Introduction

In this paper we use methods from the geometry of convex figures and geometric inequalities. Both the above mathematical subjects are old but have been very convenient, fruitful and active in recent times. A classical textbook in the convexity is the excellent, “Theory of Convex Bodies” by T. Bonnesen and W. Fenchel [1]. Another very nice tool is the “Convex Figures” of I. Yaglom and V. Boltyanski [2]. The Yugoslavian and Romanian school, with Mitvinovic and Andrescu, produced a very interesting theorem in algebraic and geometric Inequalities. Here, the problem is to find solutions to three interesting inequalities for convex figures in the plane. This problem came to me from a former student of mine, Prof. E. Symeonidis. The problem was published in AXIOMS 2018 7(1) by S.Marcus and F. Nichita. The solution of the first inequality is quite simple but the two others are sophisticated. For the solution I used two lemmas that have particular interest and could be useful to solve other problems.

2. Problems

Let f be a convex figure in the plane (that is a compact convex set). We denote by G its centroid. D is the maximal chord and d the minimal chord through G. Moreover, L stands for the perimeter, $D_F$ the diameter, $d_F$ the minimal breadth, and A the area of F.

We have to prove:

(a)

$L\ge d\pi .$

(b)

$d.D>A.$

(c)

$L.D\ge 4A.$

Proof. 

Inequality (a).

The formula for the perimeter of a convex figure F see [3] is:

$$L=\frac{1}{2}{\int }_0^{2\pi }B\left(\vartheta \right)d\vartheta$$

where $B\left(\vartheta \right)$ is the breadth of F to the direction $\vartheta ,d_F$ is the min. breadth of F. So we have:

$$L\ge \frac{1}{2}{\int }_0^{2\pi }{d}_F.d\vartheta \ge d\pi .$$

This is because of the obvious $d_F\ge d$

The equality holds for the circle and the convex figures with constant breadth. □

For (b) and (c) we need two lemmas.

Lemma 1.

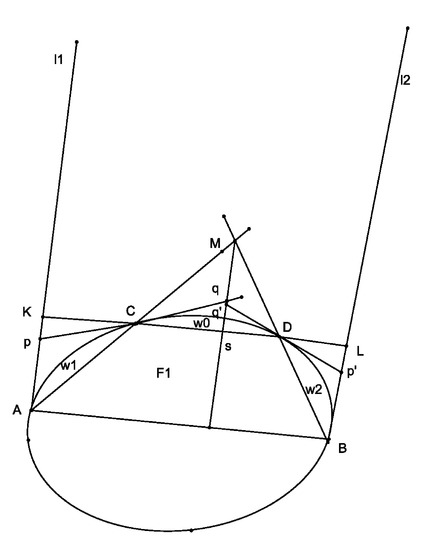
Let F be a convex figure and $AB$ a diametrical chord. We denote by $l_1,l_2$ the support lines at the points $A,B$ respectively. We take the chord $CD$ parallel to $AB$, so that $CD=AB/2$. The str.line $CD$ intersects $l_1,l_2$ at the points $K,L$. The chord $AB$ disects F into two parts. We denote the one part by $F_1$ as in the Figure 1. Then we have: $area\left(ABLK\right)\ge area{F}_1$.

Figure 1. Lemma 1.

Proof. 

Let $AC$ intersect $BD$ at the point M and $MS$ parallel to $AK$, The support line at the point C intrsects $AK,MS$ at the points $p,q$. The support line at the point D intersects $BL,MS$ at the points $p^{\prime },q^{\prime }$. In the triangle $AMB$ the points C and D are the midle points of the sides, so we use equalities of triangles without the proofs. The triangles $pKC,qSC$ are equal, the same for $ApC,MqC$, the same for $LD{p}^{\prime },SD{q}^{\prime }$ and $M{q}^{\prime }D,B{p}^{\prime }D$. We denote $w_1,w_2,w_0$ the area of the segments of the $arcAC$, $arcBD$, $arcCD$.

We have

$Area\left(ABLK\right)=Area\left(AKC\right)+Area\left(ABDC\right)+Area\left(BLD\right)$

$Area\left(ABLK\right)=w_1+w_2+w_1^{\prime }+w_2^{\prime }+Area\left(CKp\right)+Area\left(DL{p}^{\prime }\right)+Area\left(ABDC\right)\ge (w_0+w_1+w_2)+Area\left(ABDC\right)=Area{F}_1$. Because $Area\left(CKp\right)+Area\left(DL{p}^{\prime }\right)>w_0$.

By $w_1^{\prime }$ we denote the area of the triangle $ApC$ with sides $Ap,pC,arcAC$. Analogously $w_2^{\prime }$. Hence we conclude $Area\left(ABLK\right)>Area{F}_1$. □

Lemma 2.

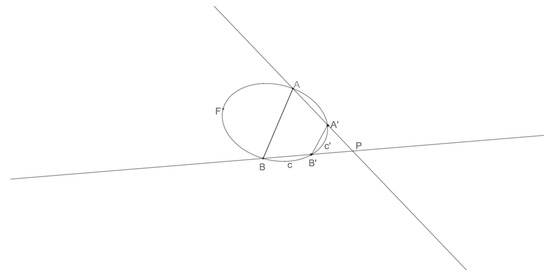
In the perimeter $\vartheta F$ of the convex set F there are the points $A,B,A^{\prime },B^{\prime }$. The chord $AB$ and $A^{\prime }{B}^{\prime }$ are parallel and the point $P=A{A}^{\prime }\cap B{B}^{\prime }$ is outside of F. We denote by $arcAB=c,arc{A}^{\prime }{B}^{\prime }=c^{\prime }$ on the $\vartheta F$ and $c\supset c^{\prime }$, like in the Figure 2. We will prove that:

$$\frac{L\left(c\right)}{|A-B|}\ge \frac{L\left(c^{\prime }\right)}{|A^{\prime }-B^{\prime }|}$$

Figure 2. Lemma 2.

Proof. 

We denote by M the vector $\overrightarrow{O}M$.

We have $A-B=\mu (A^{\prime }-B^{\prime })$ We easily find

$$P=\frac{\mu A^{\prime }-A}{\mu -1}=\frac{\mu B^{\prime }-B}{\mu -1}$$

hence

$$P-A^{\prime }=\frac{A^{\prime }-A}{\mu -1}$$

(1)

and

$$P-B^{\prime }=\frac{B^{\prime }-B}{\mu -1}$$

(2)

but

$$L\left(c\right)\ge |A-A^{\prime }|+|B-B^{\prime }|+L\left(c^{\prime }\right)$$

(3)

From the above (1), (2) follows

$$|A-A^{\prime }|+|B-B^{\prime }|=|\mu -1\left|\right(|P-A^{\prime }|+|P-B^{\prime }\left|\right)\ge |\mu -1|L\left(c^{\prime }\right)$$

(4)

From (3) and (4) we take

$$L\left(c\right)\ge |\mu -1|L\left(c^{\prime }\right)+L\left(c^{\prime }\right)=\mu L\left(c^{\prime }\right)$$

and finally

$$L\left(c\right)\ge \frac{|A-B|}{|A^{\prime }-B^{\prime }|}L\left(c^{\prime }\right)$$

 □

Inequality (b).

The continuity of the convexity asserts us that we can choose the diametrical chord $AB$ so that:

$$d_F\le AB\le D\le D_F$$

(5)

where $d_F$ and $D_F$ stands for the min.breadth and diameter of F respectively.

As you see in Figure 3, $l_1$ and $l_2$ are the parallel supporting lines at the points A and B.

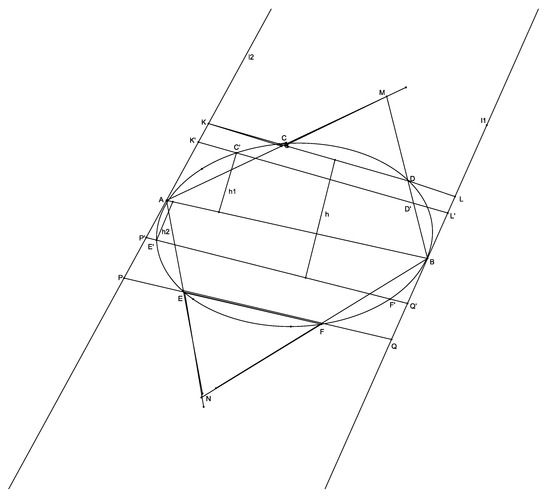
Figure 3. Proofs b, c.

We take the points $D,C,E,F$ on $\theta F$ so that $CD=EF=\frac{AB}{2},andCD\parallel EF\parallel AB$.

We easily see, according our first lemma that

$$Area\left(AKC\right)+Area\left(BLD\right)\ge Area\left(CMD\right)$$

That means

$$Area\left(F\right)<Area\left(KLQP\right)=AB.h$$

(6)

where h is the distance between $CD,EF$.

We now see that the convex F and the orthogonal $PQLK$ have common part $F\cap PQLK$; therefore, the position of the centroid G of F depends on the centroid g of the segments $arcCD$ and segment $arcEF$. The point g lies inside the orthogonal $PQLK$. So we conclude that $d\ge h$ and from (6) follows that

$$AreaF<D.d.$$

Inequality (c).

The equality only for F circle. We suppose that F is not a circle.

We translate the str. lines $KL,PQ$ closer towards to $AB$ until to $K^{\prime }{L}^{\prime },P^{\prime }Q$ such a way the parallelogram $K^{\prime }{L}^{\prime }{Q}^{\prime }{P}^{\prime }$ has

$$Area\left(K^{\prime }{L}^{\prime }{Q}^{\prime }{P}^{\prime }\right)=Area\left(F\right)$$

(7)

we have:

$$C^{\prime }{D}^{\prime }>CD,F^{\prime }{E}^{\prime }>FE$$

where $(C^{\prime },D^{\prime })=K^{\prime }{L}^{\prime }\cap F$ and ${(F^{\prime },E)}^{\prime }=P^{\prime }{Q}^{\prime }\cap F$.

Let now $L_1$ be the part of the perimeter L over of $AB$ and analogously $L_2$. We see that $C^{\prime }{D}^{\prime }/AB>1/2$ and $E^{\prime }{F}^{\prime }/AB>1/2$. So, from the lemma 2, we easily see that $arc{C}^{\prime }{D}^{\prime }>L_1/2$ and $arc{E}^{\prime }{F}^{\prime }>L_2/2$. That is $arc{C}^{\prime }{D}^{\prime }+arc{E}^{\prime }{F}^{\prime }>L/2>arc{E}^{\prime }{C}^{\prime }+arc{D}^{\prime }{F}^{\prime }$.

Moreover, $AreaF<lengtharc{E}^{\prime }{C}^{\prime }.AB,AreaF<lengtharc{D}^{\prime }F{.}^{\prime }AB$; therefore, $2AreaF<(lengtharc{E}^{\prime }{C}^{\prime }+lengtharc{D}^{\prime }{F}^{\prime })AB$ but $lengtharc{E}^{\prime }{C}^{\prime }+lengtharc{D}^{\prime }{F}^{\prime }<lengtharc{C}^{\prime }{D}^{\prime }+lengtharc{E}^{\prime }{F}^{\prime }$; hence, $4AreaF<(lengtharc{E}^{\prime }{C}^{\prime }+lengtharc{D}^{\prime }{F}^{\prime })AB+(lengtharc{C}^{\prime }{D}^{\prime }+lengtharc{E}^{\prime }F)AB<AB.L<D.L$.