Radius of Uniformly Convex γ-Spirallikeness of Combination of Derivatives of Bessel Functions

Abstract

We find the sharp radius of uniformly convex $\gamma$-spirallikeness for $N_{\nu }\left(z\right)=a{z}^2{J}_{\nu }^{″}\left(z\right)+bz{J}_{\nu }^{\prime }\left(z\right)+c{J}_{\nu }\left(z\right)$ (here $J_{\nu }\left(z\right)$ is the Bessel function of the first kind of order $\nu$) with three different kinds of normalizations of the function $N_{\nu }\left(z\right)$. As an application, we derive sufficient conditions on the parameters for the functions to be uniformly convex $\gamma$-spirallikeness and, consequently, generate examples of uniform convex $\gamma$-spirallike via $N_{\nu }\left(z\right)$. Results are well-supported by the relevant graphs and tables.

1. Introduction

Let $\mathcal{A}$ be the class of analytic functions normalized by the condition $f\left(0\right)=0=f^{\prime }\left(0\right)-1$ in the unit disk $\mathbb{D}:={\mathbb{D}}_1$, where ${\mathbb{D}}_r:=\{z\in \mathbb{C}:|z|<r\}$. Now let ${\mathsf{\Gamma }}_w$ be the image of an arc ${\mathsf{\Gamma }}_z:z=z\left(t\right)$, $(a\le t\le b)$ under the function $w=f\left(z\right)$, and let $w_0$ be a point not on ${\mathsf{\Gamma }}_w$. Let $\gamma \in \left(-\frac{\pi }{2},\frac{\pi }{2}\right)$. The arc ${\mathsf{\Gamma }}_w$ is $\gamma$-spirallike with respect to $w_0$ if

$$arg\frac{z^{\prime }\left(t\right)f^{\prime }\left(t\right)}{f\left(z\right)-w_0}$$

lies between $\gamma$ and $\gamma +\pi$. Further, an arc ${\mathsf{\Gamma }}_w$ is convex $\gamma$-spirallike if

$$arg\left(\frac{z^{″}\left(t\right)}{z^{\prime }\left(t\right)}+\frac{z^{\prime }\left(t\right)f^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)$$

lies between $\gamma$ and $\gamma +\pi$. In the form of one variable, equivalently, we say that a function $f\in \mathcal{A}$ is $\gamma$-spirallike of order $\alpha$ if and only if

$$Re\left(e^{-i\gamma }\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)>\alpha cos\gamma ,$$

where $\gamma \in \left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ and $0\le \alpha <1$. We denote the class of such functions by ${\mathcal{S}}_p^{\gamma }\left(\alpha \right)$. In view of the well-known Alexander’s relation, let ${\mathcal{CS}}_p^{\gamma }\left(\alpha \right)$ be the class of convex $\gamma$-spirallike functions of order $\alpha$, which is defined below:

$$Re\left(e^{-i\gamma }\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)\right)>\alpha cos\gamma .$$

Spacek [1] introduced and studied the class ${\mathcal{S}}_p^{\gamma }\left(0\right)$. Each function in ${\mathcal{S}}_p^{\gamma }\left(\alpha \right)$ is univalent in $\mathbb{D}$, but they are not necessarily starlike. Further, it is worth mentioning that, for general values of $\gamma \left(\right|\gamma |<\pi /2)$, a function in ${\mathcal{CS}}_p^{\gamma }\left(0\right)$ need not be univalent in $\mathbb{D}$. For example, $f\left(z\right)=i{(1-z)}^i-i\in {\mathcal{CS}}_p^{\pi /4}\left(0\right)$, but this is not univalent. In this context, see Figure 1. Indeed, $f\in {\mathcal{CS}}_p^{\gamma }\left(0\right)$ is univalent if $0<cos\gamma <1/2$; see Robertson [2] and Pfaltzgraff [3]. Note that, for $\gamma =0$, the classes ${\mathcal{S}}_p^{\gamma }\left(\alpha \right)$ and ${\mathcal{CS}}_p^{\gamma }\left(\alpha \right)$ reduce to the classes of starlike and convex functions of order $\alpha$, given by

$$Re\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)>\alpha \mathrm{and}Re\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)>\alpha ,$$

which we denote by ${\mathcal{S}}^{*}\left(\alpha \right)$ and $\mathcal{C}\left(\alpha \right)$, respectively.

In the above context and using the idea of uniformly starlike and uniformly convex functions introduced and studied in [4,5,6,7,8], Ravichandran et al. [9] introduced the concept of uniformly $\gamma$-spiral functions as described below:

Definition 1.

([9]). The function f is a uniformly convex γ-spiral function if the image of every circular arc ${\mathsf{\Gamma }}_z$ with center at ζ lying in $\mathbb{D}$ is a convex γ-spiral.

We denote the class of such functions by $\mathcal{UCSP}\left(\gamma \right)$. These functions have an analytic characterization (see [9]) as follows:

$$f\in \mathcal{UCSP}\left(\gamma \right)\iff Re\left\{e^{-i\gamma }\left(1+\frac{(z-\zeta )f^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)\right\}\ge 0,z\ne \zeta ,z,\zeta \in \mathbb{D}.$$

Indeed, authors in [9] obtained the one-variable characterization as:

$$f\in \mathcal{UCSP}\left(\gamma \right)\iff Re\left(e^{-i\gamma }\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)\right)>\left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|.$$

Special functions and their geometric properties frequently appear in univalent function theory. In the recent past, normalized function properties have been explored in terms of radius problems [10,11,12,13]. In particular, for a normalized special function f, we define

$${\mathcal{S}}^{*}\left(\alpha \right)-radius:=sup\left\{r\in {\mathbb{R}}^{+}:Re\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)>\alpha ,z\in {\mathbb{D}}_r\right\}$$

and, similarly, one may define the $\mathcal{C}\left(\alpha \right)$-radius. In this direction, the ${\mathcal{S}}^{*}\left(\alpha \right)$-radius of Bessel functions was obtained in [10], and Ramanujan-type entire functions were dealt with in [11]. A unified treatment of the radius of Ma–Minda classes [14] and more for some special functions was studied in [13,15,16].

However, to the best of our knowledge, the $\mathcal{UCSP}\left(\gamma \right)$-radius has not been studied to date for the above-mentioned special functions. Therefore, we define the $\mathcal{UCSP}\left(\gamma \right)$-radius here:

Definition 2.

Let f in $\mathcal{A}$ be a special function. Then, the radius of a uniformly convex γ-spirallike is found as:

$$R_{ucs}(\gamma ;f)=sup\left\{r\in {\mathbb{R}}^{+}:Re\left(e^{-i\gamma }\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)\right)>\left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|,z\in {\mathbb{D}}_r\right\}.$$

In the present investigation, we consider our special normalized functions to be the derivatives of Bessel functions. Recall that the Bessel function of the first kind of order $\nu$ is defined by ([17], p. 217):

$$J_{\nu }\left(z\right)=\sum _{n=0}^{\infty }\frac{{\left(-1\right)}^n}{n!\mathsf{\Gamma }(n+\nu +1)}{\left(\frac{z}{2}\right)}^{2n+\nu }\left(z\in \mathbb{C}\right).$$

(1)

We know that all its zeros are real for $\nu >-1$. Here we consider the general function

$$N_{\nu }\left(z\right)=a{z}^2{J}_{\nu }^{″}\left(z\right)+bz{J}_{\nu }^{\prime }\left(z\right)+c{J}_{\nu }\left(z\right),$$

which was studied by Mercer [18]. Here, as mentioned in [18], we take $q=b-a$ and $\left(c=0\mathrm{and}q\ne 0\right)\mathrm{or}\left(c>0\mathrm{and}q>0\right)$. From (1), we now have the power series representation

$$N_{\nu }\left(z\right)=\sum _{n=0}^{\infty }\frac{Q(2n+\nu ){\left(-1\right)}^n}{n!\mathsf{\Gamma }(n+\nu +1)}{\left(\frac{z}{2}\right)}^{2n+\nu }\left(z\in \mathbb{C}\right),$$

(2)

where $Q\left(\nu \right)=a\nu (\nu -1)+b\nu +c$ $\left(a,b,c\in \mathbb{R}\right).$ There are three important reference works dealing with the function $N_{\nu }.$ Firstly, in Mercer’s paper [18], it is proved that the $k^{th}$ positive zero of $N_{\nu }$ increases with $\nu$ in $\nu >0$. Secondly, Ismail and Muldoon [19], under the conditions $a,b,c\in \mathbb{R}$ such that $c=0$ and $b\ne a$ or $c>0$ and $b>a$, showed the following behavior of roots:

(i)

For $\nu >0$, the zeros of $N_{\nu }\left(z\right)$ are either real or purely imaginary.

(ii)

For $\nu \ge max\{0,{\nu }_0\}$, where ${\nu }_0$ is the largest real root of the quadratic $Q\left(\nu \right)=a\nu (\nu -1)+b\nu +c,$ the the zeros of $N_{\nu }\left(z\right)$ are real.

(iii)

If $\nu >0$, $\left(a{\nu }^2+(b-a)\nu +c\right)∕(b-a)>0$ and $a∕(b-a)<0$, the zeros of $N_{\nu }\left(z\right)$ are all real, except for a single pair that is conjugate and purely imaginary.

In 2016, Baricz et al. [20] obtained the sufficient and necessary conditions for the starlikeness of a normalized form of $N_{\nu }$ by using the results of Mercer [18], Ismail and Muldoon [19], and Shah and Trimble [21].

Since the function $N_{\nu }$ does not belong to $\mathcal{A}$, to prove our results, we consider the following normalizations of the function $N_{\nu }$ as given by:

$$\begin{array}{ccc}\hfill f_{\nu }\left(z\right)& =& {\left[\frac{2^{\nu }\mathsf{\Gamma }(\nu +1)}{Q\left(\nu \right)}{N}_{\nu }\left(z\right)\right]}^{\frac{1}{\nu }},\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill g_{\nu }\left(z\right)& =& \frac{2^{\nu }\mathsf{\Gamma }(\nu +1)z^{1-\nu }}{Q\left(\nu \right)}{N}_{\nu }\left(z\right),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill h_{\nu }\left(z\right)& =& \frac{2^{\nu }\mathsf{\Gamma }(\nu +1)z^{1-\frac{\nu }{2}}}{Q\left(\nu \right)}{N}_{\nu }\left(\sqrt{z}\right).\hfill \end{array}$$

(5)

In the rest of this paper, for the quadratic $Q\left(\nu \right)=a\nu (\nu -1)+b\nu +c$, we will always assume that $a,b,c\in \mathbb{R}$ $\left(c=0\mathrm{and}a\ne b\right)$ or $\left(c>0\mathrm{and}a<b\right).$ Moreover, ${\nu }_0$ is the largest real root of the quadratic $Q\left(\nu \right)$ defined according to the above conditions.

Since the functions $N_{\nu }\left(z\right)$ and $N_{\nu }^{\prime }\left(z\right)$ are entire functions of order zero, then they have infinitely many zeros. According to the Hadamard factorization theorem [22], we may write

$$N_{\nu }\left(z\right)=\frac{Q\left(\nu \right)z^{\nu }}{2^{\nu }\mathsf{\Gamma }(\nu +1)}\prod _{n\ge 1}\left(1-\frac{z^2}{{\lambda }_{\nu ,n}^2}\right)$$

(6)

and

$$N_{\nu }^{\prime }\left(z\right)=\frac{Q\left(\nu \right)z^{\nu -1}\nu }{2^{\nu }\mathsf{\Gamma }(\nu +1)}\prod _{n\ge 1}\left(1-\frac{z^2}{{\lambda }_{\nu ,n}^{\prime 2}}\right),$$

(7)

where ${\lambda }_{\nu ,n}$ and ${\lambda }_{\nu ,n}^{\prime }$ denote the $n^{th}$ positive zero of $N_{\nu }\left(z\right)$ and $N_{\nu }^{\prime }\left(z\right),$ respectively. For recent updates on the geometric properties of Bessel functions, readers are urged to see [20,23,24,25,26,27,28] and references therein.

In this paper, we find the radius of uniformly convex $\gamma$-spirallike for the functions $f_{\nu }\left(z\right),g_{\nu }\left(z\right)$, and $h_{\nu }\left(z\right)$ to be defined by (3)–(5) when $\nu \ge max\{0,{\nu }_0\}$. The key tools in their proofs are special properties of the zeros of the function $N_{\nu }$ and their derivatives.

2. Zeros of Hyperbolic Polynomials and the Laguerre–Pólya Class of Entire Functions

In this section, we recall some necessary information about polynomials and entire functions with real zeros. An algebraic polynomial is called hyperbolic if all its zeros are real. We formulate the following specific statement that we shall need; see [25] for more details. By definition, a real entire function $\psi$ belongs to the Laguerre–Pólya class $\mathcal{LP}$ if it can be represented in the form

$$\psi \left(x\right)=c{x}^m{e}^{-a{x}^2+\beta x}\prod _{k\ge 1}\left(1+\frac{x}{x_k}\right)e^{-\frac{x}{x_k}},$$

with $c,\beta ,x_k\in \mathbb{R},$ $a\ge 0,$ $m\in \mathbb{N}\cup \left\{0\right\}$, and $\sum x_k^{-2}<\infty .$ Similarly, $\varphi$ is said to be of type $\mathcal{I}$ in the Laguerre–Pólya class, written $\phi \in \mathcal{LPI}$, if $\varphi \left(x\right)$ or $\varphi (-x)$ can be represented as

$$\varphi \left(x\right)=c{x}^m{e}^{\sigma x}\prod _{k\ge 1}\left(1+\frac{x}{x_k}\right),$$

with $c\in \mathbb{R},$ $\sigma \ge 0,$ $m\in \mathbb{N}\cup \left\{0\right\},$ $x_k>0$, and $\sum x_k^{-1}<\infty .$ The class $\mathcal{LP}$ is the complement of the space of hyperbolic polynomials in the topology induced by the uniform convergence on the compact sets of the complex plane, while $\mathcal{LPI}$ is the complement of the hyperbolic polynomials whose zeros possess a preassigned constant sign. Given an entire function $\phi$ with the Maclaurin expansion

$$\phi \left(x\right)=\sum _{k\ge 0}{\mu }_k\frac{x^k}{k!},$$

its Jensen polynomials are defined by

$$P_m(\phi ;x)=P_m\left(x\right)=\sum _{k=0}^m\left(\begin{array}{c}m\\ k\end{array}\right){\mu }_k{x}^k.$$

The next result of Jensen [29] is a well-known characterization of functions belonging to $\mathcal{LP}$.

Lemma 1.

The function φ belongs to $\mathcal{LP}$ $(\mathcal{LPI}$, respectively) if and only if all the polynomials $P_m(\phi ;x)$, $m=1,2,\dots ,$ are hyperbolic (hyperbolic with zeros of equal sign). Moreover, the sequence $P_m(\phi ;z∕n)$ converges locally uniformly to $\phi \left(z\right)$.

The following result is a key tool in the proof of the main results.

Lemma 2.

([30]). The function $z⟼{\mathsf{\Psi }}_{\nu }\left(z\right)=\frac{2^{\nu }\mathsf{\Gamma }(\nu +1)}{Q\left(\nu \right)z^{\nu }}{N}_{\nu }\left(z\right)$ has infinitely many zeros, and all of them are positive, if $\nu \ge max\{0,{\nu }_0\}$. Denoting by ${\lambda }_{\nu ,n}$ the $n^{th}$ positive zero of ${\mathsf{\Psi }}_{\nu }\left(z\right),$ under the same conditions, the Weierstrassian decomposition

$${\mathsf{\Psi }}_{\nu }\left(z\right)=\prod _{n\ge 1}\left(1-\frac{z^2}{{\lambda }_{\nu ,n}^2}\right)$$

is valid, and this product is uniformly convergent on compact subsets of the complex plane. Moreover, if we denote by ${\lambda }_{\nu ,n}^{\prime }$ the nth positive zero of ${\mathsf{\Phi }}_{\nu }^{\prime }\left(z\right),$ where ${\mathsf{\Phi }}_{\nu }\left(z\right)=z^{\nu }{\mathsf{\Psi }}_{\nu }\left(z\right),$ then the positive zeros of ${\mathsf{\Psi }}_{\nu }\left(z\right)$ are interlaced with those of ${\mathsf{\Phi }}_{\nu }^{\prime }\left(z\right).$ In other words, the zeros satisfy the chain of inequalities

$${\lambda }_{\nu ,1}^{\prime }<{\lambda }_{\nu ,1}<{\lambda }_{\nu ,2}^{\prime }<{\lambda }_{\nu ,2}<{\lambda }_{\nu ,3}^{\prime }<{\lambda }_{\nu ,3}<\cdots .$$

3. Main Results

Our principal result establishes the radius of $\mathcal{UCSP}\left(\gamma \right)$, see Table 1, and reads as follows:

Theorem 1.

Let $\gamma \in \left(-\frac{\pi }{2},\frac{\pi }{2}\right).$ The following statements hold:

$\left(a\right)$

If $\nu \ge max\{0,{\nu }_0\}$, $\nu \ne 0$, then the radius of uniformly convex γ-spirallikeness of the function $f_{\nu }$ is the smallest positive root of the equation

$$\frac{r{N}_{\nu }^{″}\left(r\right)}{N_{\nu }^{\prime }\left(r\right)}+\left(\frac{1}{\nu }-1\right)\frac{r{N}_{\nu }^{\prime }\left(r\right)}{N_{\nu }\left(r\right)}=\frac{cos\gamma }{2}.$$

$\left(b\right)$

If $\nu \ge max\{0,{\nu }_0\},$ then the radius of uniformly convex γ-spirallikeness of the function $g_{\nu }$ is the smallest positive root of the equation

$$\frac{r^2{N}_{\nu }^{″}\left(r\right)+(2-\nu )r{N}_{\nu }^{\prime }\left(r\right)}{r{N}_{\nu }^{\prime }\left(r\right)+(1-\nu )N_{\nu }\left(r\right)}=\nu -\frac{cos\gamma }{2}.$$

$\left(c\right)$

If $\nu \ge max\{0,{\nu }_0\},$ then the radius of uniformly convex γ-spirallikeness of the function $h_{\nu }$ is the smallest positive root of the equation

$$\frac{\sqrt{r}{N}_{\nu }^{″}\left(\sqrt{r}\right)}{N_{\nu }^{\prime }\left(\sqrt{r}\right)}+\frac{\sqrt{r}{N}_{\nu }^{\prime }\left(\sqrt{r}\right)}{N_{\nu }\left(\sqrt{r}\right)}=1-cos\gamma .$$

Proof. 

We first prove part $\left(a\right)$. From (3), we have

$$1+\frac{z{f}_{\nu }^{″}\left(z\right)}{f_{\nu }^{\prime }\left(z\right)}=1+\frac{z{N}_{\nu }^{″}\left(z\right)}{N_{\nu }^{\prime }\left(z\right)}+\left(\frac{1}{\nu }-1\right)\frac{z{N}_{\nu }^{\prime }\left(z\right)}{N_{\nu }\left(z\right)},$$

and by means of (6) and (7), we obtain

$$1+\frac{z{f}_{\nu }^{″}\left(z\right)}{f_{\nu }^{\prime }\left(z\right)}=1-\left(\frac{1}{\nu }-1\right)\sum _{n\ge 1}\frac{2z^2}{{\lambda }_{\nu ,n}^2-z^2}-\sum _{n\ge 1}\frac{2z^2}{{\lambda }_{\nu ,n}^{\prime 2}-z^2}.$$

For $1\ge \nu >max\left\{0,{\nu }_0\right\}$, we get

$$\begin{array}{cc}\hfill & Re\left(e^{-i\gamma }\left(1+\frac{z{f}_{\nu }^{″}\left(z\right)}{f_{\nu }^{\prime }\left(z\right)}\right)\right)\hfill \\ \hfill & =Re\left(e^{-i\gamma }\right)-Re\left(e^{-i\gamma }\left(\sum _{n\ge 1}\frac{2z^2}{{\lambda }_{\nu ,n}^{\prime 2}-z^2}+\left(\frac{1}{\nu }-1\right)\sum _{n\ge 1}\frac{2z^2}{{\lambda }_{\nu ,n}^2-z^2}\right)\right)\hfill \\ \hfill & \ge cos\gamma -\left(\frac{1}{\nu }-1\right)\sum _{n\ge 1}\frac{2r^2}{{\lambda }_{\nu ,n}^2-r^2}-\sum _{n\ge 1}\frac{2r^2}{{\lambda }_{\nu ,n}^{\prime 2}-r^2}\hfill \\ \hfill & \ge cos\gamma +\frac{r{f}_{\nu }^{″}\left(r\right)}{f_{\nu }^{\prime }\left(r\right)}\hfill \end{array}$$

(8)

where $\left|z\right|=r$. Moreover, observe that if we use the inequality ([31], Lemma 2.1)

$$\mu Re\left(\frac{z}{a-z}\right)-Re\left(\frac{z}{b-z}\right)\ge \mu \frac{\left|z\right|}{a-\left|z\right|}-\frac{\left|z\right|}{b-\left|z\right|},$$

where $a>b>0,$ $\mu \in [0,1]$ and $z\in \mathbb{C}$ such that $\left|z\right|<b$, then we see that the inequality (8) is also valid when $\nu \ge 1$. Here we have seen that the zeros of $N_{\nu }$ and $N_{\nu }^{\prime }$ are interlacing according to Lemma 1. In view of the Definition 2 and the above inequalities (8), let us define $T_{f_{\nu }}:(0,{\lambda }_{\nu ,1}^{\prime })\to \mathbb{R}$, which is given by

$$T_{f_{\nu }}\left(r\right)=cos\gamma -2\left(\left(\frac{1}{\nu }-1\right)\sum _{n\ge 1}\frac{2r^2}{{\lambda }_{\nu ,n}^2-r^2}+\sum _{n\ge 1}\frac{2r^2}{{\lambda }_{\nu ,n}^{\prime 2}-r^2}\right).$$

Clearly, it can be seen that

$$T_{f_{\nu }}\left(0\right)=cos\gamma >0\mathrm{and}\underset{r\nearrow {\lambda }_{\nu ,1}^{\prime }}{lim}{T}_{f_{\nu }}\left(r\right)=-\infty$$

for all $r\in (0,{\lambda }_{\nu ,1}^{\prime })$. Moreover, for $r\in (0,{\lambda }_{\nu ,1}^{\prime })$ using Lemma 2,

$$T_{f_{\nu }}^{\prime }\left(r\right)=2\left\{-\left(\frac{1}{\nu }-1\right)\sum _{n\ge 1}\frac{4r{\lambda }_{\nu ,n}^2}{{({\lambda }_{\nu ,n}^2-r^2)}^2}-\sum _{n\ge 1}\frac{4r{\lambda }_{\nu ,n}^{{}^{\prime }2}}{{({\lambda }_{\nu ,n}^{{}^{\prime }2}-r^2)}^2}\right\}<0.$$

Now let $R_{ucs}(\gamma ;f_{\nu })$ be the smallest positive root of the equation $T_{f_{\nu }}^{\prime }\left(r\right)=0.$ Hence, the inequality

$$Re\left(e^{-i\gamma }\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)\right)>\left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|$$

holds whenever the following inequality is valid:

$$cos\gamma +\frac{r{f}_{\nu }^{″}\left(r\right)}{f_{\nu }^{\prime }\left(r\right)}>-\frac{r{f}_{\nu }^{″}\left(r\right)}{f_{\nu }^{\prime }\left(r\right)}.$$

The above inequality may be equivalently read as $T_{f_{\nu }}\left(r\right)>0$, which is valid for all $\left|z\right|=r<R_{ucs}(\gamma ;f_{\nu })$. The sharpness of the radius constant $R_{ucs}(\gamma ;f_{\nu })$ can be observed, in view of the maximum and minimum modulus principles by taking $z=r>R_{ucs}(\gamma ;f_{\nu })$ such that the following reverse inequality holds:

$$\begin{array}{cc}\hfill \underset{\left|z\right|=r}{min}Re\left(e^{-i\gamma }\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)\right)=& cos\gamma +\frac{r{f}_{\nu }^{″}\left(r\right)}{f_{\nu }^{\prime }\left(r\right)}\hfill \\ \hfill <& \underset{\left|z\right|=r}{max}\left|\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right|\hfill \\ \hfill =& -\frac{r{f}_{\nu }^{″}\left(r\right)}{f_{\nu }^{\prime }\left(r\right)}.\hfill \end{array}$$

This completes the proof of part $\left(a\right)$.

For the other parts, in view of Lemma 2, note that the functions $g_{\nu }$ and $h_{\nu }$ belong to the Laguerre–Pólya class $\mathcal{LP}$, which is closed under differentiation, that their derivatives $g_{\nu }^{\prime }$ and $h_{\nu }^{\prime }$ also belong to $\mathcal{LP}$, and that the zeros are real. Thus assuming ${\delta }_{\nu ,n}$ and ${\gamma }_{\nu ,n}$ to be the positive zeros of $g_{\nu }^{\prime }$ and $h_{\nu }^{\prime }$, respectively, we have the following representations:

$$\begin{array}{c}\hfill g_{\nu }^{\prime }\left(z\right)=\prod _{n\ge 1}\left(1-\frac{z^2}{{\delta }_{\nu ,n}^2}\right)\mathrm{and}{h}_{\nu }^{\prime }\left(z\right)=\prod _{n\ge 1}\left(1-\frac{z}{{\gamma }_{\nu ,n}}\right),\end{array}$$

which yield

$$\begin{array}{c}\hfill 1+\frac{z{g}_{\nu }^{″}\left(z\right)}{g_{\nu }^{\prime }\left(z\right)}=1-\sum _{n\ge 1}\frac{2z^2}{{\delta }_{\nu ,n}^2-z^2}\mathrm{and}1+\frac{z{h}_{\nu }^{″}\left(z\right)}{h_{\nu }^{\prime }\left(z\right)}=1-\sum _{n\ge 1}\frac{z}{{\gamma }_{\nu ,n}-z}.\end{array}$$

Further, reasoning along the same lines as in part $\left(a\right)$, the result follows at once. □

Table 1. Radii of uniformly convex $\frac{\pi }{3}-$spirallike for $f_{1/2},g_{1/2}$, and $h_{1/2}$ in Theorem 1.

	$\mathit{b}=3$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{b}=2$
	$\mathbf{a}=\mathbf{2}$	$\mathbf{a}=\mathbf{3}$	$\mathbf{a}=\mathbf{4}$	$\mathbf{b}=\mathbf{2}$	$\mathbf{b}=\mathbf{3}$	$\mathbf{b}=\mathbf{4}$	$\mathbf{c}=\mathbf{2}$	$\mathbf{c}=\mathbf{3}$	$\mathbf{c}=\mathbf{4}$
$f_{\nu }$	$0.087$	$0.067$	$0.050$	$0.099$	$0.113$	$0.121$	$0.172$	$0.192$	$0.208$
$g_{\nu }$	$0.122$	$0.094$	$0.0703$	$0.138$	$0.157$	$0.169$	$0.241$	$0.269$	$0.292$
$h_{\nu }$	$0.040$	$0.024$	$0.013$	$0.052$	$0.068$	$0.078$	$0.162$	$0.204$	$0.240$

Table 1. Radii of uniformly convex $\frac{\pi }{3}-$spirallike for $f_{1/2},g_{1/2}$, and $h_{1/2}$ in Theorem 1.

	$\mathit{b}=3$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{b}=2$
	$\mathbf{a}=\mathbf{2}$	$\mathbf{a}=\mathbf{3}$	$\mathbf{a}=\mathbf{4}$	$\mathbf{b}=\mathbf{2}$	$\mathbf{b}=\mathbf{3}$	$\mathbf{b}=\mathbf{4}$	$\mathbf{c}=\mathbf{2}$	$\mathbf{c}=\mathbf{3}$	$\mathbf{c}=\mathbf{4}$
$f_{\nu }$	$0.087$	$0.067$	$0.050$	$0.099$	$0.113$	$0.121$	$0.172$	$0.192$	$0.208$
$g_{\nu }$	$0.122$	$0.094$	$0.0703$	$0.138$	$0.157$	$0.169$	$0.241$	$0.269$	$0.292$
$h_{\nu }$	$0.040$	$0.024$	$0.013$	$0.052$	$0.068$	$0.078$	$0.162$	$0.204$	$0.240$

Example 1.

For the value $\nu =1/2$, we may express the function $N_{\nu }\left(z\right)$ in terms of the elementary trigonometric functions as follows:

$$N_{1/2}\left(z\right)=\frac{4\left(b-a\right)zcosz+\left[a\left(3-4z^2\right)-2b+4c\right]sinz}{2\sqrt{2\pi }\sqrt{z}}.$$

Consequently, we get

$$f_{1/2}\left(z\right)=\frac{{\left[4\left(a-b\right)zcosz+\left(4a{z}^2-3a+2b-4c\right)sinz\right]}^2}{{\left(a-2b-4c\right)}^{2}z},$$

$$g_{1/2}\left(z\right)=\frac{4\left(a-b\right)zcosz+\left(4a{z}^2-3a+2b-4c\right)sinz}{a-2b-4c},$$

and

$$h_{1/2}\left(z\right)=\frac{4\left(a-b\right)zcos\sqrt{z}+\left(4az-3a+2b-4c\right)\sqrt{z}sin\sqrt{z}}{a-2b-4c}.$$

An immediate consequence of the proof of Theorem 1 is the following sufficient conditions for functions to be uniformly convex $\gamma$-spirallike. In fact, Table 2, Table 3 and Table 4 explain the sufficient conditions for uniformly convex $\gamma$-spirallikeness by giving the minimum value of the $\nu$ with respect to the given equations in Corollary 1. Also, Figure 1, Figure 2 and Figure 3 represent image domains of the unit disk in view of Corollary 1.

Corollary 1.

(Sufficient condition.) Let $\gamma \in \left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ and $\nu \ge max\{0,{\nu }_0\}$. Then, the following statements hold:

$\left(a\right)$

Let $\nu \ne 0$. The function $f_{\nu }$ is uniformly convex γ-spirallike if

$$\frac{cos\gamma }{2}+\frac{N_{\nu }^{″}\left(1\right)}{N_{\nu }^{\prime }\left(1\right)}+\left(\frac{1}{\nu }-1\right)\frac{N_{\nu }^{\prime }\left(1\right)}{N_{\nu }\left(1\right)}>0.$$

$\left(b\right)$

The function $g_{\nu }$ is uniformly convex γ-spirallike if

$$\frac{cos\gamma }{2}-\nu +\frac{N_{\nu }^{″}\left(1\right)+(2-\nu )N_{\nu }^{\prime }\left(1\right)}{N_{\nu }^{\prime }\left(1\right)+(1-\nu )N_{\nu }\left(1\right)}>0.$$

$\left(c\right)$

The function $h_{\nu }$ is uniformly convex γ-spirallike if

$$\frac{N_{\nu }^{″}\left(1\right)}{N_{\nu }^{\prime }\left(1\right)}+\frac{N_{\nu }^{\prime }\left(1\right)}{N_{\nu }\left(1\right)}>1-cos\gamma .$$

• In particular, $\gamma =0$ provides sufficient conditions for functions to be uniformly convex.

Table 2. Minimum value of $\nu$ for uniformly convex $\gamma$-spirallike of $f_{\nu }$ in Corollary 1.

	$\mathit{b}=3$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{b}=2$
	$\mathbf{a}=\mathbf{2}$	$\mathbf{a}=\mathbf{3}$	$\mathbf{a}=\mathbf{4}$	$\mathbf{b}=\mathbf{2}$	$\mathbf{b}=\mathbf{3}$	$\mathbf{b}=\mathbf{4}$	$\mathbf{c}=\mathbf{2}$	$\mathbf{c}=\mathbf{3}$	$\mathbf{c}=\mathbf{4}$
$\gamma =\pi /3$	$0.8921$	$3.6136$	$1.0762$	$0.8229$	$0.7432$	$0.6999$	$0.4802$	$0.3938$	$0.3395$
$\gamma =\pi /4$	$0.8910$	$3.2130$	$1.0770$	$0.8211$	$0.7408$	$0.6973$	$0.4748$	$0.3883$	$0.3342$
$\gamma =0$	$0.8895$	$2.8790$	$1.0779$	$0.8188$	$0.7376$	$0.6937$	$0.4674$	$0.3806$	$0.3268$

Table 2. Minimum value of $\nu$ for uniformly convex $\gamma$-spirallike of $f_{\nu }$ in Corollary 1.

	$\mathit{b}=3$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{b}=2$
	$\mathbf{a}=\mathbf{2}$	$\mathbf{a}=\mathbf{3}$	$\mathbf{a}=\mathbf{4}$	$\mathbf{b}=\mathbf{2}$	$\mathbf{b}=\mathbf{3}$	$\mathbf{b}=\mathbf{4}$	$\mathbf{c}=\mathbf{2}$	$\mathbf{c}=\mathbf{3}$	$\mathbf{c}=\mathbf{4}$
$\gamma =\pi /3$	$0.8921$	$3.6136$	$1.0762$	$0.8229$	$0.7432$	$0.6999$	$0.4802$	$0.3938$	$0.3395$
$\gamma =\pi /4$	$0.8910$	$3.2130$	$1.0770$	$0.8211$	$0.7408$	$0.6973$	$0.4748$	$0.3883$	$0.3342$
$\gamma =0$	$0.8895$	$2.8790$	$1.0779$	$0.8188$	$0.7376$	$0.6937$	$0.4674$	$0.3806$	$0.3268$

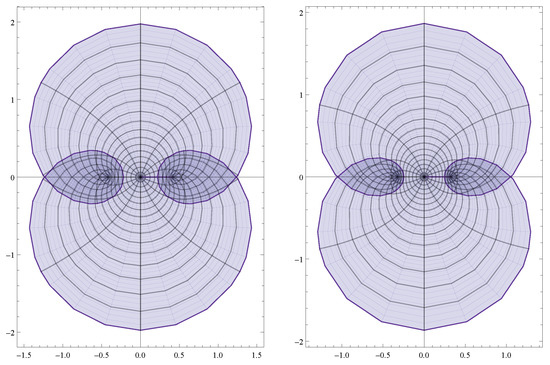
Figure 1. Image domains of the unit disk under $f_1$ with $a=2,b=3$, and $c=0$ for $\gamma =\pi /3$, and $f_{0.5}$ with $a=1,b=2$, and $c=2$ for $\gamma =\pi /4$ using Table 2.

Remark 1.

In light of Spacek [1], here we see that $f_1\in {\mathcal{CS}}_p^{\pi /3}\left(0\right)$ for $a=2,b=3$, and $c=0$, and $f_{0.5}\in {\mathcal{CS}}_p^{\pi /4}\left(0\right)$ for $a=1,b=2$, and $c=2$, but that these are not univalent in $\mathbb{D}$, as shown in Figure 1.

Table 3. Minimum value of $\nu$ for uniformly convex $\gamma$-spirallike of $g_{\nu }$ in Corollary 1.

	$\mathit{b}=3$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{b}=2$
	$\mathbf{a}=\mathbf{2}$	$\mathbf{a}=\mathbf{3}$	$\mathbf{a}=\mathbf{4}$	$\mathbf{b}=\mathbf{2}$	$\mathbf{b}=\mathbf{3}$	$\mathbf{b}=\mathbf{4}$	$\mathbf{c}=\mathbf{2}$	$\mathbf{c}=\mathbf{3}$	$\mathbf{c}=\mathbf{4}$
$\gamma =\pi /3$	$8.6224$	$8.6936$	$8.7315$	$8.5568$	$8.4404$	$8.3404$	$8.5008$	$8.4730$	$8.4455$
$\gamma =\pi /4$	$6.7337$	$6.8160$	$6.8604$	$6.6591$	$6.5297$	$6.4220$	$6.5785$	$6.5387$	$6.4993$
$\gamma =0$	$5.3610$	$5.4540$	$5.5048$	$5.2783$	$5.1385$	$5.0258$	$5.1675$	$5.1128$	$5.0586$

Table 3. Minimum value of $\nu$ for uniformly convex $\gamma$-spirallike of $g_{\nu }$ in Corollary 1.

	$\mathit{b}=3$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{b}=2$
	$\mathbf{a}=\mathbf{2}$	$\mathbf{a}=\mathbf{3}$	$\mathbf{a}=\mathbf{4}$	$\mathbf{b}=\mathbf{2}$	$\mathbf{b}=\mathbf{3}$	$\mathbf{b}=\mathbf{4}$	$\mathbf{c}=\mathbf{2}$	$\mathbf{c}=\mathbf{3}$	$\mathbf{c}=\mathbf{4}$
$\gamma =\pi /3$	$8.6224$	$8.6936$	$8.7315$	$8.5568$	$8.4404$	$8.3404$	$8.5008$	$8.4730$	$8.4455$
$\gamma =\pi /4$	$6.7337$	$6.8160$	$6.8604$	$6.6591$	$6.5297$	$6.4220$	$6.5785$	$6.5387$	$6.4993$
$\gamma =0$	$5.3610$	$5.4540$	$5.5048$	$5.2783$	$5.1385$	$5.0258$	$5.1675$	$5.1128$	$5.0586$

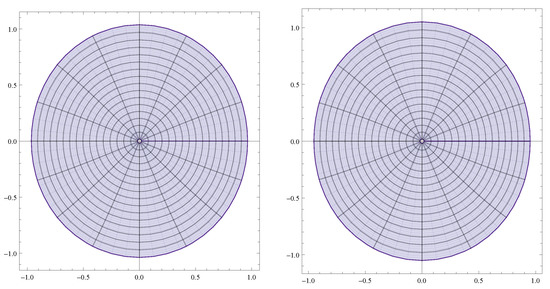
Figure 2. Image domains of the unit disk under the function $g_9$ with $a=2,b=3$, and $c=0$ for $\gamma =\pi /3$, and the function $g_7$ with $a=1,b=2$, and $c=2$ for $\gamma =\pi /4$ using Table 3.

Table 4. Minimum value of $\nu$ for uniformly convex $\gamma$-spirallike of $h_{\nu }$ in Corollary 1.

	$\mathit{b}=3$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{b}=2$
	$\mathbf{a}=\mathbf{2}$	$\mathbf{a}=\mathbf{3}$	$\mathbf{a}=\mathbf{4}$	$\mathbf{b}=\mathbf{2}$	$\mathbf{b}=\mathbf{3}$	$\mathbf{b}=\mathbf{4}$	$\mathbf{c}=\mathbf{2}$	$\mathbf{c}=\mathbf{3}$	$\mathbf{c}=\mathbf{4}$
$\gamma =\pi /3$	$1.0778$	$1.2061$	$1.2908$	$0.9895$	$0.8818$	$0.8210$	$0.5378$	$0.3990$	$0.3134$
$\gamma =\pi /4$	$1.0709$	$1.2003$	$1.2856$	$0.9818$	$0.8732$	$0.8119$	$0.5177$	$0.3741$	$0.2863$
$\gamma =0$	$1.0614$	$1.1923$	$1.2786$	$0.9713$	$0.8614$	$0.7996$	$0.4890$	$0.3377$	$0.2463$

Table 4. Minimum value of $\nu$ for uniformly convex $\gamma$-spirallike of $h_{\nu }$ in Corollary 1.

	$\mathit{b}=3$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{c}=0$			$\mathit{a}=1$ and $\mathit{b}=2$
	$\mathbf{a}=\mathbf{2}$	$\mathbf{a}=\mathbf{3}$	$\mathbf{a}=\mathbf{4}$	$\mathbf{b}=\mathbf{2}$	$\mathbf{b}=\mathbf{3}$	$\mathbf{b}=\mathbf{4}$	$\mathbf{c}=\mathbf{2}$	$\mathbf{c}=\mathbf{3}$	$\mathbf{c}=\mathbf{4}$
$\gamma =\pi /3$	$1.0778$	$1.2061$	$1.2908$	$0.9895$	$0.8818$	$0.8210$	$0.5378$	$0.3990$	$0.3134$
$\gamma =\pi /4$	$1.0709$	$1.2003$	$1.2856$	$0.9818$	$0.8732$	$0.8119$	$0.5177$	$0.3741$	$0.2863$
$\gamma =0$	$1.0614$	$1.1923$	$1.2786$	$0.9713$	$0.8614$	$0.7996$	$0.4890$	$0.3377$	$0.2463$

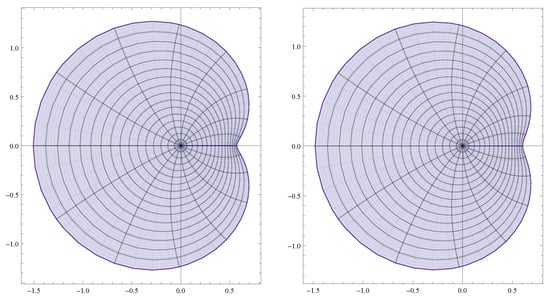
Figure 3. Image domains of the unit disk under function $h_{3.5}$ with $a=2,b=3$, and $c=0$ for $\gamma =\pi /3$, and function $h_1$ with $a=1,b=2$, and $c=2$ for $\gamma =\pi /4$ using Table 4.

Remark 2.

In Table 2, Table 3 and Table 4, the entries with the choice $\gamma =0$ generate ample examples of uniformly convex functions via the special function $N_{\nu }\left(z\right)=a{z}^2{J}_{\nu }^{″}\left(z\right)+bz{J}_{\nu }^{\prime }\left(z\right)+c{J}_{\nu }\left(z\right)$, studied by Mercer [18].

In Theorem 1, letting $\gamma =0$, we obtain the radius of uniform convexity for the functions $f_{\nu }\left(z\right),g_{\nu }\left(z\right)$, and $h_{\nu }\left(z\right)$ as defined by (3), (4), and (5), respectively.

Corollary 2.

(Radius of uniform convexity). Let $\nu \ge max\{0,{\nu }_0\}$. The following statements hold:

$\left(a\right)$

If $\nu \ne 0$, then the radius of uniform convexity of the function $f_{\nu }$ is the smallest positive root of the equation

$$\frac{r{N}_{\nu }^{″}\left(r\right)}{N_{\nu }^{\prime }\left(r\right)}+\left(\frac{1}{\nu }-1\right)\frac{r{N}_{\nu }^{\prime }\left(r\right)}{N_{\nu }\left(r\right)}=\frac{1}{2}.$$

$\left(b\right)$

The radius of uniform convexity of the function $g_{\nu }$ is the smallest positive root of the equation

$$\frac{r^2{N}_{\nu }^{″}\left(r\right)+(2-\nu )r{N}_{\nu }^{\prime }\left(r\right)}{r{N}_{\nu }^{\prime }\left(r\right)+(1-\nu )N_{\nu }\left(r\right)}=\nu -\frac{1}{2}.$$

$\left(c\right)$

Then the radius of uniform convexity of the function $h_{\nu }$ is the smallest positive root of the equation

$$\frac{\sqrt{r}{N}_{\nu }^{″}\left(\sqrt{r}\right)}{N_{\nu }^{\prime }\left(\sqrt{r}\right)}+\frac{\sqrt{r}{N}_{\nu }^{\prime }\left(\sqrt{r}\right)}{N_{\nu }\left(\sqrt{r}\right)}=0.$$

Now, from Theorem 1, we deduce that:

Example 2.

Let $\nu =1/2,$ $a=1,$ $b=2,$ $c=0$, and $\gamma =\pi /3$, see Figure 4. The following statements are true.

$\left(a\right)$

The radius of uniformly convex $\frac{\pi }{3}-$spirallikeness of the function $f_{1/2}$ is the smallest positive root of the equation

$$\frac{1+48t^4+(-1+2t^2-192t^4+32t^6)cos2t+2t(-1-16t^2+80t^4)sin2t}{(-4tcost+sint+4t^{2}sint)(2t(-1+4t^2)cost+(-1+20t^2)sint)}+\frac{1}{4}=0.$$

$\left(b\right)$

The radius of uniformly convex $\frac{\pi }{3}-$spirallikeness of the function $g_{1/2}$ is the smallest positive root of the equation

$$\frac{t(20tcost+(15-4t^2)sint)}{(-3+4t^2)cost+12tsint}+\frac{1}{4}=0.$$

$\left(c\right)$

The radius of uniformly convex $\frac{\pi }{3}-$spirallikeness of the function $h_{1/2}$ is the smallest positive root of the equation

$$\frac{(1+24t)\sqrt{t}cos\sqrt{t}+(-1+(23-4t)t)sin\sqrt{t}}{2(-7+4t)\sqrt{t}cos\sqrt{t}+2(1+16t)sin\sqrt{t}}+\frac{1}{4}=0.$$

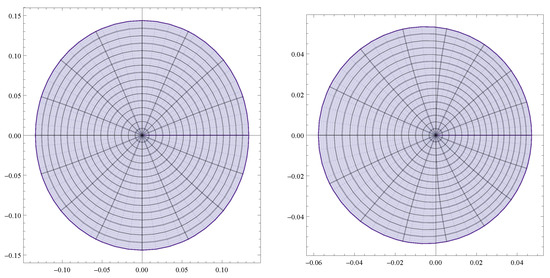
Figure 4. Image domains of $g_{1/2}$ for $\left|z\right|<0.1386$ and $h_{1/2}$ for $\left|z\right|<0.0524$, respectively, with $a=1,b=2$, and $c=0$ for $\gamma =\pi /3.$

4. Conclusions

For the three different kinds of normalizations, namely (3), (4), and (5) of the function $N_{\nu }\left(z\right)=a{z}^2{J}_{\nu }^{″}\left(z\right)+bz{J}_{\nu }^{\prime }\left(z\right)+c{J}_{\nu }\left(z\right),$ where $J_{\nu }\left(z\right)$ is the Bessel function of the first kind of order $\nu$, we obtained the sharp radius of uniformly $\gamma$-spirallikeness. As a byproduct, we obtained the conditions on parameters for the normalized forms to be uniform $\gamma$-spirallike functions. Thus, we created a category of examples of uniform $\gamma$-spirallike functions from special functions.