Local-Basis-Function Equation of State for Ice VII–X to 450 GPa at 300 K
Abstract
1. Introduction
Phase Behavior of Ice Beyond 2.2 GPa
2. Materials and Methods
2.1. Helmholtz Energy-Based Equations of State
2.2. Local-Basis-Function Representation of Helmholtz Energy
- B-spline basis function values are available in all computer environments as a call to a function/subroutine. Analogous to the use of exponential or trigonometric functions, no custom (user) programing is necessary for use of b-spline basis functions. The evaluation of equation of state properties then uses universal calling functions that are not material specific.
- The calculation of values and derivatives of a b-spline model are based on linear programing. Interpolation using b-splines is essentially a weighted average of neighboring model parameters with the basis functions providing the normalized weights. This enables efficient computer algorithms for both construction and evaluation of spline models. Arbitrary precision is possible in representing any functional behavior.
- B-spline basis functions are localized. Unlike global polynomial fits of data, spline model parameters pertain to the behavior of the underlying function in a separate restricted regime of the independent variable.
- Details of how intervals are defined allow flexibility in the behavior of function derivatives at interval boundaries. It is possible to allow discontinuities of the function or specified derivatives of the function at a location to meet the needs of a particular equation of state that might involve higher-order transitions.
2.3. Determination of Helmholtz Energy by Collocation
3. Results
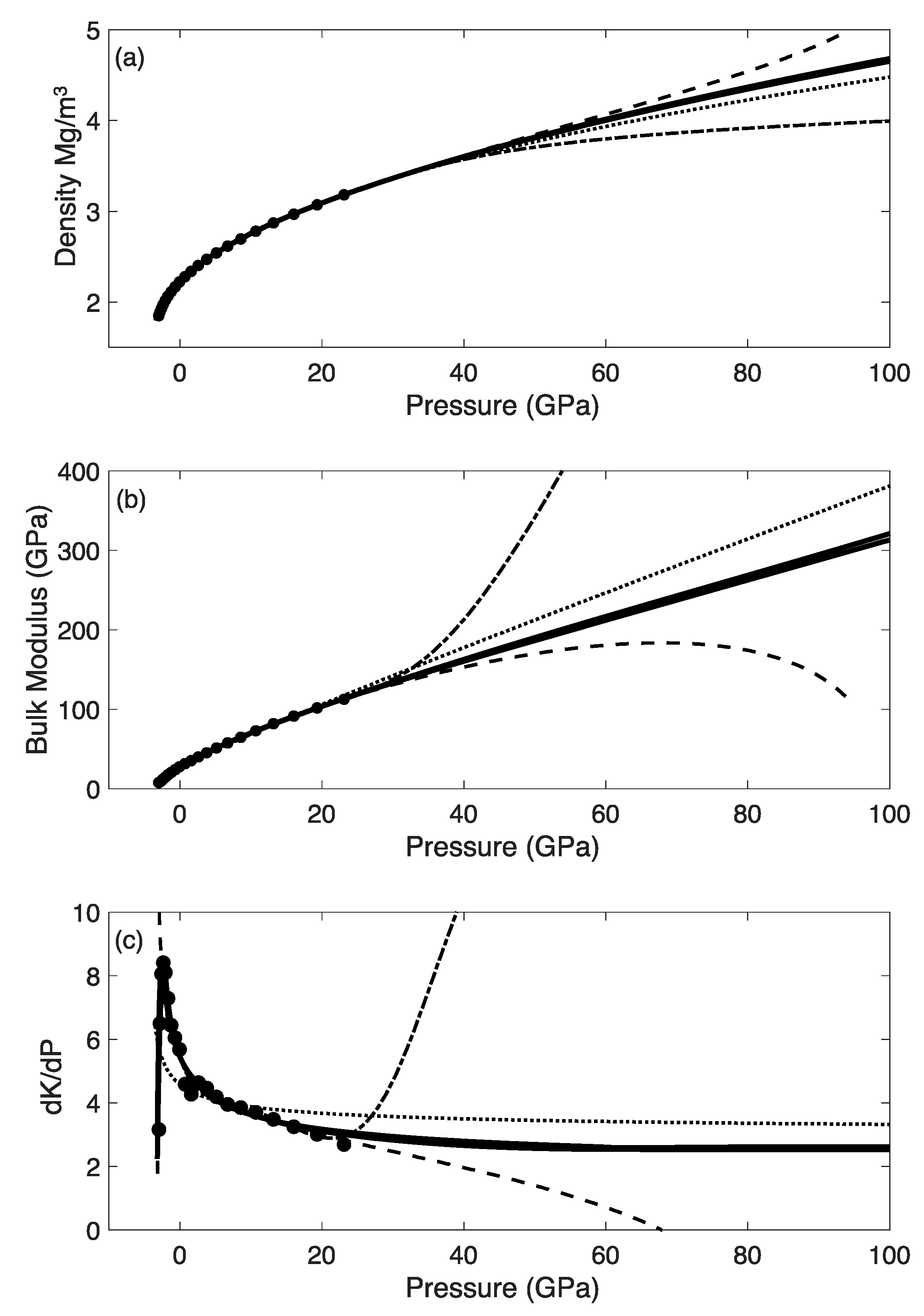
3.1. Equations of State for NaCl
3.1.1. Data and Representations
3.1.2. Discussion
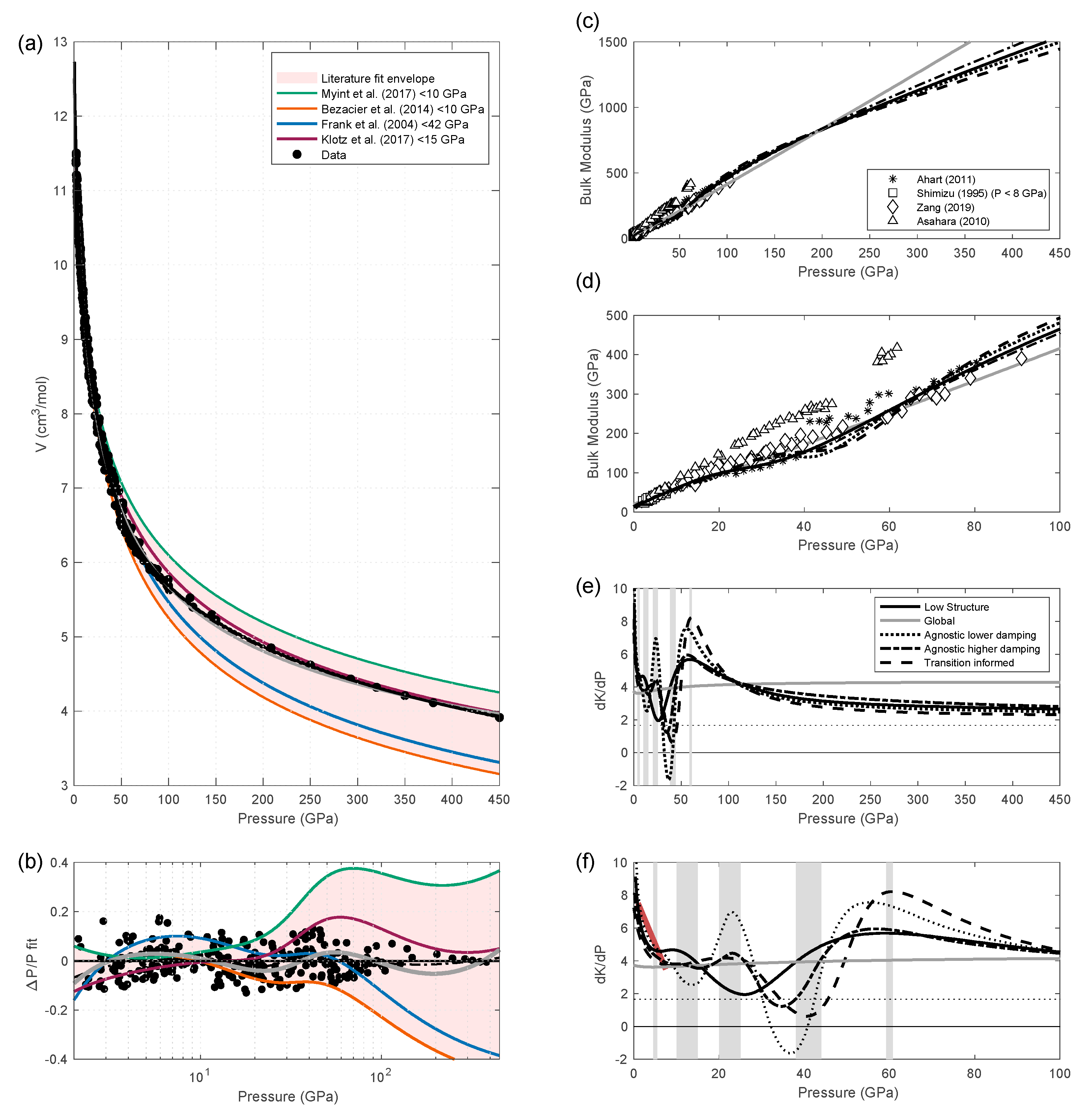
3.2. Equations of State for High Pressure Ice (Ice VII–X System)
3.2.1. Data and Representations
3.2.2. Discussion
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. B-Spline and Inverse Method Details Related to Equation of State Representations
Appendix A.1. B-Spline Basis Functions
Appendix A.2. Evaluation of B-Spline Representations
Appendix A.3. Details of B-Spline Knots and Control Points
Appendix A.4. Local-Basis-Function Equations of State Representations
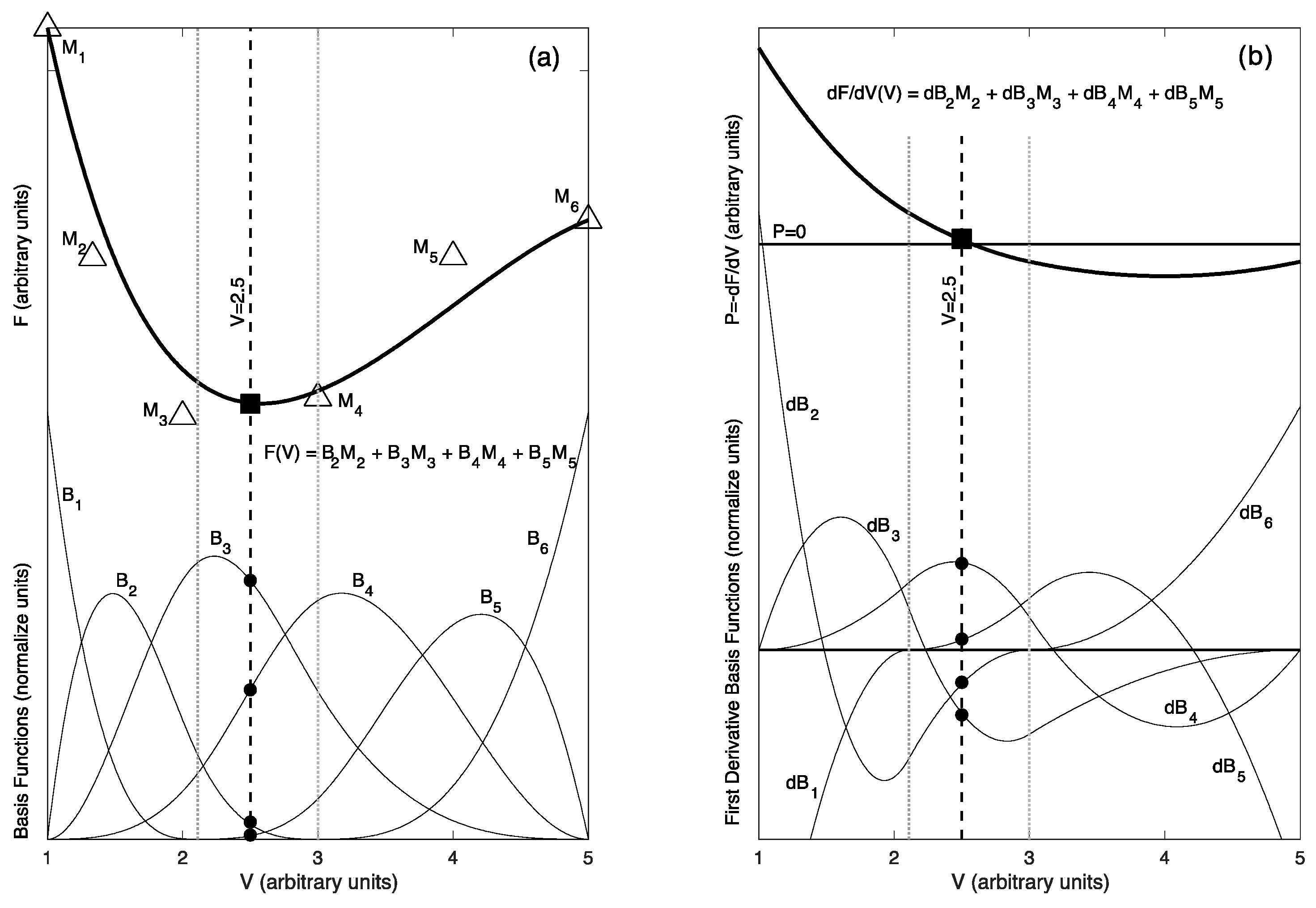
Appendix A.5. Defining Equation of State Properties with Derivatives of Helmholtz Energy
Appendix A.6. Inverse Techniques to Find Model Parameters
References
- Tschauner, O.; Huang, S.; Greenberg, E.; Prakapenka, V.B.; Ma, C.; Rossman, G.R.; Shen, A.H.; Zhang, D.; Newville, M.; Lanzirotti, A.; et al. Ice-VII inclusions in diamonds: Evidence for aqueous fluid in Earth’s deep mantle. Science 2018, 359, 1136–1139. [Google Scholar] [CrossRef]
- Léger, A.; Selsis, F.; Sotin, C.; Guillot, T.; Despois, D.; Mawet, D.; Ollivier, M.; Labèque, A.; Valette, C.; Brachet, F. A new family of planets? Icarus 2004, 169, 499–504. [Google Scholar] [CrossRef]
- Sotin, C.; Grasset, O. Mass-radius curve for extrasolar Earth-like planets and ocean planets. Icarus 2007, 191, 337–351. [Google Scholar] [CrossRef]
- Noack, L.; Höning, D.; Rivoldini, A.; Heistracher, C.; Zimov, N.; Journaux, B.; Lammer, H.; Van Hoolst, T.; Bredehöft, J.H. Water-rich planets: How habitable is a water layer deeper than on Earth? Icarus 2016, 277, 215–236. [Google Scholar] [CrossRef]
- Vance, S.D.; Panning, M.P.; Stähler, S.; Cammarano, F.; Bills, B.G.; Tobie, G.; Kamata, S.; Kedar, S.; Sotin, C.; Pike, W.T.; et al. Geophysical investigations of habitability in ice-covered ocean worlds: Geophysical habitability. J. Geophys. Res. Planets 2018, 123, 180–205. [Google Scholar] [CrossRef]
- Journaux, B.; Daniel, I.; Petitgirard, S.; Cardon, H.; Perrillat, J.-P.; Caracas, R.; Mezouar, M. Salt partitioning between water and high-pressure ices. Implication for the dynamics and habitability of icy moons and water-rich planetary bodies. Earth Planet. Sci. Lett. 2017, 463, 36–47. [Google Scholar] [CrossRef]
- Unterborn, C.T.; Desch, S.J.; Hinkel, N.R.; Lorenzo, A. Inward migration of the TRAPPIST-1 planets as inferred from their water-rich compositions. Nat. Astron. 2018, 2, 297–302. [Google Scholar] [CrossRef]
- Kite, E.S.; Ford, E.B. Habitability of exoplanet waterworlds. arXiv 2018, arXiv:1801.00748 [astro-ph]. [Google Scholar] [CrossRef]
- Hendrix, A.R.; Hurford, T.A.; Barge, L.M.; Bland, M.T.; Bowman, J.S.; Brinckerhoff, W.; Buratti, B.J.; Cable, M.L.; Castillo-Rogez, J.; Collins, G.C.; et al. The NASA Roadmap to Ocean Worlds. Astrobiology 2019, 19, 1–27. [Google Scholar] [CrossRef]
- Birch, F. Elasticity and constitution of the Earth’s interior. J. Geophys. Res. 1952, 57, 227–286. [Google Scholar] [CrossRef]
- Stacey, F.D.; Brennan, B.J.; Irvine, R.D. Finite strain theories and comparisons with seismological data. Geophys. Surv. 1981, 4, 189–232. [Google Scholar] [CrossRef]
- Benoit, M.; Bernasconi, M.; Focher, P.; Parrinello, M. New High-Pressure Phase of Ice. Phys. Rev. Lett. 1996, 76, 2934–2936. [Google Scholar] [CrossRef] [PubMed]
- Hermann, A.; Ashcroft, N.W.; Hoffmann, R. High pressure ices. Proc. Natl. Acad. Sci. USA 2012, 109, 745–750. [Google Scholar] [CrossRef]
- Millot, M.; Coppari, F.; Rygg, J.R.; Correa Barrios, A.; Hamel, S.; Swift, D.C.; Eggert, J.H. Nanosecond X-ray diffraction of shock-compressed superionic water ice. Nature 2019, 569, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Hemley, R.J.; Jephcoat, A.P.; Mao, H.K.; Zha, C.S.; Finger, L.W.; Cox, D.E. Static compression of H2O-ice to 128 GPa (1.28 Mbar). Nature 1987, 330, 737–740. [Google Scholar] [CrossRef]
- Loubeyre, P.; Letoullec, R.; Wolanin, E.; Hanfland, M.; Häusermann, D. Modulated phases and proton centering in ice observed by X-ray diffraction up to 170 GPa. Nature 1999, 397, 503–506. [Google Scholar] [CrossRef]
- Sugimura, E.; Iitaka, T.; Hirose, K.; Kawamura, K.; Sata, N.; Ohishi, Y. Compression of H2O ice to 126 GPa and implications for hydrogen-bond symmetrization: Synchrotron x-ray diffraction measurements and density-functional calculations. Phys. Rev. B 2008, 77, 214103. [Google Scholar] [CrossRef]
- Goncharov, A.F.; Struzhkin, V.V.; Somayazulu, M.S.; Hemley, R.J.; Mao, H.K. Compression of Ice to 210 Gigapascals: Infrared Evidence for a Symmetric Hydrogen-Bonded Phase. Science 1996, 273, 218–220. [Google Scholar] [CrossRef]
- Zha, C.-S.; Hemley, R.J.; Gramsch, S.A.; Mao, H.; Bassett, W.A. Optical study of H2O ice to 120GPa: Dielectric function, molecular polarizability, and equation of state. J. Chem. Phys. 2007, 126, 074506. [Google Scholar] [CrossRef]
- Meier, T.; Petitgirard, S.; Khandarkhaeva, S.; Dubrovinsky, L. Observation of nuclear quantum effects and hydrogen bond symmetrisation in high pressure ice. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef]
- Grande, Z.M.; Huang, C.; Smith, D.; Smith, J.S.; Boisvert, J.H.; Tschauner, O.; Steffen, J.H.; Salamat, A. Bond strengthening in dense H2O and implications to planetary composition. arXiv 2019, arXiv:1906.11990 [astro-ph, physics:cond-mat]. [Google Scholar]
- Hirai, H.; Kadobayashi, H.; Matsuoka, T.; Ohishi, Y.; Yamamoto, Y. High pressure X-ray diffraction and Raman spectroscopic studies of the phase change of D2O ice VII at approximately 11 GPa. Int. J. High Press. Res. 2014, 34, 289–296. [Google Scholar] [CrossRef]
- Somayazulu, M.; Shu, J.; Zha, C. In situ high-pressure x-ray diffraction study of H2O ice VII. J. Chem. Phys. 2008, 128, 064510. [Google Scholar] [CrossRef] [PubMed]
- Pruzan, P.; Chervin, J.-C.; Gauthier, M. Raman Spectroscopy Investigation of Ice VII and Deuterated Ice VII to 40 GPa. Disorder in Ice VII. Europhys. Lett. 1990, 13, 81–87. [Google Scholar] [CrossRef]
- Zha, C.-S.; Tse, J.S.; Bassett, W.A. New Raman measurements for H2O ice VII in the range of 300 cm−1 to 4000 cm−1 at pressures up to 120 GPa. J. Chem. Phys. 2016, 145, 124315. [Google Scholar] [CrossRef]
- Guthrie, M.; Boehler, R.; Tulk, C.A.; Molaison, J.J.; dos Santos, A.M.; Li, K.; Hemley, R.J. Neutron diffraction observations of interstitial protons in dense ice. Proc. Natl. Acad. Sci. USA 2013, 110, 10552–10556. [Google Scholar] [CrossRef]
- Yoshimura, Y.; Stewart, S.T.; Somayazulu, M.; Mao, H.; Hemley, R.J. High-pressure x-ray diffraction and Raman spectroscopy of ice VIII. J. Chem. Phys. 2006, 124, 024502. [Google Scholar] [CrossRef]
- Okada, T.; Iitaka, T.; Yagi, T.; Aoki, K. Electrical conductivity of ice VII. Sci. Rep. 2014, 4, 5778. [Google Scholar] [CrossRef]
- Noguchi, N.; Okuchi, T. Self-diffusion of protons in H2O ice VII at high pressures: Anomaly around 10 GPa. J. Chem. Phys. 2016, 144, 234503. [Google Scholar] [CrossRef]
- Polian, A.; Grimsditch, M. New High-Pressure Phase of H2O: Ice X. Phys. Rev. Lett. 1984, 52, 1312–1314. [Google Scholar] [CrossRef]
- Asahara, Y.; Hirose, K.; Ohishi, Y.; Hirao, N.; Murakami, M. Thermoelastic properties of ice VII and its high-pressure polymorphs: Implications for dynamics of cold slab subduction in the lower mantle. Earth Planet. Sci. Lett. 2010, 299, 474–482. [Google Scholar] [CrossRef]
- French, M.; Redmer, R. Construction of a thermodynamic potential for the water ices VII and X. Phys. Rev. B 2015, 91, 014308. [Google Scholar] [CrossRef]
- Wolanin, E.; Pruzan, P.; Chervin, J.; Canny, B.; Gauthier, M.; Häusermann, D.; Hanfland, M. Equation of state of ice VII up to 106 GPa. Phys. Rev. B 1997, 56, 5781–5785. [Google Scholar] [CrossRef]
- Davies, G.F. Quasi-harmonic finite strain equations of state of solids. J. Phys. Chem. Solids 1973, 34, 1417–1429. [Google Scholar] [CrossRef]
- Poirier, J.-P.; Tarantola, A. A logarithmic equation of state. Phys. Earth Planet. Inter. 1998, 109, 1–8. [Google Scholar] [CrossRef]
- Vinet, P.; Rose, J.H.; Ferrante, J.; Smith, J.R. Universal features of the equation of state of solids. J. Phys. Condens. Matter 1989, 1, 1941. [Google Scholar] [CrossRef]
- de Boor, C. A Practical Guide to Splines, Rev. ed.; Springer: New York, NY, USA, 2001; ISBN 978-0-387-95366-3. [Google Scholar]
- Brown, J.M. Local basis function representations of thermodynamic surfaces: Water at high pressure and temperature as an example. Fluid Phase Equilibria 2018, 463, 18–31. [Google Scholar] [CrossRef]
- Bollengier, O.; Brown, J.M.; Shaw, G.H. Thermodynamics of pure liquid water: Sound speed measurements to 700 MPa down to the freezing point, and an equation of state to 2300 MPa from 240 to 500 K. J. Chem. Phys. 2019, 151, 054501. [Google Scholar] [CrossRef]
- Journaux, B.; Brown, J.M.; Pakhomova, A.; Collings, I.E.; Petitgirard, S.; Espinoza, P.; Ballaran, T.B.; Vance, S.D.; Ott, J.; Cova, F.; et al. Holistic Approach for Studying Planetary Hydrospheres: Gibbs Representation of Ices Thermodynamics, Elasticity, and the Water Phase Diagram to 2300 MPa. J. Geophys. Res. Planets 2020, 125, e2019JE006176. [Google Scholar] [CrossRef]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems, Waltham; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Strässle, T.; Klotz, S.; Kunc, K.; Pomjakushin, V.; White, J.S. Equation of state of lead from high-pressure neutron diffraction up to 8.9 GPa and its implication for the NaCl pressure scale. Phys. Rev. B 2014, 90, 014101. [Google Scholar] [CrossRef]
- Decker, D.L. High-pressure equation of state for NaCl, KCl, and CsCl. J. Appl. Phys. 1971, 42, 3239–3244. [Google Scholar] [CrossRef]
- Brown, J.M. The NaCl pressure standard. J. Appl. Phys. 1999, 86, 5801–5808. [Google Scholar] [CrossRef]
- Stacey, F.D.; Davis, P.M. High pressure equations of state with applications to the lower mantle and core. Phys. Earth Planet. Inter. 2004, 142, 137–184. [Google Scholar] [CrossRef]
- Stacey, F.D. The K-primed approach to high-pressure equations of state. Geophys. J. Int. 2000, 143, 621–628. [Google Scholar] [CrossRef]
- Bezacier, L.; Journaux, B.; Perrillat, J.-P.; Cardon, H.; Hanfland, M.; Daniel, I. Equations of state of ice VI and ice VII at high pressure and high temperature. J. Chem. Phys. 2014, 141, 104505. [Google Scholar] [CrossRef] [PubMed]
- Bridgman, P.W. Freezings and Compressions to 50,000 kg/cm2. J. Chem. Phys. 1941, 9, 794–797. [Google Scholar] [CrossRef]
- Fei, Y.; Mao, H.; Hemley, R.J. Thermal expansivity, bulk modulus, and melting curve of H2O–ice VII to 20 GPa. J. Chem. Phys. 1993, 99, 5369–5373. [Google Scholar] [CrossRef]
- Frank, M.; Fei, Y.; Hu, J. Constraining the equation of state of fluid H2O to 80 GPa using the melting curve, bulk modulus, and thermal expansivity of Ice VII1. Geochim. Cosmochim. Acta 2004, 68, 2781–2790. [Google Scholar] [CrossRef]
- Hernandez, J.-A.; Caracas, R. Proton dynamics and the phase diagram of dense water ice. J. Chem. Phys. 2018, 148, 214501. [Google Scholar] [CrossRef]
- Journaux, B.; Caracas, R.; Carrez, P.; Gouriet, K.; Cordier, P.; Daniel, I. Elasticity and dislocations in ice X under pressure. Phys. Earth Planet. Inter. 2014, 236, 10–15. [Google Scholar] [CrossRef]
- Klotz, S.; Komatsu, K.; Kagi, H.; Kunc, K.; Sano-Furukawa, A.; Machida, S.; Hattori, T. Bulk moduli and equations of state of ice VII and ice VIII. Phys. Rev. B 2017, 95, 174111. [Google Scholar] [CrossRef]
- Liu, L. Compression of ice VII to 500 kbar. Earth Planet. Sci. Lett. 1982, 61, 359–364. [Google Scholar] [CrossRef]
- Munro, R.G.; Block, S.; Mauer, F.A.; Piermarini, G. Isothermal equations of state for H2O-VII and D2O-VII. J. Appl. Phys. 1982, 53, 6174–6178. [Google Scholar] [CrossRef]
- Olinger, B.; Halleck, P.M. Compression and bonding of ice VII and an empirical linear expression for the isothermal compression of solids. J. Chem. Phys. 1975, 62, 94. [Google Scholar] [CrossRef]
- Sugimura, E.; Komabayashi, T.; Hirose, K.; Sata, N.; Ohishi, Y.; Dubrovinsky, L.S. Simultaneous high-pressure and high-temperature volume measurements of ice VII and its thermal equation of state. Phys. Rev. B 2010, 82, 134103. [Google Scholar] [CrossRef]
- Myint, P.C.; Benedict, L.X.; Belof, J.L. Free energy models for ice VII and liquid water derived from pressure, entropy, and heat capacity relations. J. Chem. Phys. 2017, 147, 084505. [Google Scholar] [CrossRef]
- Ahart, M.; Somayazulu, M.; Gramsch, S.A.; Boehler, R.; Mao, H.; Hemley, R.J. Brillouin scattering of H2O ice to megabar pressures. J. Chem. Phys. 2011, 134, 124517. [Google Scholar] [CrossRef]
- Shimizu, H.; Nabetani, T.; Nishiba, T.; Sasaki, S. High-pressure elastic properties of the VI and VII phase of ice in dense H2O and D2O. Phys. Rev. B 1996, 53, 6107–6110. [Google Scholar] [CrossRef]
- Zhang, J.S.; Hao, M.; Ren, Z.; Chen, B. The extreme acoustic anisotropy and fast sound velocities of cubic high-pressure ice polymorphs at Mbar pressure. Appl. Phys. Lett. 2019, 114, 191903. [Google Scholar] [CrossRef]

| Pressure of Transition | Suggested Transition | Type of Measurements | References |
|---|---|---|---|
| 5 GPa | |||
| 5 GPa | Tetragonal distortion | Powder X-Ray diffraction (XRD) | Grande et al. [21] |
| 10–15 GPa | |||
| 11 GPa | Lattice distortion | XRD peak splitting | Hirai et al. [22] |
| 14 GPa | Strain in cubic lattice | Powder X-Ray diffraction | Somayazulu et al. [23] |
| 11 GPa | - | Changes in Raman line width trends for the band | Hirai et al. [22], Pruzan et al. [24] |
| 13–15 GPa | - | Raman line pressure trends | Zha et al. [25] |
| 13 GPa | - | Neutron diffraction (220/110 ratio) | Guthrie et al. [26] |
| 10–14 GPa | Lattice distortion | c/a ratio changes in ice VIII | Yoshimura et al. [27] |
| 10–14 GPa | - | Maximum in electrical conductivity | Okada et al. [28] |
| 10–15 GPa | - | Maximum in proton diffusion | Noguchi et al. [29] |
| 20–25 GPa—Possible transition to Ice VII’ with proton dynamic disorder (tunneling and thermal hoping) | |||
| 23–25 GPa | - | Bump in the 220/110 ratio from Neutron diffraction | Guthrie et al. [26] |
| 25 GPa | Proton tunneling: ice VII’ | IR reflectivity trend of and trend | Goncharov et al. [18] |
| 20–25 GPa | Proton tunneling: ice VII’ | H-NMR | Meier et al. [20] |
| 27 GPa | - | Raman line pressure trends | Zha et al. [25] |
| 40 GPa | |||
| 40 GPa | Softening | Drop in volume reported based on XRD | Hemley et al. [15], Loubeyre et al. [16], Sugimura et al. [17] |
| 44 GPa | - | Raman line pressure trends | Zha et al. [25] |
| 44 GPa | - | Discontinuity in the pressure dependence of Brillouin esound speeds | Noguchi et al. [30] |
| 40 Gpa | - | Changes in trend of reflective index | Zha et al. [19] |
| 40 GPa | - | Drop in Brillouin transverse wave speeds over a narrow P range (<2 GPa) in compression and decompression | Asahara et al. [31] |
| >60 GPa transition to ice X | |||
| 60 GPa | Proton symmetrization | IR reflectivity trend of and translation modes | Goncharov et al. [18] |
| 62 GPa | - | Raman line pressure trends | Zha et al. [25] |
| 60 Gpa | - | Changes in trend of reflective index | Zha et al. [19] |
| 59 GPa | - | Drop in Brillouin transverse wave speeds in compression | Asahara et al. [31] |
| 70 GPa | Proton symmetrization | H-NMR | Meier et al. [20] |
| 90 GPa | Proton symmetrization | Emergence of the p20 Raman mode | Zha et al. [25] |
| Type of Function | Parameters | (rms) | |||
|---|---|---|---|---|---|
| Global-Basis-Function | |||||
| Third order/degree Eulerian Finite Strain | Ko = 28.0 GPa | Ko’ = 4.5 | Prms = 0.15 GPa Krms = 2.3 GPa | ||
| Fourth order/degree Eulerian Finite Strain | Ko = 27.4 GPa | Ko’ = 5.4 | Ko” = −0.44 GPa−1 | Prms = 0.02 GPa Krms = 0.3 GPa | |
| Ninth order/degree Eulerian Finite Strain | Ko = 27.8 GPa | Ko’ = 5.4 | Ko” = −0.67 GPa−1 | Prms = 0.01 GPa Krms = 0.2 GPa | |
| (Five more parameters for the ninth order fit are not reported here. See Supplementary Materials) | |||||
| Local-Basis-Function: | |||||
| Knots (strain units): | Coefficients (GPa m3/Mg) | ||||
| Eulerian Finite Strain Order: 6 (degree 5) | [−0.08, −0.035, 0.24, 0.67] (first and last knots are repeated six times) | [0.308, 0.242, −0.155, −0.292, 4.10, 10.9, 19.8, 26.1] | Prms = 0.01 GPa Krms = 0.2 GPa | ||
| log Strain Order: 5 (degree 4) | [−0.09, −0.036, 0.2, 0.42] (first and last knots are repeated five times) | [0.326, 0.241, −0.141, −0.326 3.92 16.4 26.0] | Prms = 0.01 GPa Krms = 0.2 GPa | ||
| Type of function | Parameters | (rms) | |
|---|---|---|---|
| Global-Basis-Function | |||
| Fourth order/degree Eulerian Finite Strain | Ko = 19.2 GPa, Ko’ = 3.8, Ko” = −0.09 GPa−1 | Prms = 3.0 GPa | |
| Local-Basis-Function: | |||
| knots (dimensionless strain): | Coefficients (GPa cm3/mole) | ||
| “Agnostic” log Strain low damping Order: 6 (degree 5) | [−0.01, 0.02, 0.04, 0.06, 0.08, 0.10, 0.12, 0.15, 0.17, 0.20, 0.24, 0.27, 0.31, 0.36, 0.42] (first and last knots are repeated six times) | [−0.10, −0.07, 0.05, 0.40, 1.37, 3.75, 7.13, 12.5, 20.0, 30.7, 46.7, 72.5, 103, 157, 254, 379, 520, 647, 723] | Prms = 1.7 GPa |
| “Agnostic” log Strain higher damping Order: 6 (degree 5) | [−0.01, 0.02, 0.04, 0.06, 0.08, 0.10, 0.12, 0.15, 0.17, 0.20, 0.24, 0.27, 0.31, 0.36, 0.42] (first and last knots are repeated six times) | [0.02, −0.03, −0.03, 0.23, 1.16, 3.55, 6.96, 12.3, 19.7, 30.4, 46.9, 71.5, 103, 157, 253, 375, 516, 645, 724] | Prms = 2.0 GPa |
| “low structure” log Strain (seven intervals) Order: 7 (degree 6) | [−0.01, 0.08, 0.12, 0.16, 0.16, 0.24, 0.3, 0.42] (first and last knots are repeated seven times) | [−0.09, −0.04, 0.43, 2.21, 6.50, 17.5, 46.3, 93.1, 153, 258, 433, 595, 723] | Prms = 2.0 GPa |
| “transition informed” log Strain (seven intervals) Order: 7 (degree 6) | [−0.01, 0.12, 0.16, 0.16, 0.21, 0.23, 0.26, 0.42] (first and last knots are repeated seven times) | [0.10, −0.27, 0.26, 2.86, 10.6, 25.6, 57.3, 104, 153, 263, 396, 556, 722] | Prms = 1.7 GPa |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, J.M.; Journaux, B. Local-Basis-Function Equation of State for Ice VII–X to 450 GPa at 300 K. Minerals 2020, 10, 92. https://doi.org/10.3390/min10020092
Brown JM, Journaux B. Local-Basis-Function Equation of State for Ice VII–X to 450 GPa at 300 K. Minerals. 2020; 10(2):92. https://doi.org/10.3390/min10020092
Chicago/Turabian StyleBrown, J. Michael, and Baptiste Journaux. 2020. "Local-Basis-Function Equation of State for Ice VII–X to 450 GPa at 300 K" Minerals 10, no. 2: 92. https://doi.org/10.3390/min10020092
APA StyleBrown, J. M., & Journaux, B. (2020). Local-Basis-Function Equation of State for Ice VII–X to 450 GPa at 300 K. Minerals, 10(2), 92. https://doi.org/10.3390/min10020092





