Mathematical Modelling of Electrode Geometries in Electrostatic Fog Harvesters
Abstract
1. Introduction
1.1. Water Availability and Human Needs
1.2. Fog
1.3. Fog Water Harvesting Methods
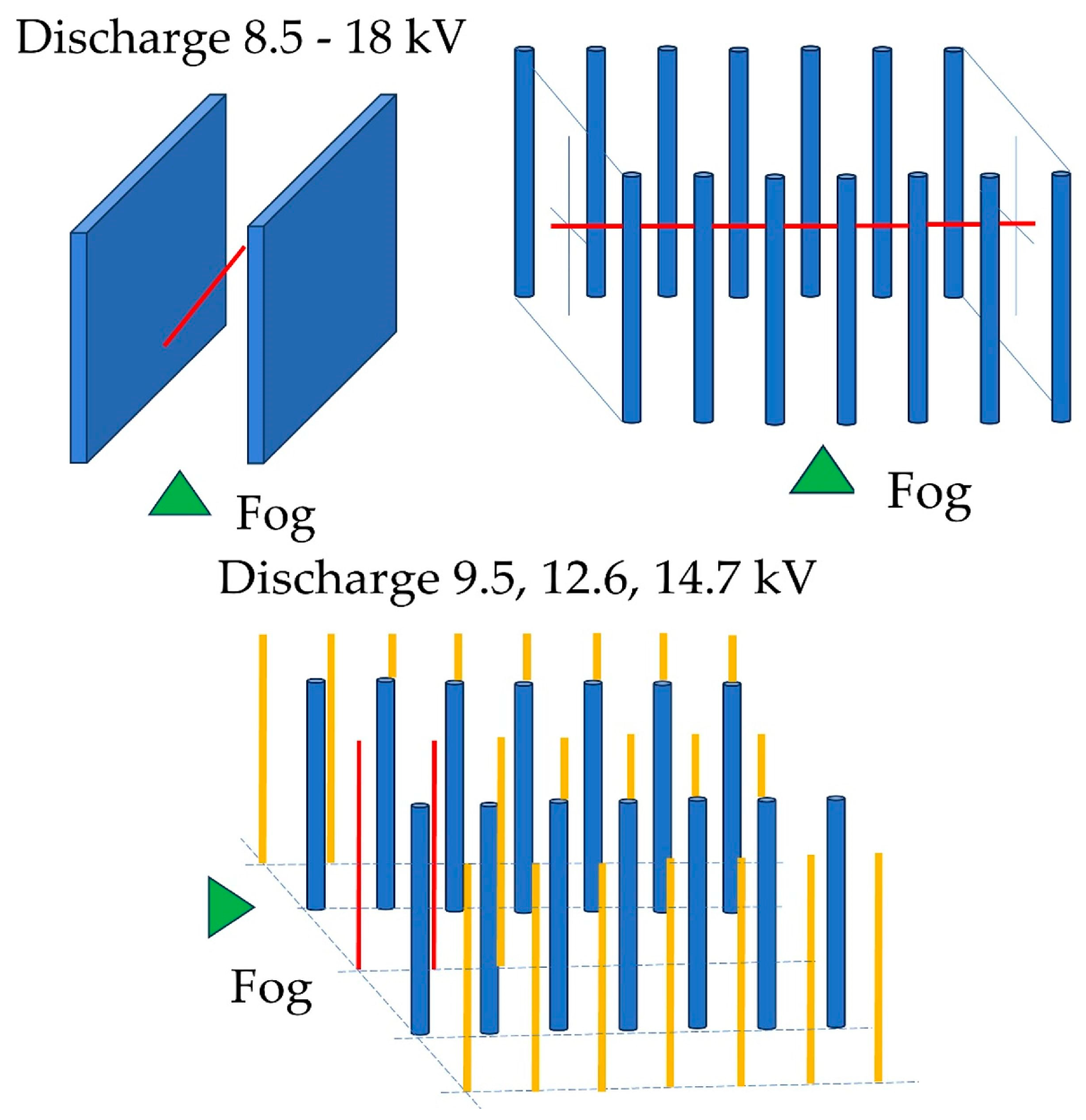
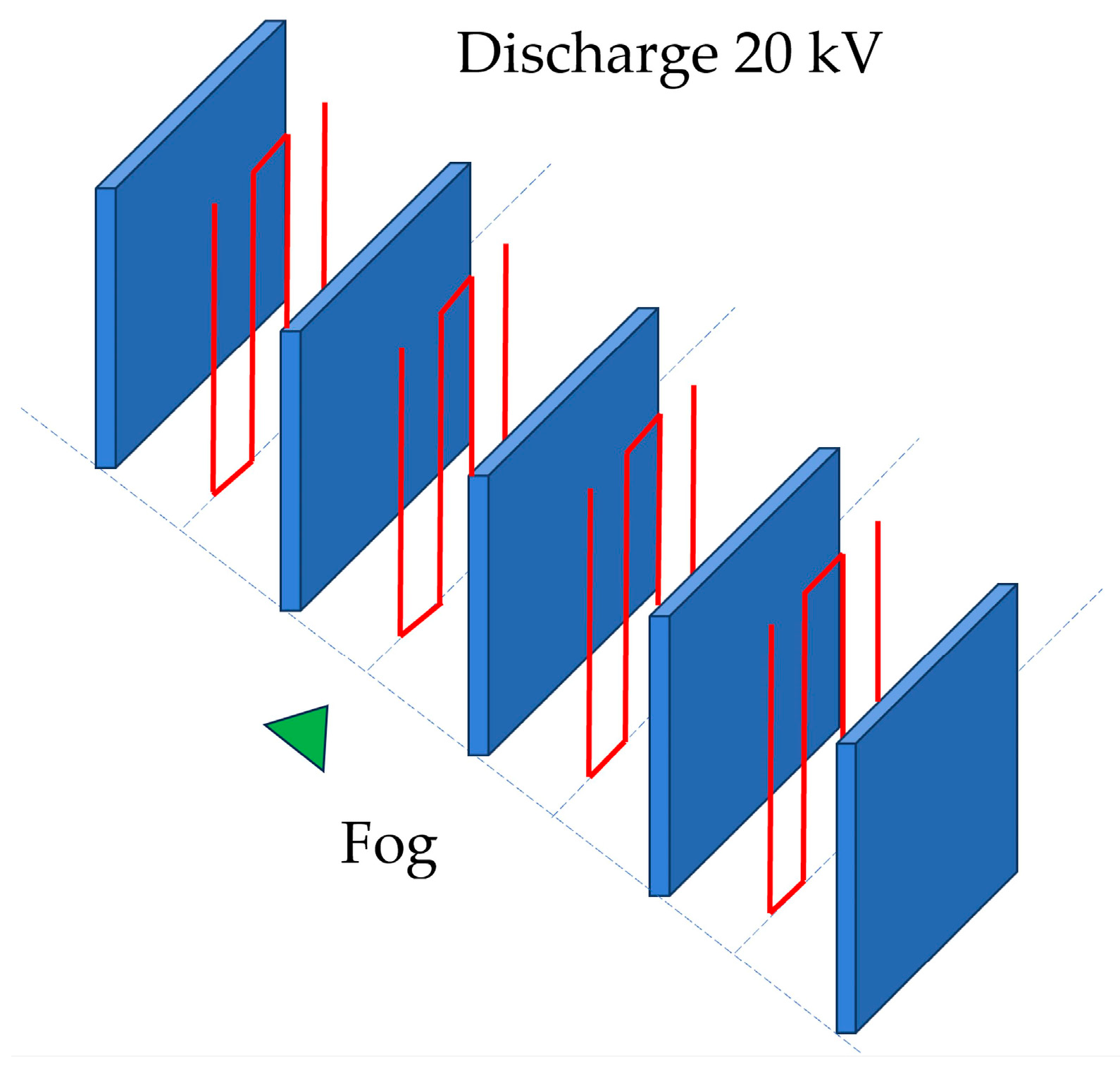
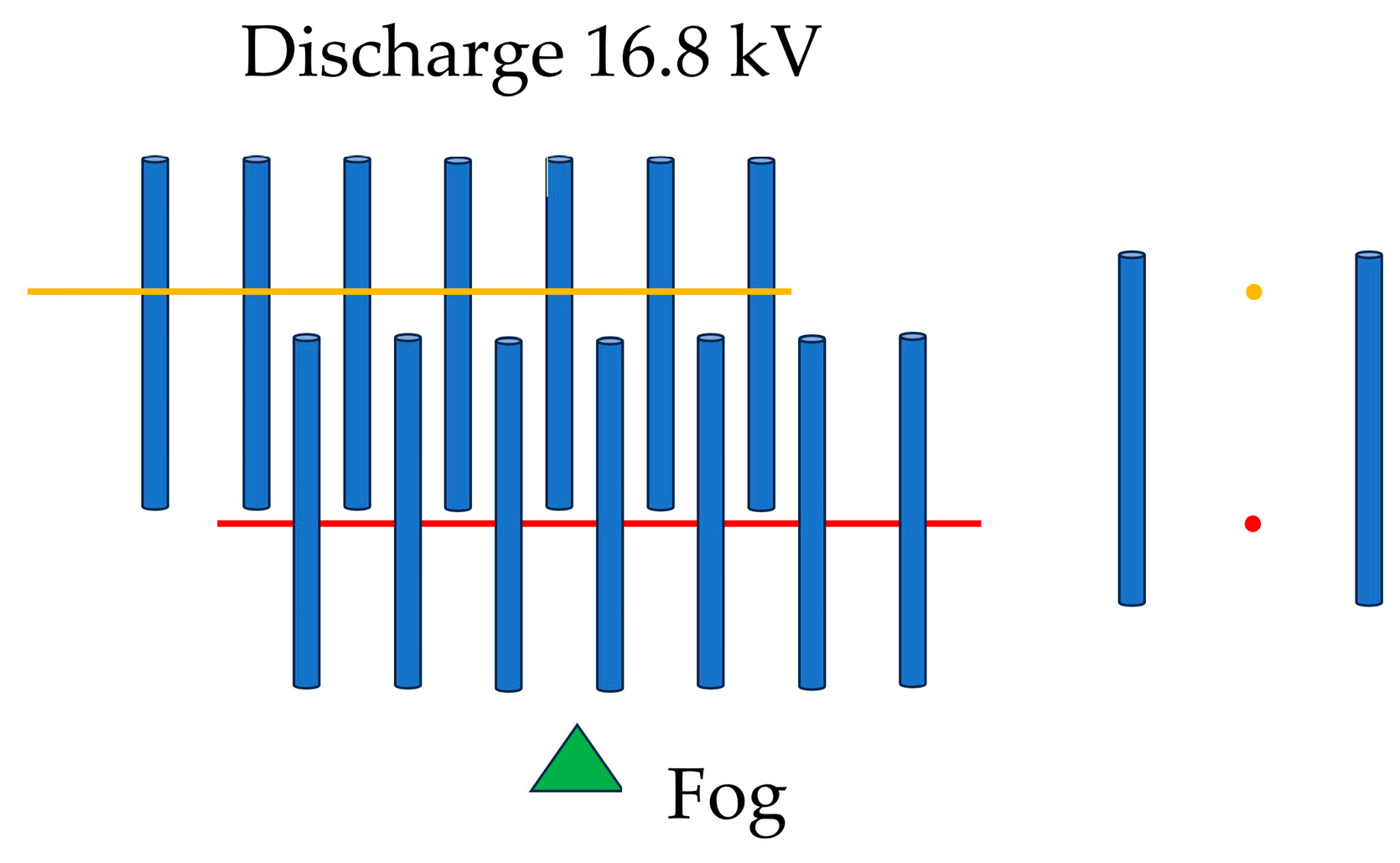
1.4. Configurations of Electrodes in Fog Water Harvesters
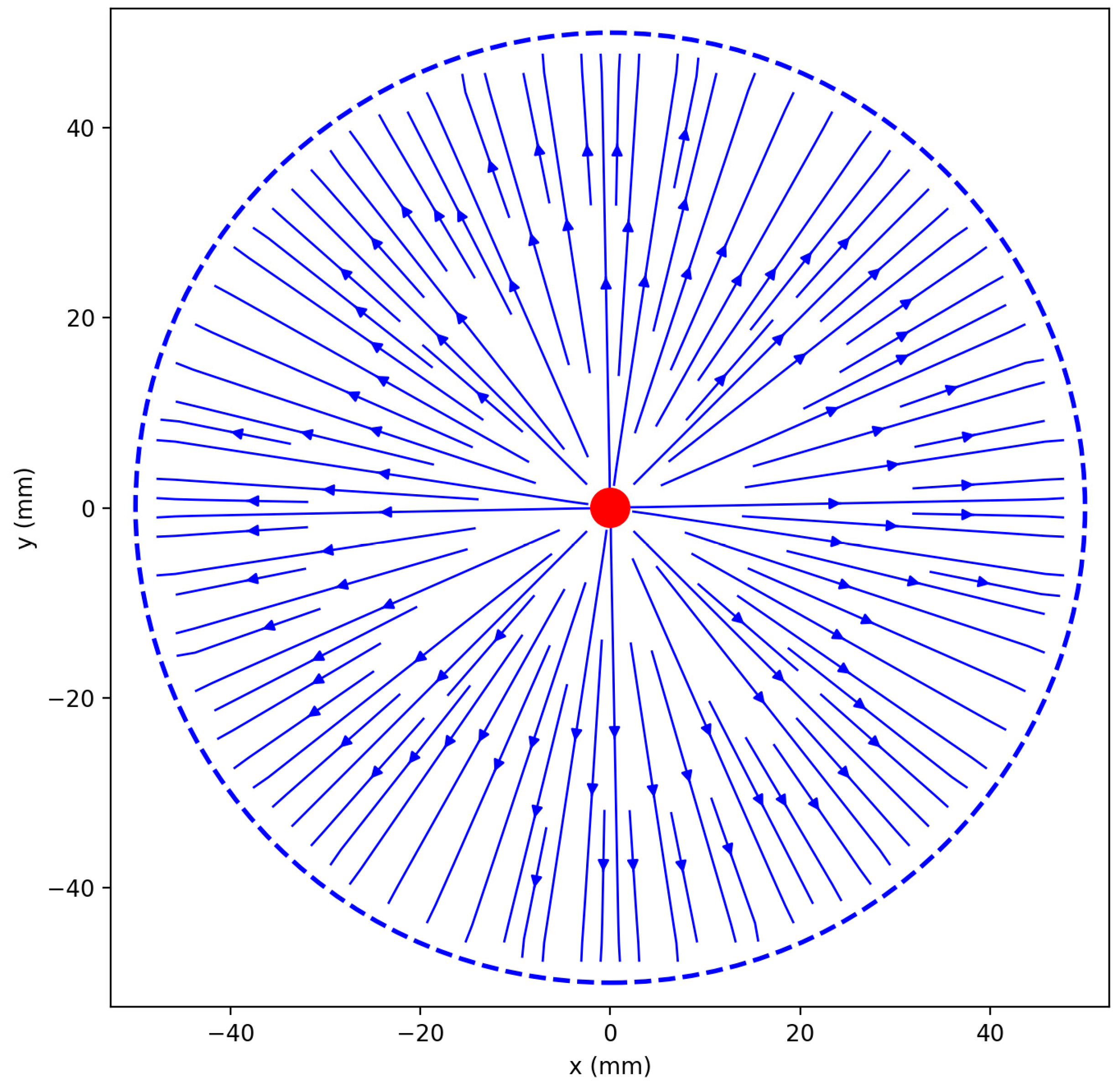
- A vertical concentric cylindrical mesh collector with a central vertical rod-type discharge electrode;
- A collector comprising two or more vertical rows of rods with a vertical or horizontal discharge electrode row positioned between the collector rows;
- A horizontal mesh collector in the form of a pipe or halved pipe with horizontal wire-type discharge electrodes positioned above.
2. Methodology
- 1.
- Libraries.
- numpy—for mathematical and matrix operations;
- matplotlib.pyplot—for plotting graphs;
- scipy.sparse.lil_matrix—to construct the difference operator matrix for solving the Laplace equation;
- scipy.sparse.spsolve—to compute the potential distribution by solving , where represents boundary conditions;
- matplotlib.patches and matplotlib.lines—for customizing the plot legend.
- 2.
- Generating the coordinate grid of electrode field potentials.
- 3.
- Formulation of initial conditions.
- 4.
- Definition of electrode masks.
- 5.
- Grid and boundary initialization.
- 6.
- Definition of a sparse matrix and Laplacian representation on the grid.
- 7.
- Computation of grid potential values.
- 8.
- Calculation of field strength projections onto the X and Y axes at grid points.
- 9.
- The visualization of the electrode region projection and the field lines.
3. Results and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WHO | World Health Organization |
| UNICEF | United Nations Children’s Fund |
| LWC | Liquid water content |
| AWG | Atmospheric water generation |
| MOF | Metal–organic framework |
| DC | Direct current |
References
- United Nations. The United Nations World Water Development Report 2023: Partnerships and Cooperation for Water; UNESCO: Paris, France, 2023; Available online: https://unesdoc.unesco.org/ark:/48223/pf0000384655 (accessed on 8 August 2025).
- World Health Organization (WHO); United Nations Children’s Fund (UNICEF). Progress on Household Drinking Water, Sanitation and Hygiene 2000–2020: Five Years into the SDGs; WHO and UNICEF: Geneva, Switzerland, 2021; Available online: https://data.unicef.org/resources/progress-on-household-drinking-water-sanitation-and-hygiene-2000-2020/ (accessed on 8 August 2025).
- Yamada, Y.; Zhang, X.; Henderson, M.E.T.; Sagayama, H.; Sekine, Y.; Tanaka, H.; Sagayama, R.; Fudge, B.W.; McCurry, K.; Speakman, J.R.; et al. Variation in Human Water Turnover Associated with Environmental and Lifestyle Factors. Science 2022, 378, 909–915. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, H.R. Hydration and Cognition: A Critical Review and Recommendations for Future Research. J. Am. Coll. Nutr. 2007, 26 (Suppl. S5), 555S–561S. [Google Scholar] [CrossRef] [PubMed]
- Cheuvront, S.N.; Kenefick, R.W.; Charkoudian, N.; Sawka, M.N. Physiologic Basis for Understanding Quantitative Dehydration Assessment. Am. J. Clin. Nutr. 2013, 97, 455–462. [Google Scholar] [CrossRef] [PubMed]
- Piantadosi, C.A. The Biology of Human Survival: Life and Death in Extreme Environments; Oxford University Press: New York, NY, USA, 2003; ISBN 9780195165012. [Google Scholar]
- Montain, S.J.; Ely, M. Water Requirements and Soldier Hydration; Borden Institute, Walter Reed Army Medical Center, US Army Medical Department Center & School: Washington, DC, USA, 2010; Available online: https://medcoeckapwstorprd01.blob.core.usgovcloudapi.net/pfw-images/borden/HydrationPDF.pdf (accessed on 8 August 2025).
- Niu, S.; Lu, C.; Yu, H.; Zhao, L.; Lü, J. Fog Research in China: An Overview. Adv. Atmos. Sci. 2010, 27, 639–662. [Google Scholar] [CrossRef]
- Toth, G.; Gultepe, I.; Hansen, B.; Milbrandt, J.; Pearson, G.; Fogarty, C.; Burrows, W. The Environment Canada Handbook on Fog and Fog Forecasting; Technical Report No. En56-231/2010E; Environment Canada, Meteorological Service of Canada: Toronto, ON, Canada, 2010; Available online: https://publications.gc.ca/collections/collection_2011/ec/En56-231-2010-eng.pdf (accessed on 8 August 2025).
- Encyclopedia Britannica. Fog. 2025. Available online: https://www.britannica.com/science/fog (accessed on 8 August 2025).
- Met Office. What Is the Difference Between Mist, Fog and Haze? Met Office. Available online: https://weather.metoffice.gov.uk/learn-about/weather/types-of-weather/fog/difference-mist-and-fog (accessed on 8 August 2025).
- Gultepe, I.; Tardif, R.; Michaelides, S.C.; Cermak, J.; Bott, A.; Bendix, J.; Müller, M.D.; Pagowski, M.; Hansen, B.; Ellrod, G.; et al. Fog Research: A Review of Past Achievements and Future Perspectives. Pure Appl. Geophys. 2007, 164, 1121–1159. [Google Scholar] [CrossRef]
- Sanders-Reed, J.N.; Fenley, S.J. Visibility in Degraded Visual Environments (DVE). In Proceedings of the SPIE, 10642, Degraded Environments: Sensing, Processing, and Display 2018, Orlando, FL, USA, 17–18 April 2018; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; p. 106420S. [Google Scholar] [CrossRef]
- Uyeda, H.; Yagi, T. The Character of Sea Fog in the Urban Area of Kushiro City, Eastern Hokkaido. J. Meteorol. Soc. Jpn. 1984, 62, 917–928. [Google Scholar] [CrossRef]
- Turkish Straits Information. Visibility Table. Available online: https://www.turkishstraits.com/info/visibilitytable (accessed on 14 April 2025).
- Luta Air. Atmospheric Water Generator LT-AWG80G (1330 W, 50 kg). Available online: https://www.lutaair.com/lt-awg80g/ (accessed on 8 August 2025).
- Kim, H.; Yang, S.; Rao, S.R.; Narayanan, S.; Kapustin, E.A.; Furukawa, H.; Umans, A.S.; Yaghi, O.M.; Wang, E.N. Water Harvesting from Air with Metal-Organic Frameworks Powered by Natural Sunlight. Science 2017, 356, 430–434. [Google Scholar] [CrossRef] [PubMed]
- Leven, R. Hand-Held Water Harvester Powered by Sunlight Could Combat Water Scarcity; UC Berkeley College of Computing, Data Science, and Society: Berkeley, CA, USA, 2023; Available online: https://cdss.berkeley.edu/news/hand-held-water-harvester-powered-sunlight-could-combat-water-scarcity (accessed on 8 August 2025).
- Li, D.; Li, C.; Xiao, M.; Zhang, M.; Li, J.; Yang, Z.; Fu, Q.; Yu, K.; Yang, Y.; Pan, Y.; et al. Sustainable Solutions for Water Scarcity: A Review of Electrostatic Fog Harvesting Technology. Commun. Eng. 2025, 4, 34. [Google Scholar] [CrossRef] [PubMed]
- Azeem, M.; Noman, M.T.; Wiener, J.; Petru, M.; Louda, P. Structural Design of Efficient Fog Collectors: A Review. Environ. Technol. Innov. 2020, 20, 101169. [Google Scholar] [CrossRef]
- Verbrugghe, N.; Khan, A.Z. Water Harvesting through Fog Collectors: A Review of Conceptual, Experimental and Operational Aspects. Int. J. Low-Carbon Technol. 2023, 18, 392–403. [Google Scholar] [CrossRef]
- Parrish, A. Virginia Tech’s Fog Harp Harvests Water Even in the Lightest Fog. Virginia Tech News. 16 April 2020. Available online: https://news.vt.edu/articles/2020/04/fogharp_results.html (accessed on 8 August 2025).
- Shi, W.; van der Sloot, T.W.; Hart, B.J.; Kennedy, B.S.; Boreyko, J.B. Harps Enable Water Harvesting under Light Fog Conditions. Adv. Sustain. Syst. 2020, 4, 2000040. [Google Scholar] [CrossRef]
- Cruzat, D.; Jerez-Hanckes, C. Electrostatic Fog Water Collection. J. Electrostat. 2018, 96, 128–133. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, R.; Liu, S.; Liu, G.; Yan, X. Electrostatic Fog Collection Mechanism and Design of an Electrostatic Fog Collector with Nearly Perfect Fog Collection Efficiency. Chem. Eng. Sci. 2022, 247, 117034. [Google Scholar] [CrossRef]
- Zeng, M.J.; Qu, J.G.; Zhang, J.F. Design and Optimization of an Electrostatic Fog Collection System for Water Harvesting: Modeling and Experimental Investigation. Sep. Purif. Technol. 2023, 323, 124422. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, G.; Ekambaram, P.; Yan, X. Lab-Scale Electrostatic Droplet Collection from a Fog Plume with Droplet Evaporation. Appl. Therm. Eng. 2023, 223, 120044. [Google Scholar] [CrossRef]
- Damak, M.; Varanasi, K.K. Electrostatically Driven Fog Collection Using Space Charge Injection. Sci. Adv. 2018, 4, eaao5323. [Google Scholar] [CrossRef] [PubMed]
- Plasma Channel. Solving Desert Water Shortages Using 20,000 Volts [Video]. YouTube, 2025. Available online: https://www.youtube.com/watch?v=G2brxBRnRH4 (accessed on 8 August 2025).
- Smythe, W.R. Static and Dynamic Electricity, 3rd ed.; Rev. Printing; Taylor & Francis: New York, NY, USA, 1989. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Hai Linh, B.; Bui Thi, K.; Kung, Y.-S. Digital Hardware Realization of Forward and Inverse Kinematics for a Five-Axis Articulated Robot Arm. Math. Probl. Eng. 2015, 2015, 906505. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers, 7th ed.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Ginters, E.; Ginters, P.V. Simulation of Electrostatic Field Lines for Different Electrode Configurations in a Fog Collector; Zenodo: Geneva, Switzerland, 2025. [Google Scholar] [CrossRef]
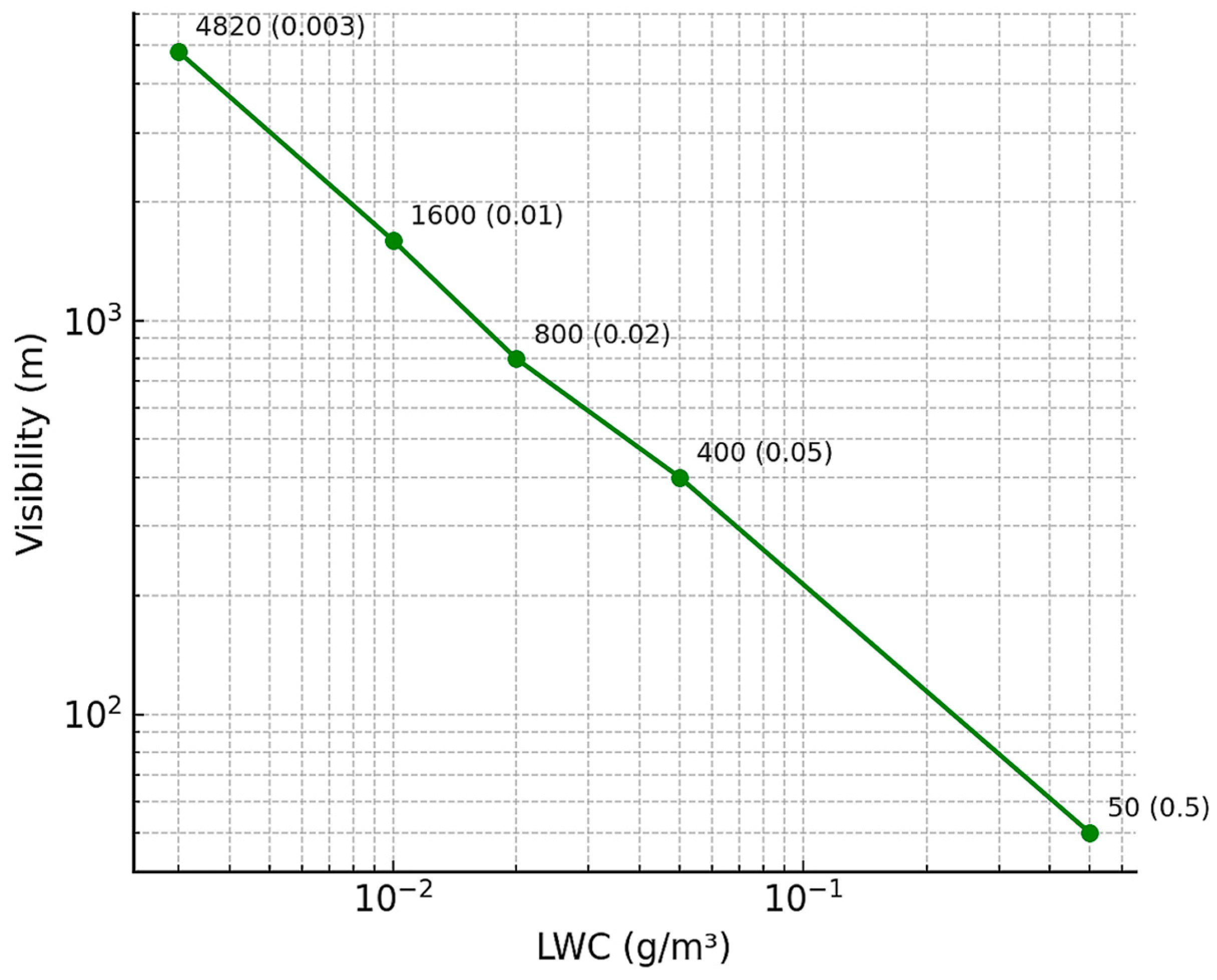

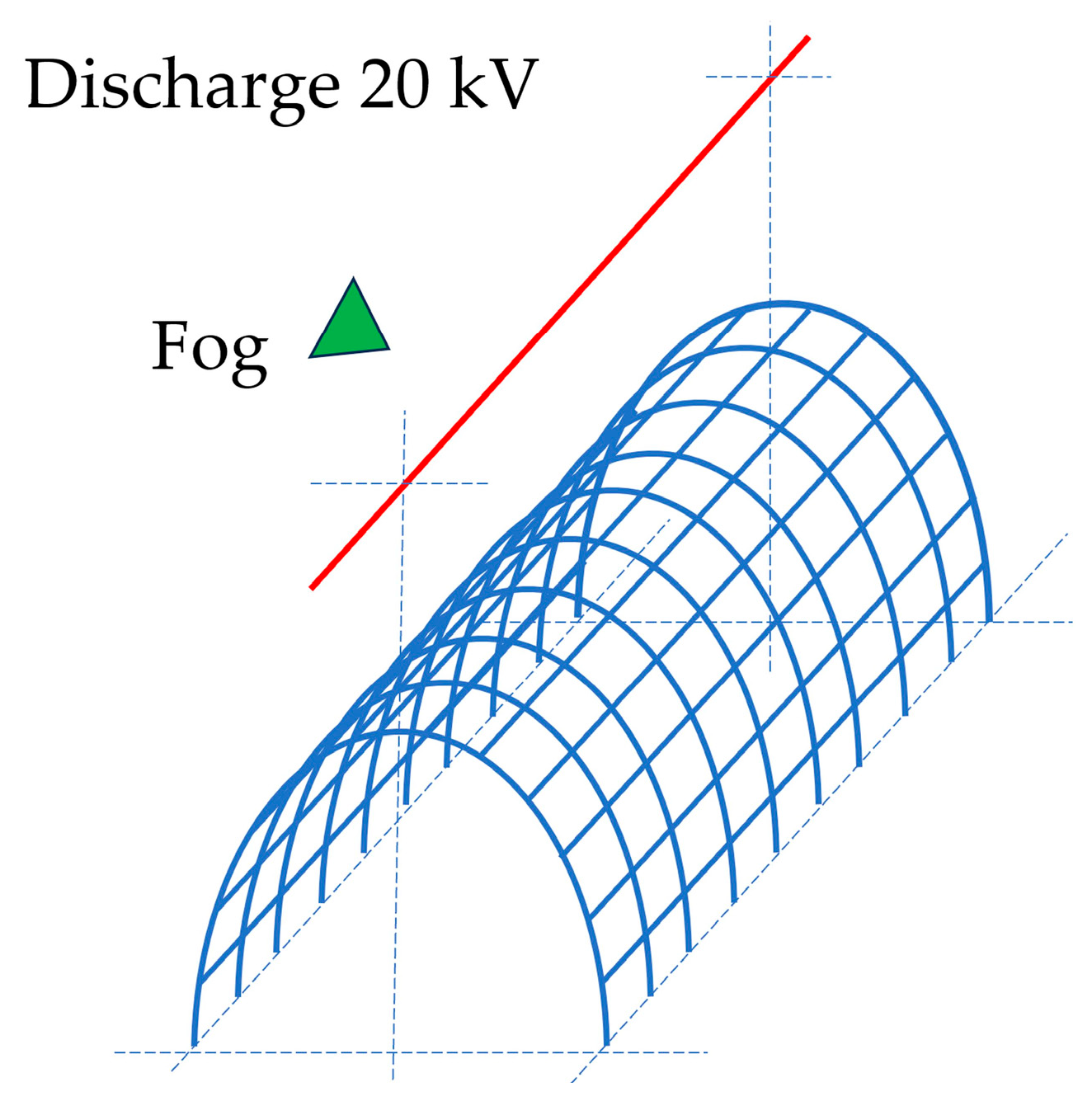


| Fog Name | Visibility (m) | Density (g/m3) |
|---|---|---|
| Haze | ≥5000 | <0.003 |
| Mist, thin fog | 1000–5000 | <0.02 |
| Moderate fog | 500–1000 | <0.05 |
| Thick or dense fog | 50–500 | ≤0.5 |
| Very dense fog | <50 | >0.5 |
| Electrode Layout | Field Direction | Benefits | Drawbacks | Amount of Collected Water |
|---|---|---|---|---|
| A vertical cylindrical mesh collector with a central vertical rod-type discharge electrode | Radial (from the center outward) | Simple structure, good symmetry, easy to deploy in the environment | Limited field control, low field line concentration, and obstructed fog flow | Low |
| A collector composed of two or more vertical rows of rods, with a vertical discharge electrode row placed centrally between the collector rows | Horizontal (toward the collectors) | Field lines are focused between the collectors, the field is efficiently utilized, and fog flow remains unobstructed | Potentially sensitive to positioning accuracy | High |
| A horizontal mesh collector in the form of a halved pipe, with a horizontal wire-type discharge electrode positioned above | Vertical (from top to bottom) | Compact design | Field utilization efficiency is low | Moderate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ginters, E.; Ginters, P.V. Mathematical Modelling of Electrode Geometries in Electrostatic Fog Harvesters. Symmetry 2025, 17, 1578. https://doi.org/10.3390/sym17091578
Ginters E, Ginters PV. Mathematical Modelling of Electrode Geometries in Electrostatic Fog Harvesters. Symmetry. 2025; 17(9):1578. https://doi.org/10.3390/sym17091578
Chicago/Turabian StyleGinters, Egils, and Patriks Voldemars Ginters. 2025. "Mathematical Modelling of Electrode Geometries in Electrostatic Fog Harvesters" Symmetry 17, no. 9: 1578. https://doi.org/10.3390/sym17091578
APA StyleGinters, E., & Ginters, P. V. (2025). Mathematical Modelling of Electrode Geometries in Electrostatic Fog Harvesters. Symmetry, 17(9), 1578. https://doi.org/10.3390/sym17091578







