A New Subclass of Bi-Univalent Functions Defined by Subordination to Laguerre Polynomials and the (p,q)-Derivative Operator

Abstract

In this work, we introduce a new subclass of bi-univalent functions using the $(p,q)$-derivative operator and the concept of subordination to generalized Laguerre polynomials ${\mathbb{L}}_t^{\varsigma }\left(k\right)$, which satisfy the differential equation $k{y}^{″}+(1+\varsigma -k)y^{\prime }+ty=0,$ with $1+\varsigma >0$, $k\in \mathbb{R}$, and $t\ge 0$. We focus on functions that blend the geometric features of starlike and convex mappings in a symmetric setting. The main goal is to estimate the initial coefficients of functions in this new class. Specifically, we obtain sharp upper bounds for $|a_2|$ and $|a_3|$ and for the Fekete–Szegö functional $|a_3-\eta a_2^2|$ for some real number $\eta$. In the final section, we explore several special cases that arise from our general results. These results contribute to the ongoing development of bi-univalent function theory in the context of $(p,q)$-calculus.

1. Introduction

Quantum calculus plays a key role in many areas such as mathematics, physics, and computer science. One notable extension is the $(p,q)$-calculus, which builds on the concept of the $(p,q)$-number. Since its introduction around 1991, this topic has attracted attention from several researchers [1,2]. For instance, Fibonacci oscillators were introduced in [3], while [4] used the $(p,q)$-number to construct a $(p,q)$-harmonic oscillator. In [1], it helped generalize certain q-oscillator algebras, and [5] applied it to compute $(p,q)$-Stirling numbers.

The importance of $(p,q)$-calculus is clear from its use in diverse fields like mathematics, physics, and chemistry. Researchers have extended this area to various applications. In ref. [6], a way to embed q-series into $(p,q)$-series was introduced. Moreover, studies on $(p,q)$-hypergeometric series produced results matching $(p,q)$-extensions of classic q-identities, as developed in works such as [7].

We begin by defining some basic terms related to $(p,q)$-calculus. The $(p,q)$-bracket number is given by [1]

$${\left[j\right]}_{p,q}=p^{j-1}+p^{j-2}q+\cdots +p^2{q}^{j-3}+p{q}^{j-2}+q^{j-1}={\displaystyle \frac{p^j-q^j}{p-q}}(p\ne q).$$

(1)

The expression ${\left[j\right]}_q={\displaystyle \frac{1-q^j}{1-q}}(q\ne 1)$ represents the q-number, and it can be extended to the form ${\left[j\right]}_{p,q}$, which is symmetric. When $p=1$, this generalized version reduces to the classical one, i.e., ${\left[j\right]}_{1,q}={\left[j\right]}_q$.

Let $\mathbb{N}$ stand for the set of positive integers, that is, $\mathbb{N}={\mathbb{N}}_0\setminus \left\{0\right\}=\{1,2,3,\dots \}$. Also, let $\mathbb{R}$ be the set of real numbers. The open unit disk in the complex plane, noted by $\Omega$, is a symmetric unit disk given by $\Omega =\{z\in \mathbb{C}:|z|<1\}$, where $\mathbb{C}$ refers to the set of complex numbers.

Definition 1 

([8]). The $(p,q)$-derivative of the function $\mathfrak{I}$ is described by

$${\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\mathfrak{I}\left(pz\right)-\mathfrak{I}\left(qz\right)}{(p-q)z}},\hfill & ifz\ne 0,\hfill \\ {\mathfrak{I}}^{\prime }\left(0\right),\hfill & ifz=0,{\mathfrak{I}}^{\prime }\left(0\right)\mathit{exists}.\hfill \end{array}\right.$$

(2)

It follows that ${\mathbb{D}}_{p,q}{z}^j={\left[j\right]}_{p,q}{z}^{j-1}$ and ${\mathbb{D}}_{p,q}ln\left(z\right)={\displaystyle \frac{ln(p/q)}{(p-q)z}}$.

Moreover, ${\left[j\right]}_{p,q}\to j$ as $p=1$ and $q\to 1^{-}$, so that ${\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)\to {\mathfrak{I}}^{\prime }\left(z\right)$. The operator ${\mathbb{D}}_{p,q}$ is linear in the sense that ${\mathbb{D}}_{p,q}(c{\mathfrak{I}}_1\left(z\right)+d{\mathfrak{I}}_2\left(z\right))=c{\mathbb{D}}_{p,q}{\mathfrak{I}}_1\left(z\right)+d{\mathbb{D}}_{p,q}{\mathfrak{I}}_2\left(z\right),$ for constants c and d. In addition, ${\mathbb{D}}_{p,q}$ satisfies the usual product and quotient rules (see [9]).

Using exponential functions, the $(p,q)$-versions of classical functions like sine, cosine, and tangent can be defined in a way similar to their Euler representations. Durani et al. [10] studied the $(p,q)$-derivatives of these functions. For more information on $(p,q)$-calculus, you can check out [11,12].

Let $\mathfrak{I}$ be a normalized analytic function in $\Omega$, expressed as

$$\mathfrak{I}\left(z\right)=z+\sum _{j=2}^{\infty }{a}_j{z}^j.$$

(3)

Here, $\mathcal{A}$ stands for the set of all such functions. We set $\mathcal{S}=\{\mathfrak{I}\in \mathcal{A}:\mathfrak{I}\mathrm{is}\mathrm{univalent}\mathrm{in}\Omega \}$. For any $\mathfrak{I}\in \mathcal{A}$, the $(p,q)$-derivative is given by

$${\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)=1+\sum _{j=2}^{\infty }{\left[j\right]}_{p,q}{a}_j{z}^{j-1},z\in \Omega .$$

We also point out that if $p=1$, the $(p,q)$-derivative simply becomes the usual q-derivative.

$${\mathbb{D}}_q\mathfrak{I}\left(z\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\mathfrak{I}\left(z\right)-\mathfrak{I}\left(qz\right)}{(1-q)z}},\hfill & \mathrm{if}z\ne 0,\hfill \\ {\mathfrak{I}}^{\prime }\left(0\right),\hfill & \mathrm{if}z=0.\hfill \end{array}\right.$$

(4)

So, for $\mathfrak{I}\in \mathcal{A}$, we have

$${\mathbb{D}}_q\mathfrak{I}\left(z\right)=1+\sum _{j=2}^{\infty }{\left[j\right]}_q{a}_j{z}^{j-1},$$

(5)

where

$${\left[j\right]}_q={\displaystyle \frac{1-q^j}{1-q}}.$$

Also, by taking $q\to 1^{-}$, ${\mathbb{D}}_q\mathfrak{I}\left(z\right)$ reduces to the usual derivative ${\mathfrak{I}}^{\prime }\left(z\right)$, for all $\mathfrak{I}\in \mathcal{A}$.

It is well known that if $\mathfrak{I}$ is univalent, then it has an inverse ${\mathfrak{I}}^{-1}$, satisfying

$${\mathfrak{I}}^{-1}\left(\mathfrak{I}\left(z\right)\right)=z=\mathfrak{I}\left({\mathfrak{I}}^{-1}\left(z\right)\right),z\in \Omega ,$$

and

$$\mathfrak{I}\left({\mathfrak{I}}^{-1}\left(\varpi \right)\right)=\varpi ,\left|\varpi \right|<r_0\left(\mathfrak{I}\right);r_0\left(\mathfrak{I}\right)\ge {\displaystyle \frac{1}{4}},$$

where

$${\mathfrak{I}}^{-1}\left(\varpi \right)=\varpi -a_2{\varpi }^2+(2a_2^2-a_3){\varpi }^3-(5a_3^2-5a_2{a}_3+a_4){\varpi }^4+\cdots$$

(6)

Levin first brought up the idea of bi-univalent functions in [13]. These are analytic functions, written as $\mathfrak{I}$, where both the function and its inverse ${\mathfrak{I}}^{-1}$ are univalent inside the unit disk $\Omega$. We use $\Sigma$ to stand for the set of all such bi-univalent functions of the form shown in (3). Some popular examples from this class are

$${\displaystyle \frac{1}{2}}log{\displaystyle \frac{1+z}{1-z}},-log(1-z),{\displaystyle \frac{z}{1-z}}.$$

On the other hand, functions like $z-{\displaystyle \frac{z^2}{2}},{\displaystyle \frac{z}{1-z^2}}$, and the Koebe function are not part of $\Sigma$, even though they do belong to the class S. For a more focused discussion and further properties of $\Sigma$, one can refer to [8,14,15,16] and references therein.

The paper by Srivastava and his collaborators [17] played a big role in reviving interest in the study of bi-univalent functions. Since then, many researchers have explored different subclasses of $\Sigma$, leading to a number of interesting findings (see [18,19,20,21,22]).

In working with univalent functions, the idea of subordination comes up a lot. Suppose $\mathfrak{I}$ and g are two functions inside the unit disk $\Omega$. We say $\mathfrak{I}$ is subordinate to g, written $\mathfrak{I}\left(z\right)\prec g\left(z\right)$, if there is a Schwarz function $\phi$ where $\phi \left(0\right)=0$ and $\left|\phi \right(z\left)\right|<1$ for all $z\in \Omega$, so that

$$\mathfrak{I}\left(z\right)=g\left(\phi \right(z\left)\right)\mathrm{for}\mathrm{all}z\in \Omega .$$

This subordination is denoted as

$$\mathfrak{I}\prec g\mathrm{or}\mathfrak{I}\left(z\right)\prec g\left(z\right)\mathrm{for}z\in \Omega .$$

Specifically, if g is univalent in $\Omega$, then the subordination condition implies that

$$\mathfrak{I}\left(0\right)=g\left(0\right)\mathrm{and}\mathfrak{I}(\Omega )\subseteq g(\Omega ).$$

The $(p,q)$-calculus has been applied in exploring different subclasses of both S and $\Sigma$. In [17], the subordination method was used to introduce the $(p,q)$-starlike and $(p,q)$-convex classes. Several works have also focused on defining and analyzing new subclasses of $\Sigma$ that are linked to $(p,q)$-type differential operators (see [23,24,25,26]).

One of the interesting problems in Geometric Function Theory is the Fekete–Szegö problem. This problem deals with the coefficients of functions $\mathfrak{I}\in \mathcal{S}$, and in [27], Fekete and Szegö established the following sharp result for such functions:

$$\left|a_3-\eta a_2^2\right|\le \left\{\begin{array}{cc}4\eta -3,\hfill & \eta \ge 1,\hfill \\ 1+2e^{{\displaystyle \frac{-2\eta }{1-\eta }}},\hfill & 0\le \eta <1,\hfill \\ 3-4\eta ,\hfill & \eta <0.\hfill \end{array}\right.$$

The fundamental inequality $\left|a_3-\eta a_2^2\right|\le 1$ is achieved when $\eta \to 1$. The combination $F_{\eta }\left(\mathfrak{I}\right)=a_3-\eta a_2^2$ plays an important role in the theory, and finding sharp bounds for $|F_{\eta }\left(\mathfrak{I}\right)|$ is a notable maximization problem.

The Laguerre equation is a second-order linear differential equation that shows up a lot in physics, especially in quantum mechanics and other physical models. It is named after Edmond Laguerre and is tied to a special group of polynomials called Laguerre polynomials; see [28,29]. Consider the differential equation below:

$$k{y}^{″}+(1+\varsigma -k)y^{\prime }+ty=0,$$

when $1+\varsigma >0$, $k\in \mathbb{R}$, and $t\ge 0$, the solution $y\left(k\right)$ to this equation is called the generalized (or associated) Laguerre polynomial, written as ${\mathbb{L}}_t^{\varsigma }\left(k\right)$. These polynomials show up in many areas of math physics, like solving Helmholtz’s equation in paraboloidal coordinates or studying how electromagnetic waves behave; see [30,31]. They also follow specific recurrence relations, such as

$${\mathbb{L}}_{t+1}^{\varsigma }\left(k\right)={\displaystyle \frac{2t+1+\varsigma -k}{t+1}}{\mathbb{L}}_t^{\varsigma }\left(k\right)-{\displaystyle \frac{t+\varsigma }{t+1}}{\mathbb{L}}_{t-1}^{\varsigma }\left(k\right)\mathrm{for}t\ge 1,$$

(7)

with initial values

$${\mathbb{L}}_0^{\varsigma }\left(k\right)=1,{\mathbb{L}}_1^{\varsigma }\left(k\right)=1+\varsigma -k,{\mathbb{L}}_2^{\varsigma }\left(k\right)={\displaystyle \frac{k^2}{2}}+(\varsigma +2)k+{\displaystyle \frac{(\varsigma +1)(\varsigma +2)}{2}},$$

(8)

and so on. For example, we can obtain ${\mathbb{L}}_3\left(k\right)$ from the recurrence relation as

$${\mathbb{L}}_3^{\varsigma }\left(k\right)={\displaystyle \frac{k^3}{6}}+{\displaystyle \frac{\varsigma +3}{2}}{k}^2+{\displaystyle \frac{(\varsigma +2)(\varsigma +3)}{2}}k+{\displaystyle \frac{(\varsigma +1)(\varsigma +2)(\varsigma +3)}{6}}.$$

(9)

Furthermore, by setting $\varsigma =0$ in the generalized Laguerre polynomial, we obtain standard Laguerre polynomials such as

$${\mathbb{L}}_t^0\left(k\right)={\mathbb{L}}_t\left(k\right).$$

(10)

Lemma 1 

([25]). Let $\mathcal{B}(k,z)$ represent the generating function for the generalized Laguerre polynomial, which is defined as

$$\mathcal{B}(k,z)=\sum _{t=0}^{\infty }{\mathbb{L}}_t^{\varsigma }\left(k\right)z^t={\displaystyle \frac{e^{-\left(\frac{kz}{1-z}\right)}}{{(1-z)}^{\varsigma +1}}}for\left|z\right|<1,k\in \mathbb{R},z\in \Omega .$$

The generalized Laguerre polynomials ${\mathbb{L}}_t^{\varsigma }\left(k\right)$, which are solutions to the second-order differential equation $k{y}^{″}+(1+\varsigma -k)y^{\prime }+ty=0,$ arise in numerous branches of applied science and engineering. One of their most prominent applications is in quantum mechanics, especially in solving the radial part of the Schrödinger equation for the hydrogen atom. In this context, the radial wave function is expressed in terms of associated Laguerre polynomials, enabling the quantization of energy levels and the accurate description of atomic orbitals [32,33]. Moreover, these polynomials appear in electromagnetic theory, particularly in solving the Helmholtz equation in paraboloidal coordinates, which is essential for modeling wave propagation in symmetric structures [34]. They also have applications in vibration analysis [35], spectral methods [35,36], and quantum optics [34], making them highly relevant across physics and engineering disciplines.

This 3D plot (Figure 1) shows the real part of the function $f\left(z\right)={\displaystyle \frac{e}{1-z}}$ over the unit disk $\left|z\right|<1$. The surface height represents $\mathrm{Re}\left(f\right(z\left)\right)$, while the color gradient reflects the imaginary part, giving a clear view of how both components behave. The black mesh and neutral lighting enhance the shape and highlight the singularity near $z=1$.

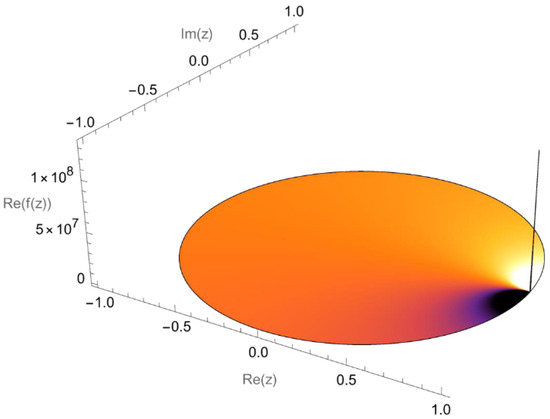
Figure 1. 3D plot represents the function ${\displaystyle \frac{e^{-\left(\frac{kz}{1-z}\right)}}{{(1-z)}^{\varsigma +1}}}$ with parameters $k=0$ and $\varsigma =0$, which simplifies to ${\displaystyle \frac{e}{1-z}}.$

These polynomials have numerous applications in physics and applied sciences:

• Quantum Mechanics: Generalized Laguerre polynomials appear in the solution of the radial part of the Schrödinger equation for the hydrogen atom. The radial wavefunctions are expressed as

  $$R_{n\ell }\left(r\right)=N_{n\ell }{r}^{\ell }{e}^{-r/\left(n{a}_0\right)}{L}_{n-\ell -1}^{2\ell +1}\left({\displaystyle \frac{2r}{n{a}_0}}\right),$$

  where $L_n^{\alpha }$ is the associated Laguerre polynomial. This form describes the behavior of an electron in a Coulomb potential.
• Laser Physics and Optics: Laguerre–Gaussian beams, which are solutions to the paraxial wave equation in cylindrical coordinates, involve Laguerre polynomials. These beams carry orbital angular momentum and are used in optical tweezers, communications, and quantum information.
• Statistical Physics and Thermodynamics: Laguerre polynomials are used to evaluate partition functions and model energy distributions in quantum gases.
• Signal Processing: In computational signal analysis, Laguerre functions based on Laguerre polynomials serve as a basis for approximating functions with exponential decay characteristics and are useful in modeling biological and electrical systems.
• Control Theory and Engineering: Laguerre polynomial-based orthogonal functions are applied in system identification and control system design to represent dynamic systems with memory.

Due to their orthogonality and completeness properties on the interval $[0,\infty )$ with the weight function $w\left(t\right)=t^{\varsigma }{e}^{-t}$, Laguerre polynomials provide a powerful basis in both analytical and numerical methods; for further details, see [32].

In [37], Wang and co-authors proposed the class ${\mathcal{C}}_s$ of convex functions related to symmetric points. This class includes all functions $\mathfrak{I}\in \mathcal{A}$ that satisfy the inequality ${\displaystyle \frac{{\left(z{\mathfrak{I}}^{\prime }\left(z\right)\right)}^{\prime }}{{\mathfrak{I}}^{\prime }\left(z\right)+{\mathfrak{I}}^{\prime }(-z)}}>0$ for every $z\in \Omega$. Crisan (see [38]) introduced the subclasses ${\mathcal{S}}_s^{*}\left(\varphi \right)$ and ${\mathcal{C}}_s\left(\varphi \right)$. A function $\mathfrak{I}\in \mathcal{A}$ is said to belong to ${\mathcal{S}}_s^{*}\left(\varphi \right)$ if it satisfies the subordination condition ${\displaystyle \frac{2z{\mathfrak{I}}^{\prime }\left(z\right)}{\mathfrak{I}\left(z\right)-\mathfrak{I}(-z)}}\prec \varphi \left(z\right),$ while $\mathfrak{I}\in {\mathcal{C}}_s\left(\varphi \right)$ if it fulfills ${\displaystyle \frac{2{\left(z{\mathfrak{I}}^{\prime }\left(z\right)\right)}^{\prime }}{{\mathfrak{I}}^{\prime }\left(z\right)+{\mathfrak{I}}^{\prime }(-z)}}\prec \varphi \left(z\right).$

Definition 2. 

A function $\mathfrak{I}\left(z\right)$ that follows the form in (3) is said to be part of the class ${\mathcal{SC}}_{p,q}(\varsigma ,\alpha ,k)$ if it satisfies these conditions:

$${\displaystyle \frac{2[(1-\alpha )z{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)+\alpha z{\mathbb{D}}_{p,q}\left[z{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)\right]]}{(1-\alpha )[\mathfrak{I}\left(z\right)-\mathfrak{I}(-z)]+\alpha z[{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)-{\mathbb{D}}_{p,q}\mathfrak{I}(-z)]}}\prec {\displaystyle \frac{e^{-\left(\frac{kz}{1-z}\right)}}{{(1-z)}^{\varsigma +1}}}=\mathcal{B}(k,z),$$

(11)

and

$${\displaystyle \frac{2[(1-\alpha )\varpi {\mathbb{D}}_{p,q}g\left(\varpi \right)+\alpha \varpi {\mathbb{D}}_{p,q}\left[\varpi {\mathbb{D}}_{p,q}g\left(\varpi \right)\right]]}{(1-\alpha )[g\left(\varpi \right)-g(-\varpi )]+2\alpha \varpi [{\mathbb{D}}_{p,q}g\left(\varpi \right)-{\mathbb{D}}_{p,q}g(-\varpi )]}}\prec {\displaystyle \frac{e^{-\left(\frac{k\varpi }{1-\varpi }\right)}}{{(1-z)}^{\varsigma +1}}}=\mathcal{B}(k,\varpi ),$$

(12)

where $k\in \mathbb{R},1+\varsigma >0,\alpha \ge 0z,\varpi \in \Omega$.

Based on the preceding definition, we can obtain the following examples by choosing specific values for the parameter $\alpha$. In particular, setting $\alpha =0$ and $\alpha =1$, respectively, yields the following two special cases:

Example 1. 

A function $\mathfrak{I}\in \Sigma$ given by (3) is said to be in the class ${\mathcal{SC}}_{p,q}(\varsigma ,0,k)$ if the following conditions are satisfied:

$${\displaystyle \frac{2{\mathbb{D}}_{p,q}\left[z{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)\right]}{{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)-{\mathbb{D}}_{p,q}\mathfrak{I}(-z)}}\prec {\displaystyle \frac{e^{-\left(\frac{kz}{1-z}\right)}}{{(1-z)}^{\varsigma +1}}}=\mathcal{B}(k,z),$$

and

$${\displaystyle \frac{2{\mathbb{D}}_{p,q}\left[\varpi {\mathbb{D}}_{p,q}g\left(\varpi \right)\right]}{[{\mathbb{D}}_{p,q}g\left(\varpi \right)-{\mathbb{D}}_{p,q}g(-\varpi )]}}\prec {\displaystyle \frac{e^{-\left(\frac{k\varpi }{1-\varpi }\right)}}{{(1-z)}^{\varsigma +1}}}=\mathcal{B}(k,\varpi ),$$

where $k\in \mathbb{R},1+\varsigma >0,z,\varpi \in \Omega$ and $\mathcal{G}={\mathfrak{I}}^{-1}$

Example 2. 

A function $\mathfrak{I}\in \Sigma$ given by (3) is said to be in the class ${\mathcal{SC}}_{p,q}(\varsigma ,1,k)$ if the following conditions are satisfied:

$${\displaystyle \frac{2\left[z{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)\right]}{\mathfrak{I}\left(z\right)-\mathfrak{I}(-z)}}\prec {\displaystyle \frac{e^{-\left(\frac{kz}{1-z}\right)}}{{(1-z)}^{\varsigma +1}}}=\mathcal{B}(k,z),$$

and

$${\displaystyle \frac{2\left[\varpi {\mathbb{D}}_{p,q}g\left(\varpi \right)\right]}{g\left(\varpi \right)-g(-\varpi )}}\prec {\displaystyle \frac{e^{-\left(\frac{k\varpi }{1-\varpi }\right)}}{{(1-z)}^{\varsigma +1}}}=\mathcal{B}(k,\varpi ),$$

where $k\in \mathbb{R},1+\varsigma >0,z,\varpi \in \Omega$ and $\mathcal{G}={\mathfrak{I}}^{-1}$.

Remark 1. 

If we set $p=1$ and let $q\to 1^{-}$, then the corresponding function ${\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)$ becomes the usual classical derivative. In this setting, when $\alpha =0$, the class ${\mathcal{S}}_{s,\Sigma }^{*}$ turns into the family of bi-univalent Ma–Minda starlike functions that are symmetric with respect to the origin. Similarly, for $\alpha =1$, the class ${\mathcal{C}}_{s,\Sigma }^{*}$ simplifies to the bi-univalent Ma–Minda convex functions symmetric about the origin, as defined in [38]. So, the classes we are working with can be seen as generalizations of these classical families using the $(p,q)$-calculus approach.

Example 3. 

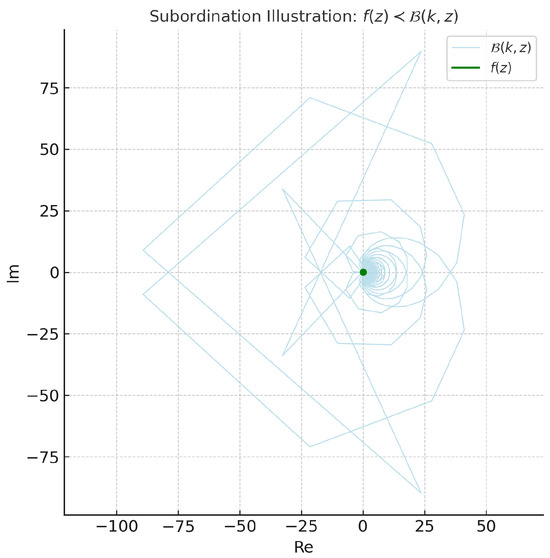
Let us consider the function:

$$f\left(z\right)=z+0.2z^2,$$

and the subordinating function:

$$\mathcal{B}(k,z)={\displaystyle \frac{e^{-\frac{kz}{1-z}}}{{(1-z)}^{\varsigma +1}}},withk=0.5,\varsigma =1.$$

We evaluate both functions over a dense grid in the open unit disk and observe that the image of $f\left(z\right)$ lies completely within the image of $\mathcal{B}(k,z)$, thereby satisfying the subordination relation $f\left(z\right)\prec \mathcal{B}(k,z)$. Figure 2 shows this containment clearly.

Figure 2. Visualization of the subordination $f\left(z\right)\prec \mathcal{B}(k,z)$ with $f\left(z\right)=z+0.2z^2$, $k=0.5$ and $\varsigma =1$.

The class discussed in this paper extends earlier known results by introducing new subclasses of bi-univalent functions that bring together starlike and convex characteristics with symmetry in mind. This is achieved using the $(p,q)$-derivative operator. Section 1 gives a short overview of quantum calculus, with a focus on $(p,q)$-calculus, and recalls some key ideas from Geometric Function Theory. In Section 2, we obtain bounds for the coefficients of functions in the class ${\mathcal{SC}}_{p,q}(\varsigma ,\alpha ,k)$. Section 3 is dedicated to proving a Fekete–Szegö-type inequality for this class. We also include several special cases of the main findings as corollaries in Section 4.

2. Coefficient Estimates for the Class ${𝓢𝓒}_{\mathit{p},\mathit{q}}(\mathsf{\varsigma },\mathsf{\alpha },\mathit{k})$

In this section, we provide the initial coefficient estimates for functions that are part of the class ${\mathcal{SC}}_{p,q}(\varsigma ,\alpha ,k)$.

Theorem 1. 

If the function $\mathfrak{I}\left(z\right)\in {\mathcal{SC}}_{p,q}(\varsigma ,\alpha ,k)$, with $k\in \mathbb{R},1+\varsigma >0,\alpha \ge 0z,\varpi \in \Omega$. Then,

$$|a_2|\le {\displaystyle \frac{|1+\varsigma -k|\sqrt{|1+\varsigma -k|}}{\sqrt{{|\left[3\right]}_{p,q}-1\left|\right|1+\alpha ({\left[2\right]}_{p,q}-1){|(1+\varsigma -k)}^2-{\left[2\right]}_{p,q}^2{[1+\alpha ({\left[2\right]}_{p,q}-1)]}^2\left|\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right|}}},$$

(13)

and

$$|a_3|\le {\displaystyle \frac{|1+\varsigma -k|}{|1+\alpha ({\left[2\right]}_{p,q}-1\left)\right|}}\left({\displaystyle \frac{1}{{|\left[3\right]}_{p,q}-1|}}+{\displaystyle \frac{|1+\varsigma -k|}{{\left[2\right]}_{p,q}^2|1+\alpha ({\left[2\right]}_{p,q}-1)|}}\right).$$

(14)

Proof. 

Assume that $\mathfrak{I}\left(z\right)\in {\mathcal{SC}}_{p,q}(\varsigma ,\alpha ,k)$, and let $g={\mathfrak{I}}^{-1}$ be given by the inverse series expansion defined in Equation (6). By using Definition (2) and from the relations (11) and (12), we can express the subordination conditions as follows:

$${\displaystyle \frac{2[(1-\alpha )z{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)+\alpha z{\mathbb{D}}_{p,q}\left[z{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)\right]]}{(1-\alpha )[\mathfrak{I}\left(z\right)-\mathfrak{I}(-z)]+\alpha z[{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)-{\mathbb{D}}_{p,q}\mathfrak{I}(-z)]}}=\mathcal{B}(k,c\left(z\right)),$$

(15)

and

$${\displaystyle \frac{2[(1-\alpha )\varpi {\mathbb{D}}_{p,q}g\left(\varpi \right)+\alpha \varpi {\mathbb{D}}_{p,q}\left[\varpi {\mathbb{D}}_{p,q}g\left(\varpi \right)\right]]}{(1-\alpha )[g\left(\varpi \right)-g(-\varpi )]+2\alpha \varpi [{\mathbb{D}}_{p,q}g\left(\varpi \right)-{\mathbb{D}}_{p,q}g(-\varpi )]}}=\mathcal{B}(k,d\left(w\right)),$$

(16)

where

$$c\left(z\right)=c_{1}z+c_2{z}^2+c_3{z}^3+\cdots$$

and

$$d\left(\varpi \right)=d_1\varpi +d_2{\varpi }^2+d_3{\varpi }^3+\cdots$$

are Schwarz functions such that $c\left(0\right)=d\left(0\right)=0$, and $\left|c\right(z\left)\right|\le 1$, $\left|d\right(\varpi \left)\right|\le 1$ for all $z,\varpi \in \Omega$. Now, since $\left|c\right(z\left)\right|\le 1$ and $\left|d\right(\varpi \left)\right|\le 1$, it follows that $|c_j|\le 1$ and $|d_j|\le 1$ for all $j\in \mathbb{N}$.

By simplifying Equations (15) and (16), we obtain

$${\displaystyle \frac{2[(1-\alpha )z{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)+\alpha z{\mathbb{D}}_{p,q}\left[z{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)\right]]}{(1-\alpha )[\mathfrak{I}\left(z\right)-\mathfrak{I}(-z)]+\alpha z[{\mathbb{D}}_{p,q}\mathfrak{I}\left(z\right)-{\mathbb{D}}_{p,q}\mathfrak{I}(-z)]}}$$

$$=1+{\left[2\right]}_{p,q}[1+\alpha ({\left[2\right]}_{p,q}-1)]a_{2}z+({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]a_3{z}^2+\cdots ,$$

(17)

$${\displaystyle \frac{2[(1-\alpha )\varpi {\mathbb{D}}_{p,q}g\left(\varpi \right)+\alpha \varpi {\mathbb{D}}_{p,q}\left[\varpi {\mathbb{D}}_{p,q}g\left(\varpi \right)\right]]}{(1-\alpha )[g\left(\varpi \right)-g(-\varpi )]+2\alpha \varpi [{\mathbb{D}}_{p,q}g\left(\varpi \right)-{\mathbb{D}}_{p,q}g(-\varpi )]}}$$

$$=1-{\left[2\right]}_{p,q}[1+\alpha ({\left[2\right]}_{p,q}-1)]a_2\varpi +({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)](2a_2^2-a_3){\varpi }^2+\cdots ,$$

(18)

and

$$\mathcal{B}(k,c\left(z\right))=1+\left[{\mathbb{L}}_1^{\varsigma }\left(k\right)c_1\right]z+[{\mathbb{L}}_1^{\varsigma }\left(k\right)c_2+{\mathbb{L}}_2^{\varsigma }\left(k\right)c_1^2]z^2+\cdots ,$$

(19)

$$\mathcal{B}(k,d\left(\varpi \right))=1+\left[{\mathbb{L}}_1^{\varsigma }\left(k\right)d_1\right]\varpi +[{\mathbb{L}}_1^{\varsigma }\left(k\right)d_2+{\mathbb{L}}_2^{\varsigma }\left(k\right)d_1^2]{\varpi }^2+\cdots .$$

(20)

Now, using Equation (15) and comparing the coefficients of the Equations (17) and (19), we obtain

$${\left[2\right]}_{p,q}[1+\alpha ({\left[2\right]}_{p,q}-1)]a_2={\mathbb{L}}_1^{\varsigma }\left(k\right)c_1,$$

(21)

$$({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]a_3={\mathbb{L}}_1^{\varsigma }\left(k\right)c_2+{\mathbb{L}}_2^{\varsigma }\left(k\right)c_1^2.$$

(22)

Similarly, from Equation (16), and by comparing the coefficients of the Equations (18) and (20), we obtain

$$-{\left[2\right]}_{p,q}[1+\alpha ({\left[2\right]}_{p,q}-1)]a_2={\mathbb{L}}_1^{\varsigma }\left(k\right)d_1,$$

(23)

$$({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)](2a_2^2-a_3)={\mathbb{L}}_1^{\varsigma }\left(k\right)d_2+{\mathbb{L}}_2^{\varsigma }\left(k\right)d_1^2.$$

(24)

Now, from Equations (21) and (23), we have

$$c_1=-d_1,$$

(25)

and

$${\displaystyle \frac{2{\left[2\right]}_{p,q}^2{[1+\alpha ({\left[2\right]}_{p,q}-1)]}^2}{{\left[{\mathbb{L}}_1^{\varsigma }\left(k\right)\right]}^2}}{a}_2^2=(c_1^2+d_1^2).$$

(26)

Also, by adding Equations (22) and (24), we immediately obtain

$$2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]a_2^2={\mathbb{L}}_1^{\varsigma }\left(k\right)(c_2+d_2)+{\mathbb{L}}_2^{\varsigma }\left(k\right)(c_1^2+d_1^2),$$

(27)

now, substituting Equation (26) into (27), we obtain

$$a_2^2={\displaystyle \frac{{\left[{\mathbb{L}}_1^{\varsigma }\left(k\right)\right]}^3(c_2+d_2)}{\left[2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]{\left[{\mathbb{L}}_1^{\varsigma }\left(k\right)\right]}^2-2{\left[2\right]}_{p,q}^2{[1+\alpha ({\left[2\right]}_{p,q}-1)]}^2{\mathbb{L}}_2^{\varsigma }\left(k\right)\right]}},$$

(28)

Using the values from Equations (7) and (8), Equation (28) becomes

$$a_2^2={\displaystyle \frac{{[1+\varsigma -k]}^3(c_2+d_2)}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]{(1+\varsigma -k)}^2-2{\left[2\right]}_{p,q}^2{[1+\alpha ({\left[2\right]}_{p,q}-1)]}^2\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}},$$

(29)

Finally, applying the triangle inequality along with the estimates from (29), we obtain the inequality (13).

Alternatively, subtracting Equation (22) from Equation (24) and applying Equation (25), we arrive at

$$a_3={\displaystyle \frac{{\mathbb{L}}_1^{\varsigma }\left(k\right)(c_2-d_2)}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]}}+a_2^2,$$

(30)

Now, by substituting Equation (26) into Equation (30) and doing a straightforward simplification, we obtain:

$$a_3={\displaystyle \frac{{\mathbb{L}}_1^{\varsigma }\left(k\right)(c_2-d_2)}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]}}+{\displaystyle \frac{{\left[{\mathbb{L}}_1^{\varsigma }\left(k\right)\right]}^2(c_1^2+d_1^2)}{2{\left[2\right]}_{p,q}^2{[1+\alpha ({\left[2\right]}_{p,q}-1)]}^2}}.$$

(31)

Using Equation (8) and applying the triangle inequality along with the bounds from (31), we obtain the inequality (14). □

Remark 2. 

We note that the coefficient bounds derived in Theorem 1 are not claimed to be sharp. Therefore, it remains an open problem whether there exists a specific function $\mathfrak{I}\left(z\right)\in {\mathcal{SC}}_{p,q}(\varsigma ,\alpha ,k)$ that attains equality in the bounds for $|a_2|$ and $|a_3|$. Identifying such extremal functions, if they exist, is an interesting direction for future work.

3. Fekete–Szegö Inequality for the Class ${𝓢𝓒}_{\mathit{p},\mathit{q}}(\mathsf{\varsigma },\mathsf{\alpha },\mathit{k})$

By using the values of $|a_2|$ and $|a_3|$, we now aim to evaluate the functional $|a_3-\eta a_2^2|$ for the class of functions ${\mathcal{SC}}_{p,q}(\varsigma ,\alpha ,k)$.

Theorem 2. 

Let $\mathfrak{I}\left(z\right)$ given by (3) be in the class ${\mathcal{SC}}_{p,q}(\varsigma ,\alpha ,k)$, with $k,\eta \in \mathbb{R},1+\varsigma >0,\alpha \ge 0,z,\varpi \in \Omega$. Then,

$$|a_3-\eta a_2^2|\le \left\{\begin{array}{cc}{\displaystyle \frac{2|1+\varsigma -k|}{|2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]|}}\hfill & for\left|h\left(\eta \right)\right|\le {\displaystyle \frac{1}{|2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]|}}\hfill \\ \\ 2|1+\varsigma -k|\left|h\right(\eta \left)\right|\hfill & for\left|h\left(\eta \right)\right|\ge {\displaystyle \frac{1}{|2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]|}}\hfill \end{array}\right.$$

where

$$h\left(\eta \right)={\displaystyle \frac{{[1+\varsigma -k]}^2(1-\eta )}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]{(1+\varsigma -k)}^2-2{\left[2\right]}_{p,q}^2{[1+\alpha ({\left[2\right]}_{p,q}-1)]}^2\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}}.$$

Proof. 

From Equations (28) and (30), it is derived that

$$a_3-\eta a_2^2={\displaystyle \frac{{\mathbb{L}}_1^{\varsigma }\left(k\right)(c_2-d_2)}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]}}+(1-\eta )a_2^2.$$

Also,

$$a_3-\eta a_2^2={\displaystyle \frac{(1+\varsigma -k)(c_2-d_2)}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]}}$$

$$\begin{array}{c}\hfill +{\displaystyle \frac{{[1+\varsigma -k]}^3(1-\eta )(c_2+d_2)}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]{(1+\varsigma -k)}^2-2{\left[2\right]}_{p,q}^2{[1+\alpha ({\left[2\right]}_{p,q}-1)]}^2\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}},\end{array}$$

Simplify to

$$\begin{array}{cc}\hfill a_3-\eta a_2^2& =(1+\varsigma -k)[\left(h\left(\eta \right)+{\displaystyle \frac{1}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]}}\right)c_2\hfill \\ \hfill & +\left(h\left(\eta \right)-{\displaystyle \frac{1}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]}}\right)d_2],\hfill \end{array}$$

where

$$h\left(\eta \right)={\displaystyle \frac{{[1+\varsigma -k]}^2(1-\eta )}{2({\left[3\right]}_{p,q}-1)[1+\alpha ({\left[2\right]}_{p,q}-1)]{(1+\varsigma -k)}^2-2{\left[2\right]}_{p,q}^2{[1+\alpha ({\left[2\right]}_{p,q}-1)]}^2\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}}.$$

□

4. Corollaries and Consequences

By substituting $\alpha =1\mathrm{and}\alpha =0$ in Theorem 1 and Theorem 2, respectively, we arrive at the following corollaries:

Corollary 1. 

Let $\mathfrak{I}\left(z\right)$ given by (3) be in the class ${\mathcal{SC}}_{p,q}(\varsigma ,1,k)$, with $k\in \mathbb{R},1+\varsigma >0,\alpha \ge 0,z,\varpi \in \Omega$. Then

$$|a_2|\le {\displaystyle \frac{|1+\varsigma -k|\sqrt{|1+\varsigma -k|}}{\sqrt{{\left[2\right]}_{p,q}|{\left[3\right]}_{p,q}-1|{(1+\varsigma -k)}^2-{\left[2\right]}_{p,q}^4\left|\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right|}}},$$

$$|a_3|\le {\displaystyle \frac{|1+\varsigma -k|}{{\left[2\right]}_{p,q}}}\left({\displaystyle \frac{1}{{|\left[3\right]}_{p,q}-1|}}+{\displaystyle \frac{|1+\varsigma -k|}{{\left[2\right]}_{p,q}^3}}\right)$$

and

$$|a_3-\eta a_2^2|\le \left\{\begin{array}{cc}{\displaystyle \frac{2|1+\varsigma -k|}{{|2\left[2\right]}_{p,q}({\left[3\right]}_{p,q}-1)|}}\hfill & \mathrm{for}\left|h\left(\eta \right)\right|\le {\displaystyle \frac{1}{{|2\left[2\right]}_{p,q}({\left[3\right]}_{p,q}-1)|}}\hfill \\ \\ 2|1+\varsigma -k|\left|h\right(\eta \left)\right|\hfill & \mathrm{for}\left|h\left(\eta \right)\right|\ge {\displaystyle \frac{1}{{|2\left[2\right]}_{p,q}({\left[3\right]}_{p,q}-1)|}}\hfill \end{array}\right.$$

where

$$h\left(\eta \right)={\displaystyle \frac{{[1+\varsigma -k]}^2(1-\eta )}{2{\left[2\right]}_{p,q}({\left[3\right]}_{p,q}-1){(1+\varsigma -k)}^2-2{\left[2\right]}_{p,q}^4\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}}.$$

Corollary 2. 

Let $\mathfrak{I}\left(z\right)$ given by (3) be in the class ${\mathcal{SC}}_{p,q}(\varsigma ,0,k)$, with $k\in \mathbb{R},1+\varsigma >0,\alpha \ge 0,z,\varpi \in \Omega$. Then,

$$|a_2|\le {\displaystyle \frac{|1+\varsigma -k|\sqrt{|1+\varsigma -k|}}{\sqrt{{|\left[3\right]}_{p,q}{-1|(1+\varsigma -k)}^2-{\left[2\right]}_{p,q}^2\left|\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right|}}},$$

$$|a_3|\le |1+\varsigma -k|\left({\displaystyle \frac{1}{{|\left[3\right]}_{p,q}-1|}}+{\displaystyle \frac{|1+\varsigma -k|}{{\left[2\right]}_{p,q}^2}}\right)$$

and

$$|a_3-\eta a_2^2|\le \left\{\begin{array}{cc}{\displaystyle \frac{2|1+\varsigma -k|}{\left|2\right({\left[3\right]}_{p,q}-1\left)\right|}}\hfill & \mathrm{for}\left|h\left(\eta \right)\right|\le {\displaystyle \frac{1}{\left|2\right({\left[3\right]}_{p,q}-1\left)\right|}}\hfill \\ \\ 2|1+\varsigma -k|\left|h\right(\eta \left)\right|\hfill & \mathrm{for}\left|h\left(\eta \right)\right|\ge {\displaystyle \frac{1}{\left|2\right({\left[3\right]}_{p,q}-1\left)\right|}}\hfill \end{array}\right.$$

where

$$h\left(\eta \right)={\displaystyle \frac{{[1+\varsigma -k]}^2(1-\eta )}{2({\left[3\right]}_{p,q}-1){(1+\varsigma -k)}^2-2{\left[2\right]}_{p,q}^2\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}}.$$

By setting $p=1$ in the previous corollaries and reverting to the standard q-derivative, we obtain the following corollaries:

Corollary 3. 

Let $\mathfrak{I}\left(z\right)$ given by (3) be in the class ${\mathcal{SC}}_q(\varsigma ,1,k)$, with $k\in \mathbb{R},1+\varsigma >0,$$\alpha \ge 0,z,\varpi \in \Omega$. Then

$$|a_2|\le {\displaystyle \frac{|1+\varsigma -k|\sqrt{|1+\varsigma -k|}}{\sqrt{{\left[2\right]}_q|{\left[3\right]}_q-1|{(1+\varsigma -k)}^2-{\left[2\right]}_q^4\left|\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right|}}},$$

$$|a_3|\le {\displaystyle \frac{|1+\varsigma -k|}{{\left[2\right]}_q}}\left({\displaystyle \frac{1}{{|\left[3\right]}_q-1|}}+{\displaystyle \frac{|1+\varsigma -k|}{{\left[2\right]}_q^3}}\right)$$

and

$$|a_3-\eta a_2^2|\le \left\{\begin{array}{cc}{\displaystyle \frac{2|1+\varsigma -k|}{{|2\left[2\right]}_q({\left[3\right]}_q-1)|}}\hfill & for\left|h\left(\eta \right)\right|\le {\displaystyle \frac{1}{{|2\left[2\right]}_q({\left[3\right]}_q-1)|}}\hfill \\ \\ 2|1+\varsigma -k|\left|h\right(\eta \left)\right|\hfill & for\left|h\left(\eta \right)\right|\ge {\displaystyle \frac{1}{{|2\left[2\right]}_q({\left[3\right]}_q-1)|}}\hfill \end{array}\right.$$

where

$$h\left(\eta \right)={\displaystyle \frac{{[1+\varsigma -k]}^2(1-\eta )}{2{\left[2\right]}_q({\left[3\right]}_q-1){(1+\varsigma -k)}^2-2{\left[2\right]}_q^4\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}}.$$

Corollary 4. 

Let $\mathfrak{I}\left(z\right)$ given by (3) be in the class ${\mathcal{SC}}_q(\varsigma ,0,k)$, with $k\in \mathbb{R},1+\varsigma >0,\alpha \ge 0,z,\varpi \in \Omega$. Then,

$$|a_2|\le {\displaystyle \frac{|1+\varsigma -k|\sqrt{|1+\varsigma -k|}}{\sqrt{{|\left[3\right]}_q{-1|(1+\varsigma -k)}^2-{\left[2\right]}_q^2\left|\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right|}}},$$

$$|a_3|\le |1+\varsigma -k|\left({\displaystyle \frac{1}{{|\left[3\right]}_q-1|}}+{\displaystyle \frac{|1+\varsigma -k|}{{\left[2\right]}_q^2}}\right)$$

and

$$|a_3-\eta a_2^2|\le \left\{\begin{array}{cc}{\displaystyle \frac{2|1+\varsigma -k|}{\left|2\right({\left[3\right]}_q-1\left)\right|}}\hfill & \mathrm{for}\left|h\left(\eta \right)\right|\le {\displaystyle \frac{1}{\left|2\right({\left[3\right]}_q-1\left)\right|}}\hfill \\ \\ 2|1+\varsigma -k|\left|h\right(\eta \left)\right|\hfill & \mathrm{for}\left|h\left(\eta \right)\right|\ge {\displaystyle \frac{1}{\left|2\right({\left[3\right]}_q-1\left)\right|}}\hfill \end{array}\right.$$

where

$$h\left(\eta \right)={\displaystyle \frac{{[1+\varsigma -k]}^2(1-\eta )}{2({\left[3\right]}_q-1){(1+\varsigma -k)}^2-2{\left[2\right]}_q^2\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}}.$$

Taking the limit as $q\to 1^{-}$ in the preceding corollaries and reverting to the classical derivative, we derive the following corollaries:

Corollary 5. 

Let $\mathfrak{I}\left(z\right)$ given by (3) be in the class $\mathcal{SC}(\varsigma ,1,k)$, with $k\in \mathbb{R},1+\varsigma >0,\alpha \ge 0,z,\varpi \in \Omega$. Then

$$|a_2|\le {\displaystyle \frac{|1+\varsigma -k|\sqrt{|1+\varsigma -k|}}{2\sqrt{{(1+\varsigma -k)}^2-4\left|\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right|}}},$$

$$|a_3|\le {\displaystyle \frac{|1+\varsigma -k|}{4}}\left(1+{\displaystyle \frac{|1+\varsigma -k|}{4}}\right)$$

and

$$|a_3-\eta a_2^2|\le \left\{\begin{array}{cc}{\displaystyle \frac{|1+\varsigma -k|}{4}}\hfill & \mathrm{for}\left|h\left(\eta \right)\right|\le {\displaystyle \frac{1}{8}}\hfill \\ \\ 2|1+\varsigma -k|\left|h\right(\eta \left)\right|\hfill & \mathrm{for}\left|h\left(\eta \right)\right|\ge {\displaystyle \frac{1}{8}}\hfill \end{array}\right.$$

where

$$h\left(\eta \right)={\displaystyle \frac{{[1+\varsigma -k]}^2(1-\eta )}{8{(1+\varsigma -k)}^2-32\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}}.$$

Corollary 6. 

Let $\mathfrak{I}\left(z\right)$ given by (3) be in the class $\mathcal{SC}(\varsigma ,0,k)$, with $k\in \mathbb{R},1+\varsigma >0,\alpha \ge 0,z,\varpi \in \Omega$. Then,

$$|a_2|\le {\displaystyle \frac{|1+\varsigma -k|\sqrt{|1+\varsigma -k|}}{\sqrt{2{(1+\varsigma -k)}^2-4\left|\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right|}}},$$

$$|a_3|\le {\displaystyle \frac{|1+\varsigma -k|}{2}}\left(1+{\displaystyle \frac{|1+\varsigma -k|}{8}}\right)$$

and

$$|a_3-\eta a_2^2|\le \left\{\begin{array}{cc}{\displaystyle \frac{|1+\varsigma -k|}{2}}\hfill & for\left|h\left(\eta \right)\right|\le {\displaystyle \frac{1}{4}}\hfill \\ \\ 2|1+\varsigma -k|\left|h\right(\eta \left)\right|\hfill & for\left|h\left(\eta \right)\right|\ge {\displaystyle \frac{1}{4}}\hfill \end{array}\right.$$

where

$$h\left(\eta \right)={\displaystyle \frac{{[1+\varsigma -k]}^2(1-\eta )}{4{(1+\varsigma -k)}^2-8\left[\frac{k^2}{2}+(\varsigma +2)k+\frac{(\varsigma +1)(\varsigma +2)}{2}\right]}}.$$

5. Conclusions

In this paper, we introduced a new subclass of bi-univalent functions by making use of the $(p,q)$-derivative operator together with subordination to generalized Laguerre polynomials ${\mathbb{L}}_t^{\varsigma }\left(k\right)$. We were able to establish upper bounds for the initial coefficients $|a_2|$, $|a_3|$, and for the Fekete–Szegö functional $|a_3-\eta a_2^2|$, where $\eta$ is a real parameter. It is worth noting that estimating the upper bounds for $|a_n|,n=4,5,6,\dots$ remains one of the open problems in the study of bi-univalent functions, and our results contribute to this ongoing discussion by providing bounds in the context of $(p,q)$-calculus. Our approach generalizes classical results using tools from quantum calculus and orthogonal polynomial theory. We also discussed several interesting special cases that arise from specific parameter choices. This work opens the door for future investigations into new subclasses of analytic and bi-univalent functions defined through other operators and special functions.