Abstract
The Internet of Vehicles (IoVs) uses vehicles as the main carrier to communicate with other entities, promoting efficient transmission and sharing of traffic data. Using real identities for communication may leak private data, so pseudonyms are commonly used as identity credentials. However, existing anonymous authentication schemes have limitations, including large vehicle storage demands, information redundancy, time-dependent pseudonym updates, and public–private key updates coupled with pseudonym changes. To address these issues, we propose a certificateless strong anonymous privacy protection authentication scheme that allows vehicles to autonomously generate and dynamically update pseudonyms. Additionally, the trusted authority transmits each entity’s partial private key via a session key, eliminating reliance on secure channels during transmission. Based on the elliptic curve discrete logarithm problem, the scheme’s existential unforgeability is proven in the random oracle model. Performance analysis shows that it outperforms existing schemes in computational cost and communication overhead, with the total computational cost reduced by 70.29–91.18% and communication overhead reduced by 27.75–82.55%, making it more suitable for privacy-sensitive and delay-critical IoV environments.
1. Introduction
With the rapid development of the information society, the IoVs, as a core component of the intelligent transportation system, is leading the technological revolution in the field of transportation. By leveraging modern technologies, such as sensing technology, network communication, cloud computing, and big data analysis, the IoVs realizes high-level connectivity among vehicles, roadside infrastructure, drivers, and cloud platforms, thus enhancing the efficiency of transmitting and sharing various traffic-related data. However, the highly dynamic and open nature of IoVs mean that it faces many threats, such as identity impersonation, message tampering, and vehicle user location tracking attacks, which will lead to the disclosure of users’ privacy data such as identity and driving trajectory. Once malicious entities obtain this private information, they may threaten traffic safety.
Against this backdrop, security in user messages and identity privacy has become a research focus of the IoVs. Although traditional digital signature technology can meet some security requirements, such as message authentication, integrity and non-repudiation, there is a risk of privacy leakage when vehicle users directly use their real identities to communicate with other entities. Therefore, researchers have proposed anonymous authentication schemes based on pseudonyms, group signatures, and ring signatures to address the above problems. Among them, the pseudonym-based method can achieve conditional privacy protection; that is, it not only allows vehicles to communicate anonymously, but also allows the trusted authority to track and revoke malicious vehicles, so this method is widely studied by researchers. However, existing pseudonym schemes have certain limitations. For instance, vehicles consistently communicate using the same pseudonym, which increases the potential risk of the malicious attacker tracking vehicles.
Some schemes involving the “pre-generation pseudonyms” strategy allow vehicles to apply for multiple pseudonyms at the same time, which may cause high storage requirements. Therefore, the periodic pseudonym mechanism is applied to reduce the storage overhead. However, the periodic replacement of pseudonyms in some schemes relies on the time factor, and frequent replacement of pseudonyms will increase system overhead, so the time interval of regular replacement of pseudonyms needs to be considered. Additionally, to implement conditional privacy protection, most of the pseudonym-based authentication protocols rely on a fully trusted third party to track the user’s real identity. However, the overly centralized tracking method may pose a risk to the privacy and security of users.
Therefore, to enhance the privacy, security, and efficiency of IoVs, we propose an autonomous dynamic pseudonym update mechanism based on collision-resistant hash function iteration () to comprehensively address the current issues—specifically filling the gaps of time-dependent updates and excessive storage in existing schemes—and provide more reliable security for vehicle communication.
1.1. Contributions
In this paper, a strong anonymous privacy protection authentication scheme based on certificateless technology is constructed by combining anonymous technology and certificateless signature technology. Our scheme not only achieves the autonomous dynamic update of vehicle pseudonyms but also realizes distributed accountability to improve the security of the system. The contributions of this paper mainly include the following aspects.
- 1.
- We design a novel autonomous dynamic pseudonym update mechanism based on collision-resistant hash functions to iteratively update pseudonyms. In this mechanism, the vehicle can update the pseudonym at any time according to the users’ needs, which eliminates the time dependence of the pseudonym updates, enhances the anonymity of the vehicle, and reduces the local storage burden of the vehicle.
- 2.
- We propose a certificateless privacy protection authentication scheme. Firstly, this scheme avoids the problems of certificate management and key escrow. Secondly, the third-party trusted authority uses the session key to transmit the partial private key to the corresponding entity, eliminating the reliance on the secure channel. Finally, in our scheme, the third-party trusted authority and pseudonym activator collaborate to track the real identity of the vehicle, which effectively prevents the trusted authority from directly and independently restoring the vehicle’s real identity.
- 3.
- We analyze the security of our scheme, evaluate the performance of our scheme, and compare the performance of our scheme with related schemes. The evaluation results show that our scheme has more advantages than the existing anonymous signature schemes in terms of computational cost and communication overhead, and is more suitable for the IoVs field with its demand for high-strength security and low transmission bandwidth and storage.
1.2. Roadmap
The rest of this paper is as follows. Section 2 presents the related work. Section 3 covers the Elliptic Curve Discrete Logarithm Problem (ECDLP), system model and scheme definition, security requirements, and security models. Section 4 introduces the proposed scheme. The security and performance of the proposed scheme are analyzed in Section 5 and Section 6, respectively. Finally, Section 7 concludes this paper.
2. Related Work
To better realize conditional privacy protection for IoVs users, driver identities remain confidential under normal circumstances but can be revealed by the Trusted Authority (TA) during incidents (e.g., hit-and-runs). Thus, scholars combine anonymity and signature technologies to achieve conditional privacy protection in IoVs.
Privacy-protection authentication schemes based on anonymity mainly include a group-based signature, a ring-based signature, and pseudonym-based methods. A group signature allows vehicles to sign messages anonymously in a group without revealing individual identities [1,2,3,4], but suffers from identity escrow (group administrators can arbitrarily disclose member identities). A ring signature, proposed by Rivest et al. [5], enables signers to remain anonymous within a ring but fails to meet IoV traceability requirements due to its “complete anonymity.”
The pseudonymous authentication system, initiated by Chaum [6], uses pseudonyms instead of real identities to enhance privacy. Wang et al. [7] proposed a PKI-based anonymous protocol with TA-generated pseudonyms, but certificate distribution and revocation list management increase computational and communication costs. Tzeng et al. [8], Li et al. [9], and Alazzawi et al. [10] developed ID-based schemes using TPDs to store master keys for dynamic pseudonym updates, but Mahanta et al. [11] showed that TPDs are vulnerable to side-channel attacks, risking key leakage.
Mei et al. [12] introduced a certificateless scheme with joint key/pseudonym generation, solving key escrow but relying on bilinear pairing, which incurs high computational costs—an issue our ECC-based design addresses to reduce overhead while retaining the advantages of certificateless technology. Thumbur et al. [13] proposed an ECC-based certificateless scheme to cut overhead, but its rigid key-update mechanism lacks adaptability to dynamic IoV topologies, motivating our flexible hash-driven key management.
Lu et al. [14], Ali et al. [15], and Al-Shareeda et al. [16] achieved anonymity but use static pseudonyms, risking tracking. Lee et al. [17] allowed dynamic pseudonyms but failed in unforgeability, while Bayat et al. [18] improved it with bilinear pairing at high cost. Raya et al. [19], Cui et al. [20], and Ali et al. [21] used pseudonym pools, but key-pseudonym coupling increases storage and Sybil attack risks. Pseudonym exchange schemes [22,23,24,25,26,27,28,29,30] reduce storage but risk impersonation via private key sharing and fail to protect pseudonym unlinkability.
Qi et al. [31] proposed a pseudonym self-generation scheme using anonymous credentials and zero-knowledge proofs, allowing repeated credential use without exposure—aligning with our focus on self-generated pseudonyms. However, their zero-knowledge proof-based verification incurs 67% higher computational cost (4.2 ms vs. our requirement of 2.3 ms for verification) due to complex proof generation. Our scheme retains self-generation but replaces proofs with lightweight hash operations, reducing latency while maintaining anonymity—directly addressing this overlapping design’s inefficiency.
Kamil et al. [32] also used self-generated pseudonyms via TA-sent random factors, overlapping with our approach to autonomous pseudonym creation. However, their time-dependent updates (tied to timestamps) create predictability: attackers can exploit time patterns to link pseudonyms, as shown in our threat analysis (§5.2). Our scheme eliminates time dependence by updating pseudonyms via collision-resistant hashing, ensuring unlinkability even in dynamic IoV scenarios, resolving this critical limitation of their overlapping mechanism.
Sucasas et al. [33] generated pseudonyms with legitimate credential association, but their static update logic lacks adaptability compared to our dynamic hash-based approach.
Notably, unlike pre-generated pseudonym pool schemes [19,20] that require storing massive pseudonyms, our hash-driven iteration () enables on-demand updates without pre-storage, directly filling the gap of storage-efficiency in dynamic scenarios.
Additionally, most of the above schemes for achieving conditional privacy protection rely on a fully trusted third party to track the real identity of the user. However, an overly centralized system configuration may threaten user privacy and security—a limitation also reflected in Table 1, where single-authority tracking (e.g., Mei et al. [12], Kamil et al. [32]) risks over-tracing. Therefore, we will design an efficient and secure strong anonymous authentication scheme to eliminate the time dependence of pseudonyms updates, and avoid the trusted authority to directly and independently restore the user’s real identity, as detailed in the comparative analysis of Table 1.

Table 1.
Comparison of core innovation dimensions.
3. Preliminaries
3.1. Definition of Entity Roles
In the proposed scheme, two core entities, namely the Pseudonym Authority (PA) and Trusted Authority (TA), are introduced with distinct functionalities to ensure a privacy–security balance is achieved in IoV authentication.
- Trusted Authority (TA): As the root authority, TA manages vehicles’ real identities (RIDs) during registration, generates partial private keys, and retains the final ability to trace real identities. It does not engage in daily pseudonym validation or updates.
- Pseudonym Authority (PA): PA handles pseudonym management: maintaining validity lists, processing initial pseudonym (PID) requests, and verifying pseudonyms during authentication without accessing real identities. In tracing, it only provides initial pseudonym queries.
The two entities operate in a complementary, permission-separated manner: TA delegates pseudonym management tasks to PA while retaining control over real identity roots, creating a “delegation–execution” hierarchy. This division ensures that no single entity holds excessive authority—TA’s inability to interfere with daily pseudonym operations reduces centralization risks, while PA’s lack of access to real identities prevents privacy breaches.This separation—TA handling identity root management and PA managing pseudonym lifecycle—reduces the risks posed by over-centralized authority.
3.2. Elliptic Curve Discrete Logarithm Problem (ECDLP)
- ECDLP Problem: Given a prime number p and an elliptic curve E, for , it is difficult to find a positive integer k less than p given .
- ECDLP hardness assumption: There is no algorithm that can solve ECDLP in probabilistic polynomial time with a non-negligible probability .
3.3. System Model
The system model includes four entities: TA, PA, RSU, and VU, as shown in Figure 1. The functionality of each entity is described as follows:
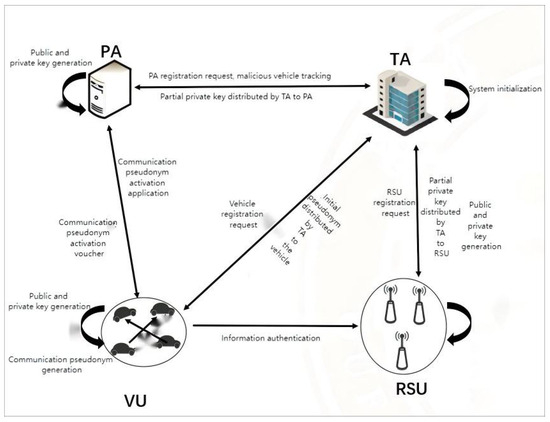
Figure 1.
System model diagram.
- 1.
- Trusted Authority (TA): TA is a fully trusted third party with powerful computing and information storage capabilities. Its responsibilities include generating the public parameters of the system, the initial pseudonyms for vehicles, and the partial private keys for roadside units and the pseudonym activator.
- 2.
- Pseudonym Activator (PA): PA is a trusted entity controlled by TA, which has better computing and information storage capabilities. Its main responsibility is to activate the pseudonym sent by the vehicle to make it valid.
- 3.
- Roadside Unit (RSU): RSU is the infrastructure deployed on side of the road, which is the most basic part of the IoVs architecture. It is a semi-trusted, honest, and curious entity with good computing and information storage capabilities. It is responsible for collecting and publishing real-time traffic information and providing message authentication and other communication services for vehicles.
- 4.
- Vehicle user (VU): In the vehicle network, vehicles communicate with other entities through On-Board Unit (OBU) devices, and their computing and storage capabilities are limited. In our scheme, vehicles can autonomously generate pseudonyms and dynamically update them.
3.4. Security Goals
To resist the potential security threats in IoVs, it is generally necessary to achieve the following security goals.
- Integrity: Protect data from tampering, forgery or replay during transmission and maintain the integrity of the message. This prevents the attacker from tampering with the communication data and ensures that the message obtained by the receiver is consistent with the original message of the sender.
- Authentication: Through the effective authentication mechanism, the identity of the communication entity is guaranteed to be legal and valid. The camouflage and identity impersonation attacks are prevented, which maintains the authenticity and credibility of the communication and prevents the malicious entity from impersonating the legal entity and participating in the communication.
- Conditional Privacy: The trusted authority is able to trace the real identity of the anonymous vehicle for the violation. It is crucial in maintaining the security and trustworthiness of IoVs.
- Unlinkability: When a vehicle sends different signatures using different communication pseudonyms in the network, the attacker cannot associate the different communication pseudonyms used by the vehicle with the same vehicle when verifying the signature. Therefore, the proposed scheme should satisfy the unlinkability between different pseudonyms.
- Non-repudiation: Ensure that the sender of a message cannot deny the fact that the message was sent by the corresponding sender to ensure non-repudiation of the communication.
3.5. Security Models
Suppose there are two types of adversaries with different attack capabilities, denoted as and , where is a malicious vehicle with the ability to replace the signer’s public key, but cannot access the TA’s main master key, and is a malicious passive TA with the ability to access the TA’s main master key, but cannot replace the signer’s public key. In this section, we will design different security models based on the capabilities of these two adversaries. Specifically, we simulate the unforgeability of the scheme through Game 1 and Game 2 executed by adversary and Challenger C. A is allowed to make the following five queries to C:
Hash query: A gives an input value, and C responds with the hash value corresponding to A.
Secret value query: A gives a pseudonym identity to C, and C responds with the secret value corresponding to the pseudonym to A.
Create user query: A gives a pseudonym identity to C, and C responds with the public key of that identity to A.
User private key query: A gives an identity to C, and C responds with the private key for that identity to A.
Replace public key query: A gives a pseudonym identity and a public key to C, and C replaces the original public key with .
Signature query: A gives a pseudonym and a message to C, and C responds with the signature for that identity to A.
Next, we will provide detailed descriptions of two games and give two definitions.
Game 1: adversary and challenger C.
- 1.
- C runs the setup algorithm to generate system parameters, then sends them to .
- 2.
- performs hash queries and creates user queries, user private key queries, replacement public key queries, and signature queries.
- 3.
- generates a signature on .
If the following conditions are simultaneously satisfied, then wins Game 1.
- 1.
- is a valid signature.
- 2.
- cannot query signatures on .
Game 2: adversary and challenger C.
- 1.
- C runs the Setup algorithm to generate system parameters and system master key, then sends them all to .
- 2.
- performs hash queries and creates user queries, user private key queries, and signature queries.
- 3.
- generates a signature on .
If the following conditions are simultaneously satisfied, then wins Game 2.
- 1.
- is a valid signature.
- 2.
- cannot query users’ private keys for .
- 3.
- cannot query signatures on .
Definition 1.
The scheme satisfies existential unforgeability under the chosen message attack (EU-CMA) if adversary and cannot win Game 1 and Game 2 with non-negligible advantage and in polynomial time, respectively.
4. Our Scheme
4.1. Construction of Scheme
This section describes the designed scheme in detail. The scheme is composed of five parts: the system initialization phase, registration phase, pseudonym generation and update phase, message authentication phase, and tracking phase. A detailed introduction of each phase is given below.
In the proposed scheme, the hash functions ∼ are designed to meet essential properties for IoV security: determinism ensures consistent pseudonym generation and verification across entities like TA, PA, and vehicles, as seen in fixed outputs for identical inputs in operations such as ; computational speed supports real-time communication in resource-constrained IoV environments, which is crucial for timely pseudonym updates and message authentication; a one-way structure and preimage resistance prevent the derivation of sensitive inputs (e.g., pseudonym seed from ), safeguarding key information; avalanche effect in functions like ensures minor input changes lead to significantly different pseudonyms, enhancing unlinkability; fixed-length results streamline data transmission, reducing overhead in processes such as pseudonym activation; and collision resistance, as already emphasized, prevents pseudonym forgery, ensuring the uniqueness of communication identities. These properties collectively reinforce the scheme’s security and efficiency in IoVs scenarios.
- 1.
- Initialization PhaseIn this phase, the TA executes the following algorithm to generate the system parameters and the public–private key pair of the system.
- (a)
- Taking the security parameter as input, the addition cyclic group of order q is selected according to , and P is selected as the generator of group . TA selects four one-way hash functions ∼, defined as fixed-length cryptographic functions with key properties: determinism (consistent outputs for identical inputs, e.g., ), a one-way structure (irreversible, protecting seeds like in ), and avalanche effect (minor input changes in yield distinct outputs, enhancing unlinkability). These lightweight functions support efficient IoV operations.
- (b)
- TA selects the random number as the system master key and calculates as the system public key.
- (c)
- TA publishes the system parameters ∼.
- 2.
- Registration PhaseAll vehicles, the PA, and RSUs must register with the TA separately before joining the connected vehicle system. This phase mainly includes PA registration, RSU registration, and vehicle registration. In PA registration and RSU registration, TA needs to generate partial private keys for PA and RSU, respectively. In vehicle registration, TA needs to generate an initial pseudonym for the vehicle, and the specific registration steps are as follows.
- PA registration:
- (a)
- PA selects the random number and calculates .
- (b)
- PA sends the registration request containing its real identity and to TA;
- (c)
- After receiving the registration request from PA, TA checks whether exists in the registration list. If it exists, the request is denied. Otherwise, TA selects a random number , calculates , , , , and sends to PA, where is the session key for communication between PA and TA.
- (d)
- After receiving from TA, PA computes , the private key , and the public key .
- RSU registrationSince the RSU registration process is similar to the PA registration process, it will not be described here.
- Vehicle Registration:
- (a)
- Vehicle chooses a random number as the secret key and calculates the public key .
- (b)
- calculates and sends the registration request containing to TA, where is the session key for communication between vehicle and TA.
- (c)
- After receiving the registration request sent by , TA calculates , checks the validity of the and checks whether exists in the registration list. If it exists, the registration request is denied. Otherwise, TA chooses two random numbers , calculates , , and , , where is the vehicle’s initial pseudonym. Finally, TA sends and to .
- 3.
- Pseudonym Generation and Autonomous Dynamic Update PhaseIn this phase, the vehicle generates the communication pseudonym according to the initial pseudonym generated by TA, and the vehicle sends the communication pseudonym activation request to PA, which activates the vehicle communication pseudonym and sends the activation credential to the vehicle. When the vehicle needs to update the communication pseudonym, the vehicle updates the communication pseudonym through the pseudonym update mechanism and sends the updated communication pseudonym to PA, which activates the updated communication pseudonym of the vehicle and sends the activation credential to the vehicle.
- Seed generation:Vehicle chooses a random number , and computes , , , , , where denotes the communication pseudonym seed.
- Pseudonym self-generation:
- (a)
- computes , ;
- (b)
- chooses random number , and computes , , where denotes the communication pseudonym of vehicle .
- Pseudonym activation:
- (a)
- chooses a random number , and computes , , , where is the current timestamp. computes , let . sends to PA.
- (b)
- After receiving from , PA determines the freshness of the message based on , where is the maximum transmission delay. If the message is fresh, steps d)-g) are performed; otherwise, the PA refuses to provide the communication pseudonym activation service for the vehicle .
- (c)
- PA needs to maintain two pseudonym lists, and , where list , and the list stores the current valid communication pseudonyms of all vehicles, and these two lists are initialized as empty.
- (d)
- PA computes and determines whether the equality holds, and if it holds, PA calculates . .
- (e)
- PA checks whether the tuple exists in the list . If it does not exist, PA lets and calculates . If it exists, PA checks whether computed in the previous step is equal to in the tuple. If they are equal, PA rejects the pseudonym activation service; otherwise, PA verifies whether the equality holds. If it holds, then PA calculates , , .
- (f)
- PA computes and checks whether the equality holds. If it holds, it means that the communication pseudonym is generated by the vehicle identity and is not activated. Then, PA sets and stores in list .
- (g)
- PA selects a random number and calculates , , , , , , where is the credential generated by PA for the vehicle . PA stores in the public valid communication pseudonym list and sends to .
- Vehicle pseudonym update and re-activation
- (a)
- When vehicle needs to update the communication pseudonym, the vehicle updates it through the pseudonym update mechanism, setting , and then repeating the pseudonym self-generation step to obtain the updated communication pseudonym.
- (b)
- Vehicle executes a) in the pseudonym activation step, sends the updated communication pseudonym to PA, repeats b)-g) in the pseudonym activation step, activates the updated communication pseudonym of the vehicle, and sends the activation credential to vehicle .
- (c)
- When vehicle needs to update the communication pseudonym again, the vehicle pseudonym update and re-activation step is repeated.
- 4.
- Message Authentication PhaseWhen vehicle sends a message to other entities using the communication pseudonym , the other entities should verify the message to prevent it from being tampered with or forged. Taking vehicle as the message sender and RSU as the message receiver as an example, the authentication steps are as follows:
- (a)
- chooses random numbers and calculates , , , , , . Let signature . send to RSU.
- (b)
- After receiving the sent by , RSU checks whether the equality holds. If it does not hold, the RSU rejects the request; otherwise, RSU calculates , .
- (c)
- Finally, the RSU verifies whetherholds. If it holds, then the message is valid and received by the RSU; otherwise, the RSU declines to accept the invalid message .
- 5.
- Malicious Vehicle Tracking PhaseAfter receiving the malicious behavior report of the vehicle, the PA tracks the initial pseudonym of the malicious vehicle based on its communication pseudonym and sends it to the trusted authority, TA. The TA tracks the real identity of the malicious vehicle according to the initial pseudonym of the malicious vehicle and holds it accountable. The specific tracing process is outlined below:
- (a)
- When the malicious vehicle is reported by other entities in the IoVs, the whistleblower sends and the malicious behavior of the vehicle to PA, and PA obtains L from , and then decrypts L with its private key to obtain z; that is, , where represents the valid credential of the vehicle, whose communication pseudonym is .
- (b)
- Based on z, PA looks up the initial pseudonym corresponding to the vehicle with the communication pseudonym in list and sends to TA.
- (c)
- TA retrieves the real identity of the malicious vehicle according to .
4.2. Correctness Proof
The correctness of the signature is ensured by the following equation:
5. Security Analysis of Our Scheme
5.1. Security Proof
It is assumed that there are two types of adversaries with different attack capabilities, namely and . is a malicious vehicle that has the ability to replace the signer’s public key but cannot access the master key of the TA. is a malicious passive TA that can access the system master key but cannot replace the signer’s public key. We will design different security models based on the capabilities of these two types of adversaries. Specifically, the unforgeability of the scheme is simulated through Game 1 and Game 2 executed by the adversary and the challenger C.
Theorem 1.
In polynomial time, if the adversary can forge a valid signature with non-negligible advantage in the ROM, then there exists an algorithm that can solve the ECDLP problem with non-negligible advantage .
(, where , , , represent the times at which the user query, secret value query, sign query, and query are created, respectively.)
Proof.
Suppose C is a solver for the elliptic curve discrete logarithm problem, where the input to the challenging problem is , with P being the generator of group G, . The objective of C is to compute the value of a. □
C needs to maintain four initially empty lists, namely , , , , , which are used to store the values of ’s queries to the oracles for , , create user, and secret value, respectively.
Phase 1: C runs the Setup algorithm to generate the system parameters ∼ and computes the public–private key pair of PA, then sends the system parameters and to .
Phase 2: adaptively makes a bounded polynomial number of queries to C.
(1) Query: When C receives an query from concerning , it first checks whether the tuple exists in the list . If it exists, it sends to . Otherwise, it performs the following operations:
- 1.
- If , C chooses and inserts the tuple into the list .
- 2.
- If , C aborts the game.
(2) Query: When C receives an query from concerning , it first checks whether the tuple exists in the list . If it exists, C sends to . Otherwise, it performs the following operations:
- 1.
- If , C chooses , sends them to , and inserts the tuple ,into the list .
- 2.
- If , C accesses the list to obtain , then chooses , , computes .Finally, C sends to , and inserts the tuple into the list .
(3) Creating User Query: When C receives the create user query from regarding the identity , it first checks whether the tuple exists in the list . If it exists, C sends to . Otherwise, it performs the following operations:
- 1.
- If , C chooses , lets , sends to , and inserts into the list .
- 2.
- If , C chooses , then sends to , and inserts , into the list .
(4) Private Key Query: When C receives a private key query about the identity , it first checks whether the tuple exists in the list .
- 1.
- If it exists, C sends to .
- 2.
- Otherwise, C outputs an error character ⊥, indicating that the user has not been created.
(5) Secret Value Query: When C receives a query about the secret value related to the identity from , it first checks whether the tuple exists in the list . If it exists, C sends to . Otherwise, it performs the following operations:
- 1.
- If , C accesses the list to obtain , chooses , computes , , sends to , and inserts into the list .
- 2.
- If , C aborts the game.
(6) Public Key Replacement Query: wants to replace the of identity , so it submits a public key replacement query to C. Upon receiving ’s query, it first checks whether the tuple exists in the list . If it exists, C updates the tuple to . Otherwise, C outputs the error character ⊥, indicating that the user has not been created.
(7) Signature Query: When submits a signature query about to C, C performs the following operations:
- (a)
- If , C accesses the lists , , and to obtain , respectively. Then, C chooses random numbers and calculates , , . C returns the signature to .
- (b)
- If , C aborts the game.
Stage 3: stops the above inquiries and outputs a forged signature about . If , C aborts the game; otherwise, using the Forking Lemma, C can successfully obtain two valid signatures and in polynomial time. Therefore, C calculates using the following formula as a valid solution to the elliptic curve discrete logarithm problem, thus solving the elliptic curve discrete logarithm problem.
Next, we analyze C’s advantage in solving the ECDLP through the following events.
Ev1: is a valid signature.
Ev2: cannot inquire about the secret value of .
Ev3: cannot inquire about the signature of .
In Stage 2, the probability that will submit secret value queries and sign queries without being aborted is .
In Stage 3, the probability that successfully forges a valid signature is , and the probability that C does not abort the game is .
According to the Forking Lemma, the probability that C successfully obtains two valid signatures is .
Therefore, C’s advantage in solving the ECDLP is .
As is non-negligible, C can solve the ECDLP problem with a non-negligible probability. This contradicts the fact that ECDLP is a hard problem. Therefore, the scheme can resist forgery attacks from .
The security proof for the second type of attacker is similar to and is not discussed here.
5.2. Security Requirement Analysis
(1) Message Authenticity and Integrity: Message Authenticity and Integrity: According to the security proof, adversaries and are incapable of successfully forging a valid signature. The RSU can verify the authenticity and integrity of the message by verifying whether the equation holds. This equality holds only if the signature is valid. Therefore, the proposed scheme satisfies the message authenticity and integrity.
(2) Conditional Privacy: In the proposed scheme, the vehicle uses the communication pseudonym to communicate anonymously with other entities in IoVs, and TA can track the real identity of the vehicle with the assistance of PA. That is, PA finds the initial pseudonym of vehicle according to the credential and sends it to TA. TA tracks the real identity of vehicle based on its initial pseudonym . Therefore, the proposed scheme satisfies conditional privacy.
(3) Unlinkability: When a vehicle generates a signature each time in the network, the communication pseudonym and credential will change accordingly, and the attacker cannot infer whether different signatures are from the same vehicle, which effectively prevents the attacker from tracking the identity of the vehicle. In addition, in the message authentication phase, each piece of verification information used by the RSU to verify the message signature will change as the signature changes; that is, the communication pseudonyms used by the vehicle cannot be associated during verification. Therefore, the proposed scheme satisfies the unlinkability of pseudonyms and real identities and the unlinkability of pseudonyms and communication pseudonyms.
(4) Autonomy and Dynamics of the Pseudonym Update: In the proposed scheme, each vehicle computes a pseudonym seed related to TA information and calculates . When vehicle wants to update its communication pseudonym, it can automatically and dynamically update its communication pseudonym through the hash function , and then it uses the new communication pseudonym to communicate with other entities. Therefore, the proposed scheme satisfies the autonomous and dynamic of pseudonym updates.
(5) Anti-Sybil attacks: The communication pseudonym generated by the vehicle will be activated by PA. After the PA is activated, the updated communication pseudonym of the vehicle is stored in the public valid fake name table, ensuring that only one pseudonym is valid for a vehicle at each time point. So the vehicle cannot use multiple simultaneously valid communication pseudonyms to communicate with other entities. Therefore, the proposed scheme can effectively resist Sybil attacks.
(6) Anti-replay attacks: There is a timestamp in the tuple , , which can be used by other entities in the IoV to check the validity of the signature. Therefore, the proposed scheme can effectively resist replay attacks.
(7) Anti-man-in-the-middle attack: The message authentication method provided by the proposed scheme was based on the certificateless public key cryptosystem, and the third party could not perform public key replacement attacks and replace the message. Therefore, the proposed scheme can effectively resist man-in-the-middle attacks.
5.3. Scyther Tool Analysis
To verify the security of the certificateless-based strong anonymous privacy protection authentication scheme proposed in this paper, the Scyther tool is used for formal modeling and verification of the protocol’s identity authentication process and pseudonym management mechanism.
In the Scyther modeling, the focus is on abstracting two core communication roles in the protocol:
- Vehicle (V): As the message sender, it uses dynamically generated pseudonyms (SPIDs) for signing and sends authentication information, including signatures, credentials, and timestamps, to the Roadside Unit (RSU).
- Roadside Unit (R): As the message receiver, the Roadside Unit is responsible for verifying the validity of the signature sent by the vehicle, checking the pseudonym status, and ensuring the freshness of the message.
The model strictly follows the core processes of the protocol, including pseudonym generation (based on a seed iterative update of hash functions), signature generation (combined with elliptic curve scalar operations), signature verification (verification through public key and elliptic curve point operations), and pseudonym activation (authorized by the Pseudonym Activator PA). Scyther claims are used to define key security attributes such as Authentication, Secrecy, and Unlinkability.
The results show that all Scyther claims are verified successfully, and the Scyther tool cannot effectively break this strong anonymous identity authentication protocol in the aforementioned malicious attack detection. The experimental results indicate that this strong anonymous identity authentication protocol can meet the preset security requirements and effectively resist common threats such as temporary key leakage attacks, pseudonym correlation attacks, Sybil attacks, replay attacks, and man-in-the-middle attacks. Additionally, it possesses forward security and flexibility in dynamic pseudonym management, making it suitable for Internet of Vehicles (IoVs) scenarios with high security demands and low latency requirements.
6. Performance Analysis
In this section, we analyze the performance of our scheme in terms of computational cost and communication overhead, and compare our scheme with five existing signature schemes. The computational cost mainly evaluates the computational amount of pseudonym generation, signature generation, and signature verification algorithms. The communication cost mainly evaluates the transmission length of signatures, pseudonyms, current timestamps, and public keys.
6.1. Computational Cost
In terms of computational cost, due to the small cost of universal hash operation and symmetric encryption and decryption, this assessment ignores them. Kamil et al. [32] simulated the basic encryption operation and obtained the running time required for the encryption operation, as shown in Table 2. To facilitate comparison, we used these data to analyze the computational overhead of our scheme, Li et al.’s scheme [29], Mei et al.’s scheme [12], Pournaghi et al.’s scheme [35], Wang et al.’s scheme [7], and Azees et al.’s scheme [34]. Table 3 shows the comparison results of computational cost between our scheme and five existing schemes.

Table 2.
Cryptographic operation symbol and execution time.

Table 3.
Calculation cost comparison.
As can be seen from Table 3, for the pseudonym and signature generation process of Li et al.’s scheme [29], vehicle users need to perform four scalar multiplication operations related to ECC, two scalar addition operations related to ECC, and one bilinear pairing operation. Therefore, the computational cost of the pseudonym and signature generation process of Li et al.’s scheme [29] is . To verify the signature, the verifier needs to perform four scalar multiplications associated with ECC and two bilinear pairing operations. Thus, the computational cost of signature verification is .
For the pseudonym and signature generation process of Mei et al.’s scheme [12], vehicle users need to perform four scalar multiplication operations related to ECC and two hash-to-point-function operations. Therefore, the computational cost of the pseudonym and signature generation process of Mei et al.’s scheme [12] is . In the process of signature verification, the verifier needs to perform two scalar multiplication operations related to ECC and two bilinear pairing operations. Thus, the computational cost of signature verification is .
For the pseudonym and signature generation process of Pournaghi et al.’s scheme [35], vehicle users need to perform four scalar multiplication operations related to ECC and one hash-to-point-function operation. Therefore, the computational cost of the pseudonym and signature generation process of Pournaghi et al.’s scheme [35] is . To verify the signature, the verifier needs to perform one scalar multiplication operation related to ECC, two bilinear pairing operations, and one hash-to-point function operation. Thus, the computational cost of signature verification is .
For the pseudonym and signature generation process of Wang et al.’s scheme [7], vehicle users need to perform four scalar multiplication operations related to ECC and two hash-to-point-function operations. Therefore, the computational cost of the pseudonym and signature generation process of Wang et al.’s scheme [7] is . To verify the signature, the verifier needs to perform one scalar multiplication operation related to ECC, three bilinear pairing operations, and one hash-to-point function operation. Thus, the computational cost of signature verification is .
For the pseudonym and signature generation process of Azees et al.’s scheme [34], vehicle users need to perform six bilinear pairing operations. Therefore, the computational cost of the pseudonym and signature generation process of Azees et al.’s scheme [34] is . To verify the signature, the verifier needs to perform five bilinear pairing operations and two hash-to-point function operations. Thus, the computational cost of signature verification is .
In the process of pseudonym and signature generation in our proposed scheme, vehicle users need to perform six scalar multiplication operations related to ECC. Therefore, the computational cost of the pseudonym and signature generation process of our scheme is . To verify the signature, the verifier needs to perform five scalar multiplication operations related to ECC. Thus, the computational cost of signature verification is .
Compared with Wang et al.’s scheme [7], Mei et al.’s scheme [12], Li et al.’s scheme [29], Pournaghi et al.’s scheme [35], and Azees et al.’s scheme [34], the total computational cost of our scheme is reduced by 82.94%, 82.82%, 70.29%, 74.99%, and 91.18%, respectively. In addition, a bar chart is presented in this subsection for a clearer view of the comparison results, as shown in Figure 2. Therefore, the proposed scheme is more efficient in pseudonym generation, signature creation, and signature verification.
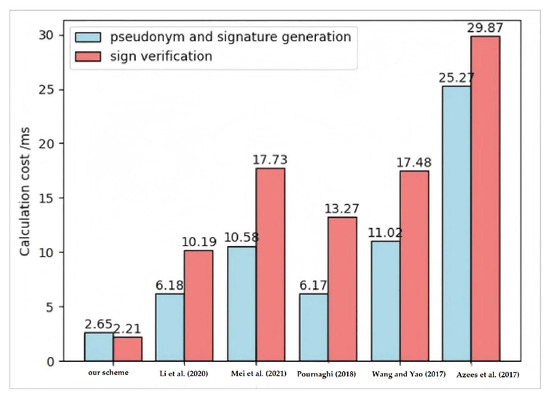
Figure 2.
Comparisons of computational overhead [7,12,29,34,35].
6.2. Communication Overhead
In terms of communication overhead, we perform simulations by using the following settings:
- 1.
- Elliptic curve cryptography scheme: Construct an addition group G with the curve of order q using generator p, where a and , bits, bits.
- 2.
- Bilinear paired cipher scheme: Use a bilinear pairing operations, where , is an addition cyclic group of order with generator , where is a point on the curve , bits, bits of prime, bits. In addition, the timestamp T is bits. Table 4 shows the comparison results of the communication cost between our scheme and the existing five schemes.
 Table 4. Communication overhead comparison.
Table 4. Communication overhead comparison.
In Wang et al.’s scheme [7], the user sends the pseudonym , signature , certificate , and timestamp to the verifier, where , . Therefore, the communication cost of sending pseudonym, signature, and timestamp in Wang et al.’s scheme [7] is .
In Mei et al.’s scheme [12], the user sends the pseudonym , signature , and timestamp to the verifier, where , . Therefore, the communication cost of sending the pseudonym, signature, and timestamp in Mei et al.’s scheme [12] is bits.
In our scheme, the user sends the pseudonym , signature , and timestamp to the verifier, where , . Therefore, the communication cost of sending the pseudonym, signature, and timestamp in our scheme is bits. Using the same approach, the communication overhead of Li et al.’s scheme [29], Pournaghi et al.’s scheme [35], and Azees et al.’s scheme [34] can be obtained.
According to Table 3, compared with Wang et al.’s scheme [7], Mei et al.’s scheme [12], Li et al.’s scheme [29], Pournaghi et al.’s scheme [35], and Azees et al.’s scheme [34], the total communication overhead of our scheme is reduced by 27.78%, 58.73%, 27.75%, and 82.55%, respectively. In addition, a bar chart pertaining to communication overhead is given for a clearer view of the comparison results, as shown in Figure 3. It can be observed in Figure 3 that the communication overhead of the proposed scheme is lower than that of other schemes; that is, the total transmission length of the pseudonym, signature and timestamp is reduced, which effectively saves the transmission bandwidth and storage overhead at the receiver. Therefore, the proposed scheme also has more advantages for communication, and is more suitable for the field of IoVs with low requirements for transmission bandwidth and storage overhead.
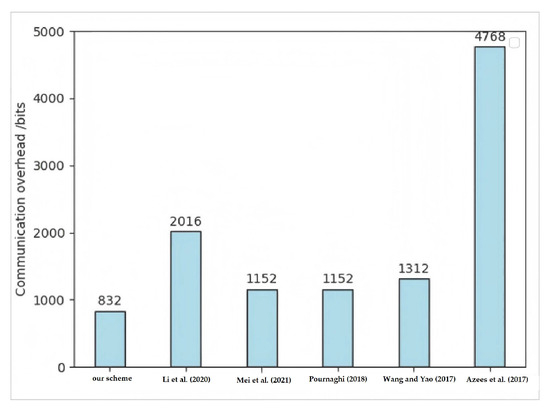
Figure 3.
Comparisons of Communication overhead [7,12,29,34,35].
7. Conclusions
This paper proposes a strong anonymous privacy protection authentication scheme. The scheme is based on a certificateless public key cryptosystem, which effectively solves the problems of certificate management and key escrow. A strong anonymity method based on a collision-resistant hash function is designed, and the vehicle can update the pseudonym in communication at any time according to the users’ needs, eliminating the time dependence of the pseudonym updates and realizing the autonomy and dynamic update of pseudonyms. In addition, the trusted authority uses the session key to transmit the partial private key of each entity to the corresponding entity, which eliminates the dependence on the secure channel in the process of partial private key transmission. In addition, TA and PA cooperated to track the real identity of vehicle users, which effectively avoided TA directly and independently restored the user’s real identity. The security analysis results show that the proposed scheme can resist adaptive chosen message attacks, replay attacks, man-in-the-middle attacks, and Sybil attacks. The performance analysis results show that compared with the existing schemes, the proposed scheme has low computational cost and small communication overhead, which is more suitable for the field of IoVs with high security strength demand and low transmission bandwidth and storage.
In summary, the originality of this scheme lies in breaking through the time dependence limitation of existing pseudonym updates and proposing an autonomous dynamic update mechanism; pioneering a method of transmitting partial private keys via session keys in a certificateless architecture to eliminate the reliance on secure channels; and designing a distributed tracking mechanism with collaboration between TA and PA to balance privacy protection and traceability. These designs collectively address the bottlenecks of existing schemes in computational efficiency, privacy security, and practicality, forming a significant distinction from existing research schemes.
Author Contributions
Conceptualization, H.W.; Methodology, S.G.; Validation, X.H.; Formal analysis, H.W.; Data curation, C.W.; Writing—original draft, S.G.; Writing—review & editing, C.W.; Visualization, C.W.; Project administration, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially funded by the Science Research Project of Weinan Science and Technology Bureau (No. ZWGX2003-1) and the Foundation for Quality Professional Degree Teaching Case Library for Graduate Students in Shandong Province (No. SDYAL2024165). The authors are indebted to these institutions for their support.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Deng, Y.-K.; Zhang, L.; Li, J. A Review of Privacy Protection in Internet of Vehicles. Appl. Res. Comput. Jisuanji Yingyong Yanjiu 2022, 39. [Google Scholar] [CrossRef]
- Pu, Y.; Xiang, T.; Hu, C.; Alrawais, A.; Yan, H. An efficient blockchain-based privacy preserving scheme for vehicular social networks. Inf. Sci. 2020, 540, 308–324. [Google Scholar] [CrossRef]
- Liu, X.; Jia, Z.; Xu, E.; Gong, B.; Wang, L. A Privacy Protection Scheme in VANETs Based on Group Signature. In Chinese Conference on Trusted Computing and Information Security; Springer: Singapore, 2018; pp. 286–300. [Google Scholar] [CrossRef]
- Jiang, Y.; Ge, S.; Shen, X. AAAS: An Anonymous Authentication Scheme Based on Group Signature in VANETs. IEEE Access 2020, 8, 98986–98998. [Google Scholar] [CrossRef]
- Maurer, U.; Renner, R. Distributed Secret Sharing over a Public Channel from Correlated Random Variables. arXiv 2021, arXiv:2110.10307v2. [Google Scholar]
- Sovrin Foundation. The Sovrin Network: A Decentralized Global Identity System. In Whitepaper; Sovrin Foundation: Provo, UT, USA, 2018. [Google Scholar]
- Wang, S.; Yao, N. LIAP: A Local Identity-Based Anonymous Message Authentication Protocol in VANETs. Comput. Commun. 2017, 112, 154–164. [Google Scholar] [CrossRef]
- Tzeng, S.F.; Horng, S.J.; Li, T.; Wang, X.; Huang, P.H.; Khan, M.K. Enhancing Security and Privacy for Identity-Based Batch Verification Scheme in VANETs. IEEE Trans. Veh. Technol. 2017, 66, 3235–3248. [Google Scholar] [CrossRef]
- Li, J.; Choo, K.K.R.; Zhang, W.; Kumari, S.; Rodrigues, J.J.; Khan, M.K.; Hogrefe, D. EPA-CPPA: An Efficient, Provably-Secure and Anonymous Conditional Privacy-Preserving Authentication Scheme for Vehicular Ad Hoc Networks. Veh. Commun. 2018, 13, 104–113. [Google Scholar] [CrossRef]
- Alazzawi, M.A.; Lu, H.; Yassin, A.A.; Chen, K. Efficient Conditional Anonymity with Message Integrity and Authentication in a Vehicular Ad-Hoc Network. IEEE Access 2019, 7, 71424–71435. [Google Scholar] [CrossRef]
- Mahanta, H.J.; Azad, A.K.; Khan, A.K. Differential Power Analysis: Attacks and Resisting Techniques. In Information Systems Design and Intelligent Applications; Springer: New Delhi, India, 2015; pp. 349–358. [Google Scholar]
- Mei, Q.; Xiong, H.; Chen, J.; Yang, M.; Kumari, S.; Khan, M.K. Efficient Certificateless Aggregate Signature with Conditional Privacy Preservation in IoV. IEEE Syst. J. 2021, 15, 245–256. [Google Scholar] [CrossRef]
- Thumbur, G.; Rao, G.S.; Reddy, P.V.; Gayathri, N.B.; Reddy, D.K.; Padmavathamma, M. Efficient and Secure Certificateless Aggregate Signature-Based Authentication Scheme for Vehicular Ad Hoc Networks. IEEE Internet Things J. 2020, 8, 1908–1920. [Google Scholar] [CrossRef]
- Lu, R.; Lin, X.; Zhu, H.; Ho, P.-H.; Shen, X. ECPP: Efficient Conditional Privacy Preservation Protocol for Secure Vehicular Communications. In Proceedings of the IEEE INFOCOM 2008, Phoenix, AZ, USA, 13–18 April 2008; pp. 1229–1237. [Google Scholar] [CrossRef]
- Ali, I.; Li, F. An Efficient Conditional Privacy-Preserving Authentication Scheme for Vehicle-To-Infrastructure Communication in VANETs. Veh. Commun. 2020, 22, 100228. [Google Scholar] [CrossRef]
- Al-Shareeda, M.A.; Anbar, M.; Manickam, S.; Hasbullah, I.H. Towards Identity-Based Conditional Privacy-Preserving Authentication Scheme for Vehicular Ad Hoc Networks. IEEE Access 2021, 9, 108889–108901. [Google Scholar] [CrossRef]
- Lee, C.-C.; Lai, Y.-M. Toward a Secure Batch Verification with Group Testing for VANET. Wirel. Netw. 2013, 19, 1441–1449. [Google Scholar] [CrossRef]
- Bayat, M.; Barmshoory, M.; Rahimi, M.; Aref, M.R. A Secure Authentication Scheme for VANETs with Batch Verification. Wirel. Netw. 2015, 21, 1733–1743. [Google Scholar] [CrossRef]
- Zhu, F.; Yi, X.; Abuadbba, A.; Khalil, I.; Huang, X.; Xu, F. A Security-Enhanced Certificateless Conditional Privacy-Preserving Authentication Scheme for Vehicular Ad Hoc Networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10456–10466. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, J.; Zhong, H.; Shi, R.; Xu, Y. An Efficient Certificateless Aggregate Signature Without Pairings for Vehicular Ad Hoc Networks. Inf. Sci. 2018, 451, 1–15. [Google Scholar] [CrossRef]
- Ali, I.; Chen, Y.; Ullah, N.; Kumar, R.; He, W. An Efficient and Provably Secure ECC-Based Conditional Privacy-Preserving Authentication for Vehicle-to-Vehicle Communication in VANETs. IEEE Trans. Veh. Technol. 2021, 70, 1278–1291. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, D.; Li, Y.; Weng, J.; Sun, M.; Yang, Y.; Li, M. Privacy-Preserving and Real-Time Detection of Vehicular Congestion Using Multilayer Perceptron Approach for Internet of Vehicles. IEEE Trans. Veh. Technol. 2022, 71, 12530–12542. [Google Scholar] [CrossRef]
- Mdee, A.P.; Khan, M.T.R.; Seo, J.; Kim, D. Infrastructure-Independent Pseudonym Swap Protocol for Vehicular Networks. In Proceedings of the 13th International Conference on Ubiquitous and Future Networks (ICUFN), Barcelona, Spain, 5–8 July 2022; pp. 351–356. [Google Scholar]
- Li, Y.; Yin, Y.; Chen, X.; Wan, J.; Jia, G.; Sha, K. A Secure Dynamic Mix Zone Pseudonym Changing Scheme Based on Traffic Context Prediction. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9492–9505. [Google Scholar] [CrossRef]
- Choudhary, S.; Dorle, S. Empirical Investigation of VANET-Based Security Models From a Statistical Perspective. In Proceedings of the International Conference on Computational Intelligence and Computing Applications (ICCICA), Nagpur, India, 11–12 December 2021; pp. 1–8. [Google Scholar]
- Li, X.; Liu, J.; Obaidat, M.S.; Vijayakumar, P.; Jiang, Q.; Amin, R. An Unlinkable Authenticated Key Agreement with Collusion Resistant for VANETs. IEEE Trans. Veh. Technol. 2021, 70, 7992–8006. [Google Scholar] [CrossRef]
- Jiang, B.; Li, J.; Yue, G.; Song, H. Differential Privacy for Industrial Internet of Things: Opportunities, Applications, and Challenges. IEEE Internet Things J. 2021, 8, 10430–10451. [Google Scholar] [CrossRef]
- Bradbury, M.; Taylor, P.; Atmaca, U.I.; Maple, C.; Griffiths, N. Privacy Challenges with Protecting Live Vehicular Location Context. IEEE Access 2020, 8, 207465–207484. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Ren, Y.; Ma, S.; Luo, B.; Weng, J.; Ma, J.; Huang, X. PAPU: Pseudonym Swap with Provable Unlinkability Based on Differential Privacy in VANETs. IEEE Internet Things J. 2020, 7, 11789–11802. [Google Scholar] [CrossRef]
- Manivannan, D.; Moni, S.S.; Zeadally, S. Secure Authentication and Privacy-Preserving Techniques in Vehicular Ad-hoc Networks (VANETs). Veh. Commun. 2020, 25, 100247. [Google Scholar] [CrossRef]
- Qi, J.; Gao, T.; Deng, X.; Zhao, C. A Pseudonym-Based Certificateless Privacy-Preserving Authentication Scheme for VANETs. Veh. Commun. 2022, 33, 100396. [Google Scholar] [CrossRef]
- Kamil, I.A.; Ogundoyin, S.O. An Improved Certificateless Aggregate Signature Scheme Without Bilinear Pairings for Vehicular Ad Hoc Networks. J. Inf. Secur. Appl. 2019, 44, 184–200. [Google Scholar] [CrossRef]
- Sucasas, V.; Mantas, G.; Bastos, J.; Damião, F.; Rodriguez, J. A Signature Scheme with Unlinkable-Yet-Accountable Pseudonymity for Privacy-Preserving Crowdsensing. IEEE Trans. Mob. Comput. 2020, 19, 752–768. [Google Scholar] [CrossRef]
- Azees, M.; Vijayakumar, P.; Deboarh, L.J. EAAP: Efficient Anonymous Authentication with Conditional Privacy-Preserving Scheme for Vehicular Ad Hoc Networks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2467–2476. [Google Scholar] [CrossRef]
- Pournaghi, S.M.; Zahednejad, B.; Bayat, M.; Farjami, Y. NECPPA: A Novel and Efficient Conditional Privacy-Preserving Authentication Scheme for VANET. Comput. Netw. 2018, 134, 78–92. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).