The Detection of a Defect in a Dual-Coupling Optomechanical System

Abstract

We provide an approach to detect a nitrogen-vacancy (NV) center, which might be a defect in a diamond nanomembrane, using a dual-coupling optomechanical system. The NV center modifies the energy-level structure of a dual-coupling optomechanical system through dressed states arising from its interaction with the mechanical membrane. Thus, we study the photon blockade in the cavity of a dual-coupling optomechanical system in which an NV center is embedded in a single-crystal diamond nanomembrane. The NV center significantly influences the statistical properties of the cavity field. We systematically investigate how three key NV center parameters affect photon blockade: (i) its coupling strength to the mechanical membrane, (ii) transition frequency, and (iii) decay rate. We find that the NV center can shift, give rise to a new dip, and even suppress the original dip in a bare quadratic optomechanical system. In addition, we can amplify the effect of the NV center on photon statistics by adding a gravitational potential when the NV center has little effect on photon blockade. Therefore, our study provides a method to detect diamond nanomembrane defects in a dual-coupling optomechanical system.

1. Introduction

Defects are an inescapable and omnipresent aspect of all materials. Their impact is profound, as they have the ability to significantly alter the electrical, optical, and mechanical characteristics of a material [1]. Since the emergence of the first electronic and optoelectronic semiconductor devices, their miniaturization has been an ongoing trend [2]. One can ultimately foresee a device consisting of merely a few atoms. Given that these atoms should not be adrift in free space, but rather embedded within a solid-state matrix, this inevitably leads to the concept of a point defect [3,4,5,6,7]. The diamond nitrogen-vacancy (NV) center is the most typical and well-investigated quantum defect, due to the fact that its quantum state is manipulable and readable [8]. These spins are highly sensitive to local fields like electric, magnetic, thermal, and strain fields. In addition, embedding the defects in nanostructures paves the way for revolutionary nanoscale sensing in physics [9,10,11], chemistry [12,13], and biology [14,15]. Thus, the detection of NV centers embedded in diamond nanostructures can facilitate the development of electronic and optoelectronic semiconductor devices.

Cavity optomechanical systems make it possible for interactions to occur between light and mechanical resonators [16,17,18]. They offer a platform that is applicable to both practical applications in precision sensing [19,20,21] and the fundamental physics of macroscopic quantum systems [22,23,24,25]. In the realm of optomechanical systems research, one of the significant milestones lies in pushing the sensitivity of weak force measurements [26,27,28] to a point where it can reach, and even far exceed, the standard quantum limit. As mentioned in the previous paragraph, there are defects in any material. Therefore, it is imperative to acknowledge the fact that an optomechanical system will exhibit a high degree of sensitivity to weak forces, and the study of the effects of defects on an optomechanical system is one of the research directions in optomechanics [29,30,31,32]. From another perspective, these are also sufficient to show that the presence of defects can exert a significant influence upon an optomechanical system. The question that naturally arises from this is whether the defects in materials can be detected by optomechanical coupling. Then, the effects of defects could be visualized through optical effects.

It is evident from the preceding discourse that the detection of defects in dual-coupling optomechanical systems is an area of significant interest. A dual-coupling optomechanical system involves quadratic optomechanical radiation pressure coupling, as well as spin–spin interactions. The quadratic optomechanical system under consideration is constituted of a high-finesse Fabry–Pérot cavity in conjunction with a flexible nano-diamond membrane, forming the basis of the theoretical framework. An NV center is embedded in a single-crystal diamond nanomembrane. The flexing of the diamond membrane strains the diamond lattice, which leads to the occurrence of spin–spin interactions [33]. An NV center will indirectly influence the optical properties of the cavity field through the mechanical membrane. Thus, we can detect the defects on the mechanical membrane by studying the changes in the optical properties of the cavity field. This paper will study the influence of defects on the second-order correlation function of the cavity field under different circumstances.

The remainder of this paper is structured as follows: Firstly, a physical model is presented, and the complete quadratic optomechanical Hamiltonian, incorporating an NV center, is furnished in its entirety. Subsequently, the eigenvalues and eigenstates of the entire system, with the exception of the external optical driving, can be obtained through the application of squeezing and supersymmetric unitary transformation. Following this, the steady state of the system can be obtained within the few-photon space in the weak-driving regime when an anti-Hermitian term is added to the Hamiltonian in a phenomenological manner. Secondly, the second-order correlation function of the cavity field was calculated numerically using Qutip. The following study will demonstrate the effects of an NV center on conventional single-photon blockade in a quadratically coupled optomechanical system. Furthermore, evidence is presented demonstrating the capacity of gravity coupling to amplify the effects of a defect by means of enhancing single-photon blockade. The conclusions of our work are presented in the conclusions section.

2. Physical Model and Solution

2.1. System Hamiltonian

Although quadratic optomechanical coupling is ordinarily extremely weak, it has the capacity to yield a photon-dependent modulation of the phonon potential. Recently, single-photon-triggered quantum phase transition [34] or entanglement [35] have been shown in quadratic optomechanical systems. Here, we consider a dual-coupling optomechanical system, in which the membrane couples to a two-level-system, e.g., the nitrogen-vacancy (NV) centers in diamond [36,37,38]. As demonstrated in Ref. [33], in order to facilitate resonance with the microwave transition of the spin triplet state of an NV center, it is necessary to achieve a mechanical frequency of approximately gigahertz. Specifically, the movement of the nano-diamond membrane exerts strain on the diamond lattice. The application of strain to the nano-diamond membrane generates an equivalent electric field at the NV centers through the piezoelectric effect, directly interacting with the spin triplet states in the NV center’s electronic ground state. In the case of near-resonance conditions being met, the mechanical vibrations of the nano-diamond membrane are known to modulate the spin triplet state energy levels of the NV center through strain or piezoelectric effects. The result is what is known as an effective spin–phonon coupling. As shown in Figure 1, here we study the photon blockade effect in a hybrid system consisting of a two-level system coupling the membrane of a quadratic optomechanical system. The Hamiltonian of this hybrid system can be expressed as follows:

$$\begin{array}{c}\hfill H_0={\omega }_c{a}^{†}a+{\omega }_m{b}^{†}b+{\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+g_0{a}^{†}a{\left(b^{†}+b\right)}^2+\mathsf{\Lambda }\left(b^{†}{\sigma }_{-}+{\sigma }_{+}b\right).\end{array}$$

(1)

It should be noted that the eigenfrequencies of cavity mode a and mechanical mode b are denoted by the symbols ${\omega }_c$ and ${\omega }_m$, respectively. The annihilation (creation) operations of the photon and phonon fields with respect to the optical cavity and mechanical membrane are denoted by $a\left(a^{†}\right)$ and $b\left(b^{†}\right)$, respectively. The Pauli operators are

$$\begin{array}{c}\hfill {\sigma }_{+}=|e\rangle \langle g|,{\sigma }_{-}=|g\rangle \langle e|,{\sigma }_z=\left(|e\rangle \langle e|-|g\rangle \langle g|\right),\end{array}$$

(2)

with the following commutation relationship:

$$\begin{array}{c}\hfill \left[{\sigma }_{+},{\sigma }_{-}\right]={\sigma }_z,\left[{\sigma }_{\pm },{\sigma }_z\right]=\mp 2{\sigma }_{\pm }.\end{array}$$

(3)

Figure 1. (Color online) A schematic diagram of a hybrid structure consisting of a two-level system coupled to the quadratic optomechanical system is presented. In conditions of near-resonance, the vibrational frequency of the nano-diamond membrane approximates the jump frequency of the spin triplet states of an NV center. An NV center in the nano-diamond membrane can thus be regarded as a two-energy system.

Figure 1. (Color online) A schematic diagram of a hybrid structure consisting of a two-level system coupled to the quadratic optomechanical system is presented. In conditions of near-resonance, the vibrational frequency of the nano-diamond membrane approximates the jump frequency of the spin triplet states of an NV center. An NV center in the nano-diamond membrane can thus be regarded as a two-energy system.

Since the photon number $a^{†}a$ is a conservable quantity, we can rewrite the Hamiltonian as

$$\begin{array}{c}\hfill H_0=\sum _{n=0}^{\infty }\left[n{\omega }_c+{\omega }_m{b}^{†}b+{\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+n{g}_0{\left(b^{†}+b\right)}^2+\mathsf{\Lambda }\left(b^{†}{\sigma }_{-}+{\sigma }_{+}b\right)\right]{\left|n\right.〉}_a{\left.〈n\right|}_a\end{array}$$

(4)

Clearly, $n{\omega }_c$ is a number and the Hamiltonian of a defect-coupled membrane can be written as

$$\begin{array}{cc}\hfill H_{md}& ={\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+{\omega }_m{b}^{†}b+n{g}_0{\left(b^{†}+b\right)}^2+\mathsf{\Lambda }\left(b^{†}{\sigma }_{-}+{\sigma }_{+}b\right).\hfill \end{array}$$

(5)

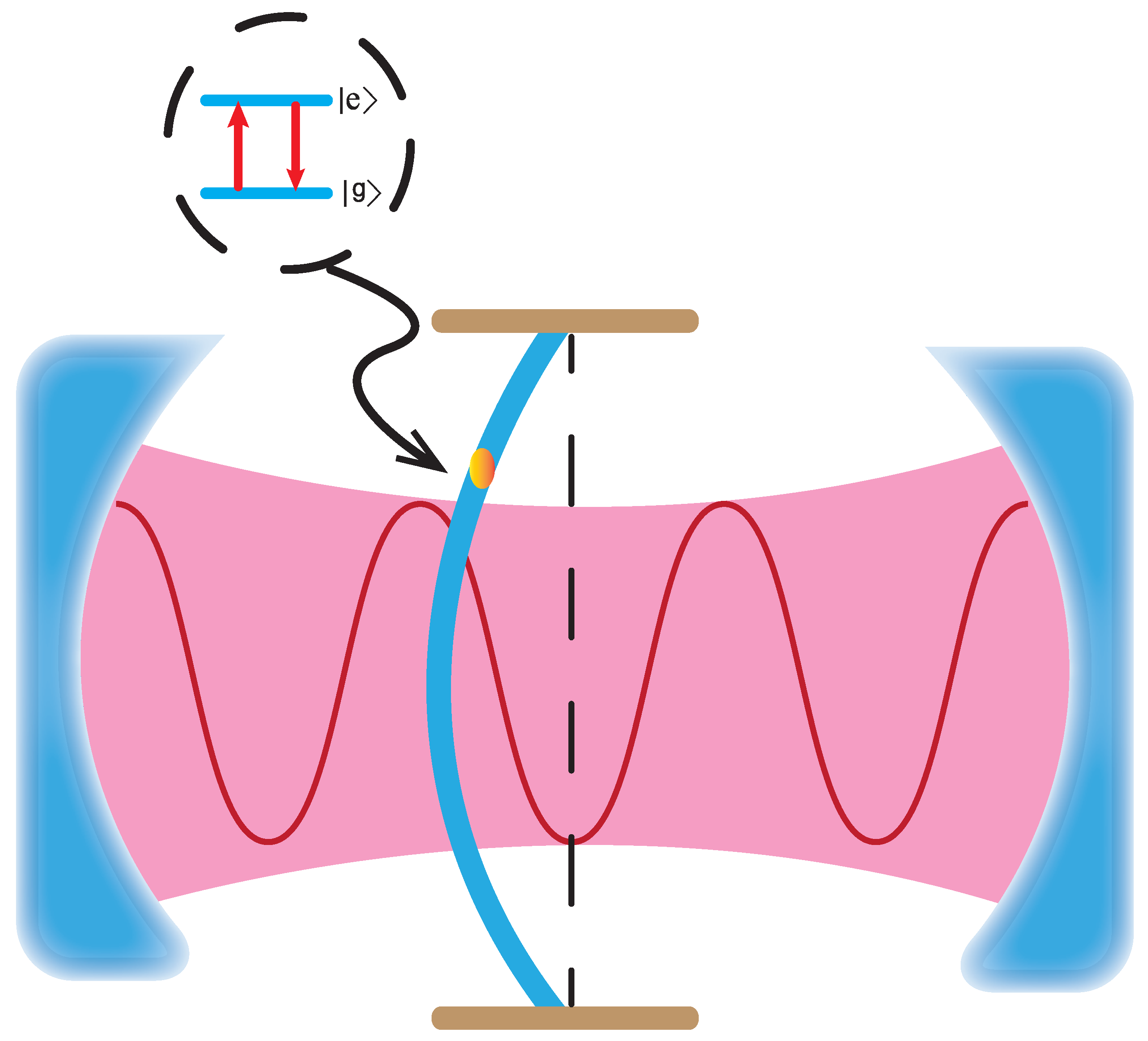
2.2. Energy Structure of the Hybrid System

It is evident that the number operator $a^{†}a$ of cavity field and Hamiltonian $H_0$ commute with each other. Thus, the excitation number of cavity photons is conservative in dynamic evolution when the system is closed. The mechanical membrane has a role to play in dual-coupling, specifically the quadratically optomechanical coupling and the Jaynes–Cummings type interaction between a NV center and mechanical membrane, respectively. Accordingly, the initial step in the process of diagonalization is the definition of the squeezing operator, as follows:

$$\begin{array}{cc}\hfill & S\left(\eta \right)=exp\left[{\displaystyle \frac{\eta }{2}}\left(b^2-b^{†2}\right)\right],\hfill \\ \hfill & S^{†}\left(\eta \right)=S(-\eta ),\hfill \end{array}$$

(6)

where $\eta =r$ is an undetermined real function of photon number n. Then, a squeezing transformation is consequently introduced

$$\begin{array}{cc}\hfill & S^{†}\left(\eta \right)bS\left(\eta \right)=b_{s}cosh\left(r\right)-b_s^{†}sinh\left(r\right),\hfill \\ \hfill & S^{†}\left(\eta \right)b^{†}S\left(\eta \right)=b_s^{†}cosh\left(r\right)-b_{s}sinh\left(r\right),\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill & S^{†}\left(\eta \right)b^{†}bS\left(\eta \right)=cosh\left(2r\right)b_s^{†}{b}_s-{\displaystyle \frac{1}{2}}sinh\left(2r\right)(b_s^{†2}+b_s^2)+sin{h}^2\left(r\right),\hfill \\ \hfill & S^{†}\left(\eta \right)b^{2}S\left(\eta \right)=sin{h}^2\left(r\right)b_s^{†2}+cos{h}^2\left(r\right)b_s^2-sinh\left(2r\right)b_s^{†}{b}_s-{\displaystyle \frac{1}{2}}sinh\left(2r\right),\hfill \\ \hfill & S^{†}\left(\eta \right)b^{†2}S\left(\eta \right)=cos{h}^2\left(r\right)b_s^{†2}+sin{h}^2\left(r\right)b_s^2-sinh\left(2r\right)b_s^{†}{b}_s-{\displaystyle \frac{1}{2}}sinh\left(2r\right).\hfill \end{array}$$

(8)

Then, the Hamiltonian $H_{md}$ becomes

$$\begin{array}{cc}\hfill H_{\mathit{md}}^{\prime }=& S^{†}\left(\eta \right)H_{md}S\left(\eta \right)=S^{†}\left(\eta \right)\left[{\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+{\omega }_m{b}^{†}b+n{g}_0{\left(b^{†}+b\right)}^2+\mathsf{\Lambda }\left(b^{†}{\sigma }_{-}+{\sigma }_{+}b\right)\right]S\left(\eta \right)\hfill \\ \hfill =& {\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+2\left[\left({\displaystyle \frac{{\omega }_m}{2}}+n{g}_0\right)cosh\left(2r\right)-n{g}_{0}sinh\left(2r\right)\right]b_s^{†}{b}_s\hfill \\ \hfill & -\left[\left({\displaystyle \frac{{\omega }_m}{2}}+n{g}_0\right)sinh\left(2r\right)-n{g}_{0}cosh\left(2r\right)\right]\left(b_s^{†2}+b_s^2\right)\hfill \\ \hfill & +\mathsf{\Lambda }\left[cosh\left(r\right)\left({\sigma }_{+}{b}_s+b_s^{†}{\sigma }_{-}\right)-sinh\left(r\right)\left({\sigma }_{+}{b}_s^{†}+b_s{\sigma }_{-}\right)\right]\hfill \\ \hfill & +\left({\omega }_m+n{g}_0\right)sin{h}^2\left(r\right)-n{g}_{0}sinh\left(2r\right)+n{g}_0.\hfill \end{array}$$

(9)

Setting the coefficient of the terms $\left({b_s^{†}}^2+b_s\right)$ to zero

$$\begin{array}{c}\hfill \left({\displaystyle \frac{{\omega }_m}{2}}+n{g}_0\right)sinh\left(2r\right)-n{g}_{0}cosh\left(2r\right)=0.\end{array}$$

(10)

Then, the squeezing parameter is obtained

$$\begin{array}{cc}\hfill r^{\left(n\right)}& ={\displaystyle \frac{1}{2}}arctanh\left({\displaystyle \frac{2n{g}_0}{{\omega }_m+2n{g}_0}}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{4}}ln(1+{\displaystyle \frac{4n{g}_0}{{\omega }_m}}).\hfill \end{array}$$

(11)

And the Hamiltonian is changed into

$$\begin{array}{cc}\hfill H_{\mathit{md}}^{\prime }=& {\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+{\omega }_m^{\left(n\right)}{b}_s^{†}{b}_s+{\mathsf{\Lambda }}_r\left({\sigma }_{+}{b}_s+b_s^{†}{\sigma }_{-}\right)-{\mathsf{\Lambda }}_c\left({\sigma }_{+}{b}_s^{†}+b_s{\sigma }_{-}\right)+{\upsilon }^{\left(n\right)},\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill & {\omega }_m^{\left(n\right)}={\omega }_m\sqrt{1+{\displaystyle \frac{4n{g}_0}{{\omega }_m}}},\hfill \\ \hfill & {\mathsf{\Lambda }}_r=\mathsf{\Lambda }cosh\left(r^{\left(n\right)}\right),\hfill \\ \hfill & {\mathsf{\Lambda }}_c=\mathsf{\Lambda }sinh\left(r^{\left(n\right)}\right),\hfill \\ \hfill & {\upsilon }^{\left(n\right)}={\displaystyle \frac{1}{2}}\left({\omega }_m^{\left(n\right)}-{\omega }_m\right).\hfill \end{array}$$

(13)

The present study investigates the eigenvalues and eigenstates of the system, under the condition that the mechanical resonator and the defect satisfy the resonant interaction criterion ${\omega }_q\approx {\omega }_m^{\left(n\right)}$. In the context of the rotating wave approximation, it was found that the Hamiltonian was reduced to the following form:

$$\begin{array}{cc}\hfill H_{\mathit{md}}^{\prime }=& {\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+{\omega }_m^{\left(n\right)}{b}_s^{†}{b}_s+{\mathsf{\Lambda }}_r\left({\sigma }_{+}{b}_s+b_s^{†}{\sigma }_{-}\right)+{\upsilon }^{\left(n\right)}\hfill \end{array}$$

(14)

We rewrite the JC Hamiltonian as

$$\begin{array}{c}\hfill H_{\mathit{md}}^{\prime }={\omega }_m^{\left(n\right)}\mathcal{M}+{\displaystyle \frac{\Delta }{2}}{\sigma }_z-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\mathsf{\Lambda }}_r\left(Q^{†}+Q\right)+{\upsilon }^{\left(n\right)},\end{array}$$

(15)

where the frequency detuning $\Delta ={\omega }_q-{\omega }_m^{\left(n\right)}$ and

$$\begin{array}{cc}\hfill & Q=b_s^{†}{\sigma }_{-}=\left(\begin{array}{cc}0& 0\\ b_s^{†}& 0\end{array}\right),Q^{†}=b_s{\sigma }_{+}=\left(\begin{array}{cc}0& b_s\\ 0& 0\end{array}\right),\hfill \\ \hfill & \mathcal{M}=b_s^{†}{b}_s+{\displaystyle \frac{1}{2}}{\sigma }_z+{\displaystyle \frac{1}{2}}=\left(\begin{array}{cc}{b}_s{b}_s^{†}& 0\\ 0& b_s^{†}{b}_s\end{array}\right),\hfill \end{array}$$

(16)

which satisfies the following relation:

$$\begin{array}{c}\hfill Q^2=Q^{†2}=0,[Q^{†},Q]=\mathcal{M}{\sigma }_z,\left\{Q,{\sigma }_z\right\}=\left\{Q^{†},{\sigma }_z\right\}=0,\\ \hfill [\mathcal{M},Q]=[\mathcal{M},Q^{†}]=0,{\left(Q^{†}-Q\right)}^2=-\mathcal{M},\left\{Q,Q^{†}\right\}=\mathcal{M}.\end{array}$$

(17)

where $\left\{\right\}$ is the anticommutator. We also note that the set $\left\{|m,e\rangle ,|m+1,g\rangle \right\}$[39,40] spans a subspace of $\mathcal{N}$ and they satisfy

$$\begin{array}{cc}\hfill & \mathcal{M}|m,e\rangle =(m+1\left)\right|m,e\rangle ,\hfill \\ \hfill & \mathcal{M}|m+1,g\rangle =(m+1\left)\right|m+1,g\rangle ,\hfill \end{array}$$

(18)

Then, the second step diagonalization of $H_{md}$ can be easily performed by introducing a supersymmetric unitary operator [41,42]

$$\begin{array}{c}\hfill \mathcal{O}\left(\theta \right)=exp\left[-{\displaystyle \frac{\theta }{2}}{\mathcal{M}}^{-1/2}(Q^{†}-Q)\right].\end{array}$$

(19)

where $\theta$ is an undetermined real number. By using Equation (17), we can expand $\mathcal{O}\left(\theta \right)$ as

$$\begin{array}{cc}\hfill \mathcal{O}\left(\theta \right)& =\sum _{k=0}^{\infty }{\displaystyle \frac{1}{\left(2k\right)!}}{\left({\displaystyle \frac{\theta }{2}}\right)}^{2k}{(-1)}^k+\sum _{k=1}^{\infty }{\displaystyle \frac{1}{(2k-1)!}}{\left(-{\displaystyle \frac{\theta }{2}}\right)}^{2k-1}{\left[{\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}\left(Q^{†}-Q\right)\right]}^{2k-1}\hfill \\ \hfill & =cos\left({\displaystyle \frac{\theta }{2}}\right)-sin\left({\displaystyle \frac{\theta }{2}}\right){\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}\left(Q^{†}-Q\right),\hfill \end{array}$$

(20)

with

$$\begin{array}{c}\hfill {\mathcal{O}}^{†}\left(\theta \right)=cos\left({\displaystyle \frac{\theta }{2}}\right)+sin\left({\displaystyle \frac{\theta }{2}}\right){\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}\left(Q^{†}-Q\right)=\mathcal{O}(-\theta ).\end{array}$$

(21)

Then, we have the following transformation:

$$\begin{array}{cc}\hfill & {\mathcal{O}}^{†}\left(\theta \right){\sigma }_z\mathcal{O}\left(\theta \right)=cos\left(\theta \right){\mathcal{M}}^{-1}\left[Q^{†},Q\right]-sin\left(\theta \right){\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}\left(Q^{†}+Q\right),\hfill \\ \hfill & {\mathcal{O}}^{†}\left(\theta \right)\left(Q^{†}+Q\right)\mathcal{O}\left(\theta \right)=cos\left(\theta \right)\left(Q^{†}+Q\right)+sin\left(\theta \right){\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}\left[Q^{†},Q\right].\hfill \end{array}$$

(22)

Based on Equation (22), we obtain

$$\begin{array}{cc}\hfill H_{\mathit{md}}^{\prime \prime }=& {\mathcal{O}}^{†}\left(\theta \right)H_{\mathit{md}}^{\prime }\mathcal{O}\left(\theta \right)={\mathcal{O}}^{†}\left(\theta \right)\left({\omega }_m^{\left(n\right)}\mathcal{M}+{\displaystyle \frac{\Delta }{2}}{\sigma }_z-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\mathsf{\Lambda }}_r\left(Q^{†}+Q\right)+{\upsilon }^{\left(n\right)}\right)\mathcal{O}\left(\theta \right)\hfill \\ \hfill =& {\omega }_m^{\left(n\right)}\mathcal{M}-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\upsilon }^{\left(n\right)}+\left({\mathsf{\Lambda }}_{r}sin\left(\theta \right)+{\displaystyle \frac{\Delta }{2}}{\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}cos\left(\theta \right)\right){\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}\left[Q^{†},Q\right]\hfill \\ \hfill & +\left({\mathsf{\Lambda }}_{r}cos\left(\theta \right)-{\displaystyle \frac{\Delta }{2}}{\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}sin\left(\theta \right)\right)\left(Q^{†}+Q\right).\hfill \end{array}$$

(23)

The last term can be eliminated by setting its coefficient to zero,

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}_{r}cos\left(\theta \right)-{\displaystyle \frac{\Delta }{2}}{\displaystyle \frac{1}{\sqrt{\mathcal{M}}}}sin\left(\theta \right)=0\end{array}$$

(24)

which can be solved by using Equation (18),

$$\begin{array}{c}\hfill {\theta }_m^{\left(n\right)}=Arctan\left({\displaystyle \frac{2{\mathsf{\Lambda }}_r\sqrt{m+1}}{\Delta }}\right)\end{array}$$

(25)

and

$$\begin{array}{c}\hfill sin\left({\theta }_m^{\left(n\right)}\right)=2{\mathsf{\Lambda }}_r\sqrt{{\displaystyle \frac{m+1}{{\Delta }^2+4(m+1){\mathsf{\Lambda }}_r^2}}},cos\left({\theta }_m^{\left(n\right)}\right)=\Delta \sqrt{{\displaystyle \frac{1}{{\Delta }^2+4(m+1){\mathsf{\Lambda }}_r^2}}}\end{array}$$

(26)

Then, Equation (23) becomes

$$\begin{array}{cc}\hfill H_{\mathit{md}}^{\prime \prime }=& {\omega }_m^{\left(n\right)}\mathcal{M}+{\displaystyle \frac{1}{2}}\left[4(m+1){\mathsf{\Lambda }}_r^2+{\Delta }^2\right]\sqrt{{\displaystyle \frac{1}{{\Delta }^2+4(m+1){\mathsf{\Lambda }}_r^2}}}{\sigma }_z-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\upsilon }^{\left(n\right)}\hfill \\ \hfill =& {\omega }_m^{\left(n\right)}\mathcal{M}+{\displaystyle \frac{\Delta }{2cos\left({\theta }_m^{\left(n\right)}\right)}}{\sigma }_z-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\upsilon }^{\left(n\right)}\hfill \end{array}$$

(27)

Obviously, $H_{\mathit{md}}^{\prime \prime }$ is a diagonalized Hamiltonian and its the eigenstate is $\left\{|m,e\rangle ,|m+1,g\rangle \right\}$ which satisfies

$$\begin{array}{cc}\hfill H_{\mathit{md}}^{\prime \prime }|m,e\rangle & ={\mathcal{O}}^{†}\left({\theta }_m^{\left(n\right)}\right)H_{\mathit{md}}^{\prime }\mathcal{O}\left({\theta }_m^{\left(n\right)}\right)|m,e\rangle =\left({\omega }_m^{\left(n\right)}(m+1)+{\displaystyle \frac{\Delta }{2cos\left({\theta }_m^{\left(n\right)}\right)}}-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\upsilon }^{\left(n\right)}\right)|m,e\rangle ,\hfill \\ \hfill H_{\mathit{md}}^{\prime \prime }|m+1,g\rangle & ={\mathcal{O}}^{†}\left({\theta }_m^{\left(n\right)}\right)H_{\mathit{md}}^{\prime }\mathcal{O}\left({\theta }_m^{\left(n\right)}\right)|m+1,g\rangle =\left({\omega }_m^{\left(n\right)}(m+1)-{\displaystyle \frac{\Delta }{2cos\left({\theta }_m^{\left(n\right)}\right)}}-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\upsilon }^{\left(n\right)}\right)|m+1,g\rangle \hfill \end{array}$$

(28)

The eigenvalue of $H_{\mathit{md}}^{\prime }$ is also

$$\begin{array}{c}\hfill E_{m\pm }\left(n\right)={\omega }_m^{\left(n\right)}(m+1)\pm {\displaystyle \frac{\Delta }{2cos\left({\theta }_m^{\left(n\right)}\right)}}-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\upsilon }^{\left(n\right)}\end{array}$$

(29)

with its associated eigenstate

$$\begin{array}{cc}\hfill & |{\nu }_m\left(n\right)\rangle =\mathcal{O}\left({\theta }_m^{\left(n\right)}\right)|m,e\rangle =cos\left({\displaystyle \frac{{\theta }_m^{\left(n\right)}}{2}}\right)|m,e\rangle +sin\left({\displaystyle \frac{{\theta }_m^{\left(n\right)}}{2}}\right)|m+1,g\rangle ,\hfill \\ \hfill & |{\mu }_m\left(n\right)\rangle =\mathcal{O}\left({\theta }_m^{\left(n\right)}\right)|m+1,g\rangle =cos\left({\displaystyle \frac{{\theta }_m^{\left(n\right)}}{2}}\right)|m+1,g\rangle -sin\left({\displaystyle \frac{{\theta }_m^{\left(n\right)}}{2}}\right)|m,e\rangle \hfill \end{array}$$

(30)

Therefore, the eigenvalue of $H_0$ is obtained,

$$\begin{array}{c}\hfill E_{nm\pm }=n{\omega }_c+{\omega }_m^{\left(n\right)}(m+1)\pm {\displaystyle \frac{\Delta }{2cos\left({\theta }_m^{\left(n\right)}\right)}}-{\displaystyle \frac{{\omega }_m^{\left(n\right)}}{2}}+{\upsilon }^{\left(n\right)},\end{array}$$

(31)

with its associated eigenstate

$$\begin{array}{cc}\hfill & |{\tilde{\nu }}_m\left(n\right)\rangle |n\rangle =S\left({\eta }^{\left(n\right)}\right)\mathcal{O}\left({\theta }_m^{\left(n\right)}\right)|m,e\rangle |n\rangle =cos\left({\displaystyle \frac{{\theta }_m^{\left(n\right)}}{2}}\right)S\left({\eta }^{\left(n\right)}\right)|m,e\rangle |n\rangle +sin\left({\displaystyle \frac{{\theta }_m^{\left(n\right)}}{2}}\right)S\left({\eta }^{\left(n\right)}\right)|m+1,g\rangle |n\rangle ,\hfill \\ \hfill & |{\tilde{\mu }}_m\left(n\right)\rangle |n\rangle =S\left({\eta }^{\left(n\right)}\right)\mathcal{O}\left({\theta }_m^{\left(n\right)}\right)|m+1,g\rangle |n\rangle =cos\left({\displaystyle \frac{{\theta }_m^{\left(n\right)}}{2}}\right)S\left({\eta }^{\left(n\right)}\right)|m+1,g\rangle |n\rangle -sin\left({\displaystyle \frac{{\theta }_m^{\left(n\right)}}{2}}\right)S\left({\eta }^{\left(n\right)}\right)|m,e\rangle |n\rangle .\hfill \end{array}$$

(32)

According to the above discussion, it is feasible to articulate a generic status of the system, as follows:

$$\begin{array}{c}\hfill |\phi \left(t\right)\rangle =\sum _{n=0}^{\infty }\sum _{m=0}^{\infty }{C}_{n,m}^{\nu }\left(t\right)|{\tilde{\nu }}_m\left(n\right)\rangle |n\rangle +C_{n,m}^{\mu }\left(t\right)|{\tilde{\mu }}_m\left(n\right)\rangle |n\rangle ,\end{array}$$

(33)

where $C_{n,m}^{\nu }$ and $C_{n,m}^{\mu }$ are the probability amplitude.

3. Analytical Solution of the Second-Order Photon Correlation

Under the weak-driving condition $\mathsf{\Omega }\ll {\gamma }_a$, where the external drive strength $\mathsf{\Omega }$ is much smaller than the cavity decay rate ${\gamma }_a$, the cavity field remains weakly excited with a low photon population. This allows us to truncate the Hilbert space to the lowest few photon-number states $|0\rangle$, $|1\rangle$, and $|2\rangle$ for calculating the second-order correlation function. Consequently, the system’s state $|\phi \left(t\right)\rangle$ can be effectively approximated within this subspace. The specific expressions are as follows:

$$\begin{array}{c}\hfill |\phi \left(t\right)\rangle =\sum _{n=0}^2\sum _{m=0}^{\infty }{C}_{n,m}^{\nu }\left(t\right)|{\tilde{\nu }}_m\left(n\right)\rangle |n\rangle +C_{n,m}^{\mu }\left(t\right)|{\tilde{\mu }}_m\left(n\right)\rangle |n\rangle .\end{array}$$

(34)

The single and two-photon probability, respectively, are

$$\begin{array}{c}\hfill P_1={\displaystyle \frac{1}{N}}\langle \phi \left(t\right)\left|\right|1\rangle \langle 1\left|\right|\phi \left(t\right)\rangle ={\displaystyle \frac{1}{N}}\sum _{m=0}^{\infty }\left({\left|C_{1,m}^{\nu }\left(t\right)\right|}^2+{\left|C_{1,m}^{\mu }\left(t\right)\right|}^2\right),\end{array}$$

(35)

$$\begin{array}{c}\hfill P_2={\displaystyle \frac{1}{N}}\langle \phi \left(t\right)\left|\right|2\rangle \langle 2\left|\right|\phi \left(t\right)\rangle ={\displaystyle \frac{1}{N}}\sum _{m=0}^{\infty }\left({\left|C_{2,m}^{\nu }\left(t\right)\right|}^2+{\left|C_{2,m}^{\mu }\left(t\right)\right|}^2\right),\end{array}$$

(36)

and

$$\begin{array}{c}\hfill N=\sum _{m=0}^{\infty }\left({\left|C_{0,m}^{\nu }\left(t\right)\right|}^2+{\left|C_{0,m}^{\mu }\left(t\right)\right|}^2\right)+\sum _{m=0}^{\infty }\left({\left|C_{1,m}^{\nu }\left(t\right)\right|}^2+{\left|C_{1,m}^{\mu }\left(t\right)\right|}^2\right)+\sum _{m=0}^{\infty }\left({\left|C_{2,m}^{\nu }\left(t\right)\right|}^2+{\left|C_{2,m}^{\mu }\left(t\right)\right|}^2\right).\end{array}$$

(37)

The second-order correlation function is

$$\begin{array}{c}\hfill g^{\left(2\right)}\left(0\right)={\displaystyle \frac{\langle a^{†}{a}^{†}aa\rangle }{{\langle a^{†}a\rangle }^2}}={\displaystyle \frac{\langle a^{†}(a{a}^{†}-1)a\rangle }{{\langle a^{†}a\rangle }^2}}={\displaystyle \frac{\langle a^{†}a{a}^{†}a\rangle -\langle a^{†}a\rangle }{{\langle a^{†}a\rangle }^2}},\end{array}$$

(38)

Since,

$$\begin{array}{cc}\hfill & \langle a^{†}a\rangle =P_1+2P_2,\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & \langle a^{†}a{a}^{†}a\rangle =P_1+4P_2,\hfill \end{array}$$

(40)

then,

$$\begin{array}{c}\hfill g^{\left(2\right)}\left(0\right)={\displaystyle \frac{2P_2}{{(P_1+2P_2)}^2}}.\end{array}$$

(41)

In the following, we calculate the photon correlation. The non-Hermitian Hamiltonian, when including the external optical driving and dissipation of the cavity, takes the following form:

$$\begin{array}{c}\hfill H_t=H_0+\mathsf{\Omega }(a^{†}{e}^{-i{\omega }_d}+a{e}^{i{\omega }_d})-i{\displaystyle \frac{{\gamma }_a}{2}}{a}^{†}a.\end{array}$$

(42)

In terms of the Schrödinger equation, i.e., $i{\displaystyle \frac{d\left|\phi \left(t\right)\right.〉}{dt}}=H_t\left|\phi \left(t\right)\right.〉$, and the completeness of the eigenstate, i.e.,

$$\begin{array}{c}\hfill \sum _{n=0}^2\sum _{m=0}^{\infty }|{\tilde{\nu }}_m\left(n\right)\rangle |n\rangle \langle n|\langle {\tilde{\nu }}_m\left(n\right)|+|{\tilde{\mu }}_m\left(n\right)\rangle |n\rangle \langle n|\langle {\tilde{\mu }}_m\left(n\right)|=\mathbf{I}.\end{array}$$

(43)

Then, we can obtain the equation of the motion of the probability amplitude

$$\begin{array}{cc}\hfill & {\dot{C}}_{0,m}^{\nu }\left(t\right)=-i{E}_{0m+}{C}_{0,m}^{\nu }\left(t\right)-i\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\nu }}_m\left(0\right)|{\tilde{\nu }}_{m^{\prime }}\left(1\right)\rangle C_{1,m^{\prime }}^{\nu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{0,m}^{\mu }\left(t\right)=-i{E}_{0m-}{C}_{0,m}^{\mu }\left(t\right)-i\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\mu }}_m\left(0\right)|{\tilde{\mu }}_{m^{\prime }}\left(1\right)\rangle C_{1,m^{\prime }}^{\mu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{1,m}^{\nu }\left(t\right)=-i\left(E_{1m+}-{\displaystyle \frac{{\gamma }_a}{2}}\right)C_{1,m}^{\nu }\left(t\right)-i\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\nu }}_m\left(1\right)|{\tilde{\nu }}_{m^{\prime }}\left(0\right)\rangle C_{0,m^{\prime }}^{\nu }\left(t\right)-i\sqrt{2}\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\nu }}_m\left(1\right)|{\tilde{\nu }}_{m^{\prime }}\left(2\right)\rangle C_{2,m^{\prime }}^{\nu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{1,m}^{\mu }\left(t\right)=-i\left(E_{1m-}-{\displaystyle \frac{{\gamma }_a}{2}}\right)C_{1,m}^{\mu }\left(t\right)-i\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\mu }}_m\left(1\right)|{\tilde{\mu }}_{m^{\prime }}\left(0\right)\rangle C_{0,m^{\prime }}^{\mu }\left(t\right)-i\sqrt{2}\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\mu }}_m\left(1\right)|{\tilde{\mu }}_{m^{\prime }}\left(2\right)\rangle C_{2,m^{\prime }}^{\mu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{2,m}^{\nu }\left(t\right)=-i\left(E_{2m+}-{\gamma }_a\right)C_{2,m}^{\nu }\left(t\right)-i\sqrt{2}\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\nu }}_m\left(2\right)|{\tilde{\nu }}_{m^{\prime }}\left(1\right)\rangle C_{1,m^{\prime }}^{\nu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{2,m}^{\mu }\left(t\right)=-i\left(E_{2m-}-{\gamma }_a\right)C_{2,m}^{\mu }\left(t\right)-i\sqrt{2}\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\mu }}_m\left(2\right)|{\tilde{\mu }}_{m^{\prime }}\left(1\right)\rangle C_{1,m^{\prime }}^{\mu }\left(t\right).\hfill \end{array}$$

(44)

Only a few photons are excited in the cavity by a weak external drive. Thus, the higher-order terms in the zero-photon, one-photon, and two-photon probability amplitudes are systematically excluded from consideration. We merely retain the terms of the same order of magnitude. Approximately, the quantum superposition coefficients of the few-photon states can be simplified to the following form:

$$\begin{array}{cc}\hfill & {\dot{C}}_{0,m}^{\nu }\left(t\right)\approx -i{E}_{0m+}{C}_{0,m}^{\nu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{0,m}^{\mu }\left(t\right)\approx -i{E}_{0m-}{C}_{0,m}^{\mu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{1,m}^{\nu }\left(t\right)\approx -i\left(E_{1m+}-{\displaystyle \frac{{\gamma }_a}{2}}\right)C_{1,m}^{\nu }\left(t\right)-i\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\nu }}_m\left(1\right)|{\tilde{\nu }}_{m^{\prime }}\left(0\right)\rangle C_{0,m^{\prime }}^{\nu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{1,m}^{\mu }\left(t\right)\approx -i\left(E_{1m-}-{\displaystyle \frac{{\gamma }_a}{2}}\right)C_{1,m}^{\mu }\left(t\right)-i\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\mu }}_m\left(1\right)|{\tilde{\mu }}_{m^{\prime }}\left(0\right)\rangle C_{0,m^{\prime }}^{\mu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{2,m}^{\nu }\left(t\right)\approx -i\left(E_{2m+}-{\gamma }_a\right)C_{2,m}^{\nu }\left(t\right)-i\sqrt{2}\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\nu }}_m\left(2\right)|{\tilde{\nu }}_{m^{\prime }}\left(1\right)\rangle C_{1,m^{\prime }}^{\nu }\left(t\right),\hfill \\ \hfill & {\dot{C}}_{2,m}^{\mu }\left(t\right)\approx -i\left(E_{2m-}-{\gamma }_a\right)C_{2,m}^{\mu }\left(t\right)-i\sqrt{2}\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }\langle {\tilde{\mu }}_m\left(2\right)|{\tilde{\mu }}_{m^{\prime }}\left(1\right)\rangle C_{1,m^{\prime }}^{\mu }\left(t\right).\hfill \end{array}$$

(45)

Note that the solution of the Linear Differential Equation ${\displaystyle \frac{dy}{dx}}+P\left(x\right)y=Q\left(x\right)$ takes the form

$$\begin{array}{c}\hfill y=e^{-\int P\left(x\right)dx}\left(\int Q\left(x\right)e^{\int P\left(x\right)dx}dx+C\right)\end{array}$$

(46)

For simplicity, we assume that the initial excitation number of both the cavity and the membrane are zero. Initially, the system is in a pair of dressed states $|{\nu }_0\left(0\right)\rangle \mathrm{and}|{\mu }_0\left(0\right)\rangle$ and

$$\begin{array}{cc}\hfill & C_{0,m}^{\nu }\left(0\right)=C_{0,m}^{\mu }\left(0\right)={\delta }_{m,0},\hfill \\ \hfill & C_{1,m}^{\nu }\left(0\right)=C_{1,m}^{\mu }\left(0\right)=0,\hfill \\ \hfill & C_{2,m}^{\nu }\left(0\right)=C_{2,m}^{\mu }\left(0\right)=0.\hfill \end{array}$$

(47)

So far, under this assumption, the quantum superposition coefficients of the system wave function in few-photon subspace can be approximated as follows:

$$\begin{array}{cc}\hfill C_{0,m}^{\nu }\left(t\right)& \approx C_{0,m}^{\nu }\left(0\right)e^{-i{E}_{0m+}t}={\delta }_{m,0}{e}^{-i{E}_{0m+}t},\hfill \\ \hfill C_{0,m}^{\mu }\left(t\right)& \approx C_{0,m}^{\mu }\left(0\right)e^{-i{E}_{0m-}t}={\delta }_{m,0}{e}^{-i{E}_{0m+}t},\hfill \\ \hfill C_{1,m}^{\nu }\left(t\right)& \approx -i\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }{\displaystyle \frac{\langle {\tilde{\nu }}_m\left(1\right)|{\tilde{\nu }}_{m^{\prime }}\left(0\right)\rangle C_{0,m^{\prime }}^{\nu }\left(0\right)e^{-i{E}_{0m^{\prime }+}t}}{i\left(E_{1m+}-E_{0m^{\prime }+}\right)-{\displaystyle \frac{{\gamma }_a}{2}}}}=-i\mathsf{\Omega }{\displaystyle \frac{\langle {\tilde{\nu }}_m\left(1\right)|{\tilde{\nu }}_0\left(0\right)\rangle e^{-i{E}_{00+}t}}{i\left(E_{1m+}-E_{00+}\right)-{\displaystyle \frac{{\gamma }_a}{2}}}},\hfill \\ \hfill C_{1,m}^{\mu }\left(t\right)& \approx -i\mathsf{\Omega }\sum _{m^{\prime }=0}^{\infty }{\displaystyle \frac{\langle {\tilde{\mu }}_m\left(1\right)|{\tilde{\mu }}_{m^{\prime }}\left(0\right)\rangle C_{0,m^{\prime }}^{\mu }\left(0\right)e^{-i{E}_{0m^{\prime }-}t}}{i\left(E_{1m-}-E_{0m^{\prime }-}\right)-{\displaystyle \frac{{\gamma }_a}{2}}}}=-i\mathsf{\Omega }{\displaystyle \frac{\langle {\tilde{\mu }}_m\left(1\right)|{\tilde{\mu }}_0\left(0\right)\rangle e^{-i{E}_{00-}t}}{i\left(E_{1m-}-E_{00-}\right)-{\displaystyle \frac{{\gamma }_a}{2}}}},\hfill \\ \hfill C_{2,m}^{\nu }\left(t\right)& \approx -\sqrt{2}{\mathsf{\Omega }}^2\sum _{k=0}^{\infty }\sum _{k^{\prime }=0}^{\infty }{\displaystyle \frac{\langle {\tilde{\nu }}_m\left(2\right)|{\tilde{\nu }}_k\left(1\right)\rangle }{i\left(E_{2m+}-E_{0k^{\prime }+}\right)-{\gamma }_a}}\times {\displaystyle \frac{\langle {\tilde{\nu }}_k\left(1\right)|{\tilde{\nu }}_{k^{\prime }}\left(0\right)\rangle C_{0,k^{\prime }}^{\nu }{e}^{-i{E}_{0k^{\prime }+}t}}{i\left(E_{1m+}-E_{0k^{\prime }+}\right)-{\displaystyle \frac{{\gamma }_a}{2}}}}\hfill \\ \hfill & =-\sqrt{2}{\mathsf{\Omega }}^2\sum _{k=0}^{\infty }{\displaystyle \frac{\langle {\tilde{\nu }}_m\left(2\right)|{\tilde{\nu }}_k\left(1\right)\rangle \langle {\tilde{\nu }}_k\left(1\right)|{\tilde{\nu }}_0\left(0\right)\rangle e^{-i{E}_{00+}t}}{\left[i\left(E_{2m+}-E_{00+}\right)-{\gamma }_a\right]\left[i\left(E_{1m+}-E_{00+}\right)-{\gamma }_a/2\right]}},\hfill \\ \hfill C_{2,m}^{\mu }\left(t\right)& \approx -\sqrt{2}{\mathsf{\Omega }}^2\sum _{k=0}^{\infty }\sum _{k^{\prime }=0}^{\infty }{\displaystyle \frac{\langle {\tilde{\mu }}_m\left(2\right)|{\tilde{\mu }}_k\left(1\right)\rangle }{i\left(E_{2m-}-E_{0k^{\prime }-}\right)-{\gamma }_a}}\times {\displaystyle \frac{\langle {\tilde{\mu }}_k\left(1\right)|{\tilde{\mu }}_{k^{\prime }}\left(0\right)\rangle C_{0,k^{\prime }}^{\mu }{e}^{-i{E}_{0k^{\prime }-}t}}{i\left(E_{1m-}-E_{0k^{\prime }-}\right)-{\displaystyle \frac{{\gamma }_a}{2}}}}\hfill \\ \hfill & =-\sqrt{2}{\mathsf{\Omega }}^2\sum _{k=0}^{\infty }{\displaystyle \frac{\langle {\tilde{\mu }}_m\left(2\right)|{\tilde{\mu }}_k\left(1\right)\rangle \langle {\tilde{\mu }}_k\left(1\right)|{\tilde{\mu }}_0\left(0\right)\rangle e^{-i{E}_{00-}t}}{\left[i\left(E_{2m-}-E_{00-}\right)-{\gamma }_a\right]\left[i\left(E_{1m-}-E_{00-}\right)-{\gamma }_a/2\right]}}.\hfill \end{array}$$

(48)

With the help of the following expansion,

$$\begin{array}{cc}\hfill & {\omega }_m^{\left(n\right)}={\omega }_m\sqrt{1+{\displaystyle \frac{4n{g}_0}{{\omega }_m}}}\approx {\omega }_m\left(1+{\displaystyle \frac{2n{g}_0}{{\omega }_m}}\right),\hfill \\ \hfill & {\eta }^{\left(n\right)}=r^{\left(n\right)}={\displaystyle \frac{1}{4}}ln\left(1+{\displaystyle \frac{4n{g}_0}{{\omega }_m}}\right)\approx {\displaystyle \frac{n{g}_0}{{\omega }_m}},\hfill \\ \hfill & S\left({\eta }^{\left(n\right)}\right)=exp\left[{\displaystyle \frac{{\eta }^{\left(n\right)}}{2}}\left(b^2-b^{†2}\right)\right]\approx 1+{\displaystyle \frac{{\eta }^{\left(n\right)}}{2}}\left(b^2-b^{†2}\right),\hfill \\ \hfill & {\upsilon }^{\left(n\right)}={\displaystyle \frac{1}{2}}\left({\omega }_m^{\left(n\right)}-{\omega }_m\right)\approx n{g}_0,\hfill \\ \hfill & {\displaystyle \frac{1}{cos\left({\theta }_m^{\left(n\right)}\right)}}\approx \sqrt{1+{\displaystyle \frac{(4m+1){\mathsf{\Lambda }}^2}{{\Delta }^2}}}.\hfill \end{array}$$

(49)

The results of the inner products such as $\langle {\tilde{\nu }}_m\left(1\right)|{\tilde{\nu }}_0\left(0\right)\rangle$, $\langle {\tilde{\mu }}_m\left(1\right)|{\tilde{\mu }}_0\left(0\right)\rangle$, $\langle {\tilde{\nu }}_m\left(2\right)|{\tilde{\nu }}_k\left(1\right)\rangle$, and $\langle {\tilde{\mu }}_m\left(2\right)|{\tilde{\mu }}_k\left(1\right)\rangle$ are shown in the Appendix A. For a weak driving, $P_1\gg P_2$, the second-order correlation function can be approximated as

$$\begin{array}{c}\hfill g^{\left(2\right)}\left(0\right)\approx {\displaystyle \frac{2P_2}{P_1^2}}.\end{array}$$

(50)

We may finally arrive at a long-time approximate analytical second-order correlation function for the few-photon state $\left|\phi \right(t)\rangle$.

4. Numerical Solution of the Second-Order Photon Correlation

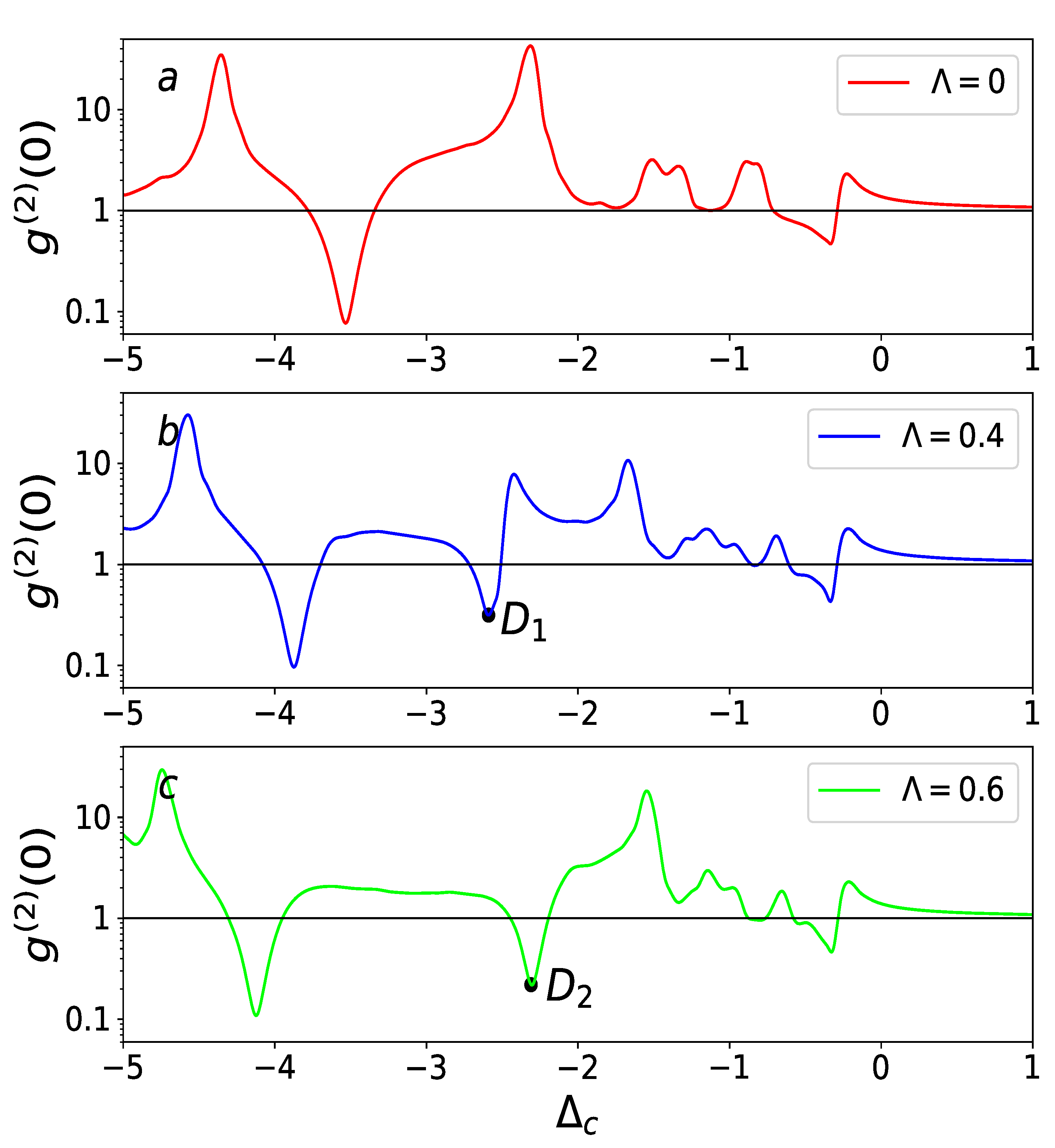
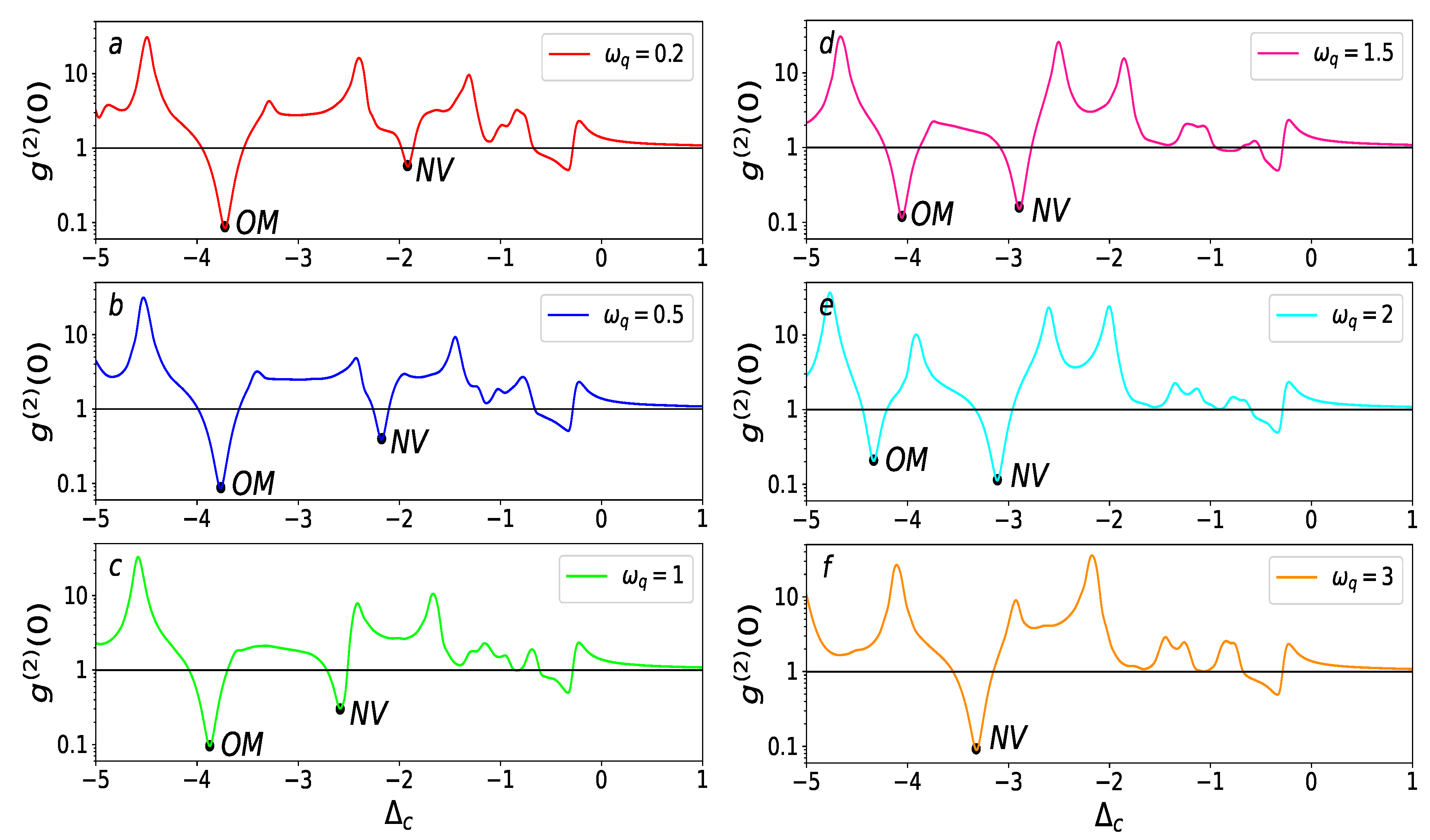
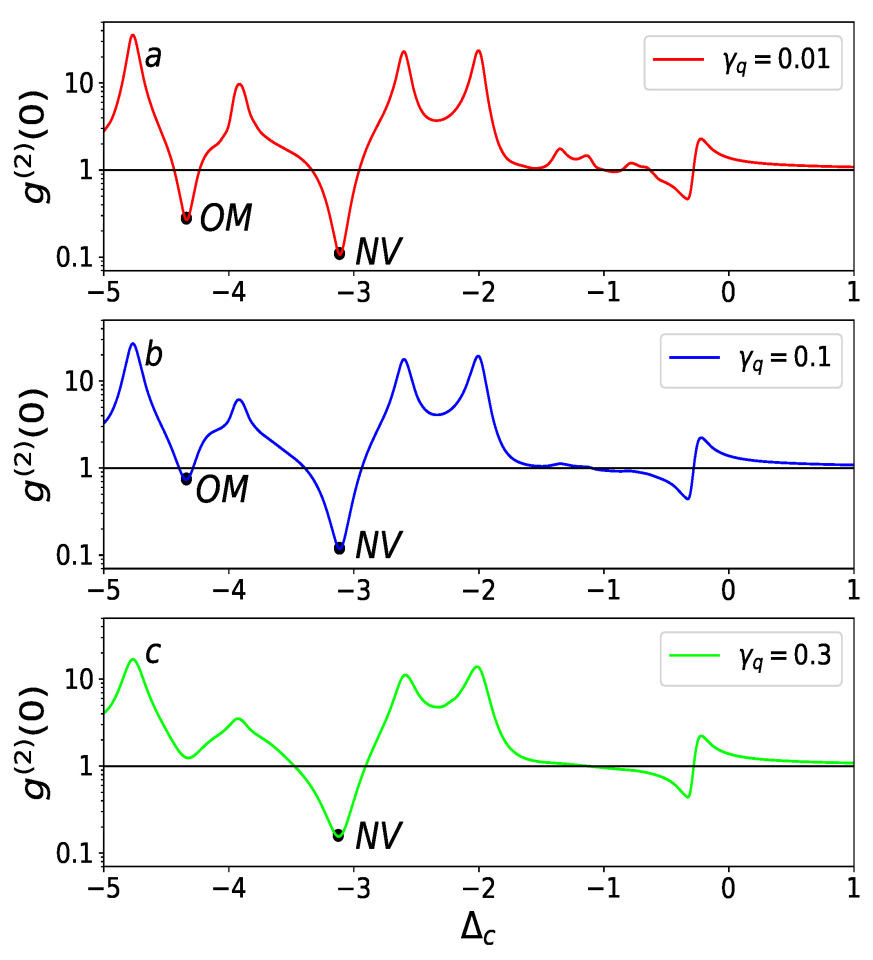
4.1. Detection of a Defect via the Second-Order Correlation Function

To study the photon blockade, a classical field with frequency ${\omega }_d$ and amplitude $\mathsf{\Omega }$ is applied to drive the cavity. The Hamiltonian of the system, in a frame rotating at frequency ${\omega }_d$, can be written as

$$\begin{array}{c}\hfill H_r={\Delta }_c{a}^{†}a+{\omega }_m{b}^{†}b+{\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+g_0{a}^{†}a{\left(b^{†}+b\right)}^2+\mathsf{\Lambda }\left(b^{†}{\sigma }_{-}+{\sigma }_{+}b\right)+i\mathsf{\Omega }\left(a^{†}-a\right).\end{array}$$

(51)

where ${\Delta }_c={\omega }_c-{\omega }_d$ represents the detuning between the external driving filed and the cavity field. Subsequent to the introduction of the environmental noise, the master equation of the density operator, denoted by $\rho$, for the driven hybrid system can be expressed as follows:

$$\begin{array}{c}\hfill \dot{\rho }=i\left[\rho ,H_r\right]+{\mathcal{L}}_a\left(\rho \right)+{\mathcal{L}}_b\left(\rho \right)+{\mathcal{L}}_{\sigma }\left(\rho \right),\end{array}$$

(52)

The Lindblad dissipators for the optical mode of the cavity field and the mechanical mode of the nano-diamond membrane are given by

$$\begin{array}{c}\hfill {\mathcal{L}}_o\left(\rho \right)={\displaystyle \frac{{\gamma }_o}{2}}(n_o+1)\left(2o\rho o^{†}-o^{†}o\rho -\rho o^{†}o\right)+{\displaystyle \frac{{\gamma }_o}{2}}{n}_o\left(2o^{†}\rho o-o{o}^{†}\rho -\rho o{o}^{†}\right),\end{array}$$

(53)

where $o=a\mathrm{or}b$ corresponds to the optical mode or mechanical mode annihilation operator, respectively. The Lindblad dissipator for a two-level system is expressed as

$$\begin{array}{c}\hfill {\mathcal{L}}_{\sigma }\left(\rho \right)={\displaystyle \frac{{\gamma }_q}{2}}(n_q+1)\left(2{\sigma }_{-}\rho {\sigma }_{+}-{\sigma }_{+}{\sigma }_{-}\rho -\rho {\sigma }_{+}{\sigma }_{-}\right)+{\displaystyle \frac{{\gamma }_q}{2}}{n}_q\left(2{\sigma }_{+}\rho {\sigma }_{-}-{\sigma }_{-}{\sigma }_{+}\rho -\rho {\sigma }_{-}{\sigma }_{+}\right).\end{array}$$

(54)

The second-order correlation function is calculated through the master equation in Equation (52). In practice, we employed the QuTiP [43,44] to solve the quantum master equations and obtain the results of the second-order correlation function. Figure 2 presents the dependence of $g^{\left(2\right)}\left(0\right)$ on ${\Delta }_c$. The different panels correspond to varying coupling strengths $\mathsf{\Lambda }$ between the diamond membrane mechanical mode and an NV center. To further examine how photon blockade can detect defects in the mechanical membrane, we compare numerical results of $g^{\left(2\right)}\left(0\right)$ with (blue and green curves) and without (red curve) the NV-membrane coupling. In Figure 2a, the red curve shows a minimum $g^{\left(2\right)}\left(0\right)<1$ near $-4<{\Delta }_c<-3$, indicating a photon blockade. However, for $-3<{\Delta }_c<-2$, $g^{\left(2\right)}\left(0\right)$ exceeds unity. The influence of an NV center becomes apparent in Figure 2b (blue curve), where its coupling modifies the photon blockade behavior compared to the uncoupled case (red curve in Figure 2a). Here, a new blockade dip $D_1$ ($g^{\left(2\right)}\left(0\right)<1$) emerges. When $\mathsf{\Lambda }$ increases, an NV center induces a stronger photon blockade effect, as seen in Figure 2c (green curve), where the dip $D_2$ becomes deeper $\left(D_2<D_1\right)$. These results demonstrate that an NV center not only introduces additional photon blockade regimes but also alters their strength. Therefore, the appearance of new blockade features can serve as an indicator of defects in the mechanical membrane.

As illustrated in Figure 3, the transition frequency of an NV center exerts a significant influence on the photon blockade within the hybrid system. The blue curve in Figure 3c illustrates the function $g^{\left(2\right)}\left(0\right)$ when the mechanical resonator interacts resonantly with a NV center, while the other subgraph corresponds to the detuning cases. Combined with the Figure 2, the NV dip of the second order correlation function with detuning between $-2$ and $-3$ is induced by the coupling of the NV center to the membrane. The OM dip with detuning between $-3$ and $-4$ is induced by the quadratically coupling between the cavity optical mode and the nano-diamond membrane mechanical mode. First, one can easily find that the NV dip will be enhanced in Figure 3a–f when the NV center transition frequency increases. Second, the OM dip remains almost constant in Figure 3a–c when ${\omega }_q/{\omega }_m\le 1$. However, the OM dip induced by the quadratic optomechanical coupling diminishes Figure 3d,e or even disappears in the orange curve of Figure 3f when ${\omega }_q/{\omega }_m>1$. So, the ratio of the depth of the NV dip to the OM dip can determine the extent of the effect of the defect.

The impact of the decay rate ${\gamma }_q$ on the photon blockade in the optomechanical system is illustrated in Figure 4. The NV dip is almost invariant when the value of ${\gamma }_q$ becomes larger. However, the OM dip changes significantly. As the decay rate ${\gamma }_q$ increases further, the OM dip will also vanish [see the green curve in Figure 4c]. For sufficiently high decay rates, the NV dip induced by the NV center vanishes. This suggests that the decay of the NV center has a greater effect on OM blockade than NV blockade. Thus, in conjunction with Figure 2, the appearance of NV blockade and the disappearance of OM blockade can be used to confirm the presence of a defect in the mechanical membrane.

4.2. Amplification of a Defect via Newtonian Gravity

The gravitational potential of a mechanical membrane can be introduced into the Hamiltonian $H_0$ by means of the tilting of the system [20,45]. The gravitational potential term of the mechanical membrane can be expressed as

$$H_g=xmgcos\theta .$$

(55)

In the given context, the position operator is defined as $x=(b+b^{†})/\sqrt{2m{\omega }_m}$ in our situation, where m is the mass of the mechanical membrane, $\theta$ is an angle from the horizontal axis, and g is the gravitational acceleration. When the gravitational potential from the Newtonian gravity is taken into account, the total Hamiltonian of the system is

$$\begin{array}{cc}\hfill H_{tot}& =H_r+H_g\hfill \\ \hfill & ={\Delta }_c{a}^{†}a+{\omega }_m{b}^{†}b+{\displaystyle \frac{{\omega }_q}{2}}{\sigma }_z+g_0{a}^{†}a{\left(b^{†}+b\right)}^2+\mathsf{\Lambda }\left(b^{†}{\sigma }_{-}+{\sigma }_{+}b\right)+i\mathsf{\Omega }\left(a^{†}-a\right)+g^{\prime }(b+b^{†}).\hfill \end{array}$$

(56)

The effective gravity coupling is given by $g^{\prime }=gcos\theta \sqrt{m/2{\omega }_m}$, while the sine component of the gravity remains dynamically irrelevant for the quadratic optomechanical coupling direction [46].

Following the introduction of the environmental noise, the master equation of the density operator $\rho$ for the dual-driven hybrid system $H_{tot}$ can be expressed as follows:

$$\begin{array}{c}\hfill \dot{\rho }=i\left[\rho ,H_{tot}\right]+{\mathcal{L}}_a\left(\rho \right)+{\mathcal{L}}_b\left(\rho \right)+{\mathcal{L}}_{\sigma }\left(\rho \right),\end{array}$$

(57)

where the form of the Lindblad dissipators for photons, phonons, and NV center can be seen in Equation (53) and Equation (54).

Figure 5 presents the influence of the gravitational potential on the NV dip, displaying $g^{\left(2\right)}\left(0\right)$ as a function of ${\Delta }_c$ calculated using the master equation in Equation (57). Each panel corresponds to different coupling strengths $g^{\prime }$ between the nano-diamond membrane and the Newtonian gravity. To better understand the influence of the Newtonian gravity on the detection of defect in the mechanical membrane, using the master equation in Equation (57), we compare the numerical results of $g^{\left(2\right)}\left(0\right)$ with (blue and green curves) and without (red curve) the gravity–membrane coupling.

The NV dip in Figure 5a is near 1. The depth of this NV dip is not very obvious. This means that it is not easy to detect a defect when the transition frequency of the NV center is small by simply observing the newly emerged photon blockade point. However, we find that we can take tilt the whole system to deepen the NV dip. The tilting of the system causes the mechanical membrane to couple with gravity. Gravity coupling can be considered as direct current phonon driving. Next, the entire system is driven through photon and phonon. We find that the NVG dip Figure 5b,c is much smaller than 1 and relatively obvious from the figure. At the same time, the value of NVG dip is smaller than the NV dip Figure 5a. This means that gravity coupling can amplify the effects of a defect through enhancing the photon blockade.

The physical mechanism behind this may be due to the fact that the tilting of the system can increase the flexion of the diamond membrane. This will further strain the diamond lattice. An NV center is embedded in a single-crystal diamond nanomembrane. Thus, the gravitational potential introduced after tilting the system increases the coupling of an NV center to the mechanical membrane.

This paper presents a dual-coupled optomechanical system consisting of a quadratic optomechanical system featuring a nano-diamond membrane with spin–spin interactions. The parameters of the quadratic optomechanical system described in this paper are experimentally feasible. The strength of the spin–spin interaction between the nano-diamond membrane and an NV center embedded in the nano-diamond membrane is much smaller than that of the quadratic optomechanical coupling in the current experiments. In this paper, we made the assumption that the strength of the spin–spin interaction was approximately equal to the quadratic optomechanical coupling. We did this to make sure that the computational results demonstrated clear effects. Thus, the research content of this paper is only theoretical at the moment. We expect that advances in the future will increase the tunability range for both photon–phonon and phonon–spin couplings.

5. Conclusions

We have presented a hybrid quadratic optomechanical system consisting of a Fabry–Pérot optical cavity, diamond nanomembrane, and a NV center. This NV center is embedded in a single-crystal diamond nanomembrane. Optical radiation pressure flexes the diamond nanomembrane. The flex of the diamond nanomembrane strains the diamond lattice, which in turn leads to a Jaynes–Cummings-type interaction between the NV center and single-crystal diamond nanomembrane. Thus, the single-crystal diamond nanomembrane is involved in both types of interactions. The application of a squeezing and supersymmetric unitary transformation enabled the determination of the eigenvalues and eigenstates of the dual-coupling optomechanical system. This approach differs from prior optomechanical studies that focused solely on single coupling mechanisms. Subsequently, the external optical driving term was considered as a perturbation to ascertain the approximate analytical expression of the steady states of the entire system. The advantage of this methodology is that it bridges photonic, phononic, and spin degrees of freedom, offering a unified platform to probe defect-induced perturbations. Finally, a numerical calculation of the second-order correlation function of the photon distribution for the cavity photons was conducted. This was undertaken in the context of considering dissipation.

The presence of a defect in a nano-diamond membrane can be detected through photon blockade effects, as the NV center’s coupling to the mechanical membrane significantly modifies the photon blockade characteristics of the optomechanical device. Compared to a bare quadratic optomechanical system, incorporating an NV center in the nanomembrane introduces modifications and creates new minima in the cavity field’s second-order correlation function. These effects become particularly pronounced when the NV–membrane coupling strength increases. The physical mechanism responsible for the observed phenomena is as follows: an NV center present within a nano-diamond membrane will modify the energy level structure of the optical microcavity through indirect interactions. We also found that an NV center can even suppress the OM dip, which is induced by the quadratic optomechanical coupling, when the transition frequency and decay rate of the NV center are greater. Thus, we can determine the presence of a defect on a membrane with the help of the effect of the NV center on photon blockade. Finally, it is worth noting that the effect of the NV center on photon blockade can be amplified by tilting the system. That is, our study may provide a new method to detect a NV center, which might be a defect in a mechanical membrane, using optomechanics.