Degenerate Appell Polynomials Connecting Beta Function as a Family of Operators and Their Approximations
Abstract
1. Overview and Foundations
1.1. Positivity of the Operators
- The generating function is analytic with
- The degenerate Appell polynomials are non-negative for and
- The parameter ƛ is chosen such that
- since all components are non-negative
- The Beta kernel for
- For any non-negative function , the integral
1.2. Recent Developments and Motivation
1.3. Role of the Parameter ƛ
- It affects the moment estimates, as seen in Lemma 1, where terms involving ƛ appear in the expansions.
- It modifies the asymptotic behavior in the Voronovskaja-type theorem (Theorem 4).
- It provides an additional degree of freedom for optimizing approximation properties for specific applications.
1.4. Function Spaces and Definitions
- denotes the space of all real-valued continuous functions on .
- is the space of bounded continuous functions.
- is the space of functions with quadratic growth.
- is continuous}.
- .
2. Preliminary Results
3. Main Results
3.1. Uniform Convergence via Korovkin’s Theorem
3.2. Direct Estimates of the Rate of Convergence
3.3. Asymptotic Behavior: A Voronovskaja-Type Theorem
4. Numerical and Graphical Analysis
4.1. Numerical Tables
4.2. Convergence Rate Analysis
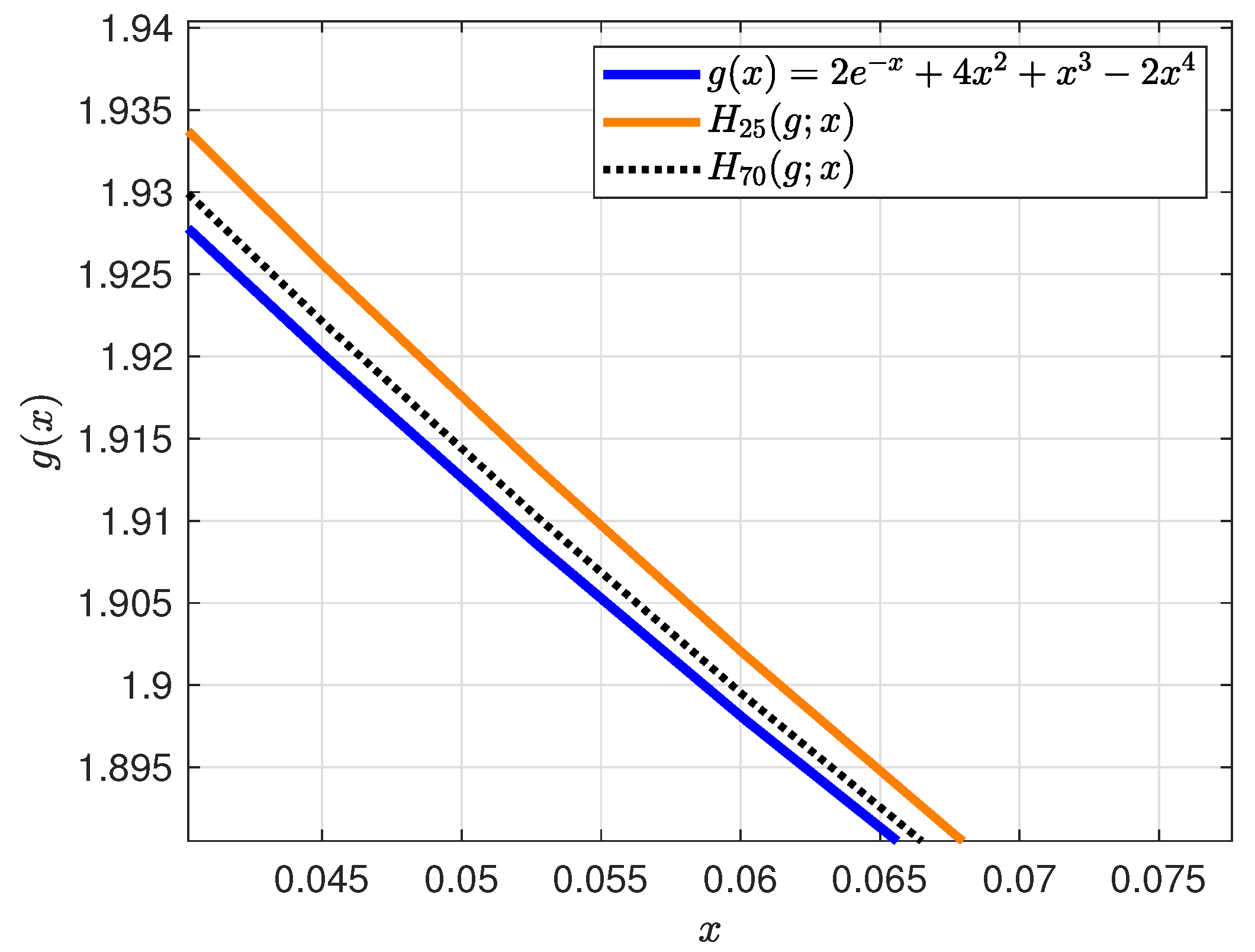
4.3. Graphical Illustration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weierstrass, K. Über die analytische Darstellbarkeit sogenannter willkürlicher Functionen reeller Argumente. Sitzungsberichte Der KöNiglich PreußIschen Akad. Der Wiss. Zu Berl. 1885, 2, 633–639. [Google Scholar]
- Korovkin, P.P. On convergence of linear positive operators in the space of continuous functions. Dokl. Akad. Nauk SSSR 1953, 90, 961–964. [Google Scholar]
- Bernstein, S.N. Démonstration du théorème de Weierstrass fondée sur le calcul des probabilités. Comm. Soc. Math. Kharkov 1912, 13, 1–2. [Google Scholar]
- Szász, O. Generalization of S. Bernstein’s polynomials to the infinite interval. J. Res. Nat. Bur. Stand. 1950, 45, 239–245. [Google Scholar] [CrossRef]
- Ismail, M.E.H. On a generalization of Szász operators. Mathematica 1974, 39, 259–267. [Google Scholar]
- Jakimovski, A.; Leviatan, D. Generalized Szász operators for the approximation in the infinite interval. Mathematica 1969, 11, 97–103. [Google Scholar]
- Aslan, R. Some approximation properties of Riemann-Liouville type fractional Bernstein-Stancu-Kantorovich operators with order of α. Iran. J. Sci. 2025, 49, 481–494. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Özger, Z.Ö.; Özger, F.; Alotaibi, A.M. Construction of a new family of modified Bernstein-Schurer operators of different order for better approximation. J. Nonlinear Convex Anal. 2024, 25, 2059–2082. [Google Scholar]
- Mansoori, M.S.; Khan, A.; Ansari, K.J. Approximation and shape preserving properties by nonlinear Lupaş type Bernstein operators of max-product kind. Arab. J. Math. 2025, 14, 107–120. [Google Scholar] [CrossRef]
- Rao, N.; Ayman-Mursaleen, M.; Aslan, R. A note on a general sequence of λ-Szász Kantorovich type operators. Comp. Appl. Math. 2024, 43, 428. [Google Scholar] [CrossRef]
- Rao, N.; Farid, M.; Jha, N.K. A study of (σ, μ)-Stancu-Schurer as a new generalization and approximations. J. Inequal. Appl. 2025, 2025, 104. [Google Scholar] [CrossRef]
- Ayman-Mursaleen, M. Quadratic function preserving wavelet type Baskakov operators for enhanced function approximation. Comp. Appl. Math. 2025, 4, 395. [Google Scholar] [CrossRef]
- Sadek, L.; Baleanu, D.; Abdo, M.S.; Shatanawi, W. Introducing novel θ-fractional operators: Advances in fractional calculus. J. King Saud Univ. Sci. 2024, 36, 103352. [Google Scholar] [CrossRef]
- Sadek, L. Controllability, observability, and stability of ϕ-conformable fractional linear dynamical systems. Asian J. Control 2024, 26, 2476–2494. [Google Scholar] [CrossRef]
- Sadek, L.; Lazar, T.A. On Hilfer cotangent fractional derivative and a particular class of fractional problems. AIMS Math. 2023, 8, 28334–28352. [Google Scholar] [CrossRef]
- Carlitz, L. A degenerate Staudt-Clausen theorem. Arch. Math. 1956, 7, 28–33. [Google Scholar] [CrossRef]
- Kim, D. A Note on the Degenerate Type of Complex Appell Polynomials. Symmetry 2019, 11, 1339. [Google Scholar] [CrossRef]
- Sergi, B.Z.; Igoz, G.; Cekim, B. Some Approximation Properties of Operators Including Degenerate Appell Polynomials. Math. Slovaca 2023, 73, 1545–1558. [Google Scholar] [CrossRef]
- Devore, R.A.; Lorentz, G.G. Constructive Approximation; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Xiong, J.; Wang, X.; Li, C. Recurrent Neural Network Based Sliding Mode Control for an Uncertain Tilting Quadrotor UAV. Int. J. Robust Nonlinear Control 2025, 35, 8030–8046. [Google Scholar] [CrossRef]
- Huang, Z.; Zheng, X.; Chao-Li; Tan, E.L.; Chen, Z.; Shi, L.; Chen, B. Piecewise Calculation Scheme for the Unconditionally Stable Chebyshev Finite-Difference Time-Domain Method. IEEE Trans. Microw. Theory Tech. 2025, 73, 4588–4596. [Google Scholar] [CrossRef]
- Wang, A.; Cheng, C.; Wang, L. On r-invertible matrices over antirings. Publ. Math. Debr. 2025, 106, 445–459. [Google Scholar] [CrossRef]
- Ali, T.A.A.; Xiao, Z.; Jiang, H.; Li, B. A Class of Digital Integrators Based on Trigonometric Quadrature Rules. IEEE Trans. Ind. Electron. 2024, 71, 6128–6138. [Google Scholar] [CrossRef]
- Savaş, R.; Patterson, R.F. Multidimensional sliding window Pringsheim convergence for measurable functions. Rend. Circ. Mat. Palermo 2024, 73, 689–698. [Google Scholar] [CrossRef]
- Savaş, E.; Mursaleen, M. Bézier Type Kantorovich q-Baskakov Operators via Wavelets and Some Approximation Properties. Bull. Iran. Math. Soc. 2023, 49, 68. [Google Scholar] [CrossRef]
- Sadek, L.; Aldawish, I. The Symmetry-Preserving Rosenbrock Approach: Application to Solve the Chaotic Lorenz System. Symmetry 2025, 17, 1844. [Google Scholar] [CrossRef]
- Haque, I.; Ali, J.; Mursaleen, M. Solvability of an infinite system of Langevin fractional differential equations in a new tempered sequence space. Fract. Calc. Appl. Anal. 2023, 26, 1894–1915. [Google Scholar] [CrossRef]
- Özger, F.; Aslan, R.; Ersoy, M. Some Approximation Results on a Class of Szász-Mirakjan-Kantorovich Operators Including Non-negative parameter α. Numer. Funct. Anal. Optim. 2025, 46, 481–484. [Google Scholar] [CrossRef]
| u | Exact | |||
|---|---|---|---|---|
| 0.2 | 0.1987 | 0.1995 | 0.1998 | 0.2000 |
| 0.4 | 0.3981 | 0.3990 | 0.3997 | 0.4000 |
| 0.6 | 0.5984 | 0.5992 | 0.5996 | 0.6000 |
| 0.8 | 0.7983 | 0.7991 | 0.7997 | 0.8000 |
| u | |||
|---|---|---|---|
| 0.2 | 1.3 × | 6.5 × | 3.2 × |
| 0.4 | 2.2 × | 1.1 × | 5.5 × |
| 0.6 | 2.1 × | 1.0 × | 5.0 × |
| 0.8 | 1.5 × | 7.3 × | 3.6 × |
| u | Exact | |||
|---|---|---|---|---|
| 0.2 | 0.5892 | 0.5878 | 0.5874 | 0.5878 |
| 0.4 | 0.9513 | 0.9510 | 0.9510 | 0.9511 |
| 0.6 | 0.9511 | 0.9510 | 0.9510 | 0.9511 |
| 0.8 | 0.5876 | 0.5877 | 0.5878 | 0.5878 |
| n | 5 | 10 | 20 | 50 |
|---|---|---|---|---|
| 0.0152 | 0.0078 | 0.0039 | 0.0016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farid, M.; Çiçek, H.; Ayman-Mursaleen, M.; Rao, N. Degenerate Appell Polynomials Connecting Beta Function as a Family of Operators and Their Approximations. Symmetry 2025, 17, 2050. https://doi.org/10.3390/sym17122050
Farid M, Çiçek H, Ayman-Mursaleen M, Rao N. Degenerate Appell Polynomials Connecting Beta Function as a Family of Operators and Their Approximations. Symmetry. 2025; 17(12):2050. https://doi.org/10.3390/sym17122050
Chicago/Turabian StyleFarid, Mohammad, Harun Çiçek, Mohammad Ayman-Mursaleen, and Nadeem Rao. 2025. "Degenerate Appell Polynomials Connecting Beta Function as a Family of Operators and Their Approximations" Symmetry 17, no. 12: 2050. https://doi.org/10.3390/sym17122050
APA StyleFarid, M., Çiçek, H., Ayman-Mursaleen, M., & Rao, N. (2025). Degenerate Appell Polynomials Connecting Beta Function as a Family of Operators and Their Approximations. Symmetry, 17(12), 2050. https://doi.org/10.3390/sym17122050








