An Innovative Algorithm Based on Chaotic Maps Amalgamated with Bit-Level Permutations for Robust S-Box Construction and Its Application in Medical Image Privacy

Abstract

Data security and privacy have become essential due to the increasingly advanced interconnectivity in today’s world, hence the reliance on cryptography. This paper introduces a new algorithm that uses a novel hybrid Tent–May chaotic map to generate pseudo-random numbers, as well as block encryption. We design a robust S-box by combining the Tent and May Maps, which yields a chaotic system with improved cryptographic properties. This S-box is a critical cryptographic primitive that significantly improves encryption security and leverages the strengths of both maps. The encryption process involves two key steps: block-wise substitution and permutation. First, we divide the image into $16\times 16$ blocks, then substitute each pixel with the $8-byte$ key and S-box. Next, we convert the encrypted image back into vector form, reorganize it using the permutation vector based on the subgroups of $S_{16}$, and finally return it to its original form. This approach greatly improves block cipher security when used, especially to protect medical images by guaranteeing their confidentiality and noninterference. Performance measures like PSNR, UACI, MSE, NCC, AD, SC, MD, and NAE prove how immune our method is to various cryptographic and statistical attacks, making it more accurate and more secure than the existing techniques.

1. Introduction

The Internet has greatly benefited humanity, mostly by offering a platform for virtual environments. In today’s world, all sectors are making vigorous efforts to virtualize their activities by employing web apps. Despite the general positive perception of the Internet and web apps, they are also associated with illegal activities like online identity theft and fraudulent purchases. Consequently, academia has developed a strong interest in enhancing the security and reliability of the Internet and online applications. Currently, there is a convergence of telemedicine technologies with Internet technologies, leading to the steady development of e-medicine [1]. The human body is subject to computerized tomography, ultrasound, magnetic resonance imaging, and other technologies to assess the condition of different organs and bones [2,3]. The Internet then transfers the image data [4]. Doctors utilize telemedicine technology to assist in diagnosing patients, effectively overcoming the obstacle of distance in delivering medical care [5]. Medical images necessitate a heightened level of security in comparison to regular photographs [6,7]. Medical photographs can compromise patient privacy, and inadequate security of medical image information can lead to issues such as the deterioration of the doctor–patient relationship [8,9]. Medical images have inherent attributes such as a large volume of data, diminished contrast, and an irregular grayscale [10,11,12]. In general, only authorized individuals have access to medical pictures. Furthermore, it is crucial to maintain the integrity of the image’s information during the doctor’s examination [3]. The unauthorized theft or use of confidential medical photographs might have severe repercussions [13]. Several studies [14,15,16,17] have demonstrated the widespread use of the chaos-based encryption method among currently known encryption algorithms. The spatiotemporal chaotic system is particularly suitable for medical imaging because of its high security requirements. This system demonstrates superior security characteristics and provides greater utility in this context [18,19,20]. Some of the latest works relate to the use of chaotic systems for image encryption, and the results show the possibility of encrypting data for transmission. Wei et al. [21] have designed a secure image encryption algorithm using hyperchaotic and the bit-level permutation while Al Sibahee et al. [22] have used a lightweight hyperchaotic map and the conditional least significant bits to hide scrambled text messages in speech signals. Rehman [23] discussed a new quantum-based method for image encryption based on the 1D sine-based chaotic maps and quantum coding. Other researchers have studied the application of chaotic maps integrated with other methods to increase the level of security of images. Abduljabbar et al. [24] presented a fast and secure method of color image encryption by using S-boxes and hyperchaotic maps and Hazzazi et al. [25] present a strong method to encrypt data using chaotic maps, Fibonacci and Tribonacci transformations, and DWT diffusion. Abduljaleel et al. [26] proposed a lightweight hybrid method to embed text messages into color images using LSB, Lah transform, and chaotic methods. Some other types of message maps have also been examined for image encryption with a view to ascertaining their utility. Riaz et al. [27] proposed a novel encryption model that possesses high levels of security and speed through using modified logistic maps while Rahman et al. [28] came up with a new compression-based 2D-chaotic sine map for biometric identification systems. Chai et al. [29] studied the application of 2D-SDMCHM and matching embedding based on flag-shaped hexagon prediction for coherent image cryptosystems in the medical domain.

1.1. Motivation

The imperative need to address the distinct security issues arising from the transmission and storage of medical pictures in digital settings motivates this research. As telemedicine gains immense popularity, there is a growing trend of concerns about the security and privacy of patients’ personal health information when communicating online. Due to the inherent characteristics of medical images, such as their large data sizes and nonuniform grayscale level distribution, the traditional encryption techniques available in the field of medical imaging may not be able to meet the necessary strict level of security. This resulted in the need for advanced cryptographic solutions, vulnerable to both cryptanalytic and statistical security attacks. Another theoretically practical solution could involve incorporating chaos theory into encryption algorithms, as chaotic systems inherently possess unpredictability and complexity, characteristics that cryptosystems seek.

1.2. Contribution

This research’s primary accomplishment is the creation of a novel encryption technique for the protection of medical images.

• The proposed cryptographic solution deals with chaos theory and an approach that combines the complexity and natural unpredictability of chaotic systems to create security models.
• This paper presents a symmetric block encryption technique using a permutation group to operate a set of pseudo-random numbers generated by the chaotic maps.
• The technique iterates the chaotic map between a pair’s changes to produce a binary output. Furthermore, we adjust these sequences to construct a solid substitution box (S-box), a crucial aspect of cryptographic systems.
• Furthermore, block substitution in the encryption process involves unique permutations that are critical for strong encryption because they create confusion and diffusion.
• The proposed method effectively demonstrates its application of medical image confidentiality through a thorough analysis based on several metrics compared to the existing methodologies.

2. Chaos Theory

Chaos theory represents an interesting branch of mathematical discipline, dealing with the behavior of dynamical systems governed by nonlinear equations, which are best known as chaotic maps [30]. These maps clearly indicate the pronounced receptivity to the starting conditions, well-known under the label “butterfly effect”. The system’s high sensitivity to initial conditions can easily cause even the smallest deviation at an earlier time, leading to significantly diverged results later. This can make long-term forecasting extremely challenging or even impossible. Since chaotic maps are nonlinear and deterministic, there is no element of randomness in their behavior, which makes them extremely sensitive to initial conditions and follow precise mathematical laws. The chaotic maps, characterized by fractal patterns and topological mixing, defy prediction. Not only are their properties highly intriguing, but they are also widely applied in various fields, ranging from biology to economics and from physics to cryptography. Rigid theoretical and experimental investigations have dealt with the well-known chaotic maps, such as the May Map, the Tent Map, the Logistic Map, and the Henon Map. Thus, in-depth study of the dynamics of a chaotic system provided researchers with great insight into chaotic systems and advanced our understanding of chaos theory in practical applications to various fields, including engineering and scientific discovery. Complex systems challenge mathematicians and scientists in this area of chaos, while the opportunities for change and innovation captivate them.

2.1. Tent Map

The bifurcation diagram of the Tent Map shows why the map got its name: the tent-like shape. This map shows the chaotic behavior in the $[2,4]$ interval as indicated by Lyapunov exponent and bifurcation diagrams. In terms of math, it is defined as [30]:

$$x_{n+1}=\left\{\begin{array}{c}{\displaystyle \frac{a{x}_n}{2}}{x}_n<0.5\\ {\displaystyle \frac{a(x_n-1)}{2}}otherwise\end{array} \right.$$

where $x_n\in [0, 1]$ and parameter $a\in [0, 4]$. Similar to the logistic map, it has a confined domain and a partially chaotic range with nonuniformity. Additionally, throughout the iteration, the Tent Map tends to remain periodic. Figure 1 displays the Lyapunov exponent and bifurcation diagram of a Tent Map.

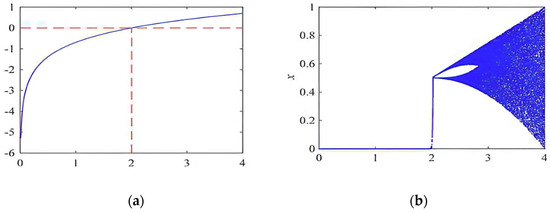
Figure 1. (a) Lyapunov exponent, (b) Bifurcation Diagram of Tent Map.

2.2. May Map

The May Map behaves similarly to the logistic map and can be represented using the following equation:

$$x_{n+1}=x_n{e}^{a(1-x_n)}$$

where $x_n\in [0, 10.9]$ and parameter $a\in [0, 5]$. This is shown in Figure 2, which displays chaotic features within the previously indicated initial condition range [31].

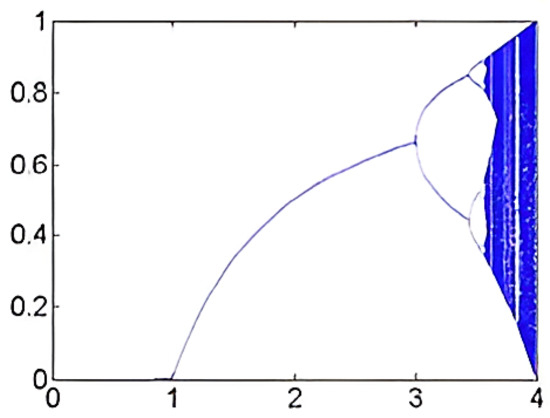
Figure 2. Bifurcation Diagram of May Map.

3. Novel Tent–May Map

The Novel Tent–May Map is a hybrid chaotic system that combines the dynamics of the Tent Map and the May Map to generate complex and unpredictable behavior suitable for cryptographic applications such as the construction of a substitution box (S-box). This map is defined mathematically as follows:

$$x_{n+1}=\left\{\begin{array}{c}{\displaystyle \frac{a{x}_n}{2}}+x_n{e}^{\left(\left(3-a\right)\left(1-x_n\right)\right)}mod 1x_n<0.5\\ {\displaystyle \frac{a(x_n-1)}{2}}+x_n{e}^{\left(\left(3-a\right)\left(1-x_n\right)\right)}mod 1otherwise\end{array} \right.$$

where $x_n\in [0, 1]$ and parameter $a\in [1.5, 4]$. This combination leverages the distinct chaotic properties of both the Tent Map and the May Map. The Tent Map contributes its well-known piecewise linearity and uniform stretching, which enhance diffusion properties essential for cryptographic strength. On the other hand, the May Map, rooted in population dynamics, introduces nonlinear exponential terms that add complexity and unpredictability. This hybrid approach aims to exploit the strengths of both maps to create a more robust and secure chaotic system.

3.1. Detailed Analysis of the Novel Tent-May Map

The Novel Tent–May Map combines the Tent Map and the May Map in a piecewise manner to generate complex chaotic behavior. The behavior of the Tent–May Map can be characterized as complex and dynamic based on its entropy spectrum, Lyapunov exponent spectrum, and bifurcation diagram. The entropy spectrum shows regions of unpredictability and randomness, especially between $a=0.5$ and $a=1.5$ and, after that, $a=2.5$, with entropy increasing and stabilizing at higher values for $a$, greater than 2.5, indicating that the system continues to exhibit chaotic behavior. The Lyapunov exponent spectrum exhibits high values for $a$ close to $0$, which is due to the strong sensitivity to the initial condition and high chaos, but this decreases near the value of $1.5$, thus explaining why it depicts less chaotic or periodic behavior before increasing and stabilizing again after $\mathrm{a}=2$. Analyzing the bifurcation diagram, one can note that it exhibits periodic or quasi-periodic oscillations for a ∼ 1.5 to 2.5 depending on its parameters by the discrete clusters of points and the transition to a chaotic behavior for $a>2.5$, as is clearly shown by the overlapping and tightly packed points for all values of $x$. These analyses collectively show that the Tent–May Map’s intricate transitions between periodic and chaotic regions are, therefore, useful for applications that need high levels of unpredicted behavior and sensitivity to initial conditions. Figure 3 displays a (a) bifurcation diagram, (b) the entropy spectrum, and (c) Lyapunov exponent spectrum, providing a comprehensive understanding of the Tent–May Map’s dynamics.

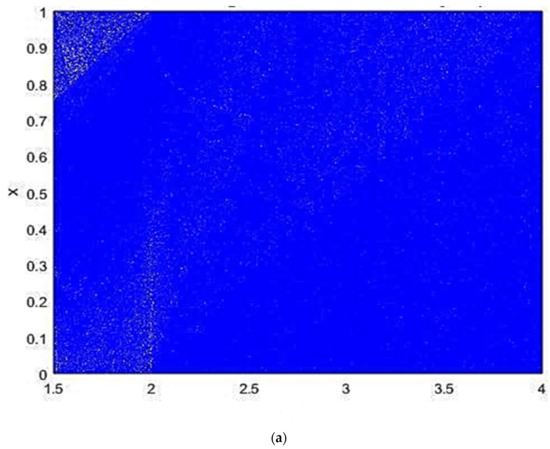
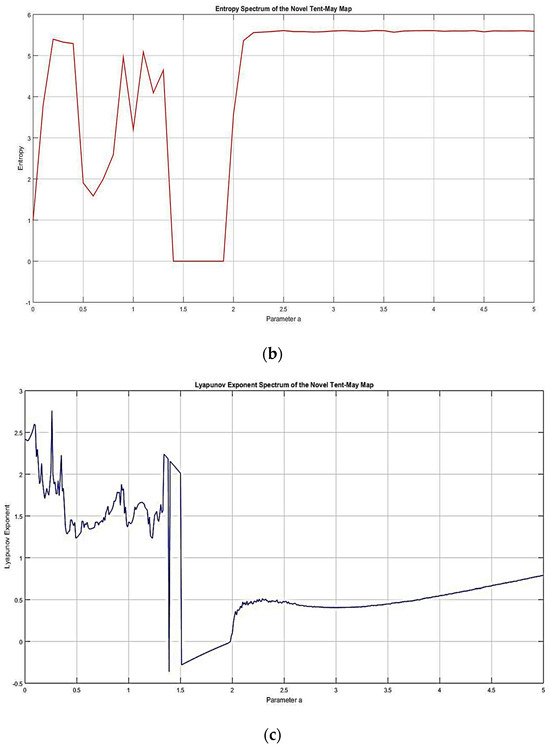
Figure 3. (a) Bifurcation Diagram, (b) Entropy Spectrum, (c) Lyapunov exponent spectrum.

Conversion between Tent and May Maps

a.

Tent Map Region $(x_n<0.5)$

When $x_n$ is less than $0.5$, the first part of the equation is used, that is,

$$x_{n+1}={\displaystyle \frac{a{x}_n}{2}}+x_n{e}^{\left(\left(3-a\right)\left(1-x_n\right)\right)}mod 1$$

This part of the map integrates both the exponential growth and decay from the May Map as well as the stretching and folding behavior characteristic of the Tent Map. The linear term ${\displaystyle \frac{a{x}_n}{2}}$ introduces stretching and folding similar to the Tent Map, while the exponential term $x_n{e}^{\left(\left(3-a\right)\left(1-x_n\right)\right)}$ adds complexity and nonlinearity.

b.

May Map Region $(x_n\ge 0.5)$

When $x_n$ is $0.5$ or greater, the second part of the equation is used, that is,

$$x_{n+1}={\displaystyle \frac{a(x_n-1)}{2}}+x_n{e}^{\left(\left(3-a\right)\left(1-x_n\right)\right)}mod 1$$

This part of the map continues to integrate both the exponential growth and decay dynamics of the May Map and the linear transformation aspect of the Tent Map. The term ${\displaystyle \frac{a(x_n-1)}{2}}$ introduces the nonlinear component similar to the May Map, creating a more complex behavior.

This intricate behavior makes the map suitable for cryptographic applications, ensuring high sensitivity to initial conditions and robust chaotic properties.

4. Cryptographic Applications

The proposed Novel Tent–May Map is particularly useful in the construction of S-boxes, which are vital components in various encryption algorithms. An S-box provides nonlinearity and confusion, two critical properties in cryptographic systems. The chaotic nature of the Novel Tent–May Map ensures that the generated S-box is highly unpredictable and resistant to linear and differential cryptanalysis. Algorithm 1 describes in detail the procedure used to develop the proposed S-box $F_{a}S-box$.

Algorithm 1: Construction of ${\mathrm{F}}_{\mathrm{a}}\mathrm{S}-\mathrm{b}\mathrm{o}\mathrm{x}$
00	Input:
01	Initialize parameter $\mathrm{a}$ and iterations
02
03	Output:
04	${\mathrm{F}}_{\mathrm{a}}\mathrm{S}-\mathrm{b}\mathrm{o}\mathrm{x}$
05
06	Iterate Tent–May Map:
07	$\mathrm{f}\mathrm{o}\mathrm{r}$ $\mathrm{i}$ from $1$ to iterations
08	Calculate $\mathrm{x}\left(\mathrm{i}\right)$ by Tent–May Map
09	$\mathrm{e}\mathrm{n}\mathrm{d}$
10	Store each value in array $\mathrm{S}$(say)
11
12	Initialize arrays $\mathrm{R}$ and $\mathrm{T}$:
13	for $\mathrm{j}$ from $1$ to iterations:
14	Calculate $\mathrm{R}$ by converting each $\mathrm{S}$ value to binary
15	End
16
17	for $\mathrm{k}$ from $1$ to iterations:
18	Calculate $\mathrm{T}$ by Transforming values of $\mathrm{S}$ to binary
19	End
20
21	Perform the $\mathrm{X}\mathrm{O}\mathrm{R}$ operation between $\mathrm{T}$ and $\mathrm{R}$
22	Convert to binary string
23
24	Make segments of $8$ bits:
25	Convert each segment to decimal
26
27	Find unique values:
28	Store the unique values in array $\mathrm{E}$
29
30	Update Array $\mathrm{E}$:
31	Add fixed integer to each value and restrict between $256$
32	Convert each to binary
33	Reordered the bits with unique pattern.
34	Convert the rearranged binary string back to decimal.
35
36	Find ${\mathrm{F}}_{\mathrm{a}}\mathrm{S}\_\mathrm{b}\mathrm{o}\mathrm{x}$:
37	${\mathrm{F}}_{\mathrm{a}}\mathrm{S}\_\mathrm{b}\mathrm{o}\mathrm{x}$ is generated by updated $\mathrm{E}$ values.
38	Interchange the position of fix point with first element in ${\mathrm{F}}_{\mathrm{a}}\mathrm{S}-\mathrm{b}\mathrm{o}\mathrm{x}$
39
40	Tweaking the Nonlinearity:
41	Take the Action of a permutation group ${\mathrm{C}}_{55860}\times {\mathrm{C}}_{70}\times {\mathrm{C}}_{70}\times {\mathrm{C}}_7\times {\mathrm{C}}_7$
	with $8$ generators and of order $13411986000$ on ${\mathrm{F}}_{\mathrm{a}}\mathrm{S}\_\mathrm{b}\mathrm{o}\mathrm{x}$, through
	right mutilation.
42
43	Update ${\mathrm{F}}_{\mathrm{a}}\mathrm{S}\_\mathrm{b}\mathrm{o}\mathrm{x}$:
44
45	End

Figure 4 displays the flowchart of Algorithm 1, which creates the proposed S-box. Table 1 provides an illustration of the proposed S-box ${ F}_{a}S\_box$.

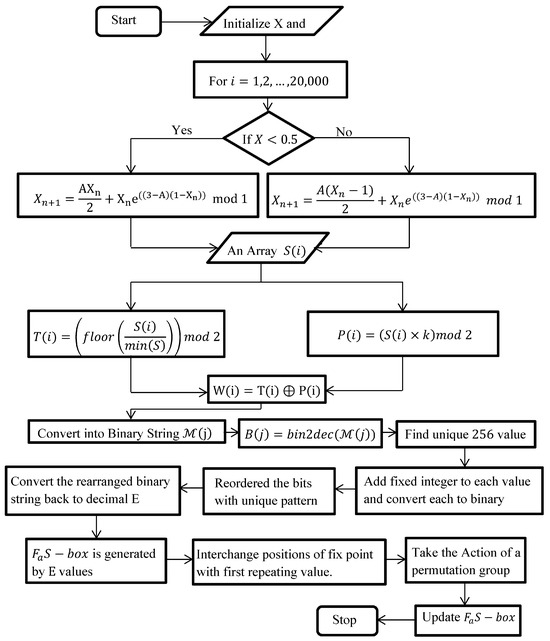
Figure 4. Flowchart of Proposed Approach.

Table 1. Proposed $F_{1.6}S-box$.

$179$	$06$	$244$	$24$	$196$	$215$	$243$	$241$	$200$	$72$	$130$	$03$	$112$	$250$	$139$	$33$
$186$	$69$	$160$	$182$	$133$	$93$	$56$	$181$	$103$	$245$	$101$	$48$	$50$	$110$	$249$	$173$
$188$	$109$	$146$	$126$	$234$	$128$	$60$	$217$	$55$	$166$	$142$	$240$	$184$	$113$	$59$	$218$
$192$	$201$	$73$	$26$	$58$	$157$	$07$	$39$	$96$	$148$	$177$	$40$	$82$	$87$	$170$	$88$
$189$	$150$	$66$	$210$	$89$	$18$	$163$	$42$	$149$	$219$	$27$	$116$	$174$	$51$	$74$	$238$
$221$	$125$	$185$	$92$	$206$	$121$	$251$	$119$	$220$	$91$	$54$	$252$	$09$	$04$	$124$	$204$
$86$	$76$	$118$	$32$	$75$	$61$	$222$	$108$	$99$	$129$	$195$	$36$	$100$	$65$	$02$	$90$
$104$	$71$	$191$	$111$	$13$	$37$	$29$	$147$	$237$	$105$	$178$	$127$	$41$	$46$	$62$	$31$
$120$	$47$	$233$	$25$	$165$	$227$	$98$	$22$	$68$	$144$	$224$	$123$	$28$	$45$	$117$	$143$
$232$	$44$	$153$	$203$	$198$	$194$	$212$	$175$	$106$	$161$	$114$	$43$	$154$	$183$	$57$	$229$
$164$	$134$	$14$	$162$	$207$	$97$	$11$	$49$	$122$	$239$	$152$	$80$	$20$	$135$	$172$	$228$
$05$	$131$	$155$	$30$	$136$	$247$	$242$	$53$	$151$	$156$	$35$	$226$	$199$	$225$	$102$	$158$
$190$	$0$	$23$	$85$	$145$	$246$	$208$	$176$	$187$	$8$	$213$	$15$	$216$	$214$	$235$	$141$
$193$	$168$	$70$	$132$	$236$	$34$	$140$	$94$	$248$	$197$	$10$	$209$	$81$	$205$	$115$	$79$
$230$	$16$	$78$	$21$	$95$	$83$	$01$	$255$	$167$	$67$	$63$	$137$	$171$	$107$	$211$	$12$
$223$	$202$	$254$	$19$	$231$	$138$	$17$	$169$	$180$	$84$	$38$	$77$	$52$	$159$	$64$	$253$

5. Performance Analysis for Proposed S-Box

New S-boxes represent an important research contribution in information security. Once created, we assess an S-box’s ability to withstand different linear and differential attacks. We have extensively evaluated the proposed S-box based on various criteria.

• $\mathrm{N}\mathrm{L}$—Nonlinearity;
• $\mathrm{S}\mathrm{A}\mathrm{C}$—Strict Avalanche Criterion;
• $\mathrm{B}\mathrm{I}\mathrm{C}$—Bit Independent Criterion;
• $\mathrm{L}\mathrm{P}$—Linear Approximation Probability;
• $\mathrm{D}\mathrm{P}$—Differential Approximation Probability.

5.1. Nonlinearity (NL)

Nonlinearity is an important factor to consider when evaluating a substitution box’s efficacy. In particular, the only nonlinear component of modern block ciphers is an S-box. If an S-box’s structure is such that the conversion between the original data and scrambled data is linear, then its resistance to distinct linear and differential attacks is weak. An effective protection against these malicious attempts requires a high value of nonlinearity. We find the nonlinearity value of a Boolean function using the following equation.

$$N_L\left(T\right)=2^{n-1}-{\displaystyle \frac{1}{2}}\left(S_{max}\left(T\right)\right)$$

where $S_{max} \left(T\right)=$ Walsh–Hadamard spectrum of a Boolean function $T$ having $n$ bits.

Table 2 displays the proposed S-box F_1.6 S-box nonlinearity scores, where the minimum, maximum, and average nonlinearity scores are 110, 112, and 111. Table 3 compares the NL scores of the proposed S-box with those of recently designed S-boxes.

Table 2. Nonlinearity score of final S-box.

Boolean Function	$T_1$	$T_2$	$T_3$	$T_4$	$T_5$	$T_6$	$T_7$	$T_8$
NL Score	$112$	$110$	$112$	$112$	$110$	$110$	$110$	$112$

Table 3. Recent S-boxes and nonlinearity values.

S-Box	Minimum NL	Maximum NL	Average NL
Proposed	$110$	$112$	$111.00$
[32]	$104$	$110$	$107.00$
[33]	$106$	$110$	$108.50$
[34]	$106$	$110$	$108.00$
[35]	$108$	$110$	$109.75$
[36]	$110$	$112$	$110.75$
[37]	$98$	$106$	$102.75$
[38]	$104$	$108$	$106.75$
[39]	$104$	$110$	$106.50$
[40]	$106$	$108$	$106.00$
[41]	$106$	$108$	$106.50$
[42]	$106$	$108$	$106.80$
[43]	$106$	$108$	$106.80$
[44]	$98$	$106$	$103.75$
[45]	$104$	$110$	$106.25$

5.2. Strict Avalanche Criterion (SAC)

Tavares and Webster first introduced the Strict Avalanche Criterion (SAC) [46]. To meet this requirement, every change to one of the input bits must result in an alteration of the ciphertext due to the use of a cipher. Using a dependency matrix, we calculate the SAC score of a substitution box. Table 4 displays the calculated and quantified values of the proposed S-box matrix.

Table 4. SAC dependence values of proposed S-box.

$0.4531$	$0.4844$	$0.4688$	$0.5469$	$0.5000$	$0.4688$	$0.4844$	$0.4688$
$0.4844$	$0.5469$	$0.4688$	$0.4531$	$0.5312$	$0.5469$	$0.5156$	$0.4688$
$0.5156$	$0.4688$	$0.5156$	$0.5312$	$0.4531$	$0.4531$	$0.5156$	$0.5312$
$0.4844$	$0.4531$	$0.5469$	$0.5312$	$0.5000$	$0.5469$	$0.5312$	$0.5312$
$0.4531$	$0.5000$	$0.4375$	$0.5312$	$0.5469$	$0.5156$	$0.5000$	$0.5312$
$0.4688$	$0.5469$	$0.5000$	$0.4688$	$0.4375$	$0.5312$	$0.5156$	$0.4688$
$0.5156$	$0.4844$	$0.5312$	$0.4844$	$0.5156$	$0.5312$	$0.5469$	$0.5156$
$0.5781$	$0.4844$	$0.4844$	$0.4844$	$0.5000$	$0.4531$	$0.5469$	$0.5000$

For an S-box, a SAC value of $0.5000$ is considered the perfect score. The proposed S-box’s average SAC score is $0.5017$, extremely close to the best value.

5.3. Bit Independence Criterion (BIC)

Tavares and Webster [46] created the Bit Independence Criterion (BIC), another criterion for rating S-box performances. According to this requirement, changes in output bits must occur independently of one another if input bits change in any way. Table 5 lists the proposed S-box’s BIC-NL values, revealing an average BIC-NL score of 111.4286.

Table 5. BIC-NL scores of proposed S-box.

$-$	$110$	$112$	$112$	$112$	$110$	$112$	$110$
$110$	$-$	$112$	$112$	$112$	$112$	$112$	$112$
$112$	$112$	$-$	$112$	$110$	$110$	$110$	$110$
$112$	$112$	$112$	$-$	$112$	$112$	$112$	$110$
$112$	$112$	$110$	$112$	$-$	$112$	$112$	$112$
$110$	$112$	$110$	$112$	$112$	$-$	$112$	$112$
$112$	$112$	$110$	$112$	$112$	$112$	$-$	$112$
$110$	$112$	$110$	$110$	$112$	$112$	$112$	$-$

BIC-SAC values of the proposed S-box are listed in Table 6.

Table 6. BIC-SAC scores of proposed S-box.

$-$	$0.4980$	$0.5137$	$0.5137$	$0.4863$	$0.4980$	$0.5039$	$0.4941$
$0.4980$	$-$	$0.5098$	$0.5000$	$0.4883$	$0.4883$	$0.5039$	$0.5039$
$0.5137$	$0.5098$	$-$	$0.5078$	$0.4980$	$0.4961$	$0.4902$	$0.5020$
$0.5137$	$0.5000$	$0.5078$	$-$	$0.5078$	$0.5195$	$0.5039$	$0.4941$
$0.4863$	$0.4883$	$0.4980$	$0.5078$	$-$	$0.5020$	$0.4844$	$0.5059$
$0.4980$	$0.4883$	$0.4961$	$0.5195$	$0.5020$	$-$	$0.5059$	$0.5195$
$0.5039$	$0.5039$	$0.4902$	$0.5039$	$0.4844$	$0.5059$	$-$	$0.5117$
$0.4941$	$0.5039$	$0.5020$	$0.4941$	$0.5059$	$0.5195$	$0.5117$	$-$

5.4. Linear Approximation Probability

In 1993, Matsui proposed linear cryptanalysis as a statistical attack to evaluate the advantages and disadvantages of the Data Encryption Standard (DES) [47,48]. Linear cryptanalysis identifies linear correlations between a cryptosystem’s inputs (key, plaintext) and outputs (cipher text). These days, cryptanalysts can investigate the weaknesses of contemporary block ciphers using linear cryptography. The National Institute of Standards and Technology (NIST) created the Advanced Encryption Standard (AES) in response to the DES cipher’s demonstrated vulnerability to linear cryptanalysis and severity [49]. Calculating the linear probability of a substitution box’s inputs and outputs and finding it small indicates that the S-box under examination is resistant to linear cryptanalysis. Equations can compute the linear probability (LP) value for an S-box.

$$LP={Max}_{t_x,t_{y\ne 0}}|{\displaystyle \frac{\{x\in V|x·t_x=S\left(x\right)·t_y\}}{2^n}}-{\displaystyle \frac{1}{2}}$$

where $t_x=input mask,t_y=output mask,$ and $V=\{0,1,\dots ,2^n-1\}$.

The proposed S-box has a low LP value of $0.0703$, indicating its effectiveness against linear cryptanalysis.

5.5. Differential Approximation Probability

Biham and Shamir [8] first presented differential cryptanalysis as a novel way to break the Data Encryption Standard (DES). Any cryptosystem that employs substitution and permutation operations, like the DES, can launch this attack. By using differential cryptanalysis, a perpetrator aims to exploit the inconsistent differences between plaintext and ciphertext by identifying similarities between related scrambled plaintexts. There may be one or more bits of variation in the original plaintext. We evaluate an S-box’s resistance to this attack using differential uniformity (DU) and differential probability (DP) measurements. We can determine the differential approximation (DP) of a specific substitution box B using the following formula:

$$DP={Max}_{∆a\ne 0,∆b} {\displaystyle \frac{[\#\{a \in P\left|B\right(a) \oplus B(a \oplus ∆a)=∆b\}]}{2^n}}$$

In this case, $P$ represents all possible inputs, and all input elements are $2^n$. Also $∆a$ and $∆b$ represent input and output differentials. Table 7 displays the projected S-box’s extremely low DP score of $0.0340$, indicating that it is capable of withstanding differential cryptanalysis.

Table 7. SAC, BIC-NL, LP, and DP scores.

S-Box	SAC	SAC-Offset	BIC-NL	LP	DP
Proposed	$0.5017$	$0.0017$	$104.70$	$0.0703$	$0.0340$
[32]	$0.5101$	$0.0100$	$106.25$	$0.1050$	$0.0390$
[33]	$0.4995$	$0.0010$	$103.85$	$0.1090$	$0.0390$
[34]	$0.4990$	$0.0010$	$104.29$	$0.1250$	$0.0390$
[35]	$0.5042$	$0.0040$	$110.60$	$0.0850$	$0.0390$
[36]	$0.4960$	$0.0040$	$102.90$	$0.1250$	$0.0390$
[37]	$0.4992$	$0.0010$	$103.10$	$0.1410$	$0.0470$
[38]	$0.4976$	$0.0020$	$102.85$	$0.1320$	$0.0390$
[39]	$0.4995$	$0.0010$	$104.57$	$0.1170$	$0.0390$
[40]	$0.5010$	$0.0010$	$100.00$	$0.0700$	$0.0390$
[41]	$0.4978$	$0.0020$	$104.21$	$0.1330$	$0.0390$
[42]	$0.5034$	$0.0030$	$103.80$	$0.1330$	$0.0390$
[43]	$0.5034$	$0.0030$	$103.79$	$0.1330$	$0.0390$
[44]	$0.5022$	$0.0020$	$112.40$	$0.1560$	$0.0390$
[45]	$0.4977$	$0.0020$	$104.10$	$0.1320$	$0.0460$

Table 7 shows the comparison of SAC, BIC-NL, LP, and DP scores with exiting well-known S-boxes.

6. Proposed Algorithm of Image Encryption

In this section, we aim to encrypt a carefully chosen set of four grayscale medical images. Our investigations have provided evidence for the strong resilience and secure qualities of the algorithm we have presented through a series of carefully conducted test experiments. While using the various capabilities of MATLAB software version R2015a, we performed all of our experimental simulations with accuracy and precision. We carefully selected four plaintext images, accessed on Saturday, 30 March 2024 for our research from the MedPix database of the National Library of Medicine (https://medpix.nlm.nih.gov/home), a reputable source. Figure 5, Figure 6, Figure 7 and Figure 8 prominently display side-by-side representations of the original images and their subsequent encrypted versions for comparison. These visual representations clearly highlight the differences, thereby confirming the effectiveness of our encryption approach in effectively protecting the integrity of the analyzed medical images. The $F_{a}S\_box$ produced by Algorithm 1 has demonstrated its security as a substitution box by achieving a high level of efficiency and security against several known attacks. Algorithm 2 displays an image encryption algorithm that utilizes the common structure of confusion and diffusion.

Algorithm 2: Image Encryption Algorithm
00.	Input:	Input image
01.		Substitution box $F_{1.6}S-box$
02.		Key (8-byte key)
03.	Output:	Encrypted image
04.	Step 1:
05.		Perform block-wise substitution for the first round:
06.		Divide the image into blocks of size $16\times 16$
07.		For each block:
08.		Extract the block.
09.		Perform substitution for each pixel in the block using the key.
10.		Update the encrypted image with the substituted block.
11.		Write the encrypted image to file Enc_round_1
12.	Step 2:
13.		Perform permutation for the second round:
14.		Reshape the encrypted image into a vector.
15.		$\mathrm{Generate} \mathrm{a} \mathrm{permutation} \mathrm{vector} \mathrm{based} \mathrm{on} \mathrm{a} \mathrm{permutation} \mathrm{subgroup} {\mathrm{S}}_{16}$
16.		Permute the reshaped vector according to the permutation vector.
17.		Reshape the permuted vector back into the image shape.
18.		Write the encrypted image to file Enc_round_2

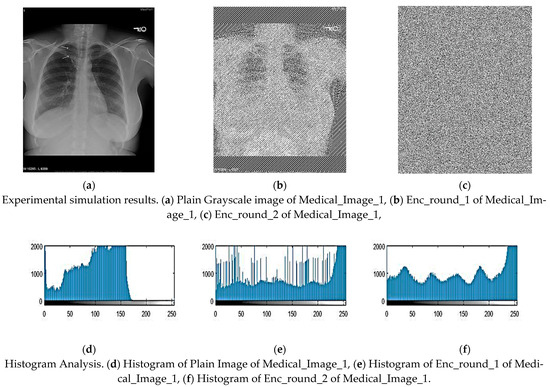
Figure 5. Experimental simulation results of Medical_Image_1 and Histogram Analysis.

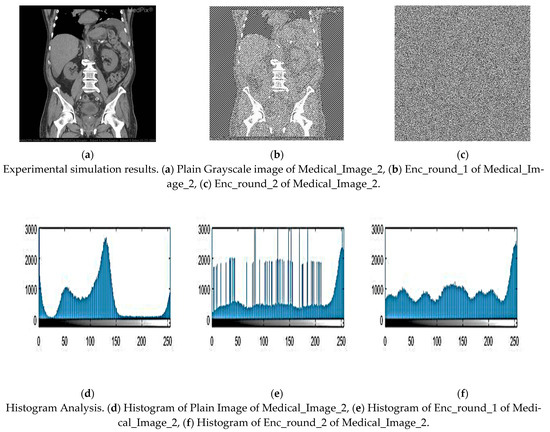
Figure 6. Experimental simulation results of Medical_Image_2 and Histogram Analysis.

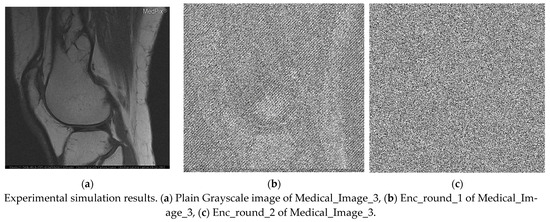
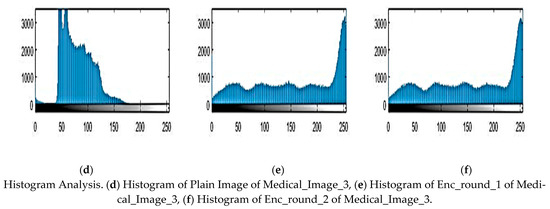
Figure 7. Experimental simulation results of Medical_Image_3 and Histogram Analysis.

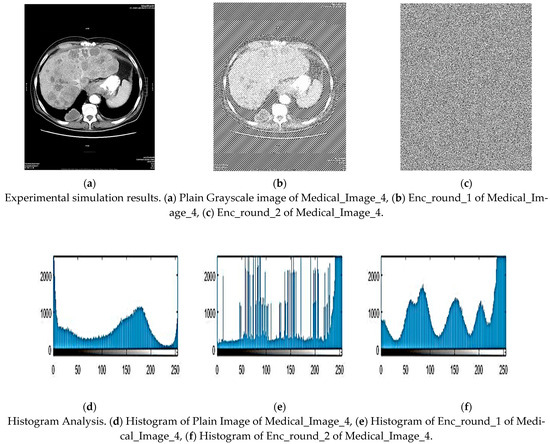
Figure 8. Experimental simulation results of Medical_Image_4 and Histogram Analysis.

7. Proposed Technique Analysis

Ensuring the security of the encryption technique is of utmost importance. This section examines the security of the method by analyzing information entropy, adjacent pixel correlation, and resistance to differential attacks through a range of experiments and studies. The testing process makes use of a wide range of images of arbitrary size and type.

Histogram

The histogram describes the frequency of each gray-level pixel in a picture and gives details on how light and dark the image is. The encryption method needs to hide the image data from the statistical and visual components of the information. Because of this, a solid encryption technique needs to have a cipher image’s smooth histogram. The encrypted Medical_Image_1, Medical_Image_2, Medical_Image_3, and Medical_Image_4 in Figure 3 have a significantly more consistent distribution of pixel values when compared to the original photos. This result demonstrates how well the suggested technique protects the image and provides support to the notion that it offers great protection against both statistical and differential attacks. These indicate that the developed encryption method is very successful at hiding the plain image’s pixel distribution information.

8. Majority Logical Criterion (MLC)

To assess the effectiveness of the encryption, various tests are employed, including energy, homogeneity, correlation, contrast, and entropy [50]. These tests assess the suitability of an S-box for the encryption process. These investigations calculate the level of unpredictability of the encrypted image. The characteristics of the encrypted image are dictated by its energy and uniformity. Correlation is employed to ascertain the degree of similarity between the original and encrypted images. The encrypted image has experienced a significant modification, as evidenced by the lowest score obtained from the correlation analysis. The luminosity of the main image is determined by its level of contrast. A stronger encryption method is characterized by a greater contrast. The encryption technique alters unencrypted images, while statistical analysis determines the effectiveness of the proposed S-box. The generated S-box is utilized for encrypting digital photographs. To conduct the MLC, we selected four JPEG images at random, namely Medical_Image_1, Medical_Image_2, Medical_Image_3, and Medical_Image_1. The encrypted images have undergone such significant alterations that they are now unrecognizable compared to the originals.

8.1. Homogeneity Analysis

Homogeneity analysis is a method employed to assess the positioning of items adjacent to the diagonal entries in the gray tone spatial dependency matrix (GTSDM) or the gray level co-occurrence matrix (GLCM). The GLCM calculates the statistical parameters of various combinations of pixel brightness values or gray levels to determine the frequencies of gray level patterns in the data. Homogeneity can be quantified by normalizing the gray-level co-occurrence matrices within the GLCM and calculating a measurement.

$$Hom=\sum _i\sum _j{\displaystyle \frac{\gamma \left(i,j\right)}{1+\left|i-j\right|}}$$

where $i,j$ are the positions of pixels of the image and $\gamma (i,j)$ is the representation position of the pixels in the image in the gray level co-occurrence matrix (GLCM).

8.2. Energy

The rate at which a picture’s pixels change in brightness or color is known as its energy. Therefore, it is expected that an encrypted image would possess a minimal amount of energy [51]. The energy measure is computed by summing the squared components of the gray-level co-occurrence matrix.

$$Energy=\sum _{i,j}{q(i,j)}^2$$

8.3. Contrast

Contrast is related to the variation of intensities of the pixels of the image. It assists viewers in identifying the various entities presented in the image. Enhancing the appearance of an image becomes feasible, making it easier to identify its individual components. The image depicting heightened uncertainty is expected to exhibit a greater level of contrast. A higher contrast level is correlated with a more robust encryption [52]. The mathematical representation is as follows:

$$Contrast=\sum _{i,j}q\left(i,j\right){|i-j|}^2$$

We performed this collection of statistical analyses to assess the applicability and stability of our suggested image encryption procedure, which is based on S-boxes. MLC analysis was conducted on the four test images, and the outcomes for both plain and encrypted images generated by our method are presented in Table 8.

Table 8. MLC Comparison of Different Approaches.

Images	Approach		Contrast	Correlation	Energy	Homogeneity
Medical_Image_1		Original	$0.0994$	$0.9814$	$0.1943$	$0.9694$
	Proposed	$Encrypted$	$13.2239$	$0.0016$	$0.0398$	$0.4175$
	Ref. [36]	$Encrypted$	$10.2390$	$0.0093$	$0.0201$	$0.3898$
	Ref. [53]	$Encrypted$	$10.1904$	$0.00298$	$0.0177$	$0.3909$
	Ref. [54]	$Encrypted$	$10.3491$	$0.00081$	$0.0161$	$0.3891$
	Ref. [55]	$Encrypted$	$10.2145$	$0.00119$	$0.0209$	$0.3925$
Medical_Image_2		Original	$0.3607$	$0.9551$	$0.2086$	$0.9009$
	Proposed	$Encrypted$	$11.9632$	$0.00219$	$0.0211$	$0.3907$
	Ref. [36]	$Encrypted$	$10.1802$	$0.00913$	$0.0334$	$0.4012$
	Ref. [53]	$Encrypted$	$10.0216$	$0.03001$	$0.0167$	$0.3916$
	Ref. [54]	$Encrypted$	$10.5286$	$0.00062$	$0.0194$	$0.4012$
	Ref. [55]	$Encrypted$	$10.2129$	$0.00381$	$0.0234$	$0.3930$
Medical_Image_3		Original	$0.0925$	$0.9498$	$0.2757$	$0.9609$
	Proposed	$Encrypted$	$11.9635$	$-0.0005$	$0.03683$	$0.4185$
	Ref. [36]	$Encrypted$	$10.4376$	$0.00121$	$0.0167$	$0.3912$
	Ref. [53]	$Encrypted$	$10.1903$	$0.00092$	$0.0183$	$0.3904$
	Ref. [54]	$Encrypted$	$10.2693$	$0.00032$	$0.0180$	$0.3944$
	Ref. [55]	$Encrypted$	$10.0061$	$0.00120$	$0.0163$	$0.4012$
		Original	$0.2256$	$0.9776$	$0.4199$	$0.9405$
	Proposed	$Encrypted$	$12.0832$	$-0.0054$	$0.0483$	$0.4337$
	Ref. [36]	$Encrypted$	$10.1283$	$0.00129$	$0.0159$	$0.3936$
Medical_Image_4	Ref. [53]	$Encrypted$	$10.1179$	$0.00213$	$0.0161$	$0.3962$
	Ref. [54]	$Encrypted$	$10.3810$	$0.00173$	$0.0188$	$0.4045$
	Ref. [55]	$Encrypted$	$10.2940$	$0.00122$	$0.0173$	$0.3981$

9. Adjacent Pixel Correlation

Correlation coefficient analysis [56,57], which is based on finding the correlation between two random variables, shows that this relationship is independent. Plaintext images typically exhibit robust correlations between pixels in different orientations. The attacker often exploits the connections between neighboring pixels to gather information about a plaintext image. Therefore, an effective encryption technique should minimize the associations between each pixel in an image [58]. The calculation of the pixel correlation coefficient can be carried out with the following formula:

$$r_{xy}={\displaystyle \frac{cov\left(x, y\right)}{\sqrt{D\left(x\right)}\sqrt{D\left(y\right)}}}$$

$$E\left(x\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{x}_i$$

$$D\left(x\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(x_i-E\left(x\right)\right)}^2$$

$$cov\left(x,y\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left(x_i-E\left(x\right)\right)\left(y_i-E\left(y\right)\right)$$

where $x_i$ and $y_i$ are gray values of the adjacent pixels. And $cov(x,y)$ is the covariance of $x$ and $y$ and $D\left(x\right)$ and $D\left(y\right)$ denote the standard deviation of $x$ and $y$, respectively.

The pixel distribution analysis and pixel correlation constitute the following Figure 9, Figure 10, Figure 11 and Figure 12, which offer the validation of image encryption techniques based on the aspects of pixel information. To compare the original image’s pixel intensity distribution to the encrypted image’s distribution, pixel distribution plots are constructed; these plots illustrate the extent of the randomization of the encryption process. In the original image, such plots give structured patterns because of inherent correlations between pixels while in the encrypted image, these plots are quite random and therefore imply successful scrambling of pixel values. The pixel correlation plots display the correlation of two neighboring pixels at different orientations: horizontal, vertical, and diagonal. High correlation coefficients in the original image imply that there is high local correlation between the corresponding pixels and when these pixels are encrypted, the correlation coefficients indicate that the local relationships are distorted. Both analyses produce a comprehensive evaluation of the encryption’s capability to randomize the image data, thereby providing the required and necessary security to the encrypted data.

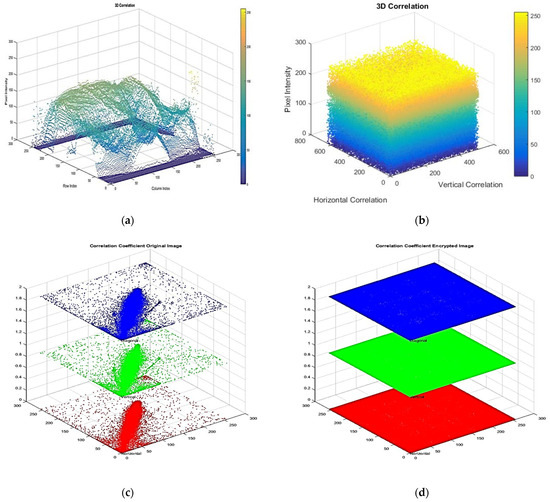
Figure 9. (a–d) Analysis of pixel distribution and pixel correlation for original Medical_Image_1 and encrypted Medical_Image_1.

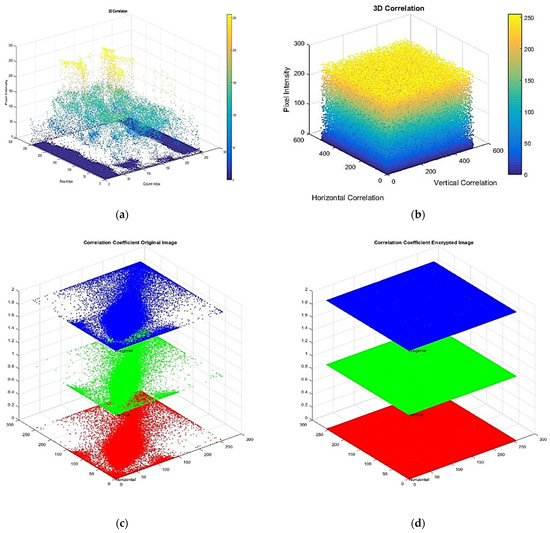
Figure 10. (a–d) Analysis of pixel distribution and pixel correlation for original Medical_Image_2 and encrypted Medical_Image_3.

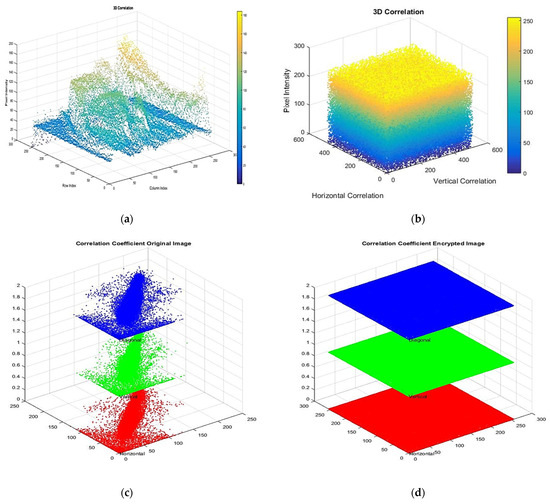
Figure 11. (a–d) Analysis of pixel distribution and pixel correlation for original Medical_Image_3 and encrypted Medical_Image_3.

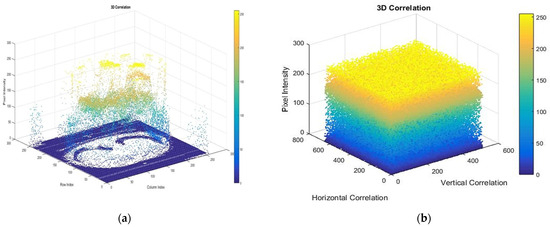
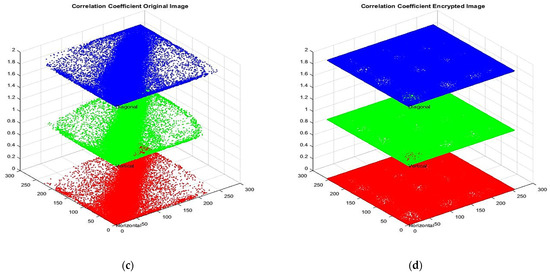
Figure 12. (a–d) Analysis of pixel distribution and pixel correlation for original Medical_Image_4 and encrypted Medical_Image_4.

Figure 9 and Figure 10: The pixel distribution plots of Medical_Image_1 to Medical_Image_4, where the original image (a) has more structured patterns (having correlations) and the encrypted image (b) is distributed uniformly and randomly, proving effective encryption. The pixel correlations of the original image are high in horizontal, vertical, and diagonal directions as shown in figure (c), while the encrypted image has small correlation coefficients as shown in figure (d), indicating that the local pixel relationship has been disrupted due to encryption.

10. Information Entropy

Information entropy is a widely used measure of information content. The information content of an image is determined through information entropy, with higher entropy indicating a lower amount of visual information in the image. To prevent entropy attacks, it is essential to use a secure encryption method that evenly and unpredictably distributes the pixels of the image. When comparing the encrypted and plain images, the information entropy of the encrypted image should be significantly higher. The theoretical information entropy of a fully random 8-bit pixel image is 7.99 [59], which can be estimated as:

$$H\left(s\right)=\sum _{i=1}^{2^N-1}\rho \left(s_i\right)\mathit{log}\left({\displaystyle \frac{1}{\rho \left(s_i\right)}}\right)$$

where $\rho \left(s_i\right)$ represents the probability of the information source, $s_i$, and $N$ represents the number of bits of $s_i$. The information entropy values for the encrypted images that our encryption method determined are shown in Table 9.

Table 9. Information Entropy Analysis Results.

Images	Information Entropy Values
Medical_Image_1 Org	$6.4605$
Medical_Image_1 Enc	$7.3128$
Medical_Image_2 Org	$5.5652$
Medical_Image_2 Enc	$7.6295$
Medical_Image_3 Org	$6.5384$
Medical_Image_3 Enc	$7.3841$
Medical_Image_4 Org	$4.7501$
Medical_Image_4 Enc	$7.1887$

11. Encrypted Image Quality Measure

This section focuses on the experimental evaluation of the proposed image encryption technique. For these tests, four JPEG images named Medical_Image_1, Medical_Image_2, Medical_Image_3, and Medical_Image_4 of arbitrary size have been selected. The results indicate that the proposed encryption scheme is robust to withstand various attacks.

11.1. Mean Square Error (MSE)

The mean square error (MSE) displays average squared deviations between corresponding elements of two images, usually the original and those for encryption. It is an indication of the overall discrepancy that exists between the two images. A greater mean square error (MSE) value shows greater dissimilarity between the images, which means that there are bigger variations in their content or quality. Mathematically, the mean square error (MSE) is:

$$MSE={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(X_i-{X^{\ast }}_i)}^2$$

N is the number of pixels in the frame, and $X_i$, ${X^{\ast }}_i$ are the $i^{th}$ pixels in the original and processed frames, respectively. Table 10 displays the mean square error (MSE) for a different image obtained using the algorithm mentioned earlier, revealing a greater level of dissimilarity between the original and encrypted images. Table 10 shows the mean square error (MSE) for a different image obtained using the above algorithm, indicating a higher degree of dissimilarity between the original and encrypted images.

Table 10. Results of different image quality metrics.

Images	MSE	PSNR	MD	AD	UQI	SSIM	NCC	NAE	SC	RMSC
Med_Imege_1	$17.409$	$5.7229$	$255$	$-81.6478$	$0.0007$	$0.0050$	$1.3286$	$1.4062$	$0.2877$	$131.95$
Med_Imege_2	$17.455$	$5.7114$	$255$	$-76.1247$	$0.0012$	$0.0047$	$1.0341$	$1.5693$	$0.3513$	$132.12$
Med_Imege_3	$15.064$	$6.3512$	$179$	$-86.9401$	$0.0006$	$0.0070$	$1.8589$	$1.3681$	$0.2011$	$122.74$
Med_Imege_4	$25.656$	$4.0389$	$255$	$-112.9976$	$0.0018$	$0.0031$	$0.9935$	$2.5353$	$0.2625$	$160.17$

11.2. Peak Signal-To-Noise Ratio (PSNR)

Peak signal-to-noise ratio (PSNR) is a quantitative measure used to assess the quality of compressed or reconstructed images by comparing them to the original image. PSNR calculates the signal-to-noise ratio by subtracting the differences between the two images. In short, it offers a more refined metric compared to MSE as it quantifies noise in relation to the intensity of the signal. A higher PSNR value corresponds to higher image quality, indicating a stronger signal relative to the level of noise. In terms of mathematics,

$$PSNR=20 {log}_{10}\left({\displaystyle \frac{MAXI}{MSE}}\right)-10{ log}_{10}\left(MSE\right)$$

where MSE is mean square error and MAXI is the maximum possible pixel value of the image.

11.3. Structural Similarity Index Method (SSIM)

The structural similarity index [60] method is a perception-based method. This approach considers the loss of quality of an image as a change in the way structural information is perceived. In addition, it is capable of exploiting contrast and brightness masking techniques, along with other notable perception-based factors. The term “structural information” refers to pixels that exhibit a significant level of interconnectivity or are subject to geographical constraints. Moreover, these closely connected pixels offer substantial details regarding the entities that are observable within the image domain. The term “luminance masking” refers to the phenomenon in which the distortion of an image becomes barely apparent as it gets closer to its edges. However, making use of contrast masking reduces the visibility of textural distortions in an image. SSIM is a metric that quantifies the perceived quality of videos and images. It quantifies the level of resemblance. Table 10 displays the structural similarity index (SSIM) values for Medical_Image_1, Medical_Image_2, Medical_Image_3, and Medical_Image_4. The table demonstrates that the similarity between the original and encrypted images is extremely small.

11.4. Average and Maximum Difference (AD and MD)

The purpose of these tests is to compute the average and maximum differences between the encrypted $E(x,y)$ and original $O(x,y)$ images. For the secure encryption process, the AD value must be more than 3 and less than −3 [61]. The AD and MD scores are calculated using the following formulas:

$$AD={\displaystyle \frac{\sum _{y=1}^R\sum _{x=1}^S\left[O\left(x,y\right)-E(x,y)\right]}{R\times S}}$$

$$MD=\mathit{max}\left|O\left(x,y\right)-E\left(x,y\right)\right|$$

where $R\times S$ are dimensions of the image.

11.5. Structural Content (SC)

This test (SC) is essentially a correlation-based metric. It is a metric to compare how structurally comparable the original $O(x,y)$ and encrypted $E(x,y)$ images are. In terms of math concepts,

$$SC={\displaystyle \frac{\sum _{y=1}^R\sum _{x=1}^S{\left[O\left(x,y\right)\right]}^2}{\sum _{y=1}^R\sum _{x=1}^S{\left[E\left(x,y\right)\right]}^2}}$$

11.6. Normalized Cross-Correlation (NCC)

The correlation function determines the degree of similarity between two images. The link between the original $\alpha (x,y)$ and ciphered $\beta (x,y)$ images is discovered by NCC. NCC is calculated using the subsequent formula:

$$NCC=\sum _{y=1}^R\sum _{x=1}^S\left({\displaystyle \frac{\alpha (x,y)\times \beta (x,y)}{\sum _{y=1}^R\sum _{x=1}^S{\left|\alpha \left(x,y\right)\right|}^2}}\right)$$

11.7. Normalized Absolute Error (NAE)

The normalized absolute error (NAE) is a performance measure that quantifies the total absolute error relative to the error in determining the mean of the actual values. NAE experiences variability due to its reliance on both the lowest and highest values. The normalized absolute error between the original $O(x,y)$ and encrypted $E(x,y)$ image can be calculated using the given formula:

$$NAE={\displaystyle \frac{\sum _{y=1}^R\sum _{x=1}^S\left[O\left(x,y\right)-E(x,y)\right]}{\sum _{y=1}^R\sum _{x=1}^S\left|O\left(x,y\right)\right|}}$$

11.8. Root Mean Square Error (RMSE)

The root mean square error (RMSE) is a commonly employed method for evaluating errors. It estimates the disparities between the predicted and observed values of an estimation. It measures the magnitude of the error. This ideal accuracy metric calculates the differences in forecasting errors between various estimators for a specific variable. The root mean square error (RMSE) is the square root of the mean square error (MSE).

12. NPCR, UACI, and & BACI Analysis

The cryptanalysis techniques of blocked average changing intensity (BACI), unified average changing intensity (UACI), and number of pixels changed rate (NPCR) [62] are employed to evaluate the level of resistance of encryption against distinguishing attacks. It is employed to ascertain the impact of minor alterations to the source images on encryption. NPCR calculates the proportion of distinct pixel values in both the original and encrypted images. The mathematical expression for MPCR is as follows:

$$NPCR=\sum _{x=1}^n\sum _{y=1}^{m}C(x,y)\times {\displaystyle \frac{100\%}{n\times m}}$$

$$C(x,y)=\left\{\begin{array}{c}0,if A\left(x,y\right)=B(x,y)\\ 1,if A\left(x,y\right)\ne B(x,y)\end{array}\right.$$

where $O(x,y)$ is the original image and the encrypted image is $E(x,y)$ and $C(x,y)$ is a specified array of the same size as A and B.

On the other hand, the unified average changing intensity (UACI) analyzes how much the intensity of the original and encrypted images changes. In terms of math,

$$UACI=\sum _{i=1}^n\sum _{j=1}^m\left[{\displaystyle \frac{|O\left(i,j\right)-E\left(i,j\right)|}{255}}\right]\times {\displaystyle \frac{100\%}{n\times m}}$$

$$BACI={\displaystyle \frac{1}{(m-1)(n-1)}}\sum _{i=1}^{(m-1)(n-1)}{\displaystyle \frac{x_i}{255}}\times 100\%$$

In these computations, the image size is denoted by $\mathrm{M}\times \mathrm{N}$, and $x_i$ displays the average of the absolute values of the difference between the two elements. A small change in the plaintext can have a maximum effect on the encrypted image’s pixel count thanks to the diffusion operation of the image encryption technique. When there is a complete difference between the two photos, the expected value of NPCR is 99.6094%. The expected value of UACI was 33.4635%, while the theoretical value of BACI is 25% [63]. Table 11 makes it evident that the NPCR for encrypted images matches the expected value, and this is also the case for UACI and BACI cases.

Table 11. UACI, NPCR, and BACI scores of all selected images.

Images	UACI%	NPCR%	BACI%
Medical_Image_1	43.6086	$99.4141$	26.6778
Medical_Image_2	$42.8617$	99.4961	$29.3678$
Medical_Image_3	$40.8491$	$99.7223$	$27.6631$
Medical_Image_4	$53.6744$	$99.1307$	$31.3947$

13. Conclusions

This study emphasizes the critical role of substitution boxes, particularly in the context of image encryption within block cipher systems. Through the implementation of a unique symmetric block encryption scheme, we have showcased the effectiveness of incorporating chaotic systems into cryptographic applications. This was achieved by implementing a permutation group $G$ on a set of pseudo-random numbers derived from the concatenation of two 8-bit arrays generated by the Tent and May chaotic maps. By employing a series of iterative generation, normalization, and additional processing techniques, we can create an S-box that plays a crucial role in strengthening the resilience of cryptographic algorithms. Specifically for medical images, the image encryption approach, which combines segmentation, block reordering via unique permutations, and pixel value substitution using the S-box, represents a significant advance in block cipher security. This cutting-edge method not only guarantees the privacy and security of medical information but also demonstrates impressive resistance to different types of attacks, both cryptographic and statistical. Our method has been extensively evaluated using various metrics, including PSNR, UACI, MSE, NCC, AD, SC, MD, and NAE. The results consistently show that our approach outperforms existing methods. Our findings confirm the effectiveness and potential of our proposed encryption scheme in enhancing the security of image encryption within block ciphers. Future research directions could explore ways to enhance and optimize our method to adapt to changing cryptographic requirements and challenges.