Sufficient Conditions for Linear Operators Related to Confluent Hypergeometric Function and Generalized Bessel Function of the First Kind to Belong to a Certain Class of Analytic Functions

Abstract

Geometric function theory has extensively explored the geometric characteristics of analytic functions within symmetric domains. This study analyzes the geometric properties of a specific class of analytic functions employing confluent hypergeometric functions and generalized Bessel functions of the first kind. Specific constraints are imposed on the parameters to ensure the inclusion of the confluent hypergeometric function within the analytic function class. The coefficient bound of the class is used to determine the inclusion properties of integral operators involving generalized Bessel functions of the first kind. Different results are observed for these operators, depending on the specific values of the parameters. The results presented here include some previously published findings as special cases.

1. Introduction

The incredible use of special functions has provoked great interest among researchers in the last few decades. Geometric function theory has extensive literature addressing the geometric and analytic characteristics of various kinds of hypergeometric functions, such as the Gaussian hypergeometric function [1,2,3,4], confluent hypergeometric function [1,5,6,7,8], Bessel function [9,10,11,12], Struve function [13,14,15], Lommel function [13,16,17], $q–$Bessel–Wright function [18] and other generalized hypergeometric functions [19,20]. The authors employed many methods to determine various conditions on the parameters of these special functions to be in the class of normalized analytic functions.

Let $\mathcal{A}$ denote the class of analytic functions of the form

$$\begin{array}{c}\hfill f\left(z\right)=z+\sum _{k=0}^{\infty }{a}_k{z}^k\end{array}$$

(1)

in the open unit disk $\mathbb{D}$$(\mathbb{D}=\{z:\left|z\right|<1\left\}\right)$ and $\mathcal{S}$ be the class of univalent functions, that is

$$\begin{array}{c}\hfill \mathcal{S}:=\left\{f\in \mathcal{A}:f\left(z\right)\mathrm{is}\mathrm{univalent}\mathrm{in}\mathbb{D}\right\}.\end{array}$$

There are many subclasses of $\mathcal{S}$ (see [1,21,22]) from which ${\mathcal{S}}^{*}$ and $\mathcal{K}$ are known as the classes of starlike functions and convex functions, respectively

$$\begin{array}{c}\hfill {\mathcal{S}}^{*}:=\left\{f\in \mathcal{A}:f\left(z\right)\mathrm{is}\mathrm{starlike}\mathrm{in}\mathbb{D}\right\}\end{array}$$

and

$$\begin{array}{c}\hfill \mathcal{K}:=\left\{f\in \mathcal{A}:f\left(z\right)\mathrm{is}\mathrm{convex}\mathrm{in}\mathbb{D}\right\}.\end{array}$$

A function $f\in \mathcal{A}$ is said to be close-to-convex if and only if $\mathrm{Re}\left\{{\displaystyle e^{i\lambda }\frac{z{f}^{\prime }\left(z\right)}{g\left(z\right)}}\right\}>0$, $z\in \mathbb{D}$, where $g\left(z\right)$ is a fixed starlike function and $\lambda \in \mathbb{R}$. The class of all close-to-convex functions is denoted by $\mathcal{C}$. In this study, we considered the following definitions:

Definition 1 

([23,24]). For $\lambda >0$ then the classes ${\mathcal{S}}_{\lambda }^{*}$ and ${\mathcal{K}}_{\lambda }$ are defined as

$$\begin{array}{c}\hfill {\mathcal{S}}_{\lambda }^{*}=\left\{f\in \mathcal{A}:\left|\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}-1\right|<\lambda ,z\in \mathbb{D}\right\}\end{array}$$

and

$$\begin{array}{c}\hfill {\mathcal{K}}_{\lambda }=\left\{f\in \mathcal{A}:\left|\frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}\right|<\lambda ,z\in \mathbb{D}\right\}.\end{array}$$

Let a function $f\left(z\right)\in {\mathcal{K}}_{\lambda }$ if and only if $z{f}^{\prime }\left(z\right)\in {\mathcal{S}}_{\lambda }^{*}$.

Definition 2 

([25]). Let $f\left(z\right)\in \mathcal{A}$, for $0\le k<\infty ,0\le \sigma <1$ then the function $f\left(z\right)$ to be in $k-\mathcal{UCV}\left(\sigma \right)$ if and only if

$$\begin{array}{c}\hfill \mathrm{Re}\left(1+\frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}\right)\ge k\left|\frac{z{f}^{\prime \prime }\left(z\right)}{h^{\prime }\left(z\right)}\right|+\sigma .\end{array}$$

When $\sigma =0$, then $k-\mathcal{UCV}\left(0\right)=k-\mathcal{UCV}$, and when $k=1$, then $1-\mathcal{UCV}=\mathcal{UCV}$.

Definition 3 

([25]). Let $f\left(z\right)$ be of the form (1) and $z\in \mathbb{D}$, then $\mathcal{CP}\left(\delta \right)$ is defined as

$$\begin{array}{c}\hfill \mathcal{CP}\left(\delta \right)=\left\{f\left(z\right)\in \mathcal{S}:\left|\frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}+1-\delta \right|\le \mathrm{Re}\left(\frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}\right)+1+\delta ,0<\delta <\infty \right\}.\end{array}$$

A function $f\left(z\right)\in \mathcal{A}$ is said to be parabolic starlike if

$$\begin{array}{c}\hfill \mathrm{Re}\left(\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\right)>\left|\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}-1\right|+\sigma ,z\in \mathbb{D},\end{array}$$

the class of such functions denoted by ${\mathcal{S}}_p\left(\sigma \right)$ (see [26]). A related class $k-{\mathcal{S}}_p\left(\sigma \right)$ is defined by using the Alexander transform as $f\left(z\right)\in k-\mathcal{UCV}\left(\sigma \right)$ if and only if $z{f}^{\prime }\in k-{\mathcal{S}}_p\left(\sigma \right)$. For $\sigma =0$ the classes $k-{\mathcal{S}}_p\left(\sigma \right)$ reduce to $k-{\mathcal{S}}_p$, of functions $k–$parabolic starlike in $\mathbb{D}$ (see [27,28]). In particular, when $k=1$, then $1-{\mathcal{S}}_p\equiv {\mathcal{S}}_p$ is the parabolic starlike functions in $\mathbb{D}$ (see [29,30]). The inclusion properties of several subclasses of S are investigated for various linear operators in the literature (see [3,4]). In this work, we are interested to study the following subclass [3]:

$$\begin{array}{c}\hfill R_{\gamma ,\alpha }^{\tau }\left(\beta \right)=\left\{f\left(z\right)\in \mathcal{A}:\left|\frac{(1-\alpha +2\gamma )\frac{f}{z}+(\alpha -2\gamma )f^{\prime }+\gamma z{f}^{\prime \prime }-1}{2\tau (1-\beta )+(1-\alpha +2\gamma )\frac{f}{z}+(\alpha -2\gamma )f^{\prime }+\gamma z{f}^{\prime \prime }-1}\right|<1,z\in \mathbb{D}\right\},\end{array}$$

where $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$.

The coefficient bound for the function $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ is given by

$$\begin{array}{c}\hfill |a_n|\le \frac{2\left|\tau \right|(1-\beta )}{1+(n-1)(\alpha -2\gamma +\gamma n)},n=2,3,\cdots .\end{array}$$

(2)

The extreme function of the classes $R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ is

$$\begin{array}{c}\hfill f\left(z\right)=\frac{1}{z^{(1/v)-1}}\frac{1}{uv}{\int }_0^z\frac{1}{t^{\frac{1}{u}-\frac{1}{v}+1}}{\int }_0^t{\omega }^{\frac{1}{1-\frac{1}{u}}}\left(1+\frac{2(1-\beta )\tau {\omega }^{n-1}}{1-{\omega }^{n-1}}\right)d\omega ,\end{array}$$

where $u+v=\alpha -\gamma$ and $uv=\gamma$. Since $1+(n-1)(\alpha -2\gamma +\gamma n)=(1-\alpha )+\gamma (2+n^2)+n(\alpha -3\gamma )\ge n(\alpha -3\gamma )$, the inequality (2) can be rewritten as (see [3])

$$\begin{array}{c}\hfill |a_n|\le \frac{2\left|\tau \right|(1-\beta )}{n(\alpha -3\gamma )},n=2,3,\cdots .\end{array}$$

(3)

The main objective of this work is to find several conditions on the parameters involved in the confluent hypergeometric function and generalized Bessel function of the first kind to belong to the class of normalized analytic functions. The confluent hypergeometric function $F(a;b;z)$ is defined as (see [1]), for $a,b\in \mathbb{C}$ with $b\ne 0,-1,-2,\cdots$

$$F(a;b;z)=\sum _{n=0}^{\infty }\frac{{\left(a\right)}_n}{{\left(b\right)}_{n}n!}{z}^n=\sum _{n=0}^{\infty }{a}_n{z}^n,z\in \mathbb{D},$$

(4)

where

$$\begin{array}{c}\hfill a_n=\frac{{\left(a\right)}_n}{{\left(b\right)}_{n}n!}.\end{array}$$

(5)

The series in (4) is convergent for all finite values of z. The function $F(a;b;z)$ satisfies the following conditions

$$\begin{array}{c}\hfill F(a+1;b+1;z)=\frac{b}{a}{F}^{\prime }(a;b;z)\end{array}$$

and

$$\begin{array}{c}\hfill F(a;a;z)=e^z.\end{array}$$

(6)

Confluent hypergeometric functions have a connection with symmetry about an axis. Several confluent hypergeometric functions map the unit disc to a domain symmetric with respect to the real axis, for example, $F(a;a;z)=e^z$ maps the unit disc to the region as shown below Figure 1.

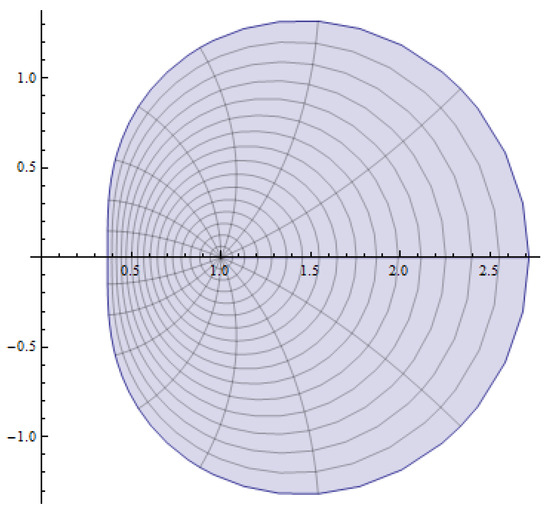
Figure 1. Mapping of unit disc by $F(a;a;z)=e^z$.

Inspired by the findings presented in references [31,32], our objective is to establish sufficient conditions for the parameter of the normalized Bessel function of the first kind. To initiate our discussion, let us revisit the definition of the generalized Bessel function of the first kind.

Let $p,q\in \mathbb{R}$ and $r\in \mathbb{C}$. The generalized Bessel function of the first kind ${\omega }_{p,q,r}\left(z\right)$ (see [9,31]) is defined as the particular solution of the second-order linear homogenous differential equation

$$\begin{array}{c}\hfill z^2{\omega }^{\prime \prime }\left(z\right)+qz{\omega }^{\prime }\left(z\right)+[r{z}^2-p^2+(1-q)p]\omega \left(z\right)=0,\end{array}$$

(7)

which is a natural generalization of Bessel’s equation. This function has the familiar representation

$$\begin{array}{c}\hfill {\omega }_p\left(z\right)={\omega }_{p,q,r}\left(z\right)=\sum _{n=0}^{\infty }\frac{{(-1)}^n{r}^n}{\left(n\right)!\Gamma \left(p+n+\frac{q+1}{2}\right)}{\left(\frac{z}{2}\right)}^{2n+p},\forall z\in \mathbb{C}.\end{array}$$

(8)

Equation (7) allows us to look into Bessel, modified Bessel, and spherical Bessel functions. The solutions to Equation (7) are called the generalized Bessel function of order p. The particular solution described in Equation (8) is known as the generalized Bessel function of the first kind of order p. However, the series mentioned earlier converges everywhere in $\mathbb{C}$. Now, let us consider the function ${\mathcal{U}}_p\left(z\right)$, defined through the transformation

$$\begin{array}{c}\hfill {\mathcal{U}}_p\left(z\right)={\left[{\alpha }_0\left(p\right)\right]}^{-1}{z}^{-\frac{p}{2}}{\omega }_p\left(\sqrt{z}\right).\end{array}$$

The series representation of ${\mathcal{U}}_p\left(z\right)$ is

$$\begin{array}{c}\hfill {\mathcal{U}}_p\left(z\right)={}_0\mathrm{F}_1\left({\mathtt{t}}_p,-\frac{rz}{4}\right)=\sum _{n=0}^{\infty }\frac{{(-1)}^n{r}^n}{4^n{\left({\mathtt{t}}_p\right)}_n{\left(1\right)}_n}{z}^n,\end{array}$$

(9)

where ${\mathtt{t}}_p=p+(q+1)/2\ne 0,-1,-2,\cdots$. It also satisfies the following conditions [31]

$$\sum _{n=0}^{\infty }\frac{{(-r/4)}^n}{{\left({\mathtt{t}}_p\right)}_n{\left(1\right)}_{n+1}}=\frac{-4({\mathtt{t}}_p-1)}{r}[{\mathcal{U}}_{p-1}\left(1\right)-1],$$

(10)

and

$$\begin{array}{c}\hfill {\mathcal{U}}_{p+1}\left(z\right)=\frac{-4{\mathtt{t}}_p}{r}{\mathcal{U}}_p^{\prime }\left(z\right),\forall z\in \mathbb{C},\end{array}$$

(11)

where $r<0,{\mathtt{t}}_p>1$ and ${\mathtt{t}}_p\ne 0,-1,-2,\cdots$.

For $f\left(z\right)\in \mathcal{A}$, using a convolution operator ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)$ is defined as (see [32])

$$\begin{array}{c}\hfill {\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)=z{\mathcal{U}}_p\left(z\right)\ast f\left(z\right)\end{array}$$

(12)

where ∗ denotes the Hadamard product or convolution of two functions, which is defined for the functions $f\left(z\right)$ of form (1) and

$$\begin{array}{c}\hfill g\left(z\right)=z+\sum _{n=2}^{\infty }{b}_n{z}^n\end{array}$$

as

$$\begin{array}{c}\hfill (f\ast g)\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{b}_n{z}^n.\end{array}$$

The series representation of Equation (12) is given by

$$\begin{array}{c}\hfill {\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)=z+\sum _{n=2}^{\infty }\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}(n-1)!}{a}_n{z}^n=z+\sum _{n=2}^{\infty }{A}_n{z}^n.\end{array}$$

(13)

In this article, we discuss the inclusion characteristics of confluent hypergeometric functions ${}_{1}F_1(a,b,z)$ and associated integral operator to the class $R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$. We mainly derive sufficient conditions involving the parameter of a, b, $\gamma$, $\alpha$, $\tau$ and $\beta$. All the results are stated and proved in Section 3. Several geometric characteristics of operator ${\mathcal{H}}_{{\mathtt{t}}_p,r}f\left(z\right)$ for $f\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ are also given in Section 3. Special cases leads to known results. For this purpose, we recall few basic results from the literature in Section 2, while the concluding remark is stated in Section 4.

2. Preliminary Results

Lemma 1 

([1]). For $a,b\in \mathbb{C}$ and $b\ne 0,-1,-2,-3,\cdots$, the confluent hypergeometric function ${}_{1}F_1(a;b;z)$ satisfies the following contiguous relations:

i 

$$\begin{array}{c}\hfill (a-b+1){}_{1}F_1(a;b;z)=a{}_{1}F_1(a+1;b;z)-(b-1){}_{1}F_1(a;b-1;z).\end{array}$$

(14)

ii 

$$\begin{array}{c}\hfill b(a+z){}_{1}F_1(a;b;z)=ab{}_{1}F_1(a+1;b;z)-(a-b)z{}_{1}F_1(a;b+1;z).\end{array}$$

(15)

iii 

$$\begin{array}{c}\hfill b{}_{1}F_1(a;b;z)=b{}_{1}F_1(a-1;b;z)+z{}_{1}F_1(a;b+1;z).\end{array}$$

(16)

Lemma 2 

([3]). Let $f\left(z\right)\in \mathcal{A}$ be of the form (1), then a sufficient condition for $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ is

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }\left[1+(n-1)(\alpha -2\gamma +\gamma n)\right]|a_n|\le |\tau |(1-\beta ).\end{array}$$

(17)

Lemma 3 

([32]). Let $f\left(z\right)\in \mathcal{A}$ be the form (1), if it satisfies

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }(\lambda +n-1)\left|a_n\right|\le \lambda ,\lambda >0\end{array}$$

(18)

then $f\left(z\right)\in {\mathcal{S}}_{\lambda }^{*}$.

Lemma 4 

([32]). Let $f\left(z\right)\in \mathcal{A}$ be the form (1), if it satisfies

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }n(\lambda +n-1)\left|a_n\right|\le \lambda ,\lambda >0\end{array}$$

(19)

then $f\left(z\right)\in {\mathcal{K}}_{\lambda }$.

Lemma 5 

([25]). Let $f\left(z\right)\in \mathcal{A}$ be in $k-\mathcal{UCV}\left(\sigma \right)$ if

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }n[n(1+k)-(k+\sigma )]\left|a_n\right|\le 1-\sigma .\end{array}$$

(20)

Lemma 6 

([25]). Let $f\left(z\right)\in \mathcal{A}$ be in $k-{\mathcal{S}}_p\left(\sigma \right)$ if it satisfies the following condition

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }[n(1+k)-(k+\sigma )]\left|a_n\right|\le 1-\sigma .\end{array}$$

(21)

Lemma 7 

([25]). Let $f\left(z\right)\in \mathcal{A}$ and it is of the form (1), if

$$\sum _{n=2}^{\infty }[n+2(\delta -1)]n\left|a_n\right|\le 2\delta -1,0<\delta <\infty$$

(22)

then $f\left(z\right)\in \mathcal{CP}\left(\delta \right)$.

3. Main Results

The parameters of the confluent hypergeometric function satisfy several conditions, letting ${}_{1}F_1(a;b;z)$ be in $R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$. The following theorem states the inclusion characteristics associated with confluent hypergeometric functions.

Theorem 1. 

Let $a,b\in \mathbb{C}$ with $b\ne 0,-1,-2,-3,\cdots$, if a and b are satisfied by one of the following conditions, then ${}_{1}F_1(a;b;z)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$. For $\left|b\right|>max\{0,|a|+1\}$

i. 

$$\begin{array}{cc}\hfill & \left(1-b\alpha +\gamma (a+b^2+1)\right){}_{1}F_1(a;b;1)+\left(\alpha (b-1)-\gamma (b^2-1)\right){}_{1}F_1(a;b-1;1)\hfill \\ & \le \frac{a}{b}+(1-\alpha +2\gamma )+\left|\tau \right|(1-\beta ).\hfill \end{array}$$

ii. 

$$\begin{array}{cc}\hfill & \left(1-b\alpha +\gamma (b^2-a^2+a+1)\right){}_{1}F_1(a;b;1)+\gamma a(a-b){}_{1}F_1(a-1;b;1)\hfill \\ & +(b-1)\left(\alpha -\gamma (1-a+b)\right){}_{1}F_1(a;b-1;1)\le \frac{a}{b}+(1-\alpha +2\gamma )+\left|\tau \right|(1-\beta ).\hfill \end{array}$$

Proof. 

The sufficient condition from Lemma 2 for the class $R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ is

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }\left[1+(n-1)(\alpha -2\gamma +\gamma n)\right]|a_n|\le |\tau |(1-\beta ).\end{array}$$

(23)

Applying (5) in (23), we obtain

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }\left[(1-\alpha +2\gamma )+n(\alpha -2\gamma )+n(n-1)\gamma \right]\frac{{\left(a\right)}_n}{{\left(b\right)}_n{\left(1\right)}_n}\le \left|\tau \right|(1-\beta )\\ \hfill (1-\alpha +2\gamma )\sum _{n=2}^{\infty }\frac{{\left(a\right)}_n}{{\left(b\right)}_n{\left(1\right)}_n}+(\alpha -2\gamma )\sum _{n=2}^{\infty }\frac{{\left(a\right)}_n}{{\left(b\right)}_n{\left(1\right)}_{n-1}}+\gamma \sum _{n=2}^{\infty }\frac{{\left(a\right)}_n}{{\left(b\right)}_n{\left(1\right)}_{n-2}}\le \left|\tau \right|(1-\beta ).\end{array}$$

(24)

Further from (24), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & (1-\alpha +2\gamma ){}_{1}F_1(a;b;1)+(\alpha -2\gamma )\frac{a}{b}{}_{1}F_1(a+1;b+1;1)+\gamma \frac{{\left(a\right)}_2}{{\left(b\right)}_2}{}_{1}F_1(a+2;b+2;1)\hfill \\ & -\left[\frac{a}{b}+(1-\alpha +2\gamma )\right]\le \left|\tau \right|(1-\beta ).\hfill \end{array}\end{array}$$

(25)

We will use (25) to prove both the cases of the Theorem 1.

i

From (14)–(16), we obtain

$$\begin{array}{c}\hfill {}_{1}F_1(a+1;b+1;1)=\frac{b(1-b)}{a}\left[{}_{1}F_1(a;b;1)-{}_{1}F_1(a;b-1;1)\right]\end{array}$$

(26)

and

$$\begin{array}{c}\hfill {}_{1}F_1(a+2;b+2;1)=\frac{[a+{(b-1)}^2]{\left(b\right)}_2}{{\left(a\right)}_2}{}_{1}F_1(a;b;1)-\frac{(1-b){(b-1)}_3}{{\left(a\right)}_2}{}_{1}F_1(a;b-1;1).\end{array}$$

(27)

Using (26) and (27) in (25), we obtain

$$\begin{array}{cc} & (1-\alpha +2\gamma ){}_{1}F_1(a;b;1)+(\alpha -2\gamma )\frac{a}{b}\frac{b(1-b)}{a}\left[{}_{1}F_1(a;b;1)-{}_{1}F_1(a;b-1;1)\right]\hfill \\ & +\gamma \frac{{\left(a\right)}_2}{{\left(b\right)}_2}\left[\frac{[a+{(b-1)}^2]{\left(b\right)}_2}{{\left(a\right)}_2}{}_{1}F_1(a;b;1)-\frac{(1-b){\left(b_1\right)}_3}{{\left(a\right)}_2}{}_{1}F_1(a;b-1;1)\right]\hfill \\ & \le \frac{a}{b}+(1-\alpha +2\gamma )+\left|\tau \right|(1-\beta ).\hfill \end{array}$$

(28)

Simplifying (24), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & [(1-\alpha +2\gamma )+(\alpha -2\gamma )(1-b)+\gamma (a+{(b-1)}^2)]{}_{1}F_1(a;b;1)\hfill \\ & -[(\alpha -2\gamma )(1-b)+\gamma {(b-1)}^2]{}_{1}F_1(a;b-1;1)\le \frac{a}{b}+(1-\alpha +2\gamma )+\left|\tau \right|(1-\beta ).\hfill \end{array}\end{array}$$

(29)

From (29), we will obtain the required result.

ii

From (14)–(16), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_{1}F_1(a+2;b+2;1)& =[{(b-1)}^2+a(1-a)]\frac{{\left(b\right)}_2}{{\left(a\right)}_2}{}_{1}F_1(a;b;1)\hfill \\ & +\frac{(a-b+1){(b-1)}_3}{{\left(a\right)}_2}{}_{1}F_1(a;b-1;1)+\frac{(a-b){\left(b\right)}_2}{(a+1)}{}_{1}F_1(a-1;b;1).\hfill \end{array}\end{array}$$

(30)

Applying (26) and (30) in (25), it follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & (1-\alpha +2\gamma ){}_{1}F_1(a;b;1)+(\alpha -2\gamma )\frac{a}{b}\frac{b(1-b)}{a}\left[{}_{1}F_1(a;b;1)-{}_{1}F_1(a;b-1;1)\right]\hfill \\ & +\gamma \frac{{\left(a\right)}_2}{{\left(b\right)}_2}\frac{[{(b-1)}^2+a(1-a)]{\left(b\right)}_2}{{\left(a\right)}_2}{}_{1}F_1(a;b;1)+\gamma \frac{{\left(a\right)}_2}{{\left(b\right)}_2}\frac{(a-b+1){(b-1)}_3}{{\left(a\right)}_2}{}_{1}F_1(a;b-1;1)\hfill \\ & +\gamma \frac{{\left(a\right)}_2}{{\left(b\right)}_2}\frac{(a-b){\left(b\right)}_2}{(a+1)}{}_{1}F_1(a-1;b;1)\le \frac{a}{b}+(1-\alpha +2\gamma )+\left|\tau \right|(1-\beta ).\hfill \end{array}\end{array}$$

(31)

Finally from (31), we will obtain the required result. □

The above result will have a different expression for some particular values of the parameters $a,b$. We consider a few special cases and presented below as example.

Example 1. 

In our first example, we consider $b=a$. Then, ${}_{1}F_1(a;b;z)={}_{1}F_1(a;a;z)=e^z$. Now, for $\left|a\right|>0$, if the inequality

$$\begin{array}{c}\hfill (1+\gamma )e+\alpha -2\gamma -2\le \left|\tau \right|(1-\beta )\end{array}$$

holds, then $e^z\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$.

The verification of the above claim can be performed as follows: From Lemma 2, it is sufficient to establish the inequality

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }\left[(1-\alpha +2\gamma )+n(\alpha -2\gamma )+n(n-1)\gamma \right]|a_n|\le |\tau |(1-\beta ).\end{array}$$

(32)

Applying the coefficient of ${}_{1}F_1(a;a;z)$ in (32), we obtain

$$\begin{array}{cc}\hfill & \sum _{n=2}^{\infty }\left[(1-\alpha +2\gamma )+n(\alpha -2\gamma )+n(n-1)\gamma \right]\frac{1}{{\left(1\right)}_n}\le \tau |(1-\beta )\hfill \\ \hfill \Rightarrow & (1-\alpha +2\gamma )\sum _{n=2}^{\infty }\frac{1}{{\left(1\right)}_n}+(\alpha -2\gamma )\sum _{n=2}^{\infty }\frac{1}{{\left(1\right)}_{n-1}}+\gamma \sum _{n=2}^{\infty }\frac{1}{{\left(1\right)}_{n-2}}\le \tau |(1-\beta ).\hfill \end{array}$$

(33)

Using (6) in (33), we obtain

$$\begin{array}{c}\hfill (1-\alpha +2\gamma )\left(e-2\right)+(\alpha -2\gamma )\left(e-1\right)+\gamma e\le \left|\tau \right|(1-\beta ).\end{array}$$

(34)

From (34), we will obtain the conclusion.

Example 2. 

If $a=1$ and $b=2$ then ${}_{1}F_1(1;2;z)=(e^z-1)/z$. If

$$\begin{array}{cc}\hfill (1-\alpha +3\gamma )e-\left(\frac{5}{2}-3\alpha +8\gamma \right)\le & \left|\tau \right|(1-\beta ),\hfill \end{array}$$

holds, then $(e^z-1)/z\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$.

The verification of the above claim can be performed as follows: Again from Lemma 2, it is sufficient to validate the inequality

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }\left[(1-\alpha +2\gamma )+n(\alpha -2\gamma )+n(n-1)\gamma \right]|a_n|\le |\tau |(1-\beta ).\end{array}$$

(35)

Applying the coefficient of ${}_{1}F_1(1;2;z)$ in (35), we obtain

$$\begin{array}{cc} & \sum _{n=2}^{\infty }\left[(1-2\alpha +6\gamma )+(n+1)(\alpha -4\gamma )+n(n+1)\gamma \right]\frac{1}{(n+1)!}\le \tau |(1-\beta )\hfill \\ \Rightarrow \hfill & (1-2\alpha +6\gamma )\sum _{n=2}^{\infty }\frac{1}{(n+1)!}+(\alpha -4\gamma )\sum _{n=2}^{\infty }(n+1)\frac{1}{(n+1)!}+\gamma \sum _{n=2}^{\infty }n(n+1)\frac{1}{(n+1)!}\le \tau \left|\right(1-\beta )\hfill \\ \Rightarrow \hfill & (1-2\alpha +6\gamma )\left(e-\frac{5}{2}\right)+(\alpha -4\gamma )(e-2)+\gamma (e-1)\le \tau |(1-\beta ).\hfill \end{array}$$

(36)

From (36), we will obtain the required results.

Example 3. 

If $a=1$ and $b=3$, then ${}_{1}F_1(1;3;z)=2!(e^z-1-z/z^2$.If

$$\begin{array}{c}\hfill 2(1-2\alpha +11\gamma )e-\frac{2}{3}\left(8-19\alpha +104\gamma \right)\le \left|\tau \right|(1-\beta ),\end{array}$$

holds, then $2!(e^z-1-z)/z^2\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$.

The verification of the above claim can be performed as follows: Again apply the coefficient of ${}_{1}F_1(1;3;z)$ in (35), we obtain

$$\begin{array}{cc}\hfill & \sum _{n=2}^{\infty }\left[(1-\alpha +2\gamma )+n(\alpha -2\gamma )+n(n-1)\gamma \right]\frac{{\left(1\right)}_n}{{\left(3\right)}_{n}n!}\le \left|\tau \right|(1-\beta )\hfill \\ \hfill \Rightarrow & (1-3\alpha +16\gamma )\sum _{n=2}^{\infty }\frac{2}{(n+2)!}+(\alpha -6\gamma )\sum _{n=2}^{\infty }\frac{2}{(n+1)!}+\gamma \sum _{n=2}^{\infty }\frac{2}{n!}\le \left|\tau \right|(1-\beta )\hfill \\ \hfill \Rightarrow & (1-3\alpha +16\gamma )2\left(e-\frac{8}{3}\right)+(\alpha -6\gamma )2\left(e-\frac{5}{3}\right)+2\gamma \left(e-2\right)\le \left|\tau \right|(1-\beta )\hfill \\ \hfill \Rightarrow & 2(1-2\alpha +11\gamma )e-\frac{2}{3}\left(8-19\alpha +104\gamma \right)\le \left|\tau \right|(1-\beta ).\hfill \end{array}$$

Example 4. 

When $a=-n$ and $b=1$, the confluent hypergeometric function ${}_{1}F_1(-n;1;z)$ becomes the Laguerre polynomial $L_n\left(z\right)$. Thus, if for $a=-n$, $b=1$, and the inequality

$$\begin{array}{cc}\hfill (1+\gamma )e^{-1}-\alpha +2\gamma \le & \left|\tau \right|(1-\beta )\hfill \end{array}$$

holds, then $L_n\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$.

To verify this claim, now we apply the coefficient of ${}_{1}F_1(-n;1;z)$ in (35). Then, we have

$$\begin{array}{cc}\hfill & \sum _{n=2}^{\infty }\left[(1-\alpha +2\gamma )+n(\alpha -2\gamma )+n(n-1)\gamma \right]\frac{{(-1)}^n}{n!}\le \left|\tau \right|(1-\beta )\hfill \\ \hfill \Rightarrow & (1-\alpha +2\gamma )\sum _{n=2}^{\infty }\frac{{(-1)}^n}{n!}+(\alpha -2\gamma )\sum _{n=2}^{\infty }\frac{{(-1)}^n}{(n-1)!}+\gamma \sum _{n=2}^{\infty }\frac{{(-1)}^n}{(n-2)!}\le \left|\tau \right|(1-\beta )\hfill \\ \hfill \Rightarrow & (1-\alpha +2\gamma )e^{-1}+(\alpha -2\gamma )(e^{-1}-1)+\gamma e^{-1}\le \left|\tau \right|(1-\beta ).\hfill \end{array}$$

(37)

From (37), we will obtain the required results.

Next, we consider the operator

$$T(a;b;z)={\int }_0^{z}F(a;b;\lambda )d\lambda .$$

Term by term integration for the series of $F(a;b;\lambda )$, leads to

$$T(a;b;z):=z+\sum _{n=2}^{\infty }\frac{{\left(a\right)}_{n-1}}{{\left(b\right)}_{n-1}{\left(1\right)}_n}{z}^n=z+\sum _{n=2}^{\infty }{A}_n{z}^n,$$

where

$$\begin{array}{c}\hfill A_n=\frac{{\left(a\right)}_{n-1}}{{\left(b\right)}_{n-1}{\left(1\right)}_n}.\end{array}$$

(38)

The next result provides conditions for which $T(a;b;z)$ is in $R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$.

Theorem 2. 

Suppose that $a\in \mathbb{C}\setminus \left\{1\right\}$ and $\left|b\right|>\left|a\right|+1$. Further, if

$$\begin{array}{cc}\hfill & (\alpha +\gamma -3){}_{1}F_1(a;b;1)+\gamma \frac{a}{b}{}_{1}F_1(a+1;b+1;1)\hfill \\ & +(3-\alpha ){}_{1}F_1(a-1;b-1;1)\le \gamma +\frac{(3-\alpha )(b-1)}{(a-1)}+\left|\tau \right|(1-\beta ),\hfill \end{array}$$

then $T(a;b;z)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$.

Proof. 

For class $R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$, the sufficient conditions form Lemma 2 is

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }\left[(\alpha +\gamma -3)n+\gamma n(n-1)+(3-\alpha )\right]|A_n|\le |\tau |(1-\beta ).\end{array}$$

(39)

Applying (38) in (39), then

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }\left[(\alpha +\gamma -3)n+\gamma n(n-1)+(3-\alpha )\right]\frac{{\left(a\right)}_{n-1}}{{\left(b\right)}_{n-1}{\left(1\right)}_n}\le \left|\tau \right|(1-\beta ).\end{array}$$

(40)

Simplifying (40), we obtain

$$\begin{array}{cc}\hfill & (\alpha +\gamma -3){}_{1}F_1(a;b;1)-(\alpha +\gamma -3)+\gamma \frac{a}{b}{}_{1}F_1(a+1;b+1;1)\hfill \\ & +(3-\alpha ){}_{1}F_1(a-1;b-1;1)-(3-\alpha )-\frac{(3-\alpha )(b-1)}{a-1}\le \left|\tau \right|(1-\beta ).\hfill \end{array}$$

(41)

From (41) and the hypothesis of the theorem will obtain the result. □

Taking $a=b$ in the above result then the following result is direct.

Corollary 1. 

If for $a\in \mathbb{C}$ and $\left|a\right|>1$, the inequality

$$\begin{array}{cc}\hfill & 2e-1\le \frac{1}{\gamma }\left(3-\alpha +\left|\tau \right|(1-\beta )\right),\hfill \end{array}$$

holds, then $T(a;a;z)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$.

Let the linear operator ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)$ belong to the class of univalent functions or to its subclasses of ${\mathcal{S}}_{\lambda }^{*}$, ${\mathcal{K}}_{\lambda }$, $k-\mathcal{UCV}\left(\sigma \right)$, $k-{\mathcal{S}}_p\left(\sigma \right)$ and $\mathcal{CP}\left(\delta \right)$, by satisfying several relevant criteria on the parameters involved in these special functions. From (13), the coefficient of the operator ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)$ is

$$\begin{array}{c}\hfill A_n=\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}(n-1)!}{a}_n.\end{array}$$

(42)

Then the geometric characteristics related to $f\left(z\right)$ in $R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ are given in the following results.

Theorem 3. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds for $\lambda >0$:

$$\begin{array}{c}\hfill (1-\lambda ){\mathcal{U}}_{p-1}\left(1\right)-{\mathcal{U}}_{p-1}^{\prime }\left(1\right)-(\lambda -1)\le \frac{r\lambda }{4({\mathtt{t}}_p-1)}\left(1+\frac{\alpha -3\gamma }{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

Then, for $r<0$, ${\mathtt{t}}_p>1$, ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in {\mathcal{S}}_{\lambda }^{*}$.

Proof. 

In Lemma 3, the sufficient conditions for the class ${\mathcal{S}}_{\lambda }^{*}$ is given as

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }(\lambda +n-1)\left|A_n\right|\le \lambda .\end{array}$$

(43)

If $A_n$ as given in (42), then (43) can be rewritten as

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }(\lambda +n-1)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}(n-1)!}\left|a_n\right|\le \lambda .\end{array}$$

(44)

Using (3) on the left side of the inequality (44), we obtain

$$\begin{array}{cc}\hfill & \sum _{n=2}^{\infty }(\lambda +n-1)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}(n-1)!}\left|a_n\right|\hfill \\ \hfill \le & \sum _{n=2}^{\infty }(\lambda +n-1)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}(n-1)!}\frac{2\left|\tau \right|(1-\beta )}{n(\alpha -3\gamma )}\hfill \\ \hfill =& \frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left((\lambda -1)\sum _{n=2}^{\infty }\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}n!}+\sum _{n=2}^{\infty }n\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}n!}\right)\hfill \\ \hfill =& \frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left((\lambda -1)\sum _{n=0}^{\infty }\frac{{(-r/4)}^n}{{\left({\mathtt{t}}_p\right)}_n(n+1)!}+\sum _{n=0}^{\infty }\frac{{(-r/4)}^n}{{\left({\mathtt{t}}_p\right)}_n\left(n\right)!}-\lambda \right).\hfill \end{array}$$

(45)

Using (10) in (45) and applying it in the inequality (44), then

$$\begin{array}{c}\hfill \frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left((\lambda -1)\frac{-4({\mathtt{t}}_p-1)}{r}\left({\mathcal{U}}_{p-1}\left(1\right)-1\right)+{\mathcal{U}}_p\left(1\right)-\lambda \right)\le \lambda .\end{array}$$

(46)

Using (11) in (46), then

$$\begin{array}{c}\hfill (\lambda -1)\frac{-4({\mathtt{t}}_p-1)}{r}\left({\mathcal{U}}_{p-1}\left(1\right)-1\right)+\frac{-4({\mathtt{t}}_p-1)}{r}{\mathcal{U}}_{p-1}^{\prime }\left(1\right)-\lambda \le \lambda \frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}.\end{array}$$

(47)

From (47) and the hypothesis of the theorem will obtain the result. □

Remark 1. 

For $\gamma =0$, Theorem 3 leads to the Theorem 2 of [32].

Theorem 4. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds for $\lambda >0$:

$$\begin{array}{c}\hfill \lambda {\mathcal{U}}_p\left(1\right)+{\mathcal{U}}_p^{\prime }\left(1\right)\le \lambda \left(1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

Then, for $r<0$, ${\mathtt{t}}_p>1$, ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in {\mathcal{K}}_{\lambda }$.

Proof. 

From Lemma 4, it follows that the sufficient condition for the class ${\mathcal{K}}_{\lambda }$ is

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }n(\lambda +n-1)\left|A_n\right|\le \lambda .\end{array}$$

(48)

Considering $A_n$ as given in (42), the inequality (48) reduces to

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }n(\lambda +n-1)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}(n-1)!}\left|a_n\right|\le \lambda .\end{array}$$

(49)

Using (3) on the left side of (49), we obtain

$$\begin{array}{cc}\hfill & \sum _{n=2}^{\infty }n(\lambda +n-1)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\left|a_n\right|\hfill \\ \hfill \le & \sum _{n=2}^{\infty }n(\lambda +n-1)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\frac{2\left|\tau \right|(1-\beta )}{n(\alpha -3\gamma )}\hfill \\ \hfill =& \frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left(\sum _{n=2}^{\infty }\lambda \frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}+\sum _{n=2}^{\infty }(n-1)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\right)\hfill \\ \hfill =& \frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left(\lambda \sum _{n=0}^{\infty }\frac{{(-r/4)}^n}{{\left({\mathtt{t}}_p\right)}_n{\left(1\right)}_n}-\frac{r}{4{\mathtt{t}}_p}\sum _{n=0}^{\infty }\frac{{(-r/4)}^n}{{({\mathtt{t}}_p+1)}_n{\left(1\right)}_n}-\lambda \right)\hfill \\ \hfill =& \frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left(\lambda {\mathcal{U}}_p\left(1\right)-\frac{r}{4{\mathtt{t}}_p}{\mathcal{U}}_{p+1}\left(1\right)-\lambda \right).\hfill \end{array}$$

(50)

Using (11) in (50) and applying it in the inequality (49), then

$$\begin{array}{c}\hfill \lambda {\mathcal{U}}_p\left(1\right)+{\mathcal{U}}_p^{\prime }\left(1\right)-\lambda \le \lambda \frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}.\end{array}$$

(51)

From (51) and the hypothesis of the theorem will obtain the result. □

Remark 2. 

Note that when $\gamma =0$ in Theorem 4, it is equivalent to Theorem 3 of [32].

Theorem 5. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds for $k\ge 0$ and $0\le \sigma <1$:

$$\begin{array}{c}\hfill (1+k){\mathcal{U}}_p^{\prime }\left(1\right)+(1-\sigma ){\mathcal{U}}_p\left(1\right)\le (1-\sigma )\left(1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

Then, for $r<0$, ${\mathtt{t}}_p>1$, ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in k-\mathcal{UCV}\left(\sigma \right)$.

Proof. 

Note that the Lemma 5 gives the sufficient condition for the class $k-\mathcal{UCV}\left(\sigma \right)$ as

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }n\left(n(1+k)-(k+\sigma )\right)\left|A_n\right|\le 1-\sigma .\end{array}$$

(52)

Choosing $A_n$ as in (42), the inequality (52) reduces to

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }n\left(n(1+k)-(k+\sigma )\right)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\left|a_n\right|\le 1-\sigma .\end{array}$$

(53)

Using (3) on the left side of (53), we obtain

$$\begin{array}{cc}\hfill & \sum _{n=2}^{\infty }n\left(n(1+k)-(k+\sigma )\right)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\left|a_n\right|\hfill \\ \hfill \le & \sum _{n=2}^{\infty }n\left((n-1)(1+k)+(1-\sigma )\right)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\frac{2\left|\tau \right|(1-\beta )}{n(\alpha -3\gamma )}\hfill \\ \hfill =& \frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left((1+k)\sum _{n=2}^{\infty }\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-2}}+(1-\sigma )\sum _{n=2}^{\infty }\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\right)\hfill \\ \hfill =& \frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left(\frac{(1+k)(-r)}{4{\mathtt{t}}_p}{\mathcal{U}}_{p+1}\left(1\right)+(1-\sigma ){\mathcal{U}}_p\left(1\right)-(1-\sigma )\right).\hfill \end{array}$$

(54)

Using (11) in (54) and apply in (53), we obtain

$$\begin{array}{c}\hfill \frac{(1+k)(-r)}{4{\mathtt{t}}_p}\frac{4{\mathtt{t}}_p}{(-r)}{\mathcal{U}}_p^{\prime }\left(1\right)+(1-\sigma ){\mathcal{U}}_p\left(1\right)-(1-\sigma )\le (1-\sigma )\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}.\end{array}$$

(55)

From (55) and the hypothesis of the theorem will obtain the result. □

Remark 3. 

For $\gamma =0$, Theorem 5 is equivalent to Theorem 1 in [32].

Theorem 6. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds for $k\ge 0$ and $0\le \sigma <1$:

$$\begin{array}{c}\hfill (k+\sigma ){\mathcal{U}}_{p-1}\left(1\right)-(1+k){\mathcal{U}}_{p-1}^{\prime }\left(1\right)-(k+\sigma )\le \frac{r(1-\sigma )}{4({\mathtt{t}}_p-1)}\left(1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

Then, for $r<0$, ${\mathtt{t}}_p>1$, ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in k-{\mathcal{S}}_p\left(\sigma \right)$.

Proof. 

From Lemma 6, we have the sufficient condition for the class $k-{\mathcal{S}}_p\left(\sigma \right)$ as

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }(n(1+k)-(k+\sigma ))\left|A_n\right|\le 1-\sigma .\end{array}$$

(56)

Now, the coefficient $A_n$ as given in (42) leads the inequality (56) to

$$\begin{array}{c}\hfill \sum _{n=2}^{\infty }(n(1+k)-(k+\sigma ))\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\left|a_n\right|\le 1-\sigma .\end{array}$$

(57)

Using (3) on the left side of (57), we obtain

$$\begin{array}{cc}\hfill & \sum _{n=2}^{\infty }(n(1+k)-(k+\sigma ))\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\left|a_n\right|\hfill \\ \hfill & \le \sum _{n=2}^{\infty }(n(1+k)-(k+\sigma ))\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\frac{2\left|\tau \right|(1-\beta )}{n(\alpha -3\gamma )}\hfill \\ \hfill & =\frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left((1+k)\sum _{n=2}^{\infty }\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}-(k+\sigma )\sum _{n=2}^{\infty }\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_n}\right)\hfill \\ \hfill & =\frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left((1+k)\left(\sum _{n=0}^{\infty }\frac{{(-r/4)}^n}{{\left({\mathtt{t}}_p\right)}_n{\left(1\right)}_n}-1\right)-(k+\sigma )\left(\sum _{n=0}^{\infty }\frac{{(-r/4)}^n}{{\left({\mathtt{t}}_p\right)}_n{\left(1\right)}_{n+1}}-1\right)\right).\hfill \end{array}$$

(58)

Using (10) in second sum of (58) and applying it in the inequality (57), we obtain

$$\begin{array}{c}\hfill (1+k)\left({\mathcal{U}}_p\left(1\right)-1\right)-(k+\sigma )\left(\frac{-4({\mathtt{t}}_p-1)}{r}[{\mathcal{U}}_{p-1}\left(1\right)-1]-1\right)\le (1-\sigma )\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}.\end{array}$$

(59)

Applying (11) in the inequality (59), then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & (1+k)\left(\frac{-4({\mathtt{t}}_p-1)}{r}{\mathcal{U}}_{p-1}^{\prime }\left(1\right)-1\right)\hfill \\ & -(k+\sigma )\left(\frac{-4({\mathtt{t}}_p-1)}{r}({\mathcal{U}}_{p-1}\left(1\right)-1)-1\right)\le (1-\sigma )\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}.\hfill \end{array}\end{array}$$

(60)

From (60) and the hypothesis of the theorem will obtain the result. □

If $k=1$ then the following results are direct.

Corollary 2. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds for $0\le \sigma <1$:

$$\begin{array}{c}\hfill 2{\mathcal{U}}_p^{\prime }\left(1\right)+(1-\sigma ){\mathcal{U}}_p\left(1\right)\le (1-\sigma )\left(1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

Then, for $r<0$, ${\mathtt{t}}_p>1$, ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in \mathcal{UCV}\left(\sigma \right)$.

Corollary 3. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds for $0\le \sigma <1$:

$$\begin{array}{c}\hfill (1+\sigma ){\mathcal{U}}_{p-1}\left(1\right)-2{\mathcal{U}}_{p-1}^{\prime }\left(1\right)-(1+\sigma )\le \frac{r(1-\sigma )}{4({\mathtt{t}}_p-1)}\left(1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

Then, for $r<0$, ${\mathtt{t}}_p>1$, ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in {\mathcal{S}}_p\left(\sigma \right)$.

If $k=1$ and $\sigma =0$, then the following results are direct.

Corollary 4. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds:

$$\begin{array}{c}\hfill 2{\mathcal{U}}_p^{\prime }\left(1\right)+{\mathcal{U}}_p\left(1\right)\le 1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}.\end{array}$$

Then, for $r<0$, ${\mathtt{t}}_p>1$, ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in \mathcal{UCV}$.

Corollary 5. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds:

$$\begin{array}{c}\hfill {\mathcal{U}}_{p-1}\left(1\right)-2{\mathcal{U}}_{p-1}^{\prime }\left(1\right)-1\le \frac{r}{4({\mathtt{t}}_p-1)}\left(1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

Then, for $r<0$, ${\mathtt{t}}_p>1$,${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in {\mathcal{S}}_p$.

Theorem 7. 

Let $f\left(z\right)\in \mathcal{A}$ be of the form (1) and $f\left(z\right)\in R_{\gamma ,\alpha }^{\tau }\left(\beta \right)$ with $0\le \alpha <1$, $0\le \gamma <1$, $\tau \in \mathbb{C}\setminus \left\{0\right\}$ and $\beta <1$. Suppose that the following inequality holds for $0<\delta <\infty$:

$$\begin{array}{c}\hfill {\mathcal{U}}_p^{\prime }\left(1\right)+(2\delta -1){\mathcal{U}}_p\left(1\right)\le (2\delta -1)\left(1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

Then, for $r<0$,${\mathtt{t}}_p>1$, ${\mathcal{H}}_{{\mathtt{t}}_p,r}\left(f\right)\left(z\right)\in \mathcal{CP}\left(\delta \right)$.

Proof. 

From Lemma 7, the sufficient condition for the class $\mathcal{CP}\left(\delta \right)$ is

$$\sum _{n=2}^{\infty }n\left(n+2(\delta -1)\right)\left|A_n\right|\le 2\delta -1.$$

(61)

Applying (42) in (61), then

$$\sum _{n=2}^{\infty }n\left(n+2(\delta -1)\right)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\left|a_n\right|\le 2\delta -1.$$

(62)

Using (3) on the left side of (62), we obtain

$$\begin{array}{cc}\hfill & \sum _{n=2}^{\infty }n\left(n+2(\delta -1)\right)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\left|a_n\right|\hfill \\ \hfill & \le \sum _{n=2}^{\infty }n\left(n-1+2\delta -1\right)\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\frac{2\left|\tau \right|(1-\beta )}{n(\alpha -3\gamma )}\hfill \\ \hfill & =\frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left(\sum _{n=2}^{\infty }\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-2}}+(2\delta -1)\sum _{n=2}^{\infty }\frac{{(-r/4)}^{n-1}}{{\left({\mathtt{t}}_p\right)}_{n-1}{\left(1\right)}_{n-1}}\right)\hfill \\ \hfill & =\frac{2\left|\tau \right|(1-\beta )}{(\alpha -3\gamma )}\left(\frac{-r}{4{\mathtt{t}}_p}{\mathcal{U}}_{p+1}\left(1\right)+(2\delta -1){\mathcal{U}}_p\left(1\right)-(2\delta -1)\right).\hfill \end{array}$$

(63)

Using (11) in (63) and applying it in (62), we obtain

$$\begin{array}{c}\hfill \frac{-r}{4{\mathtt{t}}_p}\left(\frac{-4{\mathtt{t}}_p}{r}{\mathcal{U}}_p^{\prime }\left(1\right)\right)+(2\delta -1){\mathcal{U}}_p\left(1\right)\le (2\delta -1)\left(1+\frac{(\alpha -3\gamma )}{2\left|\tau \right|(1-\beta )}\right).\end{array}$$

(64)

From (64) and the hypothesis of the theorem will obtain the required result. □

4. Conclusions

In this work, confluent hypergeometric functions and generalized Bessel functions of the first kind are used to study the geometric properties of a particular class. For the confluent hypergeometric function to be in the class, a few limitations were imposed on the parameters. The coefficient bound of the class was used to determine the geometric characteristics of integral operators using confluent hypergeometric functions and the generalized Bessel function of the first kind. For specific parameter values, these operators produce a variety of results. The presented findings included several previously published special cases.