A Generalization of Secondary Characteristic Classes on Lie Pseudoalgebras

Abstract

The aim of the paper is to construct a secondary characteristic homomorphism for Lie pseudoalgebras. The case of inner product modules is under consideration.

1. Introduction

Secondary characteristic classes were discovered in the 1970s as global invariants of a principal fiber bundle with a connection whose curvature form vanishes (cf. [1,2]). These classes may depend on the connection. However, the classes of the principal bundle of a Riemannian manifold depend only on the conformal structure of the manifold. Various approaches to secondary characteristic classes have also been studied by, among others, Bott [3], Lehmann [4] and Heitsch [5]. The classes considered in this paper are related to the approach of defining the characteristic homomorphism of flat principal bundles determined by the connection of and the reduction of the structure of the Lie group, as considered by Kamber and Tondeur (cf. [6,7]). It has important topological properties such as homotopy independence, functoriality and rigidity. The secondary characteristic homomorphism defined in this paper is a generalization of the homomorphism considered for Lie algebroids (cf. [8,9,10]) to Lie pseudoalgebras.

Let A be a commutative algebra over a commutative ring R (not necessarily with a unital element). A Lie pseudoalgebra over$(R,A)$, or an $\left(R,A\right)$-Lie algebra, is defined as an A-module L equipped with the structure of an R-Lie algebra featuring a Lie bracket $\left[·,·\right]$ and a Lie algebra homomorphism ${\omega }_L:L\to Der\left(A\right)$, mapping from L into the Lie algebra $Der\left(A\right)$ of the derivations of A (with the bracket $\left[{\delta }_1,{\delta }_2\right]={\delta }_1\circ {\delta }_2-{\delta }_2\circ {\delta }_1$). This homomorphism, referred to as the anchor of L, is a morphism of A-modules such that

$$\left[\alpha ,b\beta \right]=b\left[\alpha ,\beta \right]+{\omega }_L\left(\alpha \right)\left(b\right)\beta$$

for $\alpha ,\beta \in L,b\in A$ (cf. [11,12,13,14,15,16]). If L is a Lie pseudoalgebra over $(R,A)$, then the pair $\left(A,L\right)$ is referred to as a Lie–Rinehart algebra (cf. [17,18]). For historical and substantive commentary on $(R,A)$-Lie algebras, we recommend referring to [18].

Lie pseudoalgebras are algebraic counterparts of Lie algebroids, which were first introduced by Pradines in [19] as infinitesimal objects of Lie groupoids. We should note that any smooth manifold M defines the Lie algebroid $TM$, which is the tangent bundle of M, with the identity anchor and the Lie algebra of vector fields on M. Other examples of Lie algebroids include Lie algebras, integrable distributions (especially foliations), cotangent bundles of Poisson manifolds (particularly symplectic manifolds) [20], Lie algebroids of principal bundles [21,22], Lie algebroids of transversal foliations [23] and Lie algebroids with Riemannian [24] or symplectic structure [25]. On the other hand, some algebraic structures can be considered as Lie pseudoalgebras. Some basic examples include the following: every Lie algebra $\left(\mathfrak{g},\left[·,·\right]\right)$ over a commutative ring R with the zero anchor and the module $Der\left(A\right)$ of all derivations of A for every commutative R-algebra A as the Lie subalgebra of ${End}_R\left(A\right)$ with the inclusion map as the anchor. In particular, the polynomial ring $R\left[t\right]$ of a commutative ring R over the algebra $R\left[t\right]$, with a chosen polynomial ${\nu }_0\in R\left[t\right]$, has a Lie bracket determined by $[f,g]={\nu }_0(f{g}^{\prime }-f^{\prime }g)$, and the anchor $\omega :R\left[t\right]\to Der\left(R\right[t\left]\right)$ is given by $\omega \left(f\right)={\nu }_{0}f\frac{d}{dt}$ (cf. [26]). In [27], further examples of Lie pseudoalgebras are defined by derived preinfintesimal modules as the algebraic counterparts of the derived Lie almost vector bundles introduced in [28].

Other sources of Lie pseudoalgebras, which do not necessarily define Lie algebroids, include certain Poisson algebras and foliations. For examples arising from singular distributions, you can refer to the examples of Lie pseudoalgebras associated with an almost Lie structure discussed in [29]. Additionally, each Poisson algebra A over a commutative ring R determines the A-module of Kähler differentials ${\Omega }_{A/R}^1$, which serves as an analog of the module of 1-forms in the case of $A=C^{\infty }\left(M\right)$ for a smooth manifold M. In [17], it is demonstrated that in ${\Omega }_{A/R}^1$, the structure of a Lie pseudoalgebra over $\left(R,A\right)$ can be introduced. Furthermore, Poisson algebras can serve as a source of Lie pseudoalgebras that are not Lie algebroids.

We generalize known secondary characteristic classes related to Lie algebroids and flat connections to include objects such as Lie pseudoalgebras. This extension is twofold. On the one hand, it is a generalization because Lie pseudoalgebras are the algebraic counterparts of Lie algebroids. On the other hand, this generalization encompasses a specific class of connections that are not necessarily flat but have curvature tensors assuming certain values.

The result of this article constitutes an algebraic generalization of distinctive characteristic classes discussed in the paper [8], where certain unique characteristic homomorphisms for Lie algebroids were defined. The distinctive characteristic homomorphism ${\Delta }_{\left(A,B,\nabla \right)\#}$ is introduced for a pair of regular Lie algebroids, denoted as $B\subset A$, both on the same manifold M with identical anchor images. This is established within the context of a flat L-connection in A, where L is any Lie algebroid over M, whether regular or irregular (see also [9]).

Some exotic characteristic classes have been documented in the literature [30,31]. We aim to further develop such characteristic classes within somewhat more general cases, formulated in the context of pairs of extensions of $(R,A)$-Lie algebras.

Given two splitting extensions of Lie pseudoalgebras, denoted as ${\mathbf{e}}_L:0\to L^{\prime }\to L\to L^{\prime \prime }\to 0$ and ${\mathbf{e}}_K:0\to K^{\prime }\to K\to L^{\prime \prime }\to 0$, associated with their morphism and some connection $\nabla :M\to L$ with the curvature tensor taking values in $K^{\prime }$, we construct the characteristic homomorphism $D_{\#}^{\nabla }$ that operates from the cohomology of basic forms (as explained in Section 4) to the total cohomology of the given Lie pseudoalgebra M. If ∇ has values in K, the $D_{\#}^{\nabla }$ homomorphism becomes trivial. Consequently, the appearance of a cohomology class from the image of $D_{\#}^{\nabla }$ can be considered as an obstruction to ∇ having values in K. Next, we calculate the secondary characteristic homomorphism for pairs of inner product modules. For an inner product module $\left(E,h\right)$, the following is a pair of pseudoalgebras: the algebra of covariant derivatives $CO\left(E\right)$ and its subalgebra $CO(E,h)$ consisting of their skew-symmetric endomorphisms concerning the pseudometric h. An inner product A-module E is a finitely generated projective A-module, where A is a commutative algebra over a unital commutative ring R equipped with a pseudometric, i.e., a symmetric, nondegenerate, A-bilinear map $h:E\times E\to A$ (cf. [32] and the recent article [33]).

We arrive at a specific conclusion when an inner product module $(E,h)$ is isometric with every other inner product module $(E,g)$, and $\nabla :M\to CO\left(E\right)$. In such cases, the secondary characteristic homomorphism $D_{\#}^{\nabla }$ for the triple $(CO(E),CO(E,h),\nabla )$ remains independent of the choice of the pseudometric h. Consequently, nontrivial secondary characteristic classes become obstructions to the existence of the pseudometric that is invariant with respect to the connection. Therefore, the classes from the image of the characteristic homomorphism generalize the flat secondary characteristic classes discussed in [34].

2. Preliminaries

Connections of Lie pseudoalgebras and their extensions are important concepts in the presented approach to characteristic classes and in the definition of the notion of a connection. A key element in this framework is the algebra of covariant derivatives, which has been previously explored, for instance, in [17,30,31]. Let A be a commutative algebra over a commutative ring R and E be a module over A. Furthermore, consider $CO\left(E\right)$ as a submodule of ${End}_R\left(E\right)$ in such a way that for every element $D\in CO\left(E\right)$, there exists precisely one ${\delta }_D\in Der\left(A\right)$ such that

$$D(a·e)=a·D\left(e\right)+{\delta }_D\left(a\right)·e\mathrm{for}a\in A,e\in E.$$

(1)

Notice that $CO\left(E\right)$ is an R-Lie subalgebra of ${End}_R\left(E\right)$. Consequently, $CO\left(E\right)$ forms a Lie pseudoalgebra over $\left(R,A\right)$ with the anchor ${\omega }_{CO\left(E\right)}:CO\left(E\right)\ni D\mapsto {\delta }_D\in Der\left(A\right)$ and is referred to as the algebra of covariant derivatives. It is worth noting that the kernel of the anchor is ${End}_A\left(E\right)$, and if the representation ${\rho }_A:A\to {End}_A\left(E\right),$${\rho }_A\left(a\right)=\left(e\mapsto a·e\right)$ is faithful, $CO\left(E\right)$ comprises all $D\in {End}_R\left(E\right)$ satisfying (1). It is important to observe that the algebra $CO\left(E\right)$ serves as a generalization of the Lie algebroid of a vector bundle (cf. [22,35]).

In the classical approach, a linear connection on a manifold M, for a vector bundle V over M, is represented by a $C^{\infty }\left(M\right)$-linear operator $\nabla :\Gamma \left(TM\right)\to {End}_R(\Gamma \left(V\right))$ that satisfies the Leibniz condition:

$${\nabla }_X(f·\nu )=f·{\nabla }_X\left(\nu \right)+X\left(f\right)·\nu$$

(2)

for $X\in \Gamma \left(TM\right)$, $f\in C^{\infty }\left(M\right)$, $\nu \in \Gamma \left(V\right)$, which means that ∇ has values in $CO(\Gamma (V\left)\right)$, and (2) ensures that

$${\omega }_{CO(\Gamma (V\left)\right)}\circ \nabla ={id}_{\Gamma \left(TM\right)}.$$

Now, we extend the notion of connection to Lie pseudoalgebras, adopting a notation similar to the initial concept of generalizing the definition of connections in [36].

Let $\left(L,\left[·,·\right],\omega \right)$, $\left(L^{\prime },\left[·,·\right],{\omega }^{\prime }\right)$ be $\left(R,A\right)$-Lie pseudoalgebras. We say that a homomorphism of A-modules $\nabla :L\to L^{\prime }$ is an L-connection in $L^{\prime }$ if

$${\omega }^{\prime }\circ \nabla =\omega .$$

When referring to the curvature of the connection $\nabla :L\to L^{\prime }$, we are describing the R-bilinear homomorphism

$${\mathcal{R}}^{\nabla }:L\times L\to Ker{\omega }^{\prime },$$

$${\mathcal{R}}_{\alpha ,\beta }^{\nabla }={\left[{\nabla }_{\alpha },{\nabla }_{\beta }\right]}^{\prime }-{\nabla }_{\left[\alpha ,\beta \right]},\alpha ,\beta \in L.$$

One can observe that ${\mathcal{R}}^{\nabla }$ is alternating. Therefore, ${\mathcal{R}}^{\nabla }\in {Alt}_A^2(L,Ker{\omega }^{\prime })$. We refer to ∇ as flat if ${\mathcal{R}}^{\nabla }$ equals zero. It is evident that ${\mathcal{R}}^{\nabla }$ is equal to zero iff ∇ is also a homomorphism of R-Lie algebras.

We will now clarify the relationship between this concept of connection and the one discussed in [36]. Consider $L^{\prime },L$ and $L^{\prime \prime }$ as Lie pseudoalgebras over $\left(R,A\right)$ with anchors ${\omega }_{L^{\prime }}$, ${\omega }_L$ and ${\omega }_{L^{\prime \prime }}$, respectively. Let

$${\mathbf{e}}_L:0⟶L^{\prime }\stackrel{\iota }{⟶}L\stackrel{\pi }{⟶}{L}^{\prime \prime }⟶0$$

be a short exact sequence in the category of A-modules. Assuming that $\nabla :L^{\prime \prime }\to L$ is a splitting of ${\mathbf{e}}_L$ as a homomorphism of A-modules, it can be observed that

$${\omega }_L\circ \nabla ={\omega }_{L^{″}},$$

which means that ∇ is an $L^{″}$-connection in L. This implies that every splitting of the exact sequence ${\mathbf{e}}_L$ which is a morphism of A-modules qualifies as a connection in the generalized sense.

Given a Lie pseudoalgebra $\left(L,\left[·,·\right],\omega \right)$ over $\left(R,A\right)$, the anchor $\omega$ can be interpreted as a flat L-connection in $CO\left(A\right)$. Additionally, the map $ad:L\to {End}_A(Ker\omega )$, where $ad\left(\alpha \right)=\left[\alpha ,·\right]$, represents a flat L-connection in $CO(Ker\omega )$, and it is referred to as the adjoint representation of L.

Consider $\left(L,\left[·,·\right],\omega \right)$ as a Lie pseudoalgebra over $\left(R,A\right)$, and let $\nabla :L\to End\left(E\right)$ be an L-connection in $CO\left(E\right)$. Define $E_A^{*}={Hom}_R(E;A)$. Let $⟨·,·⟩$ denote the duality $⟨·,·⟩:E_A^{*}\times E\to A$ defined as $⟨f,e⟩=f\left(e\right)$ for $f\in {Hom}_R(E;A)$ and $e\in E$. Then, the map

$${\nabla }^{♮}\equiv Hom(\nabla ):L\to {End}_R\left(E_A^{*}\right)$$

given by

$$⟨{\nabla }_{\alpha }^{♮}\left(e^{*}\right),e⟩=\omega \left(\alpha \right)\left(⟨e^{*},e⟩\right)-⟨e^{*},{\nabla }_{\alpha }\left(e\right)⟩,\alpha \in L,e^{*}\in E_A^{*},e\in E,$$

is an L-connection in $CO\left({Hom}_R(E;A)\right)$. ${\nabla }^{♮}$ is called the contragredient connection to ∇. If ∇ is flat, so is ${\nabla }^{♮}$, because $⟨{\mathcal{R}}_{\alpha ,\beta }^{{\nabla }^{♮}}\left(e^{*}\right),e⟩=⟨e^{*},-{\mathcal{R}}_{\alpha ,\beta }^{\nabla }e⟩$ for $\alpha ,\beta \in L$, $e\in E$, $e^{*}\in E_A^{*}$.

When referring to a homomorphism

$$H:\left(K,{\left[·,·\right]}_K,{\omega }_K\right)\to \left(L,{\left[·,·\right]}_L,{\omega }_L\right)$$

of Lie pseudoalgebras $\left(K,{\left[·,·\right]}_K,{\omega }_K\right)$ and $\left(L,{\left[·,·\right]}_L,{\omega }_L\right)$ over $\left(R,A\right)$, we mean a flat K-connection $H:K\to L$ in L. If $\left(L,\left[·,·\right],{\omega }_L\right)$ is a Lie pseudoalgebra over $\left(R,A\right)$, then $Ker\omega$ and $Im\omega$ have induced structures of Lie pseudoalgebras with the zero map ${\omega }_{Ker\omega }=0$ and the inclusion ${\iota }_{Im\omega }:Im\omega \hookrightarrow Der\left(A\right)$ as the anchor. Consequently, the inclusion $\iota :Ker{\omega }_L\hookrightarrow L$ and ${\omega }_L$ commute with anchors. Therefore, we have the following short exact sequence of Lie pseudoalgebras, known as the Atiyah sequence:

$$0⟶Ker{\omega }_L\stackrel{\iota }{\hookrightarrow }L\stackrel{{\omega }_L}{⟶}Im{\omega }_L⟶0.$$

We review some well-known facts about the cohomology of Lie pseudoalgebras (as found in, for example, [17,30,37,38]). Consider $\left(L,\left[·,·\right],\omega \right)$ as a Lie pseudoalgebra over $\left(R,A\right)$, and let E be an A-module. Put:

$${\mathcal{C}}^n(L;E)={Alt}_A^n(L;E)$$

as the space of all alternating, n-linear mappings. Let $\mathcal{C}(L;E)={\displaystyle {⨁}_{n\ge 0}}{\mathcal{C}}^n(L;E)$, where ${\mathcal{C}}^0(L;E)=E$. For abbreviation, we write $\mathcal{C}\left(L\right)$ instead of $\mathcal{C}(L;A)$. The module $\mathcal{C}(L;E)$ serves as an A-algebra and is an algebra over $\mathcal{C}\left(L\right)$ with left multiplication ∧ defined as:

$$\left(\nu \wedge f\right)(x_1,\dots ,x_{p+q})={\displaystyle \sum _{\sigma \in S\left(p,q\right)}}sgn\sigma \nu (x_{\sigma \left(1\right)},\dots ,x_{\sigma \left(p\right)})f(x_{\sigma \left(p+1\right)},\dots ,x_{\sigma \left(p+q\right)})$$

for $\nu \in {\mathcal{C}}^p\left(L\right)$, $f\in {\mathcal{C}}^q(L;E)$, where the sum is taken over $\left(p,q\right)$-shuffles of permutations. In other words, $S\left(p,q\right)$ represents the subset of $S_{p+q}$, which consists of all permutations $\sigma \in S_{p+q}$ such that $\sigma \left(1\right)<\cdots <\sigma \left(p\right)$ and $\sigma (p+1)<\cdots <\sigma (p+q)$.

Suppose that $\nabla :L\to CO\left(E\right)$ is an L-connection in $CO\left(E\right)$. We define the covariant derivative $d^{\nabla }:{\mathcal{C}}^n(L;E)\to {\mathcal{C}}^{n+1}(L;E)$ as follows:

$$\begin{array}{cc}\hfill \left(d^{\nabla }f\right)(x_1,\dots ,x_{n+1})& ={\displaystyle \sum _{i=1}^{n+1}}{\left(-1\right)}^{i-1}{\nabla }_{x_i}\left(f(x_1,\dots \widehat{i}\dots ,x_{n+1})\right)\hfill \\ \hfill & +{\displaystyle \sum _{i<j}}{\left(-1\right)}^{i+j}f\left([x_i,x_j],x_1,\dots \widehat{i}\dots \widehat{j}\dots x_{n+1}\right).\hfill \end{array}$$

(3)

If ∇ is flat, $d^{\nabla }$ becomes a differential operator ($d^{\nabla }\circ d^{\nabla }=0$). Then, by the Lie pseudoalgebra cohomology, $H_{\nabla }(L,E)$ refers to the cohomology of the complex $\left(\mathcal{C}(L;E),d^{\nabla }\right)$.

In $\mathcal{C}(L;E)$, we also have two important operators: the substitution operator and the Lie derivative. Let $x\in L$. The substitution operator $i_x:{\mathcal{C}}^n(L;E)\to {\mathcal{C}}^{n-1}(L;E)$ is defined as $i_x\left(e\right)=0$ if $e\in E$ and by:

$$\left(i_{x}f\right)(y_1,\dots ,y_{n-1})=f(x,y_1,\dots ,y_{n-1})\mathrm{for}n\ge 1,y_1,\dots ,y_{n-1}\in L.$$

The Lie derivative ${\Theta }_x^{\nabla }:{\mathcal{C}}^n(L;E)\to {\mathcal{C}}^n(L;E)$ is defined as ${\Theta }_x^{\nabla }\left(e\right)=0$ if $e\in E$ and by:

$$\left({\Theta }_x^{\nabla }f\right)(y_1,\dots ,y_n)={\nabla }_x\left(f(y_1,\dots ,y_k)\right)-\sum _{i=1}^{k}f\left(y_1,\dots ,{\left[x,y_i\right]}^L,\dots ,y_k\right)$$

for $n\ge 1$, $f\in {\mathcal{C}}^n(L;E)$, $y_1,\dots ,y_{n-1}\in L$. These operators satisfy the following properties:

(a)

${\Theta }_x^{\nabla }\circ i_y-i_y\circ {\Theta }_x^{\nabla }=i_{\left[x,y\right]}$ for all $x,y\in L$.

(b)

$i_x{d}^{\nabla }+d^{\nabla }{i}_x={\Theta }_x^{\nabla }$ for all $x\in L$ (Cartan formula for the Lie derivative).

Furthermore, ${\Theta }_x^{\nabla }\circ {\Theta }_y^{\nabla }-{\Theta }_y^{\nabla }\circ {\Theta }_x^{\nabla }={\Theta }_{\left[x,y\right]}^{\nabla }$ and $d^{\nabla }\circ {\Theta }_x^{\nabla }={\Theta }_x^{\nabla }\circ d^{\nabla }$ for all $x\in L$ if ∇ is flat, and as a result, $d^{\nabla }\circ d^{\nabla }=0$. When $\nabla =\omega$, we will denote $d^{\omega }$ by $d_L$ and the cohomology of the complex $\left(\mathcal{C}(L;A),d_L\right)$ as $H\left(L\right)$.

3. Algebra of Invariant Homomorphisms

Consider $\left(L,\left[·,·\right],\omega \right)$ as a Lie pseudoalgebra over $\left(R,A\right)$, and let $\nabla :L\to {End}_R\left(L^{\prime }\right)$ be a connection in the A-module $CO\left(L^{\prime }\right)$. We define an L-connection ${Hom}^n(\nabla )$ in the A-module $CO\left({Hom}_A^n(L^{\prime };A)\right)$ by:

$$\begin{array}{cc}\hfill & \left({Hom}^n(\nabla )\left(\alpha \right)\left(f\right)\right)\left({\alpha }_1^{\prime },\dots ,{\alpha }_n^{\prime }\right)\hfill \\ \hfill & =\omega \left(\alpha \right)\left(f({\alpha }_1^{\prime },\dots ,{\alpha }_n^{\prime })\right)-{\sum }_{i=1}^{n}f\left({\alpha }_1^{\prime },\dots ,{\alpha }_{i-1}^{\prime },{\nabla }_{\alpha }\left({\alpha }_i^{\prime }\right),\dots ,{\alpha }_n^{\prime }\right)\hfill \end{array}$$

(4)

for $f\in {Hom}_A^n(L^{\prime };A)$, $n\in \mathbb{N}$, $\alpha \in L$, ${\alpha }_1^{\prime },\dots ,{\alpha }_n^{\prime }\in L^{\prime }$, and additionally, we put ${Hom}^0(\nabla )=\omega$. In this way, we define the following L-connection in $CO\left({Hom}_A(L^{\prime };A)\right)$, where ${Hom}_A(L^{\prime };A)={\displaystyle \underset{n\ge 0}{⨁}}{Hom}_A^n(L^{\prime };A)$:

$$\tilde{\nabla }=Hom(\nabla )={\displaystyle \underset{n\ge 0}{⨁}}{Hom}^n(\nabla ).$$

Lemma 1.

If $\nabla :L\to {End}_R\left(L^{\prime }\right)$ is a flat L-connection in the A-module $CO\left(L^{\prime }\right)$, then $Hom(\nabla )$is a flat L-connection in$CO\left({Hom}_A(L^{\prime };A)\right)$.

Proof. 

A standard calculation. □

Corollary 1.

For every Lie pseudoalgebra $\left(L,\left[·,·\right],\omega \right)$ over $\left(R,A\right)$, the L-connection:

$$Hom(ad):L⟶{End}_R\left({Hom}_A(L;A)\right)$$

in $CO\left({Hom}_A(L;A)\right)$ is flat.

Let $\nabla :L\to {End}_R\left(L^{\prime }\right)$ be an L-connection in an A-module $CO\left(L^{\prime }\right)$. We say that a map $f\in {Hom}_A(L^{\prime };A)$ is invariant with respect to the L-connection $\tilde{\nabla }=Hom(\nabla )$, or $\tilde{\nabla }$-invariant, if

$$f\in {\displaystyle {\bigcap }_{\alpha \in L}}Ker\tilde{\nabla }\left(\alpha \right).$$

We will denote the set of all $\tilde{\nabla }$-invariant homomorphisms by ${Hom}_A{(L^{\prime };A)}^{I\left(\tilde{\nabla }\right)}$. We have the structure of the algebra with the standard exterior multiplication in the module ${Hom}_A(L^{\prime };A)$. For any $\alpha \in L$, the map ${\tilde{\nabla }}_{\alpha }$ is a differentiation of degree zero. Hence, ${Hom}_A{(L^{\prime };A)}^{I\left(\tilde{\nabla }\right)}$ is a subalgebra of ${Hom}_A(L^{\prime };A)$.

By ${Alt}_A{(L^{\prime };A)}^{I\left(\tilde{\nabla }\right)}$, we will denote the set of all alternating, $\tilde{\nabla }$-invariant homomorphisms from ${Hom}_A(L^{\prime };A)$. Observe that ${\tilde{\nabla }}_{\alpha }\left({Alt}_A(L^{\prime };A)\right)\subset {Alt}_A(L^{\prime };A)$. Therefore, we can restrict ${\tilde{\nabla }}_{\alpha }$ to endomorphisms of ${Alt}_A(L^{\prime };A)$. Moreover, the product of alternating homomorphisms is alternating. Therefore, ${Alt}_A{(L^{\prime };A)}^{I\left(\tilde{\nabla }\right)}$ is a subalgebra of algebras ${Alt}_A(L^{\prime };A)$ and ${Hom}_A{(L^{\prime };A)}^{I\left(\tilde{\nabla }\right)}$.

4. Construction of the Secondary Characteristic Homomorphism for Pairs of Extensions of Lie Pseudoalgebras

Let

$${\mathbf{e}}_L:0⟶L^{\prime }\stackrel{\iota }{⟶}L\stackrel{\pi }{⟶}{L}^{\prime \prime }⟶0,{\mathbf{e}}_K:0⟶K^{\prime }\stackrel{{\iota }_K}{⟶}K\stackrel{{\pi }_K}{⟶}{L}^{″}⟶0$$

be two split extensions of $\left(R,A\right)$-Lie pseudoalgebras L and K, where A is a commutative algebra over a commutative ring R, i.e., ${\mathbf{e}}_L$, ${\mathbf{e}}_K$ are short exact sequences of $\left(R,A\right)$-Lie pseudoalgebras, which split in the category of A-modules. Denote by ${\left[·,·\right]}_P$ and ${\omega }_P$ the Lie bracket and the anchor in a Lie pseudoalgebra P, respectively. Clearly, ${\omega }_{L^{\prime }}=0$ and ${\omega }_{K^{\prime }}=0$. Let us assume the commutativity of the diagram:

$$\begin{array}{ccccccc}{\mathbf{e}}_K:0\to & K\prime & \stackrel{{\iota }_K}{⟶}& K& \stackrel{{\pi }_K}{⟶}& L^{″}& ⟶0\\ & \downarrow j\prime & & \downarrow j& & \Vert & \\ {\mathbf{e}}_L:0\to & L\prime & \stackrel{\iota }{⟶}& L& \stackrel{\pi }{⟶}& L^{″}& ⟶0\end{array}$$

(5)

where $j:K\to L$, $j^{\prime }:K^{\prime }\to L^{\prime }$ are homomorphisms of R-Lie algebras.

We define the pair $\left(j,j^{\prime }\right)$ as a morphism of extensions ${\mathbf{e}}_K$,${\mathbf{e}}_L$. We also let $(A,M,{\left[·,·\right]}_M,{\omega }_M)$ be a Lie pseudoalgebra over $\left(R,A\right)$ and $\nabla :M\to L$ be an M-connection in L with the curvature tensor ${\mathcal{R}}^{\nabla }$ having values in $Im(\iota \circ j^{\prime })$. Let ${\lambda }_K:L^{\prime \prime }\to K$ be a splitting of ${\mathbf{e}}_K$ in the category of A-modules. Equivalently, there exist homomorphisms of A-modules ${\lambda }_K:L^{\prime \prime }\to K$, ${\omega }^{{\lambda }_K}:K\to K^{\prime }$ such that:

• ${\pi }_K\circ {\lambda }_K={id}_{L^{\prime \prime }},{\omega }^{{\lambda }_K}\circ {\iota }_K={id}_{K^{\prime }}.$
• ${\pi }_K\circ {\iota }_K=0,{\omega }^{{\lambda }_K}\circ {\lambda }_K=0.$
• ${\iota }_K\circ {\omega }^{{\lambda }_K}+{\lambda }_K\circ {\pi }_K={id}_K.$

Since ${\omega }_K\circ {\lambda }_K={\omega }_{L^{″}}$, it follows that ${\lambda }_K$ is an $L^{\prime \prime }$-connection in K, known as an ${\mathbf{e}}_K$-connection. The homomorphism ${\omega }^{{\lambda }_K}$ is referred to as a form of the ${\mathbf{e}}_K$-connection ${\lambda }_K$ (for ${\mathbf{e}}_K$-connections, see [17,22,35,39] —in the case of Lie algebroids). We observe that $\pi \circ \left(j\circ {\lambda }_K\right)={id}_{L^{″}}$. Therefore, $\lambda :=j\circ {\lambda }_K:L^{\prime \prime }\to L$ is a splitting of ${\mathbf{e}}_L$ (consequently, $\lambda$ is an ${\mathbf{e}}_L$-connection). Since ${\mathbf{e}}_L$ splits, there exists a homomorphism of A-modules ${\omega }^{\lambda }:L\to L^{\prime }$, such that:

$$\iota \circ {\omega }^{\lambda }+\lambda \circ \pi ={id}_L,{\omega }^{\lambda }\circ \iota ={id}_{L^{\prime }},{\omega }^{\lambda }\circ \lambda =0,$$

i.e., ${\omega }^{\lambda }$ is the form of the connection $\lambda$.

Remark 1.

If the A-module $L^{″}$ is projective, the short exact sequence $e_K$ splits in the category of A-modules.

By the ${\mathbf{e}}_L$-curvature of the ${\mathbf{e}}_L$-connection$\lambda :L^{\prime \prime }\to L$, we mean ${\Omega }_{{\mathbf{e}}_L}^{\lambda }\in {\mathcal{C}}^2(L^{″};L^{\prime })$ given by

$${\Omega }_{{\mathbf{e}}_L}^{\lambda }={\omega }^{\lambda }\circ {\left[·,·\right]}_L\circ \left(\lambda \times \lambda \right),$$

i.e.,

$$\left(\iota \circ {\Omega }_{{\mathbf{e}}_L}^{\lambda }\right)({\alpha }^{″},{\beta }^{″})={\left[\lambda {\alpha }^{\prime \prime },\lambda {\beta }^{\prime \prime }\right]}_L-\lambda {\left[{\alpha }^{\prime \prime },{\beta }^{\prime \prime }\right]}_{L^{″}}\mathrm{for}{\alpha }^{\prime \prime },{\beta }^{\prime \prime }\in L^{\prime \prime }.$$

Corollary 2.

It follows from the definition of ${\Omega }_{{\mathbf{e}}_L}^{\lambda }$ that

$$\iota \circ {\Omega }_{{\mathbf{e}}_L}^{\lambda }={\left[\lambda ,\lambda \right]}_L+d^{″}\left(\lambda \right)$$

where ${\left[\lambda ,\lambda \right]}_L\in {\mathcal{C}}^2(L^{\prime \prime };L^{\prime })$ is defined by ${\left[\lambda ,\lambda \right]}_L(x^{\prime \prime },y^{\prime \prime })={\left[\lambda \left(x^{\prime \prime }\right),\lambda \left(y^{\prime \prime }\right)\right]}_L$ and $d^{″}$ is a differential operator in $\mathcal{C}(L^{\prime \prime };L^{\prime })$ induced by the zero $L^{″}$-connection in L.

Lemma 2.

${\omega }^{j\circ {\lambda }_K}\circ j=j^{\prime }\circ {\omega }^{{\lambda }_K}.$

Proof. 

Since

$$\begin{array}{cc}\hfill \iota \circ \left({\omega }^{j\circ {\lambda }_K}\circ j\right)& =\left(\iota \circ {\omega }^{j\circ {\lambda }_K}\right)\circ j=\left({id}_L-\lambda \circ \pi \right)\circ j=j-\left(j\circ {\lambda }_K\right)\circ {\pi }_K\hfill \\ \hfill & =j\circ \left({id}_K-{\lambda }_K\circ {\pi }_K\right)=j\circ \left({\iota }_K\circ {\omega }^{{\lambda }_K}\right)=\left(j\circ {\iota }_K\right)\circ {\omega }^{{\lambda }_K}=\left(\iota \circ j^{\prime }\right)\circ {\omega }^{{\lambda }_K}\hfill \\ \hfill & =\iota \circ \left(j^{\prime }\circ {\omega }^{{\lambda }_K}\right)\hfill \end{array}$$

and $\iota$ is injective, it follows that ${\omega }^{j\circ {\lambda }_K}\circ j=j^{\prime }\circ {\omega }^{{\lambda }_K}$. □

Corollary 3.

${\Omega }_{{\mathbf{e}}_L}^{j\circ {\lambda }_K}=j^{\prime }\circ {\Omega }_{{\mathbf{e}}_K}^{{\lambda }_K}.$

Proof. 

Since ${\left[·,·\right]}_L\circ \left(j\times j\right)=j\circ {\left[·,·\right]}_K$, Lemma 2 now yields:

$$\begin{array}{cc}\hfill \iota \circ {\Omega }_{\mathbf{e}}^{j\circ {\lambda }_K}& ={\omega }^{j\circ {\lambda }_K}\circ {\left[·,·\right]}_L\circ \left(\lambda \times \lambda \right)={\omega }^{j\circ {\lambda }_K}\circ {\left[·,·\right]}_L\circ \left(j\times j\right)\circ \left({\lambda }_K\times {\lambda }_K\right)\hfill \\ \hfill & =\left({\omega }^{j\circ {\lambda }_K}\circ j\right)\circ {\left[·,·\right]}_K\circ \left({\lambda }_K\times {\lambda }_K\right)=\left({\omega }^{j\circ {\lambda }_K}\circ j\right)\circ {\left[·,·\right]}_K\circ \left({\lambda }_K\times {\lambda }_K\right)\hfill \\ \hfill & =j^{\prime }\circ {\omega }^{{\lambda }_K}\circ {\left[·,·\right]}_K\circ \left({\lambda }_K\times {\lambda }_K\right)=j^{\prime }\circ {\Omega }_{{\mathbf{e}}_K}^{{\lambda }_K}.\hfill \end{array}$$

□

The anchors ${\omega }_L$ and ${\omega }_M$, serving as flat connections in $CO\left(A\right)$, determine the differential operators $d_L=d^{{\omega }_L}$ and $d_M=d^{{\omega }_M}$ in $\mathcal{C}\left(L\right)$ and $\mathcal{C}\left(M\right)$, respectively. We will denote their cohomology spaces by $H\left(L\right)$ and $H\left(M\right)$, respectively.

The extension ${\mathbf{e}}_L$ induces the following L-connection ${\nabla }^{\prime }:L\to {End}_R\left(L^{\prime }\right)$ in $CO\left(L^{\prime }\right)$ defined by

$$\iota \left({\nabla }_{\alpha }^{\prime }\left({\alpha }^{\prime }\right)\right)={\left[\alpha ,\iota {\alpha }^{\prime }\right]}_L,\alpha \in L,{\alpha }^{\prime }\in L^{\prime }.$$

(6)

Lemma 3.

${\nabla }^{\prime }$ is a flat L-connection which satisfies the properties: ${\nabla }^{\prime }\circ \iota ={\left[·,·\right]}_{L^{\prime }}$,

$${\nabla }_{j\left(\kappa \right)}^{\prime }\left(j^{\prime }\left(K^{\prime }\right)\right)\subset j^{\prime }\left(K^{\prime }\right),$$

(7)

$${\left({\nabla }^{\prime }\circ j\right)}_{\kappa }{\left[{\alpha }^{\prime },{\beta }^{\prime }\right]}_{L^{\prime }}={\left[{\left({\nabla }^{\prime }\circ j\right)}_{\kappa }\left({\alpha }^{\prime }\right),{\beta }^{\prime }\right]}_{L^{\prime }}+{\left[{\alpha }^{\prime },{\left({\nabla }^{\prime }\circ j\right)}_{\kappa }\left({\beta }^{\prime }\right)\right]}_{L^{\prime }}$$

(8)

for $\kappa \in K$, ${\alpha }^{\prime },{\beta }^{\prime }\in L^{\prime }$.

Proof. 

Let $\kappa \in K$, ${\kappa }^{\prime }\in K^{\prime }$. Since ${\pi }_K\left[\kappa ,{\iota }_K\left({\kappa }^{\prime }\right)\right]=0$ and $\iota \left({\nabla }_{j\left(\kappa \right)}^{\prime }\left(j^{\prime }\left({\kappa }^{\prime }\right)\right)\right)=j{\left[\kappa ,{\iota }_K\left({\kappa }^{\prime }\right)\right]}_K$, we deduce that

$$\iota \left({\nabla }_{j\left(\kappa \right)}^{\prime }\left(j^{\prime }\left({\kappa }^{\prime }\right)\right)\right)\in j(Ker{\pi }_K)=j(Im{\iota }_K)=(j\circ {\iota }_K)\left(K^{\prime }\right)=(\iota \circ j^{\prime })\left(K^{\prime }\right).$$

The flatness of ∇ and (8) are consequences of the Jacobi identity in L. □

The L-connection ${\nabla }^{\prime }\circ j:K\to {End}_R\left(L^{\prime }\right)$ in $L^{\prime }$ induces the K-connection

$$\widetilde{{\nabla }^{\prime }}:=Hom({\nabla }^{\prime }\circ j):K⟶{End}_R\left(\mathcal{C}\left(L^{\prime }\right)\right)$$

in $\mathcal{C}\left(L^{\prime }\right)$ by the formula given in (4) and following suitable restriction to alternating homomorphisms. Lemma 1 implies that $\widetilde{{\nabla }^{\prime }}$ is flat. Based on the definitions of $\widetilde{{\nabla }^{\prime }}$ and the invariance, we have:

Lemma 4.

Any $f\in {\mathcal{C}}^n\left(L^{\prime }\right)$ is $\widetilde{{\nabla }^{\prime }}$-invariant if and only if

$${\omega }_K\left(\kappa \right)\left(f({\alpha }_1^{\prime },\dots ,{\alpha }_n^{\prime })\right)={\displaystyle \sum _{p=1}^n}f\left({\alpha }_1^{\prime },\dots ,{\alpha }_{p-1}^{\prime },({\nabla }^{\prime }\circ j)\left(\kappa \right)\left({\alpha }_p^{\prime }\right),\dots ,{\alpha }_n^{\prime }\right)$$

for $\kappa \in K$, ${\alpha }_1^{\prime },\dots ,{\alpha }_n^{\prime }\in L^{\prime }$.

We define the set:

$$\mathcal{C}{(L^{\prime },K^{\prime })}^K=\left\{f\in {Alt}_A{(L^{\prime };A)}^{I\left(\widetilde{{\nabla }^{\prime }}\right)}:i_{\kappa }f=0\mathrm{for}\mathrm{all}\kappa \in j^{\prime }\left(K^{\prime }\right)\right\}.$$

Since for every ${\alpha }^{\prime }\in L^{\prime }$, the substitution operator $i_{{\alpha }^{\prime }}:\mathcal{C}\left(L^{\prime }\right)\to \mathcal{C}\left(L^{\prime }\right)$ is an antiderivation, $\mathcal{C}{(L^{\prime },K^{\prime })}^K$ is a subalgebra of $\mathcal{C}\left(L^{\prime }\right)$ called a basic subalgebra, and its elements are referred to as basic forms.

Let ${\Theta }_{{\alpha }^{\prime }}^0:\mathcal{C}\left(L^{\prime }\right)\to \mathcal{C}\left(L^{\prime }\right)$, where ${\alpha }^{\prime }\in L^{\prime }$, be the Lie derivative, and $d_{L^{\prime }}$ the differential operator in $\mathcal{C}\left(L^{\prime }\right)$ induced by ${\omega }_L^{\prime }=0$. We recall that $d_{L^{\prime }}\left(a\right)=0$ if $a\in A={\mathcal{C}}^0\left(L^{\prime }\right)$ and:

$$\left(d_{L^{\prime }}f\right)(x_1,\dots ,x_{n+1})={\displaystyle {\sum }_{i<j}}{\left(-1\right)}^{i+j}f\left({\left[x_i,x_j\right]}_{L^{\prime }},x_1,\dots \widehat{i}\dots \widehat{j}\dots ,x_{n+1}\right)$$

for $n\ge 1$, $f\in {\mathcal{C}}^n\left(L^{\prime }\right)$.

Lemma 5.

$d_{L^{\prime }}\circ \widetilde{{\nabla }^{\prime }}\left(\kappa \right)=\widetilde{{\nabla }^{\prime }}\left(\kappa \right)\circ d_{L^{\prime }}$ for any $\kappa \in K$.

Proof. 

The proof is conducted through a calculation and relies on property (8). □

Lemma 6.

$Hom({\nabla }^{\prime }\circ j)\left({\iota }_K\left({\kappa }^{\prime }\right)\right)={\Theta }_{j^{\prime }\left({\kappa }^{\prime }\right)}^0$ for all ${\kappa }^{\prime }\in K^{\prime }$.

Proof. 

It is sufficient to observe that ${\left[j{\iota }_K\left({\kappa }^{\prime }\right),\iota {\alpha }^{\prime }\right]}_L={\left[\iota j^{\prime }\left({\kappa }^{\prime }\right),\iota {\alpha }^{\prime }\right]}_L=\iota {\left[j^{\prime }\left({\kappa }^{\prime }\right),{\alpha }^{\prime }\right]}_{L^{\prime }}$ and ${\omega }_K\left({\iota }_K\left({\kappa }^{\prime }\right)\right)=0$ for ${\kappa }^{\prime }\in K^{\prime }$, ${\alpha }^{\prime }\in L^{\prime }$. □

Now, Lemma 6 and the Cartan formula for the Lie derivative (see page 5) imply that

$$i_{j^{\prime }\left({\kappa }^{\prime }\right)}{d}_{L^{\prime }}f={\Theta }_{j^{\prime }\left({\kappa }^{\prime }\right)}f-d_{L^{\prime }}{\iota }_{j^{\prime }\left({\kappa }^{\prime }\right)}f=Hom({\nabla }^{\prime }\circ j)\left({\iota }_K\left({\kappa }^{\prime }\right)\right)\left(f\right)=0$$

for $f\in \mathcal{C}{(L^{\prime },K^{\prime })}^K$ and ${\kappa }^{\prime }\in K^{\prime }$. Hence, from Lemma 5, we see that the image of $\mathcal{C}{(L^{\prime },K^{\prime })}^K$ under $d_{L^{\prime }}$ is included in $\mathcal{C}{(L^{\prime },K^{\prime })}^K$. Consequently, we have a differential operator

$$d^0=-d_{L^{\prime }}:\mathcal{C}{(L^{\prime },K^{\prime })}^K⟶\mathcal{C}{(L^{\prime },K^{\prime })}^K$$

(9)

in the algebra $\mathcal{C}{(L^{\prime },K^{\prime })}^K$. The cohomology of the complex $\left(\mathcal{C}{(L^{\prime },K^{\prime })}^K,d^0\right)$ will be denoted by $H(L^{\prime },{\mathbf{e}}_K)$.

We define homomorphisms of A-modules

$$W^{\nabla ,\lambda }=-{\omega }^{\lambda }\circ \nabla :M⟶L^{\prime }$$

and a homomorphism of A-algebras

$$D^{\nabla }:\mathcal{C}{(L^{\prime },K^{\prime })}^K⟶\mathcal{C}\left(M\right),D^{\nabla }\left(f\right)=f\circ \begin{array}{c}\\ \left(\underbrace{W^{\nabla ,\lambda }\times \cdots \times W^{\nabla ,\lambda }}\right).\\ n\mathrm{times}\end{array}$$

Lemma 7.

$D^{\nabla }$ is independent of the choice of the ${\mathbf{e}}_K$-connection ${\lambda }_K$.

Proof. 

Let ${\overline{\lambda }}_K:L^{″}\to K$ be a homomorphism of A-modules such that ${\pi }_K\circ {\overline{\lambda }}_K={id}_{L^{\prime \prime }}$, $\overline{\lambda }=j\circ {\overline{\lambda }}_K$. Then:

$$\begin{array}{cc}\hfill \iota \circ \left({\omega }^{\lambda }\circ \nabla -{\omega }^{\overline{\lambda }}\circ \nabla \right)& =\left(\left({id}_L-\lambda \circ \pi \right)-\left({id}_L-\overline{\lambda }\circ \pi \right)\right)\circ \nabla \hfill \\ \hfill & =\left(\overline{\lambda }-\lambda \right)\circ \pi \circ \nabla =j\circ \left({\overline{\lambda }}_K-{\lambda }_K\right)\circ \pi \circ \nabla .\hfill \end{array}$$

Moreover, ${\pi }_K\circ \left({\overline{\lambda }}_K-{\lambda }_K\right)\circ \pi \circ \nabla =\left({id}_{L^{\prime \prime }}-{id}_{L^{\prime \prime }}\right)\circ \pi \circ \nabla =0$. Hence, by the equality $j\circ {\iota }^{\prime }=\iota \circ j^{\prime }$, we conclude that $\iota \circ \left({\omega }^{\lambda }\circ \nabla -{\omega }^{\overline{\lambda }}\circ \nabla \right)\left(m\right)\in \left(\iota \circ j^{\prime }\right)\left(K^{\prime }\right)$ for $m\in M$. The injectivity of $\iota$ shows that ${\omega }^{\lambda }\circ \nabla -{\omega }^{\overline{\lambda }}\circ \nabla$ has values in $j^{\prime }\left(K^{\prime }\right)$. □

By the definition of $D^{\nabla }$,

$$D^{\nabla }={\nabla }^{*}\circ {\left(-{\omega }^{\lambda }\right)}^{*}\mathrm{on}\mathcal{C}{(L^{\prime },K^{\prime })}^K,$$

(10)

where ${\nabla }^{*}:\mathcal{C}\left(L\right)⟶\mathcal{C}\left(M\right)$ is a homomorphism of A-algebras given by

$$\left({\nabla }^{*}h\right)(m_1,\dots ,m_p)=h(\nabla m_1,\dots ,\nabla m_p)$$

for $h\in \mathcal{C}\left(L\right)$, $m_1,\dots ,m_p\in M$, and

$$\left({(-{\omega }^{\lambda })}^{*}f\right)({\alpha }_0,\dots ,{\alpha }_n)=f(-{\omega }^{\lambda }{\alpha }_0,\dots ,-{\omega }^{\lambda }{\alpha }_n)$$

for $f\in {\mathcal{C}}^n{(L^{\prime },K^{\prime })}^K$, ${\alpha }_0,\dots ,{\alpha }_n\in L$. The pair of extensions ${\mathbf{e}}_L$, ${\mathbf{e}}_K$ and the L-connection ${id}_L$ induces the homomorphism

$$D_o:=D^{{id}_L}={\left(-{\omega }^{\lambda }\right)}^{*}:\mathcal{C}{(L^{\prime },K^{\prime })}^K⟶\mathcal{C}\left(L\right).$$

Theorem 1.

$D_o=D^{{id}_L}$ is an injective homomorphism of A-algebras.

Proof. 

It remains to observe that ${\omega }^{\lambda }:L\to L^{\prime }$ is a surjection. It is satisfied because ${\omega }^{\lambda }\circ \iota ={id}_{L^{\prime }}$. □

Theorem 2.

Let ${\nabla }^o:L^{\prime \prime }\to L$ be a flat splitting of ${\mathbf{e}}_L$ in the category of A-modules. Then, for $f\in {\mathcal{C}}^n{(L^{\prime },K^{\prime })}^K$ and $l_1^{{}^{\prime \prime }},\dots ,l_n^{\prime \prime }\in L^{\prime \prime }$, we have

$$\left(D^{{\nabla }^o}f\right)(l_1^{\prime \prime },\dots ,l_n^{\prime \prime })=f\left({\omega }^{{\nabla }^o}\left(j\widetilde{l_1^{\prime \prime }}\right),\dots ,{\omega }^{{\nabla }^o}\left(j\widetilde{l_n^{\prime \prime }}\right)\right),$$

(11)

where $\widetilde{l_p^{\prime \prime }}$ is an element of K such that ${\pi }_K\left(\widetilde{l_p^{\prime \prime }}\right)=l_p^{\prime \prime }$.

Proof. 

We first recall that ${\nabla }^o$ is a flat $L^{\prime \prime }$-connection in L. Let $f\in {\mathcal{C}}^n{(L^{\prime },K^{\prime })}^K$ and $l_1^{″},\dots ,l_n^{″}\in L^{″}$. We next observe that the right-hand side of (11) does not depend on the choice of elements $\widetilde{l_p^{\prime \prime }}\in K$, such that ${\pi }_K\left(\widetilde{l_p^{\prime \prime }}\right)=l_p^{″}$. Indeed, let $\widehat{l_1^{\prime \prime }},\dots ,\widehat{l_n^{\prime \prime }}$ be elements of K such that ${\pi }_K\left(\widehat{l_1^{\prime \prime }}\right)=l_1^{″},\dots ,{\pi }_K\left(\widehat{l_n^{\prime \prime }}\right)=l_n^{″}$. Then, $\widetilde{l_p^{\prime \prime }}-\widehat{l_p^{\prime \prime }}\in Ker{\pi }_K={\iota }_K\left(K\right)$, and hence:

$$\left(\iota \circ {\omega }^{{\nabla }^o}\circ j\right)\left(\widetilde{l_p^{\prime \prime }}-\widehat{l_p^{\prime \prime }}\right)=j\left(\widetilde{l_p^{\prime \prime }}-\widehat{l_p^{\prime \prime }}\right)\in \iota \left(j^{\prime }\left(K^{\prime }\right)\right)$$

which gives $\widetilde{l_p^{\prime \prime }}-\widehat{l_p^{\prime \prime }}\in j^{\prime }\left(K^{\prime }\right)$. Now, we take $\widetilde{l_p^{\prime \prime }}={\lambda }_K\left(l_p^{\prime \prime }\right)$. Since $\lambda =j\circ {\lambda }_K$, $\iota \circ {\omega }^{{\nabla }^o}+{\nabla }^o\circ \pi ={id}_L$ and $\iota$ is injective,

$${\omega }^{{\nabla }^o}\circ \lambda =-{\omega }^{\lambda }\circ {\nabla }^o.$$

We thus obtain

$$\left(D^{{\nabla }^o}f\right)\left(l_1^{{}^{\prime \prime }},\dots ,l_n^{\prime \prime }\right)=f\left({\omega }^{{\nabla }^o}\left(j\widetilde{l_1^{\prime \prime }}\right),\dots ,{\omega }^{{\nabla }^o}\left(j\widetilde{l_n^{\prime \prime }}\right)\right).$$

□

Theorem 3.

$D^{\nabla }$ commutes with the differentials $d^0$ and $d_M$.

Proof. 

Let $f\in {\mathcal{C}}^n{(L^{\prime },K^{\prime })}^K$, $m_0,\dots ,m_n\in M$. Then:

$$\begin{array}{cc}\hfill & \left(\left(d_M\circ D^{\nabla }\right)f\right)(m_0,\dots ,m_n)\hfill \\ \hfill & =\sum _{p=0}^n{\left(-1\right)}^p{\omega }_M\left(m_p\right)\left(f\left(-{\omega }^{\lambda }\nabla m_0,\dots \widehat{p}\dots ,-{\omega }^{\lambda }\nabla m_n\right)\right)\hfill \\ \hfill & +\sum _{p<q}{\left(-1\right)}^{p+q}f\left(-{\omega }^{\lambda }\nabla {\left[m_p,m_q\right]}_M,-{\omega }^{\lambda }\nabla m_0,\dots \widehat{p}\dots \widehat{q}\dots ,-{\omega }^{\lambda }\nabla m_n\right).\hfill \end{array}$$

Since ${\omega }_M={\omega }_L\circ \nabla$, ${\omega }_L={\omega }_K\circ {\lambda }_K\circ \pi$ and $j\circ {\lambda }_K\circ \pi ={id}_L-\iota \circ {\omega }^{\lambda }$, the $\widetilde{{\nabla }^{\prime }}$-invariance of f (see Lemma 4) implies:

$$\begin{array}{cc}\hfill & {\sum }_{p=0}^n{\left(-1\right)}^p{\omega }_M\left(m_p\right)\left(f\left(-{\omega }_0^{\lambda }\nabla m_0,\dots \widehat{p}\dots ,-{\omega }^{\lambda }\nabla m_n\right)\right)\hfill \\ \hfill & ={\sum }_{p=0}^n{\left(-1\right)}^p{\omega }_K({\lambda }_K\pi \nabla m_p)\left(f\left(-{\omega }_0^{\lambda }\nabla m_0,\dots \widehat{p}\dots ,-{\omega }^{\lambda }\nabla m_n\right)\right)\hfill \\ \hfill & ={\sum }_{p<q}{\left(-1\right)}^{p+q+1}f\left({\nabla }_{j{\lambda }_K\pi \nabla m_p}^{\prime }(-{\omega }^{\lambda }\nabla m_q),-{\omega }^{\lambda }\nabla m_0,\dots \widehat{p}\dots \widehat{q}\dots ,-{\omega }^{\lambda }\nabla m_n\right)\hfill \\ \hfill & +{\sum }_{p<q}{\left(-1\right)}^{p+q}f\left({\nabla }_{j{\lambda }_K\pi \nabla m_q}^{\prime }(-{\omega }^{\lambda }\nabla m_p),-{\omega }^{\lambda }\nabla m_0,\dots \widehat{p}\dots \widehat{q}\dots ,-{\omega }^{\lambda }\nabla m_n\right).\hfill \end{array}$$

One can verify that:

$$\begin{array}{cc}\hfill & \left(\iota \circ {\Omega }_{\mathbf{e}}^{j\circ {\lambda }_K}\right)(\pi \nabla m_p,\pi \nabla m_q)+{\omega }^{\lambda }\left({\mathcal{R}}^{\nabla }(m_p,m_q)\right)\hfill \\ \hfill & ={\nabla }_{\nabla m_q}^{\prime }({\omega }^{\lambda }\nabla m_p)-{\nabla }_{\iota ({\omega }^{\lambda }\nabla m_q)}^{\prime }({\omega }^{\lambda }\nabla m_p)-{\nabla }_{\nabla m_p}^{\prime }({\omega }^{\lambda }\nabla m_q)+{\omega }^{\lambda }\nabla {\left[m_p,m_q\right]}_M,\hfill \end{array}$$

Hence, based on Corollary 3 and the assumption that the curvature of ∇ has values in $Im(\iota \circ j^{\prime })$, we conclude that:

$${\nabla }_{\nabla m_q}^{\prime }({\omega }^{\lambda }\nabla m_p)-{\nabla }_{\iota ({\omega }^{\lambda }\nabla m_q)}^{\prime }({\omega }^{\lambda }\nabla m_p)-{\nabla }_{\nabla m_p}^{\prime }({\omega }^{\lambda }\nabla m_q)+{\omega }^{\lambda }\nabla {\left[m_p,m_q\right]}_M$$

equals $\left(j^{\prime }\circ {\Omega }_{{\mathbf{e}}_K}^{{\lambda }_K}\right)(\pi \nabla m_p,\pi \nabla m_q)+{\omega }^{\lambda }\left({\mathcal{R}}^{\nabla }(m_p,m_q)\right)$ and belongs to $j^{\prime }\left(K^{\prime }\right)$. For this reason, one can verify that:

$$\begin{array}{cc}\hfill & \left(\left(d_M\circ D^{\nabla }\right)f\right)\left(m_0,\dots ,m_n\right)\hfill \\ \hfill & ={\sum }_{p<q}{\left(-1\right)}^{p+q+1}f\left({\nabla }_{\iota (-{\omega }^{\lambda }\nabla m_p)}^{\prime }(-{\omega }^{\lambda }\nabla m_q),-{\omega }^{\lambda }\nabla m_0,\dots \widehat{p}\dots \widehat{q}\dots ,-{\omega }^{\lambda }\nabla m_n\right)\hfill \\ \hfill & =0+{\sum }_{p<q}{\left(-1\right)}^{p+q+1}f\left({\left[-{\omega }^{\lambda }\nabla m_p,-{\omega }^{\lambda }\nabla m_q\right]}_{L^{\prime }},-{\omega }^{\lambda }\nabla m_0,\dots \widehat{p}\dots \widehat{q}\dots ,-{\omega }^{\lambda }\nabla m_n\right)\hfill \\ \hfill & =\left(\left(D^{\nabla }\circ d^0\right)f\right)(m_0,\dots ,m_n).\hfill \end{array}$$

□

Since $D^{\nabla }$ commutes with the differential operators $d_L$ and $d_M$, it induces the homomorphism

$$D_{\#}^{\nabla }:H(L^{\prime },{\mathbf{e}}_K)⟶H\left(M\right).$$

Analogously, $D_o$ induces the homomorphism

$$D_{o\#}:H(L^{\prime },{\mathbf{e}}_K)⟶H\left(L\right)$$

which depends only on the structures of ${\mathbf{e}}_L,{\mathbf{e}}_K$. The homomorphism $D_{\#}^{\nabla }$ is called the secondary characteristic homomorphism for the triple $\left({\mathbf{e}}_L,{\mathbf{e}}_K,\nabla \right)$, whereas $D_{o\#}$ is said to be the secondary characteristic homomorphism for the pair $\left({\mathbf{e}}_L,{\mathbf{e}}_K\right)$. Elements of the A-module $Im{D}_{\#}^{\nabla }\subset H\left(M\right)$ are called secondary characteristic classes for $\left({\mathbf{e}}_L,{\mathbf{e}}_K,\nabla \right)$.

Remark 2.

If ∇ has values in K ($Im\nabla \subset K$), it follows that $D_{\#}^{\nabla }$ is trivial. Based on this, we consider $D_{\#}^{\nabla }$ as a measure of the incompatibility of ∇ with the extension ${\mathbf{e}}_K$.

Remark 3.

This construction is an extension of one of the Lie algebroids (cf. [8]) in the category of Lie pseudoalgebras.

Consider a third short exact sequence, denoted as ${\mathbf{e}}_S:0⟶S^{\prime }\stackrel{{\iota }_S}{⟶}S\stackrel{{\pi }_S}{⟶}{L}^{\prime \prime }⟶0$, of Lie pseudoalgebras, which splits in the category of A-modules. Moreover, assuming that there exists a morphism $\left(j_S^{\prime },j_S\right)$ of extensions ${\mathbf{e}}_S$, ${\mathbf{e}}_K$, i.e., we have the commutative diagram:

$$\begin{array}{ccccccc}{\mathbf{e}}_S:0\to & S\prime & \stackrel{{\iota }_S}{⟶}& S& \stackrel{{\pi }_S}{⟶}& L^{″}& ⟶0\\ & \downarrow j_S^{\prime }& & \downarrow j_S& & \Vert & \\ {\mathbf{e}}_K:0\to & K\prime & \stackrel{{\iota }_K}{⟶}& K& \stackrel{{\pi }_K}{⟶}& L^{″}& ⟶0\\ & \downarrow j\prime & & \downarrow j& & \Vert & \\ {\mathbf{e}}_L:0\to & L\prime & \stackrel{\iota }{⟶}& L& \stackrel{\pi }{⟶}& L^{″}& ⟶0\end{array}$$

and let ${\lambda }_S:L^{\prime \prime }\to S$ be a splitting of ${\mathbf{e}}_S$.

We define the K-connnection ${\nabla }^{\prime K}:K\to {End}_R\left(K^{\prime }\right)$ by ${\iota }_K\left({\nabla }_{\kappa }^{\prime K}\left({\kappa }^{\prime }\right)\right)={\left[\kappa ,{\iota }_K{\kappa }^{\prime }\right]}_K$, $\kappa \in K$, ${\kappa }^{\prime }\in K^{\prime }$ (see the definition of ${\nabla }^{\prime }$ in (6) for the pair ${\mathbf{e}}_L$, ${\mathbf{e}}_K$). Let us denote by $D^{K,L}$, $D^{S,K}$ and $D^{S,L}$ the characteristic homomorphism (on the level of forms) for $\left({\mathbf{e}}_L,{\mathbf{e}}_K\right)$, $\left({\mathbf{e}}_K,{\mathbf{e}}_S\right)$, $\left({\mathbf{e}}_L,{\mathbf{e}}_S\right)$ and identities connections, respectively. Since $j_S\circ {\lambda }_S$ is a splitting of ${\mathbf{e}}_K$, we have

$$D^{S,L}={\left(-{\omega }^{\left(j\circ j_S\right)\circ {\lambda }_S}\right)}^{*}={\left(-{\omega }^{j\circ \left(j_S\circ {\lambda }_S\right)}\right)}^{*}=D^{K,L}.$$

Notice that in view of $i_{{\kappa }^{\prime }}\circ {\left(j^{\prime }\right)}^{*}={\left(j^{\prime }\right)}^{*}\circ i_{j^{\prime }\left({\kappa }^{\prime }\right)}$ for ${\kappa }^{\prime }\in K^{\prime }$ (here, we have the substitution operators) and ${\omega }_K\circ j_S={\omega }_S$ and ${\nabla }_{j\left(\kappa \right)}^{\prime }\circ j^{\prime }=j^{\prime }\circ {\nabla }_{\kappa }^{\prime K}$ for $\kappa \in K$, we observe that the image of the space $\mathcal{C}{(L^{\prime },K^{\prime })}^K$ under ${\left(j_K^{\prime }\right)}^{*}$ is included in $\mathcal{C}{(L^{\prime },S^{\prime })}^S$. Lemma 2 now yields:

$$\begin{array}{cc}\hfill j^{*}\circ D^{K,L}& ={\left(-{\omega }^{j\circ \left(j_S\circ {\lambda }_S\right)}\circ j_K\right)}^{*}=\left(-j^{\prime }\circ {\omega }^{j_S\circ {\lambda }_S}\right)={\left(-{\omega }^{j_S\circ {\lambda }_S}\right)}^{*}\circ {\left(j^{\prime }\right)}^{*}\hfill \\ \hfill & =D^{S,K}\circ {\left(j^{\prime }\right)}^{*}.\hfill \end{array}$$

In this way, we have proven:

Theorem 4.

$D^{S,K}\circ {\left(j^{\prime }\right)}^{*}=j^{*}\circ D^{K,L}=j^{*}\circ D^{S,L}$.

5. Application for Inner Product Modules

Let R be a unital and commutative ring, A an algebra over R and E a finitely generated projective A-module. It is demonstrated in [30] that the anchor ${\omega }_{CO\left(E\right)}$ of $CO\left(E\right)$ is surjective and the Atiyah sequence ${\mathbf{e}}_{CO\left(E\right)}:0⟶{End}_A\left(E\right)\stackrel{\iota }{⟶}CO\left(E\right)\stackrel{{\omega }_{CO\left(E\right)}}{\to }Der\left(A\right)⟶0$ splits. Assume that E is endowed with a nondegenerate, symmetric, A-bilinear map $h:E\times E\to A$. In this context, we refer to h as a pseudometric.

A finitely generated projective A-module E with a pseudometric h is referred to as an inner product module (see [32]). Let $\left(M,{\omega }_M,\left[·,·\right]\right)$ be a Lie pseudoalgebra over $\left(R,A\right)$. An M-connection $\nabla :M\to CO\left(E\right)$ within $CO\left(E\right)$ is considered compatible with h if

$${\omega }_M\left(m\right)\left(h\left(x,y\right)\right)=h\left({\nabla }_{m}x,y\right)+h\left(x,{\nabla }_{m}y\right)$$

for all $m\in M$, $x,y\in E$ (see [32]). Additionally, we assume that R includes $\frac{1}{2}$, i.e., the element $\frac{1}{2}\in R$, satisfying $\frac{1}{2}+\frac{1}{2}=1$. For any $g\in CO\left(E\right)$, by $\tilde{g}$, we will denote the endomorphism $\tilde{g}=\frac{1}{2}\left(g+g^{*}\right)$, where $g^{*}$ represents the element of $CO\left(E\right)$ with the property that

$$h\left(g^{*}\left(x\right),y\right)={\omega }_{CO\left(E\right)}\left(g\right)\left(h\left(x,y\right)\right)+h\left(x,g\left(y\right)\right),x,y\in E.$$

Now, we define two modules:

$$CO(E,h)=\left\{f\in CO\left(E\right):f+f^{*}=0\right\}$$

and

$${Sk}_A\left(E\right)=CO(E,h)\cap {End}_A\left(E\right).$$

In $CO(E,h)$, we also establish the structure of a Lie–Rinehart subalgebra within $CO\left(E\right)$ with the Atiyah sequence ${\mathbf{e}}_{CO(E,h)}:0⟶{Sk}_A\left(E\right)\stackrel{{\iota }^{\prime }}{⟶}L\stackrel{{\omega }_{CO(E,h)}}{\to }Der\left(A\right)⟶0$. As a result, we have the following commutative diagram:

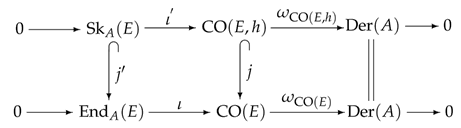where $\iota$, ${\iota }^{\prime }$, j, $j^{\prime }$ are suitable inclusions. In the terminology of differential geometry, we refer to ${\mathbf{e}}_{CO(E,h)}$ as a reduction of ${\mathbf{e}}_{CO\left(E\right)}$.

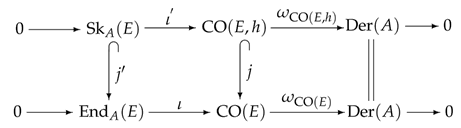
Now, let $\nabla :M\to CO\left(E\right)$ be any flat connection in $CO\left(E\right)$. Define a connection ${\nabla }^h:M\to CO\left(E\right)$ by

$${\omega }_M\left(m\right)\left(h\left(x,y\right)\right)=h\left({\nabla }_{m}x,y\right)+h\left(x,{\nabla }_m^{h}y\right)\mathrm{for}\mathrm{all}m\in M,x,y\in E.$$

We see that

$${\nabla }^h={id}^h\circ \nabla$$

(12)

where id denotes the identity map on $CO\left(E\right)$, considered as a $CO\left(E\right)$-connection on $CO\left(E\right)$. Moreover, ${\nabla }^h$ is also flat because ${\mathcal{R}}_{m,n}^{{\nabla }^h}=-{\left({\mathcal{R}}_{m,n}^{\nabla }\right)}^{*}$.

We derive $D_{\#}^{\nabla }$ using ∇ and ${\nabla }^h$. To simplify the notation, we briefly write ${\mathcal{C}}^n(E,h)$ instead of ${\mathcal{C}}^n{({End}_A\left(E\right),{Sk}_A\left(E\right))}^{CO(E,h)}$.

Let $\lambda :{Der}_R\left(A\right)\to CO\left(E\right)$ be a connection compatible with h, i.e., ${\lambda }^h=\lambda$. The existence of such a connection is proved in [32] (Theorem 1.3, p. 278). However, one can check that if $\nabla :M\to CO\left(E\right)$ is any connection in $CO\left(E\right)$, then $\frac{1}{2}\left(\nabla +{\nabla }^h\right)$ is compatible with h.

Lemma 8.

If $f\in CO\left(E\right)$, then $\widetilde{-{\omega }^{\lambda }\left(f\right)}=\frac{1}{2}({id}^h-id)\left(f\right)$.

Proof. 

Let $f\in CO\left(E\right)$. Then, from (12) and the definition of ${\omega }^{\lambda }$, we deduce

$${\omega }^{\lambda }=id-{id}^h+{id}^h\circ {\omega }^{\lambda }.$$

Since ${id}^h\left({\omega }^{\lambda }f\right)=-{\left({\omega }^{\lambda }f\right)}^{*h}$, we see that $\widetilde{-{\omega }^{\lambda }\left(f\right)}=\frac{1}{2}({id}^h-id)\left(f\right)$. □

As a result, we obtain the following:

Theorem 5.

For all $\varphi \in {\mathcal{C}}^n(E,h)$, we have

$$D_o\left(\varphi \right)={\left(\frac{1}{2}\left({id}^h-id\right)\right)}^{*}\left(\varphi \right),D^{\nabla }\left(\varphi \right)={\left(\frac{1}{2}\left({\nabla }^h-\nabla \right)\right)}^{*}\left(\varphi \right).$$

Proof. 

Let $f_1,\dots ,f_n\in CO\left(E\right)$. From Lemma 8, we deduce that:

$$\begin{array}{cc}\hfill \left(D_o\varphi \right)\left(f_1,\dots ,f_n\right)& =\varphi \left(-{\omega }^{\lambda }\left(f_1\right),\dots ,-{\omega }^{\lambda }\left(f_n\right)\right)\hfill \\ \hfill & =\varphi \left(-\widetilde{{\omega }^{\lambda }\left(f_1\right)},\dots ,-\widetilde{{\omega }^{\lambda }\left(f_n\right)}\right)\hfill \\ \hfill & =\left({\left(\frac{1}{2}\left({id}^h-id\right)\right)}^{*h}\varphi \right)(f_1,\dots ,f_n).\hfill \end{array}$$

Moreover, (10) and (12) now yield $D^{\nabla }={\left(\frac{1}{2}\left({\nabla }^h-\nabla \right)\right)}^{*}$. □

From Theorem 5, we obtain the following:

Corollary 4.

$D^{{\nabla }^h}\varphi ={\left(-1\right)}^n{D}^{\nabla }\varphi$ for all $\varphi \in {\mathcal{C}}^n(E,h).$

Proof. 

Theorem 5 gives

$$\begin{array}{cc}\hfill D^{\nabla }\varphi & ={\left(\frac{1}{2}\left({\nabla }^h-\nabla \right)\right)}^{*}\left(\varphi \right)={\left(-1\right)}^n{\left(\frac{1}{2}\left(\nabla -{\nabla }^h\right)\right)}^{*}\left(\varphi \right)\hfill \\ \hfill & ={\left(-1\right)}^n{\left(\frac{1}{2}\left({\left({\nabla }^h\right)}^h-{\nabla }^h\right)\right)}^{*}\left(\varphi \right)={\left(-1\right)}^n{D}^{{\nabla }^h}\varphi .\hfill \end{array}$$

□

We intend to prove that every basic form is closed. In the proof, we use the following:

Lemma 9.

For any $\alpha ,\beta \in {End}_A\left(E\right)$, we have $\left[\alpha ,{\beta }^{*}\right]+\left[{\alpha }^{*},\beta \right]\in {Sk}_A(E,h)$.

Proof. 

Let $\alpha ,\beta \in {End}_A\left(E\right)$. Since ${End}_A\left(E\right)$ is the kernel of ${\omega }_{CO\left(E\right)}$, it follows that

$${\left(\alpha \circ \beta \right)}^{*}={\beta }^{*}\circ {\alpha }^{*},{\left({\alpha }^{*}\right)}^{*}=\alpha ,{\left({\beta }^{*}\right)}^{*}=\beta ,$$

and hence

$${\left[\alpha ,\beta \right]}^{*}=-\left[{\alpha }^{*},{\beta }^{*}\right].$$

This implies:

$${\left[\alpha ,{\beta }^{*}\right]}^{*}+\left[{\alpha }^{*},\beta \right]=0={\left[{\alpha }^{*},\beta \right]}^{*}+\left[\alpha ,{\beta }^{*}\right],$$

and, in consequence, $\left[\alpha ,{\beta }^{*}\right]+\left[{\alpha }^{*},\beta \right]\in {Sk}_A(E,h)$. □

Theorem 6.

Every form $f\in {\mathcal{C}}^n(E,h)$ of degree $n\ge 1$ is closed.

Proof. 

Let ${\alpha }_1,\dots ,{\alpha }_{n+1}\in {End}_A\left(E\right)$. Then:

$$\begin{array}{cc}\hfill 2\left(d^{0}f\right)({\alpha }_1,\dots ,{\alpha }_{n+1})& =2{\displaystyle {\sum }_{i<j}}{\left(-1\right)}^{i+j+1}f\left(\left[{\alpha }_i,{\alpha }_j\right],{\alpha }_1,\dots \widehat{i}\dots \widehat{j}\dots ,{\alpha }_{n+1}\right)\hfill \\ \hfill & ={\displaystyle {\sum }_{i\ne j}}{\epsilon }_{ij}·f\left(\left[{\alpha }_i,{\alpha }_j\right],{\alpha }_1,\dots \widehat{i}\dots \widehat{j}\dots ,{\alpha }_{n+1}\right),\hfill \end{array}$$

where:

$${\epsilon }_{ij}=\left\{\begin{array}{cc}{\left(-1\right)}^{i+j+1}\hfill & \mathrm{if}i<j,\hfill \\ {\left(-1\right)}^{i+j}\hfill & \mathrm{if}i>j.\hfill \end{array}\right.$$

Observe that

$$\begin{array}{cc}\hfill & {\displaystyle {\sum }_{i\ne j}}{\epsilon }_{ij}·f\left(\left[{\alpha }_i,{\alpha }_j^{*}\right],{\alpha }_1,\dots \widehat{i}\dots \widehat{j}\dots ,{\alpha }_{n+1}\right)\hfill \\ \hfill & ={\displaystyle {\sum }_{i<j}}{\left(-1\right)}^{i+j+1}·f\left(\left[{\alpha }_i,{\alpha }_j^{*}\right]+\left[{\alpha }_i^{*},{\alpha }_j\right],{\alpha }_1,\dots \widehat{i}\dots \widehat{j}\dots ,{\alpha }_{n+1}\right)=0,\hfill \end{array}$$

because $\left[{\alpha }_i,{\alpha }_j^{*}\right]+\left[{\alpha }_i^{*},{\alpha }_j\right]\in {Sk}_A(E,h)$ (see Lemma 9). By applying this, we can observe that

$$\begin{array}{cc}\hfill 2\left(d^{0}f\right)\left({\alpha }_1,\dots ,{\alpha }_{n+1}\right)& ={\displaystyle {\sum }_{i\ne j}}{\epsilon }_{ij}·f\left(\left[{\alpha }_i,{\alpha }_j-{\alpha }_j^{*}\right],{\alpha }_1,\dots \widehat{i}\dots \widehat{j}\dots ,{\alpha }_{n+1}\right)\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^n}{\left(-1\right)}^{j+1}{\displaystyle \sum _{i=1\dots \widehat{j}\dots n}}f\left({\alpha }_1,\dots ,{\alpha }_{i-1},\left[{\alpha }_j-{\alpha }_j^{*},{\alpha }_i\right],\dots \widehat{j}\dots ,{\alpha }_{n+1}\right).\hfill \end{array}$$

By the invariance of f, we can deduce that the last sum is equal to

$${\displaystyle \sum _{j=1}^n}{\left(-1\right)}^{j+1}{\omega }_{CO(E,h)}\left({\alpha }_j-{\alpha }_j^{*}\right)\left(f({\alpha }_1,\dots \widehat{j}\dots ,{\alpha }_{n+1})\right),$$

and hence zero since ${\alpha }_j-{\alpha }_j^{*}\in {Sk}_A(E,h)$. Consequently, $d^{0}f=0$. □

Let ${Tr}_n\in {\mathcal{C}}^n(CO\left(E\right))$ be a multilinear trace form. We set the trace form ${\widetilde{Tr}}_n$ by ${\widetilde{Tr}}_n(f_1,\dots ,f_n)={Tr}_n(\widetilde{f_1},\dots ,\widetilde{f_n})$. Explicitly,

$${\widetilde{Tr}}_n(f_1,\dots ,f_n)={\displaystyle {\sum }_{\sigma \in S_n}}sgn\sigma ·tr\left(\widetilde{f_{\sigma \left(1\right)}},\dots ,\widetilde{f_{\sigma \left(n\right)}}\right).$$

Let ${\widetilde{Tr}}_n^A$ denote its restriction to ${\mathcal{C}}^n\left({End}_A\left(E\right)\right)$. By the definition of ${\widetilde{Tr}}_n^A$, we see immediately that $i_g\left({\widetilde{Tr}}_n^A\right)=0$ for all $g\in {Sk}_A\left(E\right)$. ${\widetilde{Tr}}_n^A$ is ${Hom}^n\left({\nabla }^{\prime }\right)$-invariant where ${\nabla }^{\prime }:CO\left(E\right)\to {End}_R\left({End}_A\left(E\right)\right)$ is defined by ${\nabla }_f^{\prime }\left(g\right)={\left[f,g\right]}_{CO\left(E\right)}$ (see [30]). Since ${\omega }_{CO(E,h)}={\omega }_{CO\left(E\right)}\circ j$ and ${\widetilde{[j\kappa ,f]}}_{CO\left(E\right)}={[j\kappa ,\tilde{f}]}_{CO\left(E\right)}$ for all $\kappa \in CO(E,h)$ and $f\in {End}_A\left(E\right)$, we deduce that ${\widetilde{Tr}}_n^A$ is ${Hom}^n({\nabla }^{\prime }\circ j)$-invariant (see Lemma 4), and consequently, ${\widetilde{Tr}}_n^A\in {\mathcal{C}}^n(E,h)$. Moreover, by Theorem 6, ${\widetilde{Tr}}_n^A$ is closed with respect to $d^0$. So, by Theorem 5, ${\widetilde{Tr}}_n^A$ induces the secondary characteristic class $D_{\#}^{\nabla }\left(\left[{\widetilde{Tr}}_n^A\right]\right)\in H^n(CO\left(E\right))$ for the triple $\left(CO\left(E\right),CO(E,h),\nabla \right)$ by

$$D_{\#}^{\nabla }\left(\left[{\widetilde{Tr}}_n^A\right]\right)=\left[{\left(\frac{1}{2}\left({\nabla }^h-\nabla \right)\right)}^{*}\left({Tr}_n\right)\right].$$

(13)

In this way, we have obtained the Chern–Simons-type classes for $CO\left(E\right)$, its reduction $CO(E,h)$ and arbitrary flat connection $\nabla :M\to CO\left(E\right)$. These classes generalize the secondary characteristic classes stated in [34] for Lie algebroids.

By an isometry between inner product of finitely generated A-modules $\left(E_1,h_1\right)$ and $\left(E_2,h_2\right)$, we mean an isomorphism $\vartheta :E_1\to E_2$ of A-modules such that

$$h_1(x,y)=h_2(\vartheta x,\vartheta y)\mathrm{for}\mathrm{all}x,y\in E_1.$$

Then, we say that $\left(E_1,h_1\right)$, $\left(E_2,h_2\right)$ are isometric.

Let $\left(E_1,h_1\right)$ and $\left(E_2,h_2\right)$ be two isometric inner product A-modules with an isometry $\vartheta :E_1\to E_2$. Observe that if f is an element of $CO\left(E_2\right)$ with the anchor ${\omega }_{CO\left(E_2\right)}\left(f\right)$, then ${\vartheta }^{-1}\circ f\circ \vartheta \in CO\left(E_1\right)$ and

$${\omega }_{CO\left(E_1\right)}({\vartheta }^{-1}\circ f\circ \vartheta )={\omega }_{CO\left(E_2\right)}\left(f\right).$$

(14)

The map

$$\Phi :CO\left(E_2\right)⟶CO\left(E_1\right),f⟼{\vartheta }^{-1}\circ f\circ \vartheta$$

is an isomorphism of Lie pseudoalgebras. Indeed, $\Phi$ preserves the Lie brackets and, by (14), commutes with the anchors. The pullback

$${\Phi }^{*}:\mathcal{C}(CO\left(E_1\right))⟶\mathcal{C}(CO\left(E_2\right)),\left({\Phi }^{*}f\right)(g_1,\dots ,g_n)=f(\Phi \left(g_1\right),\dots ,\Phi \left(g_n\right))$$

of forms via $\Phi$ is an isomorphism of algebras. Moreover, the restriction $\Phi$ to $CO(E_2,h_2)$ is also an isomorphism of Lie pseudoalgebras:

$$\Phi |CO(E_2,h_2):CO(E_2,h_2)\stackrel{\cong }{⟶}CO(E_1,h_1).$$

Let $k\in \left\{1,2\right\}$, ${Sk}_A(E_k,h_k)=CO(E_k,h_k)\cap {End}_A\left(E_k\right)$, $j_k:CO(E_k,h_k)\hookrightarrow CO\left(E_k\right)$ and $j_k^{\prime }:{Sk}_A(E_k,h_k)\hookrightarrow {End}_A\left(E_k\right)$ denote suitable inclusions. Observe that the anchor ${\omega }_{CO(E_h,h_k)}$ of $CO(E_k,h_k)$ equals ${\omega }_{CO(E_k,h_k)}\circ j_k$. Now, let $f\in {\mathcal{C}}^n(E_1,h_1)$, ${\alpha }_1\dots ,{\alpha }_n\in {End}_A\left(E_2\right)$, ${\kappa }_2\in CO\left(E_2\right)$, ${\kappa }_1=\Phi \left({\kappa }_2\right)$. Since $\Phi$ commutes with anchors, $j_1{\kappa }_1=\Phi j_2{\kappa }_2$ and f is invariant, we have:

$${\omega }_{CO(E_2,h_2)}\left({\kappa }_2\right)\left(\left({\Phi }^{*}f\right)({\alpha }_1,\dots ,{\alpha }_n)\right)=\sum _{i=1}^n\left({\Phi }^{*}f\right)\left({\alpha }_1,\dots ,{\left[j_2{\kappa }_2,{\alpha }_i\right]}_{CO\left(E_2\right)},\dots ,{\alpha }_n\right).$$

Moreover, $i_g\left({\Phi }^{*}f\right)={\Phi }^{*}\left(i_{\Phi \left(g\right)}f\right)$ for all $g\in {End}_A\left(E_1\right)$. These properties indicate that ${\Phi }^{*}f$ is an element of the basic algebra. Therefore, we observe that the restriction of ${\Phi }^{*}$ to the basic algebra $\mathcal{C}(E_1,h_1)$ is an isomorphism onto the algebra $\mathcal{C}(E_2,h_2)$ with the inverse homomorphism induced by ${\Phi }^{-1}$.

Lemma 10.

${id}^{h_1}\circ \Phi =\Phi \circ {id}^{h_2}.$

Proof. 

Let $f\in CO\left(E_2\right)$, $x,y\in E_2$. Since $\vartheta$ is an isometry and $\Phi$ commutes with the anchors of $CO\left(E_1\right)$ and $CO\left(E_2\right)$, we obtain the desired equality. □

Consequently, we obtain:

Theorem 7.

${\Phi }^{*}\circ D_o^1=D_o^2\circ {\Phi }^{*}$ where $D_o^1$ and $D_o^2$ denote the secondary characteristic homomorphisms for the pairs $\left(CO\left(E_1\right),CO(E_1,h_1)\right)$ and $\left(CO\left(E_2\right),CO(E_2,h_2)\right)$, respectively.

Proof. 

We conclude from Lemma 10 that $\left(\frac{1}{2}\left({id}^{h_1}-id\right)\right)\circ \Phi =\Phi \circ \left(\frac{1}{2}\left({id}^{h_2}-id\right)\right)$, and hence, by Theorem 5:

$${\Phi }^{*}\circ D_o^1={\left(\frac{{id}^h-id}{2}\circ \Phi \right)}^{*}={\left(\Phi \circ \frac{{id}^h-id}{2}\right)}^{*}=D_o^2\circ {\Phi }^{*}.$$

□

${\Phi }^{*}$ commutes with suitable differential operators. Hence, using Theorem 7, we obtain the following:

Theorem 8.

The secondary characteristic homomorphism for the triple

$$(CO(E),CO(E,h),\nabla )$$

where $\left(E,h\right)$ is isomorphic to each other inner product module $\left(E,h_2\right)$, is independent of the choice of the metric.

Therefore, if in the A-module $\left(E,h_1\right)$, which is isometric with each other $\left(E,h_2\right)$, there exists a pseudometric h such that ∇ is compatible with h, i.e., $\nabla ={\nabla }^h$, then secondary characteristic classes for $\left(CO\left(E\right),CO(E,h),\nabla \right)$ are equal to zero. Hence, nontrivial secondary characteristic classes are obstructions to the existence of an invariant pseudometric with respect to the connection. Moreover, we can describe the secondary characteristic homomorphism for $\left(CO\left(E\right),CO(E,h),\nabla \right)$ using an arbitrary compatible connection. Namely, we have the following:

Theorem 9.

Let $\nabla :M\to CO\left(E\right)$ be a flat M-connection on $CO\left(E\right)$ and $\mathring{\nabla }:M\to CO\left(E\right)$ be any M-connection on $CO\left(E\right)$ compatible with h. Then

$$D^{\nabla }={\left(\mathring{\nabla }-\nabla \right)}^{*}.$$

Proof. 

Let $m\in M$, $x,y\in E$. Since ${\mathring{\nabla }}_m-{\nabla }_m\in {End}_A\left(E\right)$ and $\mathring{\nabla }$ is compatible with h, we have:

$$\begin{array}{cc}\hfill h\left({\left({\mathring{\nabla }}_m-{\nabla }_m\right)}^{*}x,y\right)& ={\omega }_{CO\left(E\right)}\left({\mathring{\nabla }}_m-{\nabla }_m\right)\left(h\left(x,y\right)\right)+h\left(x,\left({\mathring{\nabla }}_m-{\nabla }_m\right)\left(y\right)\right)\hfill \\ \hfill & ={\omega }_M\left(m\right)\left(h\left(x,y\right)\right)-h\left({\mathring{\nabla }}_{m}x,y\right)-{\omega }_M\left(m\right)\left(h\left(x,y\right)\right)+h\left({\nabla }_m^{h}x,y\right)\hfill \\ \hfill & =h\left({\left({\nabla }^h-\mathring{\nabla }\right)}_{m}x,y\right);\hfill \end{array}$$

and hence, ${\left(\mathring{\nabla }-\nabla \right)}_m^{*}={\left({\nabla }^h-\mathring{\nabla }\right)}_m$. It follows that

$$\widetilde{{\left(\mathring{\nabla }-\nabla \right)}_m}=\frac{1}{2}\left({\left(\mathring{\nabla }-\nabla \right)}_m^{*}+{\left(\mathring{\nabla }-\nabla \right)}_m\right)=\frac{1}{2}{\left({\nabla }^h-\nabla \right)}_m.$$

Finally, we obtain:

$$D^{\nabla }={\left(\frac{1}{2}\left({\nabla }^h-\nabla \right)\right)}^{*}={\left(\widetilde{\mathring{\nabla }-\nabla }\right)}^{*}={\left(\mathring{\nabla }-\nabla \right)}^{*}.$$

□

We have analyzed the pseudoalgebra $CO\left(E\right)$ associated with an inner product module E and its reduction, which is a more general case compared to a Lie algebroid of a vector bundle and its Riemannian reduction. In the specific case of Lie algebroids, we derive novel characteristic classes in the sense of [34]. Clearly, in this context, any Riemannian structure $\left(E,h_1\right)$ is isometric to any other such structure $\left(E,h_2\right)$.

6. Conclusions

The considered characteristic homomorphism generalizes the concept of secondary characteristic classes to more general structures, including pairs of Lie pseudoalgebras $K\subset L$. It also encompasses connections with curvatures that fall within the kernel of the anchor of the Lie pseudoalgebra K. We have demonstrated this construction in the context of inner product modules equipped with flat connections, revealing that Chern–Simons-type classes are included in the image of the characteristic homomorphism.

There is another concept of Lie pseudoalgebras that in general differs from the one discussed in this paper. The theory of the second type of Lie pseudoalgebras was developed in [40]. It is a module over commutative Hopf algebra endowed with a specific Lie bracket which satisfies some generalized version of the Jacobi identity (for more details, we refer the reader to [40,41]). In some situations, this different approach generalizes the one under consideration. We claim that the study of characteristic homomorphisms on the second kind of Lie pseudoalgebras in the sense of [40] can give interesting results in the future.