A Modified Parallel Algorithm for a Common Fixed-Point Problem with Application to Signal Recovery

Abstract

In this work, an algorithm is introduced for the problem of finding a common fixed point of a finite family of G-nonexpansive mappings in a real Hilbert space endowed with a directed graph G. This algorithm is a modified parallel algorithm inspired by the inertial method and the Mann iteration process. Moreover, both weak and strong convergence theorems are provided for the algorithm. Furthermore, an application of the algorithm to a signal recovery problem with multiple blurring filters is presented. Consequently, the numerical experiment shows better results compared with the previous algorithm.

1. Introduction

In the mathematical literature, the correlation between symmetry and fixed-point problems is significant, as symmetries can be viewed as fixed points of transformation. For example, consider the problem of finding the fixed points of a reflection or rotation transformation. The fixed points of a reflection transformation are the points on the reflection axis and the symmetry concerning the reflection. Similarly, the fixed points of a rotation transformation are the points that are unchanged after rotation, and so there is symmetry concerning rotation.

A fixed-point problem is one of the problems that can be applied to various real-world problems including signal recovery problems. In addition, the fixed-point problem can be considered in the context of graph theory. In 2015, Tiammee et al. [1] developed some iterative procedures for G-nonexpansive mappings in Hilbert spaces involving a directed graph G. Furthermore, Tripak [2] estimated common fixed points of G-nonexpansive mappings in a Banach space involving a directed graph G using the Ishikawa iteration process. Subsequently, there has been numerous research studies involving iteration processes; see refs. [3,4,5].

In 2015 and 2016, Anh and Hieu [6,7] proposed a parallel monotone hybrid algorithm for a finite family of quasi $\varphi$-nonexpansive mappings in a Banach space. Recently, Charoensawan et al. [8] presented an algorithm called the Inertial Ishikawa-type parallel algorithm (IITPA) to estimate common fixed points of a finite family of G-nonexpansive mappings in a real Hilbert space endowed with a directed graph G. This algorithm was constructed according to the parallel monotone hybrid algorithm, the Ishikawa iteration, and the inertial method. They obtained a weak convergence theorem for the algorithm. There are numerous works related to parallel algorithms; see refs. [9,10,11].

Furthermore, another approach to developing the algorithm is to achieve a higher rate of convergence. Polyak [12] suggested an inertial extrapolation to accelerate the process of solving smooth convex minimization problems. The inertial extrapolation-type algorithms have been studied by several authors; see refs. [13,14,15].

Motivated by the previous research, our study suggests Algorithm 1 with the ideas of the parallel monotone hybrid algorithm, the Mann iteration process, and the inertial method. Then we prove some weak and strong convergence results for approximating a common fixed point of a finite family of G-nonexpansive mappings in a real Hilbert space endowed with a directed graph G under some suitable conditions. Finally, we apply our results to a signal recovery problem involving multiple blurring filters and compare them to the previous algorithms.

2. Preliminaries

First, let us recall some definitions in graph theory. To begin, assume throughout this section that $G=\left(V\right(G),E(G\left)\right)$ is a directed graph.

Definition 1.

G is said to be transitive if $(u,v),(v,z)\in E\left(G\right)$ implies $(u,z)\in E\left(G\right)$ for any $u,v,z\in V\left(G\right)$.

Definition 2.

Let $C\subseteq V\left(G\right)$ and $v\in V\left(G\right)$.

(i) 

C is said to be dominated by v if $(v,c)\in E\left(G\right)$ for all $c\in C$;

(ii) 

C is said to dominate v if $(c,v)\in E\left(G\right)$ for all $c\in C$.

Next, definitions of a metric space involving a directed graph are stated. These definitions are common and often found in literature, for example, see [8].

Definition 3.

A metric space $\mathcal{X}$ is said to be endowed with G if $V\left(G\right)=\mathcal{X}$ and $\left\{\right(v,v):v\in \mathcal{X}\}\subseteq E\left(G\right)$, where G has no parallel edges.

Definition 4.

Let C be a nonempty subset of a Hilbert space $\mathcal{H}$. Assume that $V\left(G\right)=C$ and $\mathcal{S}$ is a self-mapping on C. Then S is said to be G-nonexpansive if

(i) 

$\mathcal{S}$ is edge-preserving, that is, for $u,v\in V\left(G\right)$,

$$(u,v)\in E\left(G\right)\Rightarrow (\mathcal{S}u,\mathcal{S}v)\in E\left(G\right);$$

(i) 

$\mathcal{S}$ non-increases weights of edges of G, that is, for $u,v\in V\left(G\right)$,

$$(u,v)\in E\left(G\right)\Rightarrow \parallel \mathcal{S}u-\mathcal{S}v\parallel \le \parallel u-v\parallel .$$

Also, we need some known lemmas as follows.

Lemma 1

([16]). Let $\left\{{\sigma }_n\right\}$ and $\left\{{\theta }_n\right\}$ be sequences in ${\mathbb{R}}^{+}\cup \left\{0\right\}$ satisfying ${\sigma }_{n+1}\le {\sigma }_n+{\theta }_n$ and ${\displaystyle \sum _{n=1}^{\infty }{\theta }_n<\infty }$. Then the sequence $\left\{{\sigma }_n\right\}$ converges.

Lemma 2

([17] Opial). Let C be a nonempty subset of a Hilbert space $\mathcal{H}$, and let $\left\{{\kappa }_n\right\}$ be a sequence in $\mathcal{H}$. Assume that:

(i) 

the sequence $\left\{\parallel {\kappa }_n-\varkappa \parallel \right\}$ converges for all $\varkappa \in C$;

(ii) 

all weak sequential cluster points of $\left\{{\kappa }_n\right\}$ belong to C.

Then $\left\{{\kappa }_n\right\}$ converges weakly to some point in C.

Lemma 3

([18]). Let C be a nonempty closed convex subset of a Hilbert space $\mathcal{H}$. Assume that $V\left(G\right)=C$ and that $\mathcal{S}$ is a G-nonexpansive self-mapping on C. Given that $\left\{u_n\right\}$ is a sequence in C satisfying $u_n\rightharpoonup u$ and $\{u_n-\mathcal{S}{u}_n\}\to v$, where $u\in C$ and $v\in \mathcal{H}$, if there is a subsequence $\left\{u_{n_k}\right\}$ of $\left\{u_n\right\}$ satisfying $(u_{n_k},u)\in E\left(G\right)$ for all $k\in \mathbb{N}$, then $(I-\mathcal{S})u=v$.

For convenience, we define condition $\left(SK\right)$ of a family of mappings.

Definition 5.

Let C be a nonempty subset of a metric space $(X,d)$. For each $i=1,2,\dots ,N$, assume that $S_i$ is a self-mapping on C. Then the set $\{S_i:i=1,2,\dots ,N\}$ is said to satisfy condition $\left(SK\right)$ if there is a non-decreasing function $\phi :[0,\infty )\to [0,\infty )$ with $\phi \left(0\right)=0$, and $\phi \left(r\right)>0$ for $r>0$ such that for each $c\in C$,

$$\phi \left(d(c,\mathbb{F})\right)\le \underset{1\le i\le N}{max}d(c,S_{i}c),$$

(1)

where $\mathbb{F}:=\bigcap _{i=1}^{N}Fix\left({\mathcal{S}}_i\right)$ and ${\displaystyle d(c,\mathbb{F})=\underset{v\in \mathbb{F}}{inf}d(c,v)}$.

3. Results

To begin, assume throughout this section that $\mathcal{H}$ is a real Hilbert space endowed with a directed graph G, where $E\left(G\right)$ is convex, and that ${\mathcal{S}}_i:\mathcal{H}\to \mathcal{H}$ is a G-nonexpansive mapping for all $i=1,2,\dots ,N$, where $\mathbb{F}:={\displaystyle \bigcap _{i=1}^N}Fix\left({\mathcal{S}}_i\right)\ne \varnothing$. Define the inertial Mann-type parallel algorithm (IMTPA) as follows.

Algorithm 1: Inertial Mann-type parallel algorithm (IMTPA)

Initialization: Choose ${\kappa }_0,{\kappa }_1\in \mathcal{H}$, and let $n:=1.$ Iterative Steps: Construct a sequence $\left\{{\kappa }_n\right\}$ as the following: Step 1. Compute $$\begin{array}{c}\hfill {\varpi }_n={\kappa }_n+{\vartheta }_n({\kappa }_n-{\kappa }_{n-1}),\end{array}$$ where $\left\{{\vartheta }_n\right\}\subset [0,\infty )$. Step 2. Compute $$\begin{array}{c}\hfill {\varrho }_n^i={\lambda }_n^i{\mathcal{S}}_i{\kappa }_n+{\delta }_n^i{\mathcal{S}}_i{\varpi }_n+(1-{\lambda }_n^i-{\delta }_n^i){\varpi }_n,\end{array}$$ where $\left\{{\lambda }_n^i\right\},\left\{{\delta }_n^i\right\},\{{\lambda }_n^i+{\delta }_n^i\}\subset [0,1]$ for all $i=1,2,\dots ,N$. Step 3. Define $$\begin{array}{c}\hfill {\kappa }_{n+1}=argmax\left\{∥{\varrho }_n^i-{\varpi }_n∥:i=1,2,\dots ,N\right\}.\end{array}$$ Repeat all steps by replacing n with $n+1$.

Next, we prove some lemmas to support our main theorems. Assume that $\left\{{\kappa }_n\right\}$ is a sequence generated by IMTPA.

Lemma 4.

Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

$\left\{{\kappa }_n\right\}$ and $\left\{{\varpi }_n\right\}$ dominate ϰ for all $\varkappa \in \mathbb{F}$.

Then the sequence $\left\{{\kappa }_n\right\}$ is bounded, and the limit ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_n-\varkappa \parallel }$ exists for all $\varkappa \in \mathbb{F}$.

Proof. 

Let $\varkappa \in \mathbb{F}$. By assumption $\left(ii\right)$, we have that $({\kappa }_n,\varkappa ),({\varpi }_n,\varkappa )\in E\left(G\right)$. Fix i for some $i=1,2,\dots ,N$. Since ${\mathcal{S}}_i$ is edge-preserving, $({\mathcal{S}}_i{\kappa }_n,\varkappa ),({\mathcal{S}}_i{\varpi }_n,\varkappa )\in E\left(G\right)$. Moreover, using the fact that ${\mathcal{S}}_i$ is G-nonexpansive, we obtain the following result:

$$\begin{array}{cc}∥{\varrho }_n^i-\varkappa ∥\hfill & =∥{\lambda }_n^i\left({\mathcal{S}}_i{\kappa }_n-\varkappa \right)+{\delta }_n^i\left({\mathcal{S}}_i{\varpi }_n-\varkappa \right)+(1-{\lambda }_n^i-{\delta }_n^i)\left({\varpi }_n-\varkappa \right)∥\hfill \\ \hfill & \le {\lambda }_n^i∥{\mathcal{S}}_i{\kappa }_n-\varkappa ∥+{\delta }_n^i∥{\mathcal{S}}_i{\varpi }_n-\varkappa ∥+(1-{\lambda }_n^i-{\delta }_n^i)∥{\varpi }_n-\varkappa ∥\hfill \\ \hfill & \le {\lambda }_n^i∥{\kappa }_n-\varkappa ∥+(1-{\lambda }_n^i)∥{\varpi }_n-\varkappa ∥\hfill \\ \hfill & \le ∥{\kappa }_n-\varkappa ∥+{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel .\hfill \end{array}$$

Note that the above inequality is true for all $i=1,2,\dots ,N$. By the definition of ${\kappa }_{n+1}$, ${\kappa }_{n+1}={\varrho }_n^j$ for some $j=1,2,\dots ,N$. Thus,

$$∥{\kappa }_{n+1}-\varkappa ∥\le ∥{\kappa }_n-\varkappa ∥+{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel .$$

By assumption $\left(i\right)$ and Lemma 1, we conclude that ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_n-\varkappa \parallel }$ exists. Hence, $\left\{{\kappa }_n\right\}$ is bounded.    □

Lemma 5.

Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\delta }_n^i\le \underset{n\to \infty }{lim\; sup}{\delta }_n^i<1-{\lambda }_n^i}$ for all $i=1,2,\dots ,N$;

(iii) 

$\left\{{\kappa }_n\right\}$ and $\left\{{\varpi }_n\right\}$ dominate ϰ for all $\varkappa \in \mathbb{F}$;

(iv) 

G is transitive and $\left\{{\varpi }_n\right\}$ is dominated by ϰ for all $\varkappa \in \mathbb{F}$.

Then ${\displaystyle \underset{n\to \infty }{lim}\parallel {\mathcal{S}}_i{\kappa }_n-{\kappa }_n\parallel =0}$ for all $i=1,2,\dots ,N$.

Proof. 

Let $\varkappa \in \mathbb{F}$. From Lemma 4, we have that ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_n-\varkappa \parallel }$ exists, and $\left\{{\kappa }_n\right\}$ is bounded. This implies that $\left\{{\varpi }_n\right\}$ and $\left\{{\varrho }_n^i\right\}$ are bounded for all $i=1,2,\dots ,N$. Next, by using assumption $\left(iii\right)$ and some known equality in Hilbert spaces, see equality (8) in [19], we can gain the result below for all $i=1,2,\dots ,N$:

$$\begin{array}{cc}{∥{\varrho }_n^i-\varkappa ∥}^2\hfill & ={∥{\lambda }_n^i{\mathcal{S}}_i{\kappa }_n+{\delta }_n^i{\mathcal{S}}_i{\varpi }_n+(1-{\lambda }_n^i-{\delta }_n^i){\varpi }_n-\varkappa ∥}^2\hfill \\ \hfill & ={∥{\lambda }_n^i({\mathcal{S}}_i{\kappa }_n-\varkappa )+{\delta }_n^i({\mathcal{S}}_i{\varpi }_n-\varkappa )+(1-{\lambda }_n^i-{\delta }_n^i)({\varpi }_n-\varkappa )∥}^2\hfill \\ \hfill & ={\lambda }_n^i{∥{\mathcal{S}}_i{\kappa }_n-\varkappa ∥}^2+{\delta }_n^i{∥{\mathcal{S}}_i{\varpi }_n-\varkappa ∥}^2+(1-{\lambda }_n^i-{\delta }_n^i){∥{\varpi }_n-\varkappa ∥}^2\hfill \\ \hfill & -{\lambda }_n^i(1-{\lambda }_n^i-{\delta }_n^i){∥{\mathcal{S}}_i{\kappa }_n-{\varpi }_n∥}^2-{\delta }_n^i(1-{\lambda }_n^i-{\delta }_n^i){∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥}^2\hfill \\ \hfill & -{\lambda }_n^i{\delta }_n^i{∥{\mathcal{S}}_i{\kappa }_n-{\mathcal{S}}_i{\varpi }_n∥}^2\hfill \\ \hfill & \le {\lambda }_n^i{∥{\kappa }_n-\varkappa ∥}^2+(1-{\lambda }_n^i){∥{\varpi }_n-\varkappa ∥}^2-{\delta }_n^i(1-{\lambda }_n^i-{\delta }_n^i){∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥}^2\hfill \\ \hfill & \le \parallel {\kappa }_n{-\varkappa \parallel }^2+2{\vartheta }_n⟨{\kappa }_n-{\kappa }_{n-1},{\varpi }_n-\varkappa ⟩-{\delta }_n^i(1-{\lambda }_n^i-{\delta }_n^i){∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥}^2.\hfill \end{array}$$

By rearranging the terms, the following inequality holds for some $M_1>0$:

$${\delta }_n^i(1-{\lambda }_n^i-{\delta }_n^i){∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥}^2\le \parallel {\kappa }_n{-\varkappa \parallel }^2-{∥{\varrho }_n^i-\varkappa ∥}^2+M_1{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel .$$

(2)

Note that Inequality (2) is true for each $i=1,2,\dots ,N$. Then there exists $i_n\in \{1,2,\dots ,N\}$ such that

$${\delta }_n^{i_n}(1-{\lambda }_n^{i_n}-{\delta }_n^{i_n}){∥{\mathcal{S}}_{i_n}{\varpi }_n-{\varpi }_n∥}^2\le \parallel {\kappa }_n{-\varkappa \parallel }^2-\parallel {\kappa }_{n+1}{-\varkappa \parallel }^2+M_1{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel .$$

Since ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_n-\varkappa \parallel }$ exists, by assumption $\left(i\right)$, all terms on the right-hand side of the inequality approach zero as n goes to infinity. Notice that, by assumption $\left(ii\right)$, the term on the left-hand side of the inequality is nonnegative. Consequently,

$$\underset{n\to \infty }{lim}∥{\mathcal{S}}_{i_n}{\varpi }_n-{\varpi }_n∥=0.$$

(3)

Since $({\kappa }_n,\varkappa )\in E\left(G\right)$, by assumption $\left(iv\right)$, $({\kappa }_n,{\varpi }_n)\in E\left(G\right)$ for all $n\in \mathbb{N}$. Notice that

$$\begin{array}{cc}\parallel {\kappa }_{n+1}-{\varpi }_n\parallel \hfill & =∥{\lambda }_n^{i_n}\left({\mathcal{S}}_{i_n}{\kappa }_n-{\varpi }_n\right)+{\delta }_n^{i_n}\left({\mathcal{S}}_{i_n}{\varpi }_n-{\varpi }_n\right)∥\hfill \\ \hfill & \le ∥{\mathcal{S}}_{i_n}{\kappa }_n-{\mathcal{S}}_{i_n}{\varpi }_n∥+2∥{\mathcal{S}}_{i_n}{\varpi }_n-{\varpi }_n∥\hfill \\ \hfill & \le ∥{\kappa }_n-{\varpi }_n∥+2∥{\mathcal{S}}_{i_n}{\varpi }_n-{\varpi }_n∥\hfill \\ \hfill & ={\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel +2∥{\mathcal{S}}_{i_n}{\varpi }_n-{\varpi }_n∥.\hfill \end{array}$$

By assumption $\left(i\right)$ and Equation (3), we have that ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_{n+1}-{\varpi }_n\parallel =0}$. Due to the definition of ${\kappa }_{n+1}$, we conclude that for all $i=1,2,\dots ,N$,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel {\varrho }_n^i-{\varpi }_n\parallel =0.\end{array}$$

(4)

Now, reconsider Inequality (2) as follows:

$$\begin{array}{cc}{\delta }_n^i(1-{\lambda }_n^i-{\delta }_n^i){∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥}^2\hfill & \le \parallel {\kappa }_n{-\varkappa \parallel }^2-{∥{\varrho }_n^i-\varkappa ∥}^2+M_1{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel \hfill \\ \hfill & \le \left(\parallel {\kappa }_n-\varkappa \parallel +∥{\varrho }_n^i-\varkappa ∥\right)∥{\varrho }_n^i-{\kappa }_n∥+M_1{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel \hfill \\ \hfill & \le M_2\left(∥{\varrho }_n^i-{\kappa }_n∥+{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel \right)\hfill \\ \hfill & \le M_2\left(∥{\varrho }_n^i-{\varpi }_n∥+2{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel \right)\hfill \end{array}$$

for some $M_2>0$. Similarly, by using Equation (4), and assumptions $\left(i\right)$ and $\left(ii\right)$, we get that ${\displaystyle \underset{n\to \infty }{lim}∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥=0}$ for all $i=1,2,\dots ,N$. It remains to show that ${\displaystyle \underset{n\to \infty }{lim}∥{\mathcal{S}}_i{\kappa }_n-{\kappa }_n∥=0}$. Observe that

$$\begin{array}{cc}∥{\mathcal{S}}_i{\kappa }_n-{\kappa }_n∥\hfill & \le 2∥{\kappa }_n-{\varpi }_n∥+∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥\hfill \\ \hfill & ={\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel +∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥.\hfill \end{array}$$

Since ${\displaystyle \underset{n\to \infty }{lim}∥{\mathcal{S}}_i{\varpi }_n-{\varpi }_n∥=0}$, by assumption $\left(i\right)$, ${\displaystyle \underset{n\to \infty }{lim}∥{\mathcal{S}}_i{\kappa }_n-{\kappa }_n∥=0}$ for all $i=1,2,\dots ,N$.    □

From the proof of Lemma 5, it can be observed that if $({\kappa }_n,{\varpi }_n)\in E\left(G\right)$ for all $n\in \mathbb{N}$, then we can omit assumption $\left(iv\right)$ and still obtain the same result.

Lemma 6.

Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\delta }_n^i\le \underset{n\to \infty }{lim\; sup}{\delta }_n^i<1-{\lambda }_n^i}$ for all $i=1,2,\dots ,N$;

(iii) 

$\left\{{\kappa }_n\right\}$ and $\left\{{\varpi }_n\right\}$ dominate ϰ for all $\varkappa \in \mathbb{F}$;

(iv) 

$({\kappa }_n,{\varpi }_n)\in E\left(G\right)$ for all $n\in \mathbb{N}$.

Then ${\displaystyle \underset{n\to \infty }{lim}∥{\mathcal{S}}_i{\kappa }_n-{\kappa }_n∥=0}$ for all $i=1,2,\dots ,N$.

3.1. Weak Convergence Theorem

In this part, we provide some weak convergence theorems for IMTPA.

Theorem 1.

Let $\left\{{\kappa }_n\right\}$ be a sequence generated by IMTPA. Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\delta }_n^i\le \underset{n\to \infty }{lim\; sup}{\delta }_n^i<1-{\lambda }_n^i}$ for all $i=1,2,\dots ,N$;

(iii) 

$\left\{{\kappa }_n\right\}$ and $\left\{{\varpi }_n\right\}$ dominate ϰ for all $\varkappa \in \mathbb{F}$;

(iv) 

G is transitive, and $\left\{{\varpi }_n\right\}$ is dominated by ϰ for all $\varkappa \in \mathbb{F}$;

(v) 

if there is a subsequence $\left\{{\kappa }_{n_k}\right\}$ of $\left\{{\kappa }_n\right\}$, ${\kappa }_{n_k}\rightharpoonup \nu$ for some $\nu \in \mathcal{H}$, then $({\kappa }_{n_k},\nu )\in E\left(G\right)$.

Then the sequence $\left\{{\kappa }_n\right\}$ converges weakly to an element in $\mathbb{F}$.

Proof. 

First notice that, by Lemmas 4 and 5, ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_n-\varkappa \parallel }$ exists for all $\varkappa \in \mathbb{F}$, and that ${\displaystyle \underset{n\to \infty }{lim}∥{\mathcal{S}}_i{\kappa }_n-{\kappa }_n∥=0}$ for all $i=1,2,\dots ,N$, respectively. Next, we show that $\mathbb{F}$ contains all weak sequential cluster points of $\left\{{\kappa }_n\right\}$. Let $\overline{\varkappa }$ be a weak sequential cluster point of $\left\{{\kappa }_n\right\}$. Then there exists a subsequence $\left\{{\kappa }_{n_k}\right\}$ such that $\left\{{\kappa }_{n_k}\right\}\rightharpoonup \overline{\varkappa }$. By assumption $\left(v\right)$, we obtain that $({\kappa }_{n_k},\overline{\varkappa })\in E\left(G\right)$. Therefore, by Lemma 3, $\overline{\varkappa }\in \mathbb{F}$. Hence, by Opial’s lemma (Lemma 2), $\left\{{\kappa }_n\right\}$ converges weakly to an element in $\mathbb{F}$.    □

Similarly, we can replace assumption $\left(iv\right)$ in Theorem 1 with assumption $\left(iv\right)$ in Lemma 6 and obtain the following theorem.

Theorem 2.

Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\delta }_n^i\le \underset{n\to \infty }{lim\; sup}{\delta }_n^i<1-{\lambda }_n^i}$ for all $i=1,2,\dots ,N$;

(iii) 

$\left\{{\kappa }_n\right\}$ and $\left\{{\varpi }_n\right\}$ dominate ϰ for all $\varkappa \in \mathbb{F}$;

(iv) 

$({\kappa }_n,{\varpi }_n)\in E\left(G\right)$ for all $n\in \mathbb{N}$;

(v) 

if there is a subsequence $\left\{{\kappa }_{n_k}\right\}$ of $\left\{{\kappa }_n\right\}$, ${\kappa }_{n_k}\rightharpoonup \nu \in \mathcal{H}$, then $({\kappa }_{n_k},\nu )\in E\left(G\right)$.

Then the sequence $\left\{{\kappa }_n\right\}$ converges weakly to an element in $\mathbb{F}$.

Additionally, we have the following weak convergence theorem for a family of nonexpansive mappings in a real Hilbert space.

Theorem 3.

Let $\{{\mathcal{S}}_i:i=1,2,\dots ,N\}$ be a family of nonexpansive mappings on a real Hilbert space $\mathcal{H}$ such that $\mathbb{F}\ne \varnothing$, and let $\left\{{\kappa }_n\right\}$ be a sequence generated by IMTPA. Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\delta }_n^i\le \underset{n\to \infty }{lim\; sup}{\delta }_n^i<1-{\lambda }_n^i}$ for all $i=1,2,\dots ,N$.

Then the sequence $\left\{{\kappa }_n\right\}$ converges weakly to an element in $\mathbb{F}$.

Proof. 

First, we show that ${\mathcal{S}}_i$ is a G-nonexpansive mapping for each $i=1,2,\dots ,N$. Define $G=\left(V\right(G),E(G\left)\right)$ as a directed graph by $V\left(G\right)=\mathcal{H}$ and $E\left(G\right)=\left\{\right(x,y):x,y\in \mathcal{H}\}$ such that $E\left(G\right)$ contains no parallel edges. Furthermore, ${\mathcal{S}}_i$ is a G-nonexpansive mapping for all $i=1,2,\dots ,N$. Note that, by the definition of G, conditions $\left(iii\right)$–$\left(v\right)$ in Theorem 1 hold. As a consequence, $\left\{{\kappa }_n\right\}$ converges weakly to an element in $\mathbb{F}$.    □

3.2. Strong Convergence Theorem

In this subsection, we present some strong convergence theorems for a family of G-nonexpansive mappings in a real Hilbert space endowed with a directed graph G. To prove the theorem, the condition $\left(SK\right)$ is needed as follows.

Theorem 4.

Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

$\left\{{\kappa }_n\right\}$ and $\left\{{\varpi }_n\right\}$ dominate ϰ for all $\varkappa \in \mathbb{F}$;

(iii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\delta }_n^i\le \underset{n\to \infty }{lim\; sup}{\delta }_n^i<1-{\lambda }_n^i}$ for all $i=1,2,\dots ,N$;

(iv) 

G is transitive, and $\left\{{\varpi }_n\right\}$ is dominated by ϰ for all $\varkappa \in \mathbb{F}$;

(v) 

$\{S_i:i=1,2,\dots ,N\}$ satisfies the condition $\left(SK\right)$, where $\mathbb{F}$ is closed.

Then the sequence $\left\{{\kappa }_n\right\}$ converges strongly to an element in $\mathbb{F}$.

Proof. 

From Lemma 4, we have that ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_n-\varkappa \parallel }$ exists for all $\varkappa \in \mathbb{F}$, and so ${\displaystyle \underset{n\to \infty }{lim}d({\kappa }_n,\mathbb{F})}$ exists. By assumption $\left(v\right)$, there exists a nondecreasing function $\phi :[0,\infty )\to [0,\infty )$ such that $\phi \left(0\right)=0$, $\phi \left(r\right)>0$ for all $r>0$ and ${\displaystyle \phi \left(d({\kappa }_n,\mathbb{F})\right)\le \underset{1\le i\le N}{max}∥{\mathcal{S}}_i{\kappa }_n-{\kappa }_n∥.}$ From Lemma 5, we get that ${\displaystyle \underset{n\to \infty }{lim}∥{\mathcal{S}}_i{\kappa }_n-{\kappa }_n∥=0}$ for all $i=1,2,\dots ,N$. Consequently, ${\displaystyle \underset{n\to \infty }{lim}\phi \left(d({\kappa }_n,\mathbb{F})\right)=0}$. By the property of $\phi$, we obtain that ${\displaystyle \underset{n\to \infty }{lim}d({\kappa }_n,\mathbb{F})=0}$. Thus, we can find a subsequence $\left\{{\kappa }_{n_j}\right\}$ of $\left\{{\kappa }_n\right\}$ and a sequence $\left\{{\varkappa }_j\right\}$ in $\mathbb{F}$ such that $\parallel {\kappa }_{n_j}-{\varkappa }_j\parallel \le 2^{-j}$. Let $n_{j+1}=n_j+p$ for some $p\in \mathbb{N}$. From the proof of Lemma 4, recall $∥{\kappa }_{n+1}-\varkappa ∥\le ∥{\kappa }_n-\varkappa ∥+{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel$. Furthermore, it follows that

$$\begin{array}{cc}\parallel {\kappa }_{n_{j+1}}-{\varkappa }_j\parallel \hfill & =\parallel {\kappa }_{n_j+p}-{\varkappa }_j\parallel \hfill \\ \hfill & \le \parallel {\kappa }_{n_j+p-1}-{\varkappa }_j\parallel +{\vartheta }_{n_j+p-1}\parallel {\kappa }_{n_j+p-1}-{\kappa }_{n_j+p-2}\parallel \hfill \\ \hfill & ⋮\hfill \\ \hfill & \le \parallel {\kappa }_{n_j}-{\varkappa }_j\parallel +{\vartheta }_{n_j}\parallel {\kappa }_{n_j}-{\kappa }_{n_j-1}\parallel +\dots +{\vartheta }_{n_j+p-1}\parallel {\kappa }_{n_j+p-1}-{\kappa }_{n_j+p-2}\parallel \hfill \\ \hfill & \le 2^{-j}+{\vartheta }_{n_j}\parallel {\kappa }_{n_j}-{\kappa }_{n_j-1}\parallel +\dots +{\vartheta }_{n_j+p-1}\parallel {\kappa }_{n_j+p-1}-{\kappa }_{n_j+p-2}\parallel .\hfill \end{array}$$

As a consequence,

$$\parallel {\varkappa }_{j+1}-{\varkappa }_j\parallel \le 3·2^{-(j+1)}+{\vartheta }_{n_j}\parallel {\kappa }_{n_j}-{\kappa }_{n_j-1}\parallel +\dots +{\vartheta }_{n_j+p-1}\parallel {\kappa }_{n_j+p-1}-{\kappa }_{n_j+p-2}\parallel .$$

By assumption $\left(i\right)$, it is easy to see that the right-hand side of the inequality tends to zero as $j\to \infty$. Then it follows that $\left\{{\varkappa }_j\right\}$ is a Cauchy sequence in $\mathbb{F}$. Given the fact that $\mathbb{F}$ is closed, there exists an $\widehat{\varkappa }\in \mathbb{F}$ such that ${\displaystyle \underset{j\to \infty }{lim}{\varkappa }_j=\widehat{\varkappa }}$. Since $\parallel {\kappa }_{n_j}-{\varkappa }_j\parallel \le 2^{-j}$, ${\displaystyle \underset{j\to \infty }{lim}\parallel {\kappa }_{n_j}-\widehat{\varkappa }\parallel =0}$. Note that ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_n-\widehat{\varkappa }\parallel }$ exists. Therefore, ${\displaystyle \underset{n\to \infty }{lim}\parallel {\kappa }_n-\widehat{\varkappa }\parallel =0}$. Hence, the sequence $\left\{{\kappa }_n\right\}$ converges strongly to $\widehat{\varkappa }\in \mathbb{F}$.    □

Similarly, it can be noted from the proof of Theorem 4 that assumption $\left(iv\right)$ can be replaced by assumption $\left(iv\right)$ in Lemma 6. Accordingly, we have Theorem 5.

Theorem 5.

Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

$\left\{{\kappa }_n\right\}$ and $\left\{{\varpi }_n\right\}$ dominate ϰ for all $\varkappa \in \mathbb{F}$;

(iii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\delta }_n^i\le \underset{n\to \infty }{lim\; sup}{\delta }_n^i<1-{\lambda }_n^i}$ for all $i=1,2,\dots ,N$;

(iv) 

$({\kappa }_n,{\varpi }_n)\in E\left(G\right)$ for all $n\in \mathbb{N}$;

(v) 

$\{S_i:i=1,2,\dots ,N\}$ satisfies the condition $\left(SK\right)$, where $\mathbb{F}$ is closed.

Then the sequence $\left\{{\kappa }_n\right\}$ converges strongly to an element in $\mathbb{F}$.

Similar to Theorem 3, we have the strong convergence theorem for a family of nonexpansive mappings in a real Hilbert space. Remarkably, the common fixed point set of nonexpansive mappings is closed. Thus, the following theorem is obtained.

Theorem 6.

Let $\{{\mathcal{S}}_i:i=1,2,\dots ,N\}$ be a family of nonexpansive mappings on a real Hilbert space $\mathcal{H}$ such that $\mathbb{F}\ne \varnothing$, and let $\left\{{\kappa }_n\right\}$ be a sequence generated by IMTPA. Assume that:

(i) 

${\displaystyle \sum _{n=1}^{\infty }{\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel <\infty }$;

(ii) 

${\displaystyle 0<\underset{n\to \infty }{lim\; inf}{\delta }_n^i\le \underset{n\to \infty }{lim\; sup}{\delta }_n^i<1-{\lambda }_n^i}$ for all $i=1,2,\dots ,N$;

(iii) 

$\{S_i:i=1,2,\dots ,N\}$ satisfies the condition $\left(SK\right)$.

Then the sequence $\left\{{\kappa }_n\right\}$ converges strongly to an element in $\mathbb{F}$.

4. Application to Signal Recovery Problem

Symmetry considerations can be related to signal processing, especially when signals satisfy certain symmetries. In this section, we focus on applying IMTPA to signal recovery problems and then compare its numerical result to that of IITPA. Recall the definition of IITPA [8] shown as Algorithm 2 below.

Algorithm 2: Inertial Ishikawa-type parallel algorithm (IITPA)

Initialization: Select arbitrary elements ${\kappa }_0,{\kappa }_1\in \mathcal{H}$ and set $n:=1.$ Iterative Steps: Construct $\left\{{\kappa }_n\right\}$ by using the following steps: Step 1. Define $$\begin{array}{c}\hfill {\omega }_n={\kappa }_n+{\vartheta }_n({\kappa }_n-{\kappa }_{n-1}),\end{array}$$ where $\left\{{\vartheta }_n\right\}\subset [0,\infty )$. Step 2. Compute, for all $i=1,2,\dots ,N$, $$\begin{array}{c}\hfill {\zeta }_n^i=(1-{\alpha }_n^i){\omega }_n+{\alpha }_n^i{\mathcal{S}}_i\left[(1-{\beta }_n^i){\omega }_n+{\beta }_n^i{\mathcal{S}}_i{\omega }_n\right],\end{array}$$ where $\left\{{\alpha }_n^i\right\},\left\{{\beta }_n^i\right\}\subset [0,1]$. Step 3. Compute $$\begin{array}{c}\hfill {\kappa }_{n+1}=argmax\left\{∥{\zeta }_n^i-{\omega }_n∥:i=1,2,\dots ,N\right\}.\end{array}$$ Replace n by $n+1$ and then repeat Step 1.

Consider a signal recovery problem with various types of noises mathematically interpreted as:

$$b_i=A_{i}x+{\epsilon }_i,$$

where $x\in {\mathbb{R}}^P$ represents the initial signal, $b_i\in {\mathbb{R}}^M$ is the observed signal with noise ${\epsilon }_i$, and $A_i\in {\mathbb{R}}^{M\times P}$ ($M<P$) is a filter matrix for each $i=1,2,\dots ,N$. This problem is equivalently expressed below:

$$\begin{array}{c}\underset{x\in {\mathbb{R}}^P}{min}\frac{1}{2}\parallel A_{1}x-b_1{\parallel }_2^2+{\parallel x\parallel }_1;\\ \underset{x\in {\mathbb{R}}^P}{min}\frac{1}{2}\parallel A_{2}x-b_2{\parallel }_2^2+{\parallel x\parallel }_1;\\ \underset{x\in {\mathbb{R}}^P}{min}\frac{1}{2}\parallel A_{3}x-b_3{\parallel }_2^2+{\parallel x\parallel }_1;\\ ⋮\\ \underset{x\in {\mathbb{R}}^P}{min}\frac{1}{2}\parallel A_{N}x-b_N{\parallel }_2^2+{\parallel x\parallel }_1\end{array}$$

(5)

To apply Algorithms 1 and 2, this problem can be established as a common fixed-point problem as follows. Let $\mathcal{H}={\mathbb{R}}^P$ and ${\mathcal{S}}_i(·)={\mathrm{prox}}_{{\zeta }_i{\parallel ·\parallel }_1}(I-{\zeta }_i\nabla r_i)(·)$, where $r_i(·)=\frac{1}{2}{\parallel A_i(·)-b_i\parallel }_2^2$ and ${\zeta }_i>0$ for each $i=1,2,\dots ,N$. With this setting, ${\mathcal{S}}_i$ is a nonexpansive mapping when ${\zeta }_i\in \left(0,\frac{2}{\parallel A_i{\parallel }_2^2}\right)$.

Now we perform a numerical experiment on IMTPA using Matlab R2021a. First, we choose the signal size $P=2048$ and $M=1024$ and generate x using the uniform distribution on $[-2,2]$ with k nonzero elements. Then we obtain the Gaussian matrix $A_i$ using the command $randn(M,P)$ and also the observation $b_i$ using white Gaussian noise with a signal-to-noise ratio SNR=40 with ${\zeta }_i=\frac{3}{2\parallel A_i{\parallel }_2^2}$ for all $i=1,2,3$. Furthermore, select vectors ${\kappa }_0$ and ${\kappa }_1$ randomly and apply them to IMTPA, where ${\lambda }_n^i=0.8$, ${\delta }_n^i=\frac{n}{10(n+1)}$, and

$${\vartheta }_n=\left\{\begin{array}{ccc}& min\left\{\frac{1}{{(n+100)}^2{\parallel {\kappa }_n-{\kappa }_{n-1}\parallel }_2},0.3\right\}& \mathrm{if}{\kappa }_n\ne {\kappa }_{n-1};\\ & 0.3& \mathrm{otherwise}\end{array}\right.$$

for each $n\in \mathbb{N}$ and $i=1,2,3$. An easy observation is that all conditions in Theorem 3 are satisfied. To be more specific, ${\vartheta }_n\parallel {\kappa }_n-{\kappa }_{n-1}\parallel \le {\displaystyle \frac{1}{{(n+100)}^2}}$ for all $n\in \mathbb{N}$, and so assumption $\left(i\right)$ holds. Further, consider that ${\displaystyle 0<\underset{n\to \infty }{lim}{\delta }_n^i=0.1<1-{\lambda }_n^i}$. Furthermore, the assumption $\left(ii\right)$ of Theorem 3 is also true. This guarantees that the sequence $\left\{{\kappa }_n\right\}$ converges to a solution of such a common fixed-point problem in ${\mathbb{R}}^P$. In addition, for IITPA, set ${\beta }_n^i=0.8$ and ${\alpha }_n^i=\frac{n}{10(n+1)}$ for all $n\in \mathbb{N}$ and $i=1,2,3$. Furthermore, the result is shown in Table 1. In this numerical test, we use four different numbers of nonzero elements: $k=50,100,150,200$. From the table, notice that the CPU time (in seconds) of IMTPA is less than that of IITPA, at least five seconds in each case. Moreover, the number of iterations of IMTPA is also less than that of IITPA by at least a thousand iterations. Furthermore, we illustrate the recovery signals for both algorithms in the case where $k=200$ in Figure 1.

Table 1. Numerical results for IITPA and IMTPA.

		k Nonzero Elements
		$\mathit{k}\mathbf{=}\mathbf{50}$	$\mathit{k}\mathbf{=}\mathbf{100}$	$\mathit{k}\mathbf{=}\mathbf{150}$	$\mathit{k}\mathbf{=}\mathbf{200}$
IITPA	No. of Iterations	1290	1332	1383	1474
	CPU Time	5.9837	6.5560	6.4376	6.5130
IMTPA	No. of Iterations	203	205	218	245
	CPU Time	0.8378	1.0953	0.9076	1.0110

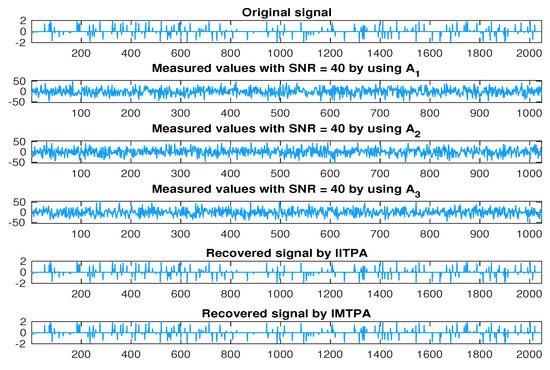
Figure 1. The initial signal, the measurements, and the recovered signals by IITAPA and IMTPA for $k=200$.

Additionally, we use the mean squared error $MS{E}_n=\frac{1}{P}{\parallel {\kappa }_n-x\parallel }_2^2<{10}^{-5}$ to measure the restoration accuracy. The error of each reconstructed signal is displayed in Figure 2. As can be seen in the figure, the error of IMTPA is less than that of IITPA. Overall, the signal obtained from IMTPA in this experiment gives a better numerical result than the signal obtained from IITPA.

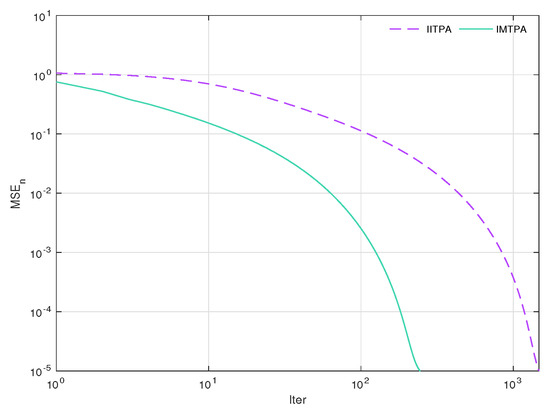
Figure 2. Plots of MSE${}_n$ over the number of iterations when $k=200$.

5. Conclusions

Taking everything into account, we present an algorithm called IMTPA for finding a common fixed point of a family of G-nonexpansive mappings on a Hilbert space endowed with a directed graph. This algorithm is a modified parallel algorithm with the inertial method and the Mann iteration concept. Under some extra conditions, we prove weak and strong convergence theorems for IMTPA. Lastly, we do a numerical experiment on a signal recovery problem using IMTPA and the previous algorithm called IITPA. The results show that the numerical outcome of IMTPA is better than that of IITPA. For future research, one can study results from different types of distances besides metrics. Another approach is that one can investigate a contraction in a Banach algebra instead of a Hilbert space.