Extension of the Reproducing Kernel Hilbert Space Method’s Application Range to Include Some Important Fractional Differential Equations

Abstract

Fractional differential equations are becoming more and more indispensable for modeling real-life problems. Modeling and then analyzing these fractional differential equations assists researchers in comprehending and predicting the system they want to study. This is only conceivable when their solutions are available. However, the majority of fractional differential equations lack exact solutions, and even when they do, they cannot be assessed precisely. Therefore, in order to analyze the symmetry analysis and acquire approximate solutions, one must rely on numerical approaches. In order to solve several significant fractional differential equations numerically, this work presents an effective approach. This method’s versatility and simplicity are its key benefits. To verify the RKHSM’s applicability, the convergence analysis and error estimations related to it are discussed. We also provide the profiles of a variety of representative numerical solutions to the problem at hand. We validated the potential, reliability, and efficacy of the RKHSM by testing some examples.

1. Introduction

The derivative concept has gained a lot of attention and significance in numerous fields of applied mathematics. This concept is used to build some ordinary or partial differential equations that model nearly all the behavior of dynamic processes in nature. However, utilizing the classical derivative doesn’t fill the gap that exists in several domains. Due to this latter need, the classical concept of the derivative was modernized to include the notion of a fractional derivative [1,2]. Fractional differential equations (also abbreviated as FDEs) have become more and more common for modeling real-world problems in recent years. The majority of natural processes are described by non-linear differential equations. Non-linear processes must be multiplied in order to solve engineering, applied mathematics, and physics problems [3]. FDEs, therefore, need either analytical or numerical methods to be solved. Since there is currently no analytical solution to the majority of FDEs, mathematicians have long sought to create successful numerical methods for addressing them [4,5,6,7,8]. This is what our research aims to do. Our general idea is to extend the application of the RKHSM to obtain numerical simulations for non-linear ordinary differential equations of fractional order (also abbreviated as NFODEs).

In numerical analysis, the RKHSM has been extensively employed. Starting from Cui and Lin [9], who discussed the solutions to many problems. Then, the RKHSM has been selected as a substitute method for solving various differential equations and integral problems, and even fractional types of problems [10,11,12,13,14,15]. A reproducing kernel collocation approach for nonlocal fractional BVPs was recently described in [16]. Du and Chen offer a stable LSM based on RK in [17,18] for variable order time-fractional advection-diffusion equations and nonlinear FIDEs. For the solution of fuzzy fractional integrodifferential equations, a modified RKSM is used in [19]. In [10], Chen et al. proposed resolving an RK space with a nonlinear time-delay singly perturbed BVP. The RKHSM is characterized by its simplicity of use and flexibility in solving a wide variety of difficult differential equations, without forgetting the fact that it is mesh-free.

We will discuss some fundamental tools for using the RKHSM in Section 2. After making the necessary preparations, Section 3 of this paper will describe how to implement the RKHSM. Some applications are presented in Section 4. The conclusion is presented at the end.

2. Preliminaries

This section is focused on introducing some theory requirements for understanding the RKHSM that we will apply to solve some non-linear and linear fractional ODEs.

Definition 1. 

A function $\mathrm{K}(·,\mathrm{t})$ defined from $\mathrm{X}\times \mathrm{X}$ to $\mathbb{C}$ (where $\mathrm{X}\ne \varnothing ),$ is a reproducing kernel of H provided

1. 

$\mathrm{K}(·,\mathrm{t})\in H,$

2. 

$⟨\mathrm{u},\mathrm{K}(·,\mathrm{t})⟩=\mathrm{u}\left(\mathrm{t}\right),\forall \mathrm{u}\in H.$

Note carefully that H is a Hilbert space.

Definition 2. 

We set [9]

$$\begin{array}{cc}\hfill W_2^{m+1}[0,T]=\left\{\mathrm{u}\right|& \mathit{The}\mathit{functions}{\mathrm{u}}^{\left(\mathfrak{j}\right)}\mathit{are}\mathit{absolutely}\mathit{continuous}\mathit{in}[0,T],{\mathrm{u}}^{(m+1)}\in L^2[0,T],\hfill \\ \hfill & \mathit{and}{\mathrm{u}}^{\left(\mathfrak{j}\right)}\left(0\right)=0\mathit{with}\mathfrak{j}=0,1,\dots m\},\hfill \end{array}$$

where $m=0,1.$ An inner product on $W_2^{m+1}[0,T]$ is

$${⟨\mathrm{u},\mathrm{g}⟩}_{W_2^{m+1}}=\sum _{\mathfrak{j}=0}^m{\mathrm{u}}^{\left(\mathfrak{j}\right)}\left(0\right){\mathrm{g}}^{\left(\mathfrak{j}\right)}\left(0\right)+{\int }_0^T{\mathrm{u}}^{(m+1)}\left(\mathrm{t}\right){\mathrm{g}}^{(m+1)}\left(\mathrm{t}\right)d\mathrm{t},$$

(1)

while the norm is

$${∥\mathrm{u}∥}_{W_2^{m+1}}=\sqrt{{⟨\mathrm{u},\mathrm{u}⟩}_{W_2^{m+1}}},$$

for all $\mathrm{u},\mathrm{g}\in W_2^{m+1}[0,T].$

Theorem 1. 

The function

$$R_{\tau }\left(\mathrm{t}\right)=\left\{\begin{array}{cc}\hfill r(\mathrm{t},\tau )& ,\tau <\mathrm{t},\hfill \\ \hfill r(\tau ,\mathrm{t})& ,\tau \ge \mathrm{t},\hfill \end{array}\right.$$

(2)

is the reproducing kernel function of $W_2^1[0,T].$ Where $r(\mathrm{t},\tau )=1+\tau .$

See [15] for the proof.

Theorem 2. 

The function

$$S_{\tau }\left(\mathrm{t}\right)=\left\{\begin{array}{cc}\hfill \varsigma (\mathrm{t},\tau )& ,\tau <\mathrm{t},\hfill \\ \hfill \varsigma (\tau ,\mathrm{t})& ,\tau \ge \mathrm{t},\hfill \end{array}\right.$$

(3)

is the reproducing kernel function of $W_2^2[0,T],$ Where $\varsigma (\mathrm{t},\tau )=\tau \mathrm{t}+\frac{1}{2}{\tau }^2\mathrm{t}-\frac{1}{6}{\tau }^3.$

See [15] for the proof.

Definition 3. 

The Caputo derivative of $\mathrm{u}$ is

$$D_a^{\alpha }\mathrm{u}\left(\mathrm{t}\right)=J_a^{m-\alpha }{D}_a^m\mathrm{u}\left(\mathrm{t}\right)={\displaystyle \frac{1}{\Gamma (m-\alpha )}}\underset{a}{\overset{\mathrm{t}}{\int }}{(\mathrm{t}-\eta )}^{-\alpha -1+m}{\mathrm{u}}^m\left(\eta \right)\mathrm{d}\eta ,\alpha \in (m-1,m].$$

(4)

RKHS Method

Consider the 1st-order non-linear ODE,

$$\left\{\begin{array}{cc}{\mathrm{D}}_0^{\alpha }\mathrm{u}\left(\mathrm{t}\right)=\mathrm{F}(\mathrm{t},\mathrm{u}\left(\mathrm{t}\right)),\hfill & 0\le \mathrm{t}\le T,T\in {\mathbb{R}}^{\ast },\hfill \\ \mathrm{u}\left(0\right)=\mu ,\hfill \end{array}\right.$$

(5)

$\mathrm{F}$ is a function of $\mathrm{u}$ and $\mathrm{t}$, $\mathrm{u}$ is the unknown, ${\mathrm{D}}_0^{\alpha }$ is the Caputo derivative, and $\mu$ is a constant.

Making the variable change: $\mathrm{v}\left(\mathrm{t}\right)=\mathrm{u}\left(\mathrm{t}\right)-\mu$ to homogenize $\mathrm{u}\left(0\right)=\mu .$ Replacing $\mathrm{u}\left(\mathrm{t}\right)$ by $\mathrm{v}\left(\mathrm{t}\right)+\mu$ in (5), gives

$$\left\{\begin{array}{cc}{\mathrm{D}}_0^{\alpha }\mathrm{v}\left(\mathrm{t}\right)=\overline{\mathrm{F}}(\mathrm{t},\mathrm{v}\left(\mathrm{t}\right)),\hfill & 0\le \mathrm{t}\le T,T\in {\mathbb{R}}^{\ast },\hfill \\ \mathrm{v}\left(0\right)=0,\hfill \end{array}\right.$$

(6)

the function $\overline{\mathrm{F}}$ is non-linear.

Using the linear operator $\mathrm{L}:W_2^2[0,T]\to W_2^1[0,T]$ such that $\mathrm{L}\mathrm{v}\left(\mathrm{t}\right)={\mathrm{D}}_0^{\alpha }\mathrm{v}\left(\mathrm{t}\right)$ in (6) to get

$$\left\{\begin{array}{cc}\mathrm{L}\mathrm{v}\left(\mathrm{t}\right)=\overline{\mathrm{F}}(\mathrm{t},\mathrm{v}\left(\mathrm{t}\right)),\hfill & 0\le \mathrm{t}\le T,T\in {\mathbb{R}}^{\ast },\hfill \\ \mathrm{v}\left(0\right)=0.\hfill \end{array}\right.$$

(7)

The next step is to build an orthogonal function system of $W_2^2[0,T].$ Letting

$${\psi }_{\mathfrak{i}}\left(\mathrm{t}\right)={\mathrm{L}}^{\ast }{\kappa }_{\mathfrak{i}}\left(\mathrm{t}\right),$$

(8)

where

• ${\kappa }_{\mathfrak{i}}\left(\mathrm{t}\right)=R_{{\mathrm{t}}_{\mathfrak{i}}}\left(\mathrm{t}\right)$; $R_{{\mathrm{t}}_{\mathfrak{i}}}\left(\mathrm{t}\right)$ is given by (2).
• The set ${\left\{{\mathrm{t}}_{\mathfrak{i}}\right\}}_{\mathfrak{i}=1}^{\infty }$ is dense in $[0,T].$
• ${\mathrm{L}}^{\ast }$ means the adjoint of $\mathrm{L}.$

And, to find ${\left\{{\mathsf{{\rm Y}}}_{\mathfrak{i}}\right\}}_{\mathfrak{i}=1}^{\infty },$ we need to use Gram-Schmidt’s process:

$${\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)=\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}{\psi }_k\left(\mathrm{t}\right),0<{\beta }_{\mathfrak{i}\mathfrak{i}},\mathfrak{i}\in {\mathbb{N}}^{\ast }.$$

(9)

where $\{{\psi }_1,{\psi }_2,{\psi }_3,\dots \}$ represents the function system in $W_2^2[0,T]$ obtained by

$$\begin{array}{cc}\hfill {\psi }_{\mathfrak{i}}\left(\mathrm{t}\right)={\mathrm{L}}^{\ast }{\kappa }_{\mathfrak{i}}\left(\mathrm{t}\right)={⟨{\mathrm{L}}^{\ast }{\kappa }_{\mathfrak{i}}\left(\eta \right),S_{\mathrm{t}}\left(\eta \right)⟩}_{W_2^2}={⟨{\kappa }_{\mathfrak{i}}\left(\eta \right),\mathrm{L}{S}_{\mathrm{t}}\left(\eta \right)⟩}_{W_2^1}& ={⟨R_{{\eta }_{\mathfrak{i}}}\left(\eta \right),\mathrm{L}{S}_{\mathrm{t}}\left(\eta \right)⟩}_{W_2^1}\hfill \\ \hfill & ={\mathrm{L}}_{\eta }{S}_{\mathrm{t}}{\left(\eta \right)|}_{\eta ={\mathrm{t}}_{\mathfrak{i}}}.\hfill \end{array}$$

(10)

The coefficients ${\beta }_{\mathfrak{i}k}$ can be found by

$${\beta }_{\mathfrak{i}\mathfrak{j}}=\left\{\begin{array}{cc}-\frac{1}{e_{\mathfrak{i}}}\sum _{k=\mathfrak{j}}^{\mathfrak{i}-1}{C}_{\mathfrak{i}k}{\beta }_{k\mathfrak{j}},\hfill & \mathfrak{i}>\mathfrak{j},\hfill \\ \frac{1}{e_{\mathfrak{i}}},\hfill & \mathfrak{i}=\mathfrak{j}\ne 1,\hfill \\ \frac{1}{∥{\psi }_1∥},\hfill & \mathfrak{i}=\mathfrak{j}=1,\hfill \end{array}\right.$$

(11)

where $e_{\mathfrak{i}}=\sqrt{{∥{\psi }_{\mathfrak{i}}∥}^2-{\sum }_{k=1}^{\mathfrak{i}-1}{C}_{\mathfrak{i}k}^2},C_{\mathfrak{i}k}={⟨{\psi }_{\mathfrak{i}},{\mathsf{{\rm Y}}}_k⟩}_{W_2^2}.$

Theorem 3. 

Suppose ${\left\{{\mathrm{t}}_{\mathfrak{i}}\right\}}_{\mathfrak{i}=1}^{\infty }$ is dense in $[0,T],$ then ${\left\{{\psi }_{\mathfrak{i}}\right\}}_{\mathfrak{i}=1}^{\infty }$ is the complete system of $W_2^2[0,T].$

Proof. 

Observe that ${\psi }_{\mathfrak{i}}\left(\mathrm{t}\right)\in W_2^2[0,T].$ Thus, fixing $\mathrm{v}\in W_2^2,$ we can write

$${⟨\mathrm{v}\left(\mathrm{t}\right),{\psi }_{\mathfrak{i}}\left(\mathrm{t}\right)⟩}_{W_2^2}=0,\mathfrak{i}=1,2,\dots .$$

Since

$${⟨\mathrm{v}\left(\mathrm{t}\right),{\psi }_{\mathfrak{i}}\left(\mathrm{t}\right)⟩}_{W_2^2}={⟨\mathrm{v}\left(\mathrm{t}\right),{\mathrm{L}}^{\ast }{\kappa }_{\mathfrak{i}}\left(\mathrm{t}\right)⟩}_{W_2^2}={⟨\mathrm{L}\mathrm{v}\left(\mathrm{t}\right),{\kappa }_{\mathfrak{i}}\left(\mathrm{t}\right)⟩}_{W_2^1}=\mathrm{L}\mathrm{v}\left({\mathrm{t}}_{\mathfrak{i}}\right)=0,$$

and ${\left\{{\mathrm{t}}_{\mathfrak{i}}\right\}}_{\mathfrak{i}=1}^{\infty }$ is dense on the interval $[0,T],$

$$\mathrm{L}\mathrm{v}\left(\mathrm{t}\right)=0.$$

Then,

$${\mathrm{L}}^{-1}\left(\mathrm{L}\mathrm{v}\left(\mathrm{t}\right)\right)={\mathrm{L}}^{-1}\left(0\right),$$

that gives

$$\mathrm{v}\left(\mathrm{t}\right)=0.$$

□

Lemma 1. 

Assume $\mathrm{v}\in W_2^2,$ then

$${∥{\mathrm{v}}^{\left(\mathfrak{i}\right)}\left(\mathrm{t}\right)∥}_C\le \mathfrak{C}{∥\mathrm{v}\left(\mathrm{t}\right)∥}_{W_2^2},\mathfrak{i}=0,1,$$

(12)

where $\mathfrak{C}\ge 0$ and ${∥\mathrm{v}\left(\mathrm{t}\right)∥}_C=\underset{\mathrm{t}\in [0,T]}{max}\left|\mathrm{v}\left(\mathrm{t}\right)\right|.$

Proof. 

$\forall \mathrm{t}\in [0,T]$ we have

$${\mathrm{v}}^{\left(\mathfrak{i}\right)}\left(\mathrm{t}\right)={⟨\mathrm{v}(🞍),{\partial }_{\mathrm{t}}^{\left(\mathfrak{i}\right)}{S}_{\mathrm{t}}(🞍)⟩}_{W_2^2},\mathfrak{i}\in \{0,1\}.$$

We obtain, utilizing the expression of ${\partial }_{\mathrm{t}}^{\left(\mathfrak{i}\right)}{S}_{\mathrm{t}}(🞍)$

$${∥{\partial }_{\mathrm{t}}^{\left(\mathfrak{i}\right)}{S}_{\mathrm{t}}∥}_{W_2^2}\le {\mathfrak{C}}_{\mathfrak{i}},\mathfrak{i}=0,1.$$

Consequently,

$$\left|{\mathrm{v}}^{\left(\mathfrak{i}\right)}\left(\mathrm{t}\right)\right|=\left|{⟨\mathrm{v}(🞍),{\partial }_{\mathrm{t}}^{\left(\mathfrak{i}\right)}{S}_{\mathrm{t}}(🞍)⟩}_{W_2^2}\right|\le {∥{\partial }_{\mathrm{t}}^{\left(\mathfrak{i}\right)}{S}_{\mathrm{t}}∥}_{W_2^2}{∥\mathrm{v}∥}_{W_2^2}\le {\mathfrak{C}}_{\mathfrak{i}}{∥\mathrm{v}∥}_{W_2^2},\mathfrak{i}=0,1,$$

(13)

where $\mathfrak{C}=\underset{\mathfrak{i}=0,1}{max}\left\{{\mathfrak{C}}_{\mathfrak{i}}\right\}.$ Then Lemma 1 follows from (13). □

Theorem 4. 

Let ${\left\{{\mathrm{t}}_{\mathfrak{i}}\right\}}_{\mathfrak{i}=1}^{\infty }$ be dense and problem (7) has a unique solution $\mathrm{v}\in W_2^2[0,T].$ Therefore, the solution of (7) is

$$\mathrm{v}\left(\mathrm{t}\right)=\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\overline{\mathrm{F}}({\mathrm{t}}_k,\mathrm{v}\left({\mathrm{t}}_k\right)){\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right).$$

(14)

While the solution of (5) is

$$\mathrm{u}\left(\mathrm{t}\right)=\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\overline{\mathrm{F}}({\mathrm{t}}_k,\mathrm{v}\left({\mathrm{t}}_k\right)){\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)+\mu .$$

(15)

Proof. 

Firstly, ${\left\{{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)\right\}}_{\mathfrak{i}=1}^{\infty }$ is a complete orthonormal basis in $W_2^2[0,T]$ that allows us to write

$$\begin{array}{ccc}\hfill \mathrm{v}\left(\mathrm{t}\right)& =\sum _{\mathfrak{i}=1}^{\infty }{⟨\mathrm{v}\left(\mathrm{t}\right),{\overline{\psi }}_{\mathfrak{i}}\left(\mathrm{t}\right)⟩}_{W_2^2}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)\hfill & \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}{⟨\mathrm{v}\left(\mathrm{t}\right),{\psi }_k\left(\mathrm{t}\right)⟩}_{W_2^2}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)\hfill \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}{⟨\mathrm{v}\left(\mathrm{t}\right),{\mathrm{L}}^{\ast }{\kappa }_k\left(\mathrm{t}\right)⟩}_{W_2^2}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)\hfill \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}{⟨\mathrm{L}\mathrm{v}\left(\mathrm{t}\right),{\kappa }_k\left(\mathrm{t}\right)⟩}_{W_2^1}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)\hfill \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}{⟨\mathrm{L}\mathrm{v}\left(\mathrm{t}\right),R_{\mathrm{t}}\left({\mathrm{t}}_k\right)⟩}_{W_2^1}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)\hfill \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\mathrm{L}\mathrm{v}\left({\mathrm{t}}_k\right){\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)\hfill \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\overline{\mathrm{F}}({\mathrm{t}}_k,\mathrm{v}\left({\mathrm{t}}_k\right)){\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right).\hfill \end{array}$$

Secondly, by replacing $\mathrm{v}\left(\mathrm{t}\right)$ by its Formula (14) in $\mathrm{u}\left(\mathrm{t}\right)=\mathrm{v}\left(\mathrm{t}\right)+\mu$, we get

$$\mathrm{u}\left(\mathrm{t}\right)=\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\overline{\mathrm{F}}({\mathrm{t}}_k,\mathrm{v}\left({\mathrm{t}}_k\right)){\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)+\mu .$$

□

Now, the RKHSM’s solution ${\mathrm{v}}_n\left(\mathrm{t}\right)$ can be represented as

$${\mathrm{v}}_n\left(\mathrm{t}\right)=\sum _{\mathfrak{i}=1}^n\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\overline{\mathrm{F}}({\mathrm{t}}_k,\mathrm{v}\left({\mathrm{t}}_k\right)){\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right).$$

(16)

The space $W_2^2[0,T]$ is a Hilbert space, hence

$$\sum _{\mathfrak{i}=1}^{\infty }\sum _{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\overline{\mathrm{F}}({\mathrm{t}}_k,\mathrm{v}\left({\mathrm{t}}_k\right)){\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)<\infty ,$$

(17)

${\mathrm{v}}_n\left(\mathrm{t}\right)$ converges to $\mathrm{v}\left(\mathrm{t}\right)$ in the norm, in other words.

Theorem 5. 

${\mathrm{v}}_n\left(\mathrm{t}\right)$ converges uniformly to $\mathrm{v}\left(\mathrm{t}\right)$ and ${\mathrm{v}}_n^{\prime }\left(\mathrm{t}\right)$ converges uniformly to ${\mathrm{v}}^{\prime }\left(\mathrm{t}\right).$

Proof. 

1.

Let us estimate the following:

$\forall \mathrm{t}\in [0,T],$

$$\begin{array}{cc}\hfill \left|{\mathrm{v}}_n\left(\mathrm{t}\right)-\mathrm{v}\left(\mathrm{t}\right)\right|& =\left|{⟨{\mathrm{v}}_n(🞍)-\mathrm{v}(🞍),S_{\mathrm{t}}(🞍)⟩}_{W_2^2}\right|\hfill \\ & \le {∥S_{\mathrm{t}}∥}_{W_2^2}{∥{\mathrm{v}}_n-\mathrm{v}∥}_{W_2^2}\hfill \\ & \le {\mathcal{C}}_0{∥{\mathrm{v}}_n-\mathrm{v}∥}_{W_2^2},\hfill \end{array}$$

where ${\mathcal{C}}_0$ is a constant.

2.

Doing the same thing to the derivative, we get

$$\left|{\mathrm{v}}_n^{\prime }\left(\mathrm{t}\right)-{\mathrm{v}}^{\prime }\left(\mathrm{t}\right)\right|\le {∥{\partial }_{\mathrm{t}}{S}_{\mathrm{t}}∥}_{W_2^2}{∥{\mathrm{v}}_n^{\prime }-{\mathrm{v}}^{\prime }∥}_{W_2^2},$$

due to the uniform boundedness of ${\partial }_{\mathrm{t}}{S}_{\mathrm{t}}(🞍),$ we have

$${∥{\partial }_{\mathrm{t}}{S}_{\mathrm{t}}∥}_{W_2^2}\le {\mathcal{C}}_1,$$

where ${\mathcal{C}}_1$ is a positive constant.

Therefore

$$\left|{\mathrm{v}}_n^{\prime }\left(\mathrm{t}\right)-{\mathrm{v}}^{\prime }\left(\mathrm{t}\right)\right|\le {\mathcal{C}}_1{∥{\mathrm{v}}_n^{\prime }-{\mathrm{v}}^{\prime }∥}_{W_2^2}.$$

□

3. Convergence Analysis

We write

$${\mathrm{v}}_n\left(\mathrm{t}\right)=\sum _{\mathfrak{i}=1}^n{A}_{\mathfrak{i}}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right),$$

(18)

to denote the numerical solution for problem (14), where

$$A_{\mathfrak{i}}=\sum _{\mathsf{k}=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\overline{\mathrm{F}}({\mathrm{t}}_k,\mathrm{v}\left({\mathrm{t}}_k\right)).$$

(19)

Here, by letting ${\mathrm{t}}_1=0,$ the values of $\mathrm{v}\left({\mathrm{t}}_1\right)$ will be known from the IC. And, ${\mathrm{v}}_0\left({\mathrm{t}}_1\right)=\mathrm{v}\left({\mathrm{t}}_1\right).$

Theorem 6. 

Assume that ${∥{\mathrm{v}}_n∥}_{W_2^2}$ is bounded, ${\left\{{\mathrm{t}}_{\mathfrak{i}}\right\}}_{\mathfrak{i}=1}^{\infty }$ is dense, and the solution $\mathrm{v}\in W_2^2$ of (18) is unique. Then

1. 

${\mathrm{v}}_n$ converges to $\mathrm{v},$

2. 

$${\mathrm{v}}_n\left(\mathrm{t}\right)=\sum _{\mathfrak{i}=1}^n{\mathrm{A}}_{\mathfrak{i}}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right).$$

Proof. 

1.

We have

$${\mathrm{v}}_{n+1}\left(\mathrm{t}\right)={\mathrm{v}}_n\left(\mathrm{t}\right)+{\mathrm{A}}_{n+1}{\mathsf{{\rm Y}}}_{n+1}\left(\mathrm{t}\right),$$

the orthogonality of ${\left\{{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right)\right\}}_{\mathfrak{i}=1}^{\infty }$ implies

$$\begin{array}{cc}\hfill {∥{\mathrm{v}}_{n+1}∥}_{W_2^2}^2=& {∥{\mathrm{v}}_n∥}_{W_2^2}^2+{\mathrm{A}}_{n+1}^2\hfill \\ \hfill =& {∥{\mathrm{v}}_{n-1}∥}_{W_2^2}^2+{\mathrm{A}}_n^2+{\mathrm{A}}_{n+1}^2\hfill \\ \hfill & ⋮\hfill \\ \hfill =& {∥{\mathrm{v}}_0∥}_{W_2^2}^2+\sum _{\mathfrak{i}=1}^{n+1}{\mathrm{A}}_{\mathfrak{i}}^2,\hfill \end{array}$$

(20)

and so

$${∥{\mathrm{v}}_n∥}_{W_2^2}\le {∥{\mathrm{v}}_{n+1}∥}_{W_2^2}.$$

Since ${∥{\mathrm{v}}_n∥}_{W_2^2}$ is bounded, we deduce ${∥{\mathrm{v}}_n∥}_{W_2^2}$ is convergent.

$$\sum _{\mathfrak{i}=1}^{\infty }{A}_{\mathfrak{i}}^2=\mathsf{\Phi },$$

where $\Theta$ is a constant.

Consequently

$$\left\{{\mathsf{\Phi }}_1^2,{\mathsf{\Phi }}_2^2,\dots \right\}\in {\ell }^2.$$

Observe that $\left({\mathrm{v}}_q\left(\mathrm{t}\right)-{\mathrm{v}}_{q-1}\left(\mathrm{t}\right)\right)\perp \cdots \perp \left({\mathrm{v}}_{n+1}\left(\mathrm{t}\right)-{\mathrm{v}}_n\left(\mathrm{t}\right)\right),$ So for $q>n:$

$$\begin{array}{cc}\hfill {∥{\mathrm{v}}_q-{\mathrm{v}}_n∥}_{W_2^2}^2& ={∥{\mathrm{v}}_q-{\mathrm{v}}_{q-1}+{\mathrm{v}}_{q-1}-\cdots +{\mathrm{v}}_{n+1}-{\mathrm{v}}_n∥}_{W_2^2}^2\hfill \\ \hfill & ={∥{\mathrm{v}}_q-{\mathrm{v}}_{q-1}∥}_{W_2^2}^2+{∥{\mathrm{v}}_{q-1}-{\mathrm{v}}_{q-2}∥}_{W_2^2}^2+\cdots +{∥{\mathrm{v}}_{n+1}-{\mathrm{v}}_n∥}_{W_2^2}^2.\hfill \end{array}$$

(21)

Furthermore,

$${∥{\mathrm{v}}_q-{\mathrm{v}}_{q-1}∥}_{W_2^2}^2={\mathrm{A}}_q^2.$$

Consequently, we have as $n\to \infty ,$

$${∥{\mathrm{v}}_q-{\mathrm{v}}_n∥}_{W_2^2}^2=\sum _{\ell =n+1}^q{\mathrm{A}}_{\ell }^2\to 0.$$

On account of the completeness of $W_2^2,$ we reach: ${\mathrm{v}}_n\to \widehat{\mathrm{v}}$ as $n\to \infty .$

2.

Taking the limit in (18), we obtain

$$\tilde{\mathrm{v}}\left(\mathrm{t}\right)=\sum _{\mathfrak{i}=1}^{\infty }{\mathrm{A}}_{\mathfrak{i}}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right).$$

(22)

Utilising the operator $\mathrm{L}$, we get

$$\mathrm{L}\tilde{\mathrm{v}}\left(\mathrm{t}\right)=\sum _{\mathfrak{i}=1}^{\infty }{\mathrm{A}}_{\mathfrak{i}}\mathrm{L}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right),$$

it follows that

$$\begin{array}{cc}\hfill \mathrm{L}\tilde{\mathrm{v}}\left({\mathrm{t}}_{\ell }\right)& =\sum _{\mathfrak{i}=1}^{\infty }{\mathrm{A}}_{\mathfrak{i}}{⟨\mathrm{L}{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right),{\kappa }_{\ell }\left(\mathrm{t}\right)⟩}_{W_2^1}\hfill \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }{\mathrm{A}}_{\mathfrak{i}}{⟨{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right),{\mathrm{L}}^{\ast }{\kappa }_{\ell }\left(\mathrm{t}\right)⟩}_{W_2^2}\hfill \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }{\mathrm{A}}_{\mathfrak{i}}{⟨{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right),{\psi }_{\ell }\left(\mathrm{t}\right)⟩}_{W_2^2}.\hfill \end{array}$$

(23)

Multiplying (23) by ${\beta }_{\mathfrak{j}\ell }$ and taking ${\sum }_{\ell =1}^{\mathfrak{j}}$ to find

$$\begin{array}{cc}\hfill \sum _{\ell =1}^{\mathfrak{j}}{\beta }_{\mathfrak{j}\ell }\mathrm{L}\tilde{\mathrm{v}}\left({\mathrm{t}}_{\ell }\right)& =\sum _{\mathfrak{i}=1}^{\infty }{\mathrm{A}}_{\mathfrak{i}}{⟨{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right),\sum _{\ell =1}^{\mathfrak{j}}{\beta }_{\mathfrak{j}\ell }{\psi }_{\ell }\left(\mathrm{t}\right)⟩}_{W_2^2}\hfill \\ \hfill & =\sum _{\mathfrak{i}=1}^{\infty }{\mathrm{A}}_{\mathfrak{i}}{⟨{\mathsf{{\rm Y}}}_{\mathfrak{i}}\left(\mathrm{t}\right),{\mathsf{{\rm Y}}}_{\mathfrak{j}}\left(\mathrm{t}\right)⟩}_{W_2^2}\hfill \\ \hfill & ={\mathrm{A}}_{\mathfrak{j}}.\hfill \end{array}$$

We conclude,

$$\mathrm{L}\tilde{\mathrm{v}}\left({\mathrm{t}}_{\ell }\right)=\overline{\mathrm{F}}({\mathrm{t}}_{\ell },\tilde{\mathrm{v}}\left({\mathrm{t}}_{\ell }\right)).$$

$\forall \mu \in [0,T],$ there exists ${\left\{{\mathrm{t}}_{n\mathfrak{j}}\right\}}_{\mathfrak{j}=1}^{\infty }$ such that

$${\mathrm{t}}_{n\mathfrak{j}}\to \mu ,\mathrm{as}\mathfrak{j}\to \infty ,$$

that resulting from the density of ${\left\{{\mathrm{t}}_{\mathfrak{i}}\right\}}_{\mathfrak{i}=1}^{\infty }$.

Now, we know that,

$$\mathrm{L}\tilde{\mathrm{v}}\left({\mathrm{t}}_{n\mathfrak{j}}\right)=\overline{\mathrm{F}}({\mathrm{t}}_{n\mathfrak{j}},\tilde{\mathrm{v}}\left({\mathrm{t}}_{n\mathfrak{j}}\right)).$$

Since $\overline{\mathrm{F}}$ is continuous and by letting $n\mathfrak{j}\to \infty ,$ we can easily deduce the result.

□

4. Numerical Experiments

In this section, we tested two examples to assure the efficiency of the RKHSM. The rate of convergence of the presented method is as follows [20]:

$${\left(O_c\right)}_n=\frac{-ln\left(E_n/E_{\frac{n}{2}}\right)}{ln\left(2\right)},$$

where

$$E_n=\underset{\mathrm{t}\in [0,T]}{max}\left|\mathrm{u}\left(\mathrm{t}\right)-{\mathrm{u}}_n\left(\mathrm{t}\right)\right|.$$

Now, the process for using the RKHSM can be summed up as follows:

• Step 1: Fix $n;$
• Step 2: Set ${\psi }_{\mathfrak{i}}\left({\mathrm{t}}_{\mathfrak{i}}\right)={\mathrm{L}}_{\eta }{S}_{\mathrm{t}}\left(\eta \right){|}_{\eta ={\mathrm{t}}_{\mathfrak{i}}};$
• Step 3: Calculate the coefficients ${\beta }_{\mathfrak{i}\mathfrak{j}}$ using (11);
• Step 4: Set ${\mathsf{{\rm Y}}}_{\mathfrak{i}}\left({\mathrm{x}}_{\mathfrak{i}}\right)={\sum }_{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}{\psi }_k\left({\mathrm{t}}_{\mathfrak{i}}\right),{\beta }_{\mathfrak{i}\mathfrak{i}}>0,\mathfrak{i}\in \{1,\dots ,n\}$
• Step 5: Choose an initial guess ${\mathrm{u}}_0\left({\mathrm{t}}_1\right);$
• Step 6: Set $\mathfrak{i}=1;$
• Step 7: Set ${\Lambda }_{\mathfrak{i}}={\sum }_{k=1}^{\mathfrak{i}}{\beta }_{\mathfrak{i}k}\overline{\mathrm{F}}({\mathrm{t}}_k,\mathrm{u}\left({\mathrm{t}}_k\right));$
• Step 8: ${\mathrm{u}}_{\mathfrak{i}}\left({\mathrm{t}}_{\mathfrak{i}}\right)={\sum }_{\ell =1}^{\mathfrak{i}}{\Lambda }_{\ell }{\mathsf{{\rm Y}}}_{\ell }\left({\mathrm{t}}_{\ell }\right);$
• Step 9: If $n>\mathfrak{i},$ set $\mathfrak{i}=\mathfrak{i}+1.$ Go to step 7. Else stop.
• where ${\mathrm{t}}_{\mathfrak{i}}=\frac{\mathfrak{i}}{n},\mathfrak{i}\in \{1,\dots ,n\}$ and n is the number of collocation points.

Example 1. 

Taking the following fractional linear ODE:

$$\left\{\begin{array}{cc}{\mathrm{D}}_0^{\alpha }\mathrm{u}\left(\mathrm{t}\right)={\mathrm{t}}^2+\frac{2}{\Gamma (3-\alpha )}{\mathrm{t}}^{2-\alpha }-\mathrm{u}\left(\mathrm{t}\right),\hfill & \mathrm{t}\in [0,1],\alpha \in (0,1]\hfill \\ \mathrm{u}\left(0\right)=0.\hfill \end{array}\right.$$

(24)

Taking $n=100$ collocation points in which ${\mathrm{t}}_{\mathfrak{i}}=\frac{\mathfrak{i}}{n},$ where $\mathfrak{i}$ is an integer that varies from 1 to $n.$ The numerical solution for (24) is obtained via the RKHSM for different fractional derivatives $\alpha .$ The outcomes are compared with the exact solution $\mathrm{u}\left(\mathrm{t}\right)={\mathrm{t}}^2.$ Figure 1 shows the exact solution and the RKHSM’s solution with $\alpha =1.$ The absolute error, in this case, is plotted in Figure 2. In Figure 3, the blue (exact solution) and green (proposed method) lines overlap for $\alpha =0.9$, and its absolute error is given in Figure 4. When $\alpha =0.8,$ Figure 5 shows that the exact solution and proposed method lines also overlap, and its absolute error is displayed in Figure 6. In Table 1 and Table 2, we combined the obtained results for $\alpha =1,0.9,$ and $0.8.$ The very small difference between the numerical and exact results confirms that the proposed method is effective.

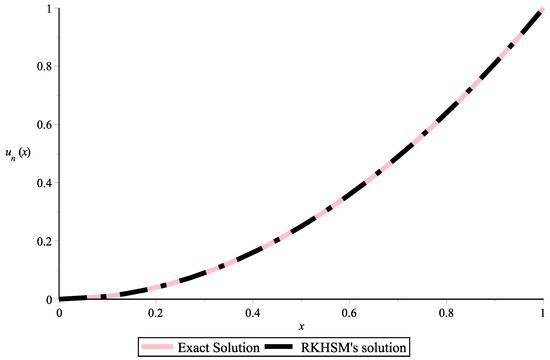
Figure 1. Two-dimensional plot of the solutions obtained via the Exact formula and RKHSM for Example 1 with $\alpha =1$.

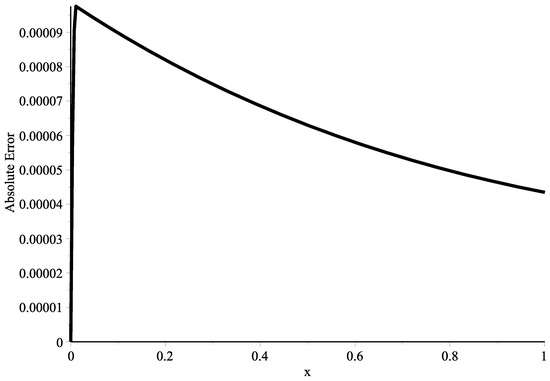
Figure 2. Two-dimensional plot of the absolute error for Example 1 with $\alpha =1$.

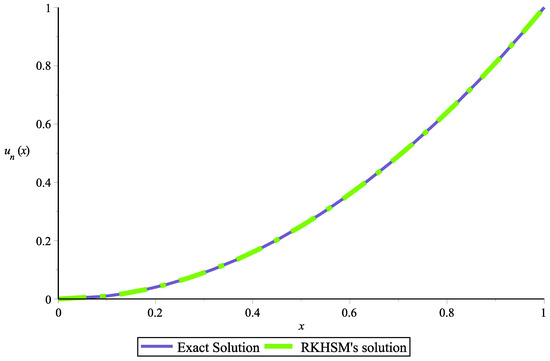
Figure 3. Two-dimensional plot of the solutions obtained via the Exact formula and RKHSM for Example 1 with $\alpha =0.9$.

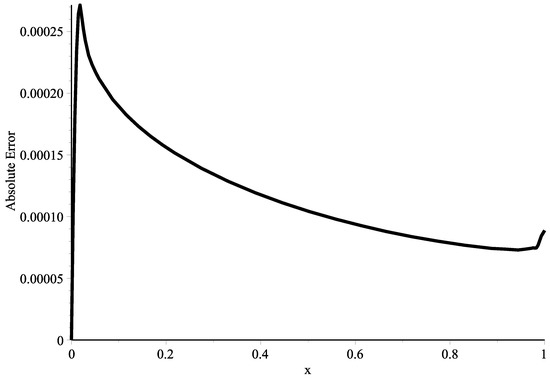
Figure 4. Two-dimensional plot of the absolute error for Example 1 with $\alpha =0.9$.

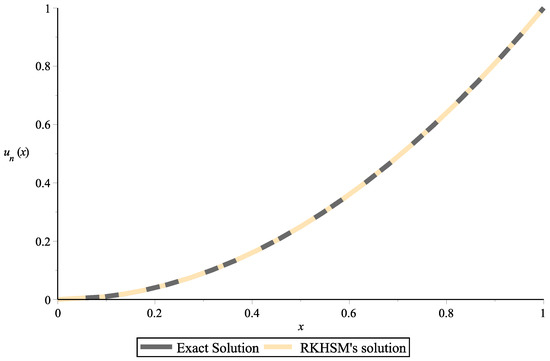
Figure 5. Two-dimensional plot of the solutions obtained via the Exact formula and RKHSM for Example 1 with $\alpha =0.8$.

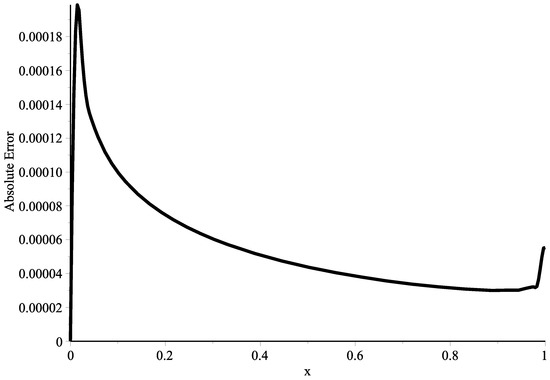
Figure 6. Two-dimensional plot of the absolute error for Example 1 with $\alpha =0.8$.

Table 1. Numerical outcomes for (24) with $\alpha =1$.

t	Exact Solution	RKHSM	Absolute Error
0	0	0	0
$0.1$	$0.01$	$0.010089787$	$8.979\times {10}^{-5}$
$0.2$	$0.04$	$0.040081922$	$8.192\times {10}^{-5}$
$0.3$	$0.09$	$0.090074877$	$7.488\times {10}^{-5}$
$0.4$	$0.16$	$0.160068581$	$6.858\times {10}^{-5}$
$0.5$	$0.25$	$0.250062970$	$6.297\times {10}^{-5}$
$0.6$	$0.36$	$0.360057994$	$5.799\times {10}^{-5}$
$0.7$	$0.49$	$0.490053597$	$5.360\times {10}^{-5}$
$0.8$	$0.64$	$0.640049733$	$4.973\times {10}^{-5}$
$0.9$	$0.81$	$0.810046365$	$4.637\times {10}^{-5}$
1	$1.00$	$1.000043466$	$4.347\times {10}^{-5}$

Table 2. Numerical outcomes for (24) with diverse of $\alpha$.

	Absolute Errors
t	$\mathbf{\alpha }=\mathbf{1}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{9}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{8}$
0	0	$1.517\times {10}^{-10}$	$4.569\times {10}^{-11}$
$0.1$	$8.979\times {10}^{-5}$	$1.891\times {10}^{-4}$	$9.985\times {10}^{-5}$
$0.2$	$8.192\times {10}^{-5}$	$1.561\times {10}^{-4}$	$7.464\times {10}^{-5}$
$0.3$	$7.488\times {10}^{-5}$	$1.342\times {10}^{-4}$	$6.0498\times {10}^{-5}$
$0.4$	$6.858\times {10}^{-5}$	$1.176\times {10}^{-4}$	$5.088\times {10}^{-5}$
$0.5$	$6.297\times {10}^{-5}$	$1.045\times {10}^{-4}$	$4.383\times {10}^{-5}$
$0.6$	$5.799\times {10}^{-5}$	$9.379\times {10}^{-5}$	$3.846\times {10}^{-5}$
$0.7$	$5.799\times {10}^{-5}$	$8.519\times {10}^{-5}$	$3.439\times {10}^{-5}$
$0.8$	$4.973\times {10}^{-5}$	$7.839\times {10}^{-5}$	$3.140\times {10}^{-5}$
$0.9$	$4.637\times {10}^{-5}$	$7.382\times {10}^{-5}$	$2.986\times {10}^{-5}$
1	$4.347\times {10}^{-5}$	$8.878\times {10}^{-5}$	$5.531\times {10}^{-5}$

Example 2. 

Taking the following fractional linear ODE:

$$\left\{\begin{array}{cc}{\mathrm{D}}_0^{\alpha }\mathrm{u}\left(\mathrm{t}\right)=\frac{\Gamma (5+\alpha )}{24}{\mathrm{t}}^4+{\mathrm{t}}^{8+2\alpha }-{\mathrm{u}}^2\left(\mathrm{t}\right),\hfill & \mathrm{t}\in [0,1],\alpha \in (0,1]\hfill \\ \mathrm{u}\left(0\right)=0.\hfill \end{array}\right.$$

(25)

Taking $n=100$ collocation points in which ${\mathrm{t}}_{\mathfrak{i}}=\frac{\mathfrak{i}}{n},$ where $\mathfrak{i}$ is an integer that varies from 1 to $n.$ The numerical solution for (25) is obtained via the RKHSM for different fractional derivative $\alpha .$ The results are compared with the exact solution $\mathrm{u}\left(\mathrm{t}\right)={\mathrm{t}}^{4+\alpha }.$ Figure 7, Figure 8 and Figure 9 show the exact solution and the RKHSM’s solution with $\alpha =1,0.9,$ and $0.8,$ respectively. In Table 3 and Table 4, we combined the obtained results for $\alpha =1,0.9,$ and $0.8.$ The very small difference between the numerical and exact results confirms that the proposed method is effective.

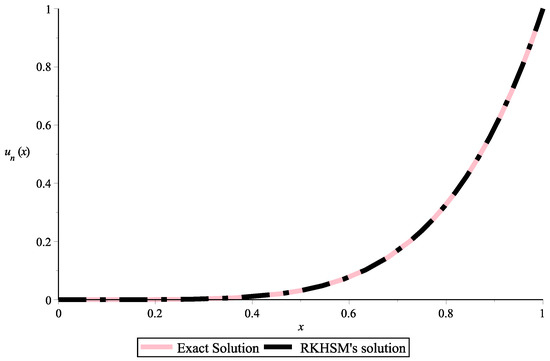
Figure 7. Two-dimensional plot of the solutions obtained via the Exact formula and RKHSM for Example 2 with $\alpha =1$.

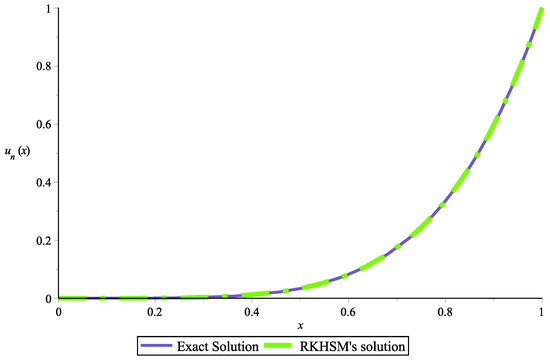
Figure 8. Two-dimensional plot of the solutions obtained via the Exact formula and RKHSM for Example 2 with $\alpha =0.9$.

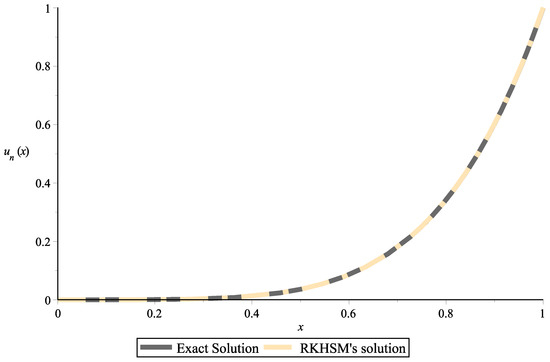
Figure 9. Two-dimensional plot of the solutions obtained via the Exact formula and RKHSM for Example 2 with $\alpha =0.8$.

Table 3. Numerical outcomes for (25) with $\alpha =1$.

t	Exact Solution	RKHSM	Absolute Error
0	0	0	0
$0.1$	$0.00001$	$0.000010170$	$1.697\times {10}^{-7}$
$0.2$	$0.00032$	$0.000321337$	$1.337\times {10}^{-6}$
$0.3$	$0.00243$	$0.002434509$	$4.509\times {10}^{-6}$
$0.4$	$0.01024$	$0.010250711$	$1.071\times {10}^{-5}$
$0.5$	$0.03125$	$0.031271189$	$2.119\times {10}^{-5}$
$0.6$	$0.07776$	$0.077797788$	$3.779\times {10}^{-5}$
$0.7$	$0.16807$	$0.168134319$	$6.432\times {10}^{-5}$
$0.8$	$0.32768$	$0.327788758$	$1.088\times {10}^{-4}$
$0.9$	$0.59049$	$0.590676921$	$1.869\times {10}^{-4}$
1	$1.00000$	$1.000326163$	$3.262\times {10}^{-4}$

Table 4. Numerical outcomes for (25) with diverse $\alpha$.

	Absolute Errors
t	$\mathbf{\alpha }=\mathbf{1}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{9}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{8}$
0	0	$1.962\times {10}^{-9}$	$5.110\times {10}^{-10}$
$0.1$	$1.697\times {10}^{-7}$	$2.038\times {10}^{-6}$	$1.710\times {10}^{-6}$
$0.2$	$1.337\times {10}^{-6}$	$1.789\times {10}^{-6}$	$2.132\times {10}^{-6}$
$0.3$	$4.509\times {10}^{-6}$	$1.400\times {10}^{-6}$	$1.410\times {10}^{-6}$
$0.4$	$1.071\times {10}^{-5}$	$9.240\times {10}^{-6}$	$1.381\times {10}^{-6}$
$0.5$	$2.119\times {10}^{-5}$	$2.459\times {10}^{-5}$	$8.770\times {10}^{-6}$
$0.6$	$3.779\times {10}^{-5}$	$5.417\times {10}^{-5}$	$2.878\times {10}^{-5}$
$0.7$	$6.432\times {10}^{-5}$	$1.151\times {10}^{-4}$	$8.200\times {10}^{-5}$
$0.8$	$1.088\times {10}^{-4}$	$2.460\times {10}^{-4}$	$2.144\times {10}^{-4}$
$0.9$	$1.869\times {10}^{-4}$	$5.246\times {10}^{-4}$	$5.114\times {10}^{-4}$
1	$3.262\times {10}^{-4}$	$1.239\times {10}^{-3}$	$1.327\times {10}^{-3}$

5. Conclusions

In the current work, we successfully applied a numerical approach to provide numerical solutions to the proposed problem. The two key steps for using the RKHS method are creating an orthonormal function system of the suitable RKHS and defining an acceptable bounded linear operator. It is demonstrated that the proposed approaches have good convergence. To demonstrate the capability and dependability of the RKHSM, two examples were used. When exact results are compared to our acquired results, it is seen that they are in strong agreement. The applicability, simplicity, and efficacy of the suggested method for solving such classes of fractional differential equations may be seen from the numerical results. This work opens up the possibility for the RKHSM to be used in studying NFODEs that are described with novel fractional derivatives. As part of our purpose, we plan to suggest a general numerical algorithm for systems of non-linear fractional differential equations, which will be new in the literature.