On Rotationally Symmetrical Planar Networks and Their Local Fractional Metric Dimension

Abstract

The metric dimension has various applications in several fields, such as computer science, image processing, pattern recognition, integer programming problems, drug discovery, and the production of various chemical compounds. The lowest number of vertices in a set with the condition that any vertex can be uniquely identified by the list of distances from other vertices in the set is the metric dimension of a graph. A resolving function of the graph G is a map $\vartheta :V\left(G\right)\to [0,1]$ such that ${\sum }_{u\in \mathcal{R}\{v,w\}}\vartheta \left(u\right)\ge 1,$ for every pair of adjacent distinct vertices $v,w\in V\left(G\right)$. The local fractional metric dimension of the graph G is defined as ${\mathrm{ldim}}_{\mathrm{f}}\left(G\right)$ = $min\{{\sum }_{v\in V\left(G\right)}\vartheta \left(v\right)$, where $\vartheta$ is a local resolving function of $G\}$. This paper presents a new family of planar networks namely, rotationally heptagonal symmetrical graphs by means of up to four cords in the heptagonal structure, and then find their upper-bound sequences for the local fractional metric dimension. Moreover, the comparison of the upper-bound sequence for the local fractional metric dimension is elaborated both numerically and graphically. Furthermore, the asymptotic behavior of the investigated sequences for the local fractional metric dimension is addressed.

1. Introduction

Slater [1] and Harary [2] independently established the issue of the metric dimension in the 1970s, which involved calculating the smallest number of vertices in a graph that could be uniquely represented by their corresponding vector of distances. Imran et al. [3,4] required the characterization of families of (rotationally symmetric) planar graphs with a constant metric dimension in this regard (see, for example, [5,6]). The problem of the metric dimension is important not only in research on graph structural features, but also in the solution of real-world problems, such as robot navigation [6], pattern recognition and image processing [7], combinatorial optimization [8], and networking [9], which are only a few examples among other things. Particularly, the problem of the hexagonal metric dimension, because of its application and graphs [10,11,12], has taken on a new significance.

The metric dimension problem was redeveloped as an integer programming problem by Chartrand et al. [13] in 2000. Currie and Oellermann [14] proposed a linear programming relaxation, which they named the fractional metric dimension of the graph, as the best solution. Benish et al. [15] proposed a local variant of the fractional metric dimension involving only nearby vertices in 2018. In [16], this was determined for a variety of graph types. Liu et al. [17] recently published a paper on this topic, where they calculated the local fractional metric dimension of a rotationally symmetric family of symmetric planar networks produced from a cycle of edge combinations $n\in \{3,4,5\}$ of order m.

A network N is an ordered 2-tuple consisting of two sets: a set of nodes (termed vertices $V\left(N\right)$) and a set of edges $E\left(N\right)$ that connect nodes/vertices. The number of items in N is the order of N. The number of items in $V\left(N\right)$ is denoted by p, and the size of N is the number of elements. $E\left(N\right)$ is denoted by the letter q. $d(x,y)$ represents the distance between x and y. For additional information, we refer the reader to [18,19,20] as a connection to graph theory.

We live in a silicon age with technological advancements. Robots and other devices are progressing at a fast rate. Personnel is being replaced by machines. In the meantime, this is necessary in order to connect the above-mentioned landmarks due to financial restrictions and the management of massive queues. There are fewer of these on production lines or in servicing areas. In this way, distance-based dimensions address these issues’ limits without difficulty. A collection of numbers $Y=\{y_1,y_2,\dots ,y_k\}$ from $V\left(N\right)$ is defined as an ordered set of vertices on which an object can be placed. We refer to a k-tuple as $r\left(x\right|Y)=(d(x,y_1),d(x,y_2),d(x,y_3),\cdots ,d(x,y_k)$ in metric notation, where $d(x,y_t)$ for $1\le t\le k$ denotes the distance between two points, $y_t$ and x. The set Y is transformed into a resolving set with k elements if, for each pair of different vertices, $x,z,r\left(x\right|Y)\ne r(z\left|Y\right)$.

The resolving set Y in N has the smallest number of elements. The base of N is a collection of elements. The cardinality of the letter Y is N. In [21], this denotes the metric dimension, and Slatter [22,23] invented the phrase “resolving set of a problem”. The concept of a locating set is used to create a connected network. Harary and Melter [24] discovered the above-mentioned terms and declared them to be the metric dimension of a component of a network. Following that, a group of researchers tested various networks for the evaluation of the metric dimension of a group of interconnected networks, where F was defined as a bounded function.

In a collection of interconnected networks, if all of the networks in a family have the same metric dimension, then F is said to be of a constant metric dimension [25]. Furthermore, given that a generalized Peterson antiprism in a $P(n,2)$ network C is a network that is a circulant network $C_2^n$, every one of these forms a family with a constant metric dimension. Similarly, the metric dimensions of wheels and Jahangir networks were explored. With the support of IPP, we were able to acquire a more accurate solution of this concept. FMD was also utilized by Fehr et al. [26] to find an improved solution to a linear programming relaxation problem. Arumugam and Mathew [27] provided clarification of the situation. FMD has many new features. Several graph theorists discussed several results related to the metric dimension and graph labelings on various families of graphs in [28,29,30,31,32]. Many researchers have discussed several aspects of graph theory [33,34,35,36,37,38,39,40].

Several networks have surfaced in relation to FMD, including Cartesian and hierarchical networks, which are examples of these types of networks. Linked networks’ lexicographic and comb products were discussed in [41,42]. Furthermore, Liu et al. [43] calculated the generalized Jahangir network’s FMD. Aisyah et al. recently defined and computed the idea of the local fractional metric dimension (LFMD) for the corona product of two networks [44]. Circular ladders are a type of rotationally symmetric and planar network that consists of distinct faces. The triangle, quadrangle, and pentagon are all geometric shapes. It was found that for quadrangular circular ladders $\left(Q_1^n\mathrm{and}{Q}_2^n\right)$ and a pentagonal circular ladder $P_n^1$, the LFMD is constant for each $n\ge 4$ and $n\equiv 0\left(\mathrm{mod}2\right)$ value, where n signifies that each of these circular ladders has a different number of steps. Moreover, it has been established that a triangular circular ladder $T_n$ and a pentagonal circular ladder $P_n$ are equivalent ladders in a circle $(P_k^k,2\le k\le 7)$. They have an LFMD that is variable. Recently, Poulik and Ghorai discussed the determination of journey order based on a graph’s Wiener absolute index with the help of bipolar fuzzy information, and they elaborated on the estimation of the most affected cycles and the busiest network routes based on the complexity function of a graph in a fuzzy environment in [45,46].

The following lemma will be used throughout this manuscript.

Lemma 1

([15,47,48]). Let G be a finite connected graph of order $n\ge 2$. Then, the following bounds hold.

$${\mathrm{ldim}}_{\mathrm{f}}\left(G\right)\le {dim}_{\mathrm{f}}\left(G\right),$$

(1)

$$\frac{n}{n-\mathrm{ldim}\left(G\right)+1}\le {\mathrm{ldim}}_{\mathrm{f}}\left(G\right)\le \frac{n}{\ell \left(G\right)}\le \frac{n}{2}$$

(2)

$$1\le {\mathrm{ldim}}_{\mathrm{f}}\left(G\right)\le \mathrm{ldim}\left(G\right)\le n-\mathrm{diam}\left(G\right).$$

(3)

A planar graph G with a local fractional metric dimension less than or equal to 3 is shown in Figure 1.

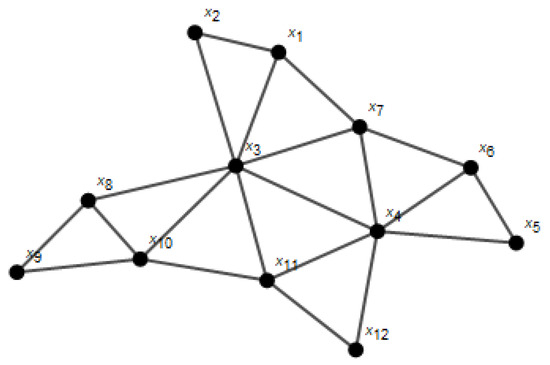
Figure 1. A planar graph G with a local fractional metric dimension less than or equal to 3.

The resolving sets with respect to adjacent vertices are:

• $\mathcal{R}\{x_1,x_2\}=V\left(G\right)\setminus \left\{x_3,x_4,x_5,x_8,x_9,x_{10},x_{11},x_{12}\right\},\left|\mathcal{R}\{x_1,x_2\}\right|=4.$
• $\mathcal{R}\{x_2,x_3\}=V\left(G\right)\setminus \left\{x_1\right\},\left|\mathcal{R}\{x_2,x_3\}\right|=11.$
• $\mathcal{R}\{x_3,x_4\}=V\left(G\right)\setminus \left\{x_7,x_{11}\right\},\left|\mathcal{R}\{x_3,x_4\}\right|=10.$
• $\mathcal{R}\{x_4,x_5\}=V\left(G\right)\setminus \left\{x_6\right\},\left|\mathcal{R}\{x_1,x_2\}\right|=11.$
• $\mathcal{R}\{x_5,x_6\}=V\left(G\right)\setminus \left\{x_2,x_3,x_4,x_8,x_9,x_{10},x_{11},x_{12}\right\},\left|\mathcal{R}\{x_5,x_6\}\right|=4.$
• $\mathcal{R}\{x_6,x_7\}=V\left(G\right)\setminus \left\{x_4,x_{11},x_{12}\right\},\left|\mathcal{R}\{x_6,x_7\}\right|=9.$
• $\mathcal{R}\{x_7,x_1\}=V\left(G\right)\setminus \left\{x_3,x_8,x_9,x_{10},x_{11}\right\},\left|\mathcal{R}\{x_7,x_1\}\right|=7.$
• $\mathcal{R}\{x_1,x_3\}=V\left(G\right)\setminus \left\{x_2,x_6,x_7\right\},\left|\mathcal{R}\{x_1,x_2\}\right|=9.$
• $\mathcal{R}\{x_3,x_7\}=V\left(G\right)\setminus \left\{x_1,x_4,x_5,x_{12}\right\},\left|\mathcal{R}\{x_1,x_2\}\right|=8.$
• $\mathcal{R}\{x_7,x_4\}=V\left(G\right)\setminus \left\{x_2,x_3,x_6,x_8,x_9,x_{10}\right\},\left|\mathcal{R}\{x_1,x_2\}\right|=6.$
• $\mathcal{R}\{x_4,x_6\}=V\left(G\right)\setminus \left\{x_1,x_5,x_7\right\},\left|\mathcal{R}\{x_1,x_2\}\right|=9.$
• $\mathcal{R}\{x_3,x_8\}=V\left(G\right)\setminus \left\{x_{10}\right\},\left|\mathcal{R}\{x_3,x_8\}\right|=11.$
• $\mathcal{R}\{x_8,x_9\}=V\left(G\right)\setminus \left\{x_{10},x_{11},x_{12}\right\},\left|\mathcal{R}\{x_8,x_9\}\right|=9.$
• $\mathcal{R}\{x_9,x_{10}\}=V\left(G\right)\setminus \left\{x_8\right\},\left|\mathcal{R}\{x_9,x_{10}\}\right|=11.$
• $\mathcal{R}\{x_{12},x_4\}=V\left(G\right)\setminus \left\{x_9,x_{10},x_{11}\right\},\left|\mathcal{R}\{x_{12},x_4\}\right|=9.$
• $\mathcal{R}\{x_8,x_{10}\}=V\left(G\right)\setminus \left\{x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_9\right\},\left|\mathcal{R}\{x_8,x_{10}\}\right|=4.$
• $\mathcal{R}\{x_{10},x_3\}=V\left(G\right)\setminus \left\{x_8,x_{11},x_{12}\right\},\left|\mathcal{R}\{x_{10},x_3\}\right|=9.$
• $\mathcal{R}\{x_3,x_{11}\}=V\left(G\right)\setminus \left\{x_4,x_5,x_6,x_9,x_{10}\right\},\left|\mathcal{R}\{x_3,x_{11}\}\right|=7.$
• $\mathcal{R}\{x_{11},x_4\}=V\left(G\right)\setminus \left\{x_1,x_2,x_3,x_8,x_{12}\right\},\left|\mathcal{R}\{x_{11},x_4\}\right|=7.$
• $\mathcal{R}\{x_{10},x_{11}\}=V\left(G\right)\setminus \left\{x_1,x_2,x_3,x_7\right\},\left|\mathcal{R}\{x_{10},x_{11}\}\right|=8.$
• $\mathcal{R}\{x_{11},x_{12}\}=V\left(G\right)\setminus \left\{x_4,x_5,x_6,x_7\right\},\left|\mathcal{R}\{x_{11},x_{12}\}\right|=8.$

Since the minimum cardinality of the resolving set is 4, by relation (2), we have ${\mathrm{ldim}}_{\mathrm{f}}\left(G\right)\le \frac{12}{4}=3.$

The remaining sections proceed as follows: In Section 2, Section 3 and Section 4, the upper-bound sequences of the local fractional metric dimension over heptagonal rotationally symmetric planar graphs with up to four cords are discussed. In Section 5, a comparison of the upper-bound sequences of the local frictional metric dimension is elaborated upon. In the last section, we will provide the concluding remarks of the proposed work and discuss some open problems for further research. Throughout the manuscript, LFMD is the local frictional metric dimension, and HRS graphs are heptagonal rotationally symmetrical planar graphs.

2. Upper-Bound Sequences of the LFMD of HRS Planar Graphs with One Cord

In this section, we will find the sequences of the LFMD of HRS planar graphs with one cord. The families of planar graphs based on a heptagon with up to four cords are shown in Figure 2.

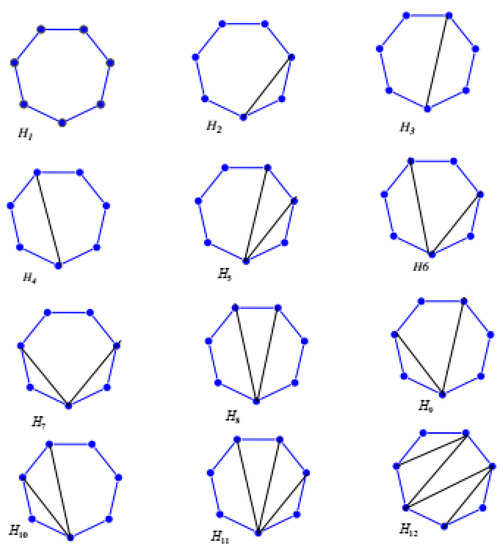
Figure 2. Heptagonal planar graphs with up to four cords.

The heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_1\right)$ and ${\mathcal{G}}^m\left(H_2\right)$ are shown in Figure 3.

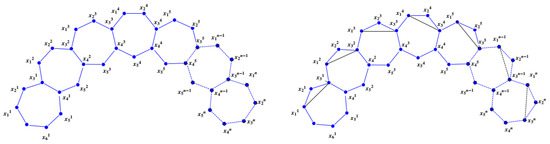
Figure 3. Heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_1\right)$ and ${\mathcal{G}}^m\left(H_2\right)$.

Proposition 1.

Let ${\mathcal{G}}^m\left(H_1\right)$ be a heptagonal rotationally symmetrical planar graph. Then, ${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_1\right)\right)=1$ and

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_1\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{4}{3},\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{11},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right..$$

Proof. 

For $m=1$, we have a unique cycle of an odd length, so ${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_1\right)\right)=1$. For $m=2$, we have:

• $\mathcal{R}\{x_1^1,x_2^1\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \left\{x_5^1\right\}.$
• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \left\{x_6^1\right\}.$
• $\mathcal{R}\{x_3^1,x_4^1\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \{x_7^1,x_3^2\}.$
• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \left\{x_1^1\right\}.$
• $\mathcal{R}\{x_5^1,x_6^1\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \left\{x_2^1\right\}.$
• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \{x_3^1,x_1^2,x_2^2\}.$
• $\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \{x_5^2,x_4^1,x_4^2\}.$
• $\mathcal{R}\{x_3^1,x_1^2\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \left\{x_4^2\right\}.$
• $\mathcal{R}\{x_1^2,x_2^2\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \left\{x_5^2\right\}.$
• $\mathcal{R}\{x_2^2,x_3^2\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \{x_4^1,x_5^1,x_6^1\}.$
• $\mathcal{R}\{x_3^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \{x_1^1,x_2^1,x_3^1\}.$
• $\mathcal{R}\{x_4^2,x_5^2\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \left\{x_1^2\right\}.$
• $\mathcal{R}\{x_5^2,x_6^2\}=V\left({\mathcal{G}}^2\left(H_1\right)\right)\setminus \left\{x_2^2\right\}.$

Since the minimum cardinality of the resolving set is 9, by relation (2), we have ${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^2\left(H_1\right)\right)\le \frac{4}{3}.$

For $m\ge 3$, we have the following resolving sets:

• $\mathcal{R}\{x_1^i,x_2^i\}=V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus \left\{x_5^i\right\}$, $1\le i\le m$.

• $\mathcal{R}\{x_2^i,x_3^i\}=V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus \left\{x_6^i\right\}$, $1\le i\le m$.

• $\mathcal{R}\{x_4^i,x_5^i\}=V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus \left\{x_1^i\right\}$, $1\le i\le m$.

• $\mathcal{R}\{x_5^i,x_6^i\}=V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus \left\{x_2^i\right\}$, $1\le i\le m$.

• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus \{x_3^1,x_1^2,x_2^2\}$, $1\le i\le m$.

• $\mathcal{R}\{x_3^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_7^1,x_3^2,x_2^3,x_1^3\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^{m-1},x_2^{m-1},x_3^{m-1}\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_1^{m-2},x_2^{m-2},x_3^{m-2},x_3^m\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_1^{m-i-1},x_2^{m-i-1},x_3^{m-i-1},x_3^{m-i+1},x_1^{m-i+2},x_2^{m-i+2}\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

• $\mathcal{R}\{x_7^i,x_1^i\}=V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_4^1,x_4^2,x_5^2,x_3^3,x_4^3,x_5^3\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup \hfill & \mathrm{if}i=1,\hfill \\ {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^3\right\}}_{i=1}^5,\hfill & \\ \left\{x_4^m\right\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_4^{m-1},x_4^m,x_5^m\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_4^{m-2},x_4^{m-1},x_5^{m-1},x_3^m,x_4^m,x_5^m\},\hfill & \mathrm{if}i=m-2,\hfill \\ \{x_4^2,x_4^3,x_5^3,x_3^3,x_5^4,x_4^4\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup {\left\{x_i^{m-1}\right\}}_{i=1}^5\hfill & \mathrm{otherwise}\hfill \\ \cup \cdots \cup {\left\{x_i^{m-4}\right\}}_{i=1}^5,\hfill \end{array}\hfill \end{array}\right.$

They have the following cardinalities.

• $|\mathcal{R}\{x_1^i,x_2^i\}|=|\mathcal{R}\{x_2^i,x_3^i\}|=|\mathcal{R}\{x_4^i,x_5^i\}|=|\mathcal{R}\{x_5^i,x_6^i\}|=5m+1$

• $\left|\mathcal{R}\right\{x_6^1,x_7^1\left\}\right|=5m-1.$

• $|\mathcal{R}\{x_3^i,x_4^i\}|=|V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m-2,\hfill & \mathrm{if}i=1,\hfill \\ 5m-1,\hfill & \mathrm{if}i=m,\hfill \\ 5m-2,\hfill & \mathrm{if}i=m-1,\hfill \\ 5m-4,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

• $|\mathcal{R}\{x_7^i,x_1^i\}|=|V\left({\mathcal{G}}^m\left(H_1\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}11,\hfill & \mathrm{if}i=1,\hfill \\ 5m+1,\hfill & \mathrm{if}i=m,\hfill \\ 5m-1,\hfill & \mathrm{if}i=m-1,\hfill \\ 5m-4,\hfill & \mathrm{if}i=m-2,\hfill \\ 16,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

As 11 is the minimal cardinality, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_1\right)\right)\le \frac{5m+2}{11}.$$

□

Proposition 2.

Let ${\mathcal{G}}^m\left(H_2\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_2\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{4},\hfill & \mathrm{if}m=1,\hfill \\ 3,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{4},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

Proof. 

For $m=1$, we have

• $\mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_4^1,x_5^1\}=\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^1\left(H_2\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_1^1,x_3^1\}=V\left({\mathcal{G}}^1\left(H_2\right)\right)\setminus \left\{x_2^1\right\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=V\left({\mathcal{G}}^1\left(H_2\right)\right)\setminus \{x_3^1,x_4^1,x_5^1\}.$

• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^1\left(H_2\right)\right)\setminus \{x_1^1,x_6^1,x_7^1\}.$

Since the minimum cardinality of the resolving set is 4, by relation (2), we have ${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_2\right)\right)\le \frac{7}{4}.$

For $m=2$, we have:

• $\mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_4^1,x_5^1\}=\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_7^1,x_1^1\}=\mathcal{R}\{x_3^1,x_1^2\}=\mathcal{R}\{x_3^2,x_4^2\}=\mathcal{R}\{x_4^2,x_5^2\}=\varnothing .$

• $\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_1^1,x_3^1\}=V\left({\mathcal{G}}^2\left(H_2\right)\right)\setminus \left\{x_2^1\right\}.$

• $\mathcal{R}\{x_5^2,x_4^1\}=\mathcal{R}\{x_1^2,x_3^2\}=V\left({\mathcal{G}}^2\left(H_2\right)\right)\setminus \left\{x_2^2\right\}.$

• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^2\left(H_2\right)\right)\setminus \{x_1^1,x_6^1,x_7^1\}.$

• $\mathcal{R}\{x_1^2,x_2^2\}=V\left({\mathcal{G}}^2\left(H_2\right)\right)\setminus \{x_3^2,x_4^2,x_5^2\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=V\left({\mathcal{G}}^2\left(H_2\right)\right)\setminus \{x_3^1,x_4^1,x_5^1,x_1^2,x_2^2,x_3^2,x_4^2,x_5^2\}.$

• $\mathcal{R}\{x_2^2,x_3^2\}=V\left({\mathcal{G}}^2\left(H_2\right)\right)\setminus \{x_1^1,x_2^1,x_3^1,x_4^1,x_5^1,x_6^1,x_7^1,x_1^2\}.$

Since the minimum cardinality of the resolving set is 4, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^2\left(H_2\right)\right)\le \frac{12}{4}=3.$$

For $m\ge 3$, we have the following resolving sets:

• $\mathcal{R}\{x_3^i,x_4^i\}=\mathcal{R}\{x_4^i,x_5^i\}=\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_7^i,x_1^i\}=V\left({\mathcal{G}}^m\left(H_2\right)\right)\setminus \varnothing$.

• $\mathcal{R}\{x_1^i,x_3^i\}=\mathcal{R}\{x_5^i,x_6^i\}=V\left({\mathcal{G}}^m\left(H_2\right)\right)\setminus \left\{x_2^i\right\}$.

• $\mathcal{R}\{x_3^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_2\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_3^1,x_4^1,x_5^1\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^2\right\}}_{i=1}^5,\hfill & \mathrm{if}i=1,\hfill \\ \{x_3^m,x_4^m,x_5^m\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_3^{m-1},x_4^{m-1},x_5^{m-1},x_1^m,x_2^m,x_3^m,x_4^m,x_5^m\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_3^{m-2},x_4^{m-2},x_5^{m-2}\}\cup {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup {\left\{x_i^m\right\}}_{i=1}^5,\hfill & \mathrm{if}i=m-2,\hfill \\ \{x_3^2,x_4^2,x_5^2\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^3\right\}}_{i=1}^5,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

• $\mathcal{R}\{x_2^i,x_3^i\}=V\left({\mathcal{G}}^m\left(H_2\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_1^1,x_6^1,x_7^1\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^1,x_2^1,x_3^1,x_4^1,x_5^1,x_6^1,x_7^1,x_1^2\},\hfill & \mathrm{if}i=2,\hfill \\ A_{n-1}\cup \{x_2^{m-1},x_3^{m-1},x_4^{m-1},x_5^{m-1},x_1^m\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

They have the following cardinalities.

• $|\mathcal{R}\{x_3^i,x_4^i\}|=|\mathcal{R}\{x_4^i,x_6^i\}|=|\mathcal{R}\{x_6^1,x_7^1\}|=|\mathcal{R}\{x_7^i,x_1^i\}|=5m+2.$
• $|\mathcal{R}\{x_1^i,x_3^i\}|=|\mathcal{R}\{x_5^i,x_5^i\}|=5m+1.$
• $|\mathcal{R}\{x_1^i,x_2^i\}|=|V\left({\mathcal{G}}^m\left(H_2\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}4,\hfill & \mathrm{if}i=1,\hfill \\ 5m-1,\hfill & \mathrm{if}i=m,\hfill \\ 5m-6,\hfill & \mathrm{if}i=m-1,\hfill \\ 5m-11,\hfill & \mathrm{if}i=m-2,\hfill \\ 4,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_2^i,x_3^i\}|=|V\left({\mathcal{G}}^m\left(H_2\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m-1,\hfill & \mathrm{if}i=1,\hfill \\ 5m-6,\hfill & \mathrm{if}i=2,\hfill \\ 4,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

As 4 is the minimal cardinality, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_2\right)\right)\le \frac{5m+2}{4}.$$

□

The heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_3\right)$ and ${\mathcal{G}}^m\left(H_4\right)$ are shown in Figure 4.

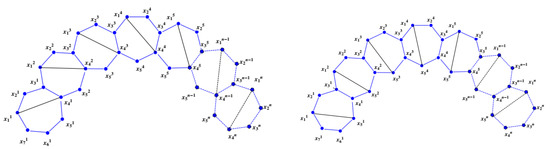
Figure 4. Heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_3\right)$ and ${\mathcal{G}}^m\left(H_4\right)$.

Proposition 3.

Let ${\mathcal{G}}^m\left(H_3\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_3\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{5},\hfill & \mathrm{if}m=1,\hfill \\ \frac{12}{5},\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{5},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

Proof. 

For $m=1$, we have:

• $\mathcal{R}\{x_1^1,x_2^1\}=\mathcal{R}\{x_3^1,x_4^1\}=V\left({\mathcal{G}}^1\left(H_3\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_2^1,x_3^1\}=\mathcal{R}\{x_1^1,x_4^1\}=V\left({\mathcal{G}}^1\left(H_3\right)\right)\setminus \left\{x_6^1\right\}.$

• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^1\left(H_3\right)\right)\setminus \left\{x_7^1\right\}.$

• $\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^1\left(H_3\right)\right)\setminus \left\{x_5^1\right\}.$

• $\mathcal{R}\{x_5^1,x_6^1\}=V\left({\mathcal{G}}^1\left(H_3\right)\right)\setminus \{x_1^1,x_2^1\}.$

• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^1\left(H_3\right)\right)\setminus \{x_3^1,x_4^1\}.$

Since the minimum cardinality of the resolving set is 5, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_3\right)\right)\le \frac{7}{5}.$$

For $m=2$, we have:

• $\mathcal{R}\{x_1^2,x_2^2\}=\mathcal{R}\{x_3^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_2^1,x_3^1\}=\mathcal{R}\{x_1^1,x_4^1\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \left\{x_6^1\right\}.$

• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \left\{x_7^1\right\}.$

• $\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \left\{x_5^1\right\}.$

• $\mathcal{R}\{x_3^1,x_1^2\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \left\{x_5^2\right\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=\mathcal{R}\{x_3^1,x_4^1\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \{x_3^2,x_4^2\}.$

• $\mathcal{R}\{x_5^1,x_6^1\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \{x_1^1,x_2^1\}.$

• $\mathcal{R}\{x_4^2,x_5^2\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \{x_2^1,x_3^1\}.$

• $\mathcal{R}\{x_5^2,x_4^1\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \{x_1^2,x_2^2\}.$

• $\mathcal{R}\{x_2^2,x_3^2\}=\mathcal{R}\{x_1^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \{x_1^1,x_4^1,x_5^1,x_6^1,x_7^1\}.$

• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^2\left(H_3\right)\right)\setminus \{x_3^1,x_4^1,x_1^2,x_2^2,x_3^2,x_4^2,x_5^2\}.$

Since the minimum cardinality of the resolving set is 5, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^2\left(H_3\right)\right)\le \frac{12}{5}.$$

For $m\ge 3$, we have the following resolving sets:

• $\mathcal{R}\{x_5^i,x_6^i\}=V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus \{x_1^i,x_2^i\}.$
• $\mathcal{R}\{x_7^i,x_1^i\}=V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus \left\{x_5^i\right\}.$
• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus \{x_3^1,x_4^1\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^2\right\}}_{i=1}^5.$
• $\mathcal{R}\{x_4^i,x_5^i\}=V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\left\{x_7^1\right\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_2^{i-1},x_3^{i-1}\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_2^i\}=\mathcal{R}\{x_3^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\varnothing ,\hfill & \mathrm{if}i=m,\hfill \\ \{x_3^2,x_4^2,x_1^3,x_2^3,x_3^3,x_4^3,x_5^3\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup \hfill & \mathrm{if}i=1,\hfill \\ {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^3\right\}}_{i=1}^5,\hfill & \\ \{x_3^{i+1},x_4^{i+1}\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_3^{m-1},x_4^{m-1},x_1^m,x_2^m,x_3^m,x_4^m,x_5^m\},\hfill & \mathrm{if}i=m-2,\hfill \\ \{x_3^2,x_4^2,x_1^3,x_2^3,x_3^3,x_4^3,x_5^3\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup \hfill & \mathrm{otherwise}\hfill \\ {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^4\right\}}_{i=1}^5,\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_4^i\}=\mathcal{R}\{x_2^i,x_3^i\}=V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\left\{x_6^1\right\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^1,x_4^1,x_5^1,x_6^1,x_7^1\},\hfill & \mathrm{if}i=2,\hfill \\ A_{n-1}\cup \{x_2^{m-2},x_3^{m-2},x_1^{m-1},x_2^{m-1},x_3^{m-1}\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

They have the following cardinalities.

• $\left|\mathcal{R}\right\{x_5^i,x_6^i\left\}\right|=5m.$
• $\left|\mathcal{R}\right\{x_7^i,x_1^i\left\}\right|=5m+1.$
• $\left|\mathcal{R}\right\{x_6^1,x_7^1\left\}\right|=5.$
• $|\mathcal{R}\{x_1^i,x_2^i\}|=\mathcal{R}\{x_3^i,x_4^i\}|=|V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5,\hfill & \mathrm{if}i=1,\hfill \\ 5m+2,\hfill & \mathrm{if}i=m,\hfill \\ 5m,\hfill & \mathrm{if}i=m-1,\hfill \\ 5m-5,\hfill & \mathrm{if}i=m-2,\hfill \\ 13,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_4^i\}|=\mathcal{R}\{x_2^i,x_3^i\}|=|V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m+1,\hfill & \mathrm{if}i=1,\hfill \\ 5m-3,\hfill & \mathrm{if}i=2,\hfill \\ 7,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_4^i,x_5^i\}|=|V\left({\mathcal{G}}^m\left(H_3\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m+1,\hfill & \mathrm{if}i=1,\hfill \\ 5m,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

As 7 is the minimal cardinality, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_3\right)\right)\le \frac{5m+2}{7}.$$

□

Proposition 4.

Let ${\mathcal{G}}^m\left(H_4\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_4\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{5},\hfill & \mathrm{if}m=1,\hfill \\ \frac{3}{2},\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{6},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

Proof. 

For $m=1$, we have

• $\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^1\left(H_4\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_1^1,x_5^1\}=V\left({\mathcal{G}}^1\left(H_4\right)\right)\setminus \left\{x_3^1\right\}.$

• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^1\left(H_4\right)\right)\setminus \left\{x_2^1\right\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=V\left({\mathcal{G}}^1\left(H_4\right)\right)\setminus \left\{x_4^1\right\}.$

• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^1\left(H_4\right)\right)\setminus \{x_5^1,x_6^1\}.$

• $\mathcal{R}\{x_3^1,x_4^1\}=V\left({\mathcal{G}}^1\left(H_4\right)\right)\setminus \{x_1^1,x_7^1\}.$

Since the minimum cardinality of the resolving set is 5, by relation (2), we have ${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_4\right)\right)\le \frac{7}{5}.$

For $m=2$, we have:

• $\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_7^1,x_1^1\}=\mathcal{R}\{x_3^1,x_1^2\}=\mathcal{R}\{x_5^2,x_4^1\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \left\{x_2^1\right\}.$

• $\mathcal{R}\{x_1^2,x_2^2\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \left\{x_4^2\right\}.$

• $\mathcal{R}\{x_4^1,x_5^2\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \left\{x_2^2\right\}.$

• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \{x_5^1,x_6^1\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \{x_4^1,x_4^2,x_5^2\}.$

• $\mathcal{R}\{x_3^1,x_4^1\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \{x_1^1,x_7^1,x_3^2\}.$

• $\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_1^1,x_5^1\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \{x_3^1,x_1^2,x_2^2\}.$

• $\mathcal{R}\{x_3^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \{x_2^1,x_3^1,x_1^2\}.$

• $\mathcal{R}\{x_3^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \{x_2^1,x_3^1,x_1^2\}.$

• $\mathcal{R}\{x_1^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \{x_1^1,x_7^1,x_3^2\}.$

• $\mathcal{R}\{x_2^2,x_3^2\}=V\left({\mathcal{G}}^2\left(H_4\right)\right)\setminus \{x_4^1,x_5^1,x_6^1,x_5^2\}.$

Since the minimum cardinality of the resolving set is 8, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^2\left(H_4\right)\right)\le \frac{12}{8}=\frac{3}{2}.$$

For $m\ge 3$, we have the following resolving sets:

• $\mathcal{R}\{x_5^i,x_6^i\}=\mathcal{R}\{x_7^i,x_1^i\}=V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus \varnothing$.
• $\mathcal{R}\{x_4^i,x_5^i\}=V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus \left\{x_2^i\right\}.$
• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus \{x_3^1,x_1^2,x_2^2\}.$
• $\mathcal{R}\{x_1^i,x_2^i\}=V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\left\{x_4^i\right\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_4^1,x_4^2,x_5^2,x_3^3,x_4^3,x_5^3\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup \hfill & \mathrm{if}i=1,\hfill \\ {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^3\right\}}_{i=1}^5,\hfill & \\ \{x_4^{m-1},x_4^m,x_5^m\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_4^{m-2},x_4^{m-1},x_5^{m-1},x_3^m,x_4^m,x_5^m\},\hfill & \mathrm{if}i=m-2,\hfill \\ \{x_4^2,x_4^3,x_5^3,x_3^4,x_4^4,x_5^4\}\cup {\left\{x_i^m\right\}}_{i=1}^5\cup \hfill & \mathrm{otherwise}\hfill \\ {\left\{x_i^{m-1}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^4\right\}}_{i=1}^5,\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_3^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_2^{m-1},x_3^{m-1},x_1^m\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_1^1,x_7^1,x_3^2,x_1^3,x_2^3\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_2^{m-2},x_3^{m-2},x_1^{m-1},x_3^m\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_2^{i-1},x_3^{i-1},x_1^i,x_3^{i+1},x_1^{i+2},x_2^{i+2}\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_2^i,x_3^i\}=V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_5^1,x_6^1\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_4^1,x_5^1,x_6^1,x_5^2\},\hfill & \mathrm{if}i=2,\hfill \\ \{x_1^1,x_4^1,x_5^1,x_6^1,x_7^1,x_4^2,x_5^2,x_5^3\},\hfill & \mathrm{if}i=3,\hfill \\ \{x_1^2,x_4^2,x_5^2,x_4^3,x_5^3,x_5^4\}\cup {\left\{x_j^1\right\}}_{j=1}^7,\hfill & \mathrm{if}i=4,\hfill \\ \{x_1^3,x_4^3,x_5^3,x_4^4,x_5^4,x_5^5\}\cup {\left\{x_j^1\right\}}_{j=1}^7\cup {\left\{x_j^2\right\}}_{j=1}^5,\hfill & \mathrm{if}i=5,\hfill \\ \{x_1^{i-2},x_4^{i-2},x_5^{i-2},x_4^{i-1},x_5^{i-1},x_5^i\}\cup \hfill & \mathrm{otherwise}\hfill \\ {\left\{x_j^1\right\}}_{j=1}^7\cup {\left\{x_j^{m-3}\right\}}_{j=1}^5\cup {\left\{x_j^{m-4}\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^2\right\}}_{j=1}^5,\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_5^i\}=V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_2^{m-2},x_3^{m-2},x_1^{m-1},x_3^m\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_3^1,x_1^2,x_2^2\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^1,x_7^1,x_3^2,x_1^3,x_2^3\},\hfill & \mathrm{if}i=2,\hfill \\ \{x_2^{m-3},x_3^{m-3},x_1^{m-2},x_3^{m-1},x_1^m,x_2^m\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

They have the following cardinalities.

• $|\mathcal{R}\{x_5^i,x_6^i\}=\mathcal{R}\{x_7^i,x_1^i\}|=5m+2.$
• $\left|\mathcal{R}\right\{x_4^i,x_5^i\left\}\right|=5m+1.$
• $\left|\mathcal{R}\right\{x_6^1,x_7^1\left\}\right|=5m-1.$
• $|\mathcal{R}\{x_1^i,x_2^i\}|=|V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m+1,\hfill & \mathrm{if}i=m,\hfill \\ 6,\hfill & \mathrm{if}i=1,\hfill \\ 5m-1,\hfill & \mathrm{if}i=m-1,\hfill \\ 5m-4,\hfill & \mathrm{if}i=m-2,\hfill \\ 11,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_3^i,x_4^i\}|=|V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m-1,\hfill & \mathrm{if}i=m,\hfill \\ 5m-3,\hfill & \mathrm{if}i=1,\hfill \\ 5m-2,\hfill & \mathrm{if}i=m-1,\hfill \\ 5m-4,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_2^i,x_3^i\}|=|V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m,\hfill & \mathrm{if}i=1,\hfill \\ 5m-2,\hfill & \mathrm{if}i=2,\hfill \\ 5m-6,\hfill & \mathrm{if}i=3,\hfill \\ 5m-11,\hfill & \mathrm{if}i=4,\hfill \\ 5m-16,\hfill & \mathrm{if}i=5,\hfill \\ 9,\hfill & \mathrm{otherwise}\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_5^i\}|=|V\left({\mathcal{G}}^m\left(H_4\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m-2,\hfill & \mathrm{if}i=m,\hfill \\ 5m-1,\hfill & \mathrm{if}i=1,\hfill \\ 5m-3,\hfill & \mathrm{if}i=2,\hfill \\ 5m-4,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

As 6 is the minimal cardinality, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_4\right)\right)\le \frac{5m+2}{6}.$$

□

3. Upper-Bound Sequences of the LFMD of HRS Planar Graphs with Two Cords

In this section, we will find the LFMD of HRS planar graphs with two cords. The heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_5\right)$ and ${\mathcal{G}}^m\left(H_6\right)$ are shown in Figure 5.

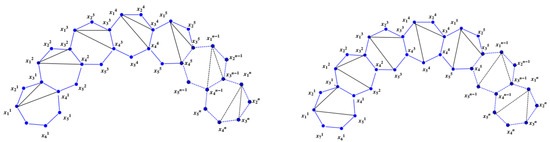
Figure 5. Heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_5\right)$ and ${\mathcal{G}}^m\left(H_6\right)$.

Proposition 5.

Let ${\mathcal{G}}^m\left(H_5\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_5\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{4},\hfill & \mathrm{if}m=1,\hfill \\ 3,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{4}\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

The proof is similar to the proof of Proposition 2.

Proposition 6.

Let ${\mathcal{G}}^m\left(H_6\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_6\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{3},\hfill & \mathrm{if}m=1,\hfill \\ 4,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{3}\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

Proof. 

For $m=1$, we have:

• $\mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_7^1,x_1^1\}=\mathcal{R}\{x_1^1,x_5^1\}=V\left({\mathcal{G}}^1\left(H_6\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_4^1,x_5^1\}=\mathcal{R}\{x_1^1,x_3^1\}=V\left({\mathcal{G}}^1\left(H_6\right)\right)\setminus \left\{x_2^1\right\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=V\left({\mathcal{G}}^1\left(H_6\right)\right)\setminus \{x_3^1,x_4^1\}.$

• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^1\left(H_6\right)\right)\setminus \{x_1^1,x_5^1,x_6^1,x_7^1\}.$

Since the minimum cardinality of the resolving set is 3, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_6\right)\right)\le \frac{7}{3}.$$

For $m=2$, we have:

• $$\begin{gathered} \mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_7^1,x_1^1\}=\mathcal{R}\{x_3^1,x_1^2\}=\mathcal{R}\{x_5^1,x_6^1\}= \\ \mathcal{R}\{x_1^1,x_5^1\}=\mathcal{R}\{x_3^1,x_1^2\}=\mathcal{R}\{x_3^2,x_4^2\}=\mathcal{R}\{x_5^2,x_4^1\}=\mathcal{R}\{x_1^2,x_5^2\}=V\left({\mathcal{G}}^2\left(H_6\right)\right)\setminus \varnothing \end{gathered}$$

• $\mathcal{R}\{x_4^1,x_5^1\}=\mathcal{R}\{x_1^1,x_3^1\}=V\left({\mathcal{G}}^2\left(H_6\right)\right)\setminus \left\{x_2^1\right\}.$

• $\mathcal{R}\{x_4^2,x_5^2\}=\mathcal{R}\{x_1^2,x_3^2\}=V\left({\mathcal{G}}^2\left(H_6\right)\right)\setminus \left\{x_2^2\right\}.$

• $\mathcal{R}\{x_1^2,x_2^2\}=V\left({\mathcal{G}}^2\left(H_6\right)\right)\setminus \{x_3^2,x_4^2\}.$

• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^2\left(H_6\right)\right)\setminus \{x_1^1,x_5^1,x_6^1,x_7^1\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=V\left({\mathcal{G}}^2\left(H_6\right)\right)\setminus \{x_3^1,x_4^1,x_1^2,x_2^2,x_3^2,x_4^2,x_5^2\}.$

• $\mathcal{R}\{x_2^2,x_3^2\}=V\left({\mathcal{G}}^2\left(H_6\right)\right)\setminus \{x_1^1,x_2^1,x_3^1,x_4^1,x_5^1,x_6^1,x_7^1,x_1^2,x_5^2\}.$

Since the minimum cardinality of the resolving set is 3, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^2\left(H_6\right)\right)\le 4.$$

For $m\ge 3$, we have the following resolving sets:

• $\mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_6^i,x_7^i\}=\mathcal{R}\{x_7^1,x_1^1\}=\mathcal{R}\{x_1^1,x_5^1\}=V\left({\mathcal{G}}^m\left(H_6\right)\right)\setminus \varnothing .$
• $\mathcal{R}\{x_4^1,x_5^1\}=\mathcal{R}\{x_1^1,x_3^1\}V\left({\mathcal{G}}^m\left(H_6\right)\right)\setminus \left\{x_2^i\right\}.$
• $\mathcal{R}\{x_1^i,x_2^i\}=V\left({\mathcal{G}}^m\left(H_6\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_3^1,x_4^1\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup {\left\{x_j^{m-1}\right\}}_{j=1}^5\cup ···\cup {\left\{x_j^2\right\}}_{j=1}^5,\hfill & \mathrm{if}i=1,\hfill \\ \{x_3^2,x_4^2\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup {\left\{x_j^{m-1}\right\}}_{j=1}^5\cup ···\cup {\left\{x_j^3\right\}}_{j=1}^5,\hfill & \mathrm{if}i=2,\hfill \\ \{x_3^m,x_4^m\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_3^{m-1},x_4^{m-1}\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup {\left\{x_j^{m-1}\right\}}_{j=1}^5\cup ···\cup {\left\{x_j^m\right\}}_{j=1}^5,\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_3^3,x_4^3\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup {\left\{x_j^{m-1}\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^4\right\}}_{j=1}^5,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_2^i,x_3^i\}=V\left({\mathcal{G}}^m\left(H_6\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_1^1,x_5^1,x_6^1,x_7^1\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^1,x_2^1,x_3^1,x_4^1,x_5^1,x_6^1,x_7^1,x_1^2,x_5^2\},\hfill & \mathrm{if}i=2,\hfill \\ \{x_1^1,x_2^1,x_3^1,x_4^1,x_5^1,x_6^1,x_7^1,x_1^m,x_5^m\cup \hfill & \mathrm{if}i=m,\hfill \\ {\left\{x_j^{m-1}\right\}}_{j=1}^5\}\cup {\left\{x_j^{m-2}\right\}}_{j=1}^5\cup ···\cup {\left\{x_j^2\right\}}_{j=1}^5,\hfill & \\ A_{j-1};j=(4,5,\cdots ,m),\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

They have the following cardinalities.

• $|\mathcal{R}\{x_3^i,x_4^i\}|=|\{x_5^i,x_6^i\}|=|\{x_6^1,x_7^1\}|=|\{x_7^i,x_1^i\}|=|\{x_1^i,x_5^i\}|=5m+2.$
• $|\mathcal{R}\{x_4^i,x_5^i\}|=|\{x_1^i,x_3^i\}|=5m+1.$
• $|\mathcal{R}\{x_1^i,x_2^i\}|=|V\left({\mathcal{G}}^m\left(H_6\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5,\hfill & \mathrm{if}i=1,\hfill \\ 10,\hfill & \mathrm{if}i=2,\hfill \\ 5m,\hfill & \mathrm{if}i=m,\hfill \\ 5m-5,\hfill & \mathrm{if}i=m-1,\hfill \\ 17,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_2^i,x_3^i\}|=|V\left({\mathcal{G}}^m\left(H_6\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m-2,\hfill & \mathrm{if}i=1,\hfill \\ 5m-7,\hfill & \mathrm{if}i=2,\hfill \\ 3,\hfill & \mathrm{if}i=m,\hfill \\ 8,\hfill & \mathrm{if}i=m-1,\hfill \\ 5n-12-5(i-3),\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

As is the minimal cardinality is 3, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_6\right)\right)\le \frac{5m+2}{3}.$$

□

The heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_7\right)$ and ${\mathcal{G}}^m\left(H_8\right)$ are shown in Figure 6.

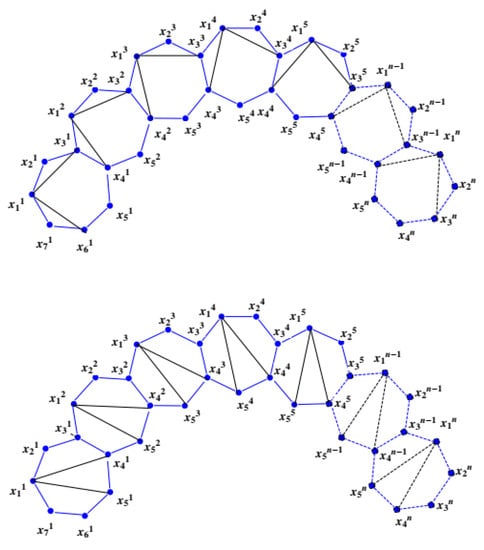
Figure 6. Heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_7\right)$ and ${\mathcal{G}}^m\left(H_8\right)$.

Proposition 7.

Let ${\mathcal{G}}^m\left(H_7\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_7\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{4},\hfill & \mathrm{if}m=1,\hfill \\ 3,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{4},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

The proof is similar to the proof of Proposition 2.

Proposition 8.

Let ${\mathcal{G}}^m\left(H_8\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_8\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{4},\hfill & \mathrm{if}m=1,\hfill \\ \frac{12}{5},\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{5},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

Proof. 

For $m=1$, we have:

• $\mathcal{R}\{x_1^1,x_2^1\}=\mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^1\left(H_8\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_2^1,x_3^1\}=\mathcal{R}\{x_1^1,x_4^1\}=V\left({\mathcal{G}}^1\left(H_8\right)\right)\setminus \{x_5^1,x_6^1\}.$

• $\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_1^1,x_5^1\}=V\left({\mathcal{G}}^1\left(H_8\right)\right)\setminus \{x_3^1,x_4^1\}.$

• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^1\left(H_8\right)\right)\setminus \{x_1^1,x_2^1,x_7^1\}.$

Since the minimum cardinality of the resolving set is 4, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_8\right)\right)\le \frac{7}{4}.$$

For $m=2$, we have:

• $\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_7^1,x_1^1\}=\mathcal{R}\{x_3^1,x_1^2\}=\mathcal{R}\{x_1^2,x_2^2\}=\mathcal{R}\{x_3^2,x_4^2\}=\mathcal{R}\{x_5^2,x_4^1\}=V\left({\mathcal{G}}^2\left(H_8\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_2^1,x_3^1\}=\mathcal{R}\{x_1^1,x_4^1\}=V\left({\mathcal{G}}^2\left(H_8\right)\right)\setminus \{x_5^1,x_6^1\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=\mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_1^2,x_5^2\}=V\left({\mathcal{G}}^2\left(H_8\right)\right)\setminus \{x_3^2,x_4^2\}.$

• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^2\left(H_8\right)\right)\setminus \{x_1^1,x_2^1,x_7^1\}.$

• $\mathcal{R}\{x_4^2,x_5^2\}=V\left({\mathcal{G}}^2\left(H_8\right)\right)\setminus \{x_2^1,x_3^1,x_1^2,x_2^2\}.$

• $\mathcal{R}\{x_2^2,x_3^2\}=\mathcal{R}\{x_1^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_8\right)\right)\setminus \{x_1^1,x_4^1,x_5^1,x_6^1,x_7^1,x_5^2\}.$

• $\mathcal{R}\{x_1^1,x_5^1\}=\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^2\left(H_8\right)\right)\setminus \{x_3^1,x_4^1,x_1^2,x_2^2,x_3^2,x_4^2,x_5^2\}.$

Since the minimum cardinality of the resolving set is 5, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^2\left(H_8\right)\right)\le \frac{12}{5}.$$

For $m\ge 3$, we have the following resolving sets:

• $\mathcal{R}\{x_5^i,x_6^i\}=\mathcal{R}\{x_7^i,x_1^i\}=V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus \varnothing .$
• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus \{x_3^1,x_4^1\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup {\left\{x_j^{m-1}\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^2\right\}}_{j=1}^5.$
• $\mathcal{R}\{x_2^i,x_3^i\}=V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_5^1,x_6^1\},\hfill & \mathrm{if}i=1,\hfill \\ \varnothing ,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_4^i,x_5^i\}=V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_1^1,x_2^1,x_7^1\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_2^{i-1},x_3^{i-1},x_1^i,x_2^i\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_5^1,x_6^1\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^1,x_4^1,x_5^1,x_6^1,x_7^1,x_5^2\},\hfill & \mathrm{if}i=2,\hfill \\ \{x_1^{m-1},x_4^{m-1},x_5^{m-1},x_5^m\cup \hfill & \mathrm{if}i=m,\hfill \\ {\left\{x_j^1\right\}}_{j=1}^7\}\cup {\left\{x_j^{m-2}\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^2\right\}}_{j=1}^5,\hfill & \\ A_{j-1};j=(4,5,\cdots ,m),\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_2^i\}=\mathcal{R}\{x_3^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_3^2,x_4^2\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^3\right\}}_{j=1}^5,\hfill & \mathrm{if}i=1,\hfill \\ \{x_3^3,x_4^3\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^4\right\}}_{j=1}^5,\hfill & \mathrm{if}i=2,\hfill \\ \varnothing ,\hfill & \mathrm{if}i=m,\hfill \\ \{x_3^m,x_4^m\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_3^4,x_4^4\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^5\right\}}_{j=1}^5,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_5^i\}=V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_3^1,x_4^1\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^2\right\}}_{j=1}^5,\hfill & \mathrm{if}i=1,\hfill \\ \{x_3^2,x_4^2\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^3\right\}}_{j=1}^5,\hfill & \mathrm{if}i=2,\hfill \\ \{x_3^m,x_4^m\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_3^{m-1},x_4^{m-1}\}\cup {\left\{x_j^m\right\}}_{j=1}^5,\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_3^3,x_4^3\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^4\right\}}_{j=1}^5,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

They have the following cardinalities.

• $|\mathcal{R}\{x_5^i,x_6^i\}|=|\mathcal{R}\{x_7^i,x_1^i\}|=5m+2.$
• $\left|\mathcal{R}\right\{x_6^1,x_7^1\left\}\right|=5.$
• $|\mathcal{R}\{x_2^i,x_3^i\}|=|V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m+1,\hfill & \mathrm{if}i=1,\hfill \\ 5m+2,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_4^i,x_5^i\}|=|V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m-1,\hfill & \mathrm{if}i=1,\hfill \\ 5m-2,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_4^i\}|=|V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m,\hfill & \mathrm{if}i=1,\hfill \\ 5m-4,\hfill & \mathrm{if}i=2,\hfill \\ 6,\hfill & \mathrm{if}i=m,\hfill \\ 5m-9-5(j-4),\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_2^i\}|=\mathcal{R}\{x_3^i,x_4^i\}|=|V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}10,\hfill & \mathrm{if}i=1,\hfill \\ 15,\hfill & \mathrm{if}i=2,\hfill \\ 5m+2,\hfill & \mathrm{if}i=m,\hfill \\ 5m,\hfill & \mathrm{if}i=m-1,\hfill \\ 20,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_5^i\}|=|V\left({\mathcal{G}}^m\left(H_8\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5,\hfill & \mathrm{if}i=1,\hfill \\ 10,\hfill & \mathrm{if}i=2,\hfill \\ 5m,\hfill & \mathrm{if}i=m,\hfill \\ 5m-5,\hfill & \mathrm{if}i=m-1,\hfill \\ 15,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

As 5 is the minimal cardinality, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_8\right)\right)\le \frac{5m+2}{5}.$$

□

The heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_9\right)$ and ${\mathcal{G}}^m\left(H_{10}\right)$ are shown in Figure 7.

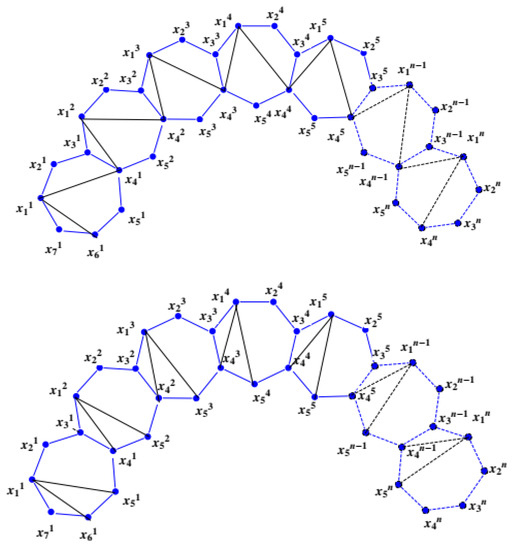
Figure 7. Heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_9\right)$ and ${\mathcal{G}}^m\left(H_{10}\right)$.

Proposition 9.

Let ${\mathcal{G}}^m\left(H_9\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_9\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{3},\hfill & \mathrm{if}m=1,\hfill \\ 3,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{3},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

Proof. 

For $m=1$, we have:

• $\mathcal{R}\{x_1^1,x_2^1\}=\mathcal{R}\{x_2^1,x_3^1\}=\mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_1^1,x_4^1\}=V\left({\mathcal{G}}^1\left(H_9\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_4^1,x_5^1\}=\mathcal{R}\{x_1^1,x_6^1\}=V\left({\mathcal{G}}^1\left(H_9\right)\right)\setminus \left\{x_7^1\right\}.$

• $\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^1\left(H_9\right)\right)\setminus \{x_5^1,x_6^1\}.$

• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^1\left(H_9\right)\right)\setminus \{x_1^1,x_2^1,x_3^1,x_4^1\}.$

Since the minimum cardinality of the resolving set is 3, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_9\right)\right)\le \frac{7}{3}.$$

For $m=2$, we have:

• $\mathcal{R}\{x_2^1,x_3^1\}=\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_1^1,x_4^1\}=\mathcal{R}\{x_1^2,x_2^2\}=\mathcal{R}\{x_2^2,x_3^2\}=\mathcal{R}\{x_3^2,x_4^2\}=\mathcal{R}\{x_5^2,x_4^1\}=\mathcal{R}\{x_1^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_9\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_4^1,x_5^1\}=\mathcal{R}\{x_1^1,x_6^1\}=V\left({\mathcal{G}}^2\left(H_9\right)\right)\setminus \left\{x_7^1\right\}.$

• $\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^2\left(H_9\right)\right)\setminus \{x_5^1,x_6^1\}.$

• $\mathcal{R}\{x_4^2,x_5^2\}=\mathcal{R}\{x_1^2,x_4^1\}=V\left({\mathcal{G}}^2\left(H_9\right)\right)\setminus \{x_2^1,x_3^1\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=\mathcal{R}\{x_3^1,x_4^1\}=V\left({\mathcal{G}}^2\left(H_9\right)\right)\setminus \{x_1^2,x_2^2,x_3^2,x_4^2\}.$

• $\mathcal{R}\{x_3^1,x_1^2\}=V\left({\mathcal{G}}^2\left(H_9\right)\right)\setminus \{x_1^1,x_4^1,x_5^1,x_6^1,x_7^1,x_5^2\}.$

• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^2\left(H_9\right)\right)\setminus \{x_1^1,x_2^1,x_3^1,x_4^1,x_1^2,x_2^2,x_3^2,x_4^2,x_5^2\}.$

Since the minimum cardinality of the resolving set is 3, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^2\left(H_9\right)\right)\le 3.$$

For $m\ge 3$, we have the following resolving sets:

• $\mathcal{R}\{x_2^i,x_3^i\}=\mathcal{R}\{x_5^i,x_6^i\}=\mathcal{R}\{x_1^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_9\right)\right)\setminus \varnothing .$
• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^m\left(H_9\right)\right)\setminus \{x_1^1,x_2^1,x_3^1,x_4^1\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^2\right\}}_{j=1}^5.$
• $\mathcal{R}\{x_4^i,x_5^i\}=\mathcal{R}\{x_1^i,x_6^1\}=V\left({\mathcal{G}}^m\left(H_9\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\left\{x_7^1\right\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_2^{i-1},x_3^{i-1}\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_7^i,x_1^i\}=V\left({\mathcal{G}}^m\left(H_9\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_5^1,x_6^1\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^1,x_4^1,x_5^1,x_6^1,x_7^1,x_5^2\},\hfill & \mathrm{if}i=2,\hfill \\ \{x_1^{m-1},x_4^{m-1},x_5^{m-1},x_5^m\cup \hfill & \mathrm{if}i=m,\hfill \\ {\left\{x_j^1\right\}}_{j=1}^7\}\cup {\left\{x_j^{m-2}\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^2\right\}}_{j=1}^5,\hfill & \\ A_{j-1};j=(4,5,\cdots ,m),\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_2^i\}=\mathcal{R}\{x_3^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_9\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_1^2,x_2^2,x_3^2,x_4^2\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^3\right\}}_{j=1}^5,\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^3,x_2^3,x_3^3,x_4^3\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^4\right\}}_{j=1}^5,\hfill & \mathrm{if}i=2,\hfill \\ \varnothing ,\hfill & \mathrm{if}i=m,\hfill \\ \{x_1^m,x_2^m,x_3^m,x_4^m\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_1^4,x_2^4,x_3^4,x_4^4\}\cup {\left\{x_j^m\right\}}_{j=1}^5\cup \cdots \cup {\left\{x_j^5\right\}}_{j=1}^5,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

They have the following cardinalities.

• $|\mathcal{R}\{x_2^i,x_3^i\}|=|\mathcal{R}\{x_5^i,x_6^i\}|=|\mathcal{R}\{x_1^i,x_4^i\}|=5m+2.$
• $\left|\mathcal{R}\right\{x_6^1,x_7^1\left\}\right|=3.$
• $|\mathcal{R}\{x_4^i,x_5^i\}|=|\mathcal{R}\{x_1^i,x_6^i\}|=|V\left({\mathcal{G}}^m\left(H_9\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m+1,\hfill & \mathrm{if}i=1,\hfill \\ 5m,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_7^i,x_1^i\}|=|V\left({\mathcal{G}}^m\left(H_9\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m,\hfill & \mathrm{if}i=1,\hfill \\ 5m-4,\hfill & \mathrm{if}i=2,\hfill \\ 6,\hfill & \mathrm{if}i=m,\hfill \\ 5m-9-5(j-4),\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_2^i\}|=|\mathcal{R}\{x_3^i,x_4^i\}|=|V\left({\mathcal{G}}^m\left(H_9\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}8,\hfill & \mathrm{if}i=1,\hfill \\ 11,\hfill & \mathrm{if}i=2,\hfill \\ 5m+2,\hfill & \mathrm{if}i=m,\hfill \\ 5m-2,\hfill & \mathrm{if}i=m-1,\hfill \\ 18,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

As 3 is the minimal cardinality, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_9\right)\right)\le \frac{5m+2}{3}.$$

□

Proposition 10.

Let ${\mathcal{G}}^m\left(H_{10}\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_{10}\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{4},\hfill & \mathrm{if}m=1,\hfill \\ 3,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{4},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

The proof is similar to the proof of Proposition 2.

4. Upper-Bound Sequences of the LFMD of HRS Planar Graphs with Three and Four Cords

In this section, we will find the LFMD of HRS planar graphs with three and four cords. The heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_9\right)$ and ${\mathcal{G}}^m\left(H_{10}\right)$ are shown in Figure 8.

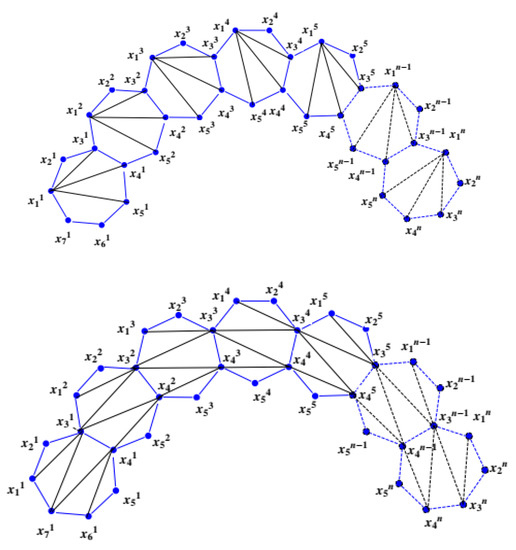
Figure 8. Heptagonal symmetrical planar graphs ${\mathcal{G}}^m\left(H_{11}\right)$ and ${\mathcal{G}}^m\left(H_{12}\right)$.

Proposition 11.

Let ${\mathcal{G}}^m\left(H_{11}\right)$ be a heptagonal rotationally symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_{11}\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{3},\hfill & \mathrm{if}m=1,\hfill \\ 4,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{3},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

Proof. 

For $m=1$, we have:

• $\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_7^1,x_1^1\}=V\left({\mathcal{G}}^1\left(H_{11}\right)\right)\setminus \varnothing .$

• $\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_1^1,x_5^1\}=V\left({\mathcal{G}}^1\left(H_{11}\right)\right)\setminus \left\{x_4^1\right\}.$

• $\mathcal{R}\{x_1^1,x_3^1\}=V\left({\mathcal{G}}^1\left(H_{11}\right)\right)\setminus \{x_2^1,x_4^1\}.$

• $\mathcal{R}\{x_3^1,x_4^1\}=V\left({\mathcal{G}}^1\left(H_{11}\right)\right)\setminus \{x_1^1,x_7^1\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=\mathcal{R}\{x_1^1,x_4^1\}=V\left({\mathcal{G}}^1\left(H_{11}\right)\right)\setminus \{x_3^1,x_5^1,x_6^1\}.$

• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^1\left(H_{11}\right)\right)\setminus \{x_1^1,x_2^1,x_7^1\}.$

• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^1\left(H_{11}\right)\right)\setminus \{x_1^1,x_5^1,x_6^1,x_7^1\}.$

Since the minimum cardinality of the resolving set is 3, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^1\left(H_{11}\right)\right)\le \frac{7}{3}.$$

For $m=2$, we have:

• $\mathcal{R}\{x_5^1,x_6^1\}=\mathcal{R}\{x_7^1,x_1^1\}=\mathcal{R}\{x_3^1,x_1^2\}=\mathcal{R}\{x_5^2,x_4^1\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \varnothing$

• $\mathcal{R}\{x_1^2,x_2^2\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \left\{x_3^2\right\}.$

• $\mathcal{R}\{x_1^2,x_3^2\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_2^2,x_3^2\}.$

• $\mathcal{R}\{x_3^1,x_4^1\}=\mathcal{R}\{x_1^2,x_5^2\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_1^1,x_7^1,x_4^2\}.$

• $\mathcal{R}\{x_6^1,x_7^1\}=\mathcal{R}\{x_1^1,x_5^1\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_4^1,x_4^2,x_5^2\}.$

• $\mathcal{R}\{x_4^1,x_5^1\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_1^1,x_2^1,x_7^1\}.$

• $\mathcal{R}\{x_1^1,x_3^1\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_2^1,x_4^1,x_5^2\}.$

• $\mathcal{R}\{x_2^1,x_3^1\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_1^1,x_5^1,x_6^1,x_7^1\}.$

• $\mathcal{R}\{x_4^2,x_5^2\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_2^1,x_3^1,x_1^2,x_2^2\}.$

• $\mathcal{R}\{x_1^1,x_2^1\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_3^1,x_1^2,x_2^2,x_3^2,x_4^2\}.$

• $\mathcal{R}\{x_3^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_1^1,x_2^1,x_3^1,x_7^1,x_1^2\}.$

• $\mathcal{R}\{x_1^2,x_4^2\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_4^1,x_5^2,x_6^2,x_3^2,x_5^2\}.$

• $\mathcal{R}\{x_1^1,x_4^1\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_3^1,x_5^1,x_6^1,x_1^2,x_2^2,x_3^2\}.$

• $\mathcal{R}\{x_2^2,x_3^2\}=V\left({\mathcal{G}}^2\left(H_{11}\right)\right)\setminus \{x_1^1,x_2^1,x_3^1,x_4^1,x_5^1,x_6^1,x_7^1,x_1^2,x_5^2\}.$

Since the minimum cardinality of the resolving set is 3, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^2\left(H_{11}\right)\right)\le 4.$$

For $m\ge 3$, we have the following resolving sets:

• $\mathcal{R}\{x_5^i,x_6^i\}=\mathcal{R}\{x_7^i,x_1^i\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus \varnothing .$
• $\mathcal{R}\{x_1^i,x_3^i\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_2^i,x_4^i,x_5^{i+1}\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_2^2,x_3^2,x_5^3\},\hfill & \mathrm{if}i=2,\hfill \\ \{x_2^i,x_4^i\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_2^{i-1},x_4^{i-1},x_5^i\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_2^i,x_3^i\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_1^1,x_5^1,x_6^1{x}_7^1\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_1^2,x_5^2,\cup {\left\{x_i^1\right\}}_{i=1}^7\},\hfill & \mathrm{if}i=2.\hfill \\ \{x_1^m,x_5^m,\cup {\left\{x_i^1\right\}}_{i=1}^7\}\cup {\left\{x_i^2\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_i^{m-1}\right\}}_{i=1}^5,\hfill & \mathrm{if}i=m\ge 3.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_4^i,x_5^i\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_1^1,x_2^1,x_7^1\},\hfill & \mathrm{if}i=1,\hfill \\ \{x_2^{i-1},x_3^{i-1},x_1^i,x_2^i\},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_6^1,x_7^1\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus \left\{x_4^1\right\}\cup {\left\{x_j^m\right\}}_{i=4}^5\cup \cdots \cup {\left\{x_j^2\right\}}_{i=4}^5.$
• $\mathcal{R}\{x_1^i,x_2^i\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_3^1,x_1^2,x_2^2,x_3^2,x_4^2\cup {\left\{x_j^{m-2}\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_j^4\right\}}_{i=1}^5\},\hfill & \mathrm{if}i=1,\hfill \\ \left\{x_3^m\right\},\hfill & \mathrm{if}i=m,\hfill \\ \{x_3^i,x_1^{i+1},x_2^{i+1},x_3^{i+1},x_4^{i+1}\},\hfill & \mathrm{if}i=m-1,\hfill \\ \{x_3^i,x_1^{i+1},x_2^{i+1},x_3^{i+1},x_4^{i+1}\}\cup {\left\{x_j^m\right\}}_{i=1}^5\cup \cdots \cup {\left\{x_j^{i+2}\right\}}_{i=1}^5,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_5^i\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_4^1,x_4^2,x_5^2,x_4^3,x_5^3\}\cup {\left\{x_j^m\right\}}_{i=4}^5\cup \cdots \cup \hfill & \mathrm{if}i=1,\hfill \\ {\left\{x_j^4\right\}}_{i=4}^5,\hfill & \\ \{x_1^1,x_7^1,x_4^2,x_4^3,x_5^3\}\cup {\left\{x_j^m\right\}}_{i=4}^5\cup {\left\{x_j^{m-1}\right\}}_{i=4}^5\hfill & \mathrm{if}i=2,\hfill \\ \cup \cdots \cup {\left\{x_j^4\right\}}_{i=4}^5,\hfill & \\ \{x_1^1,x_2^1,x_3^2,x_7^3,x_4^3,x_1^2\}\cup {\left\{x_j^m\right\}}_{i=4}^5\cup {\left\{x_j^{m-1}\right\}}_{i=4}^5\hfill & \mathrm{if}i=3,\hfill \\ \cup \cdots \cup {\left\{x_j^4\right\}}_{i=4}^5,\hfill & \\ \{x_1^1,x_2^1,x_3^1,x_7^1,x_1^2,x_4^3\cup {\left\{x_j^m\right\}}_{i=4}^5\}\cup {\left\{x_j^{m-1}\right\}}_{i=4}^5\hfill & \mathrm{if}i=m,\hfill \\ \cup \cdots \cup {\left\{x_j^4\right\}}_{i=4}^5,\hfill & \\ \{x_1^1,x_2^1,x_3^1,x_7^1,x_1^2,2^2,x_3^2,x_1^3,x_4^3\}\cup \{x_4^{m-1},x_5^{m-1}\}\hfill & \mathrm{otherwise}.\hfill \\ \cup \cdots \cup {\left\{x_j^{i+2}\right\}}_{i=1}^5,\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_3^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_1^1,x_7^1,x_4^2,x_4^3,x_5^3\}\cup {\left\{x_j^m\right\}}_{i=4}^5\cup \hfill & \mathrm{if}i=1,\hfill \\ {\left\{x_j^{m-1}\right\}}_{i=4}^5\cup \cdots \cup {\left\{x_j^4\right\}}_{i=4}^5,\hfill & \\ \{x_1^1,x_2^1,x_3^1,x_7^1,x_1^2,x_4^3\}\cup {\left\{x_j^m\right\}}_{i=4}^5\cup \hfill & \mathrm{if}i=2,\hfill \\ {\left\{x_j^{m-1}\right\}}_{i=4}^5\cup \cdots \cup {\left\{x_j^4\right\}}_{i=4}^5,\hfill & \\ \{x_1^1,x_2^1,x_3^1,x_1^2,x_7^1,x_2^2,x_3^2\}\cup \left\{x_1^i\right\}\cup \hfill & \mathrm{if}i=m,\hfill \\ {\left\{x_j^{m-1}\right\}}_{i=1}^3\cup \cdots \cup {\left\{x_j^3\right\}}_{i=1}^5,\hfill & \\ \{x_1^1,x_2^1,x_3^1,x_7^1,x_4^m,x_1^{m-1}\}\cup {\left\{x_j^{m-2}\right\}}_{i=1}^3\cup \hfill & \mathrm{if}i=m-1,\hfill \\ {\left\{x_j^{m-3}\right\}}_{j=1}^3\cup \cdots \cup {\left\{x_j^2\right\}}_{j=1}^3,\hfill & \\ \{x_1^1,x_2^1,x_3^1,x_7^1,x_1^2,2^2,x_3^2,x_1^3,x_4^4\}\cup \hfill & \mathrm{otherwise}.\hfill \\ \{x_4^m,x_5^m\}\cup \cdots \cup \{x_4^5,x_5^5\},\hfill \end{array}\hfill \end{array}\right.$
• $\mathcal{R}\{x_1^i,x_4^i\}=V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i$.
  Here,
  $A_i=\left\{\begin{array}{c}\begin{array}{cc}\{x_3^1,x_5^1,x_6^1,x_1^2,x_2^2,x_3^2\}\cup {\left\{x_j^3\right\}}_{i=1}^3\cup {\left\{x_j^m\right\}}_{i=1}^3\cup \hfill & \mathrm{if}i=1,\hfill \\ {\left\{x_j^{m-1}\right\}}_{i=1}^3\cup \cdots \cup {\left\{x_j^4\right\}}_{i=1}^3,\hfill & \\ \{x_4^1,x_5^1,x_6^1,x_3^2,x_5^2\}\cup {\left\{x_j^m\right\}}_{i=1}^3\cup {\left\{x_j^{m-1}\right\}}_{i=1}^3\cup \cdots \cup {\left\{x_j^3\right\}}_{i=1}^3,\hfill & \mathrm{if}i=2,\hfill \\ \{x_4^1,x_5^1,x_6^1,x_4^2,x_5^2,x_3^m,x_5^m\}\cup \{x_4^{m-1},x_5^{m-1}\}\cup \hfill & \mathrm{if}i=m,\hfill \\ \{x_4^{m-2},5^{m-2}\}\cup \cdots \cup \{x_4^2,x_5^2\},\hfill & \\ \{x_4^1,x_5^1,x_6^1\cup {\left\{x_j^m\right\}}_{i=1}^3\}\cup \{x_3^{m-1},x_5^{m-1}\}\cup \hfill & \mathrm{if}i=m-1,\hfill \\ \{x_3^{m-2},x_5^{m-2}\}\cup \cdots \cup \{x_4^2,x_5^2\},\hfill & \\ \{x_4^1,x_5^1,x_6^1,x_4^2,x_5^2,x_4^3,x_5^3\}\cup {\left\{x_j^m\right\}}_{i=1}^3\cup \hfill & \mathrm{otherwise}.\hfill \\ {\left\{x_j^{m-1}\right\}}_{i=1}^3\cup \cdots \cup \{x_j^4,x_1^3\},\hfill \end{array}\hfill \end{array}\right.$

They have the following cardinalities.

• $|\mathcal{R}\{x_5^i,x_6^i\}|=|\mathcal{R}\{x_7^i,x_1^i\}|=5m+2.$
• $\left|\mathcal{R}\right\{x_6^1,x_7^1\left\}\right|=3m+1.$
• $|\mathcal{R}\{x_4^i,x_5^i\}|=|V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m-1,\hfill & \mathrm{if}i=1,\hfill \\ 5m-2,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_2^i,x_3^i\}|=|V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m+1,\hfill & \mathrm{if}i=1,\hfill \\ 5m-7,\hfill & \mathrm{if}i=2,\hfill \\ 3,\hfill & \mathrm{if}i\ge 3.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_3^i\}|=|V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}5m-1,\hfill & \mathrm{if}i=1,\hfill \\ 5m-1,\hfill & \mathrm{if}i=2,\hfill \\ 5m,\hfill & \mathrm{if}i=m,\hfill \\ 5m-1,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_4^i\}|=|V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}2m+2,\hfill & \mathrm{if}i=1,\hfill \\ 3m-1,\hfill & \mathrm{if}i=2,\hfill \\ 3m,\hfill & \mathrm{if}i=m,\hfill \\ 3m-1,\hfill & \mathrm{if}i=m-1,\hfill \\ 2m+4,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_5^i\}|=|V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}3m+3,\hfill & \mathrm{if}i=1,\hfill \\ 3m+3,\hfill & \mathrm{if}i=2,\hfill \\ 3m,\hfill & \mathrm{if}i=3,\hfill \\ 3m,\hfill & \mathrm{if}i=4,\hfill \\ 3m+1,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_1^i,x_2^i\}|=|V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}22,\hfill & \mathrm{if}i=1,\hfill \\ 5m+1,\hfill & \mathrm{if}i=m,\hfill \\ 5m-3,\hfill & \mathrm{if}i=m-1,\hfill \\ 5m+2,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$
• $|\mathcal{R}\{x_3^i,x_4^i\}|=|V\left({\mathcal{G}}^m\left(H_{11}\right)\right)\setminus A_i|=$$\left\{\begin{array}{c}\begin{array}{cc}3m+3,\hfill & \mathrm{if}i=1,\hfill \\ 2m+3,\hfill & \mathrm{if}i=2,\hfill \\ 2m+5,\hfill & \mathrm{if}i=m,\hfill \\ 3m+2,\hfill & \mathrm{if}i=m-1,\hfill \\ 3m+1,\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$

As 3 is the minimal cardinality, by relation (2), we have

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_{11}\right)\right)\le \frac{5m+2}{3}.$$

□

Proposition 12.

Let ${\mathcal{G}}^m\left(H_{12}\right)$ be a heptagonal symmetrical planar graph. Then,

$${\mathrm{ldim}}_{\mathrm{f}}\left({\mathcal{G}}^m\left(H_{12}\right)\right)\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{4},\hfill & \mathrm{if}m=1,\hfill \\ 3,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{4},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$$

5. Comparison of the Investigated Upper-Bound Sequences for the Local Fractional Metric Dimension

In this section, we will discuss the asymptotic behaviors and numerical and graphical comparisons between the investigated upper-bound sequences for the local fractional metric dimension. We found the sequences of the local fractional metric dimensions of heptagonal rotationally symmetrical planar graphs. In Table 1 and Table 2, the asymptotic behaviors and the numerical comparison are, respectively, discussed. The graphical behavior of the upper-bound sequences for the local fractional metric dimensions of the heptagonal rationally symmetrical planar graphs is shown in Figure 9.

Table 1. Asymptotic behavior of the local fractional metric dimension of the graph $({\mathcal{G}}^m\left(H_i\right)$, $1\le i\le 12$) arising from a planar chorded cycle.

G	${\mathbf{ldim}}_{\mathbf{f}}\left({\mathcal{G}}^{\mathit{m}}\left(\mathit{G}\right)\right)$	Asymptotic Behavior
${\mathcal{G}}^m\left(H_1\right)$	$\le \left\{\begin{array}{c}\begin{array}{cc}1,\hfill & \mathrm{if}m=1,\hfill \\ \frac{4}{3},\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{11},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$	Unbounded
${\mathcal{G}}^m\left(H_2\right)$=${\mathcal{G}}^m\left(H_5\right)$=
${\mathcal{G}}^m\left(H_7\right)$= ${\mathcal{G}}^m\left(H_{10}\right)$=${\mathcal{G}}^m\left(H_{12}\right)$	$\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{4},\hfill & \mathrm{if}m=1,\hfill \\ 3,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{4},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$	Unbounded
${\mathcal{G}}^m\left(H_3\right)$	$\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{5},\hfill & \mathrm{if}m=1,\hfill \\ \frac{12}{5},\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{5},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$	Unbounded
${\mathcal{G}}^m\left(H_4\right)$	$\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{5},\hfill & \mathrm{if}m=1,\hfill \\ \frac{3}{2},\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{6},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$	Unbounded
${\mathcal{G}}^m\left(H_6\right)$=${\mathcal{G}}^m\left(H_{11}\right)$	$\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{3},\hfill & \mathrm{if}m=1,\hfill \\ 4,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{3}\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$	Unbounded
${\mathcal{G}}^m\left(H_8\right)$	$\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{4},\hfill & \mathrm{if}m=1,\hfill \\ \frac{12}{5},\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{5},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$	Unbounded
${\mathcal{G}}^m\left(H_9\right)$	$\le \left\{\begin{array}{c}\begin{array}{cc}\frac{7}{3},\hfill & \mathrm{if}m=1,\hfill \\ 3,\hfill & \mathrm{if}m=2,\hfill \\ \frac{5m+2}{3},\hfill & \mathrm{otherwise}.\hfill \end{array}\hfill \end{array}\right.$	Unbounded

Table 2. Numerical comparison of the upper-bound sequences for the local fractional metric dimensions of heptagonal rationally symmetrical planar graphs.

m	(5 m + 2)/11	(5 m + 2)/4	(5 m + 2)/5	(5 m + 2)/6	(5 m + 2)/3
3	1.54545	4.25	3.4	2.83333	5.66667
4	2.0	5.5	4.4	3.66667	7.33333
5	2.45455	6.75	5.4	4.5	9.0
6	2.90909	8.0	6.4	5.33333	10.6667
7	3.36364	9.25	7.4	6.16667	12.3333
8	3.81818	10.5	8.4	7.0	14.0
9	4.27273	11.75	9.4	7.83333	15.6667
10	4.72727	13.0	10.4	8.66667	17.3333
11	5.18182	14.25	11.4	9.5	19.0
12	5.63636	15.5	12.4	10.3333	20.6667
13	6.09091	16.75	13.4	11.1667	22.3333
14	6.54545	18.0	14.4	12.0	24.0
15	7.0	19.25	15.4	12.8333	25.6667

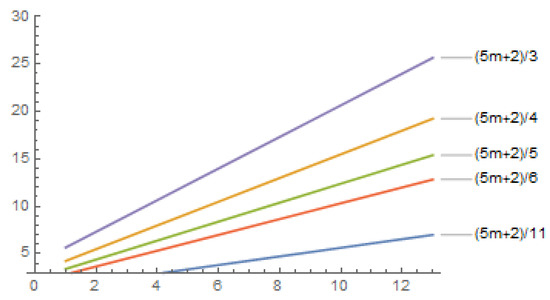
Figure 9. Graphical behavior of the upper-bound sequences for the local fractional metric dimensions of heptagonal rationally symmetrical planar graphs.

6. Conclusions

Finding the metric dimension of a given graph for a specific number is an NP-hard problem. The metric dimension has many applications in several fields, such as computer science, minimal distance problems, and chemical graph theory. In this regard, we proposed a new rotationally symmetrical heptagonal planar network and then found its upper-bound sequences for the local fractional metric dimensions. Further, in future work, anyone can solve some of the following open problems:

• The generalization of the proposed work to an n-sided polygon with up to k cords.
• Finding the upper bounds for the local fractional metric dimensions of rotationally symmetrical n-sided polygon planar networks and then finding their asymptotic behaviors.