You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Symmetry
Download PDF
  • Feature Paper
  • Article
  • Open Access

5 February 2023

New High-Pressure Structures of Transition Metal Carbonates with O3C–CO3 Orthooxalate Groups

,
,
and
1
Sobolev Institute of Geology and Mineralogy, Siberian Branch of Russian Academy of Sciences, 630090 Novosibirsk, Russia
2
Department of Geology and Geophysics, Novosibirsk State University, 630090 Novosibirsk, Russia
3
Vereshchagin Institute for High Pressure Physics, Russian Academy of Sciences, Troitsk, 108840 Moscow, Russia
4
Fersman Mineralogical Museum, Russian Academy of Sciences, 119071 Moscow, Russia
Symmetry2023, 15(2), 421;https://doi.org/10.3390/sym15020421
This article belongs to the Section Chemistry: Symmetry/Asymmetry
Version Notes
Order Reprints

Abstract

Based on the density functional theory and crystal structure prediction approaches, we found a novel high-pressure structure of Fe 2 CO 4 - P 1 ¯ . It is characterized by the presence of ethane-like O 3 C–CO 3 groups or so-called orthooxalate groups. The formation of such O 3 C–CO 3 groups has been proposed earlier in melts and aqueous carbonate solutions, but no such examples were known in inorganic crystalline materials. We found that this structure is dynamically and thermally stable at pressures of 50 GPa. Similar structures were also predicted to be dynamically stable for Mn 2 CO 4 , Ni 2 CO 4 , and Co 2 CO 4 . In addition, FeCO 3 was found to transform into a similar structure with O 3 C–CO 3 orthooxalate groups at a pressure above 275 GPa. Additionally, for the first time, we describe the self-diffusion of metal atoms in carbonates at high pressure and at high temperatures. The prediction of novel carbonate structures extends the crystal chemistry of inorganic carbonates beyond the established ones with [CO 3 ] triangles, [C 2 O 5 ] pyro-groups, and [CO 4 ] tetrahedra.

1. Introduction

Currently, theoretical methods for crystal structure predictions have proven to be an effective approach for discovering new compounds and their structures that precede real experiments. Recently, using these methods, it was shown that in the MO–CO 2 systems (where M = Mg, Ca, Sr, Ba, and Pb), in addition to the well-known MCO 3 carbonates, M 2 CO 4 , M 3 CO 5 , and MC 2 O 5 compounds became thermodynamically stable at high pressures [1,2,3,4,5]. Subsequently, the formation of the Mg 2 CO 4 [6], Ca 2 CO 4 [7], CaC 2 O 5 [8], Sr 2 CO 4 [9], Sr 3 CO 5 [10], SrC 2 O 5 [11], and PbC 2 O 5 [12] phases was experimentally confirmed.
For alkaline earth metals, the thermodynamic stabilization pressures of M 2 CO 4 structures (M = Mg, Ca, Sr, and Ba) were inversely proportional to the cation size, decreasing from 50–75 GPa for Mg 2 + [3,6] to 5 GPa for Ba 2 + [4]. Ca 2 CO 4 , Sr 2 CO 4 , and Ba 2 CO 4 have the same structure P n m a , while Mg 2 CO 4 has slightly different structure ( P 2 1 / c ) [6]. The low-pressure thermodynamic stability limits for the crystal structures of M 3 CO 5 (M = Ca, Sr, and Ba) compounds vary in the range of 11–15 GPa, and these compounds are stable in the I 4 / m c m structure [4].
The structures of M 2 CO 4 and M 3 CO 5 are characterized by the presence of orthoanion groups of [CO 4 ] tetrahedra and form a class of orthocarbonates and oxy-orthocarbonates. The s p 3 -hybridized carbon atoms in the structures of orthocarbonates are a key difference from the so-called “traditional” MCO 3 carbonates, whose structures contain s p 2 -hybridized carbon atoms only in triangular coordination at a pressure below 50 GPa. The structures of the MC 2 O 5 composition are characterized by the most diverse crystallochemistry, including [C 2 O 5 ] pyro-groups (formed by two trigonal [CO 3 ] groups), complex tetrahedra, layers, and frameworks which consist of corner-shared [CO 4 ] tetrahedra [1,8,13]. In addition, at pressures above 70 GPa, traditional carbonates MgCO 3 and CaCO 3 are known to transform into structures that consist of corner-shared [CO 4 ] tetrahedra, forming chains or rings [14,15,16,17].
For iron, in addition to the traditional carbonate FeCO 3 , Fe 4 C 3 O 12 and Fe 4 C 4 O 13 are also known [18]. Both carbonates contain tetrahedrally coordinated carbon units and are formed above ∼70 GPa [18]. However, these two carbonates contain iron in both 2+ and 3+ oxidation states and are beyond the FeO–CO 2 system. Hence, to date, FeCO 3 is the only known intermediate compound in this system. It should also be noted that, unlike MgCO 3 and CaCO 3 , iron carbonate does not undergo polymorphic phase transitions up to 110 GPa [18,19,20].
The aim of the present work is to reveal the possible stable structure of Fe 2 CO 4 and FeCO 3 using crystal structure prediction methods. The obtained results could extend the known crystal chemistry of inorganic carbonates and motivate future experimental studies of the FeO–CO 2 system, which is complicated by the presence of iron in two oxidation states.

2. Computational Methods

Crystal structure prediction has been performed using evolutionary algorithms implemented in the USPEX package [21,22,23,24] and random structure searching implemented in the AIRSS package [25,26] at 25, 50, 75, and 100 GPa for fixed-composition Fe 2 CO 4 and at 100, 200, and 300 GPa for FeCO 3 for 1–4 formula units per unit cell.
The first generation in the USPEX calculations consisted of 65 structures created using a random symmetry operator. Furthermore, to obtain the next generation, 60% of the structures with the lowest enthalpy from the previous generation were selected. In all subsequent generations, structures were produced by heredity (35%), atomic mutation (20%), lattice permutation (10%), and random generator (35%) operators. On average, 32–36 generations were produced and relaxed at each pressure.
All calculations were performed within the VASP 5.4.4 package [27,28] based on density functional theory (DFT). The exchange-correlation effects were calculated via generalized gradient approximation (GGA) in Perdew–Burke–Ernzerhof (PBE) parameterization [29]. To describe core-valence interactions, we used the projector augmented wave basis set with energy cutoff of plane waves equal to 430 eV. The first Brillouin zone was sampled according to the Monkhorst–Pack scheme with a k-point mesh of 0.5 Å − 1 and Gaussian smearing with a parameter σ = 0.1 eV. The most promising predicted structures were relaxed with higher accuracy as follows: the cutoff energy was 600 eV, k-point sampling grid of spacing was 0.25 Å − 1 , and σ = 0.05 eV. Pseudopotentials with 3 d 7 4 s 1 (Fe), 2 s 2 2 p 2 (C), and 2 s 2 2 p 4 (O) electronic configurations were used.
It is well-known that standard DFT tends to over-delocalize the electronic states for transition metals, which prevents them from describing the systems with strongly localized d-electrons appropriately. In order to describe the properties of considered structures more accurately, Dudarev’s DFT+U method was used [30]. In our study, U was set to 2 eV, since in [31], it was found to give the best agreement with the experimental values for the spin transition pressure of iron in FeCO 3 .
Calculations of the phonon spectra were performed using the PHONOPY program [32]. The real space force constants were calculated using supercell and finite displacement approaches, with 2 × 2 × 2 supercells for the considered structures. In this case, high-quality settings were used: the cutoff energy was 800 eV, k-point sampling grid of spacing was 0.2 Å − 1 , and σ = 0.05 eV.
To examine the thermal stability of Fe 2 CO 4 , ab initio molecular dynamic (AIMD) simulations based on DFT were performed using a supercell with 255 atoms at 300, 1000, and 2000 K. The time step was set to 1 fs. In the simulations at 300 and 1000 K, the total simulation time was 10 ps, and in the simulations at 2000 K, it was 20 ps. The NPT ensemble (where N is the number of particles, P is pressure, and T is the temperature) were used. During the simulation, the frequency of the temperature oscillations was controlled by the Langevin thermostat.
Images of the structures were produced using VESTA software [33]. The MD simulation animation was made in OVITO software [34].

3. Results

Experiments performed for Fe 2 CO 4 crystal structure predictions have revealed the known structures of Ca 2 CO 4 - P n m a [2] and Mg 2 CO 4 - P n m a (Olivine type) [3]. However, these structures are not the most favorable among the predicted ones. According to the results obtained, the structure with P 1 ¯ symmetry had the lowest enthalpy in the entire studied pressure range of 10–100 GPa (Figure 1a). The predicted Fe 2 CO 4 - P 1 ¯ was dynamically stable, as evidenced by the absence of imaginary frequencies in the calculated phonon spectrum (Figure 1b).
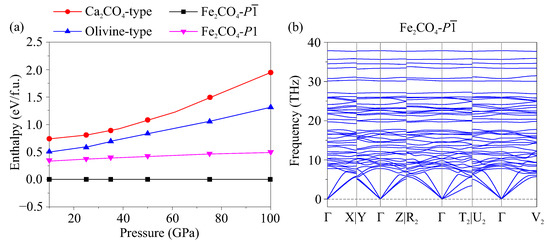
Figure 1. (a) Relative enthalpy-pressure dependencies of Fe 2 CO 4 modifications. (b) Phonon dispersion curves of Fe 2 CO 4 - P 1 ¯ at 50 GPa.
In DFT+U calculations, the total energy of a phase strongly depends on the Hubbard correction U. Since U must vary for each compound, it makes no sense to compare the total energies obtained from the calculations with the same values of U, and it is incorrect to compare the energies obtained with different U values. Consequently, estimation of the pressure at which Fe 2 CO 4 - P 1 ¯ became stable relative to decomposition into carbonate and oxide is currently difficult. For instance, we estimated the stability of Fe 2 CO 4 - P 1 ¯ relative to FeO in the wustite structure and FeCO 3 in the siderite structure without consideration of Hubbard correction (U = 0) and with U = 2 eV (Figure 2), respectively. In the first case, Fe 2 CO 4 - P 1 ¯ stabilizes with respect to a mechanical mixture of FeO + FeCO 3 above 40 GPa. In the second case, it stabilizes at sufficiently higher pressures above 100 GPa. Thus, the stability of Fe 2 CO 4 - P 1 ¯ relative to FeO + FeCO 3 remains an open question.
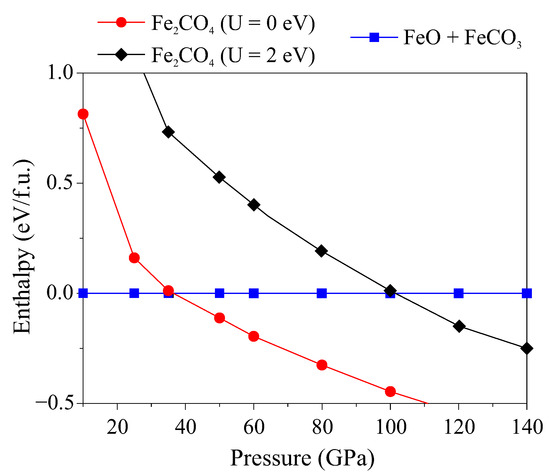
Figure 2. The enthalpy-pressure dependency of Fe 2 CO 4 - P 1 ¯ relative to the mechanical mixture of FeO + FeCO 3 .
The structural data of the predicted Fe 2 CO 4 - P 1 ¯ are given in Table 1. The structure was characterized by the presence of ethane-like [C 2 O 6 ] groups, in which two carbon atoms were bonded together and, in addition, each of them bonded to three more oxygen atoms (Figure S1). By analogy with orthocarbonates, we will call such a group an orthooxalate group and label it as O 3 C–CO 3 . The found Fe 2 CO 4 - P 1 ¯ is the first example of inorganic compounds with the O 3 C–CO 3 group. However, there exists one example of an organic compound with an orthooxalate group, namely a unique orthooxalate: 2,5,7,10,11,14-hexaoxa[4.4.4]propellane [35].
Table 1. Structural data of predicted Fe 2 CO 4 and FeCO 3 modifications with the lowest enthalpy.
At 50 GPa, the C–C distances between two neighboring carbon atoms were equal to 1.53 Å, and the C–O distances varied in the range of 1.35–1.40 Å. These distances were almost equal to the bond lengths observed for the mentioned organic orthooxalate [35], in which the C–C bond length was 1.55 Å and the C–C bond was 1.395 Å. As expected, in the crystal structure of siderite FeCO 3 - R 3 ¯ c , the C–O distances were shorter, and they were equal to 1.27 Å at 50 GPa.
Similar to siderite, the crystal structure of Fe 2 CO 4 - P 1 ¯ can be described as the filling of octahedral voids by cations in the close packing of anions. The array of oxygen atoms in it corresponds to a slightly distorted hcp structure. Half of the octahedral voids are filled with Fe atoms, with 1/8 of them being filled with covalently bonded carbon atoms which are part of orthooxalate groups. In the structure, slabs A and B of the partially filled close-packed octahedra of oxygen atoms can be distinguished (Figure 3a). In slab A, half of the octahedra were filled with Fe atoms. The FeO 6 octahedra were connected in chains as shown in Figure 3b. In slab B, half of the octahedra were filled with Fe atoms, and one-fourth of the octahedra were filled with C–C groups (Figure 3c). Slabs A’ and B’ were similar to A and B in atomic arrangement but shifted in one octahedron, which could also be distinguished.
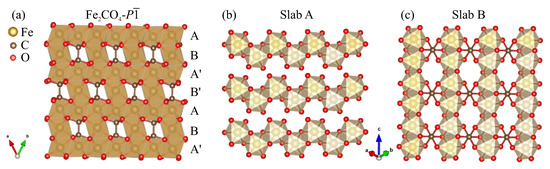
Figure 3. Crystal structure of predicted Fe 2 CO 4 - P 1 ¯ .
The atomic environment around the iron atoms had some similarities with the well-known ferrioxalate anion [Fe(C 2 O 4 ) 3 ] 3 − [36] present in the tri-hydrated potassium tris(oxalato) ferrate(III) K 3 [Fe(C 2 O 4 ) 3 ]·3H 2 O. Similar to this transition metal complex, in the found Fe 2 CO 4 - P 1 ¯ structure, iron was in octahedral coordination with an Fe–O distance nearly equal to 2 Å. The ferrioxalate anion consisted of an [FeO 6 ] octahedron and three [C 2 O 4 ] 2 − oxalate groups acting as bidentate ligands, while in the found Fe 2 CO 4 structure, there was an [FeO 6 ] octahedron and two bidentate orthooxalate [C 2 O 6 ] groups.
It should be noted that the second low-enthalpy phase Fe 2 CO 4 - P 1 also had O 3 C–CO 3 orthooxalate groups in its structure (Figure 1). Fe 2 CO 4 - P 1 and Fe 2 CO 4 - P 1 ¯ were similar in the manner that they represented different fillings of octahedral voids in the h c p array of oxygen with Fe atoms and C–C groups (Table S1 and Figure S2).
In order to analyze the bonding nature, we calculated the Bader charges, the charge density differences (crystal density minus superposition of isolated atomic densities), and electron localization functions (ELFs) of Fe 2 CO 4 - P 1 ¯ at 50 GPa. The obtained Bader charge of C 4 + in Fe 2 CO 4 - P 1 ¯ was lower than that of C 4 + in FeCO 3 - R 3 ¯ c , being +1.609 and +2.109 for C 4 + in Fe 2 CO 4 - P 1 ¯ and in FeCO 3 - R 3 ¯ c , respectively. This indicates that part of the electrons which were used for the formation of C–O bonds within the [CO 3 ] triangle was spent on the formation of a C – C bond. The calculated Bader charges of other atoms are summarized in Table 2. As shown in Figure 4, the charge accumulation occurred halfway through the C–C and C–O vectors. The maximum ELF value between two carbon atoms was about 0.9, and between the carbon and oxygen atoms, it was about 0.7 (Figure 4b), which is indicative of the covalent bonding between these atoms. Thus, we can argue that there was covalent bonding between the carbon atoms, and the carbon in this structure was in the s p 3 -hybridized state.
Table 2. Effective Bader charges on each atom in the relaxed FeCO 3 - R 3 ¯ c and Fe 2 CO 4 - P 1 ¯ at 50 GPa.
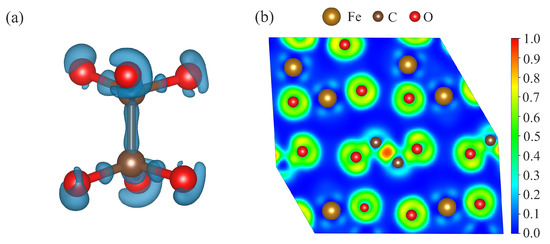
Figure 4. (a) Charge density difference and (b) electron localization functions of Fe 2 CO 4 - P 1 ¯ at 50 GPa.
To investigate the thermal stability of the predicted Fe 2 CO 4 - P 1 ¯ structure, we performed AIMD calculations at 50 GPa and different temperatures. Although small shifts and Fe 2 + cation displacements were observed during the entire 10 ps AIMD simulations at temperatures of 300 and 1000 K, the covalent C–C and C–O bonds were not broken, and the Fe atoms were roughly in the same position. At 1000 K, the C–C and C–O distances varied from 1.35 to 1.74 Å and from 1.17 to 1.63 Å, respectively, confirming that there was no breaking of these bonds. At 2000 K, there was also no observed breaking of the C–C and C–O bonds. The C–C and C–O distances varied from 1.29 to 1.81 Å and from 1.11 to 1.72 Å through MD simulation. From Figure 5, it can clearly be seen that at 2000 K, the structure changed. Specifically, some Fe atoms migrated from one octahedral slab to another. Interestingly, with a more thorough analysis of the MD simulation performed at 2000 K, we can conclude that the process of migration of Fe atoms was continuous (Video S1). A similar self-diffusion of iron atoms was observed for the structure of bcc iron at pressures of the Earth’s inner core and high temperatures [37]. However, nothing similar was observed earlier for carbonate compounds, and only continuous rotation of [CO 3 ] groups (the so-called dynamical disorder) was described for alkaline earth carbonates [38].
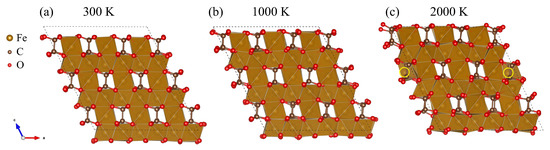
Figure 5. Snapshots of Fe 2 CO 4 at the end of the AIMD simulations at 50 GPa and (a) 300, (b) 1000, and (c) 2000 K. The migrated atoms are highlighted in yellow. The dashed line represents the simulated cell.
In addition, the thermal stability of the second low-enthalpy phase Fe 2 CO 4 - P 1 was investigated. According to the results, it was also stable at 300 and 1000 K, and at 2000 K, a continuous migration of Fe 2 + cations was observed (Figure S3), but compared with Fe 2 CO 4 - P 1 ¯ , it was more intense (Video S2).
In traditional carbonates, the cation can be replaced, and numerous alkaline earth and transition metal carbonates can be formed in the same calcite structure, among which are FeCO 3 , MnCO 3 , CoCO 3 , NiCO 3 , and ZnCO 3 . Based on this, we performed preliminary calculations to examine the dynamic stability of Mn 2 CO 4 , Co 2 CO 4 , Ni 2 CO 4 , and Zn 2 CO 4 in the P 1 ¯ structure. No imaginary modes in the phonon spectra of Mn 2 CO 4 - P 1 ¯ , Co 2 CO 4 - P 1 ¯ , and Ni 2 CO 4 - P 1 ¯ were observed, and hence these orthocarbonates were dynamically stable (Figure 6). The relaxation of Zn 2 CO 4 - P 1 ¯ was accompanied by the rearrangement of atoms with the destruction of the C–C bonds (i.e., it was not stable against small atomic displacements). Only isolated CO 3 triangles were observed in the final structure of Zn 2 CO 4 .
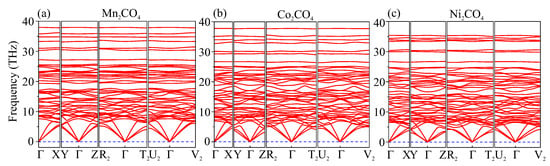
Figure 6. Phonon dispersion curves of (a) Mn 2 CO 4 , (b) Co 2 CO 4 , and (c) Ni 2 CO 4 in P 1 ¯ structure at 50 GPa.
Stable structures of CaCO 3 with [CO 4 ] tetrahedra are known to appear at pressures above 75 GPa [16,39], while Ca 2 CO 4 with [CO 4 ] tetrahedra become stable starting from a pressure of 15 GPa [2,7]. Based on this tendency, according to which the s p 3 structure in the M 2 CO 4 composition appears at much lower pressures than in the MCO 3 composition, we assumed that there was a stable structure of FeCO 3 with O 3 C–CO 3 orthooxalate groups at a pressure several times higher than that for Fe 2 CO 4 . To examine this assumption, we performed crystal structure prediction calculations at pressures of 100–300 GPa. At 100 and 200 GPa, the siderite structure (FeCO 3 - R 3 ¯ c ) was predicted to be the most favorable one. At 300 GPa, the new structure of FeCO 3 with the symmetry P 1 ¯ was predicted to be the most favorable one. As expected, the new FeCO 3 - P 1 ¯ was characterized by the presence of orthooxalate groups. According to our calculations, the phase transition from FeCO 3 - R 3 ¯ c to this structure occurred at a pressure of 275 GPa (Figure 7a). From the calculated phonon spectra, it is clear that FeCO 3 - P 1 ¯ is dynamically stable (Figure 7b). It should be noted that the previously known structures MgCO 3 - C 2 / m , - P 1 ¯ , - P 2 1 , and - P n a 2 1 [15] with [CO 4 ] tetraherda were also considered in the calculations. However, they were energetically unfavorable in the entire considered pressure range.
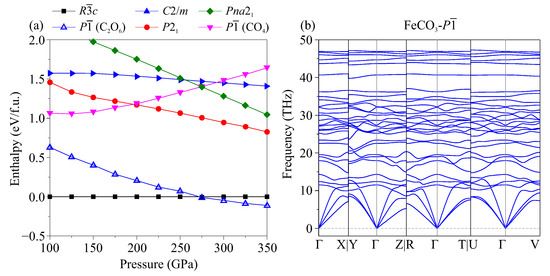
Figure 7. (a) Relative enthalpy-pressure dependencies of FeCO 3 modifications. (b) Phonon dispersion curves of FeCO 3 - P 1 ¯ with [C 2 O 6 ] groups at 300 GPa.
The structural data of the new phase FeCO 3 - P 1 ¯ are given in Table 1. Similar to Fe 2 CO 4 - P 1 ¯ , it can be described as an h c p array of oxygen atoms in which half of the octahedral voids were filled: 1/3 was filled with Fe atoms, and 1/6 was filled with C–C groups. The A, A’, A", and B octahedral slabs can be distinguished (Figure 8a). In slab A, all octahedral voids were filled with Fe and C–C groups, as shown in Figure 8b, while in slab B, all octahedra were empty. Layers A’ and A" were filled in the same way as layer A but shifted relative to each other by one octahedron.
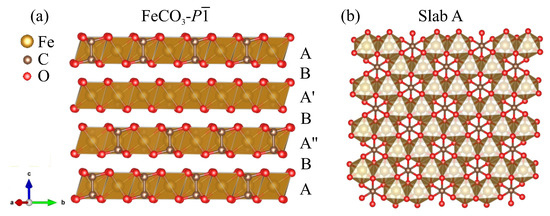
Figure 8. Crystal structure of predicted FeCO 3 - P 1 ¯ .

4. Discussion

The formation of O 3 C–CO 3 orthooxalate groups in melts and aqueous carbonate solutions was proposed earlier by AIMD simulations [40,41]. Solomatova et al. [40] reported that in pyrolite melts (NaCa 2 Fe 4 Mg 30 Al 3 Si 24 O 89 ) with 6.48 and 9.82 wt% of CO 2 at a pressure of 65 GPa, in addition to [CO 2 ], [CO 3 ], and [CO 4 ], other species with polymerized carbon were also formed. Among the polymerized carbon species, the most observed one was ethane-like [C 2 O 6 ] (i.e., O 3 C–CO 3 groups). With increasing pressure, the relative number of O 3 C–CO 3 groups in the melts increases. This could mean that with increasing pressure, O 3 C–CO 3 groups become more favorable over other polymerized (C x O y ) species. Kuang and Tse [41] investigated the reactions of hydrogen and calcium carbonate melts at high pressures. It was shown that a calcium carbonate melt contains only [CO 3 ] and [CO 4 ] species, while after reaction with H 2 , the formation of complex oxo-carbon polymers ([C x O y ]) displaying C–C bonds, including O 3 C–CO 3 groups, can be observed. Our results demonstrate the first example of possible solid structures with the same O 3 C–CO 3 groups.
For Fe 2 CO 4 , several phases with a similar structure were predicted, which differed only in the distribution of Fe and C–C atoms in the oxygen octahedrons. It is possible that, in reality, Fe 2 CO 4 has a structure in which the iron and C–C atoms are statistically distributed through the octahedral voids, especially at high temperatures.
Due to the fact that both FeCO 3 (1FeO*1CO 2 ) and Fe 2 CO 4 (2FeO*1CO 2 ) presented different filling of octahedral voids in the hcp array of oxygen atoms, it can be assumed that the enthalpies of the other structure of intermediate compositions (xFeO*yCO 2 ) will be close to the energetic convex hull, and some of them will be thermodynamically stable.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/sym15020421/s1. Figure S1: Orthooxalate group with C–O and C–C bond distances. Figure S2: Crystal structure of predicted Fe 2 CO 4 - P 1 . Figure S3: Relaxed structure and snapshots of Fe 2 CO 4 - P 1 at the end of the AIMD simulations at 50 GPa and 300, 1000, and 2000 K. Table S1: Structural data of predicted metastable Fe 2 CO 4 - P 1 . Video S1: AIMD simulation of Fe 2 CO 4 - P 1 ¯ at 50 GPa and 2000 K. Video S2: AIMD simulation of metastable Fe 2 CO 4 - P 1 at 50 GPa and 2000 K.

Author Contributions

Conceptualization, P.N.G. and K.D.L.; methodology, N.E.S. and D.N.S.; validation, N.E.S. and P.N.G.; formal analysis, N.E.S. and D.N.S.; investigation, N.E.S. and D.N.S.; writing—original draft preparation, N.E.S., P.N.G., and D.N.S.; writing—review and editing, K.D.L.; visualization, N.E.S. and D.N.S.; supervision, P.N.G. and K.D.L.; funding acquisition, P.N.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the RFBR under research project no. 20-03-00774 and the state assignment of the IGM SB RAS.

Data Availability Statement

Not applicable.

Acknowledgments

The computations were performed using resources provided by the Novosibirsk State University Supercomputer Center.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yao, X.; Xie, C.; Dong, X.; Oganov, A.R.; Zeng, Q. Novel high-pressure calcium carbonates. Phys. Rev. B 2018, 98, 014108. [Google Scholar] [CrossRef]
  2. Sagatova, D.; Shatskiy, A.; Sagatov, N.; Gavryushkin, P.N.; Litasov, K.D. Calcium orthocarbonate, Ca2CO4-Pnma: A potential host for subducting carbon in the transition zone and lower mantle. Lithos 2020, 370, 105637. [Google Scholar] [CrossRef]
  3. Gavryushkin, P.N.; Sagatova, D.N.; Sagatov, N.; Litasov, K.D. Formation of Mg-Orthocarbonate through the Reaction MgCO3+ MgO= Mg2CO4 at Earth’s Lower Mantle P–T Conditions. Cryst. Growth Des. 2021, 21, 2986–2992. [Google Scholar] [CrossRef]
  4. Gavryushkin, P.N.; Sagatova, D.N.; Sagatov, N.; Litasov, K.D. Orthocarbonates of Ca, Sr, and Ba—The Appearance of sp3-Hybridized Carbon at a Low Pressure of 5 GPa and Dynamic Stability at Ambient Pressure. ACS Earth Space Chem. 2021, 5, 1948–1957. [Google Scholar] [CrossRef]
  5. Banaev, M.V.; Sagatov, N.E.; Sagatova, D.N.; Gavryushkin, P.N. High-Pressure Crystal Structures of Pb2CO4 and PbC2O5 with Tetrahedral [CO4] and Pyrocarbonate [C2O5] atomic groups. ChemistrySelect 2022, 7, e202201940. [Google Scholar] [CrossRef]
  6. Gavryushkin, P.; Martirosyan, N.; Rashchenko, S.; Sagatova, D.; Sagatov, N.; Semerikova, A.; Fedotenko, T.; Litasov, K. First Experimental Synthesis of Mg Orthocarbonate by the MgCO3 + MgO= Mg2CO4 Reaction at Pressures of the Earth’s Lower Mantle. JETP Lett. 2022, 116, 477–484. [Google Scholar] [CrossRef]
  7. Binck, J.; Laniel, D.; Bayarjargal, L.; Khandarkhaeva, S.; Fedotenko, T.; Aslandukov, A.; Glazyrin, K.; Milman, V.; Chariton, S.; Prakapenka, V.B.; et al. Synthesis of calcium orthocarbonate, Ca2CO4-Pnma at P-T conditions of Earth’s transition zone and lower mantle. Am. Mineral. 2022, 107, 336–342. [Google Scholar] [CrossRef]
  8. König, J.; Spahr, D.; Bayarjargal, L.; Gavryushkin, P.N.; Sagatova, D.; Sagatov, N.; Milman, V.; Liermann, H.P.; Winkler, B. Novel Calcium sp3 Carbonate CaC2O5-I4 2 ¯ d May Be a Carbon Host in Earth’s Lower Mantle. ACS Earth Space Chem. 2022, 6, 73–80. [Google Scholar] [CrossRef]
  9. Laniel, D.; Binck, J.; Winkler, B.; Vogel, S.; Fedotenko, T.; Chariton, S.; Prakapenka, V.; Milman, V.; Schnick, W.; Dubrovinsky, L.; et al. Synthesis, crystal structure and structure–property relations of strontium orthocarbonate, Sr2CO4. Acta Crystallogr. Sect. B 2021, 77, 131–137. [Google Scholar] [CrossRef]
  10. Spahr, D.; König, J.; Bayarjargal, L.; Gavryushkin, P.N.; Milman, V.; Liermann, H.P.; Winkler, B. Sr3[CO4]O Antiperovskite with Tetrahedrally Coordinated sp3-Hybridized Carbon and OSr6 Octahedra. Inorg. Chem. 2021, 60, 14504–14508. [Google Scholar] [CrossRef]
  11. Spahr, D.; König, J.; Bayarjargal, L.; Milman, V.; Perlov, A.; Liermann, H.P.; Winkler, B. Sr[C2O5] is an Inorganic Pyrocarbonate Salt with [C2O5]2– Complex Anions. J. Am. Chem. Soc. 2022, 144, 2899–2904. [Google Scholar] [CrossRef] [PubMed]
  12. Spahr, D.; König, J.; Bayarjargal, L.; Luchitskaia, R.; Milman, V.; Perlov, A.; Liermann, H.P.; Winkler, B. Synthesis and Structure of Pb[C2O5]: An Inorganic Pyrocarbonate Salt. Inorg. Chem. 2022, 61, 9855–9859. [Google Scholar] [CrossRef] [PubMed]
  13. Sagatova, D.N.; Gavryushkin, P.N.; Sagatov, N.E.; Banaev, M.V. High-pressure transformations of CaC2O5—A full structural trend from double [CO3] triangles through the isolated group of [CO4] tetrahedra to framework and layered structures. Phys. Chem. Chem. Phys. 2022, 24, 23578–23586. [Google Scholar] [CrossRef] [PubMed]
  14. Oganov, A.R.; Glass, C.W.; Ono, S. High-pressure phases of CaCO3: Crystal structure prediction and experiment. Earth Planet. Sci. Lett. 2006, 241, 95–103. [Google Scholar] [CrossRef]
  15. Pickard, C.J.; Needs, R.J. Structures and stability of calcium and magnesium carbonates at mantle pressures. Phys. Rev. B 2015, 91, 104101. [Google Scholar] [CrossRef]
  16. Smith, D.; Lawler, K.V.; Martinez-Canales, M.; Daykin, A.W.; Fussell, Z.; Smith, G.A.; Childs, C.; Smith, J.S.; Pickard, C.J.; Salamat, A. Postaragonite phases of CaCO3 at lower mantle pressures. Phys. Rev. Mater. 2018, 2, 013605. [Google Scholar] [CrossRef]
  17. Binck, J.; Bayarjargal, L.; Lobanov, S.S.; Morgenroth, W.; Luchitskaia, R.; Pickard, C.J.; Milman, V.; Refson, K.; Jochym, D.B.; Byrne, P.; et al. Phase stabilities of MgCO3 and MgCO3-II studied by Raman spectroscopy, x-ray diffraction, and density functional theory calculations. Phys. Rev. Mater. 2020, 4, 055001. [Google Scholar] [CrossRef]
  18. Cerantola, V.; Bykova, E.; Kupenko, I.; Merlini, M.; Ismailova, L.; McCammon, C.; Bykov, M.; Chumakov, A.I.; Petitgirard, S.; Kantor, I.; et al. Stability of iron-bearing carbonates in the deep Earth’s interior. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef]
  19. Nagai, T.; Ishido, T.; Seto, Y.; Nishio-Hamane, D.; Sata, N.; Fujino, K. Pressure-induced spin transition in FeCO3-siderite studied by X-ray diffraction measurements. J. Phys. Conf. Ser. 2010, 215, 012002. [Google Scholar] [CrossRef]
  20. Zhao, C.; Xu, L.; Gui, W.; Liu, J. Phase Stability and Vibrational Properties of Iron-Bearing Carbonates at High Pressure. Minerals 2020, 10, 1142. [Google Scholar] [CrossRef]
  21. Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef] [PubMed]
  22. Oganov, A.R.; Lyakhov, A.O.; Valle, M. How Evolutionary Crystal Structure Prediction Works–and Why. Accounts Chem. Res. 2011, 44, 227–237. [Google Scholar] [CrossRef] [PubMed]
  23. Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
  24. Bushlanov, P.V.; Blatov, V.A.; Oganov, A.R. Topology-based crystal structure generator. Comput. Phys. Commun. 2019, 236, 1–7. [Google Scholar] [CrossRef]
  25. Pickard, C.J.; Needs, R.J. High-Pressure Phases of Silane. Phys. Rev. Lett. 2006, 97, 045504. [Google Scholar] [CrossRef] [PubMed]
  26. Pickard, C.J.; Needs, R.J. Ab initio random structure searching. J. Phys. Condens. Matter 2011, 23, 053201. [Google Scholar] [CrossRef]
  27. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  28. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  29. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
  30. Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
  31. Li, Z.; Stackhouse, S. Iron-rich carbonates stabilized by magnetic entropy at lower mantle conditions. Earth Planet. Sci. Lett. 2020, 531, 115959. [Google Scholar] [CrossRef]
  32. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
  33. Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
  34. Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
  35. Aped, P.; Fuchs, B.; Goldberg, I.; Senderowitz, H.; Tartakovsky, E.; Weinman, S. Structure and conformation of heterocycles. 21. Probing the anomeric effect in orthoesters. Structure, conformation, and dynamic behavior of a unique orthooxalate: 2, 5, 7, 10, 11, 14-hexaoxa [4.4. 4] propellane. J. Am. Chem. Soc. 1992, 114, 5585–5590. [Google Scholar] [CrossRef]
  36. Junk, P.C. Supramolecular interactions in the X-ray crystal structure of potassium tris (oxalato) ferrate (III) trihydrate. J. Coord. Chem. 2005, 58, 355–361. [Google Scholar] [CrossRef]
  37. Belonoshko, A.B.; Lukinov, T.; Fu, J.; Zhao, J.; Davis, S.; Simak, S.I. Stabilization of body-centred cubic iron under inner-core conditions. Nat. Geosci. 2017, 10, 312–316. [Google Scholar] [CrossRef]
  38. Ishizawa, N. Calcite V: A hundred-year-old mystery has been solved. Powder Diffr. 2014, 29, S19–S23. [Google Scholar] [CrossRef]
  39. Gavryushkin, P.N.; Martirosyan, N.S.; Inerbaev, T.M.; Popov, Z.I.; Rashchenko, S.V.; Likhacheva, A.Y.; Lobanov, S.S.; Goncharov, A.F.; Prakapenka, V.B.; Litasov, K.D. Aragonite-II and CaCO3-VII: New High-Pressure, High-Temperature Polymorphs of CaCO3. Cryst. Growth Des. 2017, 17, 6291–6296. [Google Scholar] [CrossRef]
  40. Solomatova, N.V.; Caracas, R.; Manning, C.E. Carbon sequestration during core formation implied by complex carbon polymerization. Nat. Commun. 2019, 10, 789. [Google Scholar] [CrossRef]
  41. Kuang, H.; Tse, J.S. High-Temperature, High-Pressure Reactions of H2 with CaCO3 Melts. Phys. Status Solidi B 2022, 259, 2100644. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Anatomic Comparison of Contralateral Maxillary Second Molars Using High-Resolution Micro-CT
Previous
On the Polarization Dependence of Two-Photon Processes including X-ray Scattering
Next