Complexity Reduction Approach for Solving Second Kind of Fredholm Integral Equations

Abstract

Initially, the concept of the complexity reduction approach was applied to solve symmetry algebraic systems that were generated from the discretization of the partial differential equations. Consequently, in this paper, the effectiveness of a complexity reduction approach based on half- and quarter-sweep iteration concepts for solving linear Fredholm integral equations of the second kind is investigated. Half- and quarter-sweep iterative methods are applied to solve dense linear systems generated from the discretization of the second kind of linear Fredholm integral equations using a repeated modified trapezoidal (RMT) scheme. The formulation and implementation of the proposed methods are presented. In addition, computational complexity analysis and numerical results of test examples are also included to verify the performance of the proposed methods.

1. Introduction

Integral equations commonly arise as mathematical models for a variety of physical phenomena and also as reformulations of other mathematical models. In this paper, the second kind of linear Fredholm integral equations, which can be represented mathematically as follows,

$$\phi \left(x\right)+{\int }_a^{b}K(x,t)\phi \left(t\right)dt=f\left(x\right),x\in [a,b]$$

(1)

are considered. The kernel $K(x,t)$ and function $f\left(x\right)$ are known, whereas the function $\phi \left(x\right)$ is unknown and has to be determined from Equation (1). The kernel $K(x,t)$ is assumed to be integrable and to satisfy properties that are sufficient to guarantee the conditions of the Fredholm alternative theorem (refer to Theorem 1 below). Equation (1) can also be rewritten in the equivalent operator form

$$(I+\kappa )\phi =f$$

(2)

where the integral operator is defined as follows:

$$\kappa \phi \left(t\right)={\int }_a^{b}K(x,t)\phi \left(t\right)dt.$$

(3)

Theorem 1

([1]). Let χ be a Banach space and let $\kappa :\chi ⟶\chi$ be compact. Then, the equation $(I+\kappa )\phi =f$ has a unique solution $x\in \chi$ if and only if the homogeneous equation $(I+\kappa )z=0$ has only the trivial solution $z=0$. In such a case, the operator $I+\kappa :\chi \stackrel{1-1}{\genfrac{}{}{0pt}{}{⟶}{onto}}\chi$ has a bounded inverse ${(I+\kappa )}^{-1}$.

Definition 1

([1]). Let χ and $\mathrm{Y}$ be a normed vector space and let $\kappa :\chi ⟶\mathrm{Y}$ be linear. Then, κ is compact if the set $\left\{\kappa x\right|\parallel x\parallel x\le 1\}$ has compact closure in $\mathrm{Y}$. This is equivalent to saying that, for every bounded sequence $\left\{x_n\right\}\subset \chi$, the sequence $\left\{\kappa x_n\right\}$ has a subsequence that is convergent to some points in $\mathrm{Y}$. Compact operators are also called completely continuous operators.

In many applications, numerical techniques are widely used to solve linear Fredholm integral equations compared to the analytical method. The basic concept is the discretization of linear Fredholm integral equations to yield linear systems, which are then solved numerically. Many methods have been proposed to discretize the linear Fredholm integral equations of the second kind into linear systems, such as projection [2,3,4,5,6] and quadrature [7,8,9,10,11,12,13] methods. Such discretizations mostly lead to dense linear systems and can be prohibitively expensive to solve using direct methods as the order of the system increases. Hence, iterative methods are an attractive alternative for efficient solutions.

Consequently, the concept of the half-sweep iteration was first envisioned by Abdullah [14] via the Explicit Decoupled Group (EDG) method to solve symmetry algebraic systems that are generated from the discretization of the two-dimensional Poisson equations. Meanwhile, Othman and Abdullah [15] extended the half-sweep iteration concept to the quarter-sweep iteration concept through the Modified Explicit Group (MEG) method. Both the iteration concepts are also known as the complexity reduction approach. The basic idea of the half- and quarter-sweep iteration concepts is to reduce the computational complexity of the method during iterations. The implementation of the half- and quarter-sweep iterations will only consider nearly a half and a quarter of all interior node points in a solution domain, respectively. Further studies to verify the effectiveness of both iteration concepts have been carried out; refer to [16,17,18,19,20,21] and references therein. In this paper, the performance of the half- and quarter-sweep iterative methods is investigated in solving dense linear systems generated by the discretization of problem (1) using a repeated modified trapezoidal (RMT) [13] scheme.

The outline of this paper is as follows. Section 2 gives the formulation of the full-, half- and quarter-sweep RMT approximation equations. Meanwhile, Section 3 discusses the application of the full-, half- and quarter-sweep iterative methods to solve problem (1). Numerical results are presented in Section 4 to demonstrate the performance of the proposed numerical techniques. The computational complexity of the proposed methods in solving problem (1) is explained in Section 5, and concluding remarks are given in Section 6.

2. Repeated Modified Trapezoidal Approximation Equations

The RMT scheme is applied to discretize problem (1) by replacing the integral by finite sums. The formula for the modified trapezoidal scheme for solving definite integral ${\int }_a^b\phi \left(t\right)dt$ is defined as follows

$${\int }_a^b\phi \left(t\right)dt=\frac{b-a}{2}[\phi \left(a\right)+\phi \left(b\right)]+\frac{{(b-a)}^2}{12}[{\phi }^{{}^{\prime }}\left(a\right)-{\phi }^{{}^{\prime }}\left(b\right)]-\frac{{(b-a)}^5}{720}{\phi }^{\left(4\right)}\left(\xi \right),$$

(4)

and its repeated formula (RMT) is

$${\int }_a^b\phi \left(t\right)dt=\frac{h}{2}\phi \left(a\right)+h\sum _{j=1}^{n-1}\phi \left(t_j\right)+\frac{h}{2}\phi \left(b\right)+\frac{h^2}{12}[{\phi }^{{}^{\prime }}\left(a\right)-{\phi }^{{}^{\prime }}\left(b\right)]$$

(5)

where the constant step size, h, is defined as

$$h=\frac{b-a}{n},$$

(6)

and, n and $t_j$$(j=0,1,2,\cdots ,n-2,n-1,n)$ are the number of subintervals in the interval $[a,b]$ and abscissas of the partition points of the integration interval $[a,b]$, respectively.

The conditions of $K(x,t)$ and $f\left(x\right)$ must be differentiable with respect to their variables should be satisfied in order to discretize problem (1) using the RMT scheme. Moreover, two cases, which are whether the derivative of $\frac{\partial K(x,t)}{\partial x\partial t}$ exists or not, also need to be considered separately. Before further explanation, the following notations are used for simplicity:

$$K_{i,j}\equiv K(x_i,t_j),$$

$${\phi }_i\equiv \phi \left(x_i\right),$$

$${\phi }_j\equiv \phi \left(t_j\right),$$

$$f_i\equiv f\left(x_i\right),$$

$$J_{i,j}\equiv \frac{\partial K(x_i,t_j)}{\partial t_j},$$

$$H_{i,j}\equiv \frac{\partial K(x_i,t_j)}{\partial x_i},$$

$$L_{i,j}\equiv \frac{\partial K(x_i,t_j)}{\partial x_i\partial t_j},$$

$${\phi }_i^{{}^{\prime }}\equiv {\phi }^{{}^{\prime }}\left(x_i\right)$$

and

$$f_i^{{}^{\prime }}\equiv f^{{}^{\prime }}\left(x_i\right).$$

Now, let interval $[a,b]$ be divided uniformly into n subintervals and the discrete set of points of x and t given by $x_i=a+ih$ and $t_j=a+jh$. Based on [13], the RMT approximation equations for both cases are shown as follows.

Case 1: $\frac{\partial K(x,t)}{\partial x\partial t}$ does not exist

$$\left.\begin{array}{c}{\phi }_i+A_{i,0}{\phi }_0+h\sum _{j=1}^{n-1}{K}_{i,j}{\phi }_j+B_{i,n}{\phi }_n,i=0,1,2,\cdots ,n-2,n-1,n\hfill \\ +\frac{h^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }}-K_{i,n}{\phi }_n^{{}^{\prime }})=f_i\hfill \\ {\phi }_0^{{}^{\prime }}+\frac{h}{2}{H}_{0,0}{\phi }_0+h\sum _r{j=1}^{n-1}{H}_{0,j}{\phi }_j+\frac{h}{2}{H}_{0,n}{\phi }_n=f_0^{{}^{\prime }}\hfill \\ {\phi }_n^{{}^{\prime }}+\frac{h}{2}{H}_{n,0}{\phi }_0+h\sum _{j=1}^{n-1}{H}_{n,j}{\phi }_j+\frac{h}{2}{H}_{n,n}{\phi }_n=f_n^{{}^{\prime }}\hfill \end{array}\right\}$$

(7)

Case 2: $\frac{\partial K(x,t)}{\partial x\partial t}$ exists

$$\left.\begin{array}{c}{\phi }_i+A_{i,0}{\phi }_0+h\sum _{j=1}^{n-1}{K}_{i,j}{\phi }_j+B_{i,n}{\phi }_n,i=0,1,2,\cdots ,n-2,n-1,n\hfill \\ +\frac{h^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }}-K_{i,n}{\phi }_n^{{}^{\prime }})=f_i\hfill \\ {\phi }_0^{{}^{\prime }}+C_{0,0}{\phi }_0+h\sum _{j=1}^{n-1}{H}_{0,j}{\phi }_j+D_{0,n}{\phi }_n+\frac{h^2}{12}(H_{0,0}{\phi }_0^{{}^{\prime }}-H_{0,n}{\phi }_n^{{}^{\prime }})=f_0^{{}^{\prime }}\hfill \\ {\phi }_n^{{}^{\prime }}+C_{n,0}{\phi }_0+h\sum _{j=1}^{n-1}{H}_{n,j}{\phi }_j+D_{n,n}{\phi }_n+\frac{h^2}{12}(H_{n,0}{\phi }_0^{{}^{\prime }}-H_{n,n}{\phi }_n^{{}^{\prime }})=f_n^{{}^{\prime }}\hfill \end{array}\right\}$$

(8)

where

$$A_{i,j}=\frac{h}{2}{K}_{i,j}+\frac{h^2}{12}{J}_{i,j},$$

$$B_{i,j}=\frac{h}{2}{K}_{i,j}-\frac{h^2}{12}{J}_{i,j},$$

$$C_{i,j}=\frac{h}{2}{H}_{i,j}+\frac{h^2}{12}{L}_{i,j}$$

and

$$D_{i,j}=\frac{h}{2}{H}_{i,j}-\frac{h^2}{12}{L}_{i,j}.$$

The standard RMT approximation equations as defined in Equations (7) and (8) also can be referred to as full-sweep RMT approximation equations.

For further discussions on formulating the half- and quarter-sweep RMT approximation equations for problem (1), the interval that is divided uniformly, as shown in Figure 1 and Figure 2, is considered.

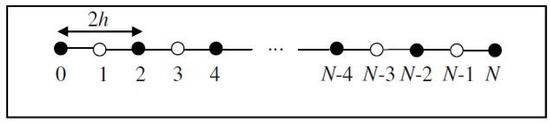
Figure 1. Distribution of uniform node points for the half-sweep case.

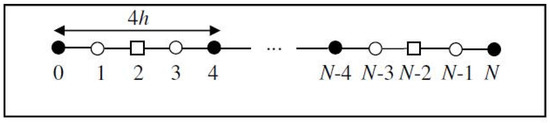
Figure 2. Distribution of uniform node points for the quarter-sweep case.

Based on Figure 1 and Figure 2, the half- and quarter-sweep iterative methods will compute estimation values for node points of type • only until the convergence criterion is satisfied. After the convergence criterion is achieved, the estimation solutions for the remaining points are computed directly [12,14,15].

By applying the half- and quarter-sweep iteration concepts, the generalized full-, half- and quarter-sweep RMT approximation equations for both cases can be expressed as follows.

Case 1: $\frac{\partial K(x,t)}{\partial x\partial t}$ does not exist

$$\left.\begin{array}{c}{\phi }_i+A_{i,0}{\phi }_0+ph\sum _{j=p,2p,3p}^{n-p}{K}_{i,j}{\phi }_j+B_{i,n}{\phi }_n,i=0,p,2p,\cdots ,n-2p,n-p,n\hfill \\ +\frac{{\left(ph\right)}^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }}-K_{i,n}{\phi }_n^{{}^{\prime }})=f_i\hfill \\ {\phi }_0^{{}^{\prime }}+\frac{ph}{2}{H}_{0,0}{\phi }_0+ph\sum _{j=p,2p,3p}^{n-p}{H}_{0,j}{\phi }_j+\frac{ph}{2}{H}_{0,n}{\phi }_n=f_0^{{}^{\prime }}\hfill \\ {\phi }_n^{{}^{\prime }}+\frac{ph}{2}{H}_{n,0}{\phi }_0+ph\sum _{j=p,2p,3p}^{n-p}{H}_{n,j}{\phi }_j+\frac{ph}{2}{H}_{n,n}{\phi }_n=f_n^{{}^{\prime }}\hfill \end{array}\right\}$$

(9)

Case 2: $\frac{\partial K(x,t)}{\partial x\partial t}$ exists

$$\left.\begin{array}{c}{\phi }_i+A_{i,0}{\phi }_0+ph\sum _{j=p,2p,3p}^{n-p}{K}_{i,j}{\phi }_j+B_{i,n}{\phi }_n,i=0,p,2p,\cdots ,n-2p,n-p,n\hfill \\ +\frac{{\left(ph\right)}^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }}-K_{i,n}{\phi }_n^{{}^{\prime }})=f_i\hfill \\ {\phi }_0^{{}^{\prime }}+C_{0,0}{\phi }_0+ph\sum _{j=p,2p,3p}^{n-p}{H}_{0,j}{\phi }_j+D_{0,n}{\phi }_n+\frac{{\left(ph\right)}^2}{12}(H_{0,0}{\phi }_0^{{}^{\prime }}-H_{0,n}{\phi }_n^{{}^{\prime }})=f_0^{{}^{\prime }}\hfill \\ {\phi }_n^{{}^{\prime }}+C_{n,0}{\phi }_0+ph\sum _{j=p,2p,3p}^{n-p}{H}_{n,j}{\phi }_j+D_{n,n}{\phi }_n+\frac{{\left(ph\right)}^2}{12}(H_{n,0}{\phi }_0^{{}^{\prime }}-H_{n,n}{\phi }_n^{{}^{\prime }})=f_n^{{}^{\prime }}\hfill \end{array}\right\}$$

(10)

where

$$A_{i,j}=\frac{ph}{2}{K}_{i,j}+\frac{{\left(ph\right)}^2}{12}{J}_{i,j},$$

$$B_{i,j}=\frac{ph}{2}{K}_{i,j}-\frac{{\left(ph\right)}^2}{12}{J}_{i,j},$$

$$C_{i,j}=\frac{ph}{2}{H}_{i,j}+\frac{{\left(ph\right)}^2}{12}{L}_{i,j}$$

and

$$D_{i,j}=\frac{ph}{2}{H}_{i,j}-\frac{{\left(ph\right)}^2}{12}{L}_{i,j}.$$

The value of p, which corresponds to 1, 2 and 4, represents the full-, half- and quarter-sweep cases, respectively. From Equations (9) and (10), it is obvious that the full-, half- and quarter-sweep RMT approximation equations can be represented in matrix form, as shown in Equation (11) with $(\frac{n}{p}+3)$ equations and $(\frac{n}{p}+3)$ unknowns

$$M\phi =f,$$

(11)

where the matrix M is dense, f is known and $\phi$ is the unknown vector to be calculated.

3. Iterative Methods

For the solution of system (11), complexity reduction approaches with the Gauss–Seidel (GS) iterative method are implemented. Combinations of the GS method with half- and quarter-sweep iterations are called the Half-Sweep Gauss–Seidel (HSGS) and Quarter-Sweep Gauss–Seidel (QSGS) methods, respectively. Meanwhile, the standard GS method is also known as the Full-Sweep Gauss–Seidel (FSGS) method.

Definition 2

([22]). Let M be a real matrix. Then, $M=S-T$ is referred to as

(i) 

a regular splitting if S is nonsingular, $S^{-1}\ge O$ and $T\ge O$,

(ii) 

a weak regular splitting if S is nonsingular, $S^{-1}\ge O$ and $S^{-1}T\ge O$,

(iii) 

a nonnegative splitting, if $S^{-1}T\ge O$, and

(iv) 

a convergent splitting if $\rho \left(S^{-1}T\right)<1$.

Theorem 2

([23]). The following statements are equivalent:

(i) 

W is a convergent matrix,

(ii) 

${lim}_{k\to \infty }\parallel W^k\parallel =0$ for some matrix norm,

(iii) 

$\rho \left(W\right)<1$.

Lemma 1

([23]). If the spectral radius satisfies $\rho \left(W\right)<1$, then ${(I-W)}^{-1}$ exists and

$${(I-W)}^{-1}=I+W+W^2+\cdots =\sum _{l=0}^{\infty }{W}^l.$$

Based on regular splitting, the GS splitting can be defined as follows.

Definition 3

([22]). Let $M=P-Q-R$, where P, $-Q$ and $-R$ are diagonal, strictly lower triangular and strictly upper triangular parts of matrices M, respectively. We call $M=S-T$ the Gauss–Seidel splitting of M, if $S=P-Q$ and $T=R$. In addition, the splitting is called

(i) 

Gauss–Seidel convergent if spectral radius, $\rho \left(S^{-1}T\right)<1$, and

(ii) 

Gauss–Seidel regular if $S^{-1}={(P-Q)}^{-1}\ge O$ and $T=R\ge O$.

The general scheme for all three GS iterative methods to solve system (11) can be written as

$${\phi }^{(k+1)}={(P-Q)}^{-1}(R{\phi }^{\left(k\right)}+f),k=0,1,2,\cdots .$$

(12)

Based on the formulation (12), the iterative forms of the FSGS, HSGS and QSGS methods for solving system (11) are of the form

$${\phi }^{(k+1)}=W_{FSGS}{\phi }^{\left(k\right)}+c_{FSGS}$$

(13)

$${\phi }^{(k+1)}=W_{HSGS}{\phi }^{\left(k\right)}+c_{HSGS}$$

(14)

and

$${\phi }^{(k+1)}=W_{QSGS}{\phi }^{\left(k\right)}+c_{QSGS}$$

(15)

respectively, where

$$W_{FSGS}=W_{HSGS}=W_{QSGS}=S^{-1}T$$

and

$$c_{FSGS}=c_{HSGS}=c_{QSGS}=S^{-1}f.$$

Theorem 3.

Let square matrices $W_{FSGS}$, $W_{HSGS}$ and $W_{QSGS}$ be in the order of $n+3$, $\frac{n}{2}+3$ and $\frac{n}{4}+3$, respectively. The successive approximations (13)–(15) for $k=0,1,2,\cdots$ converge to the unique solution of

$$\phi =W_{FSGS}\phi +c_{FSGS}$$

(16)

$$\phi =W_{HSGS}\phi +c_{HSGS}$$

(17)

and

$$\phi =W_{QSGS}\phi +c_{QSGS}$$

(18)

respectively, if and only if the spectral radius of the iteration matrices is less than one, i.e., $\rho \left(W_{FSGS}\right)<1$, $\rho \left(W_{HSGS}\right)<1$ and $\rho \left(W_{QSGS}\right)<1$.

Proof. 

The iterative form of the FSGS, HSGS and QSGS methods can be rewritten as follows:

$${\phi }^{(k+1)}=W_{FSGS}^{k+1}{\phi }^{\left(0\right)}+[W_{FSGS}^k+\cdots +W_{FSGS}+I]c_{FSGS}$$

(19)

$${\phi }^{(k+1)}=W_{HSGS}^{k+1}{\phi }^{\left(0\right)}+[W_{HSGS}^k+\cdots +W_{HSGS}+I]c_{HSGS}$$

(20)

and

$${\phi }^{(k+1)}=W_{QSGS}^{k+1}{\phi }^{\left(0\right)}+[W_{QSGS}^k+\cdots +W_{QSGS}+I]c_{QSGS}$$

(21)

respectively. Since $\rho \left(W_{FSGS}\right)<1$, $\rho \left(W_{HSGS}\right)<1$ and $\rho \left(W_{QSGS}\right)<1$ and, based on Theorem 2, $W_{FSGS}$, $W_{HSGS}$ and $W_{QSGS}$ matrices are convergent and satisfy the following conditions

$$\underset{k\to \infty }{lim}{W}_{FSGS}^{k+1}{\phi }^{\left(0\right)}=0,$$

(22)

$$\underset{k\to \infty }{lim}{W}_{HSGS}^{k+1}{\phi }^{\left(0\right)}=0$$

(23)

and

$$\underset{k\to \infty }{lim}{W}_{QSGS}^{k+1}{\phi }^{\left(0\right)}=0$$

(24)

respectively. Based on Lemma 1, this implies that

$$\underset{k\to \infty }{lim}{\phi }^{(k+1)}=\underset{k\to \infty }{lim}{W}_{FSGS}^{k+1}{\phi }^{\left(0\right)}+\left(\sum _{l=0}^{\infty }{W}_{FSGS}^l\right)c_{FSGS}={\left(I-W_{FSGS}\right)}^{-1}{c}_{FSGS}$$

(25)

$$\underset{k\to \infty }{lim}{\phi }^{(k+1)}=\underset{k\to \infty }{lim}{W}_{HSGS}^{k+1}{\phi }^{\left(0\right)}+\left(\sum _{l=0}^{\infty }{W}_{HSGS}^l\right)c_{HSGS}={(I-W_{HSGS})}^{-1}{c}_{HSGS}$$

(26)

and

$$\underset{k\to \infty }{lim}{\phi }^{(k+1)}=\underset{k\to \infty }{lim}{W}_{QSGS}^{k+1}{\phi }^{\left(0\right)}+\left(\sum _{l=0}^{\infty }{W}_{QSGS}^l\right)c_{QSGS}={(I-W_{QSGS})}^{-1}{c}_{QSGS}.$$

(27)

Hence, the sequences converge to the vectors $\phi ={(I-W_{FSGS})}^{-1}{c}_{FSGS}$, $\phi ={(I-W_{HSGS})}^{-1}{c}_{HSGS}$ and $\phi ={(I-W_{QSGS})}^{-1}{c}_{QSGS}$ and, $\phi =W_{FSGS}x+c_{FSGS}$, $\phi =W_{HSGS}x+c_{HSGS}$ and $\phi =W_{QSGS}x+c_{QSGS}$, respectively. □

By determining the values of matrices P, $-Q$ and $-R$ as stated in Definition 3, the algorithms for the FSGS, HSGS and QSGS methods with full-, half- and quarter-sweep RMT approximation equations, respectively, to solve problem (1) can generally be described by Algorithms 1 and 2.

Algorithm 1: GS methods with RMT scheme (Case 1)
Step i.	Set ${\phi }^{\left(0\right)}$ and initialize all the parameters.
Step ii.	Iteration cycle
		for$k=0,1,2,\cdots$
			for$i=0,p,2p,\cdots ,n-2p,n-p,n$
			Compute
			${\phi }_i^{(k+1)}\leftarrow \left\{\begin{array}{c}\frac{[f_i-ph{\sum }_{j=p,2p,3p}^{n-p}{K}_{i,j}{\phi }_j^{\left(k\right)}-B_{i,n}{\phi }_n^{\left(k\right)}-\frac{{\left(ph\right)}^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }\left(k\right)}-K_{i,n}{\phi }_n^{{}^{\prime }\left(k\right)})]}{1+A_{i,0}},i=0\hfill \\ \frac{\genfrac{}{}{0pt}{}{[f_i-A_{i,0}{\phi }_0^{(k+1)}-ph{\sum }_{j=p,2p,3p}^{i-p}{K}_{i,j}{\phi }_j^{(k+1)}-ph{\sum }_{j=i+p}^{n-p}{K}_{i,j}{\phi }_j^{\left(k\right)}}{-B_{i,n}{\phi }_n^{\left(k\right)}-\frac{{\left(ph\right)}^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }\left(k\right)}-K_{i,n}{\phi }_n^{{}^{\prime }\left(k\right)})]}}{1+ph{K}_{i,i}},i=p,2p,\cdots ,n-p\hfill \\ \frac{[f_i-A_{i,0}{\phi }_0^{(k+1)}-ph{\sum }_{j=p,2p,3p}^{n-p}{K}_{i,j}{\phi }_j^{(k+1)}-\frac{{\left(ph\right)}^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }\left(k\right)}-K_{i,n}{\phi }_n^{{}^{\prime }\left(k\right)})]}{1+B_{i,n}},i=n\hfill \end{array}\right.$
			${\phi }_0^{{}^{\prime }(k+1)}\leftarrow f_0^{{}^{\prime }}-\frac{ph}{2}{H}_{0,0}{\phi }_0^{(k+1)}-ph{\sum }_{j=p,2p,3p}^{n-p}{H}_{0,j}{\phi }_j^{(k+1)}-\frac{ph}{2}{H}_{0,n}{\phi }_n^{(k+1)}$
			${\phi }_n^{{}^{\prime }(k+1)}\leftarrow f_n^{{}^{\prime }}-\frac{ph}{2}{H}_{n,0}{\phi }_0^{(k+1)}-ph{\sum }_{j=p,2p,3p}^{n-p}{H}_{n,j}{\phi }_j^{(k+1)}-\frac{ph}{2}{H}_{n,n}{\phi }_n^{(k+1)}$
Step iii.	Convergence test. If the convergence criterion, i.e., the maximum norm
	$\Vert {\phi }^{(k+1)}-{\phi }^{\left(k\right)}{\Vert }_{\infty }\le ϵ$, is satisfied, go to Step iv. Otherwise, go to Step ii.
Step iv.	Stop.

Algorithm 2: GS methods with RMT scheme (Case 2)
Step i.	Set ${\phi }^{\left(0\right)}$ and initialize all the parameters.
Step ii.	Iteration cycle
		for  $k=0,1,2,\cdots$
			for  $i=0,p,2p,\cdots ,n-2p,n-p,n$
			Compute
			${\phi }_i^{(k+1)}\leftarrow \left\{\begin{array}{c}\frac{[f_i-ph{\sum }_{j=p,2p,3p}^{n-p}{K}_{i,j}{\phi }_j^{\left(k\right)}-B_{i,n}{\phi }_n^{\left(k\right)}-\frac{{\left(ph\right)}^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }\left(k\right)}-K_{i,n}{\phi }_n^{{}^{\prime }\left(k\right)})]}{1+A_{i,0}},i=0\hfill \\ \frac{\genfrac{}{}{0pt}{}{[f_i-A_{i,0}{\phi }_0^{(k+1)}-ph{\sum }_{j=p,2p,3p}^{i-p}{K}_{i,j}{\phi }_j^{(k+1)}-ph{\sum }_{j=i+p}^{n-p}{K}_{i,j}{\phi }_j^{\left(k\right)}}{-B_{i,n}{\phi }_n^{\left(k\right)}-\frac{{\left(ph\right)}^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }\left(k\right)}-K_{i,n}{\phi }_n^{{}^{\prime }\left(k\right)})]}}{1+ph{K}_{i,i}},i=p,2p,\cdots ,n-p\hfill \\ \frac{[f_i-A_{i,0}{\phi }_0^{(k+1)}-ph{\sum }_{j=p,2p,3p}^{n-p}{K}_{i,j}{\phi }_j^{(k+1)}-\frac{{\left(ph\right)}^2}{12}(K_{i,0}{\phi }_0^{{}^{\prime }\left(k\right)}-K_{i,n}{\phi }_n^{{}^{\prime }\left(k\right)})]}{1+B_{i,n}},i=n\hfill \end{array}\right.$
			${\phi }_0^{{}^{\prime }(k+1)}\leftarrow \frac{f_0^{{}^{\prime }}-C_{0,0}{\phi }_0^{(k+1)}-ph{\sum }_{j=p,2p,3p}^{n-p}{H}_{0,j}{\phi }_j^{(k+1)}-D_{0,n}{\phi }_n^{(k+1)}+\frac{{\left(ph\right)}^2}{12}{H}_{0,n}{\phi }_n^{{}^{\prime }\left(k\right)}}{1+\frac{{\left(ph\right)}^2}{12}{H}_{0,0}}$
			${\phi }_n^{{}^{\prime }(k+1)}\leftarrow \frac{f_n^{{}^{\prime }}-C_{n,0}{\phi }_0^{(k+1)}-ph{\sum }_{j=p,2p,3p}^{n-p}{H}_{n,j}{\phi }_j^{(k+1)}-D_{n,n}{\phi }_n^{(k+1)}-\frac{{\left(ph\right)}^2}{12}{H}_{n,0}{\phi }_0^{{}^{\prime }(k+1)}}{1-\frac{{\left(ph\right)}^2}{12}{H}_{n,n}}$
Step iii.	Convergence test. If the convergence criterion, i.e., the maximum norm
	$\Vert {\phi }^{(k+1)}-{\phi }^{\left(k\right)}{\Vert }_{\infty }\le ϵ$, is satisfied, go to Step iv. Otherwise, go to Step ii.
Step iv.	Stop.

After the iteration process, additional calculation is required for the HSGS and QSGS methods to compute the remaining points. In this paper, the second-order Lagrange interpolation technique [12] is applied to compute the remaining points. The formulations to calculate remaining points using the second-order Lagrange interpolation technique for HSGS and QSGS are defined as

$${\phi }_i=\left\{\begin{array}{cc}\frac{3}{8}{\phi }_{i-1}+\frac{3}{4}{\phi }_{i+1}-\frac{1}{8}{\phi }_{i+3},\hfill & i=1,3,5,\cdots ,n-3\hfill \\ \frac{3}{4}{\phi }_{i-1}+\frac{3}{8}{\phi }_{i+1}-\frac{1}{8}{\phi }_{i-3},\hfill & i=n-1\hfill \end{array}\right.$$

(28)

and

$${\phi }_i=\left\{\begin{array}{cc}\frac{3}{8}{\phi }_{i-2}+\frac{3}{4}{\phi }_{i+2}-\frac{1}{8}{\phi }_{i+6},\hfill & i=2,6,10,\cdots ,n-6\hfill \\ \frac{3}{4}{\phi }_{i-2}+\frac{3}{8}{\phi }_{i+2}-\frac{1}{8}{\phi }_{i-6},\hfill & i=n-2\hfill \\ \frac{3}{8}{\phi }_{i-1}+\frac{3}{4}{\phi }_{i+1}-\frac{1}{8}{\phi }_{i+3},\hfill & i=1,3,5,\cdots ,n-3\hfill \\ \frac{3}{4}{\phi }_{i-1}+\frac{3}{8}{\phi }_{i+1}-\frac{1}{8}{\phi }_{i-3},\hfill & i=n-1\hfill \end{array}\right.$$

(29)

respectively.

4. Numerical Simulations

For numerical simulations, two parameters, i.e., the number of iterations and computational time, are considered for comparative analysis to verify the performance of the FSGS with full-sweep RMT (FSGS-RMT), HSGS with half-sweep RMT (HSGS-RMT) and QSGS with quarter-sweep RMT (QSGS-RMT) methods in solving problem (1). The following two test problems that satisfy the conditions of the Fredholm alternative theorem have been chosen for the numerical simulations.

Test Problem 1 [24]

$$\phi \left(x\right)-{\int }_0^1(4xt-x^2)\phi \left(t\right)dt=x,x\in [0,1],$$

(30)

where the exact solution is given by

$$\phi \left(x\right)=24x-9x^2.$$

Test Problem 2 [11]

$$\phi \left(x\right)-{\int }_0^1(x^2+t^2)\phi \left(t\right)dt=x^6-5x^3+x+10,x\in [0,1],$$

(31)

where the exact solution is

$$\phi \left(x\right)=x^6-5x^3+\frac{1045}{28}{x}^2+x+\frac{2141}{84}.$$

Throughout the simulations, the convergence test considered the threshold, $ϵ={10}^{-10}$. The simulations were run sequentially by a computer with processor Intel(R) Core(TM) 2 CPU 1.66GHz and computer codes were written in C programming language. The value of initial datum ${\phi }^{\left(0\right)}$ was set to be zero for all the test problems. All results of numerical simulations obtained from the implementation of the FSGS-RMT, HSGS-RMT and QSGS-RMT methods for test problems 1 and 2 are tabulated in Table 1 and Table 2, respectively. The following Table 3 and Table 4 show the estimation solutions of $\phi \left(x\right)$ at points $x=0.00,0.25,0.50,0.75$ and $1.00$ for both test problems. Moreover, numerical results by applying FSGS with the standard repeated trapezoidal (FSGS-RT) method are also included for comparison purposes.

Table 1. Numerical results of test problem 1.

Number of Iterations
$\mathit{n}$		Methods
	FSGS-RMT	HSGS-RMT	QSGS-RMT
1024	199	198	197
2048	199	199	198
4096	199	199	199
8192	199	199	199
16,384	199	199	199
Computational Time (in seconds)
$\mathit{n}$		Methods
	FSGS-RMT	HSGS-RMT	QSGS-RMT
1024	24.41	3.10	0.75
2048	90.20	11.89	2.96
4096	345.30	47.44	12.03
8192	1366.72	183.99	48.92
16,384	4954.54	1282.61	296.14

Table 2. Numerical results of test problem 2.

Number of Iterations
$\mathit{n}$		Methods
	FSGS-RMT	HSGS-RMT	QSGS-RMT
1024	57	57	57
2048	57	57	57
4096	57	57	57
8192	57	57	57
16,384	57	57	57
Computational Time (in seconds)
$\mathit{n}$		Methods
	FSGS-RMT	HSGS-RMT	QSGS-RMT
1024	6.38	1.48	0.38
2048	26.93	5.99	1.61
4096	110.83	25.53	6.92
8192	421.51	99.67	30.31
16,384	1589.12	405.52	112.27

Table 3. Numerical discrete solutions for test problem 1.

$\mathit{x}$			$\mathit{n}=1024$
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	0.0000000000	0.0000000000	0.0000000000	0.0000000000	0.0000000000
0.25	5.4375000000	5.4375422001	5.4374999834	5.4374998680	5.4374989407
0.50	9.7500000000	9.7500758171	9.7499999703	9.7499997640	9.7499981067
0.75	12.9375000000	12.9376008511	12.9374999608	12.9374996882	12.9374974982
1.00	15.0000000000	15.0001173021	14.9999999548	14.9999996405	14.9999971150
$\mathit{x}$			$\mathit{n}=\mathbf{2048}$
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	0.0000000000	0.0000000000	0.0000000000	0.0000000000	0.0000000000
0.25	5.4375000000	5.4375105498	5.4374999978	5.4374999834	5.4374998680
0.50	9.7500000000	9.7500189538	9.7499999960	9.7499999703	9.7499997640
0.75	12.9375000000	12.9375252122	12.9374999948	12.9374999608	12.9374996882
1.00	15.0000000000	15.0000293249	14.9999999940	14.9999999548	14.9999996405
$\mathit{x}$			$\mathit{n}=\mathbf{4096}$
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	0.0000000000	0.0000000000	0.0000000000	0.0000000000	0.0000000000
0.25	5.4375000000	5.4375026372	5.4374999996	5.4374999978	5.4374999834
0.50	9.7500000000	9.7500047381	9.7499999992	9.7499999960	9.7499999703
0.75	12.9375000000	12.9375063025	12.9374999990	12.9374999948	12.9374999608
1.00	15.0000000000	15.0000073307	14.9999999989	14.9999999940	14.9999999548
$\mathit{x}$			$\mathit{n}=\mathbf{8192}$
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	0.0000000000	0.0000000000	0.0000000000	0.0000000000	0.0000000000
0.25	5.4375000000	5.4375006591	5.4374999998	5.4374999996	5.4374999978
0.50	9.7500000000	9.7500011841	9.7499999996	9.7499999992	9.7499999960
0.75	12.9375000000	12.9375015751	12.9374999995	12.9374999990	12.9374999948
1.00	15.0000000000	15.0000018321	14.9999999995	14.9999999989	14.9999999940
$\mathit{x}$			$\mathit{n}$= 16,384
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	0.0000000000	0.0000000000	0.0000000000	0.0000000000	0.0000000000
0.25	5.4375000000	5.4375001645	5.4374999998	5.4374999998	5.4374999996
0.50	9.7500000000	9.7500002956	9.7499999997	9.7499999996	9.7499999992
0.75	12.9375000000	12.9375003933	12.9374999996	12.9374999995	12.9374999990
1.00	15.0000000000	15.0000004575	14.9999999996	14.9999999995	14.9999999989

Table 4. Numerical discrete solutions for test problem 2.

$\mathit{x}$			$\mathit{n}=1024$
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	25.4880952381	25.4881398776	25.4880952013	25.4880949434	25.4880928707
0.25	27.9928036644	27.9928529780	27.9928036232	27.9928033343	27.9928010125
0.50	34.7090773810	34.7091407166	34.7090773265	34.7090769446	34.7090738755
0.75	45.3000023251	45.3000890310	45.3000022486	45.3000017117	45.2999973971
1.00	59.8095238095	59.8096432336	59.8095237020	59.8095229482	59.8095168899
$\mathit{x}$			$\mathit{n}=\mathbf{2048}$
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	25.4880952381	25.4881063979	25.4880952335	25.4880952013	25.4880949434
0.25	27.9928036644	27.9928159928	27.9928036593	27.9928036232	27.9928033343
0.50	34.7090773810	34.7090932148	34.7090773741	34.7090773265	34.7090769446
0.75	45.3000023251	45.3000240015	45.3000023155	45.3000022486	45.3000017117
1.00	59.8095238095	59.8095536654	59.8095237960	59.8095237020	59.8095229482
$\mathit{x}$			$\mathit{n}=\mathbf{4096}$
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	25.4880952381	25.4880980280	25.4880952375	25.4880952335	25.4880952013
0.25	27.9928036644	27.9928067465	27.9928036637	27.9928036593	27.9928036232
0.50	34.7090773810	34.7090813393	34.7090773800	34.7090773741	34.7090773265
0.75	45.3000023251	45.3000077441	45.3000023239	45.3000023155	45.3000022486
1.00	59.8095238095	59.8095312734	59.8095238078	59.8095237960	59.8095237020
$\mathit{x}$			$\mathit{n}=\mathbf{8192}$
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	25.4880952381	25.4880959355	25.4880952380	25.4880952375	25.4880952335
0.25	27.9928036644	27.9928044349	27.9928036643	27.9928036637	27.9928036593
0.50	34.7090773810	34.7090783705	34.7090773808	34.7090773800	34.7090773741
0.75	45.3000023251	45.3000036798	45.3000023249	45.3000023239	45.3000023155
1.00	59.8095238095	59.8095256754	59.8095238092	59.8095238078	59.8095237960
$\mathit{x}$			$\mathit{n}$= 16,384
	Exact	FSGS-RT	FSGS-RMT	HSGS-RMT	QSGS-RMT
0.00	25.4880952381	25.4880954124	25.4880952380	25.4880952380	25.4880952335
0.25	27.9928036644	27.9928038570	27.9928036644	27.9928036643	27.9928036593
0.50	34.7090773810	34.7090776283	34.7090773809	34.7090773808	34.7090773741
0.75	45.3000023251	45.3000026637	45.3000023251	45.3000023249	45.3000023155
1.00	59.8095238095	59.8095242759	59.8095238094	59.8095238092	59.8095237960

5. Computational Complexity Analysis

In order to measure the computational complexity of the methods, the amount of computational work required from each method for solving problem (1) was estimated by considering the arithmetic operations performed per iteration. In estimating the computational work of the proposed methods, it is assumed that the values of $ph$, $K_{i,j}$, $H_{i,j}$, $J_{i,j}$ and $L_{i,j}$ are stored beforehand. Based on Algorithm 1 (for Case 1), it can be observed that the number of arithmetic operations required (excluding the convergence test) per iteration for the FSGS-RMT, HSGS-RMT and QSGS-RMT methods is $({\left(\frac{n}{p}\right)}^2+\frac{8n}{p}+7)$ additions/subtractions (ADD/SUB) and $({\left(\frac{n}{p}\right)}^2+\frac{12n}{p}+17)$ multiplications/divisions (MUL/DIV). Meanwhile, for Case 2 (Algorithm 2), $({\left(\frac{n}{p}\right)}^2+\frac{8n}{p}+15)$ ADD/SUB and $({\left(\frac{n}{p}\right)}^2+\frac{12n}{p}+29)$ MUL/DIV operations are involved for an iteration.

The iteration process for the HSGS-RMT and QSGS-RMT methods is carried out only on $(\frac{n}{2}+3)$ and $(\frac{n}{4}+3)$ mesh points, respectively. Thus, an additional two ADD/SUB and six MUL/DIV operations are involved to calculate a mesh point for the remaining points after convergence by using second-order Lagrange interpolation. Hence, the total numbers of arithmetic operations involved in an iteration and in the direct solution after convergence for the FSGS-RMT, HSGS-RMT and QSGS-RMT methods are summarized in Table 5.

Table 5. Total computing operations for the FSGS-RMT, HSGS-RMT and QSGS-RMT methods.

	Case 1
Methods	Per Iteration		After Convergence
	ADD/SUB	MUL/DIV	ADD/SUB	MUL/DIV
FSGS-RMT	$n^2+8n+7$	$n^2+12n+17$	-	-
HSGS-RMT	$\frac{n^2}{4}+4n+7$	$\frac{n^2}{4}+6n+17$	n	$3n$
QSGS-RMT	$\frac{n^2}{16}+2n+7$	$\frac{n^2}{16}+3n+17$	$\frac{3n}{2}$	$\frac{9n}{2}$
	Case 2
Methods	Per Iteration		After Convergence
	ADD/SUB	MUL/DIV	ADD/SUB	MUL/DIV
FSGS-RMT	$n^2+8n+15$	$n^2+12n+29$	-	-
HSGS-RMT	$\frac{n^2}{4}+4n+15$	$\frac{n^2}{4}+6n+29$	n	$3n$
QSGS-RMT	$\frac{n^2}{16}+2n+15$	$\frac{n^2}{16}+3n+29$	$\frac{3n}{2}$	$\frac{9n}{2}$

6. Conclusions

In this paper, a complexity reduction approach based on the half- and quarter-sweep iteration concepts has been successfully employed to obtain the estimation solutions for the second kind of linear Fredholm integral equations. Through numerical results obtained for test problems 1 and 2 (refer Table 1 and Table 2), the findings show that the numbers of iterations for the FSGS-RMT, HSGS-RMT and QSGS-RMT methods are nearly the same. In terms of computational time, both the HSGS-RMT and QSGS-RMT methods are faster than the FSGS-RMT method. This is due to the reduction in the computational complexity of the HSGS-RMT and QSGS-RMT methods, which is approximately $75\%$ and $93.75\%$ less than the FSGS-RMT method, respectively. Meanwhile, accuracies of numerical solutions for the HSGS-RMT and QSGS-RMT methods are also in good agreement compared to the FSGS-RMT method. The findings also support the claim in [13] that the RMT scheme is more accurate than the repeated trapezoidal scheme; refer to Table 3 and Table 4. Overall, the results reveal that the QSGS-RMT method is superior to the FSGS-RT, FSGS-RMT and HSGS-RMT methods. For future works, the effectiveness of the proposed complexity reduction approach will be investigated in solving fractional integro-differential equations [25,26].