The Existence, Uniqueness, and Stability Analysis of the Discrete Fractional Three-Point Boundary Value Problem for the Elastic Beam Equation
Abstract
1. Introduction
2. Essential Preliminaries
3. EB Existence and Uniqueness
- (A1)
- There exists a constant , which satisfies for all and each .
- (A2)
- There exists a bounded function with for all .
4. EB Stability Analysis
- (A3)
- ,
- (A4)
- .
- ()
- For an increasing function , there exists such that, for(i) ,(ii) .
5. Applications
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cianciaruso, F.; Infante, G.; Pietramala, P. Solutions of perturbed hammerstein integral equations with applications. arXiv 2016, arXiv:1602.00976v4. [Google Scholar] [CrossRef]
- Infante, G.; Pietramala, P. A cantilever equation with nonlinear boundary conditions. Electron. J. Qual. Theory Differ. Equ. 2009, 15, 1–14. [Google Scholar] [CrossRef]
- Li, Y. Existence of positive solutions for the cantilever beam equations with fully nonlinear terms. Nonlinear Anal. Real World Appl. 2016, 27, 221–237. [Google Scholar] [CrossRef]
- Song, Y. A nonlinear boundary value problem for fourth-order elastic beam equations. Bound. Value Probl. 2014, 191, 1–11. [Google Scholar] [CrossRef]
- Li, S.; Zhai, C. New existence and uniqueness results for an elastic beam equation with nonlinear boundary conditions. Bound. Value Probl. 2015, 104, 1–12. [Google Scholar] [CrossRef][Green Version]
- Gupta, C.P. Existence and uniqueness theorems for the bending of an elastic beam equation. Appl. Anal. 1988, 26, 289–304. [Google Scholar] [CrossRef]
- Kumar, A.; Chauhan, H.V.S.; Ravichandran, C.; Nisar, K.S.; Baleanu, D. Existence of solutions of non-autonomous fractional differential equations with integral impulse condition. Adv. Differ. Equ. 2020, 434, 1–15. [Google Scholar] [CrossRef]
- Ismail, M.; Saeed, U.; Alzabut, J.; Rehman, M. Approximate solutions for fractional boundary value problems via green-cas wavelet method. Mathematics 2019, 7, 1164. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Benchohra, M.; Litimein, S.; Nieto, J.J. Semilinear fractional differential equations with infinite delay and non-instantaneous impulses. J. Fixed Point Theory Appl. 2019, 21, 1–21. [Google Scholar] [CrossRef]
- Almeida, R. What is the best fractional derivative to fit data? Appl. Anal. Discrete Math. 2017, 11, 358–368. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Fractional derivatives applied to MSEIR problems: Comparative study with real world data. Eur. Phys. J. Plus 2019, 134, 1–17. [Google Scholar] [CrossRef]
- Matar, M.M.; Abbas, M.I.; Alzabut, J.; Kaabar, M.K.A.; Etemad, S.; Rezapour, S. Investigation of the p-Laplacian nonperiodic nonlinear boundary value problem via generalized Caputo fractional derivatives. Adv. Differ. Equ. 2021, 68, 1–18. [Google Scholar]
- Pratap, A.; Raja, V.; Alzabut, J.; Dianavinnarasi, J.; Cao, J.; Rajchakit, G. Finite-time Mittag-Leffler stability of fractional-order quaternion-valued memristive neural networks with impulses. Neural Process Lett. 2020, 51, 1485–1526. [Google Scholar] [CrossRef]
- Wu, R.C.; Hei, X.D.; Chen, L.P. Finite-time stability of fractional-order neural networks with delay. Commun. Theor. Phys. 2013, 60, 189–193. [Google Scholar] [CrossRef]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process 2011, 91, 437–445. [Google Scholar] [CrossRef]
- Stamova, I. Mittag-Leffler stability of impulsive differential equations of fractional order. Q. Appl. Math. 2015, 73, 525–535. [Google Scholar] [CrossRef]
- Lijun, G.; Wang, D.; Wang, G. Further results on exponential stability for impulsive switched nonlinear time-delay systems with delayed impulse effects. Appl. Math. Comput. 2015, 268, 186–200. [Google Scholar]
- Hyers, D. On the stability of the linear functional equation. Proc. Natl. Acad Sci. USA 1941, 27, 222–224. [Google Scholar] [CrossRef] [PubMed]
- Obloza, M. Hyers stability of the linear differential equation. Rocznik Nauk-Dydakt Prace Mat. 1993, 13, 259–270. [Google Scholar]
- Ulam, S.M. Problems in Modern Mathematics; Wiley: New York, NY, USA, 1940. [Google Scholar]
- Ahmad, M.; Zada, A.; Alzabut, J. Stability analysis of a nonlinear coupled implicit switched singular fractional differential system with p-Laplacian. Adv. Differ. Equ. 2019, 436, 1–22. [Google Scholar] [CrossRef]
- Zada, A.; Alzabut, J.; Waheed, H.; Loan-Lucian, P. Ulam–Hyers stability of impulsive integrodifferential equations with Riemann-Liouville boundary conditions. Adv. Differ. Equ. 2020, 1, 1–50. [Google Scholar] [CrossRef]
- Iswarya, M.; Raja, R.; Rajchakit, G.; Cao, J.; Alzabut, J.; Huang, C. Existence, uniqueness and exponential stability of periodic solution for discrete–time delayed BAM neural networks based on coincidence degree theory and graph theoretic method. Mathematics 2019, 7, 1055. [Google Scholar] [CrossRef]
- Guo, Y.; Shu, X.; Li, Y.; Xu, F. The existence and Hyers–Ulam stability of solution for an impulsive Riemann–Liouville fractional neutral functional stochastic differential equation with infinite delay of order 1 < β < 2. Bound. Value Prob. 2019, 59. [Google Scholar] [CrossRef]
- Ahmad, M.; Zada, A.; Alzabut, J. Hyres–Ulam Stability of Coupled System of Fractional Differential Equations of Hilfer– Hadamard Type. Demonstr. Math. 2019, 52, 283–295. [Google Scholar] [CrossRef]
- Salem, A.; Alzahrani, F.; Almaghamsi, L. Fractional Langevin equations with nonlocal integral boundary conditions. Mathematics 2019, 7, 402. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. A transform method in discrete fractional calculus. Int. J. Difference Equ. 2017, 2, 165–176. [Google Scholar]
- Atici, F.M.; Eloe, P.W. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. Fractional difference calculus. In Proceedings of the International Symposium on Univalent Functions, Fractional Calculus and their Applications; Nihon University: Koriyama, Japan, 1988; pp. 139–152. [Google Scholar]
- Goodrich, C.S.; Peterson, A.C. Discrete Fractional Calculus; Springer: New York, NY, USA, 2015. [Google Scholar]
- Atici, F.M.; Eloe, P.W. Two–point boundary value problems for finite fractional difference equations. J. Differ. Equ. Appl. 2011, 17, 445–456. [Google Scholar] [CrossRef]
- Alzabut, J.; Abdeljawad, T.; Baleanu, D. Nonlinear delay fractional difference equations with applications on discrete fractional Lotka-Volterra competition model. J. Comput. Anal. Appl. 2018, 25, 889–898. [Google Scholar]
- Chen, F.; Zhou, Y. Existence and Ulam Stability of Solutions for Discrete Fractional Boundary Value Problem. Discret. Dyn. Nat. Soc. 2013, 1–7. [Google Scholar] [CrossRef]
- Chen, H.; Jin, Z.; Kang, S. Existence of positive solution for Caputo fractional difference equation. Adv. Differ. Equ. 2015, 44, 1–12. [Google Scholar] [CrossRef]
- Chen, C.; Bohner, M.; Jia, B. Ulam-Hyers stability of Caputo fractional difference equations. Math. Meth. Appl. Sci. 2019, 42, 7461–7470. [Google Scholar] [CrossRef]
- Chen, C.; Bohner, M.; Jia, B. Method of upper and lower solutions for nonlinear Caputo fractional difference equations and its applications. Fract. Calc. Appl. Anal. 2019, 22, 1307–1320. [Google Scholar] [CrossRef]
- Chen, C.; Bohner, M.; Jia, B. Existence and uniqueness of solutions for nonlinear Caputo fractional difference equations. Turk. J. Math. 2020, 44, 857–869. [Google Scholar] [CrossRef]
- Goodrich, C.S. Solutions to a discrete right-focal fractional boundary value problem. Int. J. Differ. Equ. 2010, 5, 195–216. [Google Scholar]
- Goodrich, C.S. Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions. Comput. Math. Appl. 2011, 61, 191–202. [Google Scholar] [CrossRef]
- Rehman, M.; Iqbal, F.; Seemab, A. On existence of positive solutions for a class of discrete fractional boundary value problems. Positivity 2017, 21, 1173–1187. [Google Scholar] [CrossRef]
- Selvam, A.G.M.; Dhineshbabu, R. Uniqueness of solutions of a discrete fractional order boundary value problem. AIP Conf. Proc. 2019, 2095, 1–7. [Google Scholar]
- Selvam, A.G.M.; Alzabut, J.; Dhineshbabu, R.; Rashid, S.; Rehman, M. Discrete fractional order two-point boundary value problem with some relevant physical applications. J. Inequal. Appl. 2020, 221, 1–19. [Google Scholar] [CrossRef]
- Selvam, A.G.M.; Dhineshbabu, R. Ulam stability results for boundary value problem of fractional difference equations. Adv. Math. Sci. J. 2020, 9, 219–230. [Google Scholar] [CrossRef]
- Selvam, A.G.M.; Dhineshbabu, R. Existence and uniqueness of solutions for a discrete fractional boundary value problem. Int. J. Appl. Math. 2020, 33, 283–295. [Google Scholar]
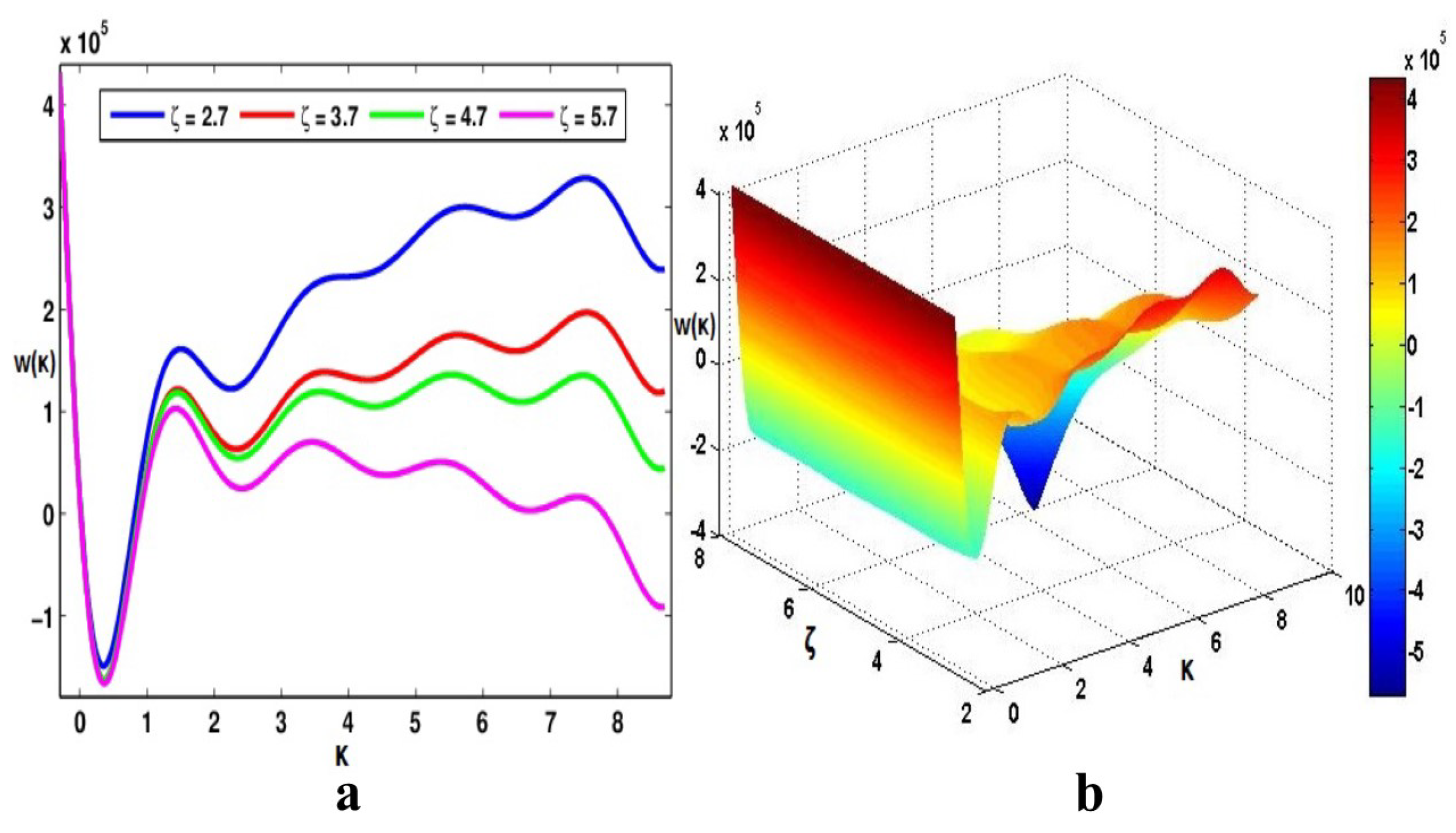
| 2.7 | 3.7 | 4.7 | 5.7 | |
| −0.3 | 4.3158 | 4.3158 | 4.3158 | 4.3158 |
| 0.7 | −0.5233 | −0.7356 | −0.7410 | −0.8078 |
| 1.7 | 1.5354 | 1.0872 | 1.0384 | 0.8468 |
| 2.7 | 1.4988 | 0.8076 | 0.6918 | 0.3413 |
| 3.7 | 2.3044 | 1.3849 | 1.1846 | 0.6559 |
| 4.7 | 2.5123 | 1.3991 | 1.1014 | 0.3865 |
| 5.7 | 3.0038 | 1.7498 | 1.3450 | 0.4457 |
| 6.7 | 2.9459 | 1.6211 | 1.1023 | 0.0290 |
| 7.7 | 3.2506 | 1.9406 | 1.3037 | 0.0745 |
| 8.7 | 2.3972 | 1.2029 | 0.4457 | −0.9137 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzabut, J.; Selvam, A.G.M.; Dhineshbabu, R.; Kaabar, M.K.A. The Existence, Uniqueness, and Stability Analysis of the Discrete Fractional Three-Point Boundary Value Problem for the Elastic Beam Equation. Symmetry 2021, 13, 789. https://doi.org/10.3390/sym13050789
Alzabut J, Selvam AGM, Dhineshbabu R, Kaabar MKA. The Existence, Uniqueness, and Stability Analysis of the Discrete Fractional Three-Point Boundary Value Problem for the Elastic Beam Equation. Symmetry. 2021; 13(5):789. https://doi.org/10.3390/sym13050789
Chicago/Turabian StyleAlzabut, Jehad, A. George Maria Selvam, R. Dhineshbabu, and Mohammed K. A. Kaabar. 2021. "The Existence, Uniqueness, and Stability Analysis of the Discrete Fractional Three-Point Boundary Value Problem for the Elastic Beam Equation" Symmetry 13, no. 5: 789. https://doi.org/10.3390/sym13050789
APA StyleAlzabut, J., Selvam, A. G. M., Dhineshbabu, R., & Kaabar, M. K. A. (2021). The Existence, Uniqueness, and Stability Analysis of the Discrete Fractional Three-Point Boundary Value Problem for the Elastic Beam Equation. Symmetry, 13(5), 789. https://doi.org/10.3390/sym13050789








