The Comparative Study for Solving Fractional-Order Fornberg–Whitham Equation via ρ-Laplace Transform
Abstract
1. Introduction
2. Basic Definitions
3. The General Methodology of -LDM
4. Convergence Analysis
5. The General Methodology of -Laplace Variational Iteration Method
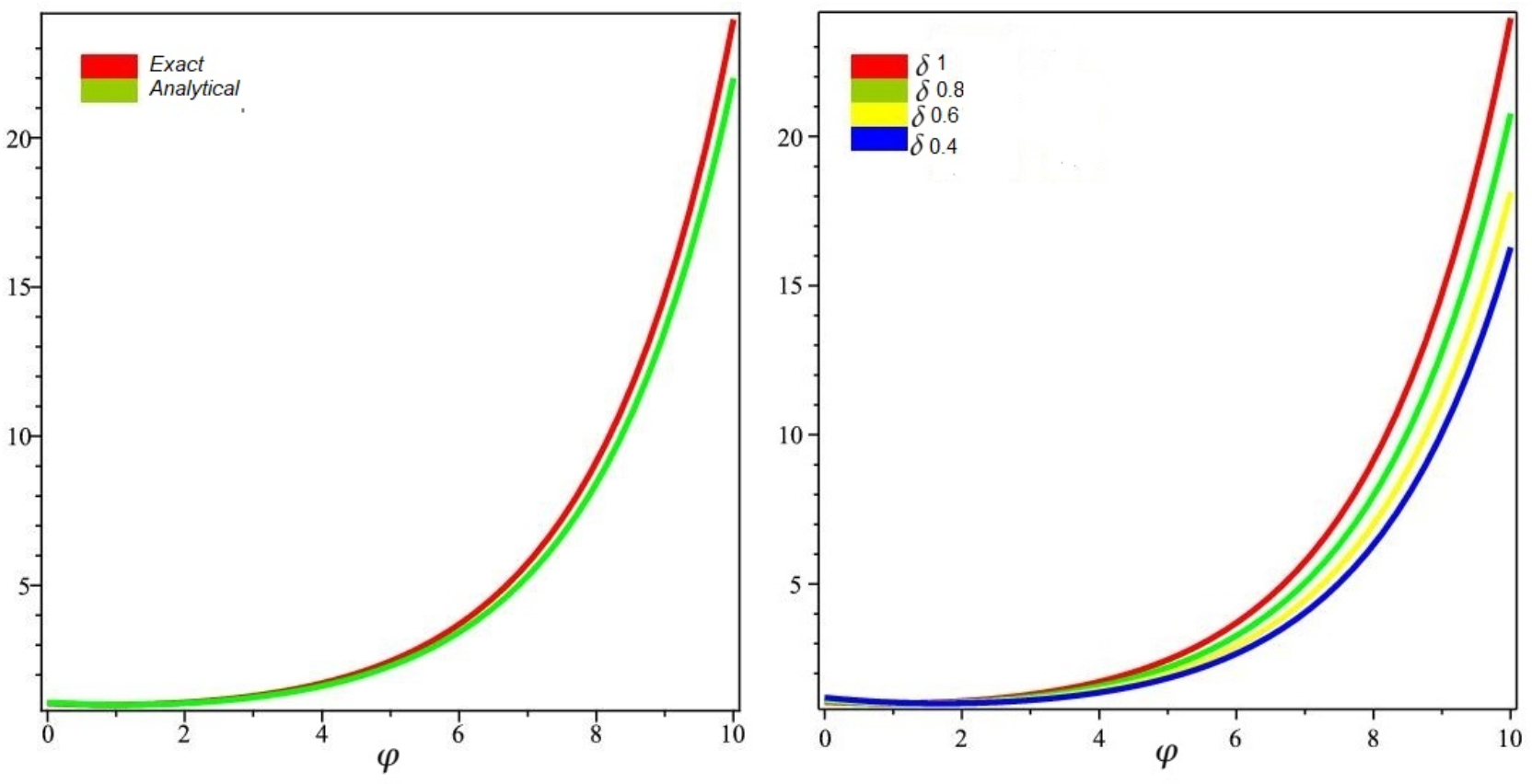
6. Implementation of Techniques
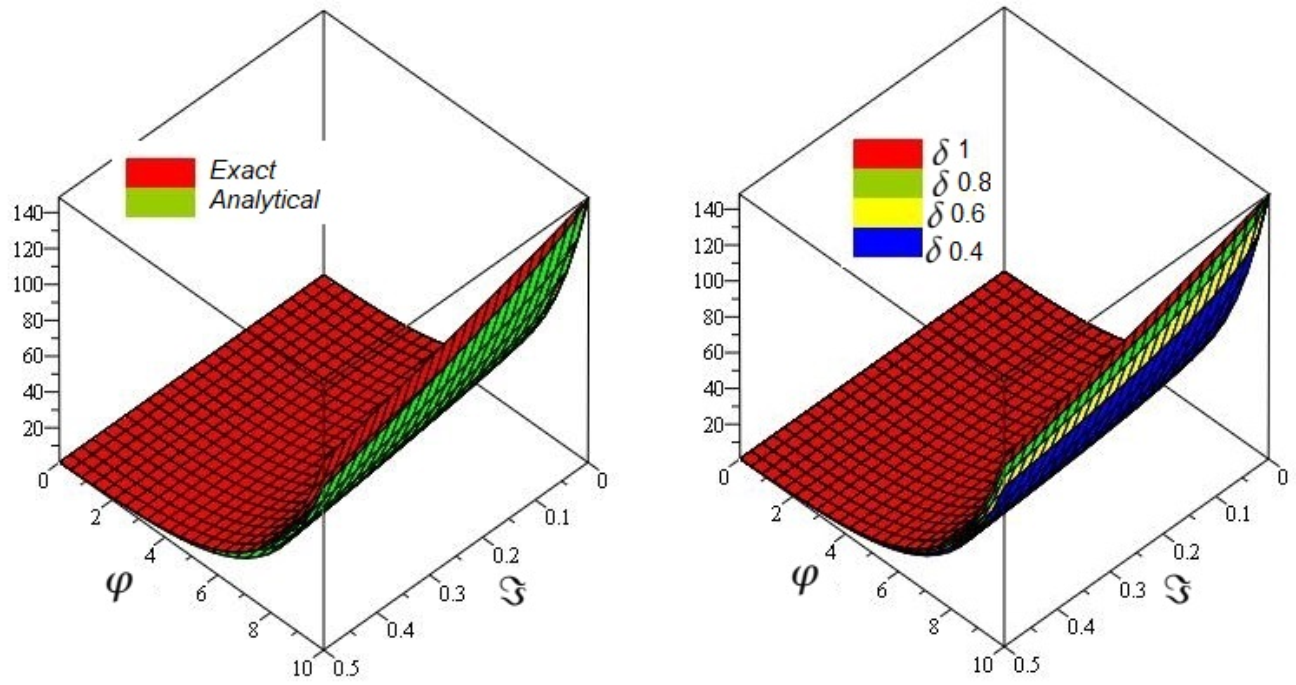
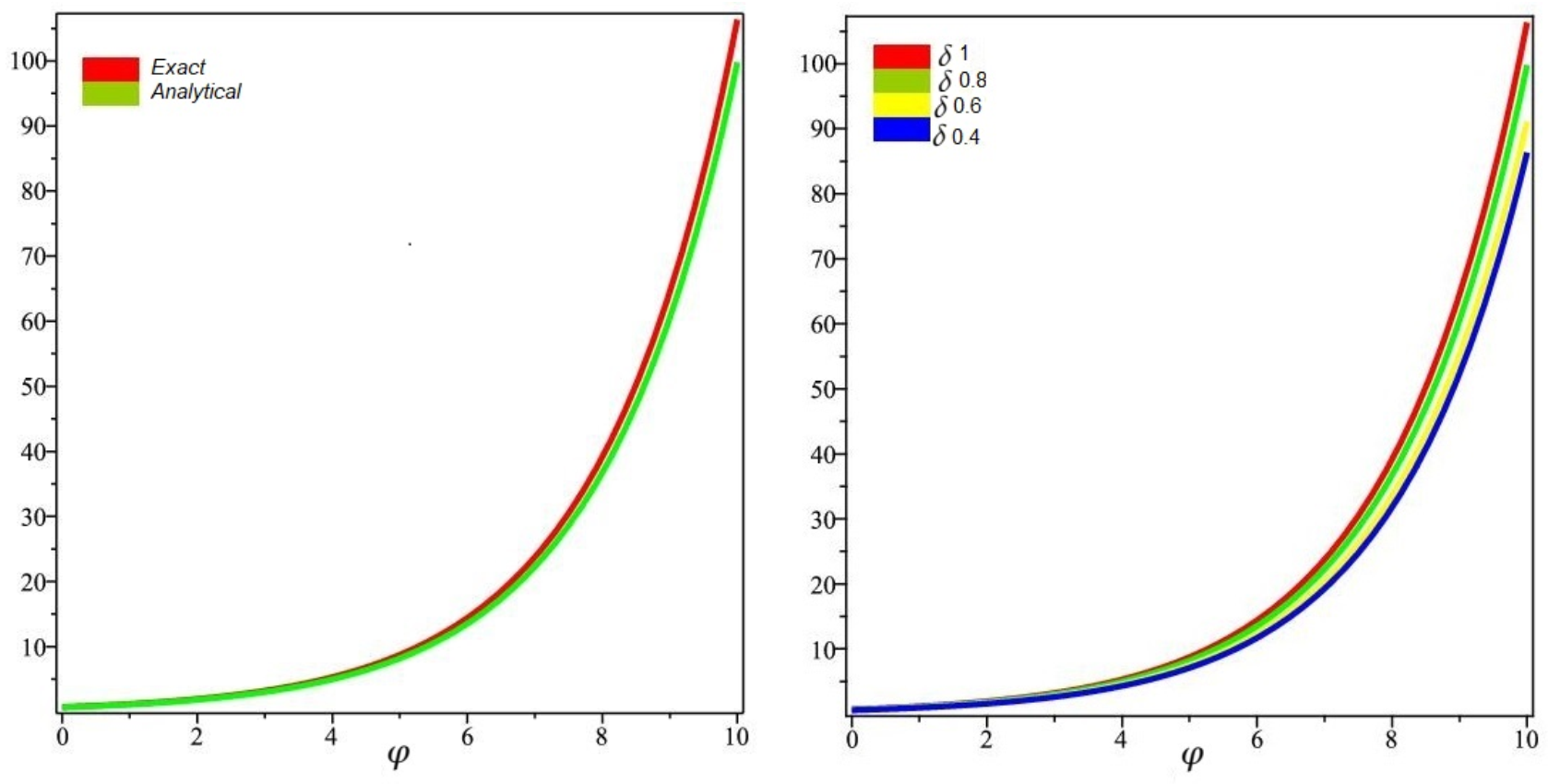
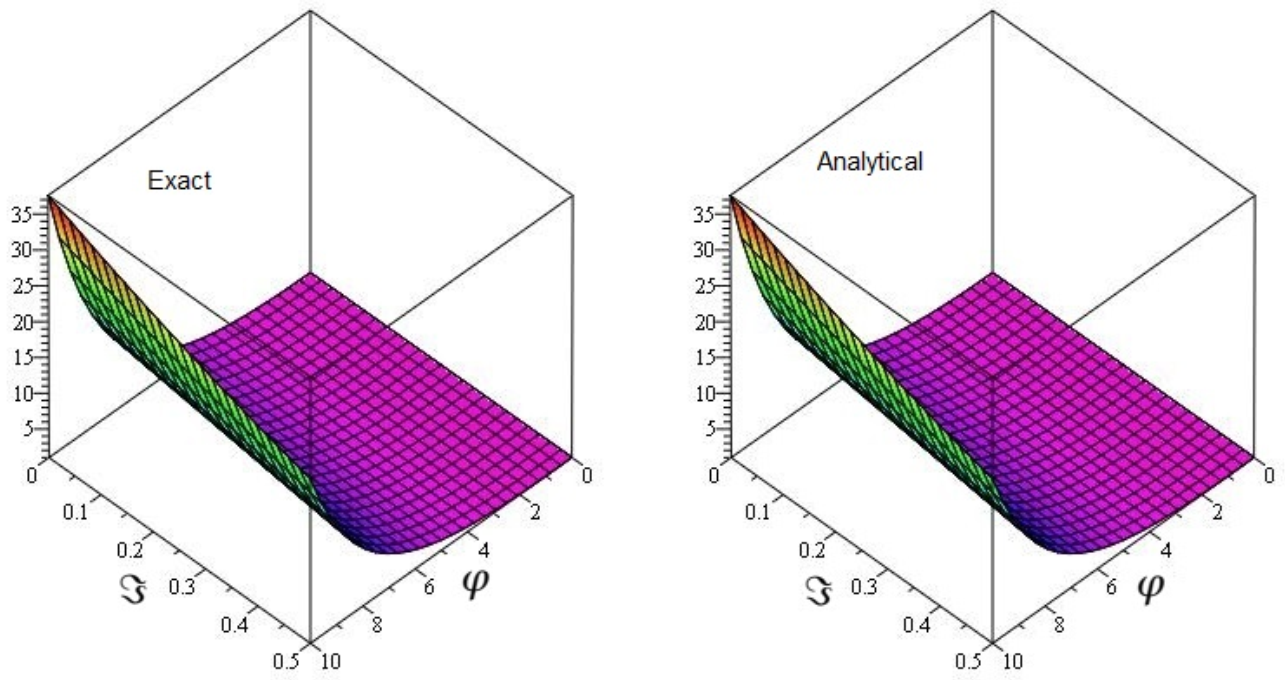
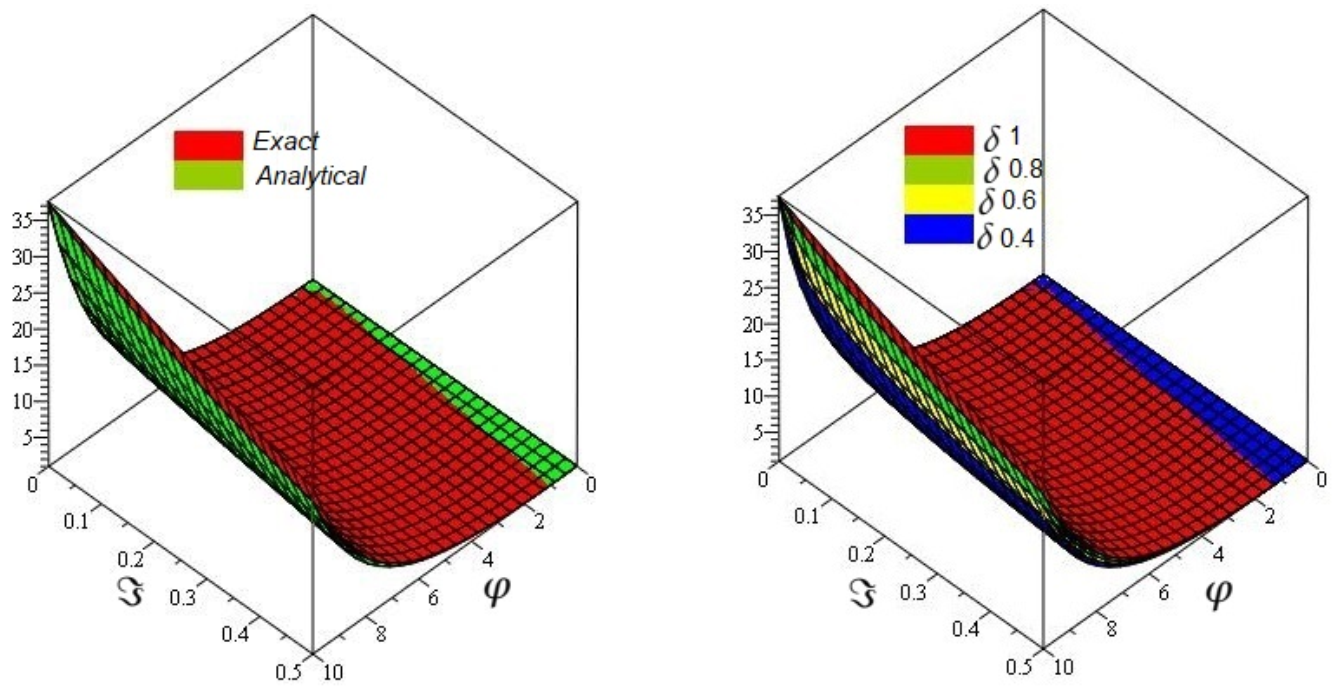
6.1. Problem
6.2. Problem
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M.; Baleanu, D. Fractional modeling of blood ethanol concentration system with real data application. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013143. [Google Scholar] [CrossRef]
- Yusuf, A.; Qureshi, S.; Inc, M.; Aliyu, A.I.; Baleanu, D.; Shaikh, A.A. Two-strain epidemic model involving fractional derivative with Mittag-Leffler kernel. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 123121. [Google Scholar] [CrossRef] [PubMed]
- Kilic, B.; Inc, M. The first integral method for the time fractional Kaup-Boussinesq system with time dependent coefficient. Appl. Math. Comput. 2015, 254, 70–74. [Google Scholar] [CrossRef]
- Inc, M.; Akgul, A.; Kilicman, A. Numerical solutions of the second-order one-dimensional telegraph equation based on reproducing kernel Hilbert space method. Abstr. Appl. Anal. 2013, 2013, 768963. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000; Volume 35, pp. 87–130. [Google Scholar]
- Cesarano, C.; Pierpaolo, N.; Paolo, E.R. Pseudo-Lucas Functions of Fractional Degree and Applications. Axioms 2021, 10, 51. [Google Scholar] [CrossRef]
- Sabatier, J.A.T.M.J.; Agrawal, O.P.; Machado, J.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007; Volume 4. [Google Scholar]
- Al-luhaibi, M.S. An analytical treatment to fractional Fornberg-Whitham equation. Math. Sci. 2017, 11, 1–6. [Google Scholar] [CrossRef]
- Agarwal, P.; Ahs, S.; Akbare, M.; Nawaz, R.; Cesarano, C. A Reliable Algorithm for solution of Higher Dimensional Nonlinear (1+1) and (2+1) Dimensional Volterra-Fredholm Integral Equations. Dolomites Res. Notes Approx. 2021, 14, 18–25. [Google Scholar]
- Zakarya, M.; Altanji, M.; AlNemer, G.; Abd El-Hamid, H.A.; Cesarano, C.; Rezk, H.M. Fractional Reverse Coposn’s Inequalities via Conformable Calculus on Time Scales. Symmetry 2021, 13, 542. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, H.; Thounthong, P.; Chu, Y.-M.; Cesarano, C. Solution of Multi-Term Time-Fractional PDE Models Arising in Mathematical Biology and Physics by Local Meshless Method. Symmetry 2020, 12, 1195. [Google Scholar] [CrossRef]
- Bazighifan, O.; Cesarano, C. A Philos-type oscillation criteria for fourth-order neutral differential equations. Symmetry 2020, 12, 379. [Google Scholar] [CrossRef]
- Camacho, J.C.; Rosa, M.; Garias, M.L.; Bruzon, M.S. Classical symmetries, travelling wave solutions and conservation laws of a generalized Fornberg-Whitham equation. J. Comput. Appl. Math. 2017, 318, 149–155. [Google Scholar] [CrossRef]
- Bruzon, M.S.; Marquez, A.P.; Garrido, T.M.; Recio, E.; de la Rosa, R. Conservation laws for a generalized seventh order KdV equation. J. Comput. Appl. Math. 2019, 354, 682–688. [Google Scholar] [CrossRef]
- Whitham, G.B. Variational methods and applications to water waves. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1967, 299, 6–25. [Google Scholar]
- Fornberg, B.; Whitham, G.B. A numerical and theoretical study of certain nonlinear wave phenomena. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1978, 289, 373–404. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. A new analysis of the Fornberg-Whitham equation pertaining to a fractional derivative with Mittag-Leffler-type kernel. Eur. Phys. J. Plus 2018, 133, 1–10. [Google Scholar] [CrossRef]
- Lu, J. An analytical approach to the Fornberg-Whitham type equations by using the variational iteration method. Comput. Math. Appl. 2011, 61, 2010–2013. [Google Scholar] [CrossRef][Green Version]
- Hashemi, M.S.; Haji-Badali, A.; Vafadar, P. Group invariant solutions and conservation laws of the Fornberg-Whitham equation. Z. Naturforschung A 2014, 69, 489–496. [Google Scholar] [CrossRef]
- Ramadan, M.A.; Al-luhaibi, M.S. New iterative method for solving the fornberg-whitham equation and comparison with homotopy perturbation transform method. J. Adv. Math. Comput. Sci. 2014, 4, 1213–1227. [Google Scholar] [CrossRef]
- Merdan, M.; Gokdogan, A.; Yildirim, A.; Mohyud-Din, S.T. Numerical simulation of fractional Fornberg-Whitham equation by differential transformation method. Abstr. Appl. Anal. 2012, 2012, 965367. [Google Scholar] [CrossRef]
- Wang, K.; Liu, S. Application of new iterative transform method and modified fractional homotopy analysis transform method for fractional Fornberg-Whitham equation. J. Nonlinear Sci. Appl. 2016, 9, 2419–2433. [Google Scholar] [CrossRef]
- Abidi, F.; Omrani, K. Numerical solutions for the nonlinear Fornberg-Whitham equation by He’s methods. Int. J. Mod. Phys. B 2011, 25, 4721–4732. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. A modifi ed Laplace transform for certain generalized fractional operators. Results Nonlinear Anal. 2018, 1, 88–98. [Google Scholar]
- He, J.H. Approximate solution of nonlinear differential equations with convolution product nonlinearities. Comput. Methods Appl. Mech. Eng. 1998, 167, 69–73. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput. 2000, 114, 115–123. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Variational iteration method for fractional calculus-a universal approach by Laplace transform. Adv. Differ. Equ. 2013, 2013, 18. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Laplace transform: Making the variational iteration method easier. Appl. Math. Lett. 2019, 92, 134–138. [Google Scholar] [CrossRef]
- Dehghan, M. Finite difference procedures for solving a problem arising in modeling and design of certain optoelectronic devices. Math. Comput. Simul. 2006, 71, 16–30. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Boston, MA, USA, 1994. [Google Scholar]
- Khalouta, A.; Kadem, A. A New Method to Solve Fractional Differential Equations: Inverse Fractional Laplace Transform Method. Appl. Appl. Math. 2019, 14, 926–941. [Google Scholar]
- Bokhari, A.; Baleanu, D.; Belgacem, R. Application of Laplace transform to Atangana-Baleanu derivatives. J. Math. Comput. Sci. 2019, 20, 101–107. [Google Scholar] [CrossRef]
- Belgacem, R.; Baleanu, D.; Bokhari, A. Laplace Transform and Applications to Caputo-Fractional Differential Equations. Int. J. Anal. Appl. 2019, 17, 917–927. [Google Scholar]
- Machado, J.; Baleanu, D.; Chen, W.; Sabatier, J. New trends in fractional dynamics. J. Vib. Control 2014, 20, 963. [Google Scholar] [CrossRef]
- Baleanu, D.; Guvenc, Z.; Machado, J. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Maitama, S.; Zhao, W. New integral transform: Laplace transform a generalization of Sumudu and Laplace transform for solving differential equations. arXiv 2019, arXiv:1904.11370. [Google Scholar]
- El-Kalla, I.L. Convergence of the Adomian method applied to a class of nonlinear integral equations. Appl. Math. Lett. 2008, 21, 372–376. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunthrayuth, P.; Zidan, A.M.; Yao, S.-W.; Shah, R.; Inc, M. The Comparative Study for Solving Fractional-Order Fornberg–Whitham Equation via ρ-Laplace Transform. Symmetry 2021, 13, 784. https://doi.org/10.3390/sym13050784
Sunthrayuth P, Zidan AM, Yao S-W, Shah R, Inc M. The Comparative Study for Solving Fractional-Order Fornberg–Whitham Equation via ρ-Laplace Transform. Symmetry. 2021; 13(5):784. https://doi.org/10.3390/sym13050784
Chicago/Turabian StyleSunthrayuth, Pongsakorn, Ahmed M. Zidan, Shao-Wen Yao, Rasool Shah, and Mustafa Inc. 2021. "The Comparative Study for Solving Fractional-Order Fornberg–Whitham Equation via ρ-Laplace Transform" Symmetry 13, no. 5: 784. https://doi.org/10.3390/sym13050784
APA StyleSunthrayuth, P., Zidan, A. M., Yao, S.-W., Shah, R., & Inc, M. (2021). The Comparative Study for Solving Fractional-Order Fornberg–Whitham Equation via ρ-Laplace Transform. Symmetry, 13(5), 784. https://doi.org/10.3390/sym13050784





