Computational Properties of General Indices on Random Networks

Abstract

We perform a detailed (computational) scaling study of well-known general indices (the first and second variable Zagreb indices, $M_1^{\alpha }\left(G\right)$ and $M_2^{\alpha }\left(G\right)$, and the general sum-connectivity index, ${\chi }_{\alpha }\left(G\right)$) as well as of general versions of indices of interest: the general inverse sum indeg index $IS{I}_{\alpha }\left(G\right)$ and the general first geometric-arithmetic index $G{A}_{\alpha }\left(G\right)$ (with $\alpha \in \mathbb{R}$). We apply these indices on two models of random networks: Erdös–Rényi (ER) random networks $G_{\mathrm{ER}}(n_{\mathrm{ER}},p)$ and random geometric (RG) graphs $G_{\mathrm{RG}}(n_{\mathrm{RG}},r)$. The ER random networks are formed by $n_{\mathrm{ER}}$ vertices connected independently with probability $p\in [0,1]$; while the RG graphs consist of $n_{\mathrm{RG}}$ vertices uniformly and independently distributed on the unit square, where two vertices are connected by an edge if their Euclidean distance is less or equal than the connection radius $r\in [0,\sqrt{2}]$. Within a statistical random matrix theory approach, we show that the average values of the indices normalized to the network size scale with the average degree $⟨k⟩$ of the corresponding random network models, where $⟨k_{\mathrm{ER}}⟩=(n_{\mathrm{ER}}-1)p$ and $⟨k_{\mathrm{RG}}⟩=(n_{\mathrm{RG}}-1)(\pi r^2-8r^3/3+r^4/2)$. That is, $⟨X\left(G_{\mathrm{ER}}\right)⟩/n_{\mathrm{ER}}\approx ⟨X\left(G_{\mathrm{RG}}\right)⟩/n_{\mathrm{RG}}$ if $⟨k_{\mathrm{ER}}⟩=⟨k_{\mathrm{RG}}⟩$, with X representing any of the general indices listed above. With this work, we give a step forward in the scaling of topological indices since we have found a scaling law that covers different network models. Moreover, taking into account the symmetries of the topological indices we study here, we propose to establish their statistical analysis as a generic tool for studying average properties of random networks. In addition, we discuss the application of specific topological indices as complexity measures for random networks.

1. Introduction

Harold Wiener can be considered the pioneer in the study of the so-called topological indices. His first investigations in this subject appeared in 1947 [1]. There, he introduced the today known as Wiener index in order tu analyze and correlate physicochemical properties of alkanes. The topological indices associate a numerical value to topological properties of discrete structures, based on its invariants. The initial goal of the study of topological indices was to establish quantitative relationships between different structures and properties of molecules. Winner’s work did not produce an immediate impact. Note that it was about 30 years later, in 1971, that Haruo Hosoya continued the research on topological indices by introducing the Z index [2]; currently known as the Hosoya Z index, which has been successfully applied in establishing quantitative structure–property relationships (QSPRs) and quantitative structure–activity relationships (QSARs).

It is also fair to recognize the relevance of the contributions made by two important groups in the study and development of topological indices. On the one hand, the extinct group of the Ruder Boskovic Institute in Zagreb, where the mathematical and computational properties of the well-known Zagreb indices were first studied. In fact, the first and second Zagreb indices appeared for the first time in 1972, a year later than the Hosoya Z index, in a paper by Gutman and Trinajstić [3,4]. On the other hand, the group leaded by Milan Randić, whose index, the Randić index (introduced in 1975 [5]), is presumably the most studied and applied topological index.

Later on, the concept of variable molecular descriptors was proposed as a way of characterizing heteroatoms in molecules (see [6,7]). The essential idea is that the variables are determined during the regression; this allows making the standard error of the estimate for a particular property (targeted in the study) as small as possible (see, e.g., [8]).

Given a network $G=\left(V\right(G),E(G\left)\right)$, the first and second variable Zagreb indices are defined as [8,9,10]

$$M_1^{\alpha }\left(G\right)=\sum _{u\in V\left(G\right)}{\left(k_u\right)}^{\alpha }$$

(1)

and

$$M_2^{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{\left(k_u{k}_v\right)}^{\alpha },$$

(2)

respectively, with $\alpha \in \mathbb{R}$, $k_u$ is the degree of the vertex u, and $uv$ denotes the edge of the network G connecting the vertices u and v. Note that $M_1^2\left(G\right)$ is the first Zagreb index $M_1\left(G\right)$ and $M_1^{-1}\left(G\right)$ is the inverse degree index $ID\left(G\right)$. Furthermore, notice that $M_2^{-1/2}\left(G\right)$ is the usual Randić index $R\left(G\right)$ and $M_2^1\left(G\right)$ is the second Zagreb index $M_2\left(G\right)$. The second variable Zagreb index has found applications in the structure-boiling point modeling of benzenoid hydrocarbons [11].

The general sum-connectivity index was defined in [12] as

$${\chi }_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{(k_u+k_v)}^{\alpha }.$$

(3)

Some relations of this and other indices are reported in [13]. Note that ${\chi }_{{}_1}\left(G\right)$ is the first Zagreb index $M_1\left(G\right)$, $2{\chi }_{{}_{-1}}\left(G\right)$ is the harmonic index $H\left(G\right)$ and ${\chi }_{{}_{-1/2}}\left(G\right)$ is the sum-connectivity index $\chi \left(G\right)$.

Moreover, here we introduce two new general indices: the general inverse sum indeg index and the general first geometric-arithmetic index, that we define as

$$IS{I}_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{\left(\frac{k_u{k}_v}{k_u+k_v}\right)}^{\alpha }$$

(4)

and

$$G{A}_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{\left(\frac{\sqrt{k_u{k}_v}}{2(k_u+k_v)}\right)}^{\alpha },$$

(5)

respectively. Evidently, $IS{I}_1\left(G\right)$ and $G{A}_1\left(G\right)$ are the standard inverse sum indeg index $ISI\left(G\right)$ and first geometric-arithmetic index $GA\left(G\right)$, respectively. We note that a general inverse sum indeg index similar to ours was recently proposed in [14]. Furthermore, for reviews on geometric-arithmetic indices and a new variant of the geometric-arithmetic index (to get a better estimates of the boiling point of alkanes) see Refs. [15,16] and [17], respectively. We stress that the goal of introducing these two general indices is to show that the statistical approach described below is so general that can be applied to any general index, even these new ones with still unknown properties. Thus, we will not focus on their mathematical properties here. Instead we discuss the application of specific topological indices as complexity measures for random networks (see Section 4) and leave the mathematical study and other possible applications for future research.

Here we consider two models of random networks G: Erdös–Rényi (ER) random networks $G_{\mathrm{ER}}(n_{\mathrm{ER}},p)$ and random geometric (RG) graphs $G_{\mathrm{RG}}(n_{\mathrm{RG}},r)$. The ER random networks, introduced by Solomonoff and Rapoport [18] and investigated later in great detail by Erdös and Rényi [19,20,21], are formed by $n_{\mathrm{ER}}$ vertices connected independently with probability $p\in [0,1]$. While the RG graphs [22,23], often used to study the structure and dynamics of spatially embedded complex systems, consist of $n_{\mathrm{RG}}$ vertices uniformly and independently distributed on the unit square, where two vertices are connected by an edge if their Euclidean distance is less or equal than the connection radius $r\in [0,\sqrt{2}]$. We stress that the statistical study of topological indices we perform here is justified by the random nature of the network models we want to explore. Since a given parameter pair $(n_{\mathrm{ER}},p)$ [$(n_{\mathrm{RG}},r)$] represents an infinite-size ensemble of ER random networks (RG graphs), the computation of a topological index on a single network is irrelevant. In contrast, the computation of a given topological index on a large ensemble of random networks, all characterized by the same parameter pair $(n_{\mathrm{ER}},p)$ [$(n_{\mathrm{RG}},r)$], may provide useful average information about the full ensemble. This statistical approach, well known in random matrix theory studies, is not widespread in studies involving topological indices, mainly because topological indices are not commonly applied to random networks; for very recent exceptions see [24,25].

Therefore, the purpose of this work is twofold. First, we propose to establish the statistical analysis of topological indices as a generic tool for studying average properties of random networks, and second, we perform for the first time (to our knowledge), a scaling study of general topological indices on random networks.

Our results are presented separately for ER random networks and RG graphs in Section 2 and Section 3, respectively. Finally, the discussion and conclusions are drawn in Section 4.

2. Erdös–Rényi Random Networks

In what follows, we present the average values of the indices listed in Equations (1)–(5). All averages are computed over ensembles of ${10}^7/n_{\mathrm{ER}}$ ER random networks characterized by the parameter pair $(n_{\mathrm{ER}},p)$.

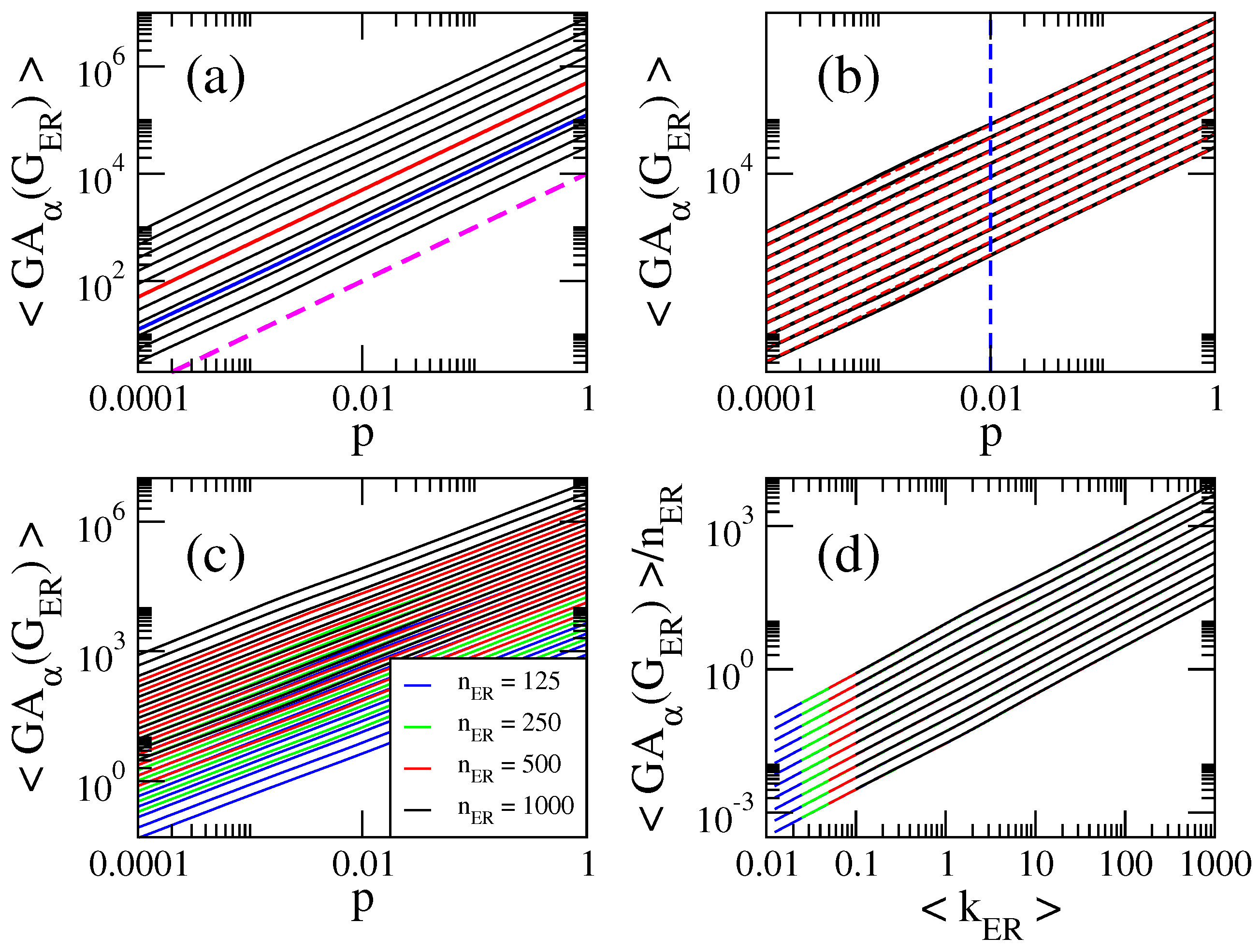
2.1. Computational Properties of General Indices on Erdös–Rényi Random Networks

In Figure 1a, Figure 2a, Figure 3a, Figure 4a and Figure 5a we present, respectively, the average first variable Zagreb index $〈M_1^{\alpha }\left(G_{\mathrm{ER}}\right)〉$, the average second variable Zagreb index $〈M_2^{\alpha }\left(G_{\mathrm{ER}}\right)〉$, the average general sum-connectivity index $〈{\chi }_{\alpha }\left(G_{\mathrm{ER}}\right)〉$, the average general inverse sum indeg index $〈IS{I}_{\alpha }\left(G_{\mathrm{ER}}\right)〉$ and the average general first geometric-arithmetic index $〈G{A}_{\alpha }\left(G_{\mathrm{ER}}\right)〉$ as a function of the probability p of ER random networks of size $n_{\mathrm{ER}}=1000$. There, we show curves for $\alpha \in [-2,2]$. As a reference, red curves correspond to $\alpha =0$ while blue curves indicate $\alpha =1$.

From these figures we observe that:

(i) 

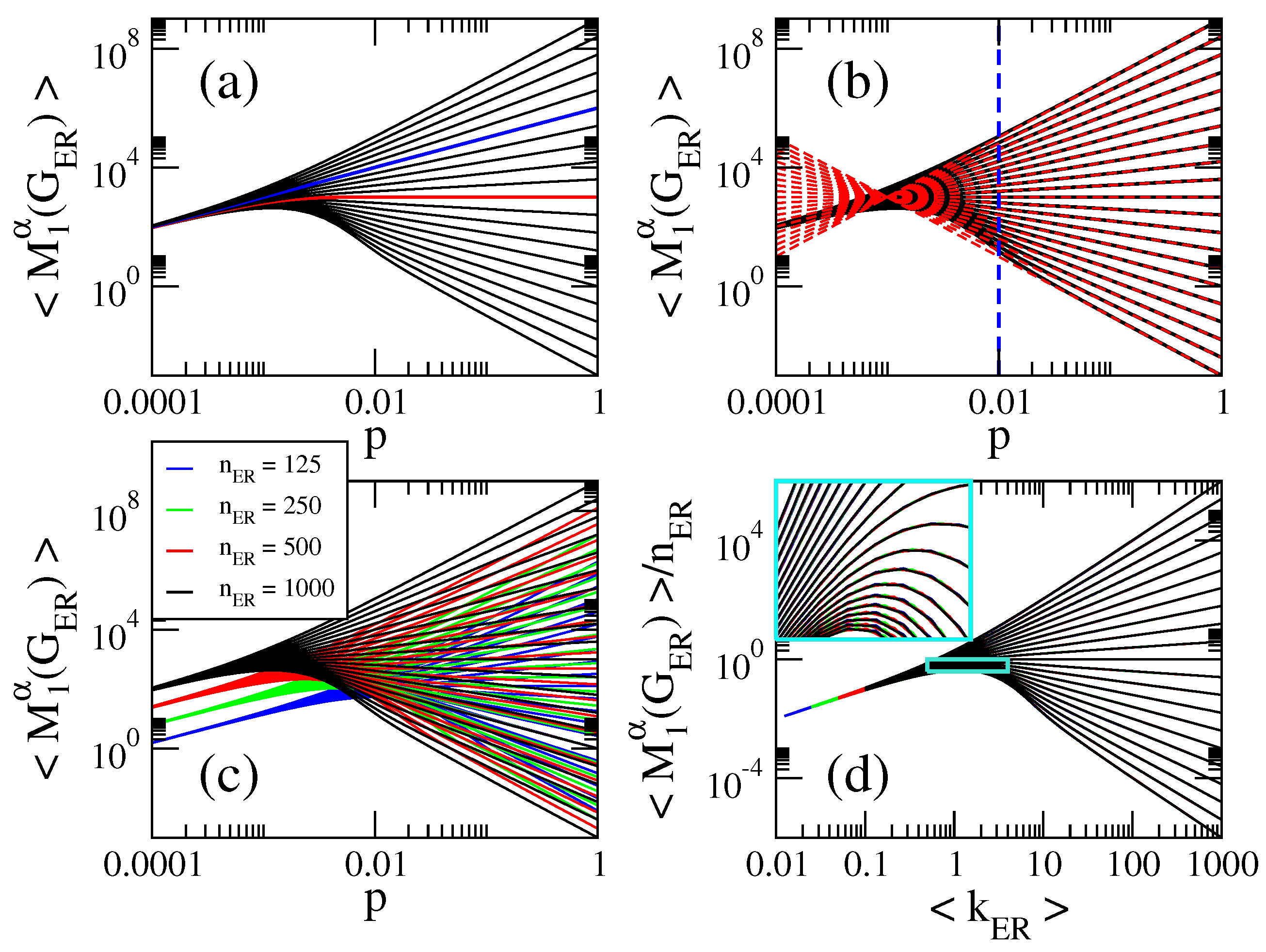
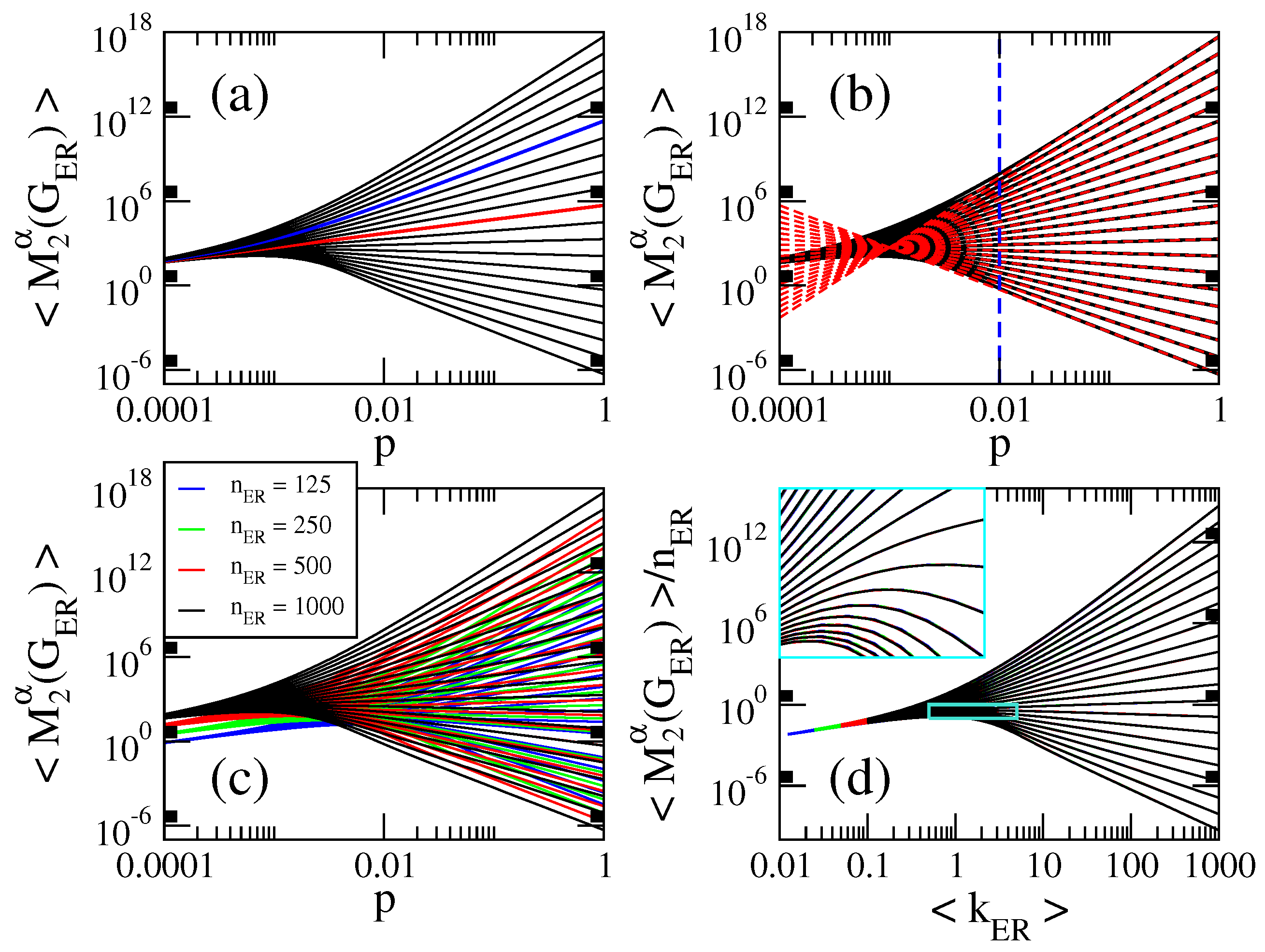
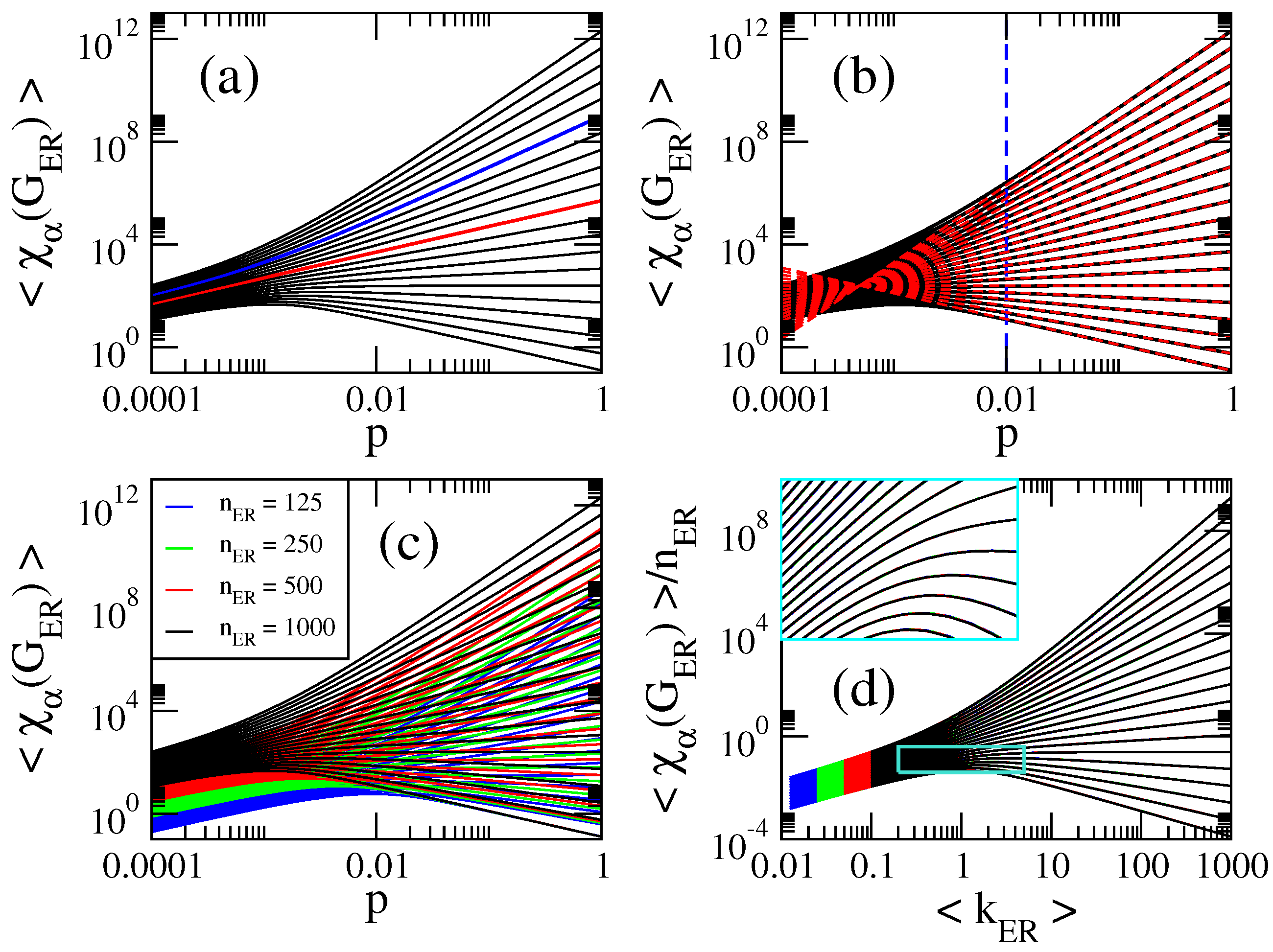
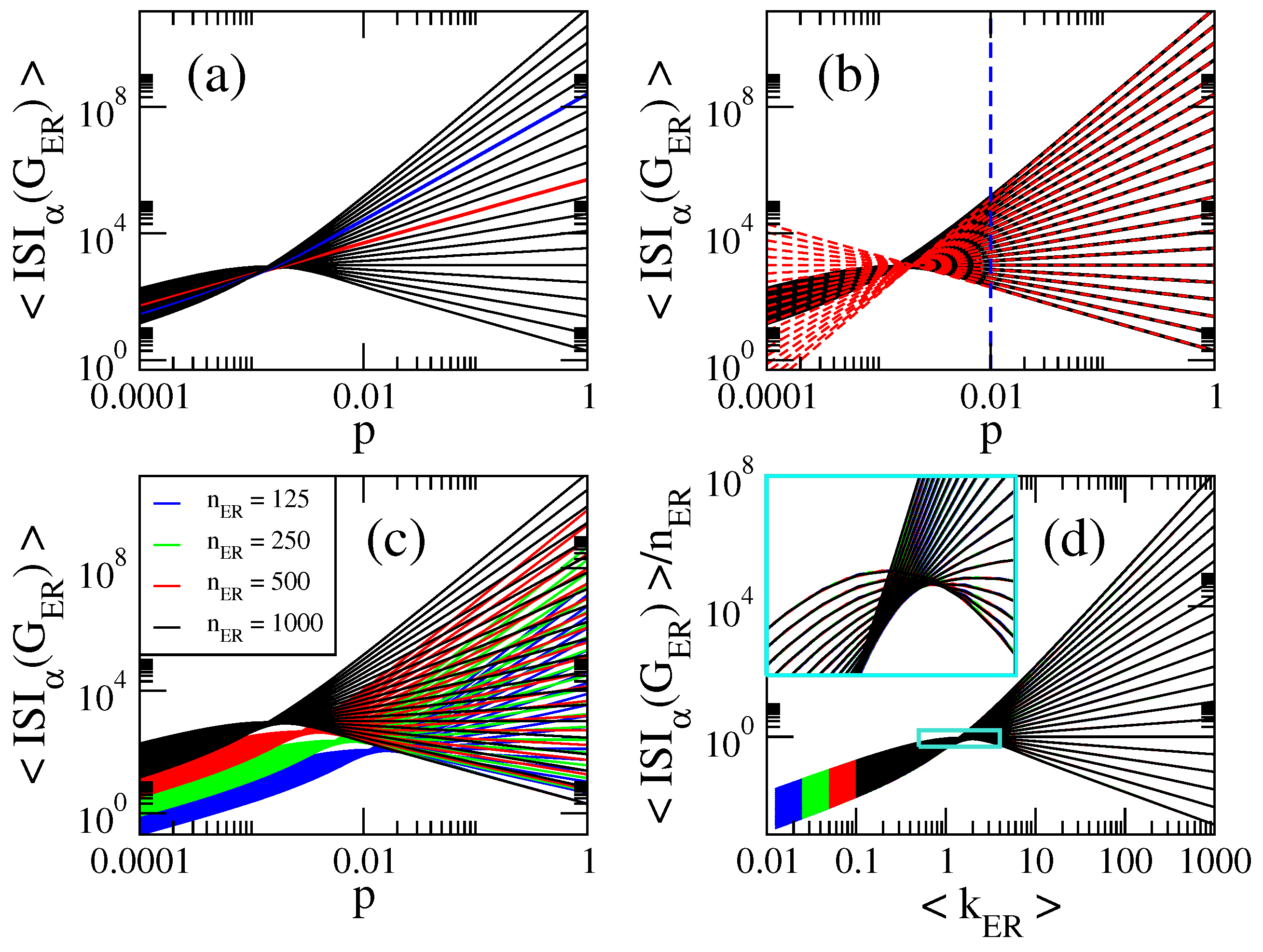
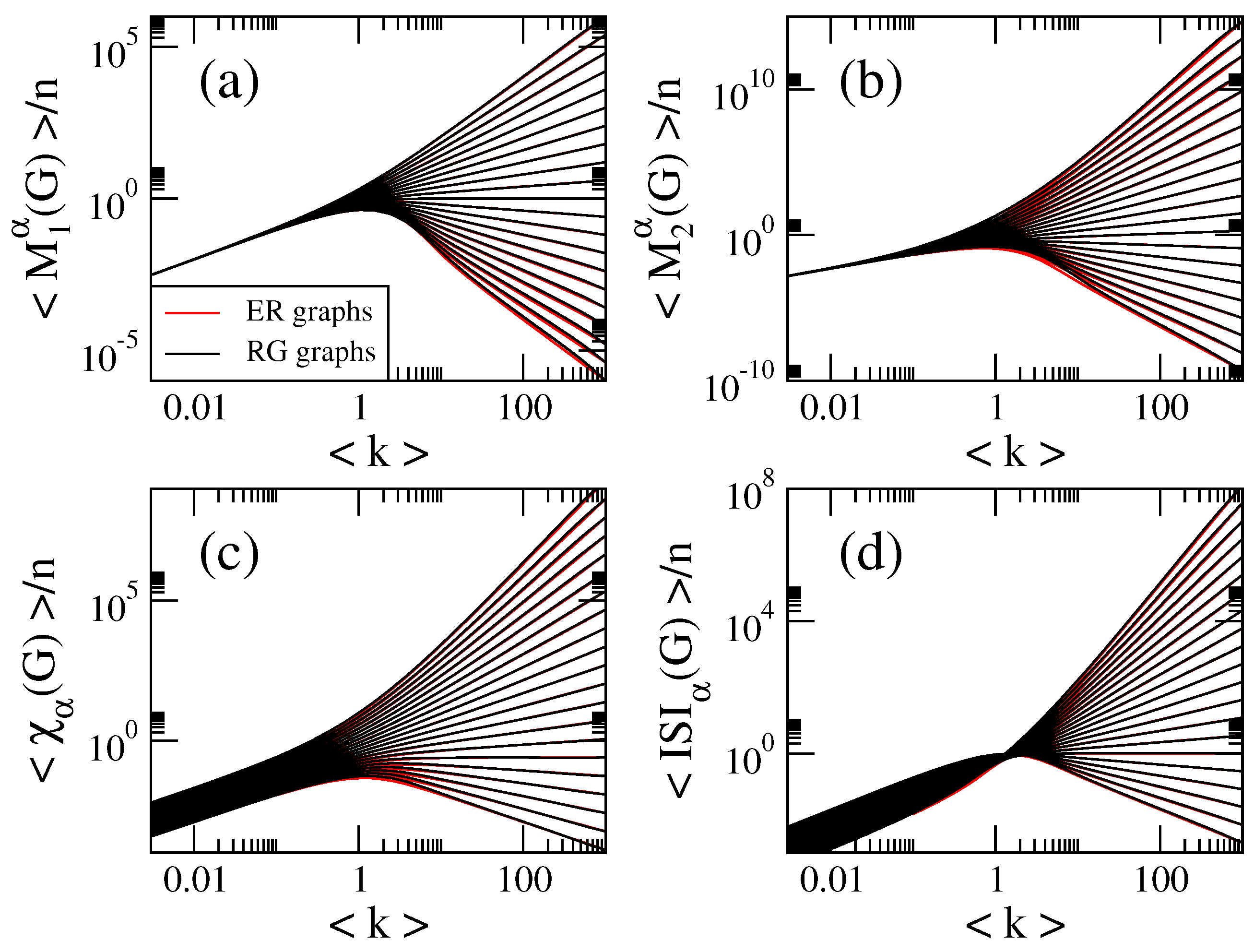
The curves of $〈M_1^{\alpha }\left(G_{\mathrm{ER}}\right)〉$, $〈M_2^{\alpha }\left(G_{\mathrm{ER}}\right)〉$, $〈{\chi }_{\alpha }\left(G_{\mathrm{ER}}\right)〉$ and $〈IS{I}_{\alpha }\left(G_{\mathrm{ER}}\right)〉$ show three different behaviors as a function of p depending on the value of $\alpha$: for $\alpha <{\alpha }_0$, they grow for small p, approach a maximum value and then decrease when p is further increased. For $\alpha >{\alpha }_0$, they are monotonically increasing functions of p. For $\alpha ={\alpha }_0$ the curves saturate above a given value of p. See Figure 1a, Figure 2a, Figure 3a and Figure 4a.

(ii) 

${\alpha }_0=0$ for $〈M_1^{\alpha }\left(G_{\mathrm{ER}}\right)〉$, where $〈M_1^{{\alpha }_0}\left(G_{\mathrm{ER}}\right)〉$ is the average number of non-isolated vertices $〈V_{\times }\left(G_{\mathrm{ER}}\right)〉$; ${\alpha }_0=-1/2$ for $〈M_2^{\alpha }\left(G_{\mathrm{ER}}\right)〉$, where $〈M_2^{{\alpha }_0}\left(G_{\mathrm{ER}}\right)〉$ is the average Randic index $〈R\left(G_{\mathrm{ER}}\right)〉$; ${\alpha }_0=-1$ for $〈{\chi }_{\alpha }\left(G_{\mathrm{ER}}\right)〉$, where $2〈{\chi }_{-1}\left(G_{\mathrm{ER}}\right)〉$ is the average Harmonic index $〈H\left(G_{\mathrm{ER}}\right)〉$; and ${\alpha }_0=-1$ for $〈IS{I}_{\alpha }\left(G_{\mathrm{ER}}\right)〉$, so $〈IS{I}_{-1}\left(G_{\mathrm{ER}}\right)〉=〈V_{\times }\left(G_{\mathrm{ER}}\right)〉$.

(iii) 

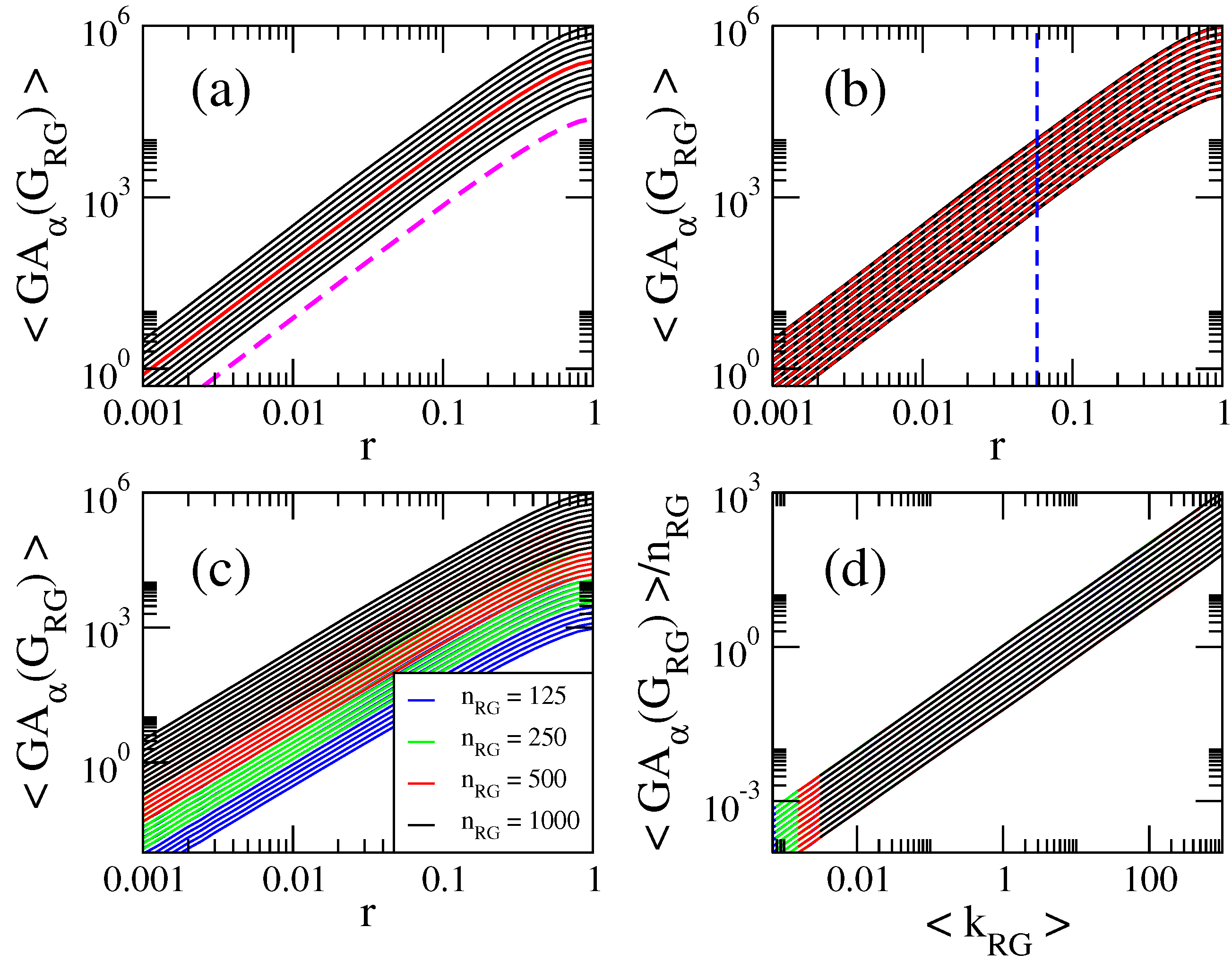
All curves of $〈G{A}_{\alpha }\left(G_{\mathrm{ER}}\right)〉$ grow linearly with p for all $\alpha$ and $n_{\mathrm{ER}}$; see the magenta dashed line in Figure 5a, plotted to guide the eye.

(iv) 

For $\alpha =0$, see the red curves in Figure 2a, Figure 3a, Figure 4a and Figure 5a, $〈M_2^0\left(G_{\mathrm{ER}}\right)〉$, $〈{\chi }_0\left(G_{\mathrm{ER}}\right)〉$, $〈IS{I}_0\left(G_{\mathrm{ER}}\right)〉$ and $〈G{A}_0\left(G_{\mathrm{ER}}\right)〉$ give the average number of edges of the ER random network. That is

$$〈M_2^0\left(G_{\mathrm{ER}}\right)〉=〈{\chi }_0\left(G_{\mathrm{ER}}\right)〉=〈IS{I}_0\left(G_{\mathrm{ER}}\right)〉=〈G{A}_0\left(G_{\mathrm{ER}}\right)〉=\frac{n_{\mathrm{ER}}(n_{\mathrm{ER}}-1)}{2}p.$$

(6)

(v) 

When $n_{\mathrm{ER}}p\gg 1$, we can write $k_u\approx k_v\approx 〈k_{\mathrm{ER}}〉$ in Equations (1)–(5), with

$$〈k_{\mathrm{ER}}〉=(n_{\mathrm{ER}}-1)p.$$

(7)

Therefore, for $n_{\mathrm{ER}}p\gg 1$, the average values of the indices we are computing here are well approximated by:

$$〈M_1^{\alpha }\left(G_{\mathrm{ER}}\right)〉=n_{\mathrm{ER}}{\left[(n_{\mathrm{ER}}-1)p\right]}^{\alpha },$$

(8)

$$〈M_2^{\alpha }\left(G_{\mathrm{ER}}\right)〉=\frac{n_{\mathrm{ER}}}{2}{\left[(n_{\mathrm{ER}}-1)p\right]}^{1+2\alpha },$$

(9)

$$〈{\chi }_{\alpha }\left(G_{\mathrm{ER}}\right)〉=\frac{n_{\mathrm{ER}}}{2^{1-\alpha }}{\left[(n_{\mathrm{ER}}-1)p\right]}^{1+\alpha },$$

(10)

$$〈IS{I}_{\alpha }\left(G_{\mathrm{ER}}\right)〉=n_{\mathrm{ER}}{\left[\frac{(n_{ER}-1)p}{2}\right]}^{1+\alpha },$$

(11)

$$〈G{A}_{\alpha }\left(G_{\mathrm{ER}}\right)〉=\frac{n_{\mathrm{ER}}(n_{\mathrm{ER}}-1)p}{2^{1+2\alpha }}.$$

(12)

In Figure 1b, Figure 2b, Figure 3b, Figure 4b and Figure 5b, we show that Equations (8)–(12) (red-dashed lines) indeed describe well the data (thick black curves) for $〈k_{\mathrm{ER}}〉\ge 10$.

2.2. Scaling Properties of General Indices on Erdös–Rényi Random Networks

Now in Figure 1c, Figure 2c, Figure 3c, Figure 4c and Figure 5c we show $〈X\left(G_{\mathrm{ER}}\right)〉$ as a function of the probability p of ER random networks of four different sizes $n_{\mathrm{ER}}$. Here and below, X represents $M_1^{\alpha }$, $M_2^{\alpha }$, ${\chi }_{\alpha }$, $IS{I}_{\alpha }$ and $G{A}_{\alpha }$. It is quite clear from these figures that the blocks of curves, characterized by the different network sizes, display similar curves but displaced on both axes. Thus, it is the goal of this section to find the scaling parameters that make the blocks of curves to coincide.

First, we recall that the average degree $〈k_{\mathrm{ER}}〉$, see Equation (7), is known to scale both topological and spectral measures applied to ER random networks. In particular, $〈k_{\mathrm{ER}}〉$ was shown to scale both the normalized Randic index [24] and the normalized Harmonic [25] index on ER random networks.

Second, we observe (not shown here) that the effect of increasing the network size is to displace the blocks of curves $〈X\left(G_{\mathrm{ER}}\right)〉$ vs. $〈k_{\mathrm{ER}}〉$, characterized by the different network sizes, upwards in the $y-$axis. Moreover, the fact that these blocks of curves, plotted in semi-log scale, are shifted the same amount on the $y-$axis when doubling $n_{\mathrm{ER}}$ is a clear signature of scalings of the form $〈X\left(G_{\mathrm{ER}}\right)〉\propto n_{\mathrm{ER}}^{\beta }〈k_{\mathrm{ER}}〉$. Furthermore, since from Equations (8)–(12) we have that $〈X\left(G_{\mathrm{ER}}\right)〉\propto n_{\mathrm{ER}}〈k_{\mathrm{ER}}〉$, we anticipate that $\beta =1$ for all $\alpha$.

Therefore, in Figure 1d, Figure 2d, Figure 3d, Figure 4d and Figure 5d we plot $〈X\left(G_{\mathrm{ER}}\right)〉/n_{\mathrm{ER}}$ as a function of $〈k_{\mathrm{ER}}〉$ showing that all indices are now properly scaled; i.e., the blocks of curves painted in different colors for different network sizes fall on top of each other. Moreover, following Equations (8)–(12), for $〈k_{\mathrm{ER}}〉\ge 10$ we have that

$$\frac{〈M_1^{\alpha }\left(G_{\mathrm{ER}}\right)〉}{n_{\mathrm{ER}}}\approx {〈k_{\mathrm{ER}}〉}^{\alpha },$$

(13)

$$\frac{〈M_2^{\alpha }\left(G_{\mathrm{ER}}\right)〉}{n_{\mathrm{ER}}}\approx \frac{{〈k_{\mathrm{ER}}〉}^{1+2\alpha }}{2},$$

(14)

$$\frac{〈{\chi }_{\alpha }\left(G_{\mathrm{ER}}\right)〉}{n_{\mathrm{ER}}}\approx \frac{{〈k_{\mathrm{ER}}〉}^{1+\alpha }}{2^{1-\alpha }},$$

(15)

and

$$\frac{〈IS{I}_{\alpha }\left(G_{\mathrm{ER}}\right)〉}{n_{\mathrm{ER}}}\approx \frac{{〈k_{\mathrm{ER}}〉}^{1+\alpha }}{2^{1+\alpha }}.$$

(16)

While

$$\frac{〈G{A}_{\alpha }\left(G_{\mathrm{ER}}\right)〉}{n_{\mathrm{ER}}}\approx \frac{〈k_{\mathrm{ER}}〉}{2^{1+2\alpha }}$$

(17)

is indeed valid for all $〈k_{\mathrm{ER}}〉$.

3. Random Geometric Graphs

As in the previous section, here we present the average values of the indices listed in Equations (1)–(5). Again, all averages are computed over ensembles of ${10}^7/n_{\mathrm{RG}}$ RG graphs, each ensemble characterized by a fixed parameter pair $(n_{\mathrm{RG}},r)$.

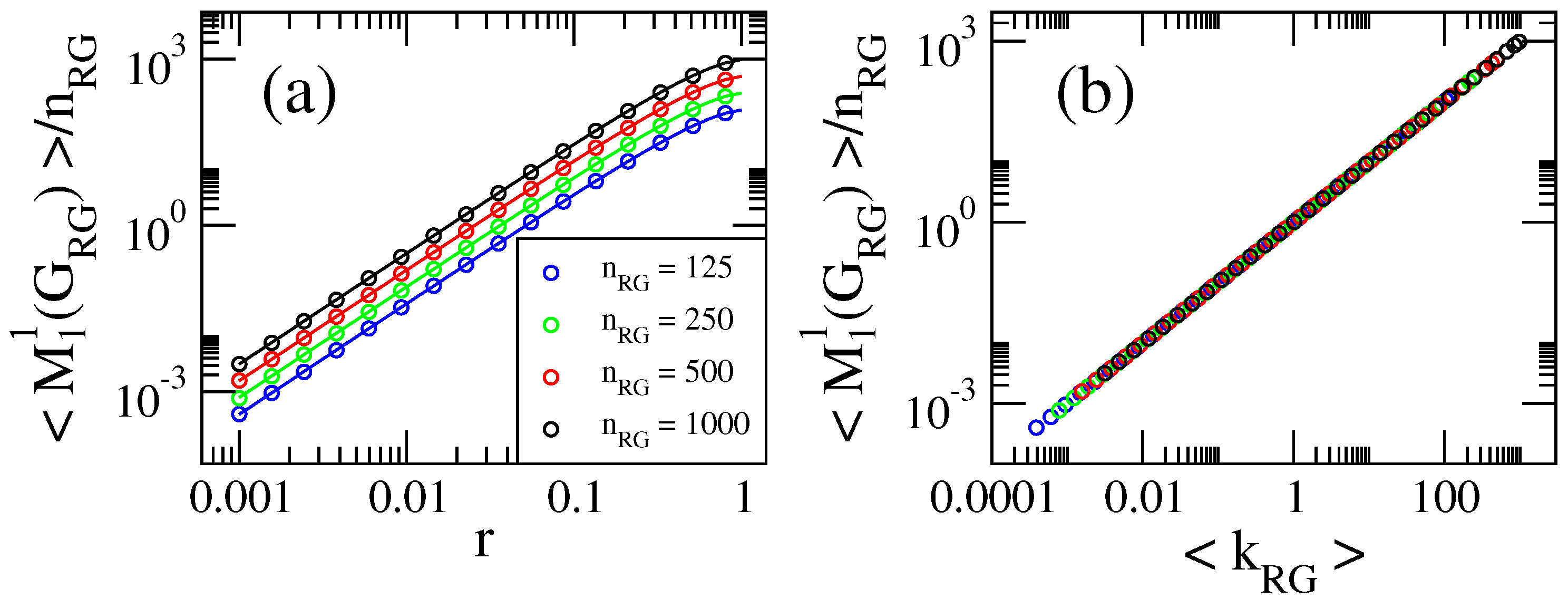
3.1. The Average Degree of Random Geometric Graphs

We want to stress that, in the previous section, the average degree was shown to be the most important quantity in the scaling of the general indices on ER random networks. Thus, since the average degree may also play a prominent role in the scaling of general indices on RG graphs, we focus on it before starting the study of $〈X\left(G_{\mathrm{RG}}\right)〉$. Then, in Figure 6a we present the average index $〈M_1^1\left(G_{\mathrm{RG}}\right)〉$ normalized to the network size (symbols), which in fact corresponds to the average degree $〈k_{\mathrm{RG}}〉$:

$$\frac{〈M_1^1\left(G_{\mathrm{RG}}\right)〉}{n_{\mathrm{RG}}}=〈k_{\mathrm{RG}}〉.$$

(18)

Moreover, an expression for $〈k_{\mathrm{RG}}〉$ was derived in Ref. [26] and reads as

$$〈k_{\mathrm{RG}}〉=(n_{\mathrm{RG}}-1)f\left(r\right),$$

(19)

where $f\left(r\right)$ is a quite non-trivial function of r:

$$f\left(r\right)=\pi r^2-\frac{8}{3}{r}^3+\frac{1}{2}{r}^4.$$

Indeed, as shown in Figure 6a, Equation (19) (full lines) coincides perfectly with $〈M_1^1\left(G_{\mathrm{RG}}\right)〉/n_{\mathrm{RG}}$ (symbols). This fact is of paramount importance to our study because given the similarity of Equation (18) with Equations (13)–(17), we can already interpret $〈k_{\mathrm{RG}}〉$ as the scaling parameter of the index $〈M_1^1\left(G_{\mathrm{RG}}\right)〉$. This trivial scaling is shown in Figure 6b where we plot $〈M_1^1\left(G_{\mathrm{RG}}\right)〉/n_{\mathrm{RG}}$ versus $〈k_{\mathrm{RG}}〉$, as given in Equation (19); there, the curves corresponding to different network sizes collapse on top of the identity function. Moreover, since $〈M_1^1\left(G_{\mathrm{RG}}\right)〉$ is a special case of the average first variable Zagreb index, $〈k_{\mathrm{RG}}〉$ becomes the perfect candidate to scale the general index $〈M_1^{\alpha }\left(G_{\mathrm{RG}}\right)〉$ and, based on the results of the previous section, also the rest of the general indices we study here.

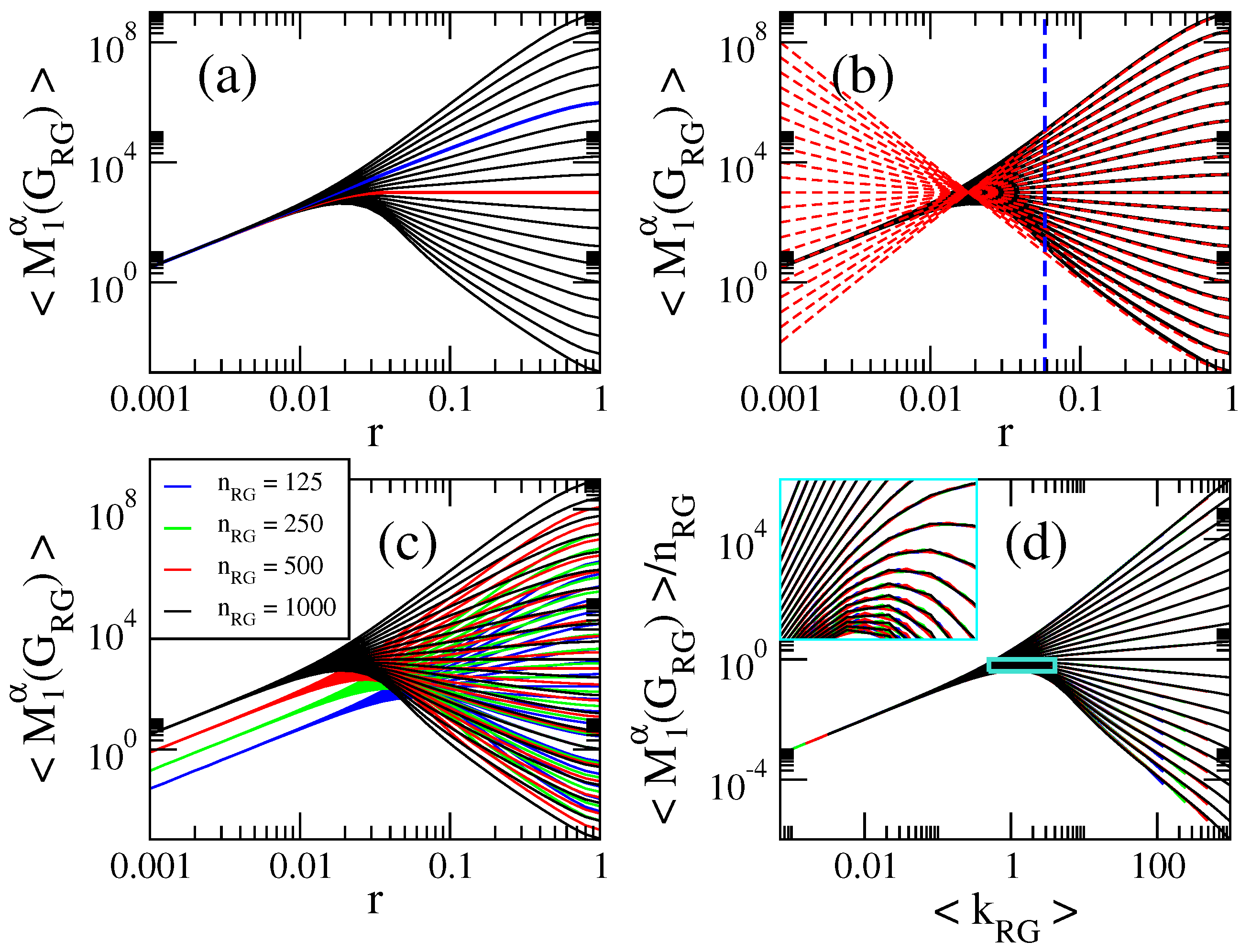
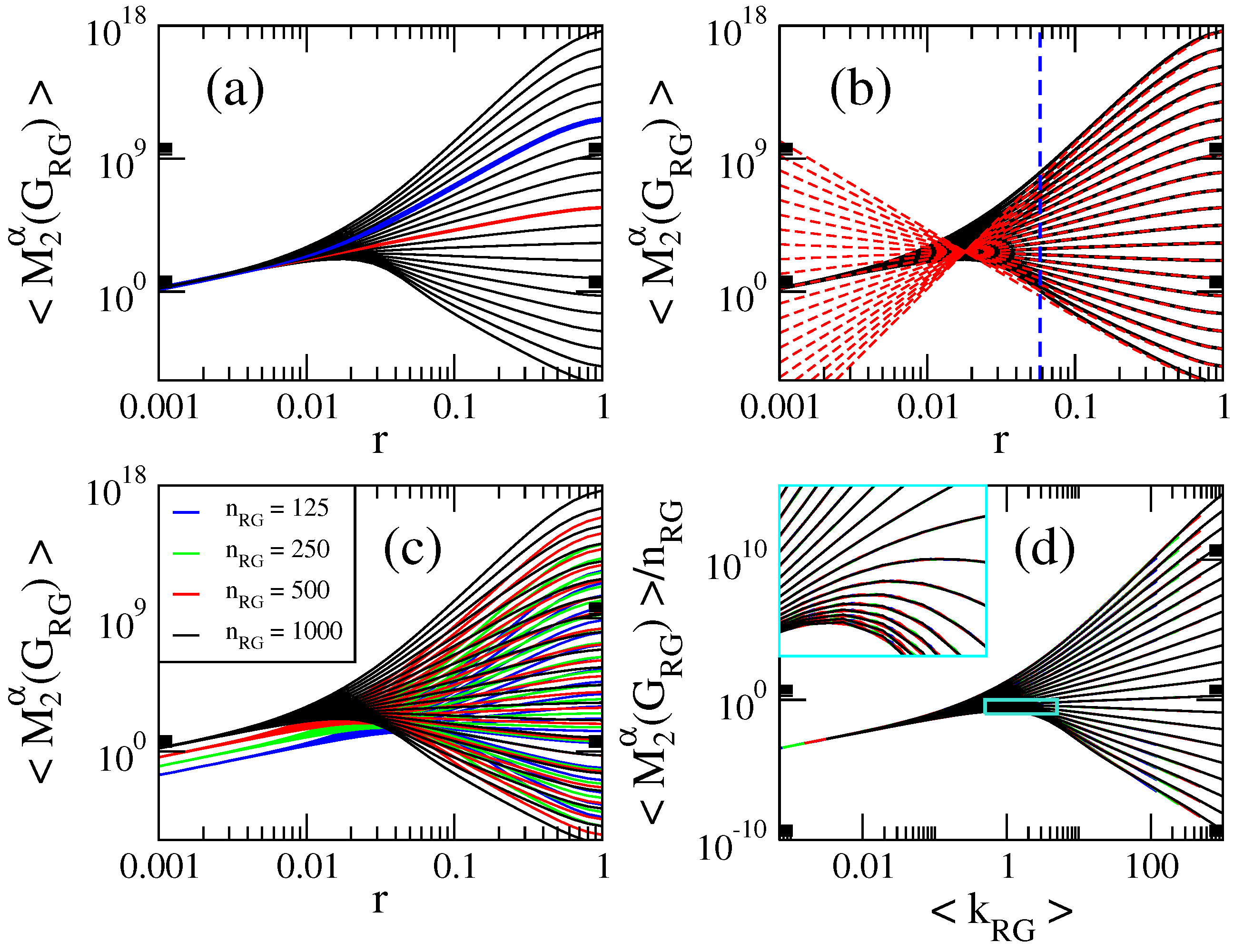
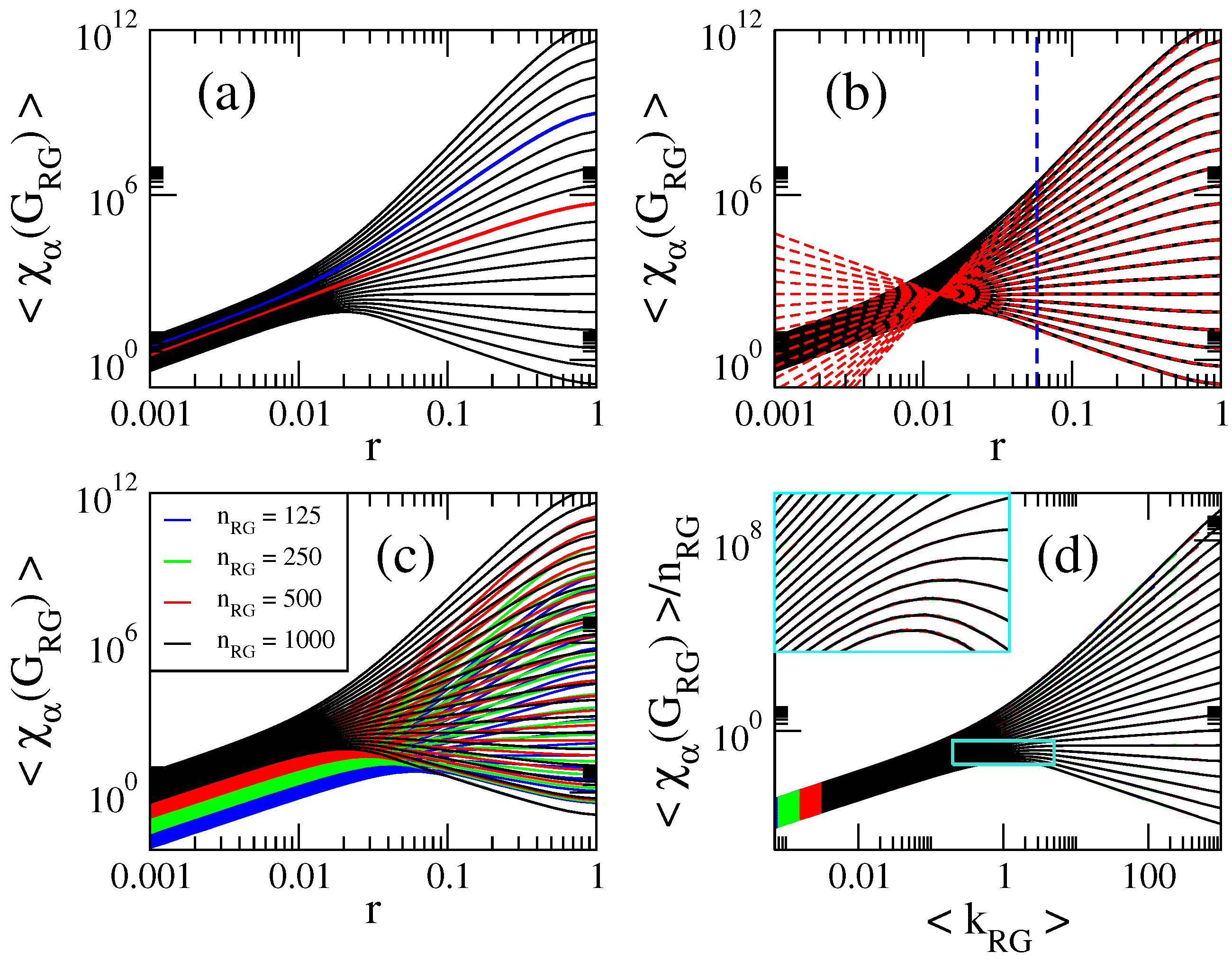
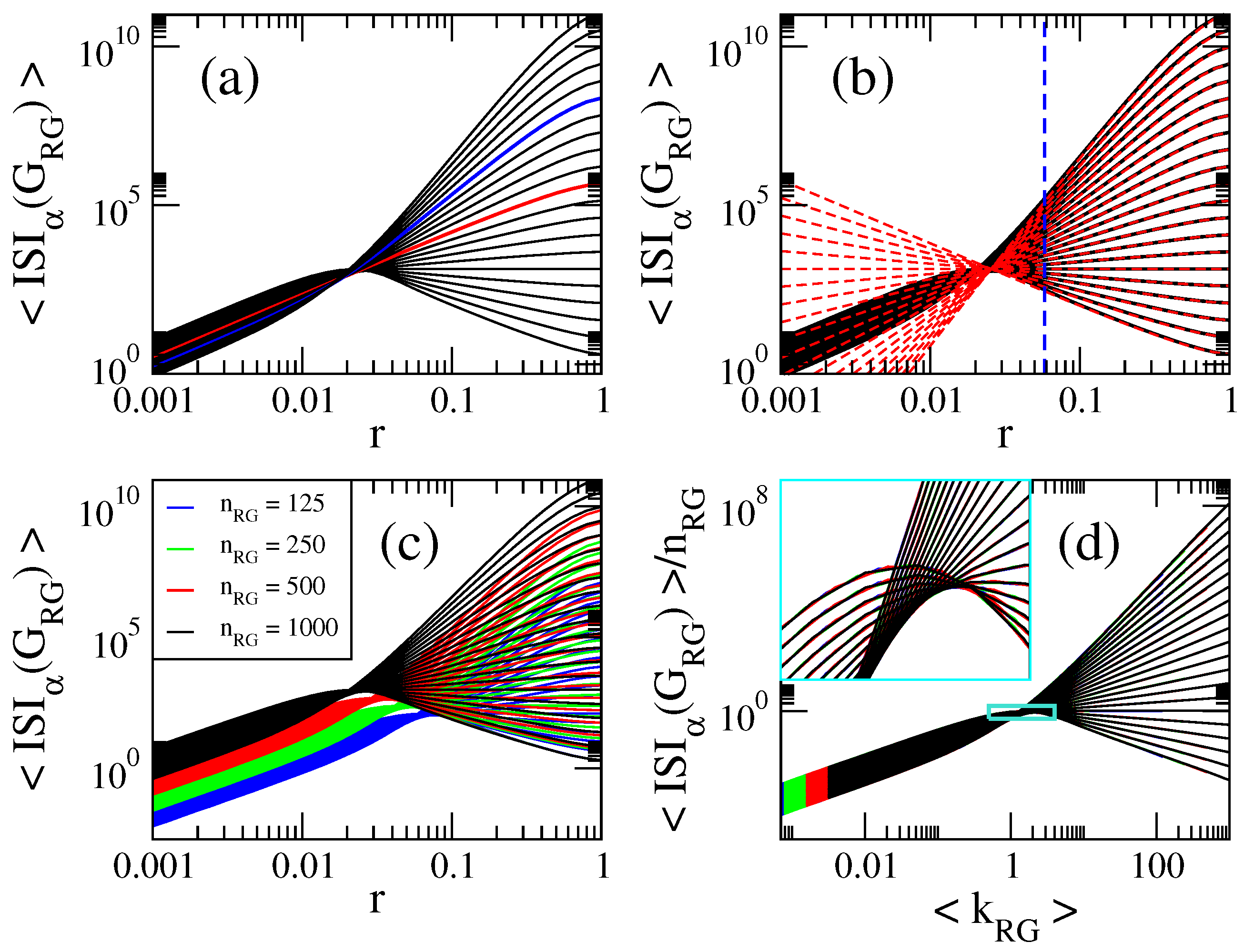
3.2. Computational Properties of General Indices on Random Geometric Graphs

Now, in Figure 7a, Figure 8a, Figure 9a, Figure 10a and Figure 11a we present, respectively, the average first variable Zagreb index $〈M_1^{\alpha }\left(G_{\mathrm{RG}}\right)〉$, the average second variable Zagreb index $〈M_2^{\alpha }\left(G_{\mathrm{RG}}\right)〉$, the average general sum-connectivity index $〈{\chi }_{\alpha }\left(G_{\mathrm{RG}}\right)〉$, the average general inverse sum indeg index $〈IS{I}_{\alpha }\left(G_{\mathrm{RG}}\right)〉$ and the average general first geometric-arithmetic index $〈G{A}_{\alpha }\left(G_{\mathrm{ER}}\right)〉$ as a function of the connection radius r of RG graphs of size $n_{\mathrm{RG}}=1000$.

For comparison purposes, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 are equivalent to Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. In fact, most of the statements (i–v) made in the previous section for ER random networks are also valid for RG graphs. Even though most statements are applicable to RG graphs by just replacing $G_{\mathrm{ER}}\to G_{\mathrm{RG}}$ and $p\to f\left(r\right)$, given the fact that this is the first study (to our knowledge) of average topological indices on RG graphs, we want to explicitly write three statements we consider relevant:

(iii’) 

The curves $〈G{A}_{\alpha }\left(G_{\mathrm{RG}}\right)〉$ grow with r, for all $\alpha$ and $n_{\mathrm{RG}}$, as $〈G{A}_{\alpha }\left(G_{\mathrm{RG}}\right)〉\propto f\left(r\right)$; see the magenta dashed line in Figure 11a, plotted to guide the eye.

(iv’) 

For $\alpha =0$, see the red curves in Figure 8a, Figure 9a, Figure 10a and Figure 11a, $〈M_2^0\left(G_{\mathrm{RG}}\right)〉$, $〈{\chi }_0\left(G_{\mathrm{RG}}\right)〉$, $〈IS{I}_0\left(G_{\mathrm{RG}}\right)〉$ and $〈G{A}_0\left(G_{\mathrm{RG}}\right)〉$ give the average number of edges of the RG graph. That is

$$〈M_2^0\left(G_{\mathrm{RG}}\right)〉=〈{\chi }_0\left(G_{\mathrm{RG}}\right)〉=〈IS{I}_0\left(G_{\mathrm{RG}}\right)〉=〈G{A}_0\left(G_{\mathrm{RG}}\right)〉=\frac{n_{\mathrm{RG}}(n_{\mathrm{RG}}-1)}{2}f\left(r\right).$$

(20)

(v’) 

When $n_{\mathrm{RG}}r\gg 1$, we can write $k_u\approx k_v\approx 〈k_{\mathrm{RG}}〉=(n_{\mathrm{RG}}-1)f\left(r\right)$ in Equations (1)–(5). Therefore, for $n_{\mathrm{RG}}r\gg 1$, the average values of the indices we are computing here are well approximated by:

$$〈M_1^{\alpha }\left(G_{\mathrm{RG}}\right)〉=n_{\mathrm{RG}}{\left[(n_{\mathrm{RG}}-1)f\left(r\right)\right]}^{\alpha },$$

(21)

$$〈M_2^{\alpha }\left(G_{\mathrm{RG}}\right)〉=\frac{n_{\mathrm{RG}}}{2}{\left[(n_{\mathrm{RG}}-1)f\left(r\right)\right]}^{1+2\alpha },$$

(22)

$$〈{\chi }_{\alpha }\left(G_{\mathrm{RG}}\right)〉=\frac{n_{\mathrm{RG}}}{2^{1-\alpha }}{\left[(n_{\mathrm{RG}}-1)f\left(r\right)\right]}^{1+\alpha },$$

(23)

$$〈IS{I}_{\alpha }\left(G_{\mathrm{RG}}\right)〉=n_{\mathrm{RG}}{\left[\frac{(n_{RG}-1)f\left(r\right)}{2}\right]}^{1+\alpha },$$

(24)

$$〈G{A}_{\alpha }\left(G_{\mathrm{RG}}\right)〉=\frac{n_{\mathrm{RG}}(n_{\mathrm{RG}}-1)f\left(r\right)}{2^{1+2\alpha }}.$$

(25)

In Figure 7b, Figure 8b, Figure 9b, Figure 10b and Figure 11b, we show that Equations (21)–(25) (red-dashed lines) indeed describe very well the data (thick black curves) for $〈k_{\mathrm{RG}}〉\ge 10$.

3.3. Scaling Properties of General Indices on Random Geometric Graphs

In Figure 7c, Figure 8c, Figure 9c, Figure 10c and Figure 11c we show $〈X\left(G_{\mathrm{RG}}\right)〉$ as a function of the connection radius r of RG graphs of four different sizes $n_{\mathrm{RG}}$. The panorama is equivalent to that observed in the previous section for ER random graphs: the blocks of curves, characterized by the different graph sizes, display similar curves but displaced on both axes.

Finally, in Figure 7d, Figure 8d, Figure 9d, Figure 10d and Figure 11d we plot $〈X\left(G_{\mathrm{RG}}\right)〉/n_{\mathrm{RG}}$ as a function of $〈k_{\mathrm{RG}}〉$ showing that all indices are now properly scaled, as anticipated in Section 3.1. Moreover, following Equations (21)–(25), for $〈k_{\mathrm{RG}}〉\ge 10$ we have that

$$\frac{〈M_1^{\alpha }\left(G_{\mathrm{RG}}\right)〉}{n_{\mathrm{RG}}}\approx {〈k_{\mathrm{RG}}〉}^{\alpha },$$

(26)

$$\frac{〈M_2^{\alpha }\left(G_{\mathrm{RG}}\right)〉}{n_{\mathrm{RG}}}\approx \frac{{〈k_{\mathrm{RG}}〉}^{1+2\alpha }}{2},$$

(27)

$$\frac{〈{\chi }_{\alpha }\left(G_{\mathrm{RG}}\right)〉}{n_{\mathrm{RG}}}\approx \frac{{〈k_{\mathrm{RG}}〉}^{1+\alpha }}{2^{1-\alpha }},$$

(28)

and

$$\frac{〈IS{I}_{\alpha }\left(G_{\mathrm{RG}}\right)〉}{n_{\mathrm{RG}}}\approx \frac{{〈k_{\mathrm{RG}}〉}^{1+\alpha }}{2^{1+\alpha }}.$$

(29)

While

$$\frac{〈G{A}_{\alpha }\left(G_{\mathrm{RG}}\right)〉}{n_{\mathrm{RG}}}\approx \frac{〈k_{\mathrm{RG}}〉}{2^{1+2\alpha }}$$

(30)

is indeed valid for all $〈k_{\mathrm{RG}}〉$.

4. Discussion and Conclusions

In this paper, within a random matrix theory (RMT) approach, we have performed a thorough statistical study of general indices on two models of random networks. In addition to well-known general indices (the first and second variable Zagreb indices, $M_1^{\alpha }\left(G\right)$ and $M_2^{\alpha }\left(G\right)$, and the general sum-connectivity index, ${\chi }_{\alpha }\left(G\right)$) we have introduced general versions of the inverse sum indeg index $IS{I}_{\alpha }\left(G\right)$ and the first geometric-arithmetic index $G{A}_{\alpha }\left(G\right)$; see Equations (3) and (4), respectively. As models of random networks we have used Erdös–Rényi (ER) random networks $G_{\mathrm{ER}}(n_{\mathrm{ER}},p)$ and random geometric (RG) graphs $G_{\mathrm{RG}}(n_{\mathrm{RG}},r)$. It is important to stress that we do not analize the information obtained from the different general indices we use here, instead we focus only on their computational properties. Furthermore, we left for a future investigation the analytical study of the general indices we have introduced in the present work: $IS{I}_{\alpha }\left(G\right)$ and $G{A}_{\alpha }\left(G\right)$.

We have found that the average value of the indices, normalized to the network size, scale with the average degree $〈k〉$ of the corresponding random network models. This means that $〈k〉$ fixes the average value of any index for different combinations of network parameters; i.e., the relevant parameter of both network models is $〈k〉$ and not the specific values of the model parameters. This result highlights the relevance of $〈k〉$ in random network studies. Moreover, the similarity between Equations (13)–(17) and Equations (26)–(30) allow us to relate the index average values of the two random network models we study here; that is,

$$\frac{〈X\left(G_{\mathrm{ER}}\right)〉}{n_{\mathrm{ER}}}\approx \frac{〈X\left(G_{\mathrm{RG}}\right)〉}{n_{\mathrm{RG}}}\mathrm{if}〈k_{\mathrm{ER}}〉=〈k_{\mathrm{RG}}〉.$$

(31)

To verify Equation (31) in Figure 12 we show four normalized indices $〈X\left(G\right)〉/n$ as a function of $〈k〉$ for both ER random networks and RG graphs; note that we use networks of different sizes. Indeed, we observe that $〈X\left(G_{\mathrm{ER}}\right)〉/n_{\mathrm{ER}}\approx 〈X\left(G_{\mathrm{RG}}\right)〉/n_{\mathrm{RG}}$ to a good numerical accuracy.

With Equation (31) we give a step forward in the scaling of topological indices since we have found a scaling law that covers different network models. Clearly, an open question we plan to address in a future investigation is whether Equation (31) could be extended to other random network models.

Finally, we want to recall that in complex systems research there is a continuous search of measures that could serve as complexity indicators. In particular, RMT has provided us with a number of measures able to distinguish between (i) integrable and chaotic (i.e. non-integrable) and (ii) ordered and disordered quantum systems [27,28]. Such measures are computed from the eigenvalues and eigenvectors of quantum Hamiltonian matrices. Examples of eigenvalue-based measures are the distribution of consecutive eigenvalue spacings, the spectrum rigidity and the ratios between consecutive eigenvalue spacings; while the inverse participation ratios and Shannon entropies are popular eigenvector-based measures [27,28]. It is interesting to notice that all these RMT measures have also been successfully applied to study networks and graphs since they can be computed from the eigenvalues and eigenvectors of adjacency matrices; see e.g., [29,30,31] and the references therein. Therefore, these measures are able to distinguish between networks composed by mostly isolated vertices and mostly connected networks. Furthermore, through scaling studies of RMT measures it has been possible to locate the percolation transition point of random graphs models [29,30]. It is worth mentioning that the scaling study of average topological indices performed in this paper has followed a statistical RMT approach; that is, from a detailed numerical study we have been able to identify the average degree as the universal parameter of our random network models: i.e. the parameter that fixes the average values of the topological indices.

Moreover, recently, it has been shown for RG graphs that there is a a huge correlation between the average-scaled Shannon entropy (of the adjacency matrix eigenvectors) and two average-scaled topological indices [32]: the Randić index $R\left(G\right)$ and the harmonic index $H\left(G\right)$. We believe that this is a remarkable result because it validates the use of average topological indices as RMT complexity measures; already suggested in Refs. [24,25] for ER random networks. Now, it is important to stress that not every index could be used as a complexity measure. From our experience, we conclude that good candidates should fulfill a particular requirement: they should be almost constant in the trivial regimes (just as RMT measures are). For example, a useful complexity measure for random networks should be constant in the regime of mostly isolated vertices as well as above the percolation transition. Indeed, this is a property that both $〈R\left(G\right)〉$ and $〈H\left(G\right)〉$ have: $〈R\left(G\right)〉\approx 〈H\left(G\right)〉\approx 0$ for mostly isolated vertices while $〈R\left(G\right)〉/n\approx 〈H\left(G\right)〉/n\approx 1/2$ once the network is well above the percolation transition.

Therefore, a straightforward application of our study on general topological indices is the identification of specific indices as complexity measure candidates. Recall that we particularly require, for an average-scaled topological index to work as complexity measure, that $〈X\left(G\right)〉/n\approx \mathrm{const}.$ for large enough $〈k〉$. In fact, from Equations (13)–(17) or Equations (26)–(30) we can see that the above condition is fulfilled for $M_1^{\alpha }\left(G\right)$, $M_2^{\alpha }\left(G\right)$, ${\chi }_{\alpha }\left(G\right)$ and $IS{I}_{\alpha }\left(G\right)$ for specific values of $\alpha$: $\alpha =0$, $\alpha =-1/2$, $\alpha =-1$ and $\alpha =-1$, respectively. In contrast, note that $G{A}_{\alpha }\left(G\right)$ does not saturate for any $\alpha$, so we discard it as possible complexity measure. Thus, in Figure 13 we plot $〈M_1^0\left(G\right)〉/n$, $〈M_2^{-1/2}\left(G\right)〉/n$, $〈{\chi }_{-1}\left(G\right)〉/n$ and $〈IS{I}_{-1}\left(G\right)〉/n$ as a function of the average degree $〈k〉$ for ER random networks and RG graphs. From the behavior of the average-scaled indices reported in Figure 13 we can identify three regimes: (i) a regime of mostly isolated vertices when $〈k〉<1/10$, where $〈X\left(G\right)〉/n\approx 0$, (ii) a regime corresponding to mostly connected networks when $〈k〉>10$, where $〈X\left(G\right)〉/n\approx \mathrm{const}.>0$, and (iii) a transition regime in the interval $1/10<〈k〉<10$, which is logarithmically symmetric around the percolation transition point $〈k〉\approx 1$. Accordingly, we propose the use of $〈M_1^0\left(G\right)〉/n$, $〈M_2^{-1/2}\left(G\right)〉/n$, $〈{\chi }_{-1}\left(G\right)〉/n$ and $〈IS{I}_{-1}\left(G\right)〉/n$ as complexity measures for random network models. (We should remark that the behavior reported in Figure 13 for $〈M_2^{-1/2}\left(G\right)〉/n$ and $〈{\chi }_{-1}\left(G\right)〉/n$ was already expected since they coincide, respectively, with $〈R\left(G\right)〉/n$ and $〈H\left(G\right)〉/2n$; already studied in Refs. [24,25,32] and used there as measures equivalent to RMT complexity measures.)

We hope that our work may motivate further analytical as well as numerical studies of general topological indices on random networks.