Extremal Trees with Respect to the Difference between Atom-Bond Connectivity Index and Randić Index

Abstract

Let G be a simple, connected and undirected graph. The atom-bond connectivity index ($ABC\left(G\right)$) and Randić index ($R\left(G\right)$) are the two most well known topological indices. Recently, Ali and Du (2017) introduced the difference between atom-bond connectivity and Randić indices, denoted as $ABC-R$ index. In this paper, we determine the fourth, the fifth and the sixth maximum chemical trees values of $ABC-R$ for chemical trees, and characterize the corresponding extremal graphs. We also obtain an upper bound for $ABC-R$ index of such trees with given number of pendant vertices. The role of symmetry has great importance in different areas of graph theory especially in chemical graph theory.

1. Introduction

Let G be a simple, connected and undirected graph. having $V\left(G\right)$ and $E\left(G\right)$ as the set of vertices and edges respectively. The number of vertices and edges in G are denoted by n m, respectively. Let $d_u$ denotes the degree of vertex u in G, while $\Delta \left(G\right)$ and $\delta \left(G\right)$ are used to denote the maximum and minimum degree of G. The distance $d_G(x,y)$ between vertices x and y is defined as the length of any shortest path in G connecting x and y. The eccentricity of $v_i$ in G is defined as $e_i={max}_{v_j\in V\left(G\right)}{d}_G(v_i,v_j)$. For more concepts and terminologies in Graph Theory, we refer to [1].

Topological indices is one of the useful tools of graph theory [2]. Molecular compounds are often modeled by molecular graphs are used to represent the molecules and molecular compounds with the help of lines and dots. In study of QSPR/QSAR, topological indices are considered as one of the useful topics [3].

In 1975, Randić [4] defined the Randić index as follows:

$$R\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d_u{d}_v}}.$$

Details about Randić index and most of its mathematical properties can be found in [5,6,7,8,9,10].

Estrada et al. [11] proposed the atom-bond connectivity ($ABC$ for short) for a molecular graph as

$$ABC\left(G\right)=\sum _{uv\in E\left(G\right)}\sqrt{\frac{d_u+d_v-2}{d_u{d}_v}}.$$

This index became popular only ten years later, when the paper [12] was published. For the details, see the surveys [13], the recent papers [14,15,16,17,18,19] and the references cited therein.

Nowadays, studying the relationship or comparison between topological indices, see [20,21,22,23], is becoming popular. Recently, Ali and Du [24] investigated extremal binary and chemical trees results for the difference between $ABC$ and R indices. A tree with maximum degree at most three or four called a binary and chemical tree, respectively.

For a connected graph G of order at least 3, the difference between $ABC$ and R is represented as (see [24])

$$(ABC-R)\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{\sqrt{d_u+d_v-2}-1}{\sqrt{d_u{d}_v}}.$$

Note that $(ABC-R)\left(G\right)\ge 0$ and equality holds if and only if $G=P_3$. So in our discussion we consider $n\ge 4$.

In this paper, motivated by the results in [24], we further investigated the extremal chemical trees for $ABC-R$. Moreover, maximal trees with fixed number of pendant vertices are also investigated for $ABC-R$ index. The techniques used in this paper are very similar to that of Refs. [19,24,25].

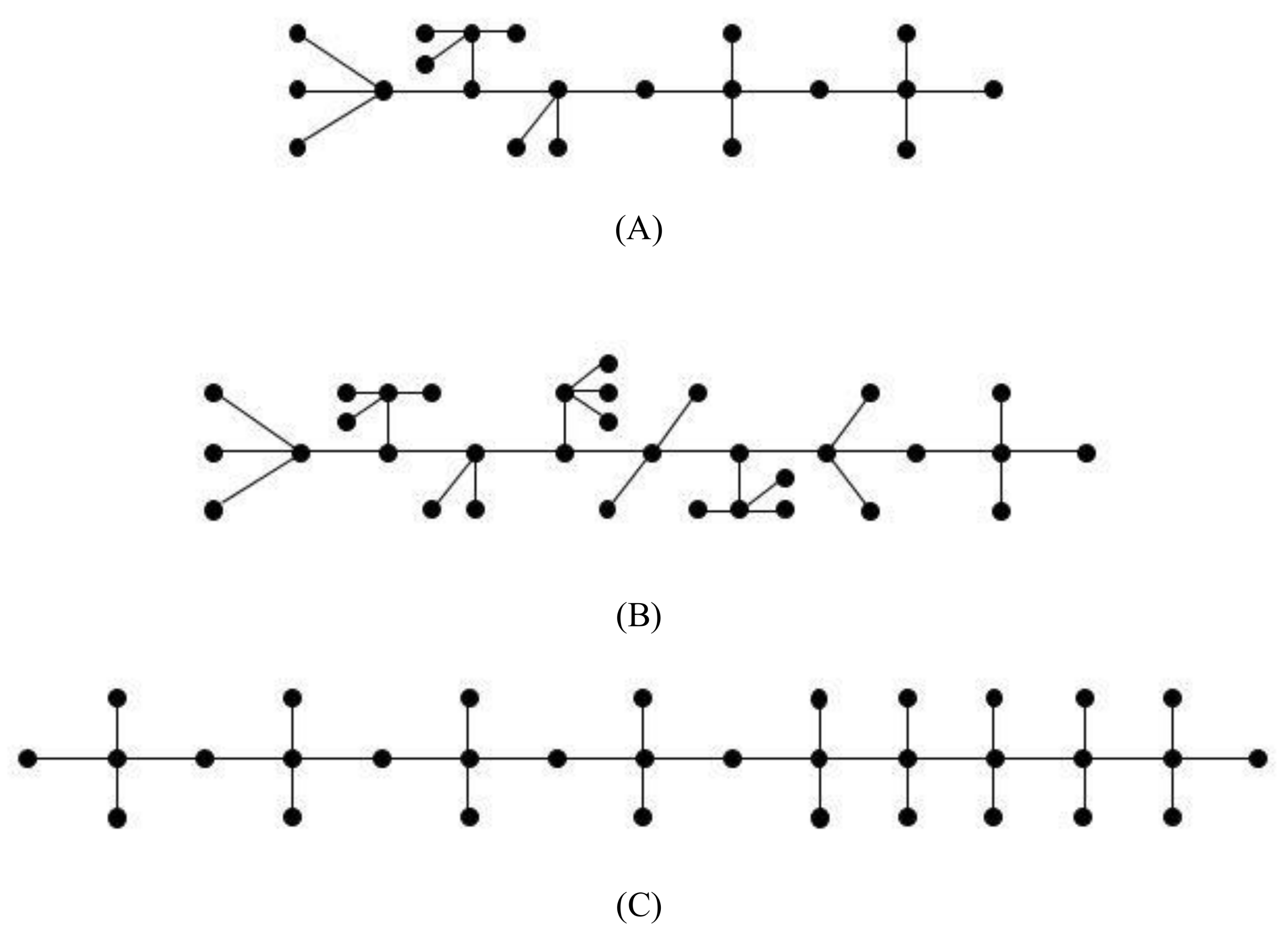
2. Preliminary Results

Let the number of edges connecting the vertices of degree p and q is denoted by $x_{p,q}$. In term of $p,q$ and $x_{p,q}$$ABC-R$ can be rewritten as follows [24]:

$$(ABC-R)\left(G\right)=\sum _{\delta \le p\le q\le \Delta }\frac{\sqrt{p+q-2}-1}{\sqrt{pq}}{x}_{p,q}.$$

(1)

Let $n_p$ be the number of vertices of degree p in G, where $1\le p\le 4$. Then for any n-vertex chemical tree the following system of equations holds (see [19,24]):

$$n_1+n_2+n_3+n_4=n,$$

(2)

$$n_1+2n_2+3n_3+4n_4=2(n-1),$$

(3)

$$x_{1,2}+x_{1,3}+x_{1,4}=n_1,$$

(4)

$$x_{1,2}+2x_{2,2}+x_{2,3}+x_{2,4}=2n_2,$$

(5)

$$x_{1,3}+x_{2,3}+2x_{3,3}+x_{3,4}=3n_3,$$

(6)

$$x_{1,4}+x_{2,4}+x_{3,4}+2x_{4,4}=4n_4.$$

(7)

From Equations (2) and (3), it follows that

$$n_2+2n_3+3n_4=n-2,$$

and thus,

$$n\equiv n_2+2n_3+2\left(\mathrm{mod}3\right).$$

(8)

By solving the sysmtem of Equations (2)–(7), the values of $x_{1,4}$ and $x_{4,4}$ are, respectively, given as below (see also Refs. [24,26]):

$$\begin{array}{c}\hfill x_{1,4}=\frac{2n+2}{3}-\frac{4}{3}{x}_{1,2}-\frac{10}{9}{x}_{1,3}-\frac{2}{3}{x}_{2,2}-\frac{4}{9}{x}_{2,3}-\frac{1}{3}{x}_{2,4}-\frac{2}{9}{x}_{3,3}-\frac{1}{9}{x}_{3,4},\\ \hfill x_{4,4}=\frac{n-5}{3}+\frac{1}{3}{x}_{1,2}+\frac{1}{9}{x}_{1,3}-\frac{1}{3}{x}_{2,2}-\frac{5}{9}{x}_{2,3}-\frac{2}{3}{x}_{2,4}-\frac{7}{9}{x}_{3,3}-\frac{8}{9}{x}_{3,4}.\end{array}$$

Note that the detailed calculation of obtaining the values for $x_{1,4}$ and $x_{4,4}$ can be referred in [26].

By substituting these values of $x_{1,4}$ and $x_{4,4}$ in Equation (1), one has:

$$\begin{array}{ccc}\hfill (ABC-R)\left(G\right)& =& \frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{4\sqrt{3}-5\sqrt{6}+1}{12}-\frac{8\sqrt{3}-\sqrt{6}-7}{12}{x}_{1,2}\hfill \\ & & -\frac{32\sqrt{3}-13\sqrt{6}-19}{36}{x}_{1,3}-\frac{4\sqrt{3}+\sqrt{6}-6\sqrt{2}+1}{12}{x}_{2,2}\hfill \\ & & -\frac{8\sqrt{3}+11\sqrt{6}-18\sqrt{2}-13}{36}{x}_{2,3}-\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}{x}_{2,4}\hfill \\ & & -\frac{4\sqrt{3}+7\sqrt{6}-23}{36}{x}_{3,3}-\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}{x}_{3,4}.\hfill \end{array}$$

(9)

Let

$$\begin{array}{ccc}\hfill \theta & =& \frac{8\sqrt{3}-\sqrt{6}-7}{12}{x}_{1,2}+\frac{32\sqrt{3}-13\sqrt{6}-19}{36}{x}_{1,3}+\frac{4\sqrt{3}+\sqrt{6}-6\sqrt{2}+1}{12}{x}_{2,2}\hfill \\ & & +\frac{8\sqrt{3}+11\sqrt{6}-18\sqrt{2}-13}{36}{x}_{2,3}+\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}{x}_{2,4}\hfill \\ & & +\frac{4\sqrt{3}+7\sqrt{6}-23}{36}{x}_{3,3}+\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}{x}_{3,4}.\hfill \end{array}$$

(10)

Then Equation (9) can be rewritten as

$$(ABC-R)\left(G\right)=\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{4\sqrt{3}-5\sqrt{6}+1}{12}-\theta .$$

(11)

since

$$\begin{array}{ccc}\hfill \theta & \approx & 0.367243x_{1,2}+0.127285x_{1,3}+0.157701x_{2,2}+0.0651375x_{2,3}\hfill \\ & & +0.0100367x_{2,4}+0.0298509x_{3,3}+0.00595623x_{3,4}.\hfill \end{array}$$

(12)

From Equation (12) we have $\theta \ge 0$. Moreover Equation (11) implies that a chemical tree which gives the minimum value of $\theta$ will produce the maximum of $(ABC-R)$.

Theorem 1

([24]). Consider the set of all n-vertex chemical trees.

(1)

Suppose that $n\equiv 0\left(mod3\right)$.

(1.1)

For $n\ge 9$, the maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{3+2\sqrt{2}-3\sqrt{6}}{4},$$

which is uniquely attained by those trees that contain a unique vertex of degree 2 and no vertex of degree 3, that is, $n_2=1$ and $n_3=0$, such that the unique vertex of degree 2 is adjacent to two vertices of degree 4, that is, $x_{1,2}=0$ and $x_{2,4}=2$.

(1.2)

For $n\ge 21$, the second maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{4\sqrt{15}-7\sqrt{6}-4\sqrt{3}+7}{4},$$

which is uniquely attained by those trees that contain no vertex of degree 2 and exactly two vertices of degree 3, that is, $n_2=0$ and $n_3=2$, such that each vertex of degree 3 is adjacent to three vertices of degree 4, that is, $x_{1,3}=x_{3,3}=0$ and $x_{3,4}=6$.

(1.3)

For $n\ge 21$, the third maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{4\sqrt{15}-4\sqrt{3}-9\sqrt{6}+11}{6},$$

which is uniquely attained by those trees that contain no vertex of degree 2 and exactly two vertices of degree 3, which are adjacent, that is, $n_2=0$, $n_3=2$, and $x_{3,3}=1$ such that each vertex of degree 3 is adjacent to exactly two vertices of degree 4, that is, $x_{1,3}=0$ and $x_{3,4}=4$.

(2)

Suppose that $n\equiv 1\left(mod3\right)$.

(2.1)

For $n\ge 13$, the maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{11+6\sqrt{15}-4\sqrt{3}-13\sqrt{6}}{12},$$

and the equality holds if and only if $n_2=0$ and $n_3=1$ such that $x_{1,3}=0$ and $x_{3,4}=3$.

(2.2)

For $n\ge 13$, the second maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{12\sqrt{2}-13\sqrt{6}-4\sqrt{3}+17}{12},$$

which is uniquely attained by those trees that contain exactly two vertices of degree 2 and no vertex of degree 3, that is, $n_2=2$ and $n_3=0$, such that either vertex of degree 2 is adjacent to two vertices of degree 4, that is, $x_{1,2}=x_{2,2}=0$ and $x_{2,4}=4$.

(2.3)

For $n\ge 25$, the third maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{12\sqrt{15}-6\sqrt{2}-25\sqrt{6}-16\sqrt{3}+29}{12},$$

which is uniquely attained by those trees that contain a unique vertex of degree 2 and exactly two vertices of degree 3, that is, $n_2=1$ and $n_3=2$, such that each vertex of degree 2 and 3 is adjacent to only vertices of degree 4, that is, $x_{1,2}=x_{1,3}=x_{2,3}=x_{3,3}=0$, $x_{2,4}=2$, and $x_{3,4}=6$.

(3)

Suppose that $n\equiv 2\left(mod3\right)$.

(3.1)

For $n\ge 5$, the maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{4\sqrt{3}-5\sqrt{6}+1}{12},$$

which is uniquely attained by those trees that contain no vertex of degree 2 or 3, that is, $n_2=n_3=0$.

(3.2)

For $n\ge 17$, the second maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{6\sqrt{15}+6\sqrt{2}-17\sqrt{6}-8\sqrt{3}+19}{12},$$

which is uniquely attained by those trees that contain a unique vertex of degree 2 and a unique vertex of degree 3, that is, $n_2=n_3=1$, such that each vertex of degree 2 and 3 is adjacent to only vertices of degree 4, that is, $x_{1,2}=x_{1,3}=x_{2,3}=0$, $x_{2,4}=2$, and $x_{3,4}=3$.

(3.3)

For $n\ge 29$, the third maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{18\sqrt{15}-29\sqrt{6}-20\sqrt{3}+31}{12},$$

which is uniquely attained by those trees that contain no vertex of degree 2 and exactly three vertices of degree 3, that is, $n_2=0$ and $n_3=3$, such that each vertex of degree 3 is adjacent to three vertices of degree 4, that is, $x_{1,3}=x_{3,3}=0$, and $x_{3,4}=9$.

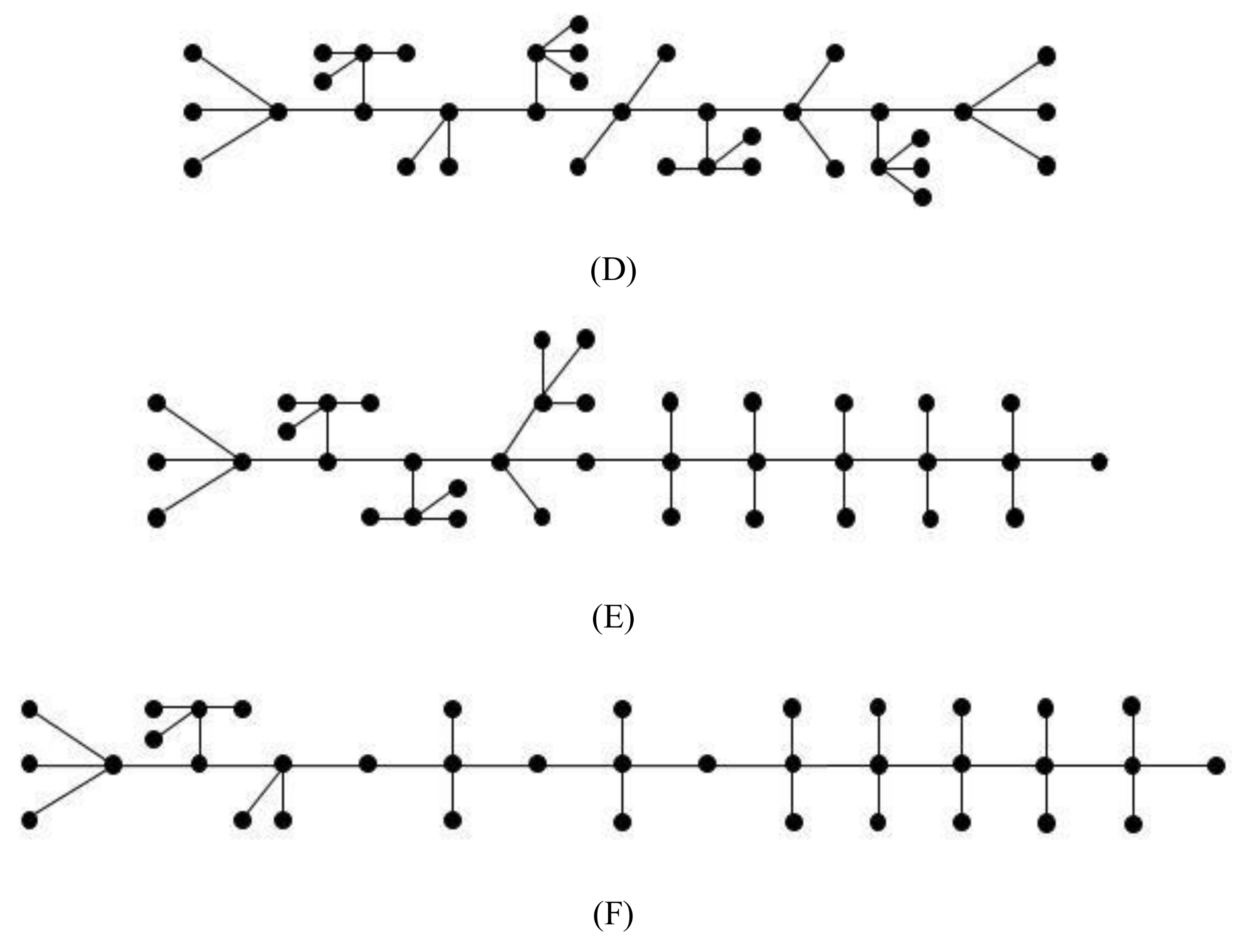
3. Maximum $\mathit{ABC}-\mathit{R}$ Index for Chemical Trees

In this section, we present a main result which deals with the maximal chemical trees for $ABC-R$ index.

Theorem 2.

Consider the set of all n-vertex chemical trees.

(1)

Suppose that $n\equiv 0\left(mod3\right)$.

(1.1)

For $n\ge 21$, the fourth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{18\sqrt{15}+36\sqrt{2}-36\sqrt{3}-63\sqrt{6}+81}{36},$$

and the equality holds if and only if $n_2=2$ and $n_3=1$ such that $x_{1,2}=x_{1,3}=x_{2,2}=x_{2,3}=0$, $x_{2,4}=4$ and $x_{3,4}=3$.

(1.2)

For $n\ge 33$, the fifth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{54\sqrt{15}+18\sqrt{2}-72\sqrt{3}-99\sqrt{6}+117}{36},$$

and the equality holds if and only if $n_2=1$ and $n_3=3$ such that $x_{1,2}=x_{1,3}=x_{2,3}=x_{3,3}=0$, $x_{2,4}=2$ and $x_{3,4}=9$.

(1.3)

For $n\ge 33$, the sixth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{24\sqrt{2}-12\sqrt{3}-21\sqrt{6}+33}{12},$$

and the equality holds if and only if $n_2=4$, $n_3=0$ such that $x_{1,2}=x_{2,2}=0$ and $x_{2,4}=8$.

(2)

Suppose that $n\equiv 1\left(mod3\right)$.

(2.1)

For $n\ge 37$, the fourth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{72\sqrt{15}-84\sqrt{3}-111\sqrt{6}+123}{36},$$

and the equality holds if and only if $n_2=0$ and $n_3=4$ such that $x_{1,3}=x_{3,3}=0$ and $x_{3,4}=12$.

(2.2)

For $n\ge 37$, the fifth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{24\sqrt{15}+18\sqrt{2}-36\sqrt{3}-66\sqrt{6}+90}{36},$$

and the equality holds if and only if $n_2=1$, $n_3=2$ such that $x_{3,3}=1,x_{1,2}=x_{1,3}=x_{2,3}=0$, $x_{2,4}=2$, and $x_{3,4}=4$.

(2.3)

For $n\ge 37$, the sixth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{18\sqrt{15}+54\sqrt{2}-48\sqrt{3}-75\sqrt{6}+105}{36},$$

and the equality holds if and only if $n_2=3$ and $n_3=1$ such that $x_{1,2}=x_{1,3}=x_{2,2}=x_{2,3}=0$, $x_{2,4}=6$, and $x_{3,4}=3$.

(3)

Suppose that $n\equiv 2\left(mod3\right)$.

(3.1)

For $n\ge 29$, the fourth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{18\sqrt{2}-8\sqrt{3}-17\sqrt{6}+25}{12},$$

and the equality holds if and only if $n_2=3$ and $n_3=0$ such that $x_{1,2}=x_{2,2}=0$ and $x_{2,4}=6$.

(3.2)

For $n\ge 29$, the fifth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{42\sqrt{15}-78\sqrt{6}-48\sqrt{3}+96}{36},$$

and the equality holds if and only if $n_2=0$ and $n_3=3$ such that $x_{1,3}=0$, $x_{3,3}=1$ and $x_{3,4}=7$.

(3.3)

For $n\ge 29$, the sixth maximum $ABC-R$ value is

$$\frac{4\sqrt{3}+\sqrt{6}-5}{12}n+\frac{36\sqrt{15}+36\sqrt{2}-60\sqrt{3}-87\sqrt{6}+111}{36},$$

and the equality holds if and only if $n_2=2$ and $n_3=2$ such that $x_{1,2}=x_{1,3}=x_{2,2}=x_{2,3}=x_{3,3}=0$, $x_{2,4}=4$ and $x_{3,4}=6$.

Proof. 

First, we claim that $\theta >0.080294$ when $x_{1,2}+x_{1,3}+x_{2,2}\ge 1$ or $x_{2,3}\ge 2$. More precisely, from Equation (12),

• when $x_{1,2}\ge 1$,

  $$\theta \ge \frac{8\sqrt{3}-\sqrt{6}-7}{12}\approx 0.367243>0.080294,$$
• when $x_{1,3}\ge 1$,

  $$\theta \ge \frac{32\sqrt{3}-13\sqrt{6}-19}{36}\approx 0.127285>0.080294,$$
• when $x_{2,2}\ge 1$,

  $$\theta \ge \frac{4\sqrt{3}+\sqrt{6}-6\sqrt{2}+1}{12}\approx 0.157701>0.080294,$$
• when $x_{2,3}\ge 2$,

  $$\theta \ge 2·\frac{8\sqrt{3}+11\sqrt{6}-18\sqrt{2}-13}{36}\approx 0.130275>0.080294.$$

So we may assume that $x_{1,2}=x_{1,3}=x_{2,2}=0$, and $x_{2,3}=0$ or 1. It follows from Equations (5) and (6) that

$$x_{2,4}=2n_2-x_{2,3}$$

(13)

and

$$2x_{3,3}+x_{3,4}=3n_3-x_{2,3}.$$

(14)

Case 1.$x_{2,3}=1$.

Observe that $n_2\ge 1$, $n_3\ge 1$, and thus $x_{2,4}\ge 1$ from Equation (13).

If $x_{2,4}\ge 2$, then by the Equation (12),

$$\theta \ge \frac{8\sqrt{3}+11\sqrt{6}-18\sqrt{2}-13}{36}+2·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}\approx 0.0852109>0.080294.$$

Suppose now that $x_{2,4}=1$. If $x_{3,3}=0$, then by Equation (14), $x_{3,4}\ge 2$, together with Equation (12), it leads to

$$\begin{array}{ccc}\hfill \theta & \ge & \frac{8\sqrt{3}+11\sqrt{6}-18\sqrt{2}-13}{36}+\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}\hfill \\ & & +2·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.08708666>0.080294.\hfill \end{array}$$

(15)

If $x_{3,3}\ge 1$, then by Equation (12),

$$\begin{array}{ccc}\hfill \theta & \ge & \frac{8\sqrt{3}+11\sqrt{6}-18\sqrt{2}-13}{36}+\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}\hfill \\ & & +\frac{4\sqrt{3}+7\sqrt{6}-23}{36}\hfill \\ & \approx & 0.1050251>0.080294.\hfill \end{array}$$

(16)

Case 2.$x_{2,3}=0$.

From Equations (13) and (14), it follows that

$$x_{2,4}=2n_2$$

(17)

and

$$2x_{3,3}+x_{3,4}=3n_3.$$

(18)

If $x_{3,3}\ge 3$, then by Equation (12),

$$\theta \ge 3·\frac{4\sqrt{3}+7\sqrt{6}-23}{36}\approx 0.0895526>0.0802936.$$

If $x_{3,3}=2$, then $n_3\ge 3$, and $x_{3,4}\ge 5$ from Equation (14), and thus by Equation (12),

$$\theta \ge 2·\frac{4\sqrt{3}+7\sqrt{6}-23}{36}+5·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\approx 0.0894829>0.0802936.$$

Now, we consider the two cases: $x_{3,3}=1$ and $x_{3,3}=0$.

Subcase 2.1.$x_{3,3}=1$.

Clearly, $n_3\ge 2$. The proofs will be partitioned into several parts according to the value of $n_3$: $n_3=2$, $n_3=3$, $n_3\ge 4$.

Firstly suppose that $n_3=2$, then, $x_{3,4}=4$ from Equation (14). Note that the case $n_2=0$ is known to belong to one of the first three minimum $\theta$ values, see Theorem 1-(1.3). If $n_2=1$, then $n\equiv 1\left(\mathrm{mod}3\right)$ from Equation (8), $x_{2,4}=2$ from Equation (17), and by Equation (12),

$$\begin{array}{ccc}\hfill \theta & =& 2·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+\frac{4\sqrt{3}+7\sqrt{6}-23}{36}+4·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.0737492.\hfill \end{array}$$

If $n_2\ge 2$, then, $x_{2,4}\ge 4$ from Equation (17), and by Equation (12),

$$\begin{array}{ccc}\hfill \theta & \ge & 4·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+\frac{4\sqrt{3}+7\sqrt{6}-23}{36}+4·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.09382262>0.0802936.\hfill \end{array}$$

Next, suppose that $n_3=3$, then $x_{3,4}=7$ from Equation (14). If $n_2=0$, then $n\equiv 2\left(\mathrm{mod}3\right)$ from Equation (8), $x_{2,4}=0$ from Equation (17), and by Equation (12),

$$\theta =\frac{4\sqrt{3}+7\sqrt{6}-23}{36}+7·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\approx 0.0715445.$$

If $n_2\ge 1$, then $x_{2,4}\ge 2$ from Equation (17), and by Equation (12),

$$\begin{array}{ccc}\hfill \theta & \ge & 2·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+\frac{4\sqrt{3}+7\sqrt{6}-23}{36}+7·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.0916179>0.0802936.\hfill \end{array}$$

Finally, if $n_3\ge 4$, then $x_{3,4}\ge 10$ from Equation (16), and by Equation (12),

$$\begin{array}{ccc}\hfill \theta & \ge & \frac{4\sqrt{3}+7\sqrt{6}-23}{36}+10·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.0894132>0.0802936.\hfill \end{array}$$

Subcase 2.2.$x_{3,3}=0$.

In this case, $x_{3,4}=3n_3$ from Equation (18). This time, we partition the proofs according to the value of $n_2$: $n_2=0$, $n_2=1$, $n_2=2$, $n_2=3$, $n_2=4$, $n_2\ge 5$.

Firstly suppose that $n_2=0$, that is, $x_{2,4}=0$ from Equation (17). Note that the cases $n_3=0,1,2,3$ were known to belong to the first three minimum $\theta$ value, see Theorem 1. If $n_3=4$, then $n\equiv 1\left(\mathrm{mod}3\right)$ from Equation (8), $x_{3,4}=12$, and by Equation (12),

$$\theta =12·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\approx 0.0714748.$$

If $n_3\ge 5$, then $x_{3,4}\ge 15$, and by Equation (12),

$$\theta \ge 15·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\approx 0.08934345>0.0802936.$$

Next, suppose that $n_2=1$, that is, $x_{2,4}=2$ from Equation (17). Note that the cases $n_3=0,1,2$ were known to belong to the first three minimum $\theta$ values, see Theorem 1. If $n_3=3$, then $n\equiv 0\left(\mathrm{mod}3\right)$ from Equation (8), $x_{3,4}=9$, and by Equation (12),

$$\theta =2·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+9·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\approx 0.0736795.$$

If $n_3\ge 4$, then $x_{3,4}\ge 12$, and by Equation (12),

$$\begin{array}{ccc}\hfill \theta & \ge & 2·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+12·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.091548>0.0802936.\hfill \end{array}$$

Now, suppose that $n_2=2$, that is, $x_{2,4}=4$ from Equation (17). The case $n_3=0$ was known to belong to one of the first three minimum $\theta$ values, see Theorem 1-(2.2). If $n_3=1$, then $n\equiv 0\left(\mathrm{mod}3\right)$ from Equation (8), $x_{3,4}=3$, and by Equation (12),

$$\theta =4·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+3·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\approx 0.0580155.$$

If $n_3=2$, then $n\equiv 2\left(\mathrm{mod}3\right)$ from Equation (8), $x_{3,4}=6$, and by Equation (12),

$$\theta =4·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+6·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\approx 0.07588419.$$

If $n_3\ge 3$, then $x_{3,4}\ge 9$, and by Equation (12),

$$\begin{array}{ccc}\hfill \theta & \ge & 4·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+9·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.09375289>0.0802936.\hfill \end{array}$$

Suppose that $n_2=3$, that is, $x_{2,4}=6$ from Equation (17). If $n_3=0$, then $n\equiv 2\left(\mathrm{mod}3\right)$ from Equation (8), $x_{3,4}=0$, and by Equation (12),

$$\theta =6·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}\approx 0.0602202.$$

If $n_3=1$, then $n\equiv 1\left(\mathrm{mod}3\right)$ from Equation (8), $x_{3,4}=3$, and by Equation (12),

$$\theta =6·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+3·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\approx 0.0780889.$$

If $n_3\ge 2$, then $x_{3,4}\ge 6$, and by Equation (12),

$$\begin{array}{ccc}\hfill \theta & \ge & 6·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+6·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.0959576>0.0802936.\hfill \end{array}$$

Suppose that $n_2=4$, that is, $x_{2,4}=8$ from Equation (17). If $n_3=0$, then $n\equiv 0\left(\mathrm{mod}3\right)$ from Equation (8), $x_{3,4}=0$, and by Equation (12),

$$\theta =8·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}\approx 0.0802936.$$

If $n_3\ge 1$, then $x_{3,4}\ge 3$, and by Equation (12),

$$\begin{array}{ccc}\hfill \theta & \ge & 8·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}+3·\frac{4\sqrt{3}+4\sqrt{6}-3\sqrt{15}-5}{18}\hfill \\ & \approx & 0.0981623>0.0802936.\hfill \end{array}$$

Finally, if $n_2\ge 5$, then $x_{2,4}\ge 10$ from Equation (17), and by Equation (12),

$$\theta \ge 10·\frac{2\sqrt{3}+2\sqrt{6}-3\sqrt{2}-4}{12}\approx 0.100367>0.0802936.$$

In conclusion, we obtain the following

(i)

If $n\equiv 0\left(\mathrm{mod}3\right)$, then the fourth, fifth and sixth minimum $\theta$ values are 0.0580155, 0.0736795 and 0.0802936, respectively.

(ii)

If $n\equiv 1\left(\mathrm{mod}3\right)$, then the fourth, fifth and sixth minimum $\theta$ values are 0.0714748, 0.0737492 and 0.0780889, respectively.

(iii)

If $n\equiv 2\left(\mathrm{mod}3\right)$, then the fourth, fifth and sixth minimum $\theta$ values are 0.0602202, 0.0715445 and 0.07588419, respectively.

Now, the Equation (11) implies the fourth, fifth and sixth maximum $ABC-R$. □

In Figure 1, Figure 2 and Figure 3, the chemical trees with the smallest numbers of vertices in Theorem 2 are listed.

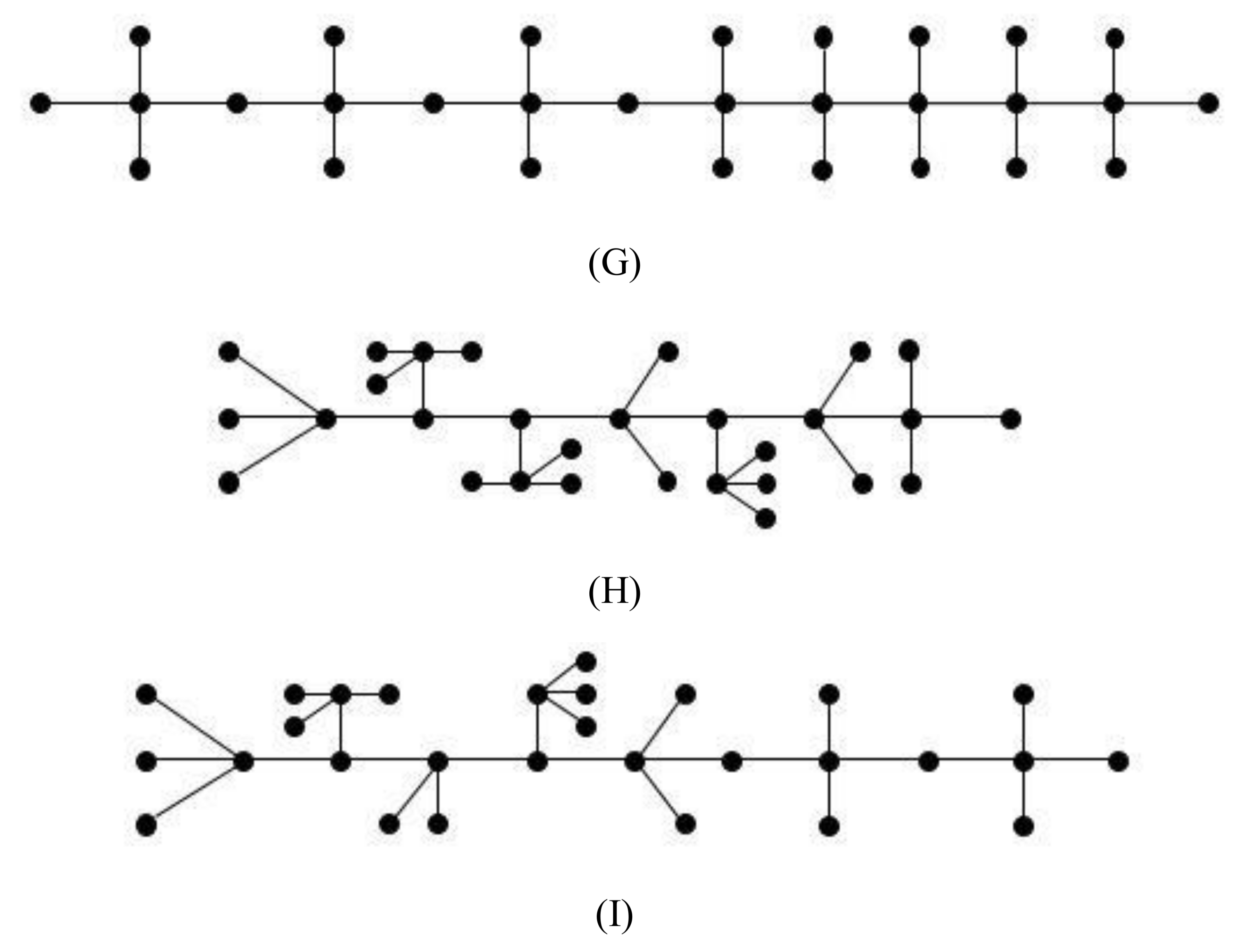
4. Upper Bound for $\mathit{ABC}-\mathit{R}$ Index of Molecular Trees

In this section, we consider the class of molecular tress and investigated the sharp bound on $ABC-R$ for this class of graphs.

Let ${\mathcal{T}}_{n,n_1}$ be the set of molecular trees satisfying

$$x_{1,4}=n_1,$$

$$x_{2,2}=n-2n_1+3-\frac{1}{3}{x}_{2,3},$$

and

$$x_{2,4}=n_1-4-\frac{2}{3}{x}_{2,3}.$$

Theorem 3

([19]). Let T be a molecular tree with n vertices, $n_1\ge 5$ of which are pendant vertices. Then

$$\left(ABC\right)\left(T\right)\le \frac{\sqrt{2}}{2}n+\frac{\sqrt{3}-\sqrt{2}}{2}{n}_1-\frac{\sqrt{2}}{2}$$

with equality holds if and only if $T\in {\mathcal{T}}_{n,n_1}$.

Obviously, from Equation (1) we obtain

$$\begin{array}{ccc}\hfill (ABC-R)\left(T\right)& =& \frac{\sqrt{2}-1}{\sqrt{3}}{x}_{1,3}+\frac{\sqrt{3}-1}{2}{x}_{1,4}+\frac{\sqrt{2}-1}{2}{x}_{2,2}+\frac{\sqrt{3}-1}{\sqrt{6}}{x}_{2,3}+\hfill \\ & & \frac{1}{\sqrt{8}}{x}_{2,4}+\frac{1}{3}{x}_{3,3}+\frac{\sqrt{5}-1}{\sqrt{12}}{x}_{3,4}+\frac{\sqrt{6}-1}{4}{x}_{4,4}\hfill \end{array}$$

(19)

Now let ${\mathcal{T}}_{n,n_1}^{\prime }$ be the set of molecular trees satisfying

$$x_{1,4}=n_1,$$

$$x_{2,2}=n-2n_1+3,$$

and

$$x_{2,4}=n_1-4.$$

Theorem 4.

Let T be a molecular tree of order n and $n_1\ge 5$ pendant vertices, then

$$(ABC-R)\left(T\right)\le \frac{\sqrt{2}-1}{2}n+\frac{2-3\sqrt{2}+2\sqrt{3}}{4}{n}_1+\frac{1}{\sqrt{2}}-\frac{3}{2}$$

with equality holds if and only if $T\in {\mathcal{T}}_{n,n_1}^{\prime }$.

Proof. 

Since T is a molecular tree, we have Equations (2)–(7). Suppose that

$$\begin{array}{ccc}\hfill f_1& =& x_{1,2}+x_{1,3}+x_{1,4}\hfill \\ \hfill f_2& =& x_{1,2}+x_{2,3}\hfill \\ \hfill f_3& =& x_{1,3}+x_{2,3}+2x_{3,3}+x_{3,4}\hfill \\ \hfill f_4& =& x_{1,4}+x_{3,4}+2x_{4,4},\hfill \end{array}$$

that is,

$$\begin{array}{ccc}\hfill f_1& =& n_1\hfill \\ \hfill f_2& =& 2n_2-2x_{2,2}-x_{2,4}\hfill \\ \hfill f_3& =& 3n_3\hfill \\ \hfill f_4& =& 4n_4-x_{2,4},\hfill \end{array}$$

we have

$$\begin{array}{ccc}\hfill \sum _{i=1}^4{f}_i& =& 2(n-1)-2(x_{2,2}+x_{2,4})\hfill \\ \hfill \sum _{i=1}^4\frac{1}{i}{f}_i& =& n-(x_{2,2}+\frac{3}{4}{x}_{2,4}),\hfill \end{array}$$

implying that

$$\begin{array}{ccc}\hfill x_{2,2}& =& \frac{3}{2}\sum _{i=1}^4{f}_i-4\sum _{i=1}^4\frac{1}{i}{f}_i+n+3\hfill \\ \hfill x_{2,4}& =& -2\sum _{i=1}^4{f}_i+4\sum _{i=1}^4\frac{1}{i}{f}_i-4.\hfill \end{array}$$

Thus we have

$$\begin{array}{ccc}\hfill x_{1,4}& =& n_1-x_{1,2}-x_{1,3}\hfill \\ \hfill x_{2,2}& =& n-2n_1+3-x_{1,2}-\frac{1}{3}{x}_{1,3}-\frac{1}{3}{x}_{2,3}+\frac{1}{3}{x}_{3,3}+\frac{2}{3}{x}_{3,4}+x_{4,4}\hfill \\ \hfill x_{2,4}& =& n_1-4+x_{1,2}+\frac{1}{3}{x}_{1,3}-\frac{2}{3}{x}_{2,3}-\frac{4}{3}{x}_{3,3}-\frac{5}{3}{x}_{3,4}-2x_{4,4}.\hfill \end{array}$$

Substituting them back into Equation (19), we have

$$\begin{array}{ccc}\hfill (ABC-R)\left(T\right)& =& \frac{\sqrt{2}-1}{2}n+\frac{2-3\sqrt{2}+2\sqrt{3}}{4}{n}_1+\frac{1}{\sqrt{2}}-\frac{3}{2}\hfill \\ & & +\frac{4-\sqrt{2}-2\sqrt{3}}{4}{x}_{1,2}+\frac{8-\sqrt{2}-10\sqrt{3}+4\sqrt{6}}{12}{x}_{1,3}\hfill \\ & & +\frac{1+\sqrt{2}-\sqrt{6}}{6}{x}_{2,3}+\frac{1-\sqrt{2}}{6}{x}_{3,3}\hfill \\ & & +\frac{2\sqrt{15}-4-\sqrt{2}-2\sqrt{3}}{12}{x}_{3,4}+\frac{\sqrt{6}-3}{4}{x}_{4,4}\hfill \\ & \approx & \frac{\sqrt{2}-1}{2}n+\frac{2-3\sqrt{2}+2\sqrt{3}}{4}{n}_1+\frac{1}{\sqrt{2}}-\frac{3}{2}\hfill \\ & & -0.219579x_{1,2}-0.078064x_{1,3}-0.005879x_{2,3}\hfill \\ & & -0.069036x_{3,3}-0.094362x_{3,4}-0.137628x_{4,4}\hfill \end{array}$$

with negative coefficients $x_{1,2}$, $x_{1,3}$, $x_{2,3}$, $x_{3,3}$, $x_{3,4}$ and $x_{4,4}$. Thus

$$(ABC-R)\left(T\right)\le \frac{\sqrt{2}-1}{2}n+\frac{2-3\sqrt{2}+2\sqrt{3}}{4}{n}_1+\frac{1}{\sqrt{2}}-\frac{3}{2}$$

and equality in above holds if and only if $x_{1,2}$ = $x_{1,3}$ = $x_{2,3}$ = $x_{3,3}$ = $x_{3,4}$ = $x_{4,4}$ = 0, or equivalently, $x_{1,4}=n_1$, $x_{2,2}=n-2n_1+3$, $x_{2,4}=n_1-4$, i.e., $T\in {\mathcal{T}}_{n,n_1}^{\prime }$. □

5. Conclusions

In this paper, we considered more maximum values of the difference $ABC-R$, where $ABC$ and R are the atom-bond connectivity index and Randić index, respectively. In particular, we characterized the fourth, the fifth and the sixth maximum chemical trees with respect to the invariant $ABC-R$, and thus extended the result by Ali and Du [24] in 2017. It is very challenging to find more maximum values of $ABC-R$ invariant unless new efficient method is introduced. By using the technique from [19], we also obtained a sharp upper bound for the $ABC-R$ index of molecular (or chemical) trees with fixed number of pendant vertices. The work on bounds for the $ABC-R$ index of general graphs and trees is widely open and one can consider many directions.