Computing Analysis of Connection-Based Indices and Coindices for Product of Molecular Networks
Abstract
1. Introduction
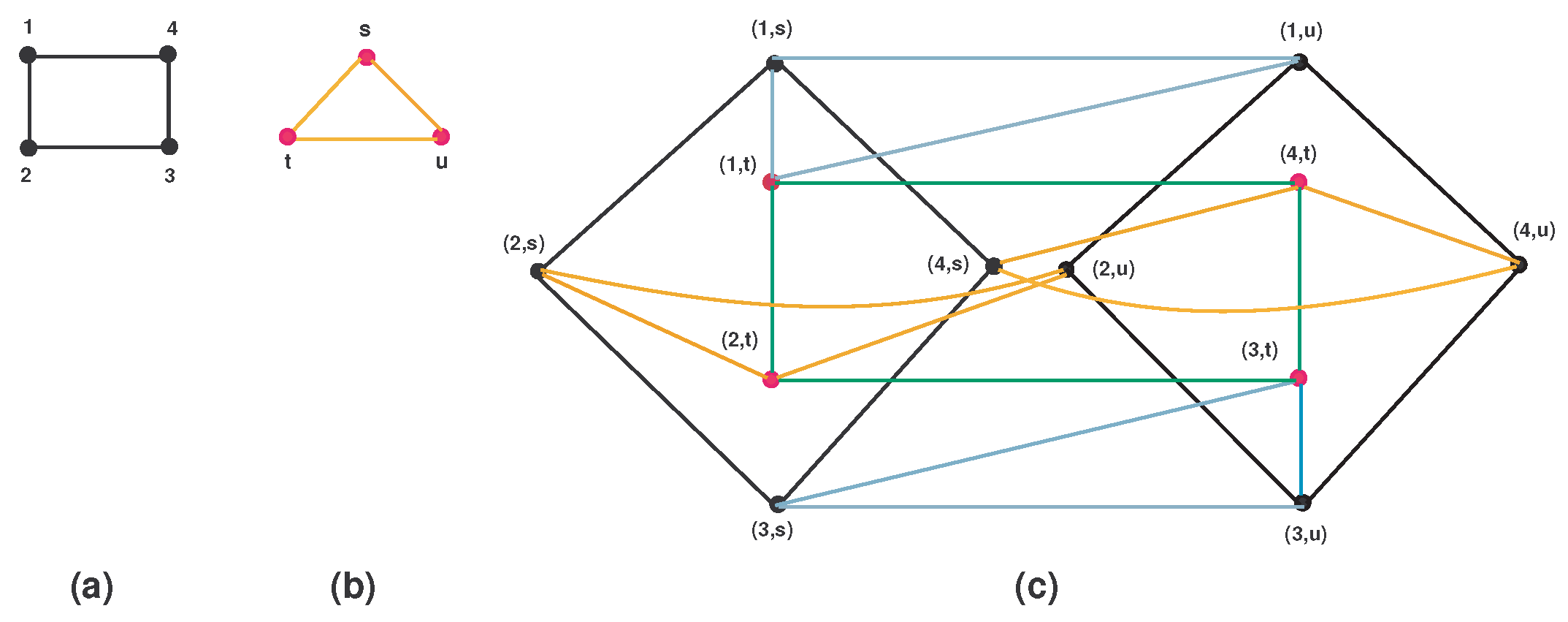
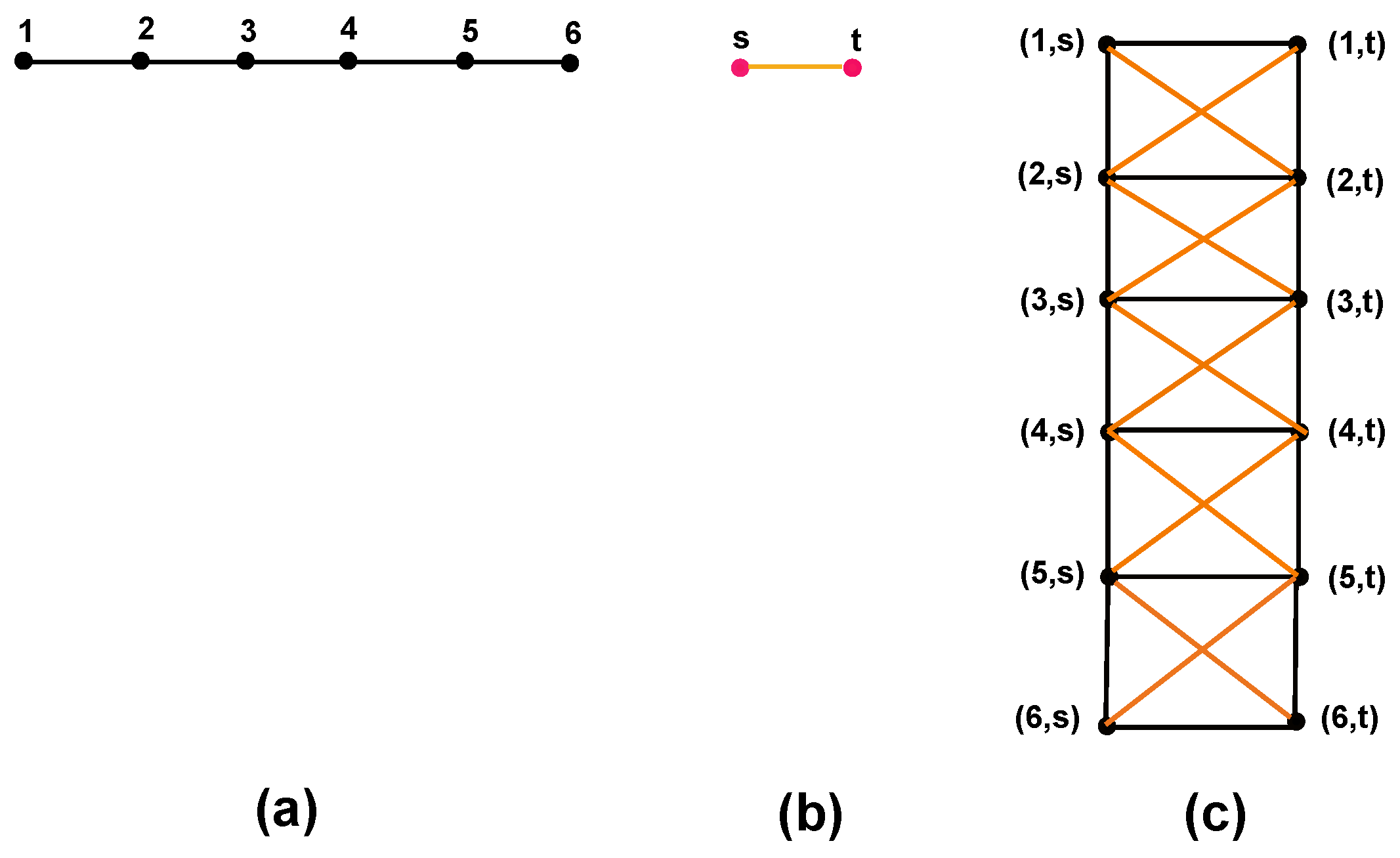
- Either or . For more detail, see Figure 1.
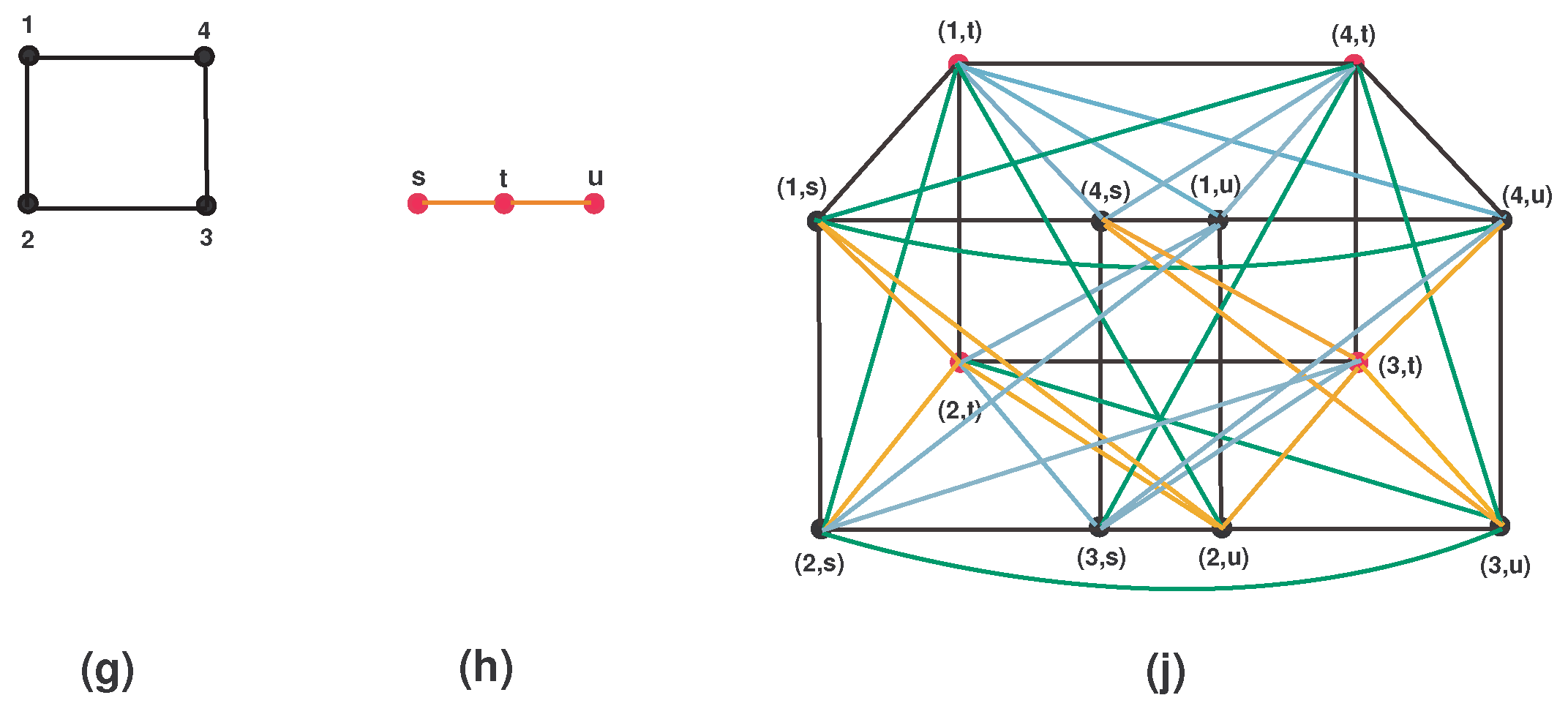
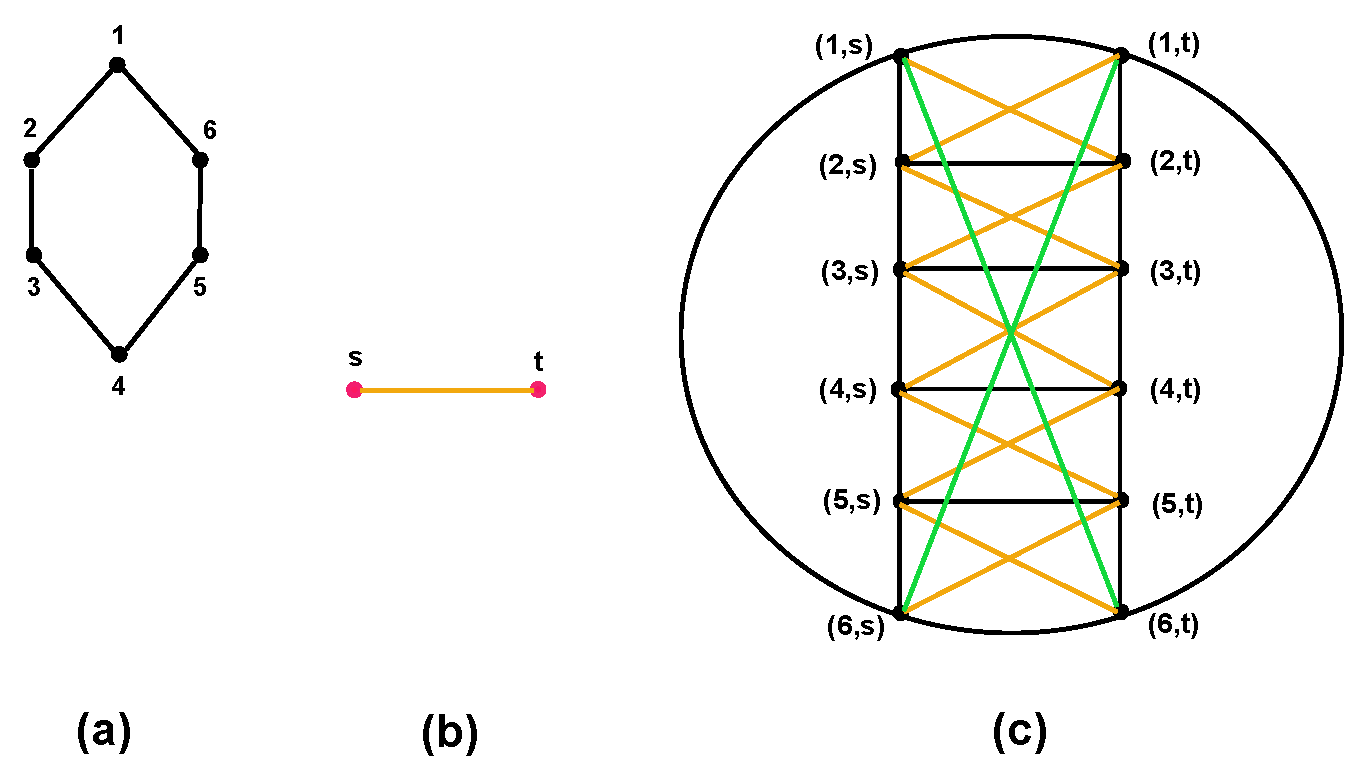
- Either or . For more detail, see Figure 3.
2. Preliminaries
3. A Few Molecular Networks
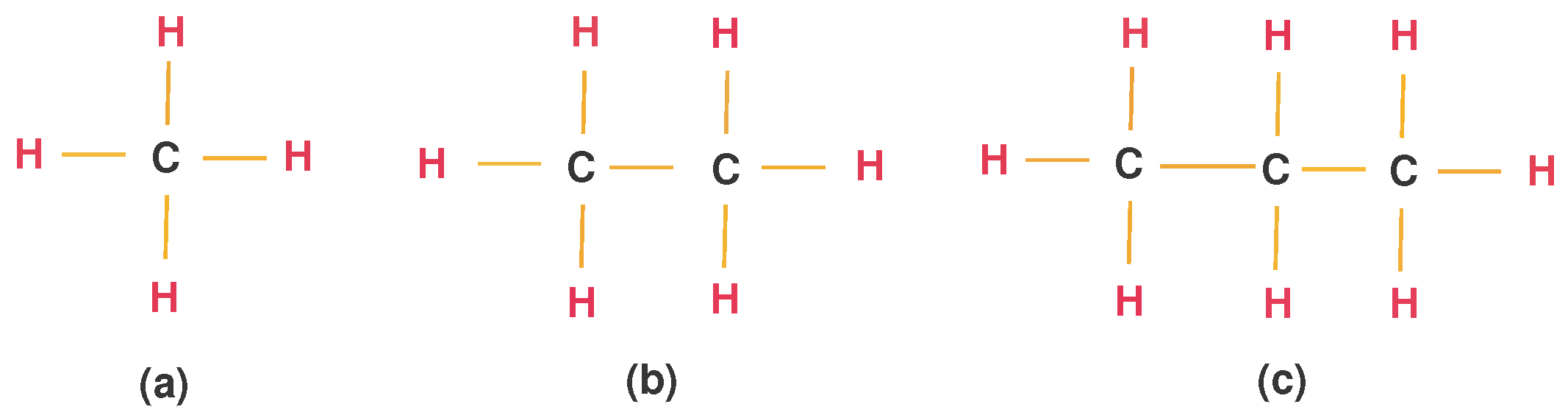
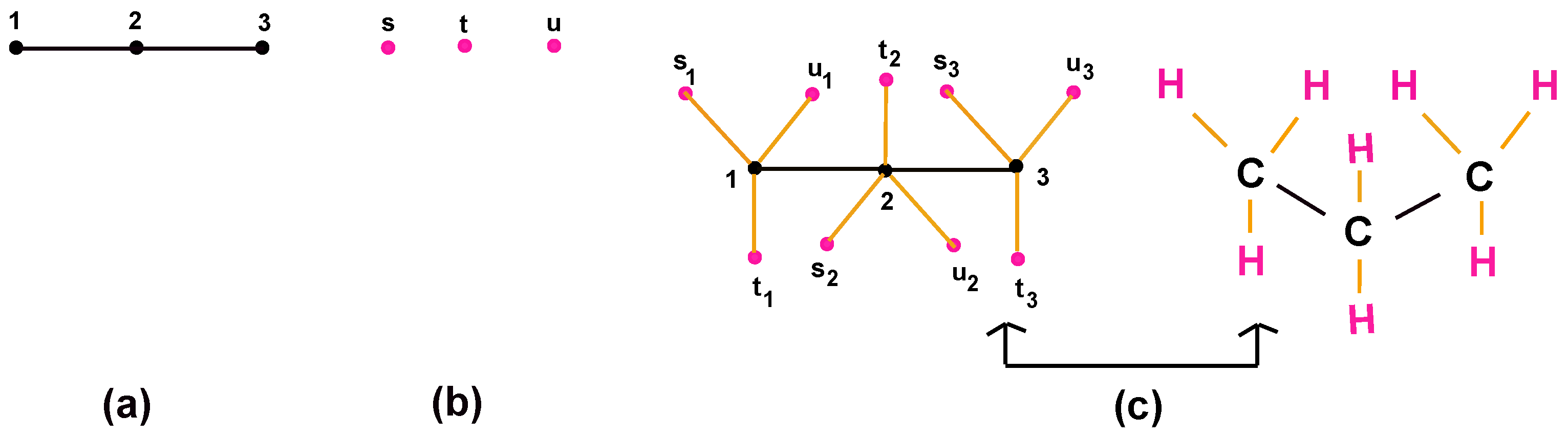
- Alkanes (hydrocarbon compounds) are organic compounds consisting of carbon atoms joined by single bounds. The simple and Lewis networks of alkanes are given in Figure 4. Moreover, methane (), ethane (), and propane () are examples of alkanes that are given in Figure 5. This alkane series continues and follows general formula as .
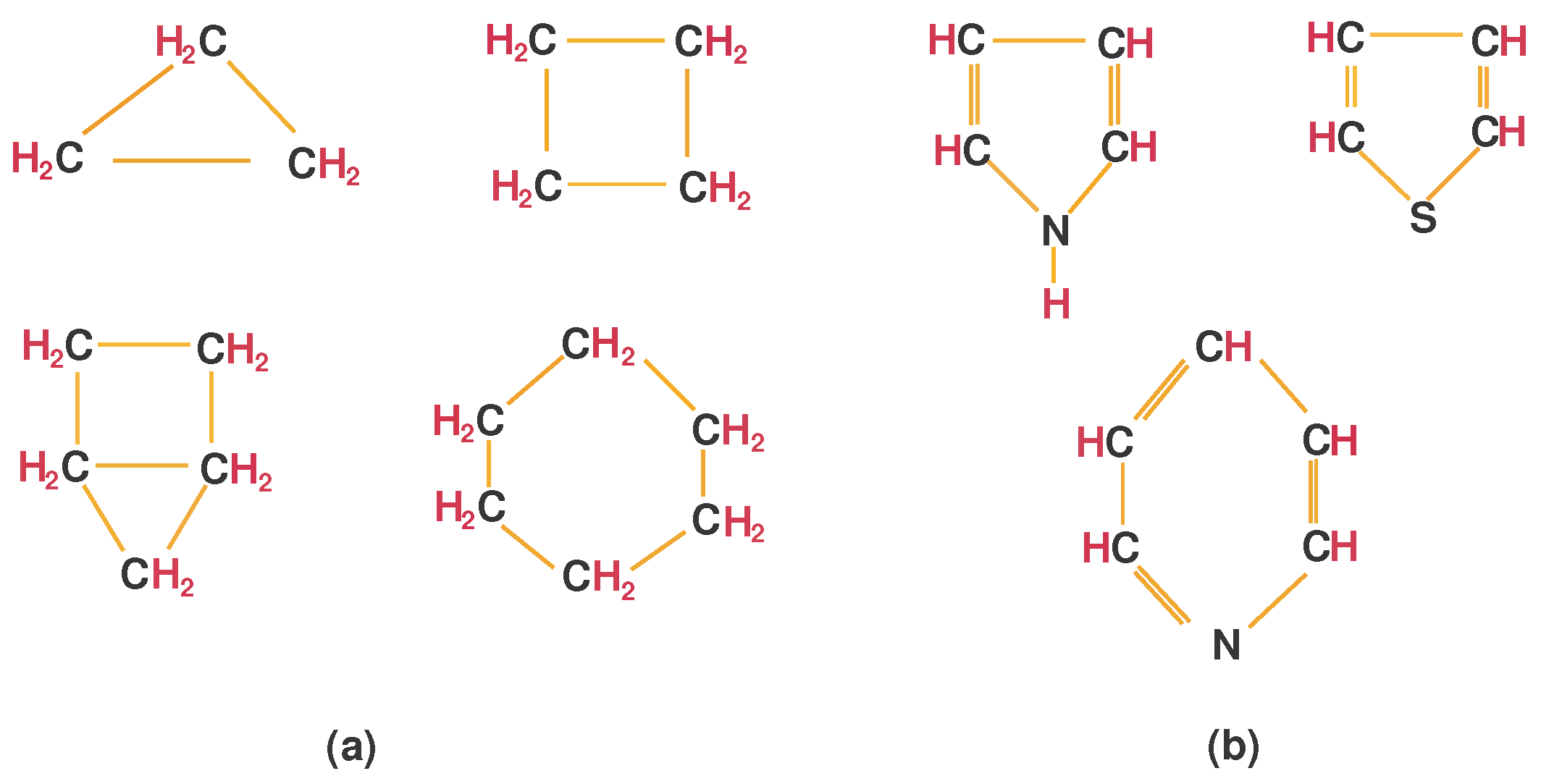
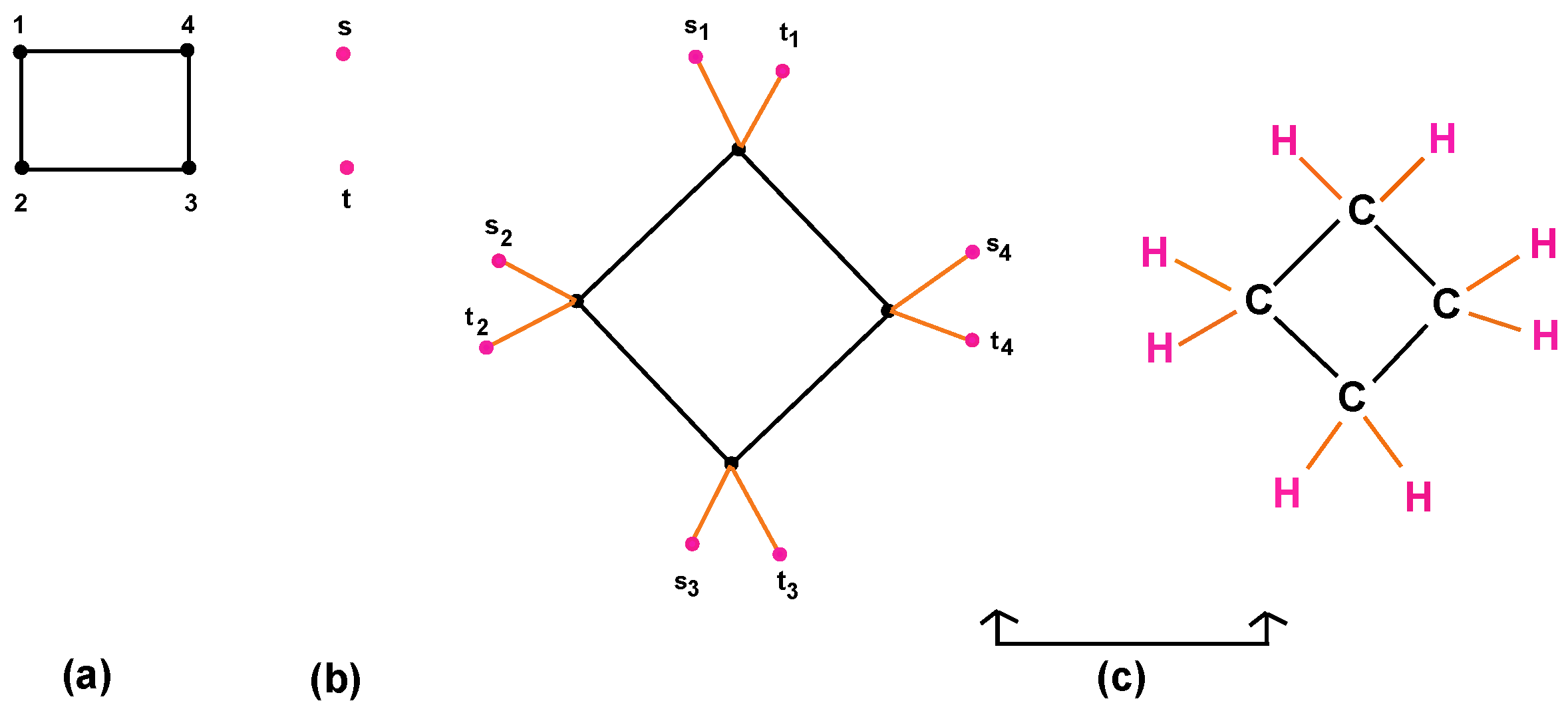
- Cyclic compounds are molecules consisting of closed chain (ring) of at least three carbon atoms. If the closed chain has only carbon atoms, then it is an organic cyclic molecule that is called by homocyclic compound. If the closed chain has both carbon and non-carbon atoms, then it is an inorganic cyclic molecule that is called the heterocyclic compound. Moreover, Cycloalkanes () are the isomers of alkenes consisting of exactly one cyclic compound joined by a single bond. Figure 6a,b presents the cyclic compounds (homocyclic and heterocyclic, respectively).
4. Main Results
5. Applications, Comparisons and Conclusions
5.1. Cartesian Product
- (a)
- (b)
- of polynomial chains: (1) If &, ; (2) If &,
- of polynomial chains: (1) If &, ; (2) If &, ; (3) If &, ; (4) If &, .
- (a)
- (b)
- (1)
- (2)
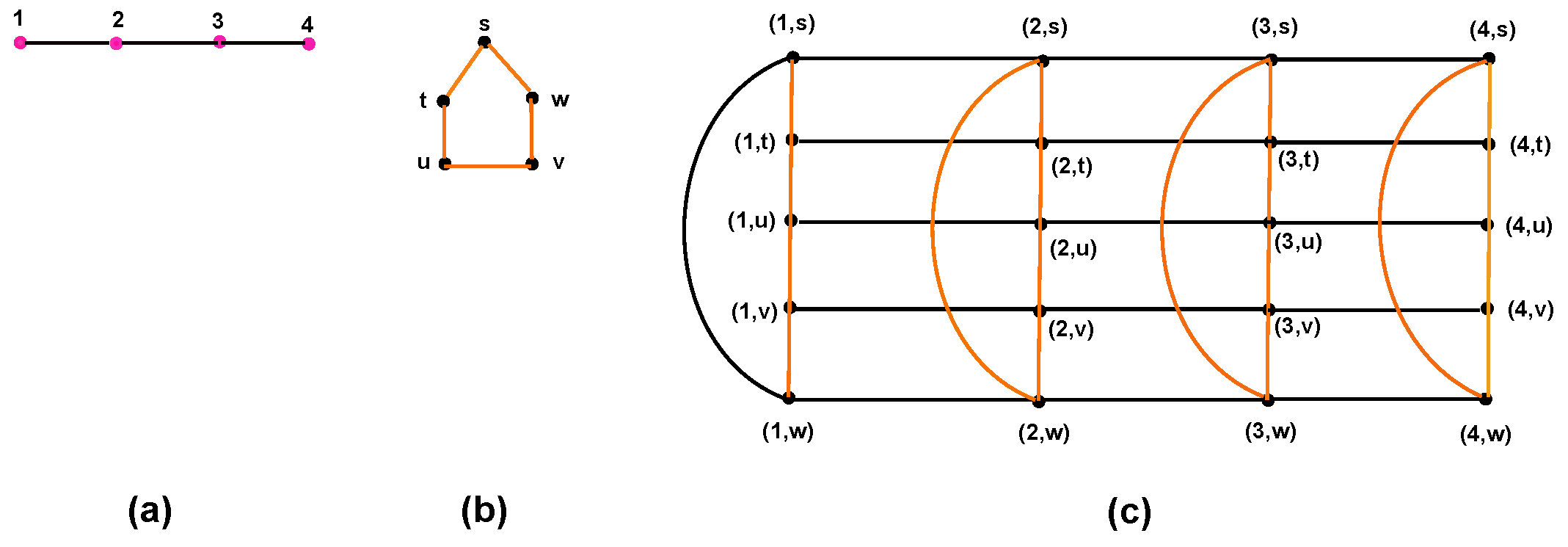
5.2. Corona Product
- (a)
- (b)
- (1)
- (2)
- (a)
- (b)
- (1)
- (2)
5.3. Lexicographic Product
- (a)
- (b)
- (1)
- (2)
- (a)
- (b)
- (1)
- (2)
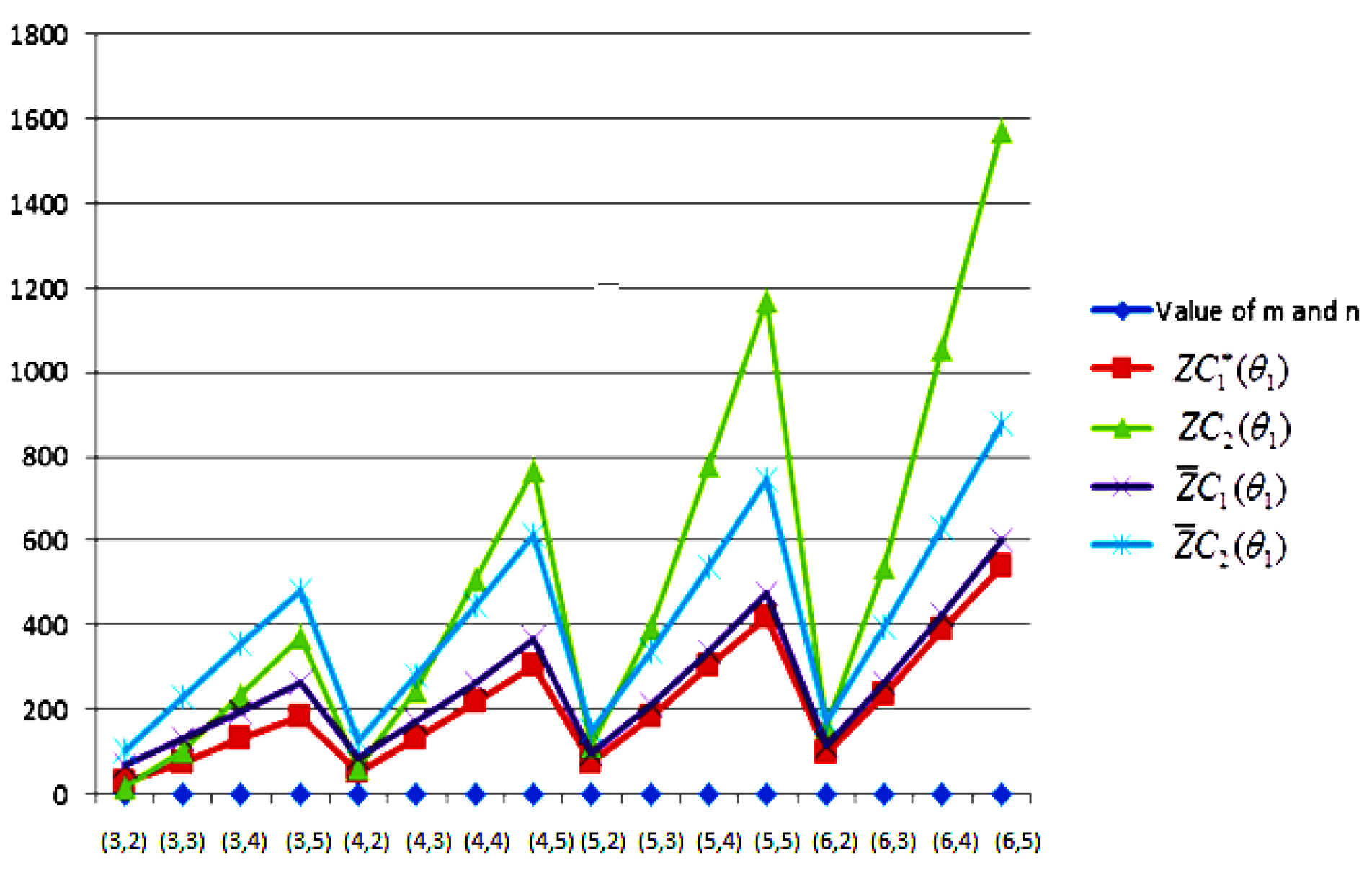
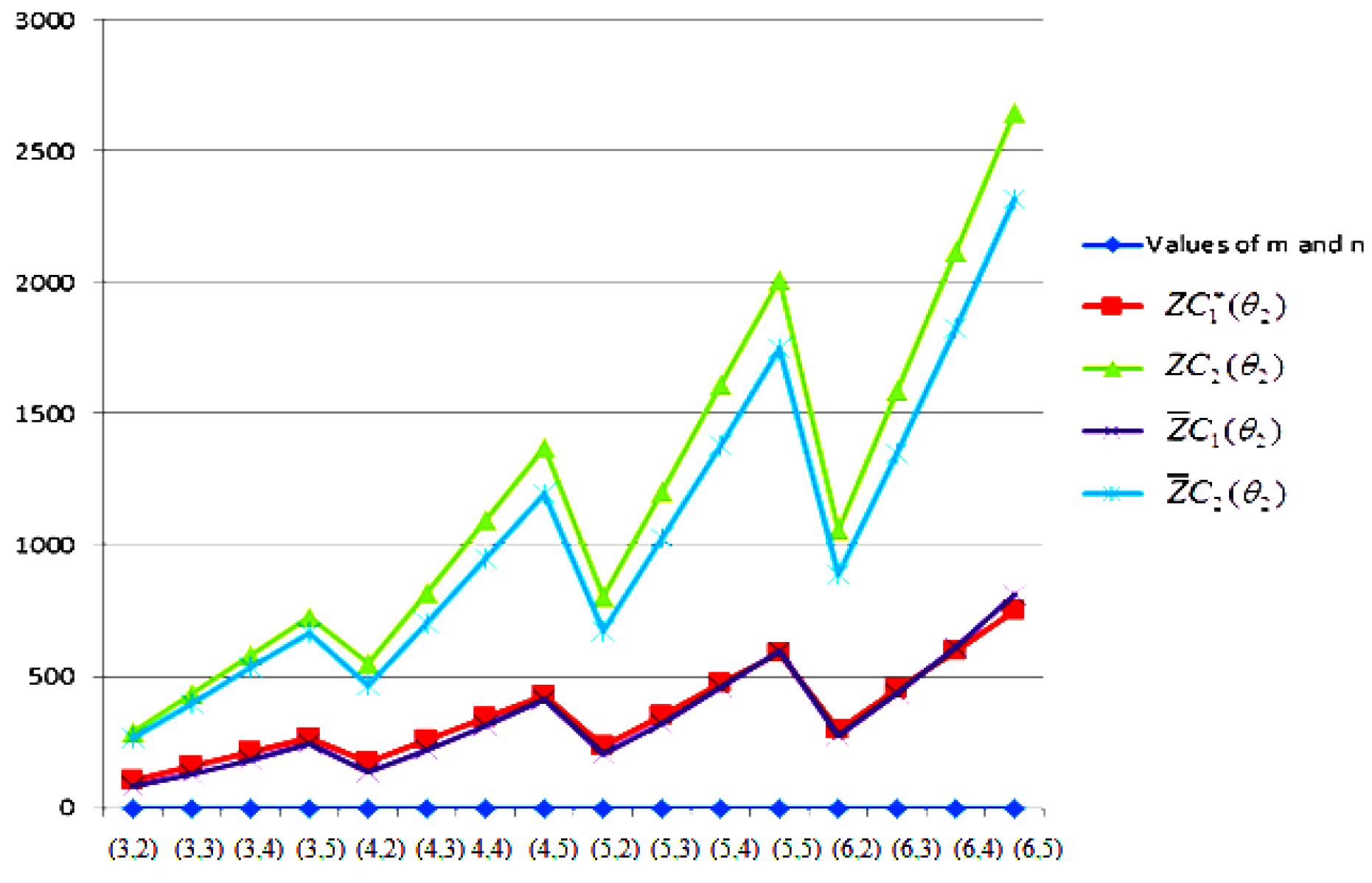
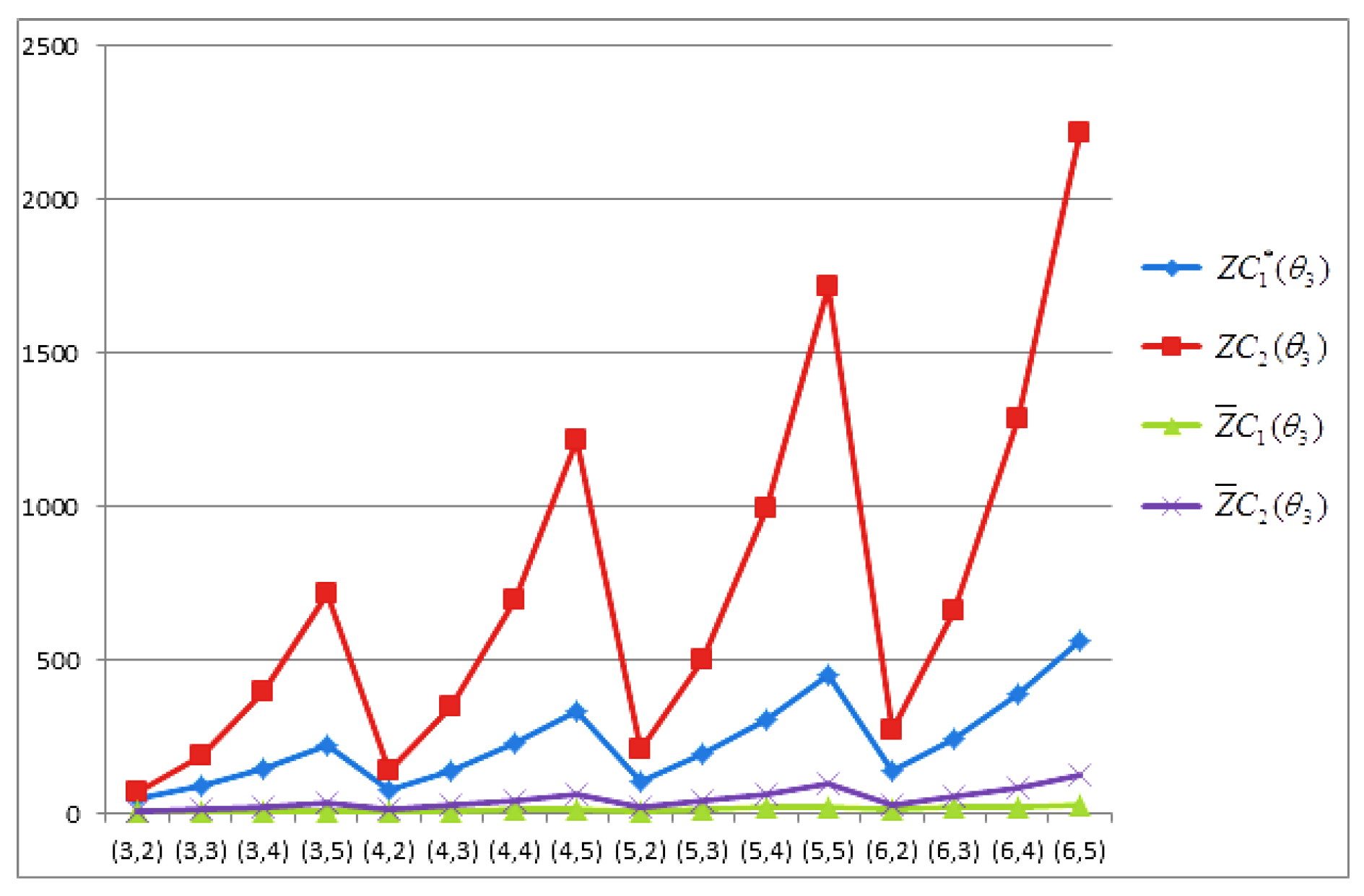
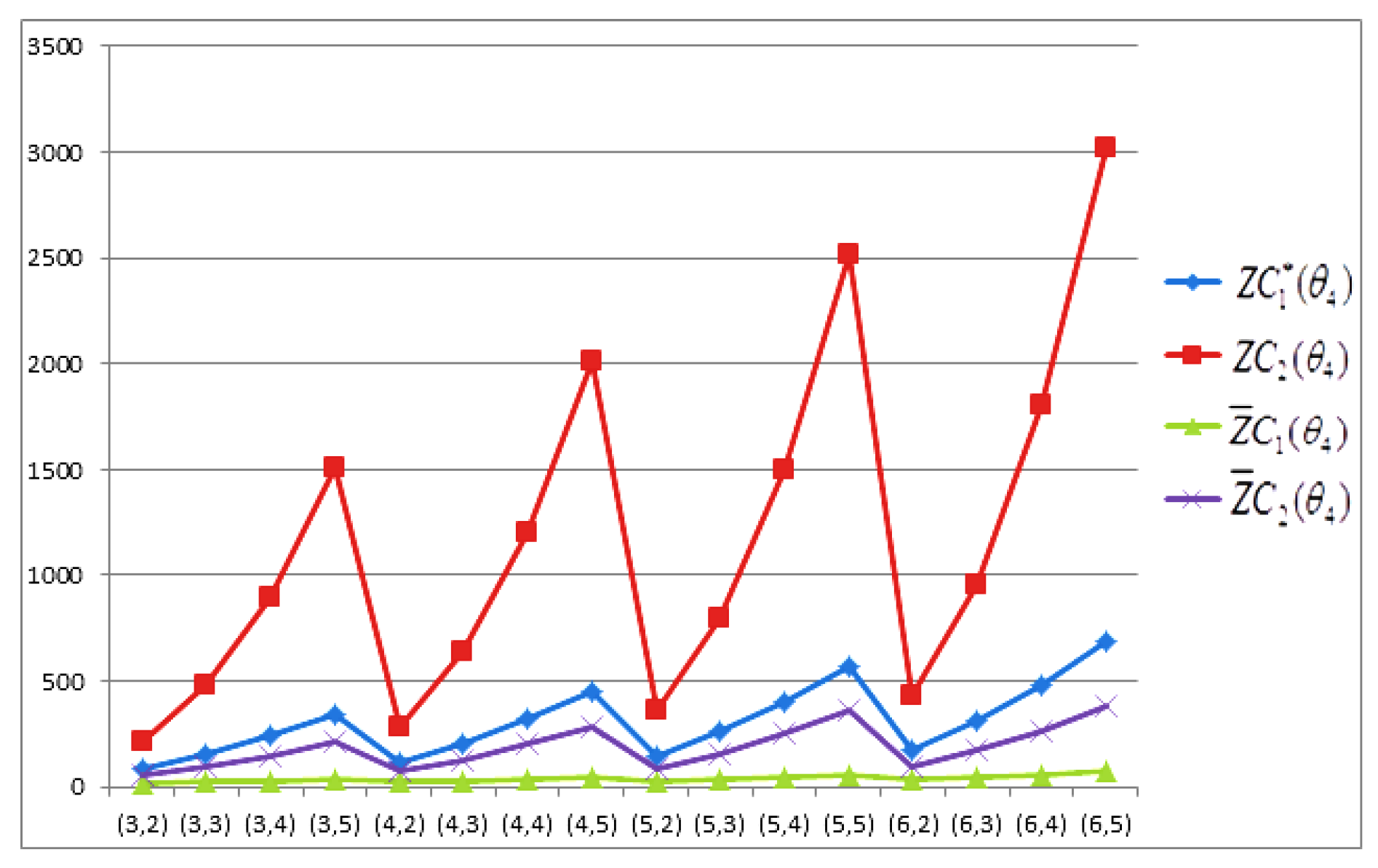
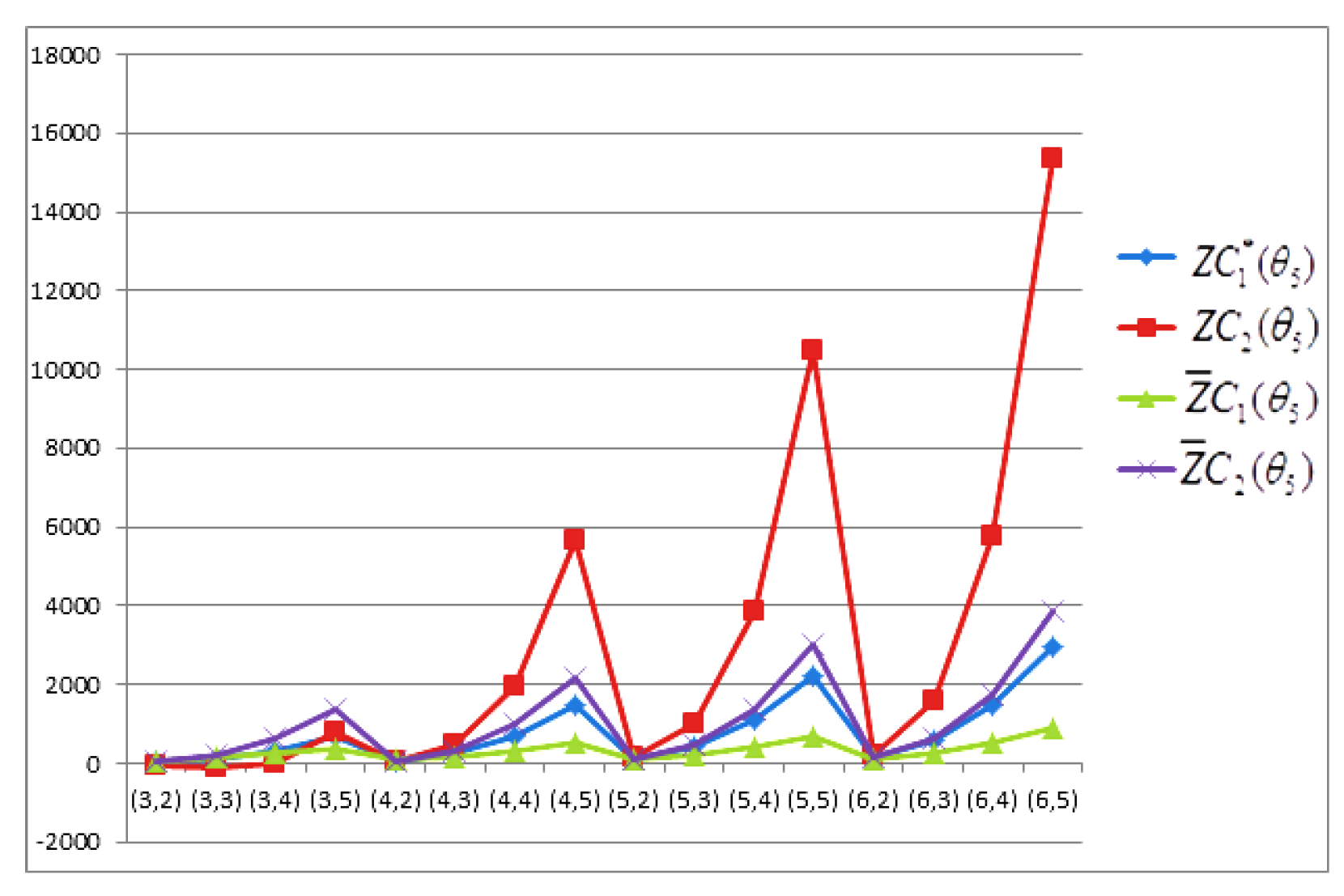
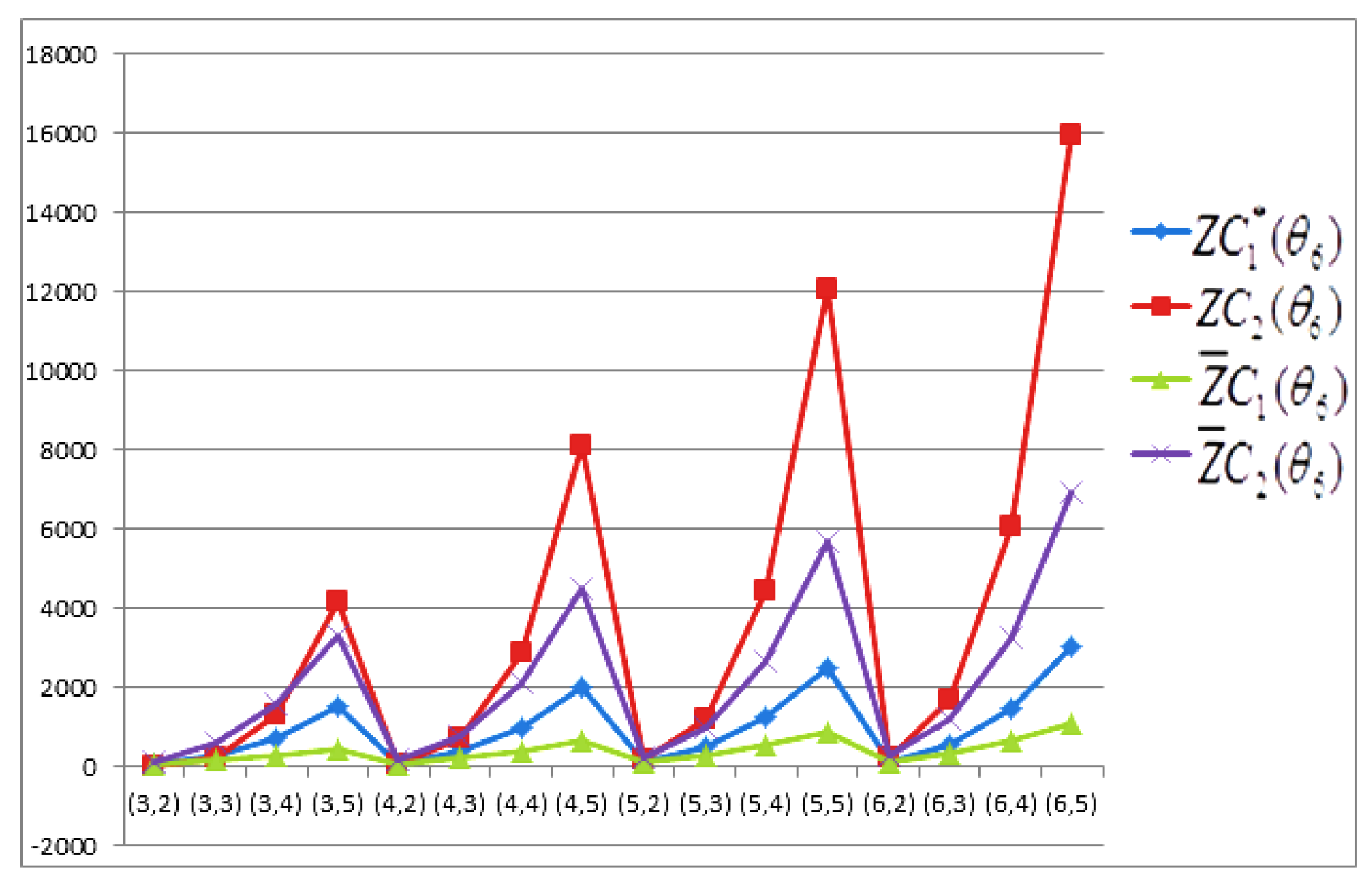
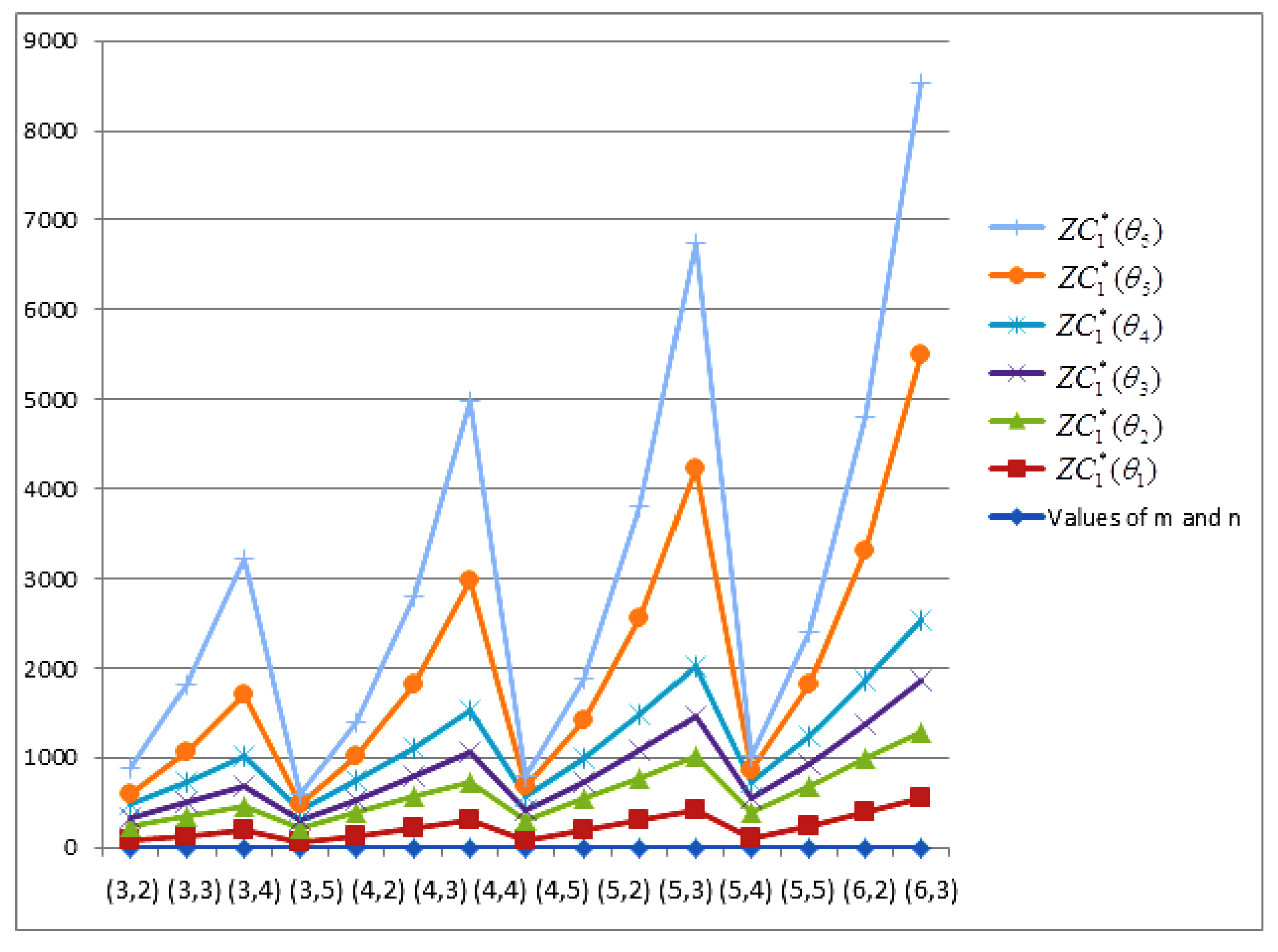
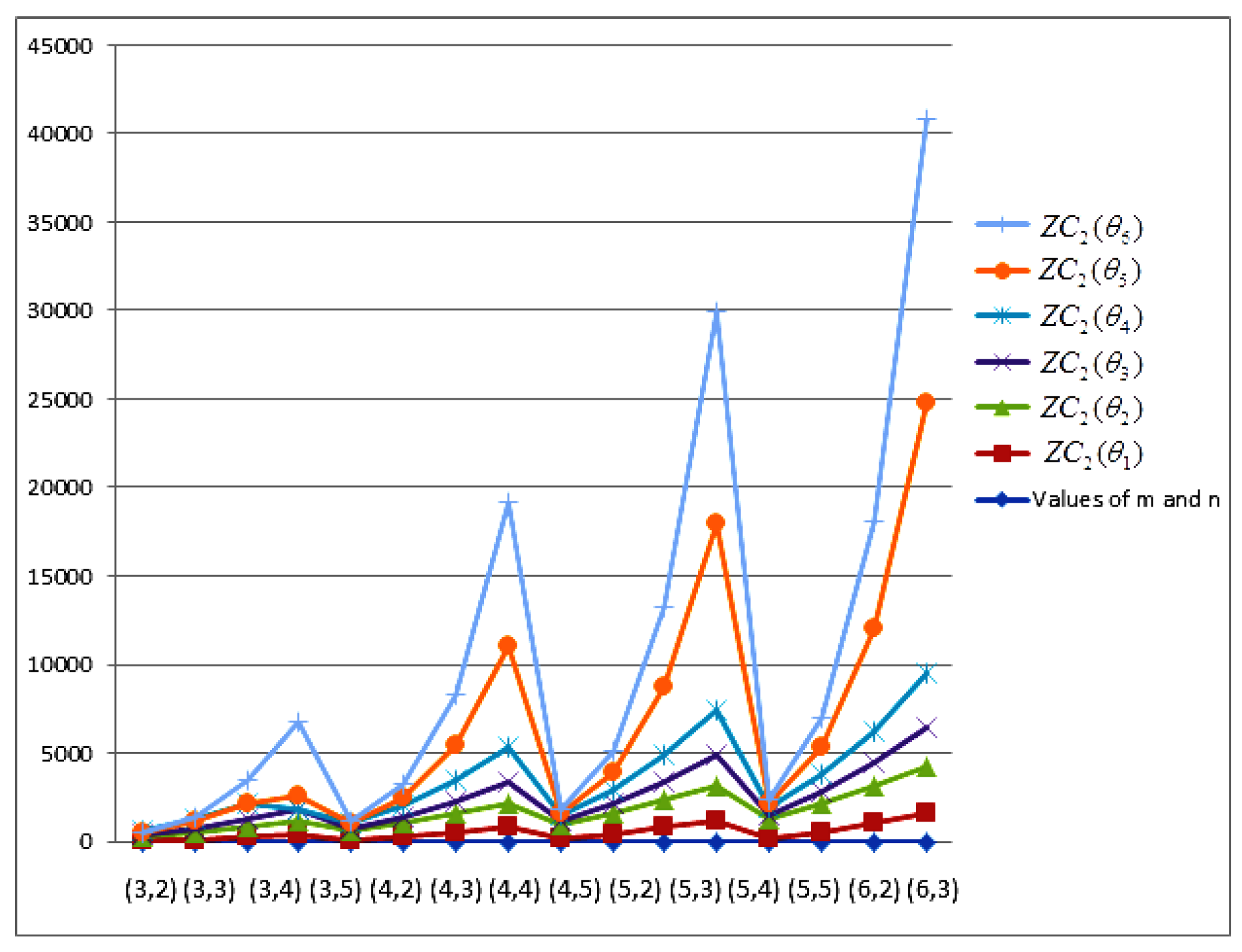
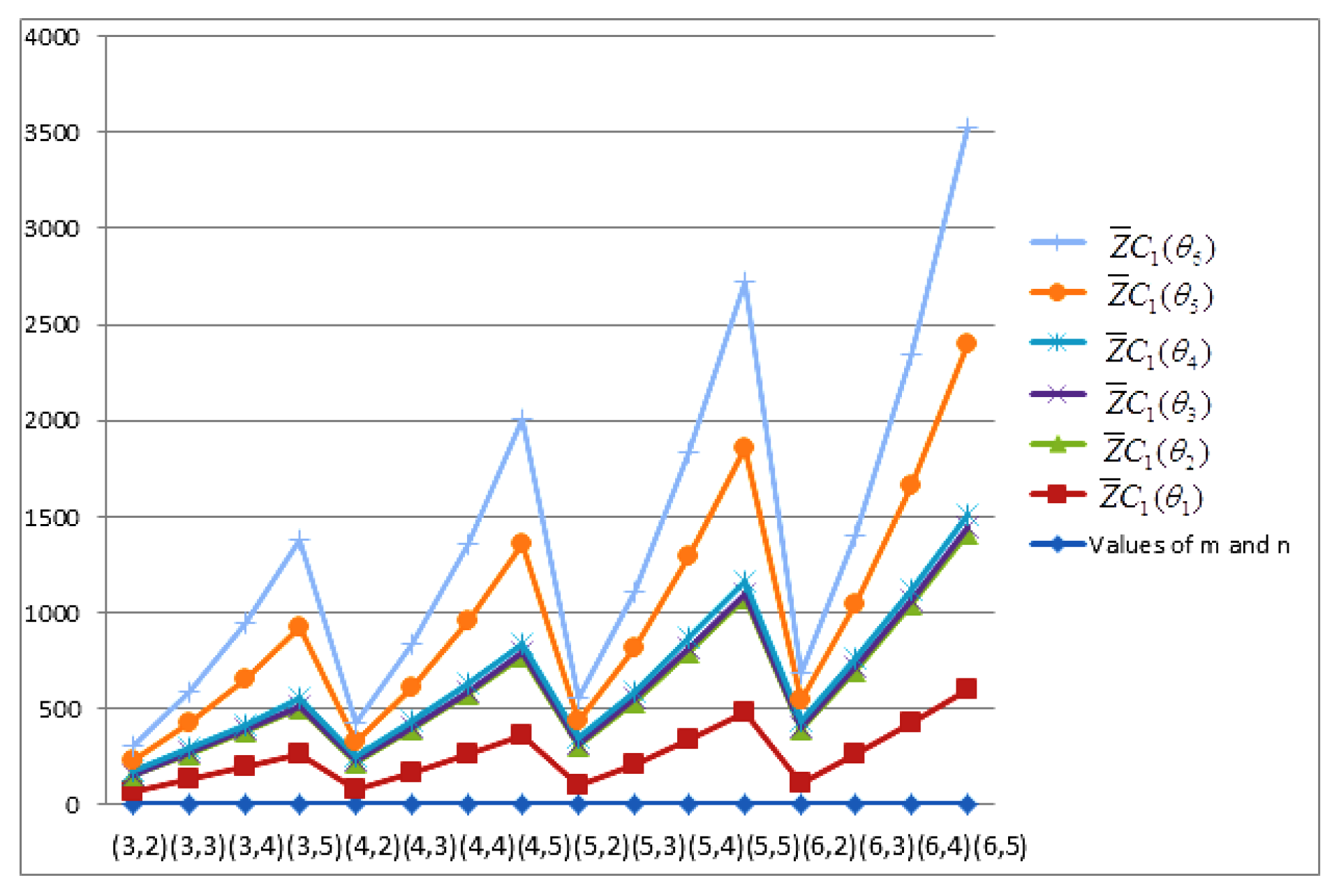
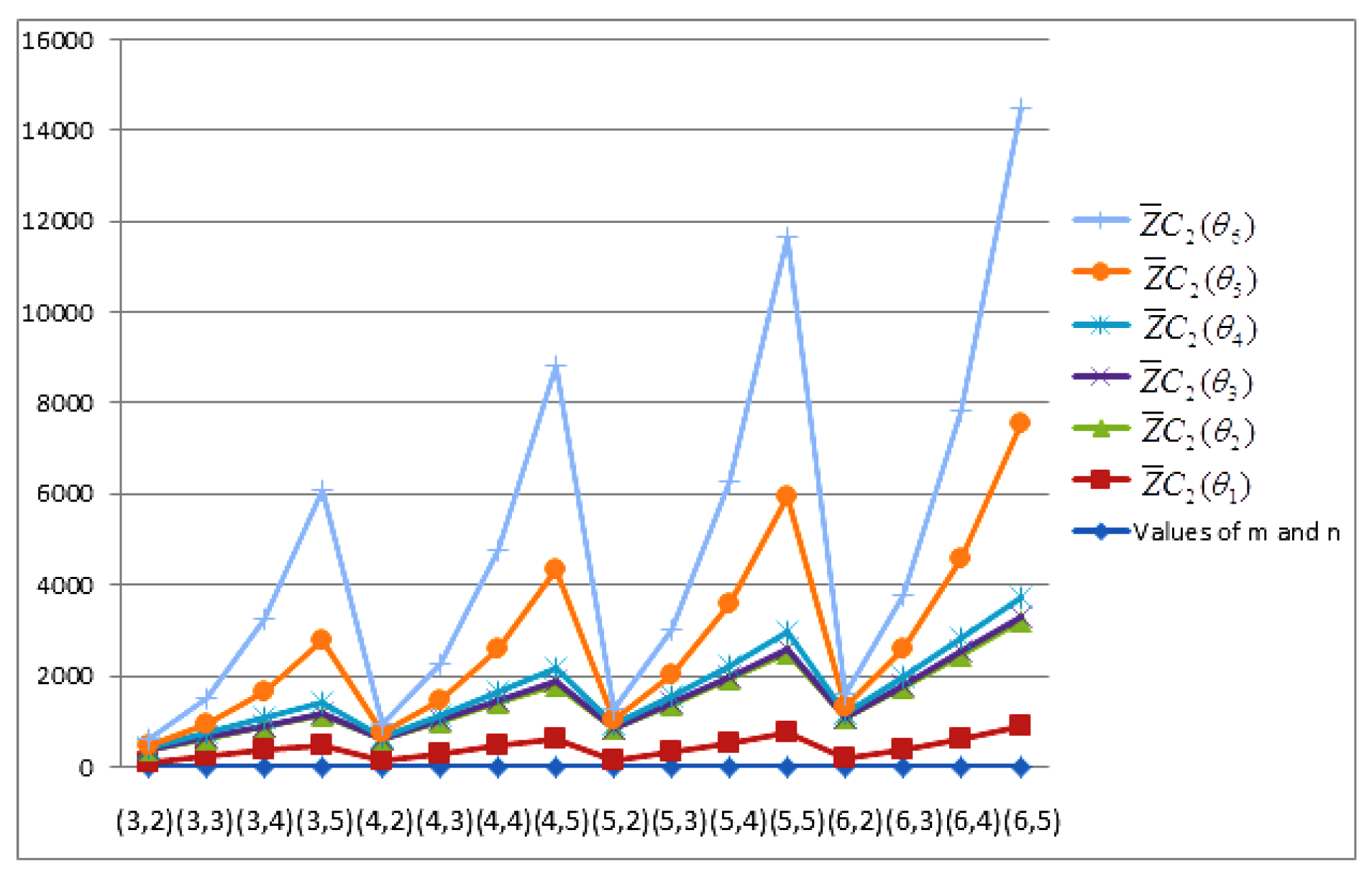
- The behaviours of all the connection-based Zagreb indices and coindices for the molecular networks (polynomial chain, carbon nanotube, alkane, cycloalkane, fence, and closed fence) are symmetrise with some less or more values and the following orderings:(i) (for polynomial chain), (ii) (for carbon nanotubes, fence and closed fence) and (iii) (for alkane and cycloalkane).
- For increasing values of m and n in all of the molecular networks (polynomial chain, carbon nanotube, alkane, cycloalkane, fence, and closed fence), the second Zagreb connection index, and the first Zagreb connection coindex are responding rapidly, and steadily, respectively.
- In the certain intervals of the values of m and n, all the connection-based indices and coindices attain the maximum and minimum values. These values are also lifting up in the intervals on increasing values of m and n in such a way that the response of maximum values is more rapid than the minimum values. In addition, we analyse that second the Zagreb connection index has attained more upper layer than other TIs in all pf the molecular networks.
- In particular, Figure 19, Figure 20, Figure 21 and Figure 22 present that first Zagreb connection index, second Zagreb connection index, first Zagreb connection coindex, and second Zagreb connection coindex are dominant and auxiliary or incapable for the molecular networks from polynomial chain to closed fence, respectively. Moreover, we analyse that last molecular network i.e., closed fence has attain more upper layer than all other molecular networks for connection-based indices and coindices.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2009; Volume 2. [Google Scholar]
- Yan, F.; Shang, Q.; Xia, S.; Wang, Q.; Ma, P. Application of topological index in predicting ionic liquids densities by the quantitative structure property relationship method. J. Chem. Eng. Data 2015, 60, 734–739. [Google Scholar] [CrossRef]
- González-D́iaz, H.; Vilar, S.; Santana, L.; Uriarte, E. Medicinal chemistry and bioinformatics-current trends in drugs discovery with networks topological indices. Curr. Top. Med. Chem. 2007, 7, 1015–1029. [Google Scholar] [CrossRef] [PubMed]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Furtula, B.; Gutman, I. A forgotten topological index. J. Math. Chem. 2015, 53, 1184–1190. [Google Scholar] [CrossRef]
- Graovac, A.; Pisanski, T. On the Wiener index of a graph. J. Math. Chem. 1991, 8, 53–62. [Google Scholar] [CrossRef]
- Azari, M.; Iranmanesh, A. Chemical graphs constructed from rooted product and their Zagreb indices. MATCH Commun. Math. Comput. Chem. 2013, 70, 901–919. [Google Scholar]
- Das, K.C.; Yurttas, A.; Togan, M.; Cevik, A.S.; Cangul, I.N. The multiplicative Zagreb indices of graph operations. J. Ineq. Appl. 2013, 90, 14. [Google Scholar] [CrossRef]
- De, N.; Pal, A.; Nayeem, S.M.A. On some bounds and exact formulae for connective eccentric indices of graphs under some graph operations. Int. J. Comb. 2014, 2014, 579257. [Google Scholar] [CrossRef]
- Luo, Z.; Wu, J. Zagreb eccentricity indices of the generalized Hierachical product graphs and their applications. J. Appl. Math. 2014, 2014, 241712. [Google Scholar] [CrossRef]
- Gao, W.; Jamil, M.K.; Farahani, M.R. The hyper-Zagreb indix and some graph operations. J. Appl. Math. Comput. 2017, 54, 263–275. [Google Scholar] [CrossRef]
- Liu, J.-B.; Javed, S.; Javaid, M.; Shabbir, K. Computing first general Zagreb index of operations on graphs. IEEE Access 2019, 7, 47494–47502. [Google Scholar] [CrossRef]
- Ali, U.; Javaid, M. Upper bounds of Zagreb connection indices of tensor and strong product on graphs. Punjab Univ. J. Math. 2020, 52, 89–100. [Google Scholar]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. III. total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Gutman, I. Degree-based topological indices. Croat. Chem. Acta 2013, 86, 351–361. [Google Scholar] [CrossRef]
- Ashrafi, A.R.; Doslic, T.; Hamzeh, A. The Zagreb coindices of graph operations. Discrete Appl. Math. 2010, 158, 1571–1578. [Google Scholar] [CrossRef]
- Hua, H.; Zhang, S. Relations between Zagreb coindices and some distance-based topological indices. MATCH Commu. Math. Comput. Chem. 2012, 68, 199–208. [Google Scholar]
- Xu, K.; Das, K.C.; Tang, K. On the multiplicative Zagreb coindices of graphs. Opuscula Math. 2013, 33, 191–204. [Google Scholar] [CrossRef]
- Gutman, I.; Furtula, B.; Vukićvić, Z.K.; Popivoda, G. On Zagreb indices and coindices. MATCH Commun. Math. Comput. Chem. 2015, 74, 5–16. [Google Scholar]
- Pattabiraman, K.; Nagarajan, S.; Chendrasekharan, M. Zagreb indices and coindices of product graphs. J. Prime Res. Math. 2015, 10, 80–91. [Google Scholar]
- Basavanagoud, B.; Gutman, I.; Gali, C.S. On second Zagreb index and coindex of some derived graphs. Kragujevac J. Sci. 2015, 37, 113–121. [Google Scholar]
- De, N.; Nayeem, S.M.A.; Pal, A. The F-coindex of some graph operations. SpringerPlus 2016, 5, 221. [Google Scholar] [CrossRef]
- Veylaki, M.; Nikmehr, M.J.; Tavallaee, H.A. The third and hyper-Zagreb coindices of some graph operations. J. Appl. Math. Comput. 2016, 50, 315–325. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry 2016, 149, 8213950. [Google Scholar] [CrossRef]
- Rajan, B.; William, A.; Grigorious, C.; Stephen, S. On certain topological indices of silicate, honeycomb and hexagonal networks. J. Comp. Math. Sci. 2012, 3, 530–535. [Google Scholar]
- Bača, M.; Horváthová, J.; Mokrišová, M.; Suhányiová, A.; Andrea, S.-F. On topological indices of carbon nanotube network. Can. J. Chem. 2015, 93, 1157–1160. [Google Scholar]
- Furtula, B.; Gutman, I. On structure-sensitivity of degree-based topological indices. Appllied Mathathematics Comput. 2013, 219, 8973–8978. [Google Scholar] [CrossRef]
- Javaid, M.; Rehman, M.A.; Cao, J. Topological indices of rhombus type silicate and oxide network. Can. J. Chem. 2016, 95, 134–143. [Google Scholar] [CrossRef]
- Hong, G.; Gu, Z.; Javaid, M.; Awais, H.M.; Siddiqui, M.K. Degree-based topological invariants of metal-organic networks. IEEE Access 2020, 8, 68288–68300. [Google Scholar] [CrossRef]
- Ali, A.; Trinajstić, N. A novel/old modification of the first Zagreb index. Mol. Inf. 2018, 37, 1–7. [Google Scholar] [CrossRef]
- Ali, U.; Javaid, M. Zagreb connection indices of disjunction and symmetric difference operations on graphs. J. Prime Res. Math. 2020, 16, 1–15. [Google Scholar]
- Ducoffe, G.; Marinescu-Ghemeci, R.; Obeja, C.; Popa, A.; Tache, R.M. Extremal graphs with respect to the modified first Zagreb connection Index. In Proceedings of the 16th Cologne-Twente Workshop on Graphs and Combinatorial Optimization, CNAM, Paris, France, 18–20 June 2018; pp. 65–68. [Google Scholar]
- Shao, Z.; Gutman, I.; Li, Z.; Wang, S.; Wu, P. Leap Zagreb indices of trees and unicyclic Graphs. Comm. Comb. Optim. 2018, 3, 179–194. [Google Scholar]
- Naji, A.M.; Soner, N.D. The first leap Zagreb index of some graph operations. Int. Jour. Appl. Graph Theory 2018, 2, 7–18. [Google Scholar]
- Gutman, I.; Milovanović, E.; Milovanović, I. Beyond the Zagreb indices. AKCE Int. J. Graphs Combin. 2018, in press. [Google Scholar] [CrossRef]
- Tang, J.-H.; Ali, U.; Javaid, M.; Shabbir, K. Zagreb connection indices of subdivision and semi-total point operations on graphs. J. Chem. 2019, 2019, 9846913. [Google Scholar] [CrossRef]
- Ali, U.; Javaid, M.; Kashif, A. Modified Zagreb Connection Indices of the T-Sum Graphs. Main Group Met. Chem. 2020, 43, 43–55. [Google Scholar] [CrossRef]
- West, D.B. An Introduction to Graph Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Gutman, I.; Ruscic, B.; Trinajstić, N.; Wilson, C.F. Graph Theory and molecular orbitals XII. acyclic polyenes. J. Chem. Phys. 1975, 62, 3399–3405. [Google Scholar] [CrossRef]
- Klavžar, S.; Gutman, I. Selected properties of the Schultz molecular topological index. J. Chem. Inf. Comp. Sci. 1996, 36, 1001–1003. [Google Scholar]
- Doslic, T. Vertex-Weighted Wiener Polynomials for Composite Graphs. Ars Math. Contemp. 2008, 1, 66–80. [Google Scholar] [CrossRef]
- Yamaguchi, S. Estimating the Zagreb indices and the spectral radius of triangle-and quadrangle-free connected graphs. Chem. Phys. Lett. 2008, 4, 396–398. [Google Scholar] [CrossRef]
- Cao, J.; Ali, U.; Javaid, M.; Huang, C. Zagreb connection indices of molecular graphs based on operations. Complexity 2020, 2020, 7385682. [Google Scholar] [CrossRef]

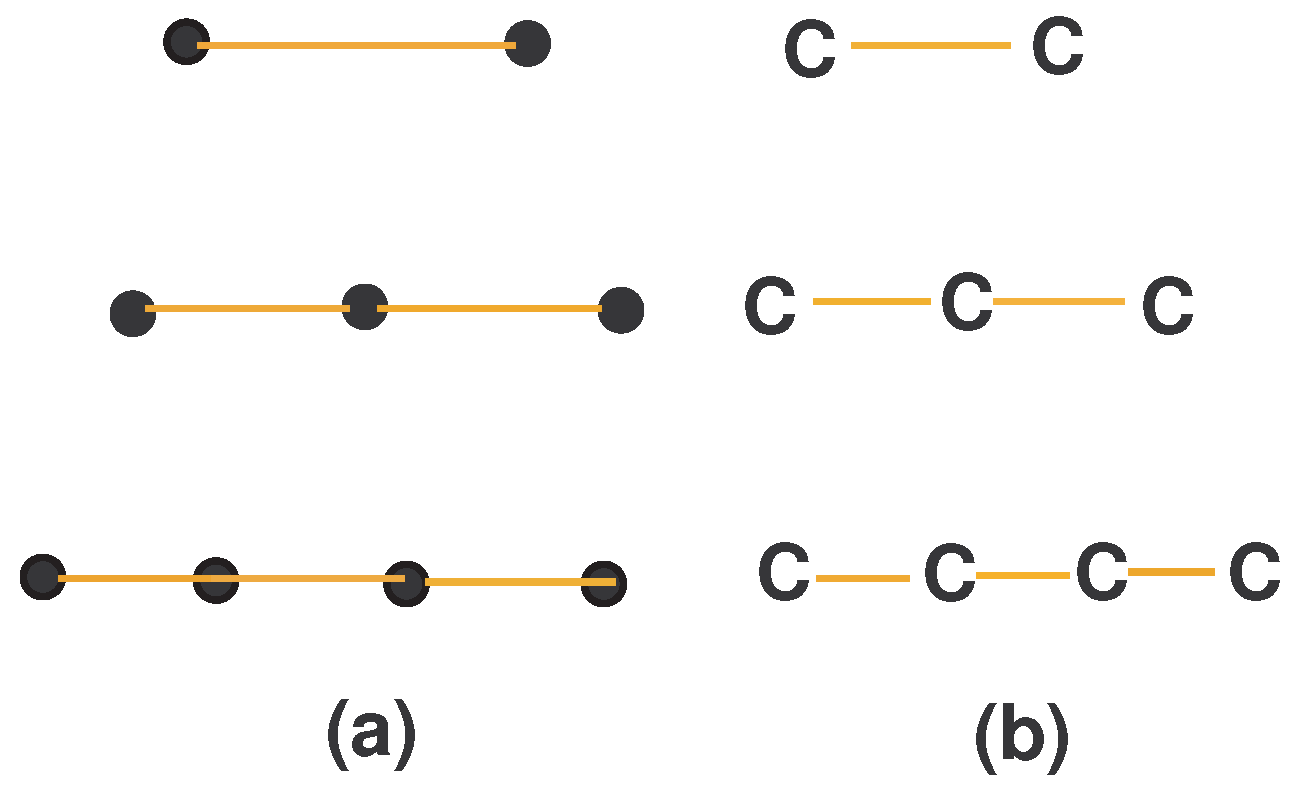
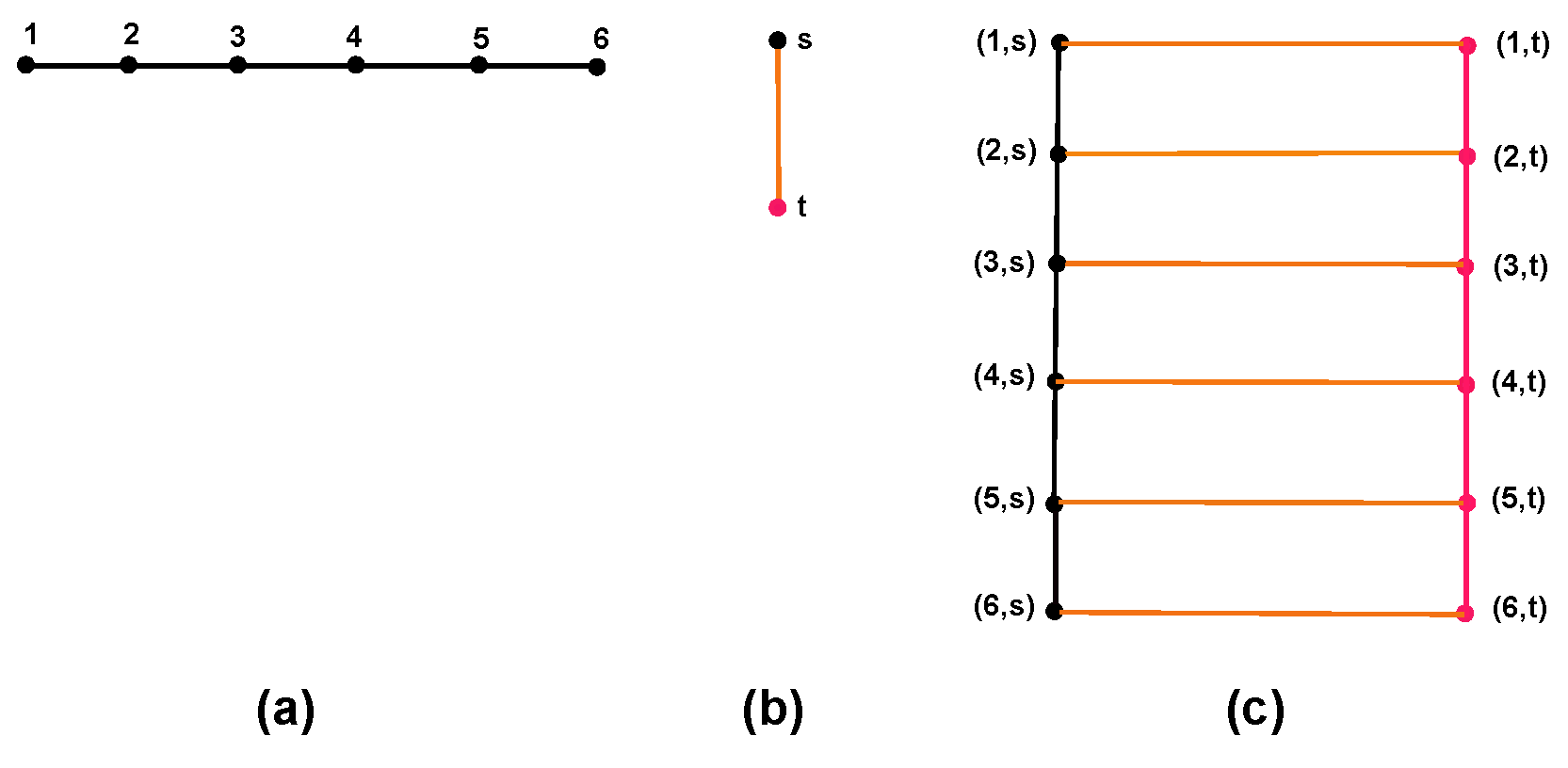
| (m,n) | ||||
|---|---|---|---|---|
| (3,2) | 28 | 18 | 68 | 102 |
| (3,3) | 76 | 102 | 130 | 228 |
| (3,4) | 130 | 237 | 196 | 354 |
| (3,5) | 184 | 372 | 266 | 480 |
| (4,2) | 52 | 66 | 84 | 126 |
| (4,3) | 130 | 248 | 170 | 284 |
| (4,4) | 216 | 510 | 264 | 446 |
| (4,5) | 302 | 772 | 366 | 612 |
| (5,2) | 76 | 114 | 100 | 150 |
| (5,3) | 184 | 394 | 214 | 340 |
| (5,4) | 302 | 783 | 340 | 538 |
| (5,5) | 420 | 1172 | 478 | 744 |
| (6,2) | 100 | 162 | 116 | 174 |
| (6,3) | 238 | 540 | 262 | 396 |
| (6,4) | 388 | 1056 | 424 | 630 |
| (6,5) | 538 | 1572 | 602 | 876 |
| (m,n) | ||||
|---|---|---|---|---|
| (3,2) | 108 | 292 | 84 | 266 |
| (3,3) | 162 | 438 | 132 | 399 |
| (3,4) | 216 | 584 | 184 | 532 |
| (3,5) | 270 | 730 | 240 | 665 |
| (4,2) | 172 | 548 | 140 | 466 |
| (4,3) | 258 | 822 | 222 | 705 |
| (4,4) | 344 | 1096 | 312 | 948 |
| (4,5) | 430 | 1370 | 410 | 1195 |
| (5,2) | 236 | 804 | 204 | 674 |
| (5,3) | 354 | 1206 | 324 | 1023 |
| (5,4) | 472 | 1608 | 456 | 1380 |
| (5,5) | 590 | 2010 | 600 | 1745 |
| (6,2) | 300 | 1060 | 276 | 890 |
| (6,3) | 450 | 1590 | 438 | 1353 |
| (6,4) | 600 | 2120 | 616 | 1828 |
| (6,5) | 750 | 2650 | 810 | 2315 |
| (m,n) | ||||
|---|---|---|---|---|
| (3,2) | 48 | 72 | 6 | 9 |
| (3,3) | 92 | 192 | 8 | 16 |
| (3,4) | 150 | 400 | 10 | 25 |
| (3,5) | 222 | 720 | 12 | 36 |
| (4,2) | 78 | 140 | 9 | 16 |
| (4,3) | 144 | 348 | 12 | 29 |
| (4,4) | 230 | 696 | 15 | 46 |
| (4,5) | 336 | 1220 | 18 | 67 |
| (5,2) | 108 | 208 | 12 | 23 |
| (5,3) | 196 | 504 | 16 | 42 |
| (5,4) | 310 | 992 | 20 | 67 |
| (5,5) | 450 | 1720 | 24 | 98 |
| (6,2) | 138 | 276 | 15 | 30 |
| (6,3) | 248 | 660 | 20 | 55 |
| (6,4) | 390 | 1288 | 25 | 88 |
| (6,5) | 564 | 2220 | 30 | 129 |
| (m,n) | ||||
|---|---|---|---|---|
| (3,2) | 90 | 216 | 18 | 54 |
| (3,3) | 156 | 480 | 24 | 96 |
| (3,4) | 240 | 900 | 30 | 150 |
| (3,5) | 342 | 1512 | 36 | 216 |
| (4,2) | 120 | 288 | 24 | 72 |
| (4,3) | 208 | 640 | 32 | 128 |
| (4,4) | 320 | 1200 | 40 | 200 |
| (4,5) | 456 | 2016 | 48 | 288 |
| (5,2) | 150 | 360 | 30 | 90 |
| (5,3) | 260 | 800 | 40 | 160 |
| (5,4) | 400 | 1500 | 50 | 250 |
| (5,5) | 570 | 2520 | 60 | 360 |
| (6,2) | 180 | 432 | 36 | 100 |
| (6,3) | 312 | 960 | 48 | 174 |
| (6,4) | 480 | 1800 | 60 | 268 |
| (6,5) | 684 | 3024 | 72 | 382 |
| (m,n) | ||||
|---|---|---|---|---|
| (3,2) | 24 | -56 | 56 | 32 |
| (3,3) | 116 | -107 | 130 | 194 |
| (3,4) | 328 | 16 | 236 | 602 |
| (3,5) | 696 | 781 | 374 | 1370 |
| (4,2) | 64 | 36 | 72 | 64 |
| (4,3) | 266 | 456 | 174 | 330 |
| (4,4) | 704 | 1934 | 324 | 974 |
| (4,5) | 1450 | 5640 | 522 | 2170 |
| (5,2) | 104 | 128 | 88 | 96 |
| (5,3) | 416 | 1019 | 222 | 468 |
| (5,4) | 1080 | 3852 | 424 | 1356 |
| (5,5) | 2204 | 10499 | 694 | 3000 |
| (6,2) | 144 | 220 | 104 | 128 |
| (6,3) | 566 | 1582 | 274 | 608 |
| (6,4) | 1456 | 5770 | 536 | 1748 |
| (6,5) | 2958 | 15358 | 890 | 3860 |
| (m,n) | ||||
|---|---|---|---|---|
| (3,2) | 72 | -4 | 72 | 144 |
| (3,3) | 288 | 245 | 162 | 594 |
| (3,4) | 744 | 1304 | 288 | 1584 |
| (3,5) | 1512 | 4169 | 450 | 3330 |
| (4,2) | 96 | 80 | 96 | 192 |
| (4,3) | 384 | 724 | 224 | 796 |
| (4,4) | 992 | 2886 | 408 | 2132 |
| (4,5) | 2016 | 8108 | 648 | 4500 |
| (5,2) | 120 | 164 | 120 | 240 |
| (5,3) | 480 | 1203 | 290 | 1000 |
| (5,4) | 1240 | 4468 | 540 | 2690 |
| (5,5) | 2520 | 12047 | 870 | 5700 |
| (6,2) | 144 | 248 | 144 | 288 |
| (6,3) | 576 | 1682 | 360 | 1206 |
| (6,4) | 1488 | 6050 | 684 | 3258 |
| (6,5) | 3024 | 15986 | 1116 | 6930 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, U.; Javaid, M.; Alanazi, A.M. Computing Analysis of Connection-Based Indices and Coindices for Product of Molecular Networks. Symmetry 2020, 12, 1320. https://doi.org/10.3390/sym12081320
Ali U, Javaid M, Alanazi AM. Computing Analysis of Connection-Based Indices and Coindices for Product of Molecular Networks. Symmetry. 2020; 12(8):1320. https://doi.org/10.3390/sym12081320
Chicago/Turabian StyleAli, Usman, Muhammad Javaid, and Abdulaziz Mohammed Alanazi. 2020. "Computing Analysis of Connection-Based Indices and Coindices for Product of Molecular Networks" Symmetry 12, no. 8: 1320. https://doi.org/10.3390/sym12081320
APA StyleAli, U., Javaid, M., & Alanazi, A. M. (2020). Computing Analysis of Connection-Based Indices and Coindices for Product of Molecular Networks. Symmetry, 12(8), 1320. https://doi.org/10.3390/sym12081320





