Sensitivity of Discrete Symmetry Tests in the Positronium System with the J-PET Detector
Abstract
1. Introduction
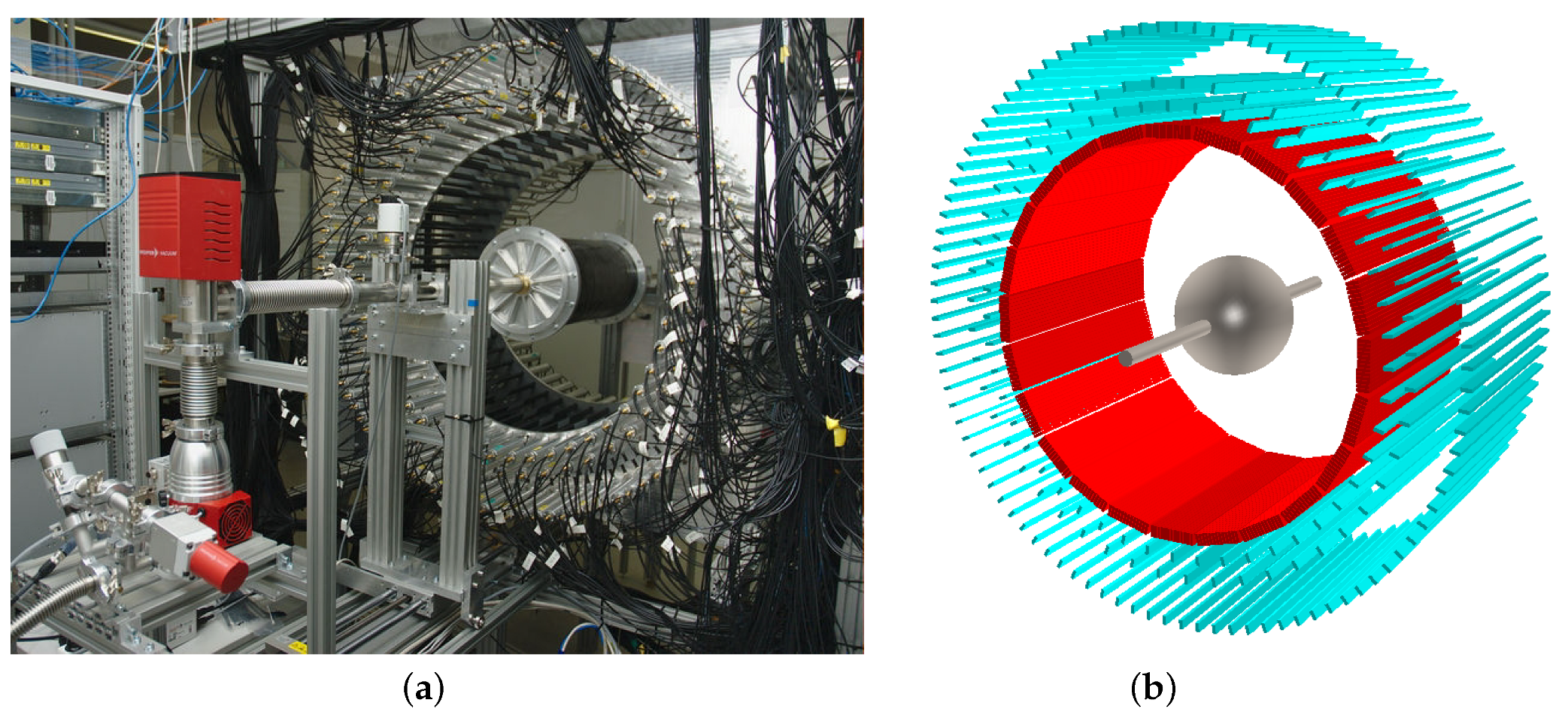
2. The J-PET Detector
3. Methods of Searching for Discrete Symmetry Violations with Ortho-Positronium in J-PET
3.1. Estimation of Positronium Spin
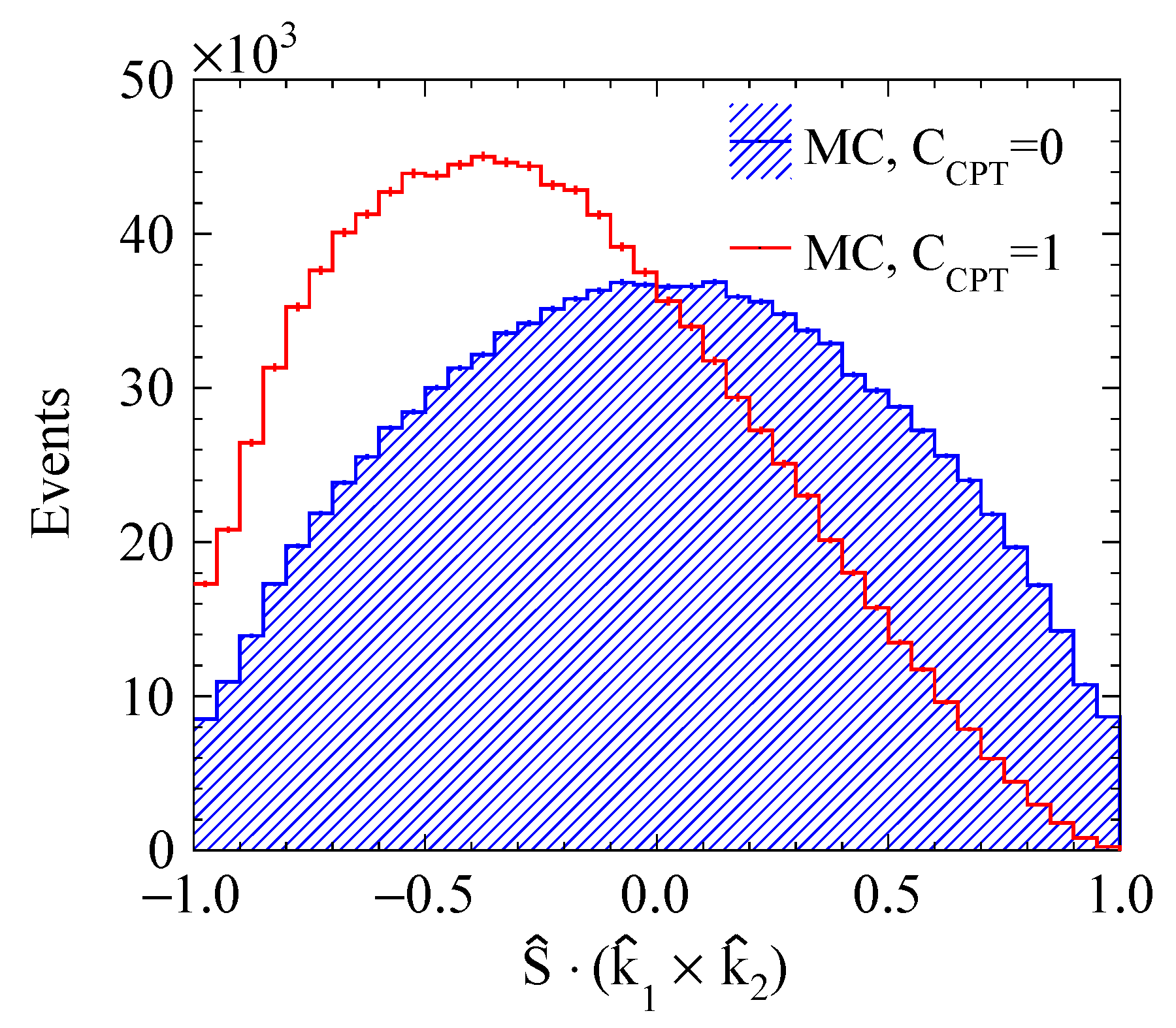
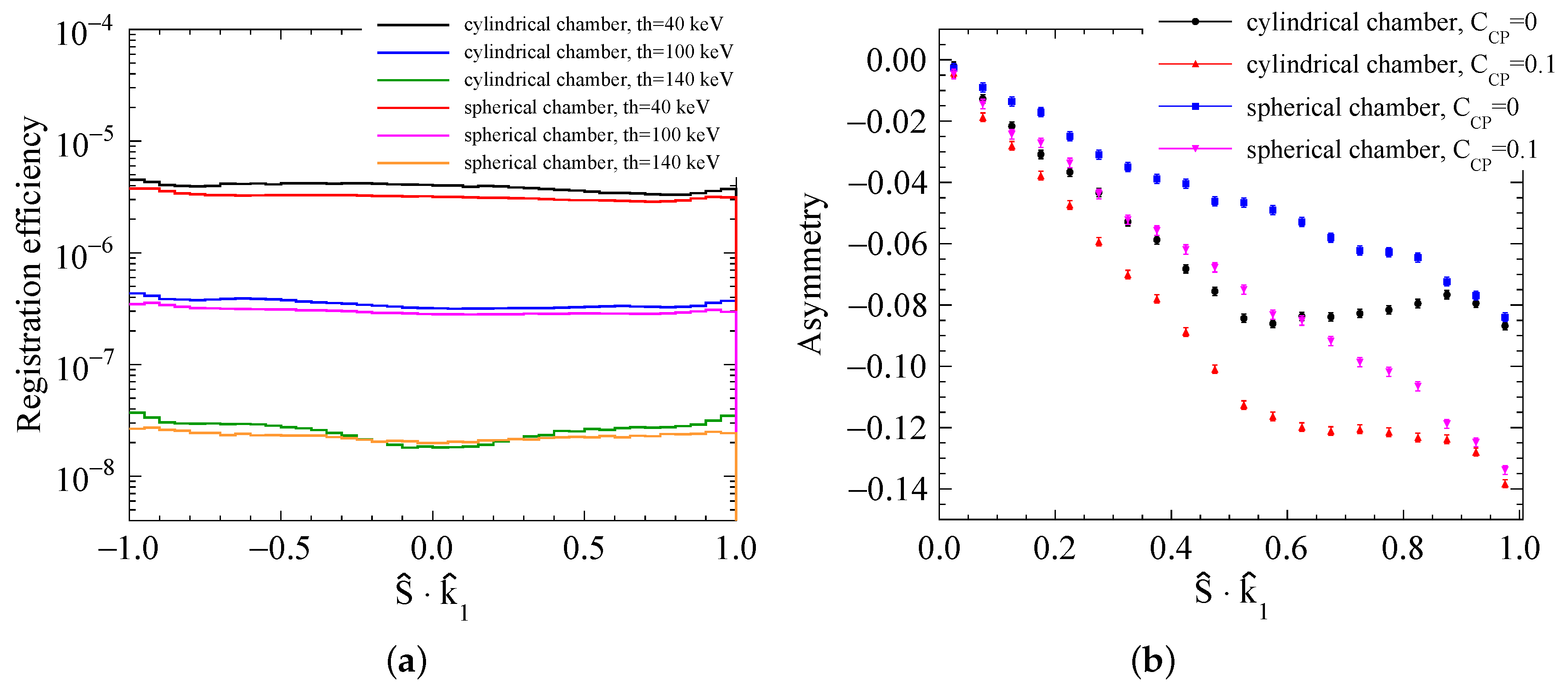
3.2. The Correlation between o-Ps Spin and Annihilation Plane
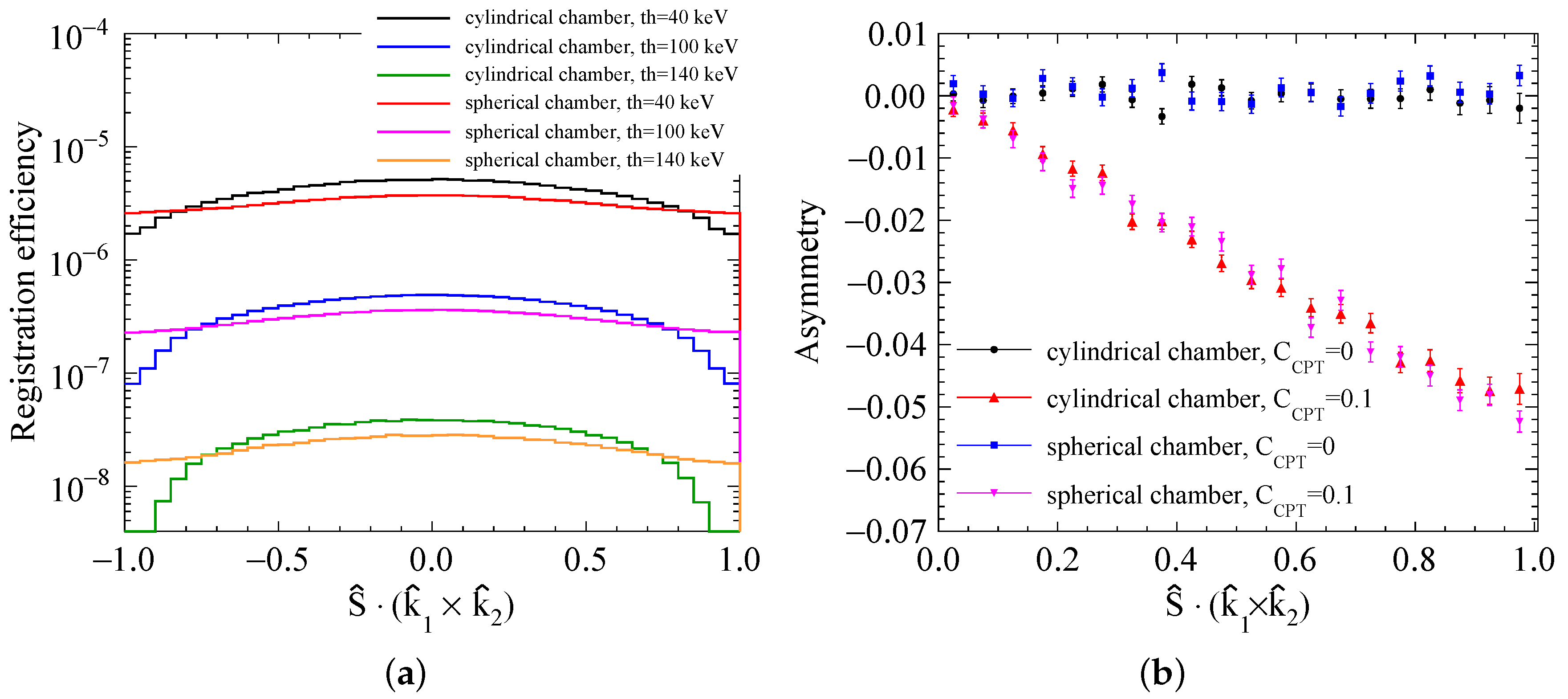
3.3. The Correlation between o-Ps Spin and Most Energetic Photon
4. Perspectives for J-PET Sensitivity to the Cpt Violation Effects
5. Conclusions
Funding
Conflicts of Interest
References
- Wu, C.S.; Ambler, E.; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. Experimental Test of Parity Conservation in Beta Decay. Phys. Rev. 1957, 105, 1413–1415. [Google Scholar] [CrossRef]
- Christenson, J.H.; Cronin, J.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π Decay of the Meson. Phys. Rev. Lett. 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Moskal, P.; Alfs, D.; Bednarski, T.; Białas, P.; Czerwiński, E.; Curceanu, C.; Gajos, A.; Głowacz, B.; Gorgol, M.; Hiesmayr, B.; et al. Potential of the J-PET detector for studies of discrete symmetries in decays of positronium atom—A purely leptonic system. Acta Phys. Polon. 2016, 47, 509. [Google Scholar] [CrossRef]
- Mills, A.P.; Berko, S. Search for C Nonconservation in Electron-Positron Annihilation. Phys. Rev. Lett. 1967, 18, 420–425. [Google Scholar] [CrossRef]
- Bernreuther, W.; Low, U.; Ma, J.P.; Nachtmann, O. How to Test CP, T and CPT Invariance in the Three Photon Decay of Polarized s Wave Triplet Positronium. Z. Phys. 1988, 41, 143–158. [Google Scholar] [CrossRef]
- Yamazaki, T.; Namba, T.; Asai, S.; Kobayashi, T. Search for CP Violation in Positronium Decay. Phys. Rev. Lett. 2010, 104, 083401. [Google Scholar] [CrossRef] [PubMed]
- Vetter, P.A.; Freedman, S.J. Search for CPT-Odd Decays of Positronium. Phys. Rev. Lett. 2003, 91, 263401. [Google Scholar] [CrossRef] [PubMed]
- Vetter, P.A.; Freedman, S.J. Branching-ratio measurements of multiphoton decays of positronium. Phys. Rev. A 2002, 66, 052505. [Google Scholar] [CrossRef]
- Matsumoto, T.; Chiba, M.; Hamatsu, R.; Hirose, T.; Yang, J.; Yu, J. Measurement of five-photon decay in orthopositronium. Phys. Rev. A 1996, 54, 1947–1951. [Google Scholar] [CrossRef] [PubMed]
- Von Busch, H.; Thirolf, P.; Ender, C.; Habs, D.; Köck, F.; Schulze, T.; Schwalm, D. Measurement of the decay e+e-→4γ at rest. Phys. Lett. B 1994, 325, 300–307. [Google Scholar] [CrossRef]
- Branco, G.C.; González Felipe, R.; Joaquim, F.R. Leptonic CP violation. Rev. Mod. Phys. 2012, 84, 515–565. [Google Scholar] [CrossRef]
- Inami, K.; Abe, K.; Abe, K.; Abe, R.; Abe, T.; Adachi, I.; Aihara, H.; Akatsu, M.; Asano, Y.; Aso, T.; et al. Search for the electric dipole moment of the τ lepton. Phys. Lett. B 2003, 551, 16–26. [Google Scholar] [CrossRef]
- Abe, K.; Akutsu, R.; Ali, A.; Amey, J.; Andreopoulos, C.; Anthony, L.; Antonova, M.; Aoki, S.; Ariga, A.; Ashida, Y.; et al. Search for CP Violation in Neutrino and Antineutrino Oscillations by the T2K Experiment with 2.2 × 1021 Protons on Target. Phys. Rev. Lett. 2018, 121, 171802. [Google Scholar] [CrossRef]
- Acero, M.A.; Adamson, P.; Alion, L.A.T.; Allakhverdian, V.; Antoshkin, N.A.A.; Arrieta-Diaz, E.; Back, A.A.A.; Backhouse, C.; Balashov, M.B.N.; Bambah, B.A.; et al. New constraints on oscillation parameters from νe appearance and νμ disappearance in the NOvA experiment. Phys. Rev. D 2018, 98, 032012. [Google Scholar] [CrossRef]
- Abe, K.; Akutsu, R.; Ali, A.; Alt, C.; Andreopoulos, C.; Anthony, L.; Antonova, M.; Aoki, S.; Ariga, A.; Asada, Y.; et al. Constraint on the matter–antimatter symmetry-violating phase in neutrino oscillations. Nature 2020, 580, 339–344. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Vargas, A.J. Lorentz and CPT tests with hydrogen, antihydrogen, and related systems. Phys. Rev. 2015, 92, 056002. [Google Scholar] [CrossRef]
- Vargas, A.J. Overview of the Phenomenology of Lorentz and CPT Violation in Atomic Systems. Symmetry 2019, 11, 1433. [Google Scholar] [CrossRef]
- Moskal, P.; Moskal, P.; Niedźwiecki, S.; Bednarski, T.; Czerwiński, E.; Kubicz, E.; Moskal, I.; Pawlik-Niedźwieckaa, M.; Sharmaa, N.G.; Silarski, M.; et al. Test of a single module of the J-PET scanner based on plastic scintillators. Nucl. Instrum. Meth. 2014, 764, 317–321. [Google Scholar] [CrossRef]
- Moskal, P.; Zoń, N.; Bednarski, T.; Białas, P.; Czerwiński, E.; Gajos, A.; Kamińska, D.; Kapłon, Ł.; Kochanowski, A.; Korcyl, G.; et al. A novel method for the line-of-response and time-of-flight reconstruction in TOF-PET detectors based on a library of synchronized model signals. Nucl. Instrum. Meth. A 2015, 775, 54–62. [Google Scholar] [CrossRef]
- Niedźwiecki, S.; Białas, P.; Curceanu, C.; Czerwiński, E.; Dulski, K.; Gajos, A.; Głowacz, B.; Gorgol, M.; Hiesmayr, B.C.; Jasińska, B.; et al. J-PET: A new technology for the whole-body PET imaging. Acta Phys. Polon. 2017, 48, 1567. [Google Scholar] [CrossRef]
- Kowalski, P.; Wiślicki, W.; Shopa, R.Y.; Raczyński, L.; Klimaszewski, K.; Curcenau, C.; Czerwiński, E.; Dulski, K.; Gajos, A.; Gorgol, M. Estimating the NEMA characteristics of the J-PET tomograph using the GATE package. Phys. Med. Biol. 2018, 63, 165008. [Google Scholar] [CrossRef] [PubMed]
- Moskal, P. Towards total-body modular PET for positronium and quantum entanglement imaging. In Proceedings of the 2018 IEEE Nuclear Science Symposium and Medical Imaging Conference Proceedings (NSS/MIC), Sydney, Australia, 10–17 November 2018; pp. 1–4. [Google Scholar]
- Moskal, P.; Stępień, E.Ł. Prospects and clinical perspectives of total-body PET imaging using plastic scintillators. PET Clin. 2020, in press. [Google Scholar]
- Moskal, P.; Kisielewska, D.; Curceanu, C.; Czerwiński, E.; Dulski, K.; Gajos, A.; Gorgol, M.; Hiesmayr, B.; Jasińska, B.; Kacprzak, K. Feasibility study of the positronium imaging with the J-PET tomograph. Phys. Med. Biol. 2019, 64, 055017. [Google Scholar] [CrossRef] [PubMed]
- Moskal, P.; Jasińska, B.; Stępień, E.Ł.; Bass, S.D. Positronium in medicine and biology. Nat. Rev. Phys. 2019, 1, 527–529. [Google Scholar] [CrossRef]
- Moskal, P.; Kisielewska, D.; Bura, Z.; Chhokar, C.; Curceanu, C.; Czerwiński, E.; Dadgar, M.; Dulski, K.; Gajewski, J.; Gajos, A.; et al. Performance assessment of the 2γ positronium imaging with the total-body PET scanners. EJNMMI Phys. 2020, 7, 44. [Google Scholar] [CrossRef] [PubMed]
- Hiesmayr, B.; Moskal, P. Genuine Multipartite Entanglement in the 3-Photon Decay of Positronium. Sci. Rep. 2017, 7, 15349. [Google Scholar] [CrossRef]
- Moskal, P.; Krawczyk, N.; Hiesmayr, B.C.; Bała, M.; Curceanu, C.; Czerwiński, E.; Dulski, K.; Gajos, A.; Gorgol, M.; Grande, R.D.; et al. Feasibility studies of the polarization of photons beyond the optical wavelength regime with the J-PET detector. Eur. Phys. J. C 2018, 78, 970. [Google Scholar] [CrossRef]
- Hiesmayr, B.C.; Moskal, P. Witnessing Entanglement In Compton Scattering Processes Via Mutually Unbiased Bases. Sci. Rep. 2019, 9, 8166. [Google Scholar] [CrossRef]
- Pałka, M.; Strzempek, P.; Korcyl, G.; Bednarski, T.; Niedźwiecki, S.; Białas, P.; Czerwiński, E.; Dulski, K.; Gajos, A.; Głowacz, B.; et al. Multichannel FPGA based MVT system for high precision time (20 ps RMS) and charge measurement. JINST 2017, 12, P08001. [Google Scholar] [CrossRef]
- Pałka, M.; Bednarski, T.; Białas, P.; Czerwiński, E.; Kapłon, L.; Kochanowski, A.; Korcyl, G.; Kowal, J.; Kowalski, P.; Kozik, T.; et al. A novel method based solely on FPGA units enabling measurement of time and charge of analog signals in Positron Emission Tomography. Bio-Algorithms Med-Syst. 2014, 10, 41–45. [Google Scholar] [CrossRef]
- Korcyl, G.; Alfs, D.; Bednarski, T.; Białas, P.; Czerwiński, E.; Dulski, K.; Gajos, A.; Głowacz, B.; Jasińska, B.; Kamińska, D.; et al. Sampling FEE and Trigger-less DAQ for the J-PET Scanner. Acta Phys. Polon. 2016, 47, 491. [Google Scholar] [CrossRef]
- Korcyl, G.; Białas, P.; Curceanu, C.; Czerwiński, E.; Dulski, K.; Flak, B.; Gajos, A.; Głowacz, B.; Gorgol, M.; Hiesmayr, B.C.; et al. Evaluation of Single-Chip, Real-Time Tomographic Data Processing on FPGA SoC Devices. IEEE Trans. Med. Imaging 2018, 37, 2526–2535. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S. Time Over Threshold as a measure of energy response of plastic scintillators used in the J-PET detector. EPJ Web Conf. 2019, 199, 05014. [Google Scholar] [CrossRef]
- Sharma, S.; Chhokar, J.; Curceanu, C.; Czerwinski, E.; Dadgar, M.; Dulski, K.; Gajewski, J.; Gajos, A.; Gorgol, M.; Gupta-Sharma, N.; et al. Estimating relationship between the Time Over Threshold and energy loss by photons in plastic scintillators used in the J-PET scanner. EJNMMI Phys. 2020, 7, 39. [Google Scholar] [CrossRef] [PubMed]
- Gajos, A.; Curceanu, C.; Czerwiński, E.; Dulski, K.; Gorgol, M.; Gupta-Sharma, N.; Hiesmayr, B.C.; Jasińska, B.; Kacprzak, K.; Kapłon, Ł.; et al. Feasibility Study of the Time Reversal Symmetry Tests in Decay of Metastable Positronium Atoms with the J-PET Detector. Adv. High Energy Phys. 2018, 2018, 8271280. [Google Scholar] [CrossRef]
- Korcyl, G.; Moskal, P.; Bednarski, T.; Białas, P.; Czerwiński, E.; Kapłon, L.; Kochanowski, A.; Kowal, J.; Kowalski, P.; Kozik, T.; et al. Trigger-less and reconfigurable data acquisition system for positron emission tomography. Bio-Algorithms Med-Syst. 2014, 10, 37–40. [Google Scholar] [CrossRef]
- Krzemień, W.; Gajos, A.; Gruntowski, A.; Stola, K.; Trybek, D.; Bednarski, T.; Białas, P.; Czerwiński, E.; Kamińska, D.; Kapłon, L.; et al. Analysis framework for the J-PET scanner. Acta Phys. Polon. A 2015, 127, 1491–1494. [Google Scholar] [CrossRef]
- Krzemień, W.; Alfs, D.; Bialas, P.; Czerwinski, E.; Gajos, A.; Glowacz, B.; Jasinska, B.; Kaminska, D.; Korcyl, G.; Kowalski, P.; et al. Overview of the software architecture and data flow for the J-PET tomography device. Acta Phys. Polon. B 2016, 47, 561. [Google Scholar] [CrossRef]
- Krzemien, W.; Gajos, A.; Kacprzak, K.; Rakoczy, K.; Korcyl, G. J-PET Framework: Software platform for PET tomography data reconstruction and analysis. SoftwareX 2020, 11, 100487. [Google Scholar] [CrossRef]
- Moskal, P.; Rundel, O.; Alfs, D.; Bednarski, T.; Białas, P.; Czerwiński, E.; Gajos, A.; Giergiel, K.; Gorgol, M.; Jasińska, B.; et al. Time resolution of the plastic scintillator strips with matrix photomultiplier readout for J-PET tomograph. Phys. Med. Biol. 2016, 61, 2025. [Google Scholar] [CrossRef]
- Skalsey, M.; Van House, J. First test of CP invariance in the decay of positronium. Phys. Rev. Lett. 1991, 67, 1993–1996. [Google Scholar] [CrossRef] [PubMed]
- Arbic, B.K.; Hatamian, S.; Skalsey, M.; Van House, J.; Zheng, W. Angular Correlation Test of CPT in Polarized Positronium. Phys. Rev. 1988, 37, 3189–3194. [Google Scholar] [CrossRef] [PubMed]
- Bernreuther, W.; Low, U.; Nachtmann, O. Possible tests of CP invariance with polarized positronium. Hyperfine Interact. 1989, 44, 139–145. [Google Scholar] [CrossRef]
- Mohammed, M.; Białas, P.; Curceanu, C.; Czerwiński, E.; Dulski, K.; Gajos, A.; Głowacz, B.; Gorgol, M.; Hiesmayr, B.C.; Jasinska, B.; et al. A method to produce linearly polarized positrons and positronium atoms with the J-PET detector. Acta Phys. Polon. 2017, 132, 1486–1489. [Google Scholar] [CrossRef]
- Gajos, A.; Kamińska, D.; Czerwiński, E.; Alfs, D.; Bednarski, T.; Białas, P.; Głowacz, B.; Gorgol, M.; Jasińska, B.; Kapłon, L.; et al. Trilateration-based reconstruction of ortho-positronium decays into three photons with the J-PET detector. Nucl. Instrum. Meth. 2016, 819, 54–59. [Google Scholar] [CrossRef]
- Gajos, A. Studies of Ortho-Positronium Decays into Three Photons with the J-PET Detector. Acta Phys. Polon. 2020, 137, 126–129. [Google Scholar] [CrossRef]
- Abe, K.; Abt, I.; Ahn, C.J.; Akagi, T.; Allen, N.J.; Ash, W.W.; Aston, D.; Baird, K.G.; Baltay, C.; Band, H.R.; et al. First Measurement of the T-Odd Correlation between the Z0 Spin and the Three-Jet Plane Orientation in Polarized Z0 Decays into Three Jets. Phys. Rev. Lett. 1995, 75, 4173–4177. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Relativistic Quantum Theory, 1st ed.; Pergamon Press: Oxford, UK; New York, NY, USA, 1971. [Google Scholar]
- Kamińska, D.; Gajos, A.; Czerwiński, E.; Alfs, D.; Bednarski, T.; Białas, P.; Curceanu, C.; Dulski, K.; Głowacz, B.; Gupta-Sharma, N.; et al. A feasibility study of ortho-positronium decays measurement with the J-PET scanner based on plastic scintillators. Eur. Phys. J. 2016, 76, 1–14. [Google Scholar] [CrossRef]
- Raj, J.; Gajos, A.; Curceanu, C.; Czerwiński, E.; Dulski, K.; Gorgol, M.; Gupta-Sharma, N.; Hiesmayr, B.C.; Jasińska, B.; Kacprzak, K.; et al. A feasibility study of the time reversal violation test based on polarization of annihilation photons from the decay of ortho-Positronium with the J-PET detector. Hyperfine Interact. 2018, 239, 56. [Google Scholar] [CrossRef][Green Version]
- Raj, J.; Kisielewska, D.; Czerwiński, E. J-PET Monte Carlo Simulations for Time-Reversal Symmetry Test in Ortho-Positronium Decay. Acta Phys. Polon. 2020, 137, 137–139. [Google Scholar] [CrossRef]
| No. | Operator | C | P | T | CP | CPT |
|---|---|---|---|---|---|---|
| 1 | + | – | + | – | – | |
| 2 | + | + | – | + | – | |
| 3 | + | – | – | – | + |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajos, A. Sensitivity of Discrete Symmetry Tests in the Positronium System with the J-PET Detector. Symmetry 2020, 12, 1268. https://doi.org/10.3390/sym12081268
Gajos A. Sensitivity of Discrete Symmetry Tests in the Positronium System with the J-PET Detector. Symmetry. 2020; 12(8):1268. https://doi.org/10.3390/sym12081268
Chicago/Turabian StyleGajos, Aleksander. 2020. "Sensitivity of Discrete Symmetry Tests in the Positronium System with the J-PET Detector" Symmetry 12, no. 8: 1268. https://doi.org/10.3390/sym12081268
APA StyleGajos, A. (2020). Sensitivity of Discrete Symmetry Tests in the Positronium System with the J-PET Detector. Symmetry, 12(8), 1268. https://doi.org/10.3390/sym12081268





