Symmetries and Their Breaking in the Fundamental Laws of Physics
Abstract
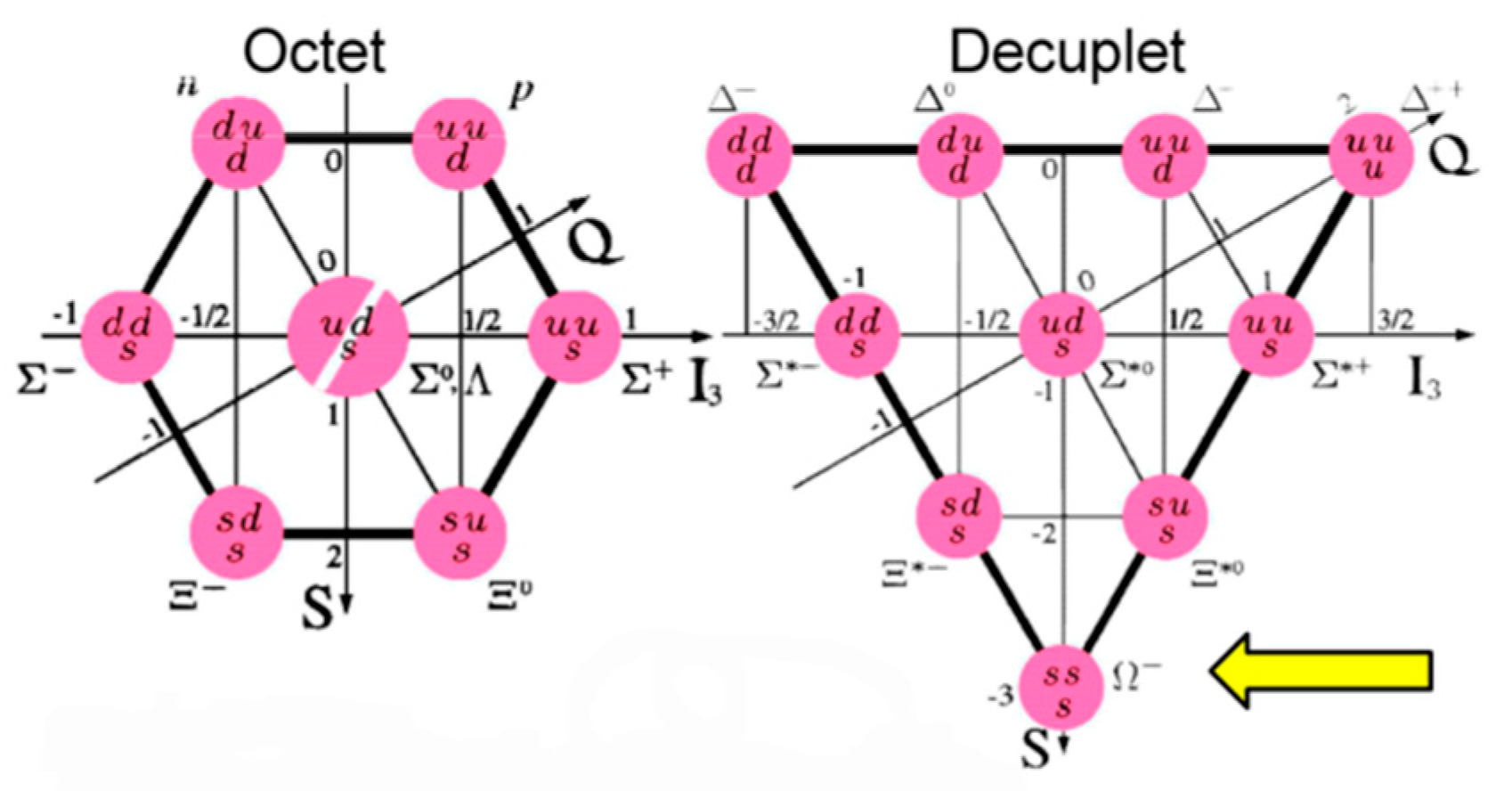
1. Symmetry as Guiding Principle for Particles and Interactions
2. Quarks and Strong Interactions
2.1. Are Quarks Real?
2.2. The Colour Charge
2.3. Asymptotic Freedom
3. Chirality and Electroweak Interaction
3.1. GIM Mechanism: Need of Charm
3.2. The Third Family
3.3. Gauge Anomalies: Quark–Lepton Symmetry
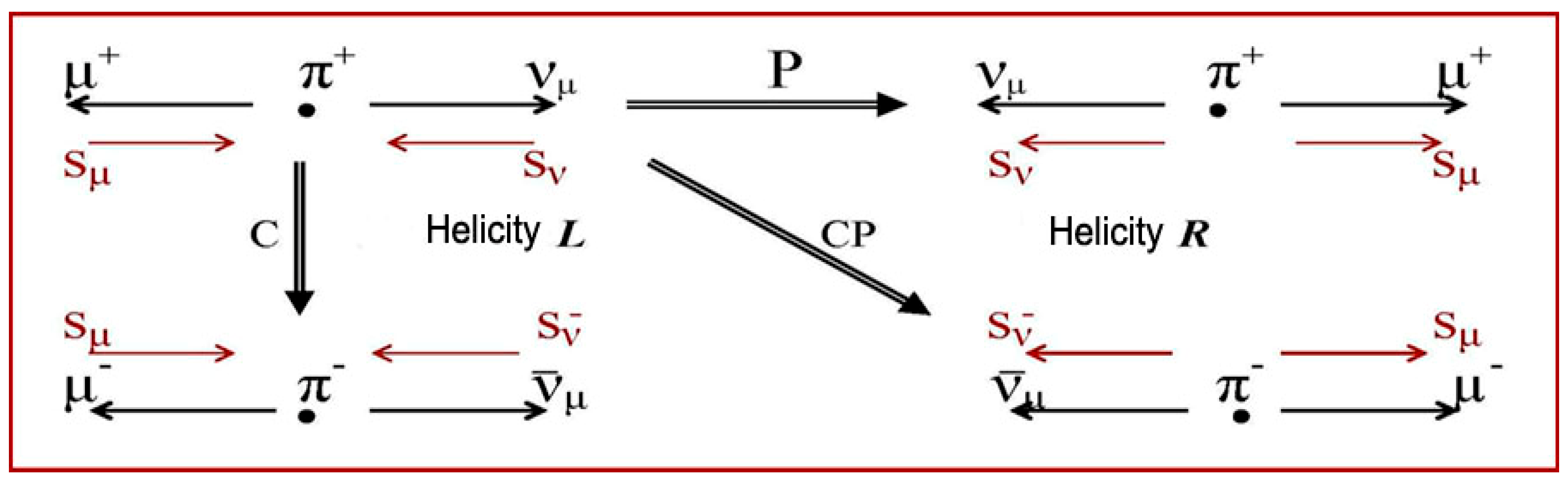
4. Discrete Symmetries CP, T, CPT
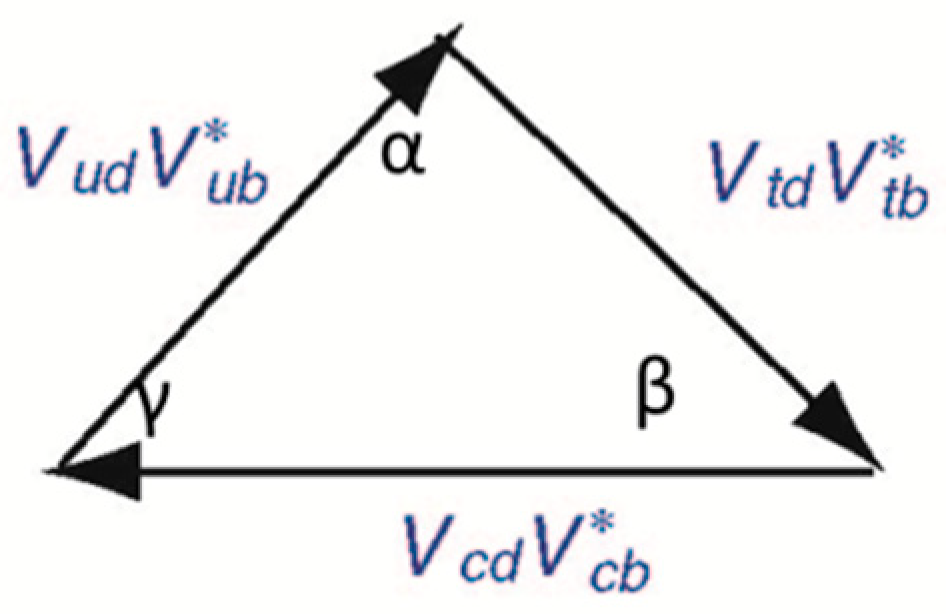
4.1. CP Violation
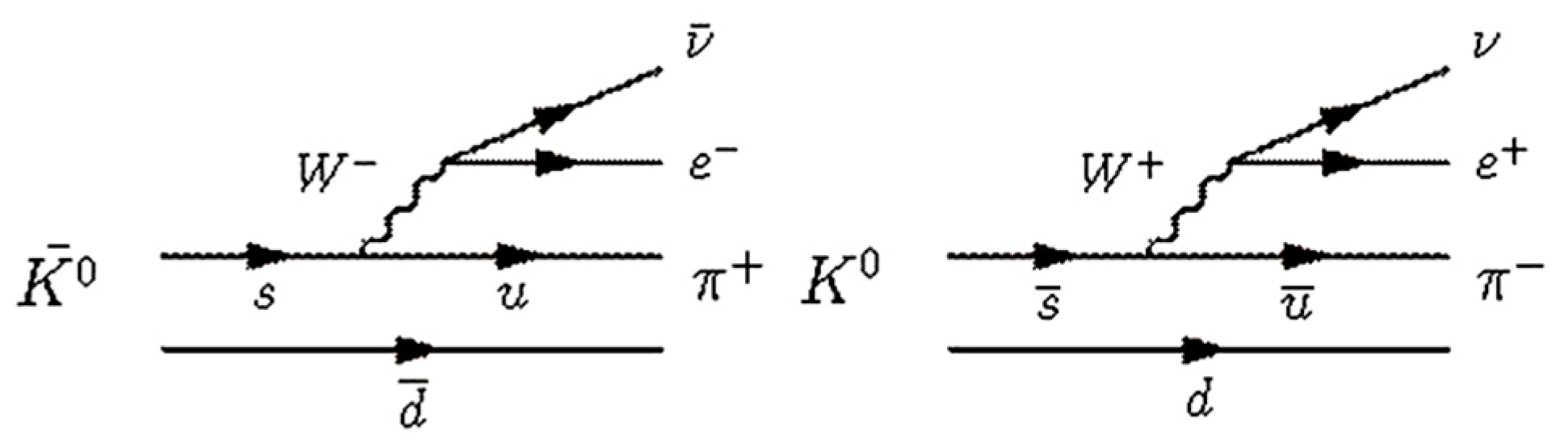
4.2. Time Reversal Violation
4.3. CPT
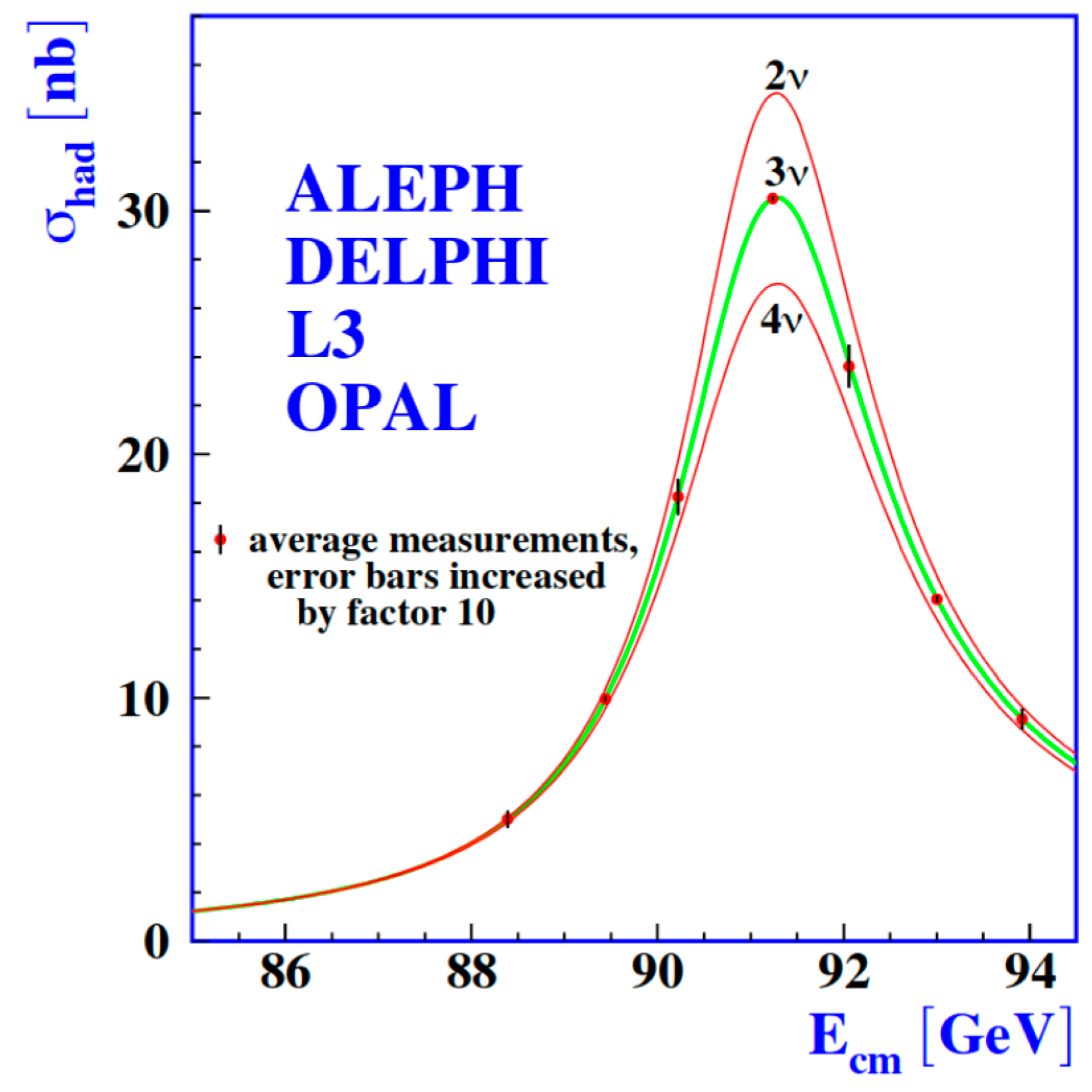
5. Neutrinos
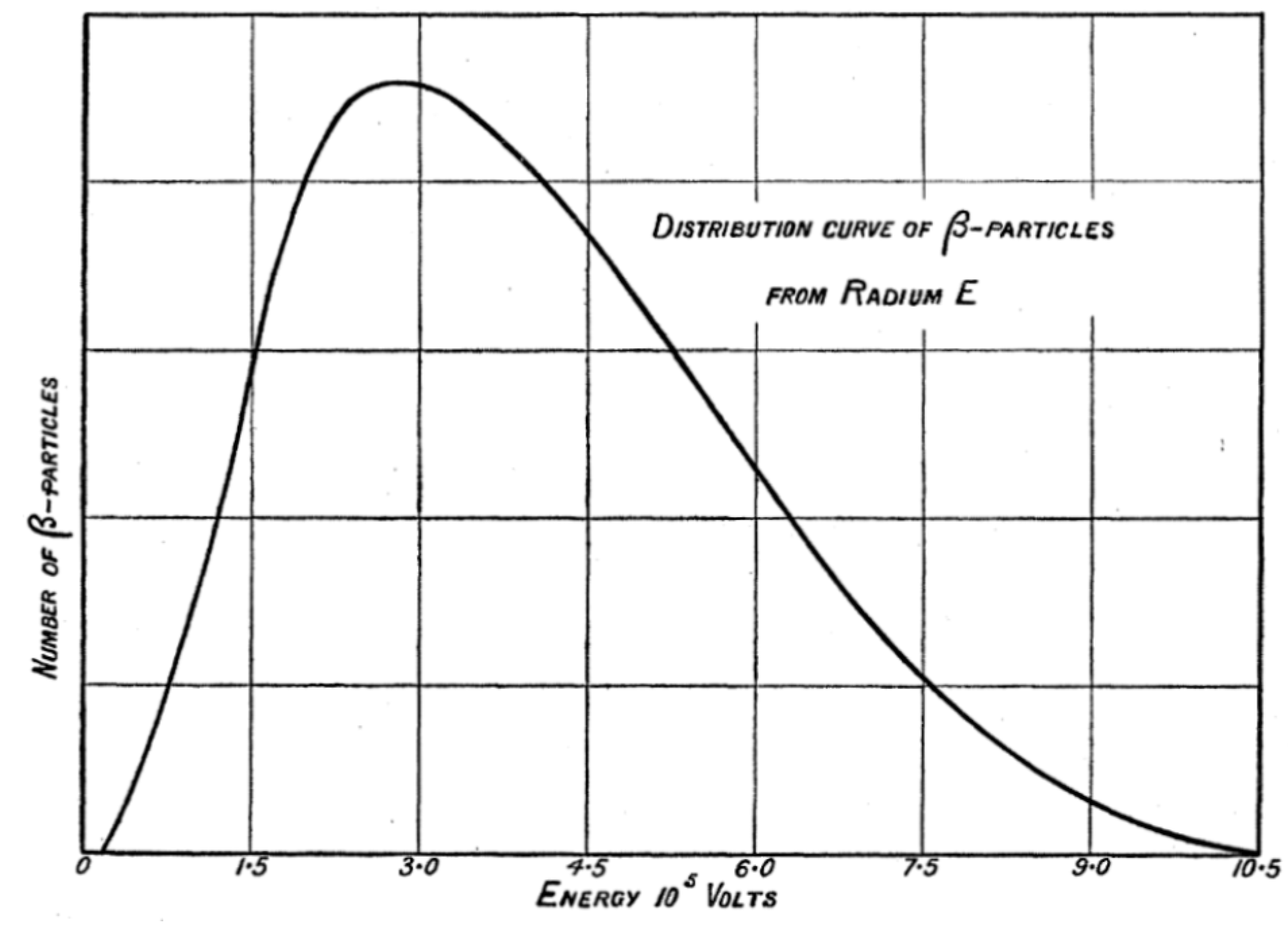
5.1. The Energy Crisis
5.2. Lepton Flavours
5.3. Neutrino Mass and Mixing: Oscillations
5.4. Genuine CP Violation
5.5. Global Lepton Number
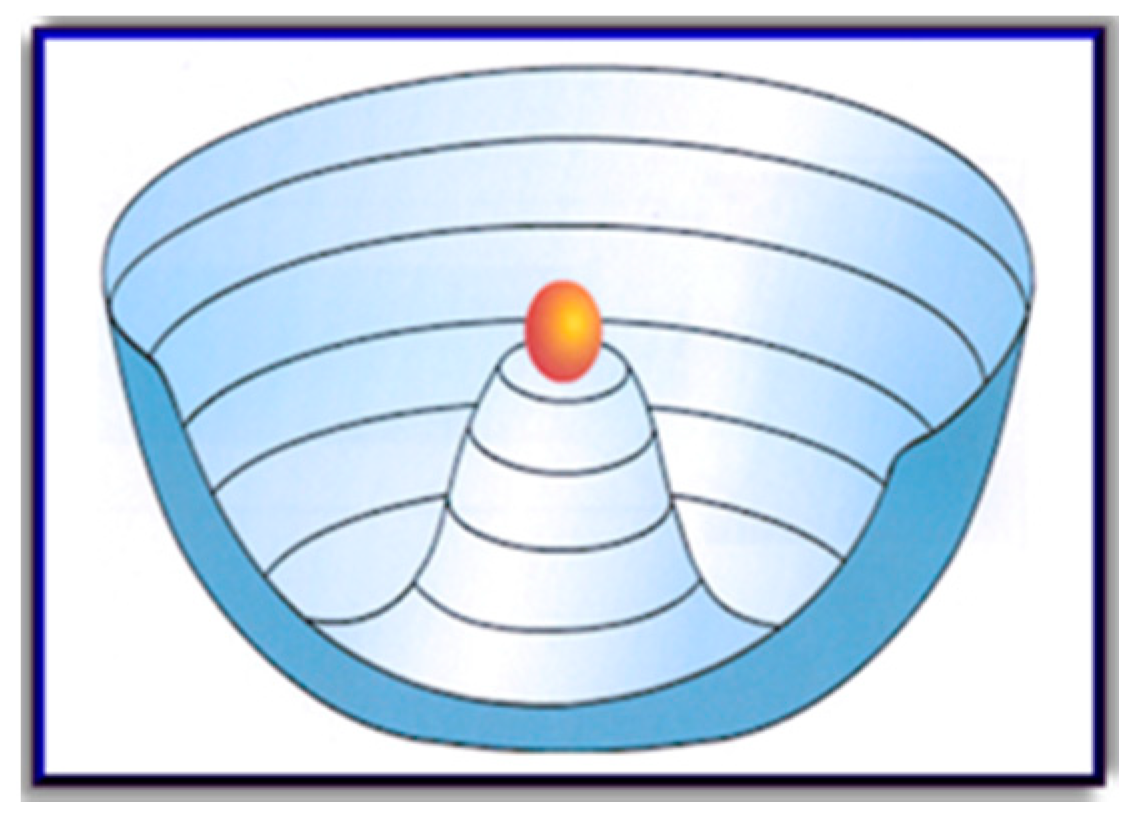
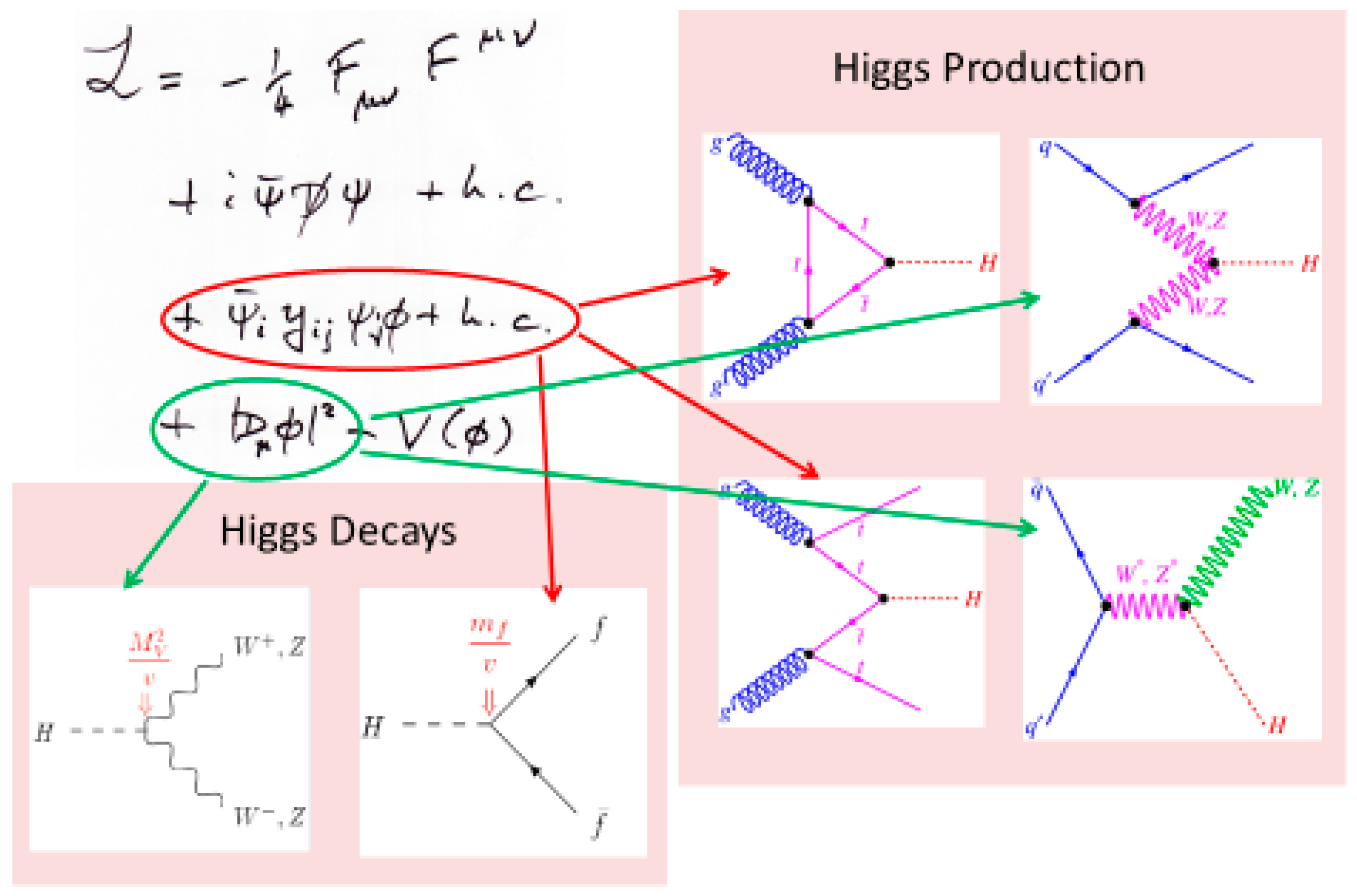
6. The Brout–Englert–Higgs Mechanism
6.1. The Higgs Boson Gauge and Yukawa Couplings
6.2. The Higgs Potential
7. Conclusions and Outlook
- -
- Mass terms are incompatible with both gauge and chirality symmetries.
- -
- Quantum loop Anomalies break conformal symmetry for vector theories and gauge symmetry for chiral field theories.
- -
- The Particle Content of the theory controls the breaking of Discrete Symmetries CP and T.
- -
- A gauge Asymmetric Vacuum leads to spontaneous symmetry breaking with hidden gauge symmetry and explaining the Origin of Mass for elementary particles.
- -
- Why the quantization of electric charge, Dual QED, Magnetic Monopoles
- -
- The principle of “Threeality” in fundamental physics.
- -
- The Hierarchy Problem for scalars, Supersymmetry.
- -
- Grand Unification, p-decay.
- -
- Neutrino Mass, Mixing, CPV, Global Lepton Number.
- -
- Charged Lepton Flavour Violation.
- -
- Baryon Asymmetry of the Universe, Leptogenesis.
- -
- Dark Matter
- -
- Dark Energy
Funding
Acknowledgments
Conflicts of Interest
References
- Gell-Mann, M. A schematic model of baryons and mesons. Phys. Lett. 1964, 8, 214. [Google Scholar] [CrossRef]
- Bloom, E.D.; Coward, D.H.; DeStaebler, H.C.; Drees, J.; Miller, G.; Mo, L.W.; Taylor, R.E.; Breidenbach, M.; Friedman, J.I.; Hartmann, G.C.; et al. High-energy inelastic e p scattering at 6 degrees and 10 degrees. Phys. Rev. Lett. 1969, 23, 930. [Google Scholar] [CrossRef]
- Hanson, G.; Abrams, G.S.; Boyarski, A.; Breidenbach, M.; Bulos, F.; Chinowsky, W.; Feldman, G.J.; Friedberg, C.E.; Fryberger, D.; Goldhaber, G.; et al. Evidence for jet structure in hadron production by e+ e− annihilation. Phys. Rev. Lett. 1975, 35, 1609. [Google Scholar] [CrossRef]
- Brandelik, R.; Braunschweig, W.; Gather, K.; Kadansky, V.; Lubelsmeyer, K.; Mattig, P.; Martyn, H.U.; Peise, G.; Rimkus, J.; Sander, H.G.; et al. Evidence for planar events in e+ e− annihilation at high energies. Phys. Lett. B 1979, 86, 243. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet behavior of nonabelian gauge theories. Phys. Rev. Lett. 1973, 30, 1343. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable perturbative results for strong interactions? Phys. Rev. Lett. 1973, 30, 1346. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Question of parity conservation in weak interactions. Phys. Rev. 1956, 104, 254. [Google Scholar] [CrossRef]
- Glashow, S.L. Partial symmetries of weak interactions. Nucl. Phys. 1961, 22, 579. [Google Scholar] [CrossRef]
- Weinberg, S. A model of leptons. Phys. Rev. Lett. 1967, 19, 1264. [Google Scholar] [CrossRef]
- Salam, A. Weak and electromagnetic interactions. Conf. Proc. C 1968, 680519, 367. [Google Scholar]
- Hasert, F.J.; Kabe, S.; Krenz, W.; von Krogh, J.; Lanske, D.; Morfin, J.; Schultze, K.; Weerts, H.; Bertrand-Coremans, G.H.; Sacton, J.; et al. Observation of neutrino-like interactions without muon on electron in the gargamelle neutrino experiment. Phys. Lett. B 1973, 46, 138. [Google Scholar] [CrossRef]
- Arnison, G.; Astbury, A.; Aubert, B.; Bacci, C.; Bauer, G.; Bézaguet, A.; Böck, R.; Bowcock, T.J.V.; Calvetti, M.; Catz, P.; et al. Experimental observation of lepton pairs of invariant mass around 95 GeV/c2 at the CERN SPS collider. Phys. Lett. B 1983, 126, 398. [Google Scholar] [CrossRef]
- Bagnaia, P.; Banner, M.; Battiston, R.; Bloch, P.; Bonaudi, F.; Borer, K.; Borghini, M.; Chollet, J.C.; Clark, A.G.; Conta, C.; et al. Evidence for Z0 → e+ e− at the CERN collider. Phys. Lett. B 1983, 129, 130. [Google Scholar] [CrossRef]
- Cabibbo, N. Unitary symmetry and leptonic decays. Phys.Rev.Lett. 1963, 10, 531. [Google Scholar] [CrossRef]
- Glashow, S.L.; Iliopoulos, J.; Maiani, L. Weak interactions with lepton-hadron symmetry. Phys. Rev. D 1970, 2, 1285. [Google Scholar] [CrossRef]
- Aubert, J.J.; Becker, U.; Biggs, P.J.; Burger, J.; Chen, M.; Everhart, G.; Goldhagen, P.; Leong, J.; McCorriston, T.; Rhoades, T.G.; et al. Experimental observation of a heavy particle J. Phys. Rev. Lett. 1974, 33, 1404. [Google Scholar] [CrossRef]
- Augustin, J.E.; Boyarski, A.; Breidenbach, M.; Bulos, F.; Dakin, J.T.; Feldman, G.J.; Fischer, G.E.; Fryberger, D.; Hanson, G.; Jean-Marie, B.; et al. Discovery of a narrow resonance in e+ e− annihilation. Phys. Rev. Lett. 1974, 33, 1406. [Google Scholar] [CrossRef]
- Kobayashi, M.; Maskawa, T. CP violation in the renormalizable theory of weak interactions. Prog. Theor. Phys. 1973, 49, 652. [Google Scholar] [CrossRef]
- Albajar, C. Search for oscillations at the CERN collider. Phys. Lett. B 1987, 186, 247, Erratum in Phys. Lett. B 1987, 197, 565. [Google Scholar] [CrossRef]
- Albrecht, H.; Andam, A.A.; Binder, U.; Bockmann, P.; Glaser, R.; Harder, G.; Nippe, A.; Schafer, M.; Schmidt-Parzefall, W.; Schroder, H.; et al. Observation of mixing. Phys. Lett. B 1987, 192, 245. [Google Scholar] [CrossRef]
- Veltman, M.J.G. Radiative corrections to vector boson masses. Phys. Lett. B 1980, 91, 95. [Google Scholar] [CrossRef][Green Version]
- Bernabeu, J.; Pich, A.; Santamaría, A. Γ(Z → ): A signature of hard mass terms for a heavy top. Phys. Lett. B 1988, 200, 569. [Google Scholar] [CrossRef][Green Version]
- Abe, F.; Akimoto, H.; Akopian, A.; Albrow, M.G.; Amendolia, S.R.; Amidei, D.; Antos, J.; Anway-Wiese, C.; Aota, S.; Apollinari, G.; et al. Observation of top quark production in collisions. Phys. Rev. Lett. 1995, 74, 2626. [Google Scholar] [CrossRef] [PubMed]
- Abachi, S.; Abbott, B.; Abolins, M.; Acharya, B.S.; Adam, I.; Adams, D.L.; Adams, M.; Ahn, S.; Aihara, H.; Alitti, J.; et al. Observation of the top quark. Phys. Rev. Lett. 1995, 74, 2632. [Google Scholar] [CrossRef] [PubMed]
- Fujikawa, K.; Suzuki, H. Path Integrals and Quantum Anomalies; Clarendon Press: Oxford, UK, 2004. [Google Scholar]
- Christenson, J.H.; Cronin, J.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π Decay of the Meson. Phys. Rev. Lett. 1964, 13, 138. [Google Scholar] [CrossRef]
- NA31 Collaboration. First evidence for direct CP violation. Phys. Lett. B 1988, 206, 169. [Google Scholar] [CrossRef]
- NA48 Collaboration. A new measurement of direct CP violation in two pion decays of the neutral kaon. Phys. Lett. B 1999, 465, 335. [Google Scholar] [CrossRef]
- CPLEAR Collaboration. Physics at CPLEAR. Phys. Rep. 2003, 374, 165. [Google Scholar] [CrossRef]
- BABAR Collaboration. Observation of CP violation in the B0 meson system. Phys. Rev. Lett. 2001, 87, 091801. [Google Scholar] [CrossRef]
- BELLE Collaboration. Observation of large CP violation in the neutral B meson system. Phys. Rev. Lett. 2001, 87, 091802. [Google Scholar] [CrossRef]
- LHCb Collaboration. Observation of CP violation in charm decays. Phys. Rev. Lett. 2019, 122, 211803. [Google Scholar] [CrossRef] [PubMed]
- Banuls, M.C.; Bernabéu, J. CP, T and CPT versus temporal asymmetries for entangled states of the B(d) system. Phys. Lett. B 1999, 464, 117–122. [Google Scholar] [CrossRef]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Tico, J.G.; Grauges, E.; Palanoab, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; et al. Observation of time reversal violation in the B0 meson system. Phys. Rev. Lett. 2012, 109, 211801. [Google Scholar] [CrossRef] [PubMed]
- Bernabeu, J.; Martinez-Vidal, F.; Villanueva-Perez, P. Time reversal violation from the entangled B0-antiB0 system. J. High Energy Phys. 2012, 2012, 64. [Google Scholar] [CrossRef]
- Bernabeu, J.; Botella, F.J.; Nebot, M. Genuine T, CP, CPT asymmetry parameters for the entangled B(d) system. J. High Energy Phys. 2016, 2016, 100. [Google Scholar] [CrossRef]
- Bernabeu, J.; Di Domenico, A.; Villanueva-Perez, P. Direct test of Time Reversal symmetry in the entangled neutral Kaon system at a ɸ-Factory. Nucl. Phys. B 2013, 868, 102. [Google Scholar] [CrossRef]
- CPLEAR Collaboration. A determination of the CPT violation parameter Re(δ) from the semileptonic decay of strangeness tagged neutral Kaons. Phys. Lett. B 1998, 444, 52. [Google Scholar] [CrossRef]
- KTeV Collaboration. A measurement of the KL charge asymmetry. Phys. Rev. Lett. 2002, 88, 181601. [Google Scholar] [CrossRef]
- KLOE Collaboration. Study of the branching ratio and charge asymmetry for the decay KS → π e ν with the KLOE detector. Phys. Lett. B 2006, 636, 173. [Google Scholar] [CrossRef][Green Version]
- Bernabeu, J.; Di Domenico, A.; Villanueva-Perez, P. Probing CPT in transitions with entangled neutral Kaons. JHEP 2015, 1510, 139. [Google Scholar] [CrossRef]
- Bernabeu, J.; Mavromatos, N.; Papavassiliou, J. Novel type of CPT Violation for correlated EPR states. Phys. Rev. Lett. 2004, 92, 131601. [Google Scholar] [CrossRef] [PubMed]
- Bernabeu, J.; Mavromatos, N.; Sarkar, S. Decoherence induced CPT Violation and entangled neutral mesons. Phys. Rev. D 2006, 74, 045014. [Google Scholar] [CrossRef]
- ALPHA Collaboration. Characterization of the 1S–2S transition in antihydrogen. Nature 2018, 557, 71. [Google Scholar] [CrossRef] [PubMed]
- ALPHA Collaboration. Observation of the hyperfine spectrum of antihydrogen. Nature 2017, 548, 66. [Google Scholar] [CrossRef]
- ASACUSA Collaboration. A hydrogen beam to characterize the ASACUSA antihydrogen hyperfine spectrometer. Nucl. Instrum. Meth. A 2019, 935, 110. [Google Scholar] [CrossRef]
- Super-Kamiokande Collaboration. Evidence for oscillation of atmospheric neutrinos. Phys. Rev. Lett. 1998, 81, 1562. [Google Scholar] [CrossRef]
- SNO Collaboration. Direct Evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2002, 89, 011301. [Google Scholar] [CrossRef]
- KamLAND Collaboration. First results from KamLAND: Evidence for reactor anti-neutrino disappearance. Phys. Rev. Lett. 2003, 90, 021802. [Google Scholar] [CrossRef]
- K2K Collaboration. Measurement of neutrino oscillation by the K2K experiment. Phys. Rev. D 2006, 74, 072003. [Google Scholar] [CrossRef]
- Pontecorvo, B. Mesonium and anti-mesonium. Sov. Phys. JETP 1957, 6, 429. [Google Scholar]
- Maki, Z.; Nakagawa, M.; Sakata, S. Remarks on the unified model of elementary particles. Prog. Theor. Phys. 1962, 28, 870. [Google Scholar] [CrossRef]
- Capozzi, F.; Fogli, G.L.; Lisi, E.; Marrone, A.; Montanino, D.; Palazzo, A. Status of three-neutrino oscillation parameters, circa 2013. Phys. Rev. D 2014, 89, 093018. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.C.; Maltoni, M.; Martinez-Soler, I.; Schwetz, T. Updated Fit to three neutrino mixing: Exploring accelerator-reactor complementarity. J. High Energy Phys. 2017, 2017, 87. [Google Scholar] [CrossRef]
- De Salas, P.F.; Forero, D.V.; Ternes, C.A.; Tortola, M.; Valle, J.W.F. Status of neutrino oscillation 2018: 3 σ hint for normal mass ordering and improved CP sensitivity. Phys. Lett. B 2018, 782, 633. [Google Scholar] [CrossRef]
- Hyper-Kamiokande Collaboration. Hyper-Kamiokande design report. arXiv 2018, arXiv:1805.04163. [physics.ins-det]. [Google Scholar]
- DUNE Collaboration. Long Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE): Conceptual design report, Volume 2: The physics program for DUNE at LBNF. arXiv 2015, arXiv:1512.06148. [physics.ins-det]. [Google Scholar]
- T2K Collaboration. Indication of electron neutrino appearance from an accelerator-produced off-axis muon neutrino beam. Phys. Rev. Lett. 2011, 107, 041801. [Google Scholar] [CrossRef]
- Double Chooz Collaboration. Indication of reactor antinue disappearance in the double chooz experiment. Phys. Rev. Lett. 2012, 108, 131801. [Google Scholar] [CrossRef]
- Daya Bay Collaboration. Observation of electron-antineutrino disappearance at Daya Bay. Phys. Rev. Lett. 2012, 108, 171803. [CrossRef]
- RENO Collaboration. Observation of electron-antineutrino diappearance at RENO. Phys. Rev. Lett. 2012, 108, 191802. [Google Scholar] [CrossRef]
- Fukugita, M.; Yanagida, T. Baryogenesis without grand unification. Phys. Lett. B 1986, 174, 45. [Google Scholar] [CrossRef]
- Thomson, J.J. XL. Cathode rays. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1897, 44, 293–316. [Google Scholar] [CrossRef]
- Rutherford, E. LIV. Collision of a particles with light atoms. IV. An anomalous effect in nitrogen. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1919, 37, 581–587. [Google Scholar] [CrossRef]
- Rutherford, E. LXXIX. The scattering of α and β particles by matter and the structure of the atom. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1911, 21, 669–688. [Google Scholar]
- Rutherford, E. VIII. Uranium radiation and the electrical conduction produced by it. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1899, 47, 109–163. [Google Scholar] [CrossRef]
- Becquerel, H. Influence d’un champ magnétique sur le rayonnement des corps radio-actifs. J. Phys. Théorique Appliquée 1900, 9, 71–78. [Google Scholar] [CrossRef][Green Version]
- Von Baeyer, O.; Hahn, O.; Meitner, L. Uber die β-Strahlen des aktiven niederschlags des thoriums. Phys. Z. 1911, 12, 273. [Google Scholar]
- Danysz, J.; Duane, W. Sur les charges électriques des rayons α et β. Le Radium 1912, 9, 417–421. [Google Scholar] [CrossRef]
- Chadwick, J. Intensitätsverteilung im magnetischen Spectrum der β-Strahlen von radium B + C. Verhandl. Dtsc. Phys. Ges. 1914, 16, 383. [Google Scholar]
- Ornstein, L.; Van Wijk, W.Z. Untersuchungen über das negative Stickstoff bandenspektrum. Für Phys. 1928, 49, 315–322. [Google Scholar] [CrossRef]
- Chadwick, J.; Ellis, C.D. A preliminary investigation of the intensity distribution in the β-ray spectra of radium B and C. In Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1922; Volume 21, p. 274. [Google Scholar]
- Ellis, C.D.; Wooster, W. The β-ray Type of Disintegration. In Mathematical Proceedings of the Cambridge Philosophical SocietyI; Cambridge University Press: Cambridge, UK, 1925; Volume 22, p. 849. [Google Scholar]
- Ellis, C.D.; Wooster, W.A. The average energy of disintegration of radium E. Proceedings of the Royal Society of London. Series A. Contain. Pap. Math. Phys. Character 1927, 117, 109–123. [Google Scholar]
- Bohr, N.R. Atomic stability and conservation laws. Accad. d’Italia 1932, 119–130. [Google Scholar]
- Chadwick, J. Possible existence of a neutrón. Nature 1932, 129, 312. [Google Scholar] [CrossRef]
- Anderson, C.D. The Positive electron. Phys. Rev. 1933, 43, 491. [Google Scholar] [CrossRef]
- Fermi, E. Tentativo di una teoria dei raggi β. Nuovo Cim. 1934, 11, 1–19. [Google Scholar] [CrossRef]
- Bethe, H.; Peierls, R. The ‘neutrino’. Nature 1934, 133, 532. [Google Scholar] [CrossRef]
- Cowan, C.L.; Reines, F.; Harrison, F.B.; Kruse, H.W.; McGuire, A.D. Detection of the free neutrino: A Confirmation. Science 1956, 124, 103. [Google Scholar] [CrossRef]
- Anderson, C.D.; Neddermeyer, S.H. Cloud chamber observations of cosmic rays at 4300 meters elevation and near sea-level. Phys. Rev. 1936, 50, 263. [Google Scholar] [CrossRef]
- Lattes, C.M.G.; Muirhead, H.; Occhialini, G.P.S.; Powell, C.F. Processes involving charged mesons. Nature 1947, 159, 694. [Google Scholar] [CrossRef]
- Feynman, R.P.; Gell-Mann, M. Theory of Fermi interaction. Phys. Rev. 1958, 109, 193. [Google Scholar] [CrossRef]
- Pontecorvo, B. Nuclear capture of mesons and the meson decay. Phys. Rev. 1947, 72, 246. [Google Scholar] [CrossRef]
- Pontecorvo, B. Electron and Muon Neutrinos. J. Phys. 1959, 43, 8–221. [Google Scholar]
- Pontecorvo, B. Electron and Muon Neutrinos. Sov. Phys. JETP 1960, 10, 1236. [Google Scholar]
- Feinberg, G. Decays of the mu meson in the intermediate-meson theory. Phys. Rev. 1958, 110, 1482. [Google Scholar] [CrossRef]
- Bartlett, D.; Devons, S.; Sachs, A.M. Search for the decay mode: μ → e + γ. Phys. Rev. Lett. 1962, 8, 120. [Google Scholar] [CrossRef]
- Danby, G.; Gaillard, J.M.; Goulianos, K.A.; Lederman, L.M.; Mistry, N.B.; Schwartz, M.; Steinberger, J. Observation of high-energy neutrino reactions and the existence of two kinds of neutrinos. Phys. Rev. Lett. 1962, 9, 36. [Google Scholar] [CrossRef]
- Perl, M.L.; Abrams, G.S.; Boyarski, A.; Breidenbach, M.; Briggs, D.; Bulos, F.; Chinowsky, W.; Dakin, J.T.; Feldman, G.J.; Friedberg, C.E.; et al. Evidence for anomalous lepton production in e+-e− annihilation. Phys. Rev. Lett. 1975, 35, 1489. [Google Scholar] [CrossRef]
- DONUT Collaboration. Observation of τ neutrino interactions. Phys. Lett. B 2001, 504, 218. [Google Scholar] [CrossRef]
- ALEPH, DELPHI, L3, OPAL, SLD, LEP Electroweak Working Group; SLD Electroweak Group; SLD Heavy Flavour Group Collaboration. Precision electroweak measurements on the Z resonance. Phys. Rept. 2006, 427, 257. [Google Scholar] [CrossRef]
- Weyl, H. Electron and gravitation. 1. Z. Phys. 1929, 56, 330. (In German) [Google Scholar] [CrossRef]
- Wu, C.S.; Ambler, E.; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. Experimental test of parity conservation in beta decay. Phys. Rev. 1957, 105, 1413. [Google Scholar] [CrossRef]
- Goldhaber, M.; Grodzins, L.; Sunyar, A.W. Helicity of neutrinos. Phys. Rev. 1958, 109, 1015. [Google Scholar] [CrossRef]
- Pontecorvo, B. Chalk river report. Rep. PD 1946, 205, 174. [Google Scholar]
- Davis, R., Jr.; Harmer, D.S. Attempt to observe the Cl37Ar37 reaction induced by reactor antineutrinos. Bull. Am. Phys. Soc. 1959, 4, 217. [Google Scholar]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Nuovo Cim. 1937, 14, 171. [Google Scholar] [CrossRef]
- Pontecorvo, B. Inverse beta processes and nonconservation of lepton charge. Sov. Phys. JETP 1958, 7, 172. [Google Scholar]
- KamLAND Collaboration Measurement of neutrino oscillation with KamLAND: Evidence for spectral distortion. Phys. Rev. Lett. 2005, 94, 081801. [CrossRef]
- Pontecorvo, B. Neutrino experiments and the problem of conservation of leptonic charge. Sov. Phys. JETP 1968, 26, 984. [Google Scholar]
- Davis, R., Jr.; Harmer, D.S.; Hoffman, K.C. Search for neutrinos from the sun. Phys. Rev. Lett. 1968, 20, 1205. [Google Scholar] [CrossRef]
- Kamiokande-II Collaboration. Experimental study of the atmospheric neutrino flux. Phys. Lett. B 1988, 205, 416. [Google Scholar] [CrossRef]
- Bernabeu, J. On the history of the PMNS Matrix... with today’s perspective. Nuovo Cim. C037 2014, 3, 145. [Google Scholar]
- T2K Collaboration. Constraint on the Matter-Antimatter Symmetry Violating Phase in neutrino oscillations. Nat. 580 2020, 7803, 39. [Google Scholar]
- Wolfenstein, L. Neutrino oscillations in matter. Phys. Rev. D 1978, 17, 2369. [Google Scholar] [CrossRef]
- Mikheyev, S.P.; Smirnov, A.Y. Resonance amplification of oscillations in matter and spectroscopy of solar neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913. [Google Scholar]
- Donini, A.; Gavela, M.B.; Hernandez, P.; Rigolin, S. Neutrino mixing and CP violation. Nucl. Phys. B 2000, 574, 23. [Google Scholar] [CrossRef]
- Akhmedov, E.K.; Maltoni, M.; Smirnov, A.Y. Neutrino oscillograms of the Earth: Effects of 1-2 mixing and CP Violation. J. High Energy Phys. 2008, 2008, 072. [Google Scholar] [CrossRef]
- Ohlsson, T.; Zhang, H.; Zhou, S. Probing the leptonic Dirac CP-violating phase in neutrino oscillation experiments. Phys. Rev. D 2013, 87, 53006. [Google Scholar] [CrossRef]
- Bernabeu, J.; Segarra, A. Disentangling genuine from matter-induced CP Violation in neutrino oscillations. Phys. Rev. Lett. 2018, 121, 211802. [Google Scholar] [CrossRef]
- Bernabeu, J.; Segarra, A. Signatures of the genuine and matter-induced components of the CP violation asymmetry in neutrino oscillations. J. High Energy Phys. 2018, 2018, 63. [Google Scholar] [CrossRef]
- Bernabeu, J.; Banuls, M.C. CP and T violation in neutrino oscillations. Nucl. Phys. Proc. Suppl. 2000, 87, 315. [Google Scholar] [CrossRef]
- Bernabeu, J.; Segarra, A. Do T-asymmetries for neutrino oscillations in uniform matter have a CP-even component? J. High Energy Phys. 2019, 2019, 103. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Hosek, J.; Petcov, S.T. On oscillations of neutrinos with dirac and majorana masses. Phys. Lett. B 1980, 94B, 495. [Google Scholar] [CrossRef]
- Doi, M.; Kotani, T.; Nishiura, H.; Okuda, K.; Takasugi, E. CP violation in majorana neutrinos. Phys. Lett. B 1981, 102B, 323. [Google Scholar] [CrossRef]
- Bernabeu, J.; Pascual, P. CP properties of the leptonic sector for majorana neutrinos. Nucl. Phys. B 1983, 228, 21. [Google Scholar] [CrossRef]
- Case, K.M. Reformulation of the majorana theory of the neutrino. Phys. Rev. 1957, 107, 307. [Google Scholar] [CrossRef]
- Ryan, C.; Okubo, S. On the equivalence of the Majorana and two-component theories of the neutrino. Nuovo Cim. Suppl. 1964, 2, 234. [Google Scholar]
- GERDA Collaboration. Improved limit on neutrinoless double-β decay of 76Ge from GERDA phase II. Phys. Rev. Lett. 2018, 120, 132503. [Google Scholar] [CrossRef]
- CUORE Collaboration. improved limit on neutrinoless double-β decay in 130Te with CUORE. Phys. Rev. Lett. 2020, 124, 122501. [Google Scholar] [CrossRef]
- KamLAND-Zen. Search for majorana neutrinos near the inverted mass hierarchy region with kamland-zen. Phys. Rev. Lett. 2016, 117, 082503, Addendum in Phys. Rev. Lett. 2016, 117, 109903. [Google Scholar] [CrossRef]
- Bernabeu, J.; De Rujula, A.; Jarlskog, C. Neutrinoless double electron capture as a tool to measure the νe mass. Nucl. Phys. B 1983, 223, 15. [Google Scholar]
- Eliseev, S.; Roux, C.; Blaum, K.; Block, M.; Droese, C.; Herfurth, F.; Kluge, H.J.; Krivoruchenko, M.I.; Novikov, Y.N.; Minaya Ramirez, E.; et al. Resonant enhancement of neutrinoless double-electron capture in Gd-152. Phys. Rev. Lett. 2011, 106, 052504. [Google Scholar] [CrossRef] [PubMed]
- Bernabeu, J.; Segarra, A. Stimulated transitions in resonant atom Majorana mixing. J. High Energy Phys. 2018, 2018, 17. [Google Scholar] [CrossRef]
- XENON Collaboration. Observation of two-neutrino double electron capture in 124Xe with XENON1T. Nature 2019, 568, 532. [Google Scholar] [CrossRef] [PubMed]
- Segarra, A.; Bernabeu, J. Absolute neutrino mass and the Dirac/Majorana distinction from the weak interaction of aggregate matter. Phys. Rev. D 2020, 101, 093004. [Google Scholar] [CrossRef]
- Englert, F.; Brout, R. Broken symmetry and the mass of gauge vector mesons. Phys. Rev. Lett. 1964, 13, 321. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken symmetries and the mass of gauge bosons. Phys. Rev. Lett. 1964, 13, 508. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30. [Google Scholar] [CrossRef]





| CPT Symmetry Test | |||
|---|---|---|---|
| Reference | CPT-conjugate | ||
| Transition | Decay products | Transition | Decay products |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernabeu, J. Symmetries and Their Breaking in the Fundamental Laws of Physics. Symmetry 2020, 12, 1316. https://doi.org/10.3390/sym12081316
Bernabeu J. Symmetries and Their Breaking in the Fundamental Laws of Physics. Symmetry. 2020; 12(8):1316. https://doi.org/10.3390/sym12081316
Chicago/Turabian StyleBernabeu, Jose. 2020. "Symmetries and Their Breaking in the Fundamental Laws of Physics" Symmetry 12, no. 8: 1316. https://doi.org/10.3390/sym12081316
APA StyleBernabeu, J. (2020). Symmetries and Their Breaking in the Fundamental Laws of Physics. Symmetry, 12(8), 1316. https://doi.org/10.3390/sym12081316




