Abstract
We investigate the dynamics of dust matter with bulk viscosity effects. We explored the analogy dynamical problem to Chaplygin gas. Due to this analogy we give exact solutions for the FRW cosmology with viscosity coefficient parameterized by the Belinskii–Khalatnikov power law dependence with respect to energy density. These exact solutions are given in the form of hypergeometrical functions. We proved simple theorem which illustrated as viscosity effects can solved the initial singularity problem present in standard cosmological model.
1. Introduction
The viscous fluid is an important subject of study in fluid mechanics [1], but starting from the 1960s this idea becomes attractive in cosmology, too. Misner was the first to study the role of viscosity during the cosmic evolution [2,3]. Effects of viscosity were also investigated by Weinberg [4] and Nightingale [5]. Murphy studied bulk viscosity effects in FRW cosmology and demonstrated that the constant bulk viscosity can solve the problem of an initial singularity in the FRW cosmology [6]. Effects of bulk viscosity can naturally remove the initial singularity. Different possibilities how the bulk viscosity effects give rise to avoiding the initial singularity were demonstrated by Heller et al. [7]. Belinskii et al. [8] studied dynamical effects of bulk viscosity, introduced a non-constant coefficient of bulk viscosity parameterized by energy density in a power-law relation, and developed dynamical system methods for study different evolutional paths in the phase space. This paper was very important from the theoretical point of view because effect of bulk viscosity was investigated beyond the constant coefficient of bulk viscosity and the language of dynamical systems opened the discussion how dynamical effects such as a singularity avoiding can depend on initial conditions. In cosmology we do not know the initial conditions for the universe, so we should study all evolutional paths admissible for all initial conditions.
In this paper, we return to these pioneering papers on bulk viscosity (see also [9]) in order to investigate the problem of bulk viscous cosmology in the modern context. In contemporary cosmology the effect of acceleration of the current Universe is investigated in terms of the standard cosmological model or CDM model. In this model role of substantial dark energy assumes the cosmological constant parameter . In the present epoch this parameter is negligible small as we know from astronomical data. Why is it not zero? it is the reflection of the cosmological constant parameter. We can describe exactly a current state of the Universe but we cannot explain why the value of the cosmological constant is so small. Another difficulty of the CDM model is the explanation why density parameters for dark energy and matter are comparable? This problem is known as the coincidence problem. For the state-of-the-art review of investigation of viscous cosmology see comprehensive reviews by Bamba et al. [10] and Brevik et al. [11]. The contemporary studies of viscous cosmological models are related to investigation of inflation [12], dark matter and dark energy problem, singularities etc. it can be also mentioned that the cosmological models with running Lambda maybe interesting [13].
In the present paper, we study dynamics of FRW Universe filled by dark matter, which is viscous. The idea of Chaplygin gas is attractive [14] because in the cosmological context it unifies effectively both dark matter (pressure) and dark energy (the parameter ) [15,16]. We show that in the same way Chaplygin gas unifies dark matter with viscosity. Obtained in such a way fluid with negative pressure we called viscous dark mater. We assume that the viscosity coefficient is parameterized by the Belinskii–Khalatnikov power law form but in a realistic case the parameterization can depend on the cosmological epoch [17].
The dynamical effects of presence of dust matter in the FRW universe is a main subject of the paper. We discuss theoretical aspects of an extended equation of state (including bulk viscosity effects). There is a strict relation between the equation of state and symmetries of dynamical equation because symmetries of the FRW equation enforce the form of the equation of state [18]. For example, the FRW equation with viscosity parameterized by and the equation of state admit scaling symmetries and vice versa scaling symmetries enforce the form of the equation of state as well as the parameterization of the coefficient of the equation of state.
2. Bulk Viscosity in FRW Cosmology
The energy-momentum tensor in the present of bulk viscosity was given by Landau and Lifshitz [1]
where , p and are the energy density, pressure and bulk viscous coefficient, respectively, and is the flow vector vector satisfying the relation .
The basic dynamical equations which govern the FRW dynamics are
In Equation (3) is the Hubble parameter, and are effective energy density and pressure
and
where , is the bulk viscosity coefficient in the correction term to the effective pressure.
is the form of the equation of state for dust matter.
Equation (3) is the conservation condition. Equations (2) and (3) admit the first integral in the form
where is curvature constant, is the scale factor from the Robertson-Walker metric space of constant curvature.
For simplicity let us consider flat model . Then
Now the effective pressure can be rewritten to the form
where A is an arbitrary positive constant and we denote
This form equation of state is known as the generalized Chaplygin gas [19]. In the special case of we obtain the equation of state for Chaplygin gas. This form of matter is important in the context of explanation for the acceleration of the current Universe in terms of substantial matter which unifies dark matter with dark energy in the form of cosmological constant (the quartessence idea).
Therefore matter with viscosity satisfies an analogous equation to the generalized Chaplygin gas.
Using conservation condition (3) and assuming that we obtain
where A, B are arbitrary constant which are useful to parameterize through parameter , and parameter . Energy density . We assume is positive, , .
It is possible to find the exact solution for viscous fluid in the form of dependence
We considered dust viscous matter and vanishing cosmological parameter .
The exact solution for the flat model filled by Chaplygin gas was found by Gorini et al. [20]. This case corresponds to .
In the same model, Chaplygin gas is a candidate for dark energy [15,16,21]. One can consider viscous fluid as natural explanation for acceleration of the current Universe.
Finally, the dimensionless density parameter for viscous fluid assumes the following form
where is the density parameter defined in the present epoch (). Please note that because (if velocity of sound becomes a complex number).
In a similar way, Chaplygin gas has an interpretation as a scalar field with the potential with energy density and pressure the viscous dust fluid can possesses interpretation as some a self-interacting scalar field with the potential [20]
Models with Chaplygin gas was tested by astronomical data (for example see [22]) and this study favors the values of the parameter m for which velocity of sound at present epoch does not exceeds velocity of light c. Note in the viscous dust fluid case . This condition is satisfied if . In addition, such an interval for the parameter (or ) is favored by astronomical data. In this interval effects of viscosity are negligible in an early universe and are important for late stages of the evolution of the universe. The latest attempt to put constraints on cosmological models with the viscosity effects was made by Odintsov et al. [23].
3. FRW Dynamics as Motion of a Particle in the Potential Well
The Friedmann first integral can be rewritten to the form analogous to the motion of a particle of unit mass in the potential [24], namely
where
and E is the total energy preserved during the motion. Therefore, in a configuration space the motion of the system takes place over levels of constant energy depending on the curvature constant (or density parameter for curvature).
Due to this analogy, one can think about the evolution of the Universe as the motion of particles which mimics the evolution of the universe because the state variable is the scale factor. Therefore, the model can be identified by a potential form as a function of the scale factor.
The corresponding dynamical system assumes the form of a dynamical system of the Newtonian type
There is a large class of models of modern cosmology formulated in terms of the particle-like description (see Table 1).

Table 1.
Cosmological models with a substantial form of dark energy and with modified gravity. The potential is obtained from ; .
The universe accelerates for some intervals of the scale factor (or redshift) if is is a decreasing function of the scale factor.
In Table 1 we complete potential forms of the theoretical models which offer the possibility of the explanation of acceleration of the Universe in the substantial dark energy or modified gravity.
If we try to generalize (18) by including dissipation effects then we should add an additional term to the right hand sides in the simplest case proportional to velocity ( for the model under consideration). The corresponding models with the bulk viscosity coefficient in the Belinskii–Khalalatnikov parameterization assumes the form of an autonomous two-dimensional dynamical system, which possesses different attractors.
The phase portrait the dynamical system representing the cosmological model with Chaplygin gas is shown in Figure 1 (drawn in XPPAUT [25]). The structure of the phase space of this model is equivalent to the structure of the phase space of the CDM model. Any cosmological model which competes with the standard cosmological model, i.e., the CDM model should have the same structure of the phase space. Moreover, this kind of phase space structure guarantees the structural stability of models. The notion of structural stability seems to be important in the context of a realistic description of the universe [26].
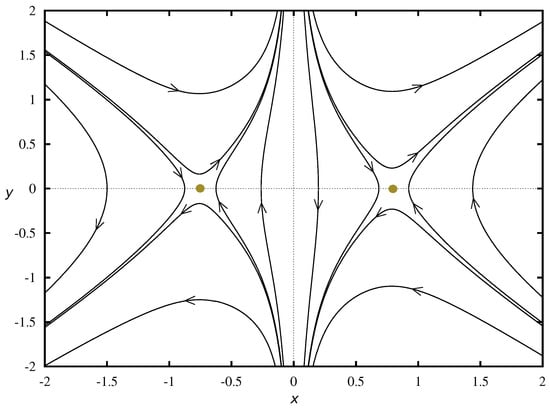
Figure 1.
The phase portrait of the cosmological model with Chaplygin gas () where , . We postulate additionally the presence of non-interacting pressureless baryonic matter. Please note that the phase portrait is structurally stable and is topologically equivalent to the CDM one.
4. Viscous Dark Energy Models—Dark Energy Models with Dissipation
In this section, we reached the class of cosmological models whose dynamics is represented by system (18) by adding bulk viscosity effect. For simplicity we assume that the model is flat and the viscosity parameter is constant.
Then motion of the system is over zero energy level and the Friedmann equation can be integrated by quadratures
One can prove the following theorem for simplest generalization of these systems in the case with bulk viscosity dissipation. Please note that now we admit the coefficient equation of state dependent on the scale factor and .
Theorem 1.
If is solution of (19) for the scale factor dependence in conservative cosmology, then
is a solution dynamical problem with constant viscosity coefficient.
The scale factor for the model under consideration satisfies the generalized equation of Newtonian type with friction which describes bulk viscosity effect
Please note that in general the bulk viscosity parameter can be parameterized by the scale factor in consequence of dependence of energy density on the scale factor.
Proof.
Let us differentiate both sides of (20) remember that . Then we obtain
Thus
Now after differentiating both sides of above formula over time we obtain the equation for a second derivative of the scale factor in the form
After introducing new time variable we can find such a function which form
guarantees dropping the dissipative term with and reducing the equation to the corresponding form in the conservative cosmology
□
This theorem has a simple application if we have the exact solution for case case of conservative cosmology then the solution with bulk viscosity can be obtained by taking . Equivalently, if we replace the cosmic time t by the new time parameter , will be a solution with bulk viscosity. The parameter can be interpreted as the Milne atomic time [27]. Finally, if we replace the cosmological time in solutions of conservative cosmology by the Milne atomic time , then we obtain exact solution with bulk viscosity.
Let us consider an anatomy of the mechanism for avoiding the initial singularity. If we start from some solution without bulk viscosity (conservative cosmology), then a generic property of its solutions is the presence of an initial singularity and generic asymptotic near this state. If the initial singularity is matter dominated, then the scale factor behave near the initial singularity following the Einstein-de Sitter solution , where is the moment when the metric is singular. Therefore, inverting this solution we have
and corresponding solution for viscous matter is
Therefore, as the scale factor goes to zero, time t is shifted to minus infinity. The scale factor behaves quasi-exponential and we obtain inflation phase for any constant coefficient of viscosity. This situation is illustrated in Figure 2 where we compare the Einstein-de Sitter model with dust matter () and the corresponding solution for viscous dust matter .
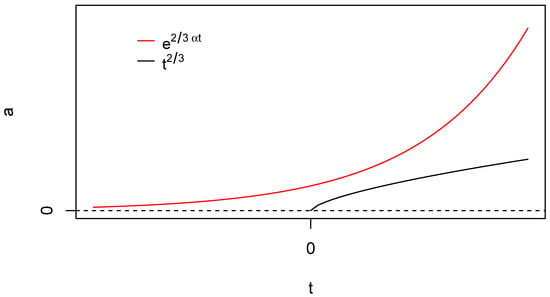
Figure 2.
The illustration of a generic mechanism of avoiding the initial singularity in the model with viscous matter and without the cosmological parameter . This mechanism can be interpreted in terms of the Milne atomic time.
5. Conclusions
In this theoretical paper, we explored an analogy of viscous FRW models with the FRW equation with Chaplygin gas. We have founded that both models are dual in this sense that there exist a 1-1 correspondence of both models. This opens the possibility to apply different analogies between them.
We introduced bulk viscosity to the dark energy models and then bulk viscosity effects are described by dynamical system of Newtonian type with friction (in principle anti-friction because energy is created in the comoving volume).
We proved the simple theorem which gives us possibility to obtain new solutions with constant bulk viscosity if we know solutions without bulk viscosity. This theorem shows explicitly how the initial singularity problem is solved by bulk viscosity effects, namely the initial singularity which is a generic property of conservative cosmology is removed to minus infinity. it is a generic effect of generation inflation phase in dark energy models. Therefore due to viscosity we realize the quintessence inflation idea.
In the paper, we showed how the initial singularity can be removed after including effect of viscous matter. It is shifted to minus infinity and the matter dominated singularity is replaced by a quasi de-Sitter solution analogous to the case found in the famous Starobinski’s paper [28]. This solution plays a very important role in the context of inflation mechanism. The same character has the exact solution obtained in our paper.
We demonstrate that for and the cosmological model with bulk viscosity is structurally stable and in the finite domain of the phase space its phase space structure is equivalent to the phase space structure of the CDM model.
The results presented in the paper have an application to the broad class of FRW models with dark energy.
Author Contributions
Conceptualization, M.S.; methodology, M.S.; formal analysis, M.S. and A.K.; investigation, M.S. and A.K.; writing—original draft preparation, M.S. and A.K.; writing—review and editing, M.S. and A.K.; visualization, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Misner, C.W. Transport processes in the primordial fireball. Nature 1967, 214, 40–41. [Google Scholar] [CrossRef]
- Misner, C.W. The isotropy of the universe. Astrophys. J. 1968, 151, 431–457. [Google Scholar] [CrossRef]
- Weinberg, C.W. Entropy generation and the survival of protogalaxies in an expanding universe. Astrophys. J. 1971, 168, 175–194. [Google Scholar] [CrossRef]
- Nightingale, J.D. Independent investigations concerning bulk viscosity in relativistic homogeneous isotropic cosmologies. Astrophys. J. 1973, 185, 105–114. [Google Scholar] [CrossRef]
- Murphy, G.L. Big-bang model without singularities. Phys. Rev. 1973, D8, 4231–4233. [Google Scholar] [CrossRef]
- Heller, M.; Klimek, Z.; Suszycki, L. Imperfect fluid Friedmannian cosmology. Astrophys. Space Sci. 1973, 20, 205–212. [Google Scholar] [CrossRef]
- Belinskii, V.A.; Nikomarov, E.S.; Khalatnikov, I.M. Investigation of the cosmological evolution of viscoelastic matter with causal thermodynamics. Sov. Phys. JETP 1979, 50, 213–221. [Google Scholar]
- Klimek, Z. Viscous Friedman cosmology. Acta Cosmol. 1981, 10, 7–19. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Brevik, I.; Grøn, Ø.; de Haro, J.; Odintsov, S.D.; Saridakis, E.N. Viscous cosmology for early- and late-time universe. Int. J. Mod. Phys. 2017, D26, 1730024. [Google Scholar] [CrossRef]
- Grøn, Ø. Viscous inflationary universe models. Astrophys. Space Sci. 1990, 173, 191–225. [Google Scholar] [CrossRef]
- Dymnikova, I.; Khlopov, M. Decay of cosmological constant in selfconsistent inflation. Eur. Phys. J. C 2001, 20, 139–146. [Google Scholar] [CrossRef]
- Chaplygin, S.A. On gas jets. Sci. Mem. Mosc. Univ. Math. Phys. 1904, 21, 1–121. [Google Scholar]
- Gorini, V.; Kamenshchik, A.; Moschella, U. Can the Chaplygin gas be a plausible model for dark energy? Phys. Rev. D 2003, 67, 063509. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion and dark energy matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Brevik, I.; Normann, B.D. Remarks on cosmological bulk viscosity in different epochs. arXiv 2020, arXiv:2006.09514. [Google Scholar]
- Szydłowski, M.; Heller, M. Equation of state and equation symmetries in cosmology. Acta Phys. Pol. B 1983, 14, 571–580. [Google Scholar]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Gorini, V.; Kamenshchik, A.; Moschella, U.; Pasquier, V. The Chaplygin gas as a model for dark energy. In On Recent Developments in Theoretical and Experimental General Relativity, Gravitation, and Relativistic Field Theories, Proceedings of the 10th Marcel Grossmann Meeting, MG10, Rio de Janeiro, Brazil, 20–26 July 2003; Novello, M., Perez Bergliaffa, S., Ruffini, R., Eds.; World Scientific: Singapore, 2004; pp. 840–859. [Google Scholar] [CrossRef]
- Szydłowski, M.; Czaja, W. Stability of FRW cosmology with generalized Chaplygin gas. Phys. Rev. D 2004, 69, 023506. [Google Scholar] [CrossRef]
- Biesiada, M.; Godłowski, W.; Szydłowski, M. Generalized Chaplygin gas models tested with SNIa. Astrophys. J. 2005, 622, 28. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Saez-Chillon Gomez, D.; Sharov, G.S. Testing the equation of state for viscous dark energy. Phys. Rev. D 2020, 101, 044010. [Google Scholar] [CrossRef]
- Szydłowski, M.; Czaja, W. Particle-like description in quintessential cosmology. Phys. Rev. D 2004, 69, 083518. [Google Scholar] [CrossRef]
- Ermentrout, B. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Perko, L. Differential Equations and Dynamical Systems, 3rd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Grünbaum, A. Philosophical Problems of Space and Time, 2nd ed.; D. Reichel: Dordrecht, The Netherlands, 1973. [Google Scholar]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).