Abstract
Kaonic atoms measure the antikaon-nucleus interaction at almost zero relative energy, allowing one to determine basic low-energy quantum chromodynamics (QCD) quantities, namely, the antikaon-nucleon (N) scattering lengths. The latter are important for extracting the sigma terms which are built on the symmetry breaking part of the Hamiltonian, thereby providing a measure of chiral and SU(3) symmetries breaking. After discussing the sigma terms and their relations to the kaonic atoms, we describe the most precise measurement in the literature of kaonic hydrogen, performed at LNF-INFN by the SIDDHARTA experiment. Kaonic deuterium is still to be measured, and two experiments are planned. The first, SIDDHARTA-2 at LNF-INFN was installed on DANE in spring 2019 and will collect data in 2020. The second, E57 at J-PARC, will become operative in 2021.
1. Introduction
Kaonic atoms experiments contribute to a deeper understanding of the quantum chromodynamics (QCD), the strong interaction theory, in the non-perturbative regime, and can also be used to investigate primary problems concerning global symmetries: the origin of symmetry breaking, its nature, the breaking mechanisms, and to what extent symmetries are broken. Kaonic atoms allow to measure the antikaon-nucleus interaction “at threshold”, from which fundamental low-energy QCD parameters, such as the antikaon-nucleon (N) scattering lengths are extracted. The latter are related to the sigma terms, which are built on the symmetry breaking part of the Hamiltonian, thereby providing a measure of chiral and SU(3) symmetries breaking. The (N) scattering lengths can be determined by measuring the shift and broadening of the ground state of kaonic hydrogen and of kaonic deuterium due to the strong interaction. In the first part of the article we discuss the low-energy strong interaction dynamics, introducing the sigma terms and their relations to the kaonic atoms. Then we introduce the most precise measurement in the literature of the kaonic hydrogen, done at LNF-INFN by the SIDDHARTA experiment. Kaonic deuterium is still to be measured and two experiments are planned. The first, SIDDHARTA-2 at LNF-INFN was installed on DANE in spring 2019 and will collect data in 2020. The second, E57 at J-PARC, will become operative in 2021. Both of these experiments, as described in the paper, have in common stringent experimental requirements which need to be satisfied in order to be ready for the difficult kaonic deuterium measurement.
2. Low-Energy Strong Interaction Dynamics
2.1. Global Symmetries
Quantum chromodynamics (QCD) is the basic theory of the strong interaction. QCD possess the feature of asymptotic freedom, meaning that as the distance scale gets smaller, the QCD constant becomes weaker and the interaction’s strength diminishes. In this high-energy regime, perturbative QCD was successfully applied. However, in the low energy domain, the (running) QCD coupling constant becomes stronger so that QCD exhibits the color confinement. In this regime, perturbative QCD ceases to be a useful tool for understanding the strong interaction dynamics. At energies smaller than ∼1 GeV, one must simplify the theory. This is done by various models which are an admixture of QCD and phenomenological treatments of confinement. At very low energies, a big simplification occurs.
Below the region of resonances (), the hadronic spectrum contains the pseudoscalar particles (, K, ) only, whose interactions can be understood from global symmetry considerations. Chiral symmetry would hold if all quark masses were to be zero (chiral limit). When quark masses are finite and equal, the SU(3)’s exact unitary symmetry scheme holds, meaning multiplets of particles (as the pseudoscalar meson and baryon octets) degenerated in mass. In our world, the quarks are massive, and then, masses are different: . Thus, in the real world the chiral symmetry is broken and the SU(3) symmetry is broken too. The chiral symmetry violation raises the masses of the pseudoscalar mesons to finite values, and the SU(3) violation splits the SU(3) multiplets.
We do not know on a fundamental level what the origin of the symmetry breaking is and what the breaking mechanisms are. One of the goals of the kaonic atoms experiments is to perform measurements which can be also useful for investigating these fundamental questions [1].
2.2. Meson-Nucleon Sigma Terms
There are two information sources about the SU(3) (and chiral) symmetry breaking. The first one is that the mass of a pseudoscalar meson comes entirely from the symmetry breaking interaction. This, however, does not tell us much about the nature of this mechanism, except getting the magnitude of the free parameters in the symmetry violating part of the strong interaction Hamiltonian.
Far more sensitive to the symmetries breaking mechanisms are the corrections to the low-energy theorems [2]. These theorems connect the symmetry breaking part of the total Hamiltonian to the massless particles scattering amplitude: they would be exact at the limit at which pseudoscalar meson masses vanish and axial vector currents are conserved. An important way to study the chiral symmetry breaking mechanisms is to study the low-energy theorems of meson-nucleon scattering. They represent the “corrections” for the real world to the exact relations which are valid only for zero mass particles.
In practice, this means to calculate the meson-nucleon sigma terms. The meson-nucleon sigma terms are quantities of fundamental importance to non-perturbative QCD. Their main point of interest lies in the fact that they provide a measure of the chiral symmetry breaking and vanish in the massless quark chiral limit of QCD. In order to define them, consider the scattering process of the meson M against the nucleon N:
where q, p and are the four-momenta of the particles and a, b denote the SU(3) indices of the two mesons. The meson-nucleon sigma term represents the expectation value in the proton state of the equal-time (sigma) double commutator for the symmetry breaking part of the strong interaction Hamiltonian, , with the axial-vector charges of the two mesons :
The next step is to relate the sigma term with the experimental meson-nucleon scattering amplitudes. This relation represents the low-energy theorem.
The axial-vector charge of the meson a is associated with the axial vector current , whose divergence is . The partially conserved axial vector current hypothesis (PCAC) identifies this divergence with the pseudoscalar meson field. In such a way, the sigma commutator in Equation (2) is replaced by the product of the two meson fields, allowing one to connect the sigma term to the meson-nucleon scattering amplitude , where the kinematic invariants describing the process are:
Finally, one obtains the low-energy theorem in the soft-meson limit together with and :
where the are the mesons decay constants.
The calculation of the sigma term from the scattering data requires an elaborate procedure. The problem is that the sigma term is not an observable. One has then to introduce an “experimental” sigma term , which can be related to the experimental meson-nucleon amplitudes. This can be done in a favored point of the (t,ν) plane, the Cheng–Dashen (C–D) point (t = 2, being the meson mass, and ) [3,4,5].
The Cheng–Dashen point is on the mass-shell but lies outside the physical meson-nucleon scattering region (). Therefore, in order to obtain from the experimental amplitudes, one has to extrapolate them to the C–D point with a procedure commonly based on dispersion relations. The last step consists of calculating at the zero momentum, for which all the kinematic variables vanish and the sigma term is defined by Equation (4) [6]. The procedure is schematically shown in Figure 1 for the kaon case.
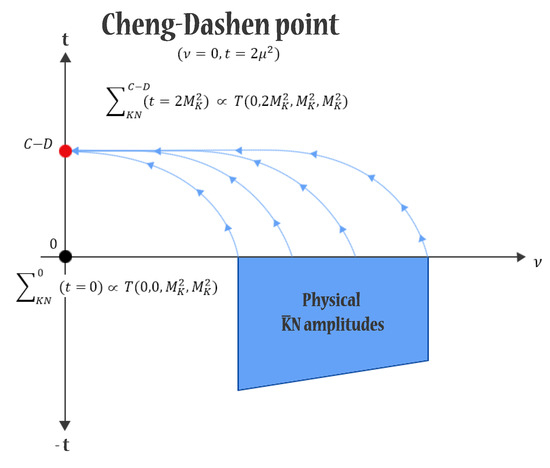
Figure 1.
Procedure for the determination of the sigma term from experimental scattering amplitudes.
The pion-nucleon sigma term has been obtained by following this approach. The range of turned out to be [7]:
This was deduced from the ( N) scattering amplitude, computed at the Cheng–Dashen point [8]. Another determination for has been obtained by the George Washington University/TRIUMF group. The range of values turned out [7]:
which is sizeably larger than Equation (5).
The situation in the kaon case is much worse than in the pion case. On the experimental side, this is due to the poor bulk of N scattering data. On the theoretical side [5], complications arise from the followings facts:
- There are channels opened below the threshold.
- There is a resonance, , just below threshold of .
- Uncertainties in the extrapolation procedure are present: the difference is larger than in the case, introducing additional uncertainty in the quantity of interest . In quantitative terms: let us refer to the case, where the “experimental” value is based on solid experimental data [9]. Here, at the C–D point is . The estimated difference [10] gives [11]; i.e., an uncertainty of about 10%.
In the case of , the uncertainty on is evaluated to be around 60%: see the estimation given in [12,13,14,15]:
It is interesting to try to evaluate how much the uncertainty of the values of the sigma terms depends on the precision of the measurement of the N scattering lengths. Kaonic atoms’ data fix the amplitudes near the threshold, giving a strong constraint to the determination of the amplitudes at zero energy, required by the definition of the scattering lengths. A measurement of the scattering length at a precision of around 10% might allow one to obtain the sigma terms with a 30% uncertainty [12,13,14,15].
Another approach, based on chiral mixing with u and d flavors only, does not introduce the Cheng–Dashen point, to be reached from the scattering amplitudes through dispersion relations. The approach has been followed by [16,17,18] who have calculated pion- and kaon-nucleon sigma terms, with large uncertainties.
An alternative method to determining the kaon-nucleon sigma terms consists of using lattice QCD simulations. This has been followed recently by different groups [19,20]. However, model assumptions cannot be fully assessed [20].
The first measurement of kaonic deuterium planned at DANE in 2020 and at J-PARC in 2021 should hopefully re-vitalize this theoretical sector.
3. Antikaon-Nucleon Scattering Lengths
In an exotic atom, an electron is substituted by a negatively charged particle, such as a kaon, which is bound by the electromagnetic interaction with the nucleus.
The hadronic atoms, in which the electron is replaced by a hadron, play a special role, because they permit one to investigate the strong interaction; i.e., the quantum chromo dynamics. In the case of a kaonic atom, the kaon interacts with the nucleus with a few keV of relative energy, to be compared to the tens of MeV of low-energy scattering experiments. This enables the unique opportunity of investigating the antikaon-nucleon/nucleus interaction almost “at threshold”, which grants access to the antikaon-nucleon scattering lengths’, basic low-energy QCD parameters.
In this context, the statement by R.H. Dalitz, made nearly 40 years ago, still holds [21]: “The most important experiment to be carried out in low energy K-meson physics today is the definitive determination of the energy level shifts in the Kp and Kd atoms, because of their direct connection with the physics of N interaction and their complete independence from all other kinds of measurements which bear on this interaction”.
3.1. Formation of a Kaonic Atom
A kaonic atom forms when a kaon stops inside a target, replacing an electron. The replacement occurs in a highly excited state [22]:
is the reduced mass, is the electron mass, and is the outermost electron shell’s principal quantum number. = 1 for hydrogen and deuterium. For the kaonic hydrogen, n is ≈ 25.
After formation, the kaonic atom undergoes a de-excitation processes until it reaches the ground state, at which it interacts with the nucleus also via the strong interaction. During the transitions to the ground state, X-ray radiation is emitted (see Figure 2).
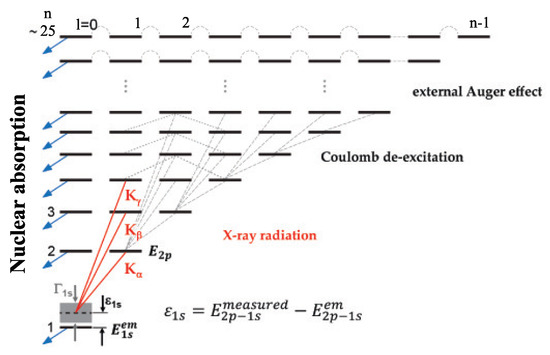
Figure 2.
Kaonic hydrogen cascade processes, down to the ground state 1s. The ground state is shifted and broadened by the strong interaction [22].
The effect of the strong interaction on the top of the electromagnetic one is the shift of the ground state with respect to the electromagnetic (e.m.) calculated value and its broadening.
The strong interaction shift is defined as:
where and are, respectively, the transition energies measured and calculated. The e.m. energy transition calculated from scalar QED, including the finite size effect and vacuum polarization, for kaonic hydrogen is [23]: 6480 ± 1 eV.
3.2. Antikaon-Nucleon Scattering Lengths
Neglecting the isospin-breaking corrections, meaning assuming , the connection between and and the complex scattering length is given by the relation (Deser–Trueman formula) [24,25]:
is the fine structure constant and is the reduced system mass.
Meissner, Raha, and Rustsky [26,27] evaluated the effects of isospin-breaking in terms of and , obtaining an improved Deser-type formula for kaonic hydrogen and kaonic deuterium
is connected to (I = 0) and (I = 1), the isospin dependent scattering lengths, through the average:
In order to extract and , one has to measure the kaonic deuterium also:
where
The first term in Equation (15) is the lowest-order impulse approximation ( scattering on each (free) nucleon of deuterium). The term C includes the contributions connected to the three-body interaction.
4. The SIDDHARTA Kaonic Hydrogen Measurement
The SIDDHARTA (Silicon Drift Detector for Hadronic Atom Research by Timing Applications) experiment at LNF-INFN [28] on DANE aimed to extract the kaonic hydrogen level shift and width with a precision higher than in the previous DEAR experiment [29], by using large area silicon drift detectors (SDDs), instead of the charge-coupled devices (CCDs) used in DEAR. The SIDDHARTA experiment could benefit from the clean, low-momentum (127 MeV/c), almost monoenergetic p/p = 0.1 kaons’ beam from the -mesons’ decay produced in collisions at the DANE collider.
The SIDDHARTA setup consisted of a kaon detector, an X-ray detection system and of a cryogenic target and is described in detail in [28].
An exploratory measurement of kaonic deuterium was performed during the 2009 run. In the kaonic hydrogen analysis, this measurement was essential to quantifying the X-rays’ fluorescence background coming from the elements of the setup materials excited by the captured kaons. No peak structures of d X-rays were visible.
A simultaneous global fit of the hydrogen and deuterium spectra was performed, and details are given in [28]. Figure 3a shows the measured X-ray kaonic hydrogen spectrum after the subtraction of fitted background. X-rays of kaonic hydrogen were observed. Figure 3b,c shows details of the fit results.
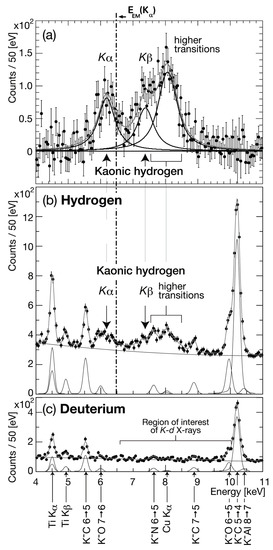
Figure 3.
The global simultaneous fit for the X-ray energy spectra for hydrogen and deuterium data (see text for details) [28].
The 1s-level shift and width turned out [28]:
This is the most precise measurement in the literature of kaonic hydrogen.
5. Kaonic Deuterium Experiments
The kaonic deuterium measurement is still missing in the study of antikaon-nucleon interaction.
As stated in [26]: “The necessity to perform measurements of the kaonic deuterium ground state observables is justified by the fact that, unlike the case of pionic atoms, the measurement of only the kaonic hydrogen spectrum does not allow, even in principle, to extract independently both s-wave -nucleon scattering lengths and .”
In the coming years, two dedicated measurements will be performed at LNF-INFN and J-PARC: SIDDHARTA-2 and E57, respectively. SIDDHARTA-2 was installed on DANE in spring 2019 and will collect data in 2020 and 2021. The E57 experiment will measure kaonic deuterium starting from 2021.
The difficulty of the measurement of kaonic deuterium is related to an X-ray yield one order of magnitude smaller than that of kaonic hydrogen and a larger width. The measurement requires a large area detector such as SDD, with good energy and timing resolutions. Moreover, dedicated veto systems are necessary to increase the S/B ratio.
5.1. The SIDDHARTA-2 Experiment at LNF-INFN
New monolithic Silicon Drift Detector arrays have been developed by the SIDDHARTA-2 Collaboration.
Two special veto systems consisting of an outer barrel of scintillators counters, called Veto-1, and an inner ring of plastic scintillation tiles (SciTiles), called Veto-2, were built and implemented.
A detailed Monte Carlo simulation was implemented within the GEANT4.
Figure 4 shows the expected spectrum. and can be determined with precisions of 30 and 80 eV, respectively; thus, together with the kaonic hydrogen values, allowing to extract the scattering lengths N with a precision of about 10%.
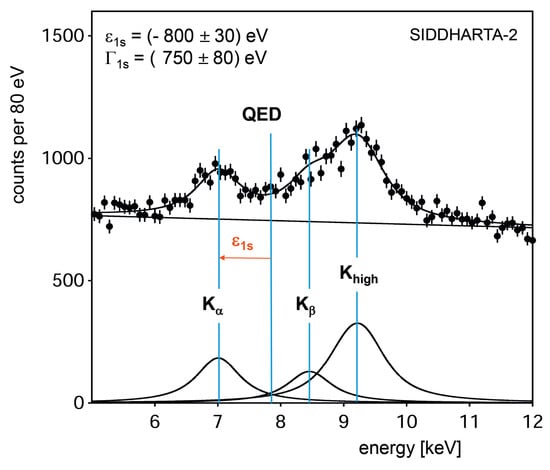
Figure 4.
Simulation of the SIDDHARTA-2 kaonic deuterium spectrum, assuming = −800 eV and = 750 eV, as well as a K yield of 10. Simulation for an integrated luminosity of 800 pb.
5.2. The E57 Experiment at J-PARC
In the E57 experiment, the cylindrical detector system (CDS), coming from the E15 experiment [30], will be used as the veto system. The experiment will use the K1.8BR multi-purpose spectrometer and the newly developed SIDDHARTA-2 SDDs for X-ray detection. Detailed Monte Carlo simulations studies (GEANT4) were performed.
Figure 5 shows the expected spectrum. and can be determined with precisions of 40 and 110 eV, respectively.
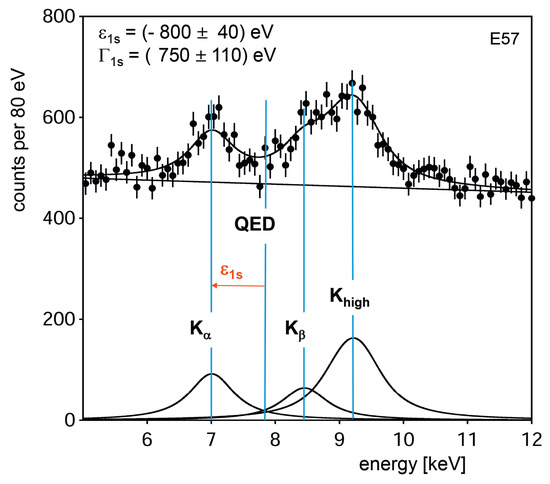
Figure 5.
E57 simulated kaonic deuterium spectrum, assuming = −800 eV and = 750 eV and a K yield of 10. Simulation for four weeks of beam time and 40 kW proton beam power.
6. Conclusions
A very useful instrument to study the chiral and SU(3) symmetries breaking mechanisms is the measurement of X-ray transitions in kaonic hydrogen and kaonic deuterium. These measurements allow to extract the antikaon-nucleon scattering lengths, which are relevant for the calculation of the kaon-nucleon sigma terms, related to the chiral and SU(3) symmetries breaking part of the Hamiltonian.
The most precise kaonic hydrogen measurement has been made by SIDDHARTA on DANE. The kaonic deuterium measurement has not yet been performed.
This situation is going to be changed in the coming years, when SIDDHARTA-2 on DANE and E57 at J-PARC, will finally measure kaonic deuterium transitions to the fundamental level. This will also fuel theoretical activities aimed to extract the kaon-nucleon sigma terms and unveil the mechanism at work in the chiral and SU(3) symmetry breaking, on which the mass of (most part) of our visible Universe depends.
Author Contributions
Conceptualization, C.C., C.G., J.M., M.I. (Mihail Iliescu), and M.I. (Masaiko Iwasaki); software, M.B., M.C. (Michael Cargnelli), R.D.G., M.I. (Mihail Iliescu), M.M., S.O., K.P., and D.S.; methodology, A.A., A.B., M.B., M.C. (Marco Carminati); L.D.P., G.B., M.B., A.C., D.B., C.F., M.I., P.K., P.L.S., M.M., P.M., S.N., S.O., A.S., F.S., M.S., M.T., G.U., O.V.D., and J.Z.; writing—original draft preparation, C.C. and C.G.; writing—review and editing, C.C. and D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Austrian Science Fund (FWF) P24756-N20 and P33037-N; the Austrian Federal Ministry of Science and Research (BMBWK), 650962/0001 VI/2/2009; the Croatian Science Foundation under project IP-2018-01-8570; the Minstero degli Affari Esteri e della Cooperazione Internazionale, Direzione Generale per la Promozione del Sistema Paese (MAECI), FWF project P33037-N “Measurement of Kaonic Deuterium X-ray Transitions,” EU STRONG-2020 project (grant agreement 824093); and the Polish Ministry of Science and Higher Education through grant number 7150/E-338/M/2018.
Acknowledgments
We thank C. Capoccia and G. Corradi from LNF-INFN, and H. Schneider, L. Stohwasser, and D. Pristauz-Telsnigg from the Stefan Meyer Institute for their fundamental contribution in designing and building the SIDDHARTA setup. We also thank the DANE staff for the excellent working conditions and constant support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guaraldo, C. The DEAR physics programme. Phys. Detect. DAΦNE 1999, XVI, 643–658. [Google Scholar]
- Reya, C. Chiral symmetry breaking and meson-nucleon sigma commutators: A Review. Rev. Mod. Phys. 1974, 46, 545–580. [Google Scholar] [CrossRef]
- Cheng, T.P.; Dashen, R.T. Experimental test of time-reversal invariance in the reaction np → γd. Phys. Rev. Lett. 1971, 26, 1659–1662. [Google Scholar]
- Altarelli, G.; Cabibbo, N.; Maiani, L. The sigma term and low-energy π-n scattering. Nucl. Phys. B 1971, 34, 621–631. [Google Scholar] [CrossRef]
- Gasser, J.; Sainio, M.E. Sigma term physics. Phys. Detect. DADAΦNE 1999, XVI, 659. [Google Scholar]
- Pavan, M.M.; Arndt, R.A.; Strakovsky, I.I.; Workman, R.I. New Result for the Pion-Nucleon Sigma Term from an Updated VPI/GW Pion-Nucleon Partial-Wave and Dispersion Relation Analysis. PiN Newslett. 1999, 15, 118–192. [Google Scholar]
- Bottino, A.; Donato, F.; Fornengo, N.; Scopel, S. Size of the neutralino nucleon cross-section in the light of a new determination of the pion nucleon sigma term. Astropart. Phys. 2002, 18, 205–211. [Google Scholar] [CrossRef][Green Version]
- Koch, R. A New Determination of the πN Sigma Term Using Hyperbolic Dispersion Relations in the (ν2, t) plane. Z. Phys. C 1982, 15, 161–168. [Google Scholar] [CrossRef]
- Jaffe, R.L. The Sigma Term Revisited. Phys. Rev. D 1980, 21, 3215–3224. [Google Scholar] [CrossRef]
- Pagels, H.J.; Pardee, W.J. Nonanalytic behavior of the sigma term in π-n scattering. Phys. Rev. D 1971, 4, 3335–3337. [Google Scholar] [CrossRef]
- Jaffe, R.L.; Korpa, C.L. The Pattern of Chiral Symmetry Breaking and the Strange Quark Content of the Proton. Comments Nucl. Part. Phys. 1987, 17, 163–175. [Google Scholar]
- Di Claudio, B.; Violini, G.; Rodríguez-Vergas, A.M. Uncertainties on the Determination of KNΣ Term Due to K−N Unphysical and Low-energy Region. Lett. Nuovo Cimento 1979, 26, 555–561. [Google Scholar] [CrossRef]
- Di Claudio, B.; Rodríguez-Vergas, A.M.; Violini, G. The Adler-Weisberger sum rule and the σ-commutator for the kaon-proton system. Z. Phys. C 1979, 3, 75–82. [Google Scholar] [CrossRef]
- Rodríguez-Vergas, A.M.; Violini, G. The Adler-Weisberger sum rule and the σ-commutator for the kaon-neutron system. Z. Phys. C 1980, 4, 135–139. [Google Scholar] [CrossRef]
- Martin, A.D.; Violini, G. The Zero Energy Kp Scattering Amplitude and the Evaluation of the Kaon-Nucleon Σ Terms. Lett. Nuovo Cimento 1981, 30, 105–110. [Google Scholar] [CrossRef]
- Chen, H.-X.; Dimitrasinovic, V.; Hosaka, A. Baryon fields with UL(3) × UR(3) chiral symmetry: Axial currents of nucleons and hyperons. Phys. Rev. D 2010, 81. [Google Scholar] [CrossRef]
- Chen, H.-X.; Dimitrasinovic, V.; Hosaka, A. Baryon fields with UL(3) × UR(3) chiral symmetry. IV. Interactions with chiral (8,1) ⨁ (1,8) vector and axial-vector mesons and anomalous magnetic moments. Phys. Rev. C 2012, 85, 055205(1)–055205(10). [Google Scholar] [CrossRef]
- Chen, H.-X.; Dimitrasinovic, V.; Hosaka, A.; Nagata, K.; Zhu, S.-L. Chiral properties of baryon fields with flavor SU(3) symmetry. Phys. Rev. D 2008, 78. [Google Scholar] [CrossRef]
- Alexandrou, C.; Drach, V.; Jansen, K.; Kallidonis, C.; Koutsou, G. Baryon spectrum with Nf = 2 + 1 + 1 twisted mass fermions. Phys. Rev. D 2014, 90, 074501(1)–074501(29). [Google Scholar] [CrossRef]
- Torrero, C. Computing the nucleon sigma terms at the physical point. In Proceedings of the 32nd International Symposium on Lattice Field Theory, New York, NY, USA, 23–28 June 2014. [Google Scholar]
- Dalitz, R.H.; McGinley, J.; Belyea, C.; Anthony, S. Theory of Low-energy Kaon-Nucleon Scattering. In Proceedings of the International Conference on Hypernuclear and Kaon Physics, Heidelberg, Germany, 20–24 June 1982; pp. 201–214. [Google Scholar]
- Zmeskal, J. From kaonic atoms to kaonic nuclei: A search for antikaon-mediated bound nuclear systems. Part. Nucl. Phys. 2008, 61, 512–550. [Google Scholar] [CrossRef]
- Iwasaki, M.; Bartlett, K.; Beer, G.A.; Gill, D.R.; Hayano, R.S.; Ito, T.M.; Lee, L.; Mason, G.; Nakamura, S.N.; Olin, A.; et al. Discovery of the repulsive energy shift of the kaonic hydrogen 1s state. Nucl. Phys. A 1998, 639, 501c–510c. [Google Scholar] [CrossRef]
- Deser, S.; Goldberger, M.L.; Baumann, K.; Thirring, W. Energy Level Displacements in Pi-Mesonic Atoms. Phys. Rev. 1954, 96, 774–776. [Google Scholar] [CrossRef]
- Trueman, T.L. Energy level shifts in atomic states of strongly-interacting particles. Nucl. Phys. 1961, 26, 57–67. [Google Scholar] [CrossRef]
- Meißner, U.-G.; Raha, U.; Rusetsky, A. Kaon-nucleon scattering lengths from kaonic deuterium experiments. Eur. Phys. J. C 2006, 47, 473–480. [Google Scholar] [CrossRef][Green Version]
- Meißner, U.-G.; Raha, U.; Rusetsky, A. Spectrum and decays of kaonic hydrogen. Eur. Phys. J. C 2004, 35, 349–357. [Google Scholar] [CrossRef]
- Bazzi, M.; Beer, G.; Bombelli, L.; Bragadireanu, A.; Cargnelli, M.; Corradi, G.; Curceanu (Petrascu), C.; d’Uffizi, A.; Fiorini, C.; Frizzi, T.; et al. A new measurement of kaonic hydrogen X-rays. Phys. Lett. B 2011, 704, 113–117. [Google Scholar] [CrossRef]
- Beer, G.; Bragadireanu, A.M.; Cargnelli, M.; Curceanu-Petrascu, C.; Egger, J.P.; Fuhrmann, H.; Guaraldo, C.; Iliescu, M.; Ishiwatari, T.; Itahashi, K.; et al. Measurement of the kaonic hydrogen X-ray spectrum. Phys. Rev. Lett. 2005, 94, 212302. [Google Scholar] [CrossRef]
- Hashimoto, T.; Ajimura, S.; Beer, G.; Bhang, H.; Bragadireanu, M.; Busso, L.; Cargnelli, M.; Choi, S.; Curceanu, C.; Enomoto, S.; et al. Search for the deeply bound K−pp state from the semi-inclusive forward-neutron spectrum in the in-flight K− reaction on helium-3. Prog. Theor. Exp. Phys. 2015, 2015. [Google Scholar] [CrossRef][Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).