Formation of the Dynamic Energy Cascades in Quartic and Quintic Generalized KdV Equations
Abstract
1. Introduction
- Big whirls have little whirls;
- Which feed on their velocity;
- And little whirls have lesser whirls;
- And so on to viscosity.
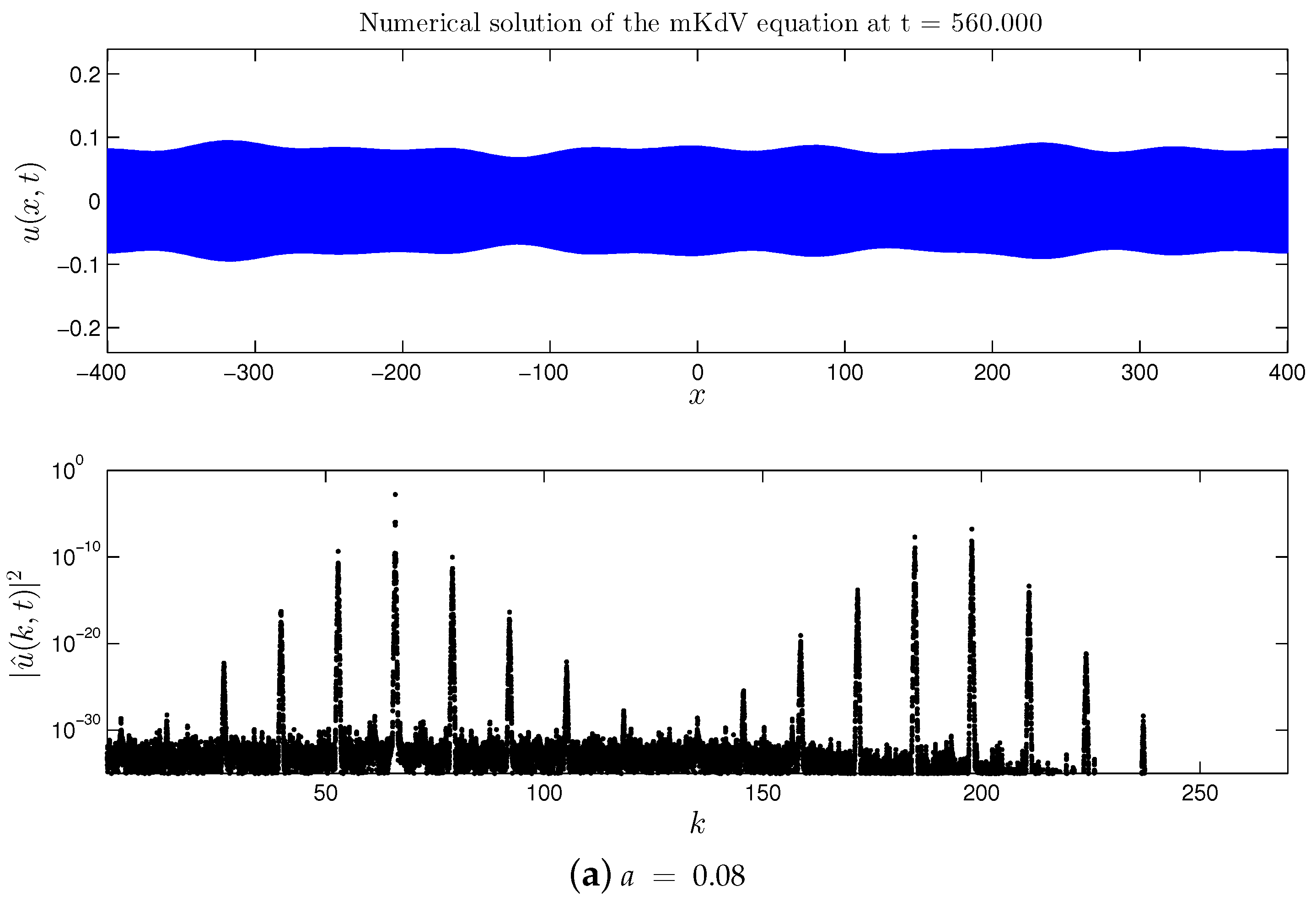
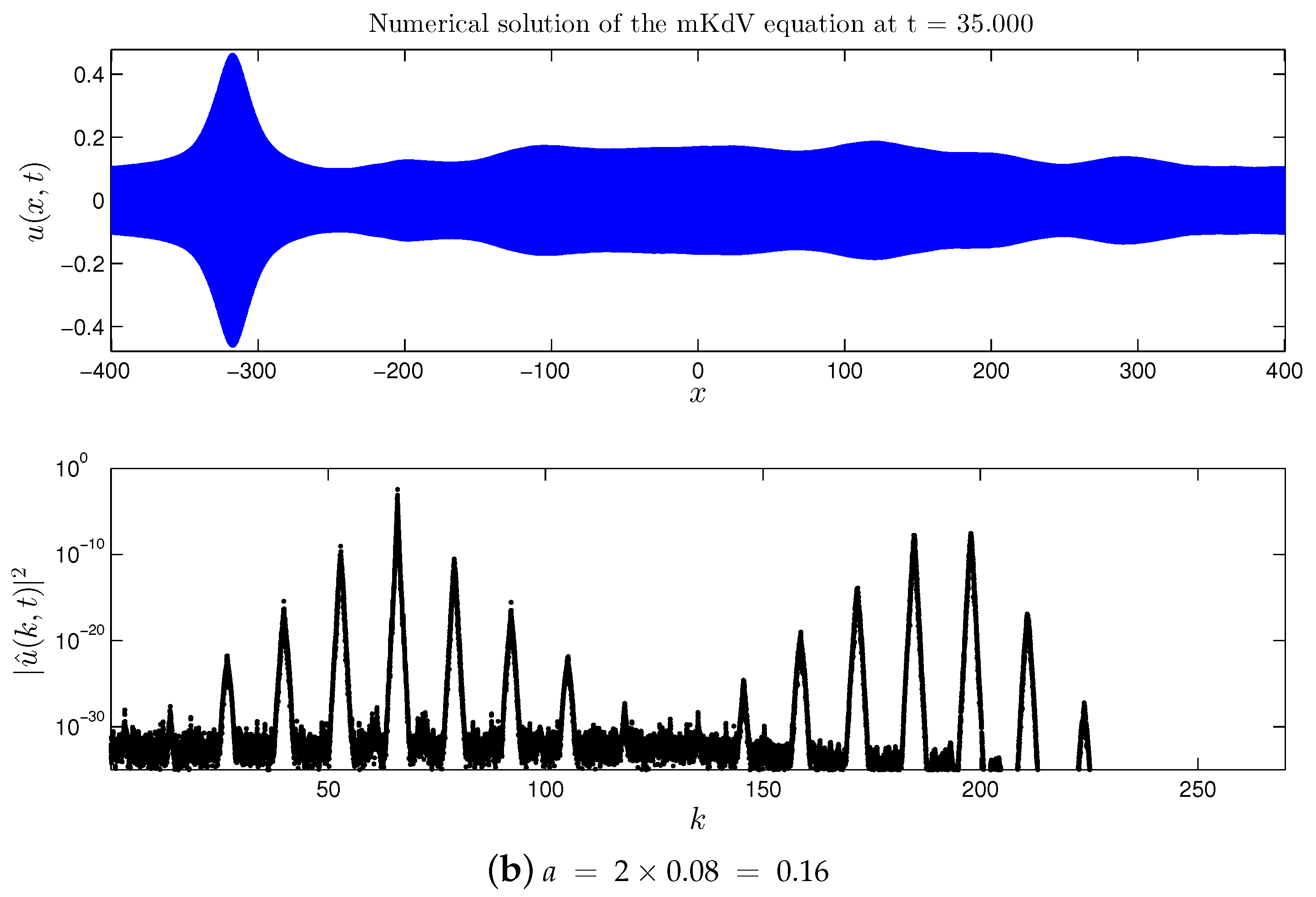
2. mKdV Equation With Broad Spectrum Initial Perturbation
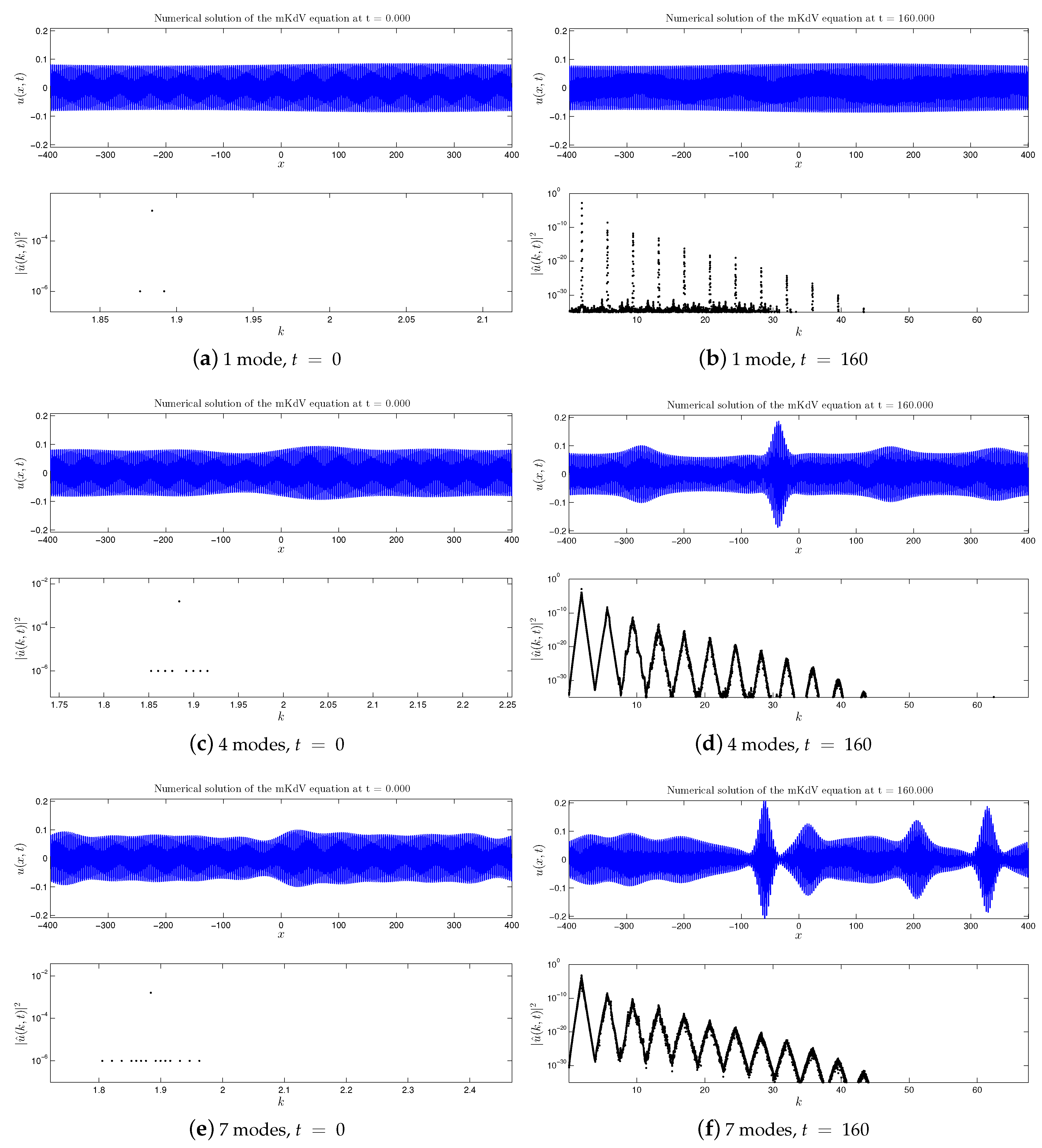
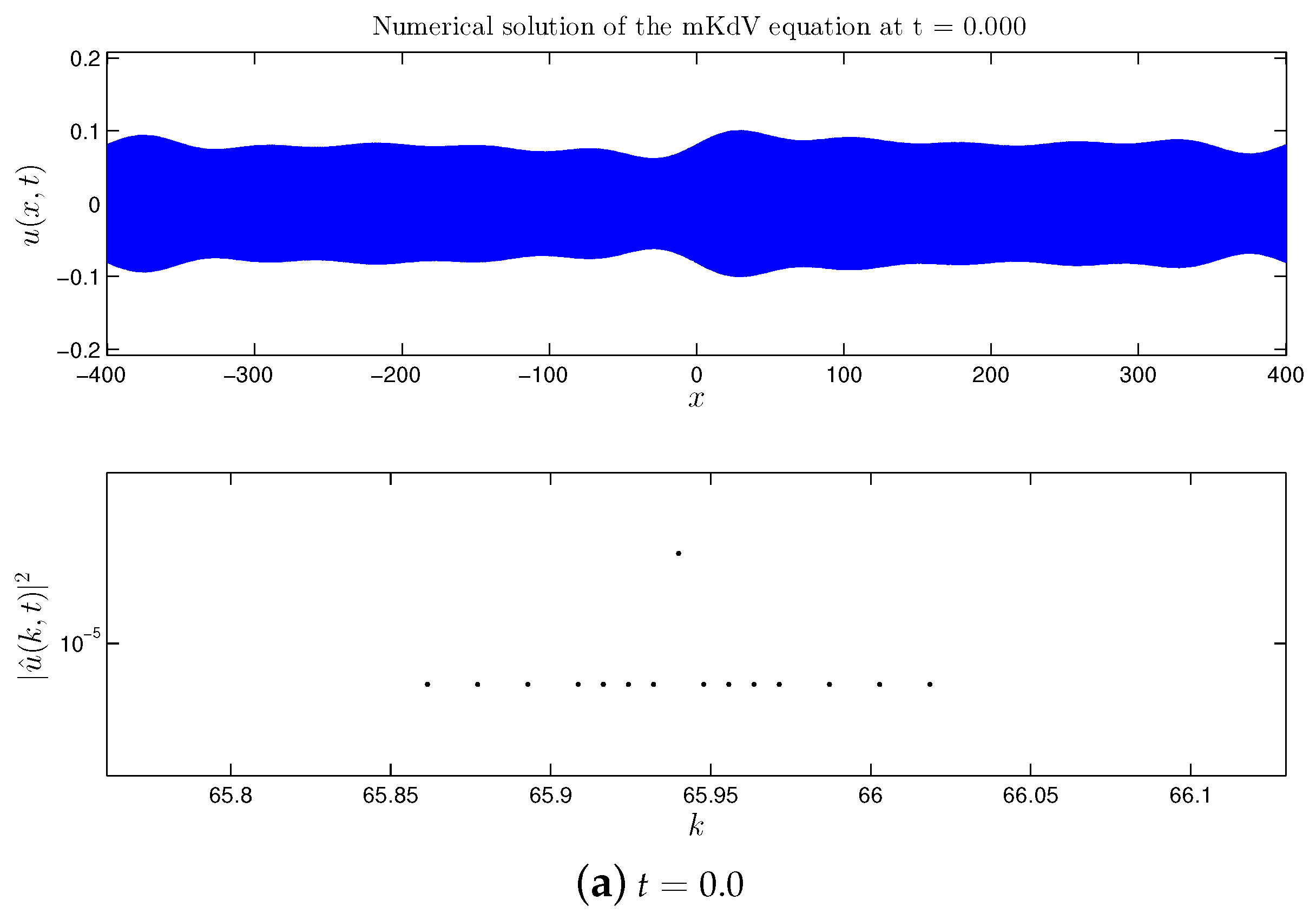
2.1. Direct cascade
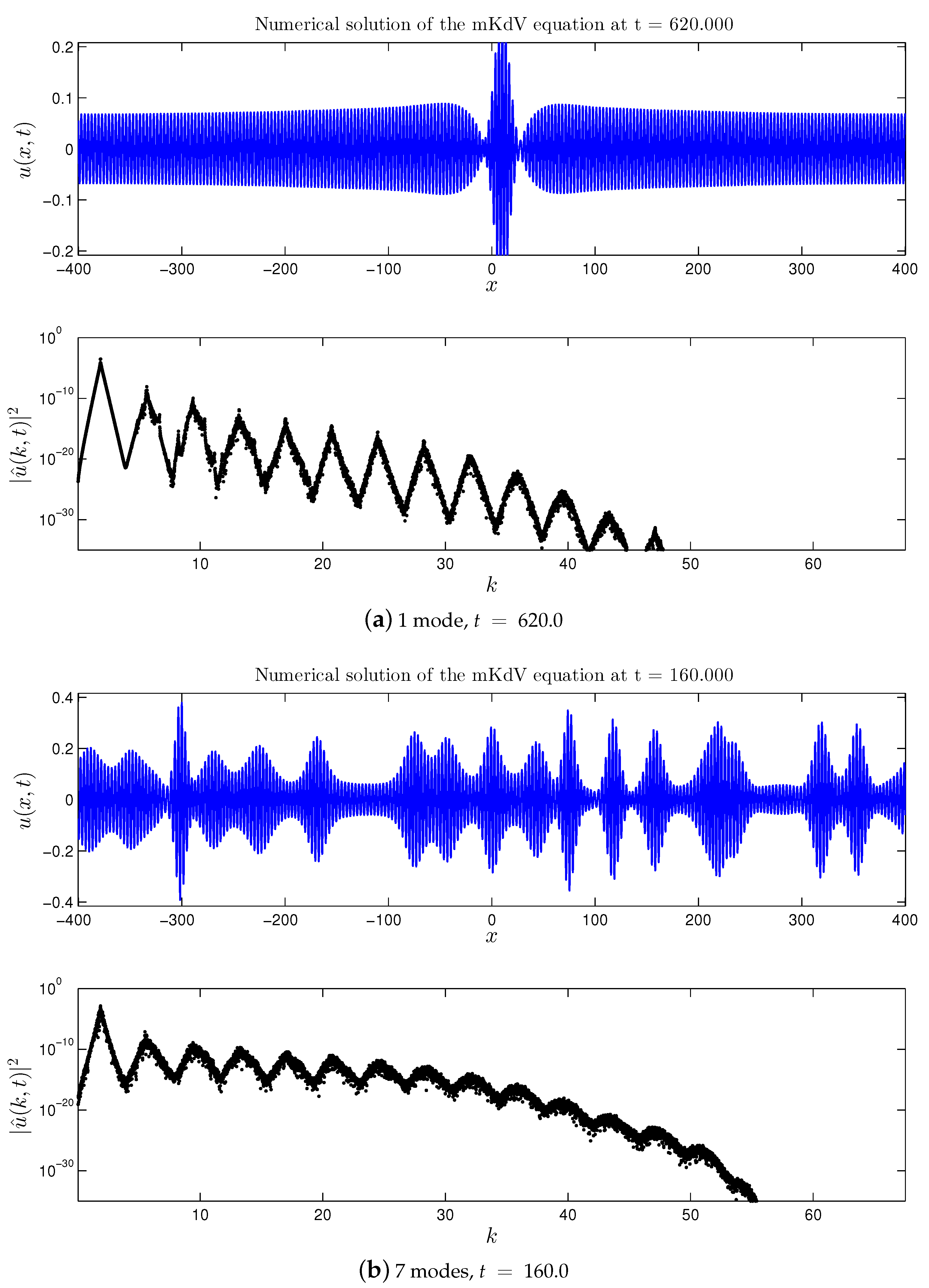
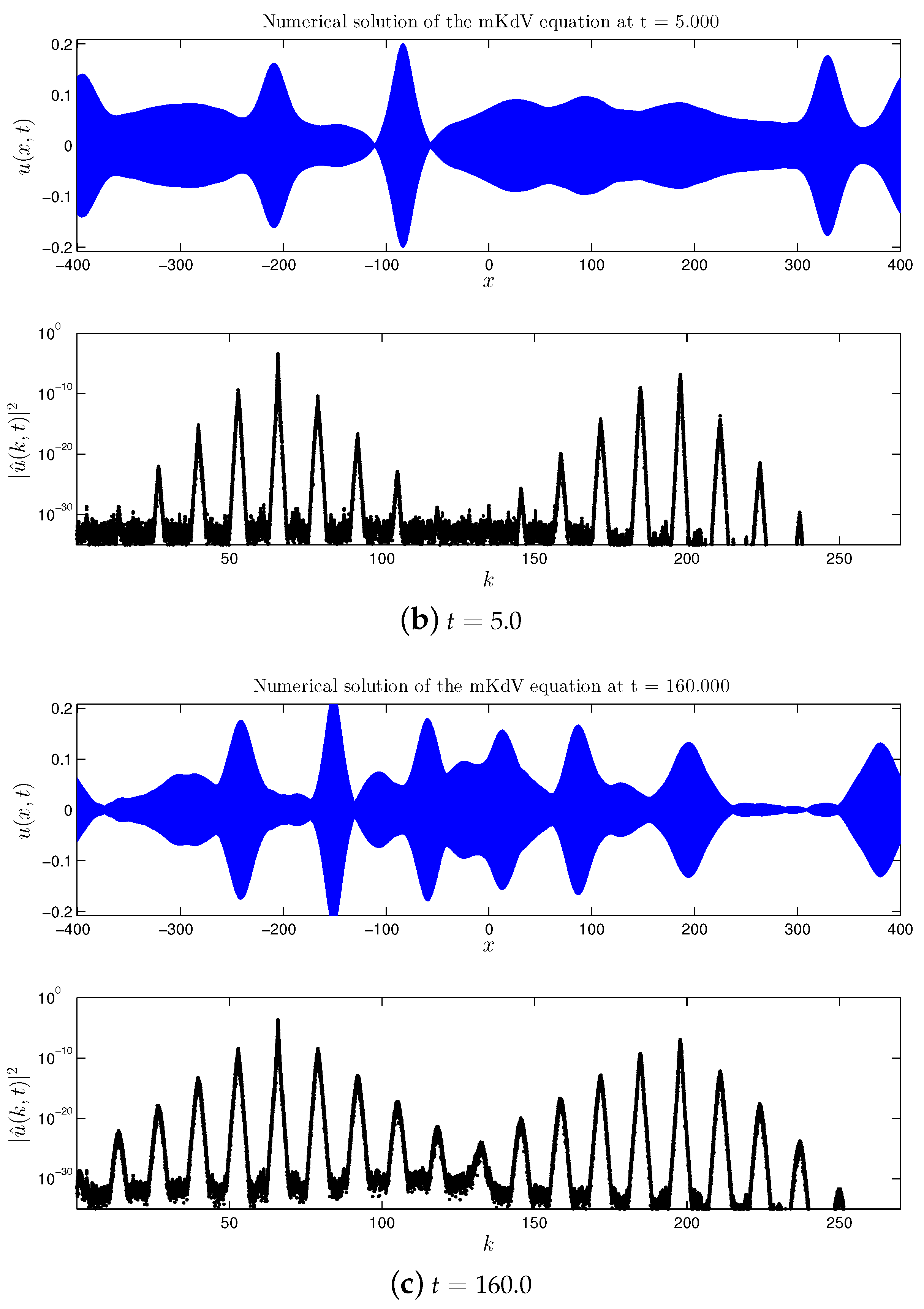
2.2. Double Cascade
3. Quartic and Quintic gKdV Equations
- Investigate the existence of the direct and inverse energy cascades
- If they exist:
- -
- To compare their formation time scales;
- -
- To compare their structure, i.e., the number of cascading modes, their location, spacing, etc.
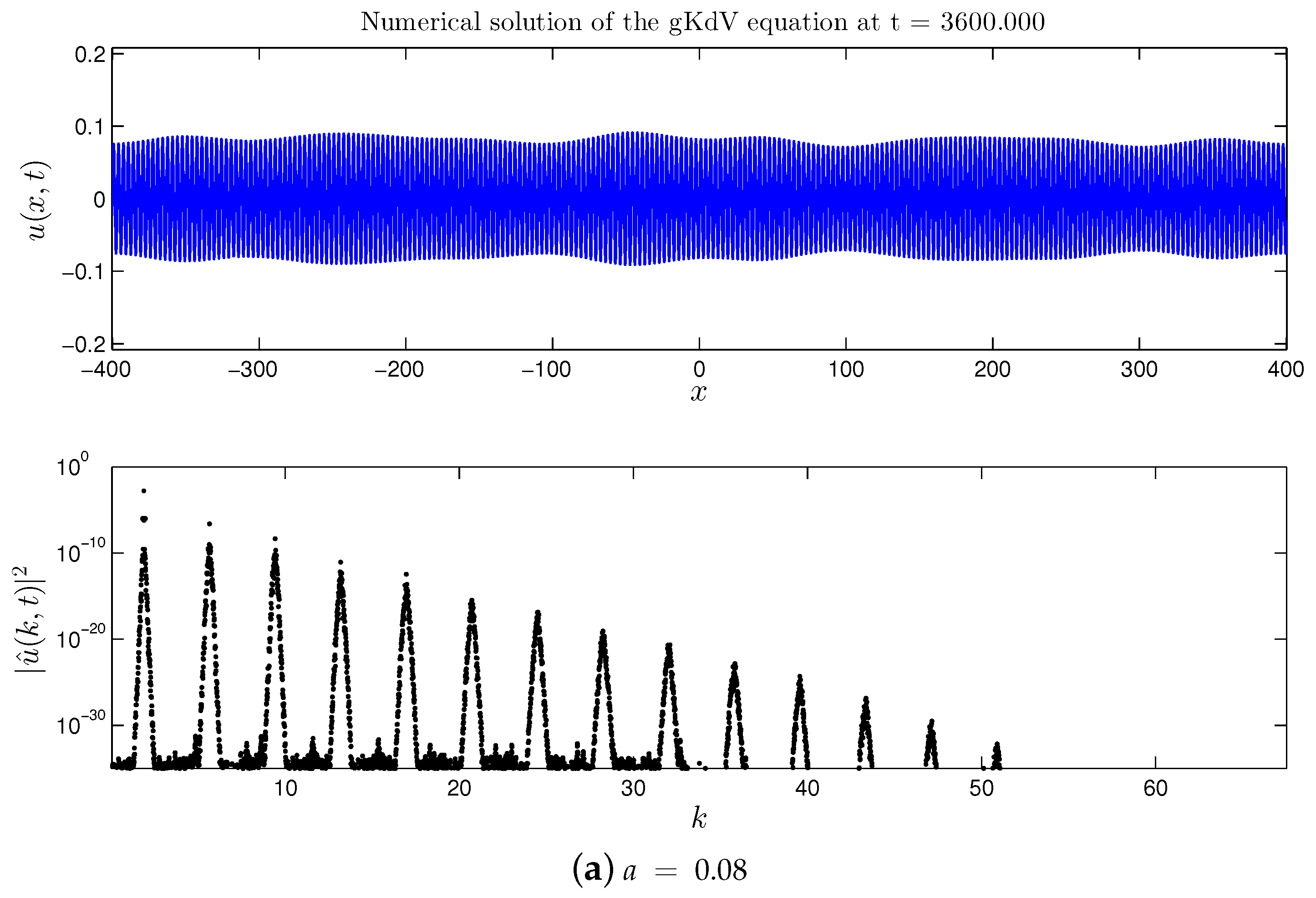
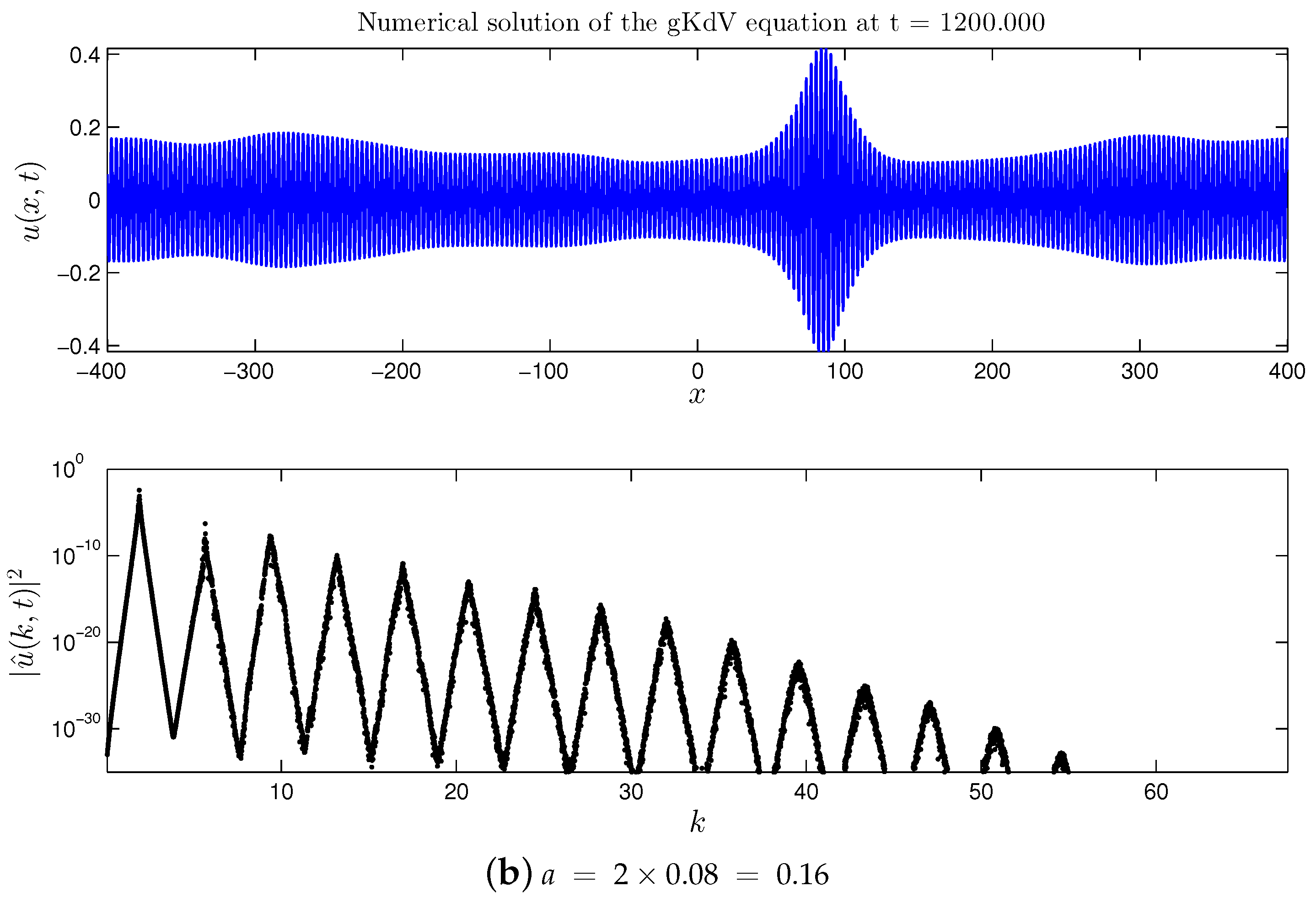
3.1. Quartic gKdV Equation
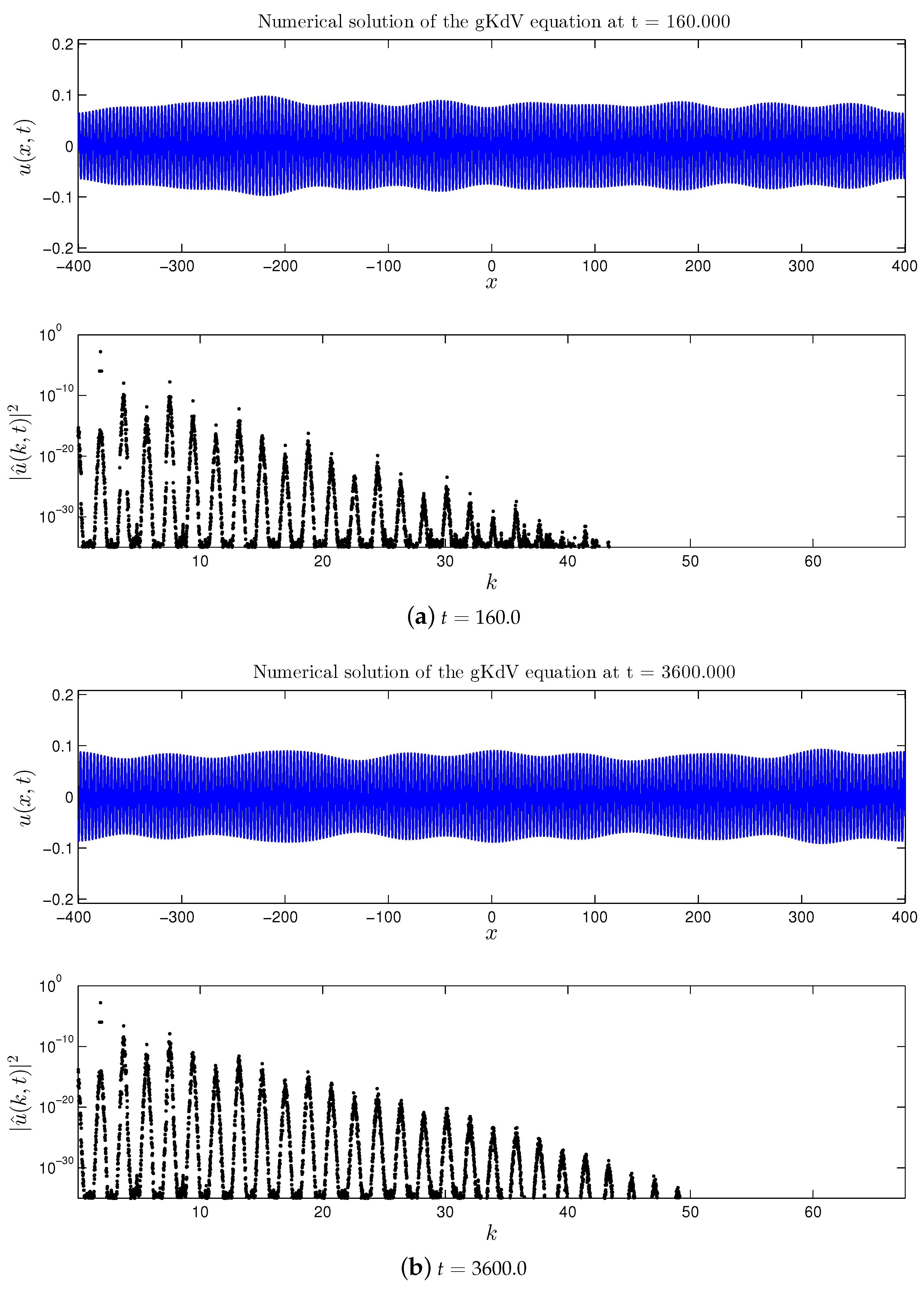
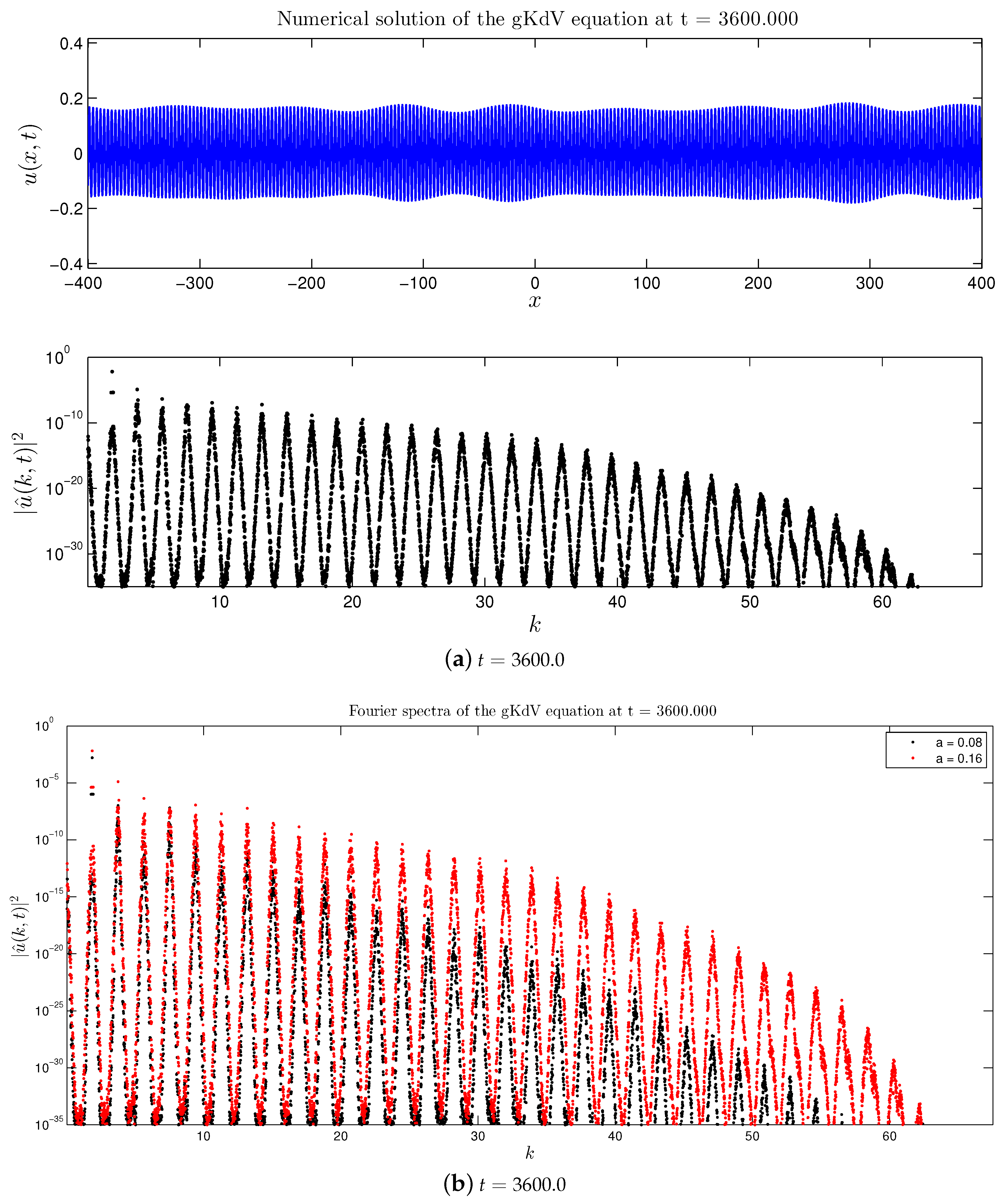
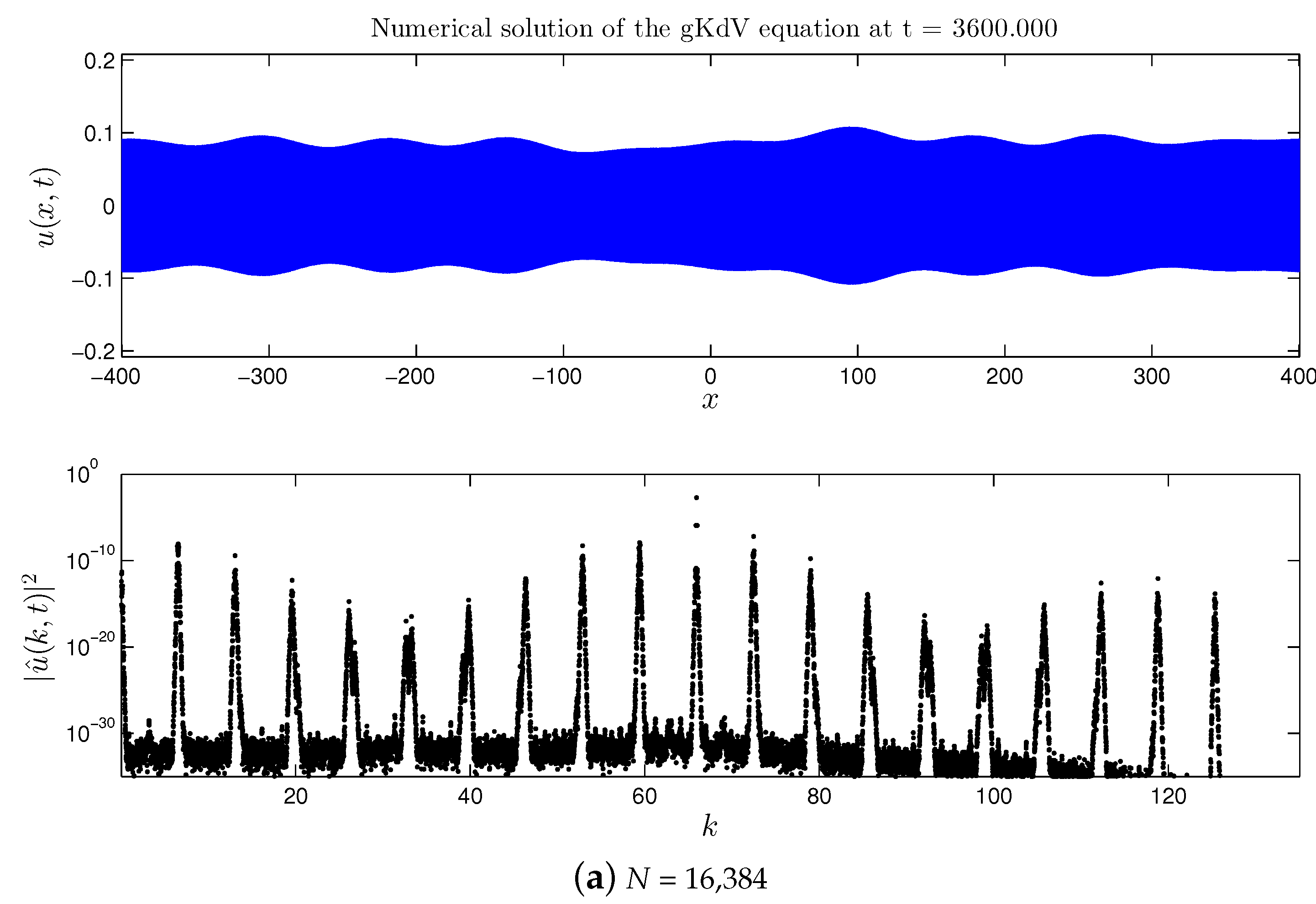
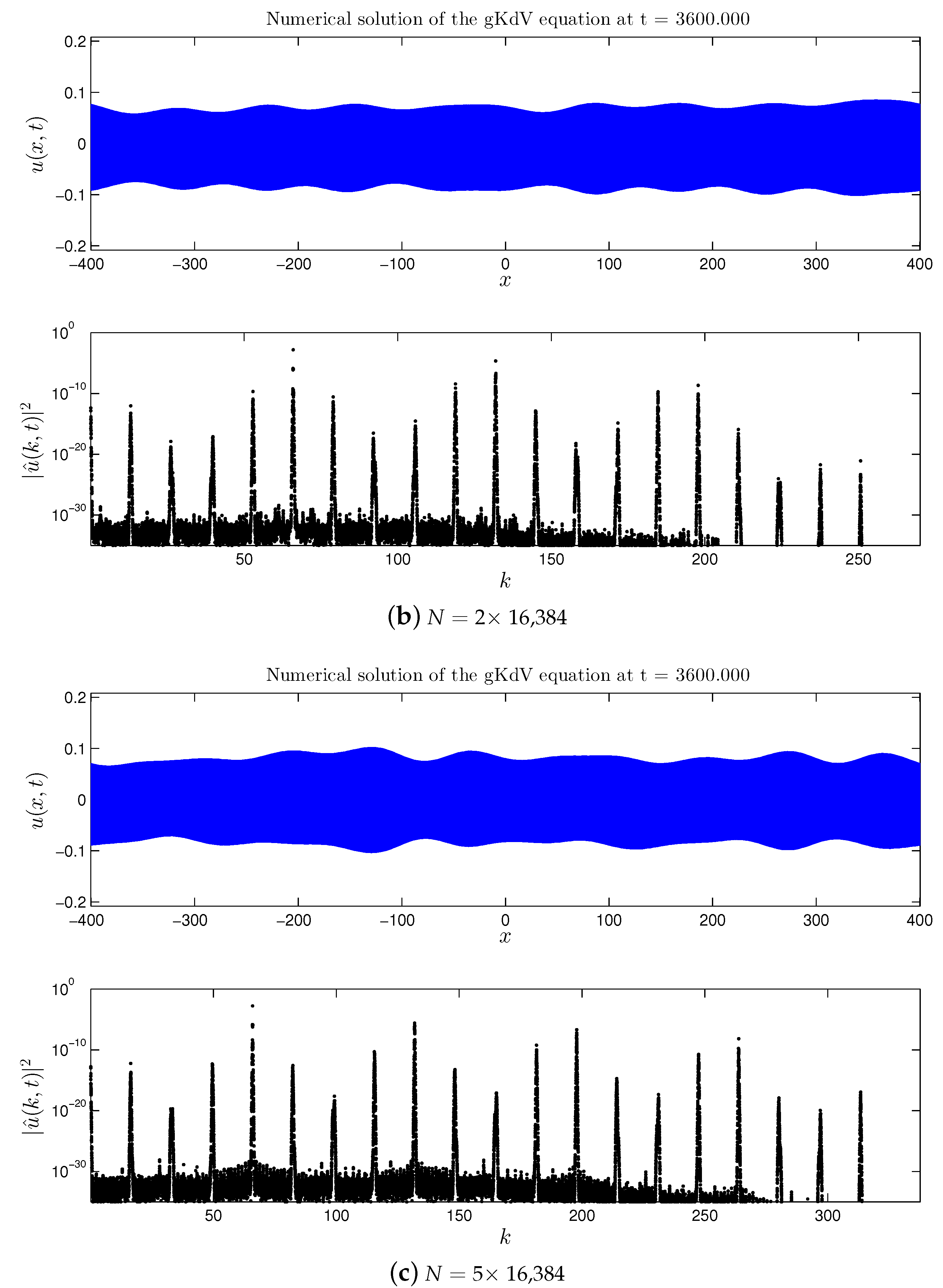
3.1.1. Direct Cascade
3.1.2. Double Cascade
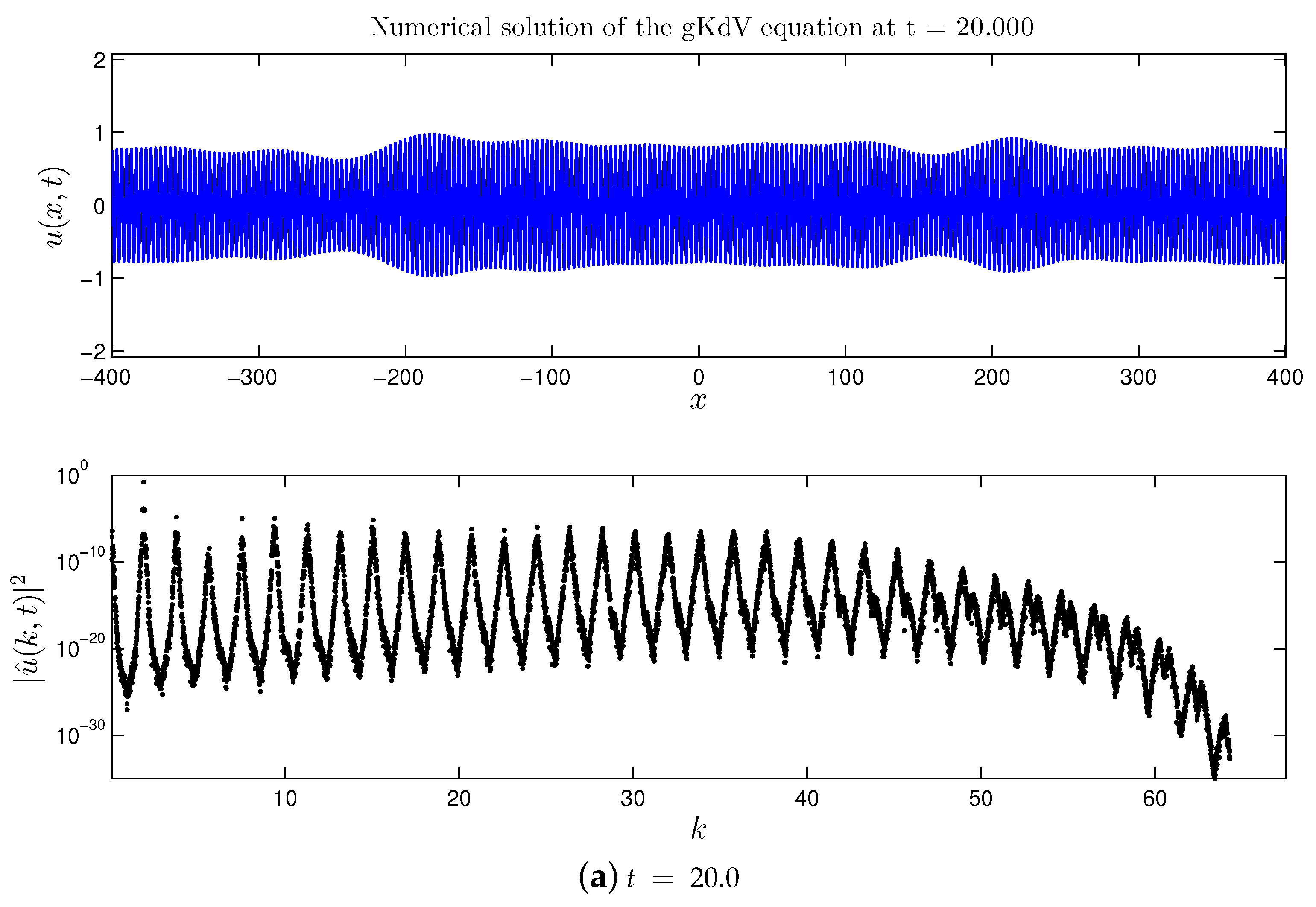
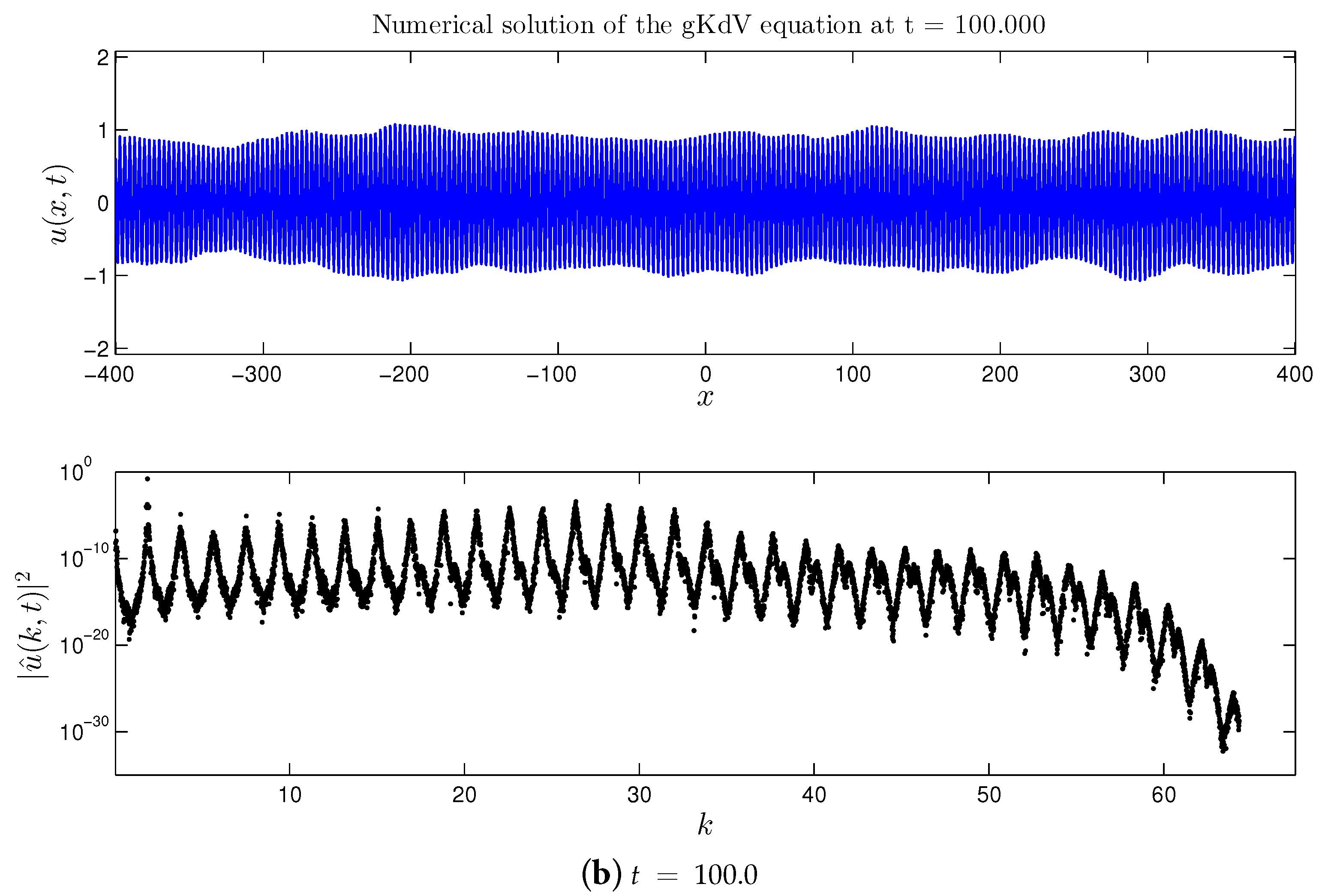
3.2. Quintic gKdV Equation
4. Discussion
- First of all, we extended the study of the mKdV equation presented in [16,17] for the case of a broader initial perturbation of the base wave. It was found that previous findings can be transposed to this case as well: formation of the direct and double cascades, their structure is preserved and appears to be quite stable. However, in the broad perturbation case all nonlinear processes are accelerated (i.e., they develop in shorter times).
- Not only the general structure of the energy cascade is preserved, but also the number of the cascading modes (for the fixed spectral domain and the base wave amplitude) and their location in the Fourier space.
- The main difference between the direct and double cascades consists in the fact that the change of the size of the spectral domain does not induce the energy redistribution in the direct cascade, while it changes completely the number of entities, and thus the energy distribution, in the double cascade(s).
- In all the mKdV cases, the formation of dynamical cascades is accompanied by the nonlinear stage of the MI development and the substantial amplification of the base wave in the physical space.
- In the case of the quartic gKdV equation, all the results about the dynamical cascades formation in the spectral domain remain the same. However, no amplification of the base wave amplitude was observed in the physical space.
- The quintic gKdV case is mostly similar to the mKdV equation (with positive nonlinearity) except for the presence of the amplitude threshold in the physical space, below which the amplification does not occur on the time horizons investigated in this study. However, if the amplitude is taken above this threshold, the base wave amplification occurs on longer time scales (virtually three times slower than in mKdV for the parameters considered in this study).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| List of acronyms | |
| BFI | Benjamin–Feir Index |
| CNRS | Centre National de la Recherche Scientifique |
| CPU | Central Processor Unit |
| FFT | Fast Fourier Transform |
| FWF | Austrian Science Foundation |
| gKdV | generalized Korteweg–de Vries equation |
| ICE | Incremental Chain Equations |
| LAMA | LAboratory of MAthematics |
| KdV | Korteweg–de Vries equation |
| MI | Modulational Instability |
| mKdV | modified Korteweg–de Vries equation |
| NLS | Nonlinear Schrödinger equation |
| PDE | Partial Differential Equation |
| WTT | Wave Turbulence Theory |
| Nomenclature | |
| a | base wave amplitude |
| coefficients in the gKdV equation | |
| Fourier coefficient corresponding to the wave number k | |
| perturbation magnitude; also appears as a coefficient in the quartic KdV equation | |
| dimensionless nonlinearity parameter | |
| k | wave number (dual variable to x) |
| base wave number | |
| modulation wave number | |
| ℓ | characteristic size of the vortex |
| coefficient in the quintic KdV equation | |
| N | the number of Fourier modes used in our numerical simulations |
| p | power of the nonlinearity in the KdV family (7) |
| t | time variable |
| T | time horizon or final simulation time |
| solution to the corresponding (m,g)KdV equation (should be clear from the context) | |
| partial derivatives of the function u with respect to its independent variables t and x correspondingly | |
| x | horizontal space coordinate |
References
- Richardson, L.F. Weather Prediction by Numerical Process; Cambridge University Press: Cambridge, UK, 1922; p. 262. [Google Scholar]
- Kolmogorov, A.N. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. Proc. R. Soc. Lond. A 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Lvov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence I. Wave Turbulence; Series in Nonlinear Dynamics; Springer: Berlin, Germany, 1992; p. 264. [Google Scholar]
- Kartashova, E. Energy spectra of 2D gravity and capillary waves with narrow frequency band excitation. Europhys. Lett. 2012, 97, 30004. [Google Scholar] [CrossRef]
- Kartashova, E. Energy transport in weakly nonlinear wave systems with narrow frequency band excitation. Phys. Rev. E 2012, 86, 041129. [Google Scholar] [CrossRef] [PubMed]
- Kartashova, E. Time scales and structures of wave interaction exemplified with water waves. Europhys. Lett. 2013, 102, 44005. [Google Scholar] [CrossRef]
- Boussinesq, J.V. Essai sur la théorie des eaux courantes. Mémoires présentés par divers savants à l’Acad. des Sci. Inst. Nat. France 1877, XXIII, 1–680. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Marchant, T.R.; Smyth, N.F. The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography. J. Fluid Mech. 1990, 221, 263–287. [Google Scholar] [CrossRef]
- Grimshaw, R. Internal Solitary Waves. In Environmental Stratified Flows; Grimshaw, R., Ed.; Springer: New York, NY, USA, 2002; pp. 1–27. [Google Scholar] [CrossRef]
- Shabat, A.B.; Adler, V.E.; Marikhin, V.G.; Mikhailov, V.V.; Sokolov, V.V. (Eds.) Encyclopedia of Integrable Systems; Landau Institute for Theoretical Physics: Chernogolovka, Russia, 2010; p. 458. [Google Scholar]
- Tobisch, E.; Pelinovsky, E. Constructive Study of Modulational Instability in Higher Order Korteweg-de Vries Equations. Fluids 2019, 4, 54. [Google Scholar] [CrossRef]
- Tao, T. Scattering for the quartic generalised Korteweg-de Vries equation. J. Differ. Equ. 2007, 232, 623–651. [Google Scholar] [CrossRef]
- Bronski, J.C.; Johnson, M.A. The Modulational Instability for a Generalized Korteweg-de Vries Equation. Arch. Ration. Mech. Anal. 2010, 197, 357–400. [Google Scholar] [CrossRef]
- Bronski, J.C.; Johnson, M.A.; Kapitula, T. An index theorem for the stability of periodic travelling waves of Korteweg-de Vries type. Proc. R. Soc. Edinb. Sect. A 2011, 141, 1141–1173. [Google Scholar] [CrossRef]
- Dutykh, D.; Tobisch, E. Direct dynamical energy cascade in the modified KdV equation. Physica D 2015, 297, 76–87. [Google Scholar] [CrossRef]
- Dutykh, D.; Tobisch, E. Observation of the Inverse Energy Cascade in the modified Korteweg-de Vries Equation. Europhys. Lett. 2014, 107, 14001. [Google Scholar] [CrossRef]
- Newell, A.C.; Rumpf, B. Wave Turbulence. Ann. Rev. Fluid Mech. 2011, 43, 59–78. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Nonlinear four-wave interactions and freak waves. Phys. Oceanogr. 2003, 33, 863–884. [Google Scholar] [CrossRef]
- Tobisch, E. Energy spectrum of ensemble of weakly nonlinear gravity-capillary waves on a fluid surface. J. Exp. Theor. Phys. 2014, 119, 359–365. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, D.E.; Pelinovsky, E.N.; Talipova, T. Wave group dynamics in weakly nonlinear long-wave models. Physica D 2001, 159, 35–57. [Google Scholar] [CrossRef]
- Dullin, H.R.; Gottwald, G.A.; Holm, D.D. On asymptotically equivalent shallow water wave equations. Physica D 2004, 190, 1–14. [Google Scholar] [CrossRef]
- Zabusky, N.J.; Galvin, C.C.J. Shallow Water Waves, the Korteweg-de Vries Equation and Solitons. J. Fluid Mech. 1971, 47, 811–824. [Google Scholar] [CrossRef]
- Johnson, R.S. Camassa-Holm, Korteweg-de Vries and related models for water waves. J. Fluid Mech. 2002, 455, 63–82. [Google Scholar] [CrossRef]
- Schamel, H. A modified Korteweg-de Vries equation for ion acoustic wavess due to resonant electrons. J. Plasma Phys. 1973, 9, 377–387. [Google Scholar] [CrossRef]
- Toida, M.; Ohsawa, Y. KdV Equations for High- and Low-Frequency Magnetosonic Waves in a Multi-Ion Plasma. J. Phys. Soc. Jpn. 1994, 63, 573–582. [Google Scholar] [CrossRef]
- Nakamura, Y.; Bailung, H.; Shukla, P.K. Observation of Ion-Acoustic Shocks in a Dusty Plasma. Phys. Rev. Lett. 1999, 83, 1602–1605. [Google Scholar] [CrossRef]
- Grue, J.; Jensen, A.; Rusas, P.O.; Sveen, J.K. Properties of large-amplitude internal waves. J. Fluid Mech. 1999, 380, 257–278. [Google Scholar] [CrossRef]
- Whitfield, A.J.; Johnson, E.R. Rotation-induced nonlinear wavepackets in internal waves. Phys. Fluids 2014, 26, 056606. [Google Scholar] [CrossRef]
- Holloway, P.; Pelinovsky, E.; Talipova, T. Internal Tide Transformation and Oceanic Internal Solitary Waves. In Environmental Stratified Flows; Grimshaw, R., Ed.; Kluwer Academic Publishers: Boston, MA, USA, 2003; pp. 29–60. [Google Scholar] [CrossRef]
- Shabat, A.B.; Kartashova, E. Computable integrability. chapter 1: General notions and ideas. arXiv 2005, arXiv:math-ph/0504020. [Google Scholar]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover Publications: New York, NY, USA, 2000; p. 688. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MatLab; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000; p. 184. [Google Scholar]
- Frigo, M.; Johnson, S.G. FFTW: An adaptive software architecture for the FFT. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP ’98 (Cat. No. 98CH36181). Seattle, WA, USA, 15 May 1998; Volume 3, pp. 1381–1384. [Google Scholar]
- Frigo, M. A fast Fourier transform compiler. In Proceedings of the 1999 ACM SIGPLAN Conf. on Programming Language Design and Implementation (PLDI), Atlanta, GA, USA, 1–4 May 1999; Volume 34, pp. 169–180. [Google Scholar]
- Frigo, M.; Johnson, S.G. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
- Hou, T.Y.; Li, R. Computing nearly singular solutions using pseudo-spectral methods. J. Comput. Phys. 2007, 226, 379–397. [Google Scholar] [CrossRef]
- Cash, J.R.; Karp, A.H. A variable order Runge-Kutta method for initial value problems with rapidly varying right-hand sides. ACM Trans. Math. Softw. 1990, 16, 201–222. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 1996; Volume 14, p. 614. [Google Scholar]
- Grimshaw, R.; Pelinovsky, E.N.; Talipova, T.; Ruderman, M.S.; Erdelyi, R. Short-Lived Large-Amplitude Pulses in the Nonlinear Long-Wave Model Described by the Modified Korteweg-De Vries Equation. Stud. Appl. Math. 2005, 114, 189–210. [Google Scholar] [CrossRef]
- Onorato, M.; Osborne, A.R.; Serio, M.; Bertone, S. Freak waves in random oceanic sea states. Phys. Rev. Lett. 2001, 86, 5831–5834. [Google Scholar] [CrossRef] [PubMed]
- Tobisch, E.; Pelinovsky, E. Conditions for modulation instability in higher order Korteweg-de Vries equations. Appl. Math. Lett. 2019, 88, 28–32. [Google Scholar] [CrossRef]
- Balajewicz, M.J.; Dowell, E.H.; Noack, B.R. Low-dimensional modelling of high-Reynolds-number shear flows incorporating constraints from the Navier-Stokes equation. J. Fluid Mech. 2013, 729, 285–308. [Google Scholar] [CrossRef]
- Kartashova, E.A. Weakly nonlinear theory of finite-size effects in resonators. Phys. Rev. Lett. 1994, 72, 2013–2016. [Google Scholar] [CrossRef]
| Base wave amplitude, a | |
| Perturbation magnitude, | |
| Base wavenumber, | |
| Perturbation wavenumber, | |
| Ratio of wavelengths, | 240 |
| Number of Fourier modes, N | 16 384 |
| Base wave amplitude, a | |
| Perturbation magnitude, | |
| Base wavenumber, | |
| Perturbation wavenumber, | |
| Ratio of wavelengths, | 240 |
| Number of Fourier modes, N | 384 |
| Property/Model | KdV (1) | mKdV (2) | Quartic gKdV (5) | Quintic gKdV (6) |
|---|---|---|---|---|
| Nonlinear Term | ||||
| MI | − | + | − | + |
| Direct cascade | − | + | + | + |
| Inverse cascade | − | − | − | − |
| Double cascade | − | + | + | + |
| Energy redistrib. | − | + | + | + |
| MI nonlin. stage | − | + | − | + |
| (amplif. ) | ||||
| Threshold | − | − | − | + |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutykh, D.; Tobisch, E. Formation of the Dynamic Energy Cascades in Quartic and Quintic Generalized KdV Equations. Symmetry 2020, 12, 1254. https://doi.org/10.3390/sym12081254
Dutykh D, Tobisch E. Formation of the Dynamic Energy Cascades in Quartic and Quintic Generalized KdV Equations. Symmetry. 2020; 12(8):1254. https://doi.org/10.3390/sym12081254
Chicago/Turabian StyleDutykh, Denys, and Elena Tobisch. 2020. "Formation of the Dynamic Energy Cascades in Quartic and Quintic Generalized KdV Equations" Symmetry 12, no. 8: 1254. https://doi.org/10.3390/sym12081254
APA StyleDutykh, D., & Tobisch, E. (2020). Formation of the Dynamic Energy Cascades in Quartic and Quintic Generalized KdV Equations. Symmetry, 12(8), 1254. https://doi.org/10.3390/sym12081254






