Abstract
We study a breather’s properties within the framework of the modified Korteweg–de Vries (mKdV) model, where cubic nonlinearity is essential. Extrema, moments, and invariants of a breather with different parameters have been analyzed. The conditions in which a breather moves in one direction or another has been determined. Two limiting cases have been considered: when a breather has an N-wave shape and can be interpreted as two solitons with different polarities, and when a breather contains many oscillations and can be interpreted as an envelope soliton of the nonlinear Schrödinger equation (NLS).
1. Introduction
Solitons exist in various physical media, such as hydrodynamics, optics, plasma, and solids. They are exact solutions of various integrable equations (nonlinear Schrödinger equation, equations of the Korteweg–de Vries class, etc.) and their properties have been well studied. Sometimes the number of solitons in the wave field is quite large, and the analysis of their dynamics using multisoliton solutions containing rapidly changing exponential functions is very complicated. That is why approximate approaches for a larger number of solitons, similar to the gas turbulence theory, when solitons behave like particles during collisions, began to develop simultaneously with the exact description of integrable systems using various methods (inverse problem, Darboux, Backlund, and Hirota transformations). In this case, it is called a soliton gas or soliton turbulence (in the general case of integrable turbulence). A kinetic equation has been obtained analytically for the distribution function of the soliton parameters [1,2,3]. Then, a broad study of soliton turbulence using numerical methods in optics and hydrodynamics began [4,5,6,7,8,9]. Obviously, wave structures with very high energy, called freak waves, can appear resulting from many particle (soliton) collisions [10,11,12,13]. Many books and reviews are devoted to this phenomenon in nonlinear physics [14,15]. Optimal focusing conditions for transforming an arbitrarily large number of solitons to the single freak wave have been found analytically in [16,17]. The fundamental role of two-soliton interactions in complex multi-soliton dynamics has been shown in [18,19,20,21].
Another class of waves that conserve their energy during propagation—oscillating wave packets (breathers)—has been much less studied. Sometimes breathers are called pulsating solitons because they propagate as isolated perturbations without losses, but they have an additional internal “oscillatory” degree of freedom. Breathers naturally arise in physical and mathematical problems [22,23,24,25,26,27,28]. Although examples of breather-like packet interactions have been considered in some works [29,30,31,32], their characteristics are not well understood. Due to the non-stationary nature of the process, even one breather leads to variations in the moments of the wave field over time, which will be important in the theory of breather turbulence [33,34]. In this paper, we study the properties of breathers with various parameters. The second section contains the studied equation; that is, the modified Korteweg–de Vries equation (mKdV), and its breather solution. Two limiting cases have been considered: when the breather is represented by two solitons of different polarity, and when it has many oscillations and can be represented by the envelope soliton of the nonlinear Schrödinger equation. Here, the breather velocities have been analyzed, and the conditions for changing the signs of speed have been determined. The third section shows the calculated extrema of breathers with different parameters. In the fourth section, the invariants of the mKdV equation have been computed for a breather. In the fifth section, the moments of breathers have been numerically and analytically determined. The Conclusion finalizes the article.
2. MKdV-Breather
The modified Korteweg–de Vries equation is used to describe different physical processes in isotropic media (dimensionally quantized films, acoustic waves in plasma, and internal waves in a symmetrically stratified fluid). Its canonical form is:
Its exact breather solution has the following form
where
where are the free parameters. Initial phases R0 and f0 can be removed by the appropriate coordinate and time conversions. The physical meaning of the other constants is as follows: p affects the number of waves in a packet, and q determines the breather’s amplitude.
In this general case, the nonlinear “phase” and “group” velocities can be easily found from Equations (3) and (4):
Several limiting cases according to the ratio of p and q can be distinguished:
- q << p: and as in the linear problem;
- q >> p: and as in the two-soliton solution;
- q = p, and as in the intermediate case.
For other cases, velocities can change signs according to Figure 1.
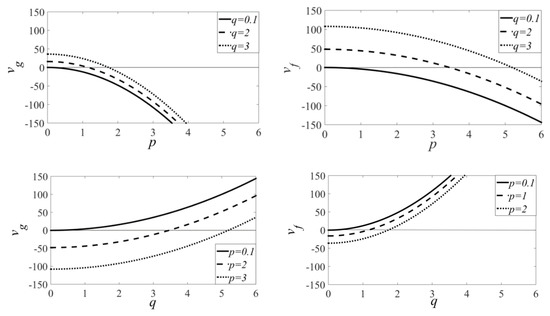
Figure 1.
“phase” and “group” velocities versus p and q.
A breather has nontrivial time-periodic behavior; it repeats its shape each time the .
If q << p, Equation (2) can be written as
In this case, the wave packet contains many oscillations and is rather symmetric (Figure 2). In this limiting case, the “phase” and “group” velocities are both negative and differ three times: . It is in full agreement with the dispersive relation in the linear approximation ().
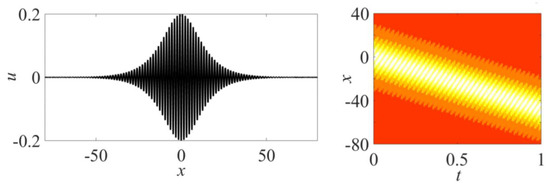
Figure 2.
Modified Korteweg–de Vries (mKdV) breather with parameters p = 2; q = 0.05; and its x-t evolution.
In this approximation, the breather is a weakly modulated wave packet, usually studied in the framework of the nonlinear Schrödinger equation. As is known, equations of the Korteweg–de Vries class can be reduced to the nonlinear Schrödinger equation on the assumption of a small amplitude and weak modulation using an asymptotic procedure [35,36]. Solution (7) coincides with the well-known solution of the nonlinear Schrödinger equation in the form of an envelope soliton, and we will often use the analogy below.
If the q >> p breather has few cycles (Figure 3) and resembles the superposition of the two mKdV solitons of different polarity :
and the soliton velocity is (A is soliton amplitude), which also follows from Equation (6). Such a breather moves rightward ).
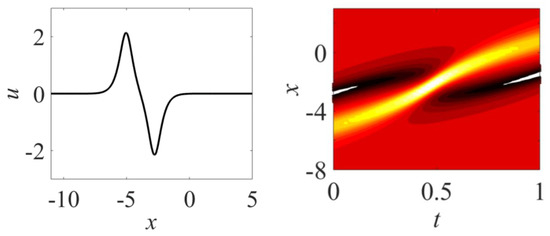
Figure 3.
MKdV breathers with parameters p = 0.2; q = 1; and its x-t evolution.
To demonstrate the breather’s dynamics, Equation (1) is numerically solved by the pseudo-spectral method. The idea of this method is to replace the initial partial differential equations with the ordinary differential equations for the coefficients of the desired functions expansion in a certain basis. At each time instant, the obtained coefficients allow one to retrieve the desired solution with the help of fast Fourier transform. This method is described in more detail in [37].
3. Breather’s Extrema
A breather’s shape and dynamics depends on p and q, so let us demonstrate three cases for the different ratios of these parameters and its extrema.
- (i)
- case: q/p >> 1. Let us fix q = 1, p = 0.2 ().
In this case, the breather contains few cycles and propagates to the right (as the mKdV soliton does). Figure 4 demonstrates the breather’s evolution. There is a periodical wave with the recurrence time of T = 1.88. The maximum of the wave field (umax) changes from 1 to 4, and the minimum (umin) changes from −4 to −1 (Figure 5). Here, the maximum value 4 is in full agreement with superposition of the two solitons with amplitudes of 2q. The height (H = umax − umin) is shown by the black curve; its variation is about 14%.
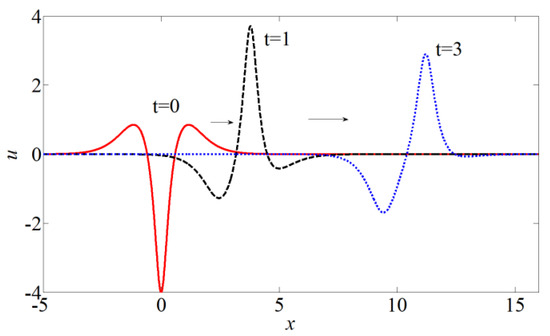
Figure 4.
Evolution of the breather with parameters q = 1, p = 0.2.
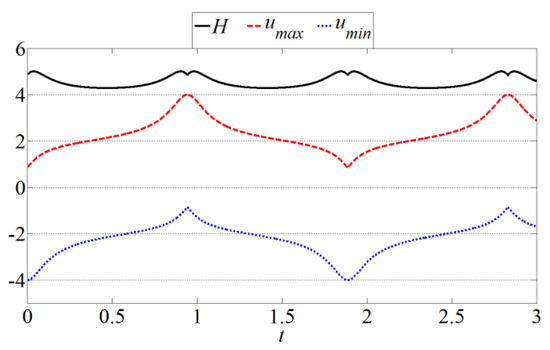
Figure 5.
Breather’s extrema over time.
- (ii)
- case: q/p << 1. Let us fix q = 0.2, p = 1 ().
In this case, the breather contains many oscillations and moves to the left ( as an envelope soliton in NLS) (Figure 6). The extrema changes less than in the previous case; its variation is about 3% (Figure 7). The curve corresponding to the breather’s height oscillates two times quicker than the umax or umin. The breather’s period is T = 0.38, and is five times less than in the previous case. Of course, with the limit of p >> q, all of the breather’s kinematic characteristics listed above are almost constant.
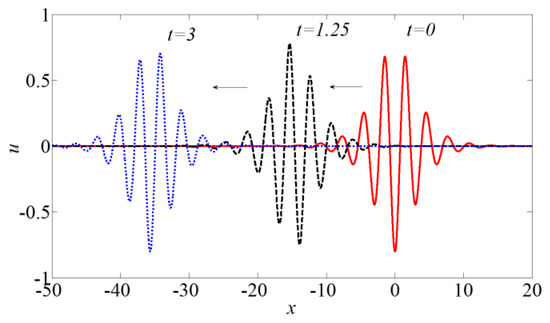
Figure 6.
Evolution of the breather with parameters q = 0.2, p = 1.
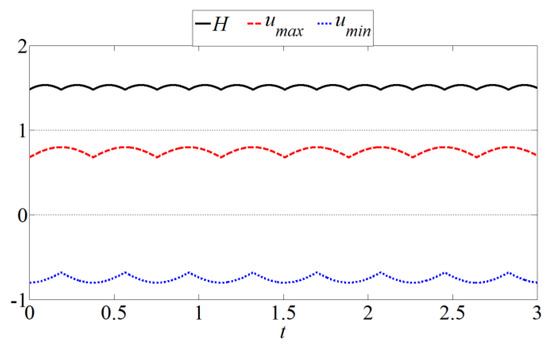
Figure 7.
Breather’s extrema over time.
- (iii)
- case: q/p = 1. Let us fix q = 1, p = 1 ().
This case is close to the first case, (i), with regard to the initial breather’s shape (Figure 8). However, the wave packet moves to the left. The behavior of the wave field’s extrema is qualitatively close to the (ii)’s one because the breather moves quite fast. The variation in the wave height is about 8%, and the amplitude is 66%. The breather oscillates with a time period of T = 0.2 (Figure 9). In fact, this case is not limiting on the solution of Equation (2) and we will not concider it further.
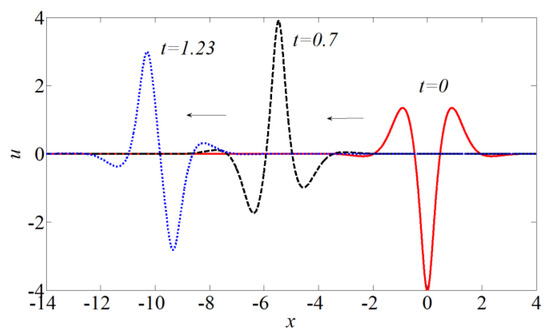
Figure 8.
Evolution of the breather with parameters q = 1, p = 1.
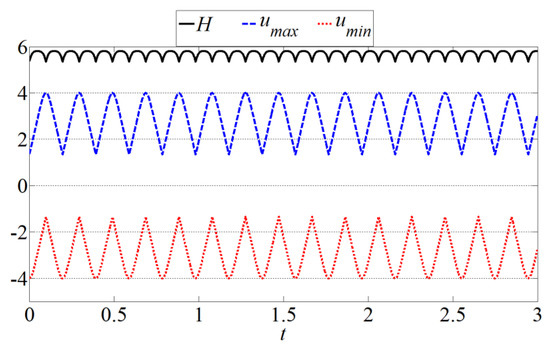
Figure 9.
Breather’s extrema over time.
4. Breather’s Invariants
The mKdV is a fully integrable equation (as well as the KdV equation). It means it has an infinite number of conserved invariants, which are not affected by the soliton interaction. The first three of them correspond to the conservation of mass, momentum, and energy [38]:
For further analysis, we also use the fourth invariant which does not have any physical meaning of the corresponding physical entities:
Invariants allow for controlling the accuracy of the numerical calculations.
We introduce variable substitutions: , , and to which then Equation (2) depends on only one parameter instead of two and can be rewritten as:
Then, Invariants (9)–(12) can be rewritten as:
Having one parameter z instead of p and q, we can obtain the dependencies of the invariants versus z.
The limiting values of the invariants are easily obtained by taking the corresponding Integrals (9)–(12) from the NLS envelope soliton (Equation (7)) and sum of two solitons (Equation (8)).
The first invariant is always zero. The second invariant in all cases is equal to 8q, that is, it does not depend on z (on p).
For the case of the two coupled solitons, when z >> 1 (A1 and A2 are the solitons’ amplitudes),
and
In the case of a strongly oscillating breather, when z << 1, the values of the invariants can be calculated analytically using the NLS approximation of the envelope soliton:
For the same z but another , the values of the invariants I2, I3, and I4 differ by the following factors: , , and . The powers of the coefficients obviously correlate with the powers in Equations (17)–(19).
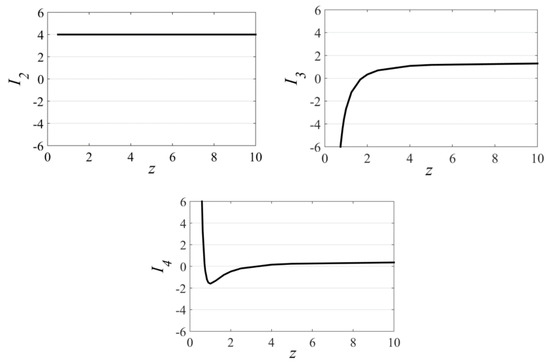
Figure 10.
Invariants via z = (q = 0.5).
By substituting q = 0.5 into Equations (20)–(23), we get the following limiting values. The second is constant for any z equal to 4. If z then . Otherwise, if , is infinitely small and is infinitely large. The third invariant is a monotonic function, while there is an inflection of I4 in the region of
5. Breather’s Moments
As is known, in the theory of turbulence, statistical moments of random fields are widely used [39].
where <…> means statistical averaging. Often, a random field is considered uniform in space (in a statistical sense), which allows one to use the ergodic hypothesis and eliminate the coordinate x.
Since here we study only one wave packet—the breather—we will use the term “moments” for the functions Mn(t) and use the terms “mean”, “variance”, “skewness”, and “kurtosis” for this quantity in the physical sense, which, strictly speaking, refer to the statistical moments . Taking into account that the mean of a breather is zero, its moments are
Knowledge of moments (26) is very important for the theory of breather turbulence [33,34], in which their statistical averaging is performed.
The first and the second moments correspond to the mean and variance, and they are constant in time (as invariants of the Korteweg–de Vries equation). The third and fourth correspond to skewness and kurtosis, i.e., the characteristics of random processes.
We study the evolution of four moments numerically. At the same time, initial values of these moments can be found analytically for two limiting cases of a breather’s solution.
If a breather has an N-shape and can be approximated by the sum of two solitons, moments can be found analytically, assuming that solitons are separated and their amplitudes are almost the same [18]:
The first moment (mean wave field) as well as the initial third one (skewness) are zero because of the breather’s symmetry. After some time, solitons exchange energy and the third moment is no longer zero. The second and fourth moments of the mKdV breather from Figure 3, calculated numerically, are M2 = 8 and M4 = 25.12. Analytical moments for the couple of separated mKdV solitons with parameters A1 = 2.14, s1 = 1, A2 = 2.15, and s2 = −1 are M2 = 8.6 and M4 = 26.3, which are very close to the numerical values. Functions M3 and M4 versus time are shown in Figure 11. Moments’ variations are huge, which is in agreement with the dramatic extrema variations (shown in Section 3). It means such breathers can have a strong impact on the multi-breather field’s characteristics.
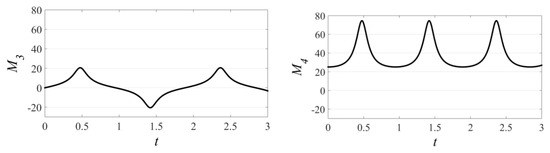
Figure 11.
Evolution of breather’s moments (p = 0.2; q = 1).
In the second limiting case, when the breather can be presented as an NLS envelope soliton (Equation (7)), the analytical formulas for initial moments are:
The second moment (as second invariant) and initial fourth moment, calculated numerically for the breather from Figure 6 (q = 0.2, p = 1), coincide with the analytical values of Formula (32): M2 = 1.6 and M4 = 0.512. A numerical evolution of M3 and M4 versus time is shown in Figure 12. Their variations are very small (Figure 12).
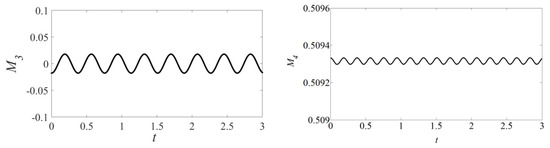
Figure 12.
Evolution of breather’s moments (q = 0.2, p = 1).
6. Conclusions
The properties of an oscillating wave packet (breather) have been considered within the modified Korteweg–de Vries equation, which is usually used to describe wave processes in isotropic media, including internal waves in fluids with symmetric stratification. The breather’s characteristics for two limiting cases have been analyzed. The extrema of a breather with many oscillations changed slightly in comparison with the case of an N-shape breather. The second invariant, corresponding to the conservation of energy, does not depend on q/p. It has been shown that the moments of the wave field for the two limiting cases can be found analytically: variations of the third and fourth moments are significant in the case of an N-shape breather, contrariwise, these moments of a breather with many oscillations change slightly. The situations when the group and phase velocities change their signs have been determined. The considered breather’s properties are essential for the further study of breather turbulence.
Author Contributions
Conceptualization, E.P.; Investigation, E.D. and E.P.; Methodology, E.D.; Writing—original draft, E.D.; Writing—review & editing, E.P. All authors have read and agreed to the published version of the manuscript.
Funding
The work was funded by RFBR grants No. 19-35-60022 and No. 19-05-00161. Studies are partially supported by Laboratory of Dynamical Systems and Applications NRU HSE, of the Ministry of science and higher education of the RF grant ag. No. 075-15-2019-1931.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zakharov, V.E. Kinetic equation for solitons. Sov. Phys. JETP 1971, 60, 993–1000. [Google Scholar]
- El, G.A.; Kamchatnov, A.M. Kinetic equation for a dense soliton gas. Phys. Rev. Lett. 2005, 95, 1–4. [Google Scholar] [CrossRef]
- El, G.A.; Kamchatnov, A.M.; Pavlov, M.V.; Zykov, S.A. Kinetic equation for a soliton gas and its hydrodynamic reductions. J. Nonlinear Sci. 2011, 21, 151–191. [Google Scholar] [CrossRef]
- Gelash, A.; Agafontsev, D.; Zakharov, V.; El, G.; Randoux, S.; Suret, P. Bound state soliton gas dynamics underlying the spontaneous modulational instability. Phys. Rev. Lett. 2019, 123, 234102. [Google Scholar] [CrossRef] [PubMed]
- Agafontsev, D.S.; Zakharov, V.E. Integrable turbulence generated from modulational instability of cnoidal waves. Nonlinearity 2016, 29, 3551–3578. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Shurgalina, E. KDV soliton gas: Interactions and turbulence. In Challenges in Complexity: Dynamics, Patterns, Cognition; Aronson, I., Pikovsky, A., Rulkov, N., Tsimring, L., Eds.; Series: Nonlinear Systems and Complexity; Springer: Berlin, Germany, 2017; Volume 20, pp. 295–306. [Google Scholar]
- Didenkulova, E.G.; Pelinovsky, E.N. The role of a thick soliton in the dynamics of the soliton gas within the framework of the Gardner equation. Radiophys. Quantum Electron. 2019, 61, 623–632. [Google Scholar] [CrossRef]
- Shurgalina, E.G.; Pelinovsky, E.N. Nonlinear dynamics of a soliton gas: Modified Korteweg-de Vries equation framework. Phys. Lett. A 2016, 380, 2049–2053. [Google Scholar] [CrossRef]
- El, G.A. Critical density of a soliton gas. Chaos 2016, 26, 023105. [Google Scholar] [CrossRef]
- Gelash, A.A.; Agafontsev, D.S. Strongly interacting soliton gas and formation of rogue waves. Phys. Rev. E 2018, 98, 1–11. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.G. Formation of freak waves in a soliton gas described by the modified Korteweg–de Vries equation. Dokl. Phys. 2016, 61, 423–426. [Google Scholar] [CrossRef]
- Didenkulova (Shurgalina), E.G. Numerical modeling of soliton turbulence within the focusing Gardner equation: Rogue wave emergence. Phys. D 2019, 399, 35–41. [Google Scholar] [CrossRef]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photonics 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer: Berlin, Germany, 2009; p. 216. [Google Scholar]
- Onorato, M.; Resitori, S.; Baronio, F. Rogue and Shock Waves in Nonlinear Dispersive Media; Lecture Notes in Physics; Springer International Publishing: New York, NY, USA, 2016. [Google Scholar]
- Slunyaev, A.V.; Pelinovsky, E.N. Role of multiple soliton interactions in the generation of rogue waves: The modified korteweg-de vries framework. Phys. Rev. Lett. 2016, 117, 214501. [Google Scholar] [CrossRef] [PubMed]
- Slunyaev, A. On the optimal focusing of solitons and breathers in long-wave models. Stud. Appl. Math. 2019, 142, 385–413. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.G.; Sergeeva, A.V.; Talipova, T.G.; El, G.A.; Grimshaw, R.H.J. Two-soliton interaction as an elementary act of soliton turbulence in integrable systems. Phys. Lett. A 2013, 377, 272–275. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.G. Two-soliton interaction in the frameworks of modified Korteweg–de Vries equation. Radiophys. Quantum Electron. 2015, 57, 737–744. [Google Scholar] [CrossRef]
- Shurgalina, E.G. The features of the paired soliton interactions within the framework of the Gardner equation. Radiophys. Quantum Electron. 2018, 60, 703–708. [Google Scholar] [CrossRef]
- Shurgalina, E.G. The mechanism of the formation of freak waves in the result of interaction of internal waves in stratified basin. Fluid Dyn. 2018, 53, 59–64. [Google Scholar] [CrossRef]
- Lamb, G.L. Elements of Soliton Theory; Wiley: New York, NY, USA, 1980; p. 289. [Google Scholar]
- Lamb, K.G.; Polukhina, O.; Talipova, T.; Pelinovsky, E.; Xiao, W.; Kurkin, A. Breather generation in fully nonlinear models of a stratified fluid. Phys. Rev. E 2007, 75, 046306. [Google Scholar] [CrossRef]
- Lee, J.H.; Lozovatsky, I.; Jang, S.-T.; Jang, C.J.; Hong, C.S.; Fernando, H.J.S. Episodes of nonlinear internal waves in the northern East China Sea. Geoph. Res. Lett. 2006, 33, L18601. [Google Scholar] [CrossRef]
- Shroyer, E.L.; Moum, J.N.; Nash, J.D. Mode 2 waves on the continental shelf: Ephemeral components of the nonlinear internal wavefield. JGR 2010, 115, C07001. [Google Scholar] [CrossRef]
- Vlasenko, V.; Stashchuk, N. Internal tides near the Celtic Sea shelf break: A new look at a well known problem. Deep Sea Res. I 2015, 103, 24–36. [Google Scholar] [CrossRef]
- Alejo, M.A.; Munoz, C. Nonlinear stability of mKdV breathers. Commun. Math. Phys. 2013, 324, 233–262. [Google Scholar] [CrossRef]
- Alejo, M.A.; Munoz, C.; Palacios, J.M. On the variational structure of Breather Solutions II: Periodic mKdV case. Electron. J. Diff. Eqns. 2017, 2017, 1–26. [Google Scholar]
- Chow, K.W.; Grimshaw, R.H.J.; Ding, E. Interactions of breathers and solitons in the extended Korteweg–de Vries equation. Wave Motion 2005, 43, 158–166. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Gelash, A. Interactions of coherent structures on the surface of deep water. Fluids 2019, 4, 83. [Google Scholar] [CrossRef]
- Kachulin, D.; Gelash, A. On the phase dependence of the soliton collisions in the Dyachenko–Zakharov envelope equation. Nonlin. Process. Geophys. 2018, 25, 553–563. [Google Scholar] [CrossRef]
- Xu, G.; Gelash, A.; Chabchoub, A.; Zakharov, V.; Kibler, B. Breather wave molecules. Phys. Rev. Lett. 2019, 122, 084101. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.M.; Devine, N. Breather turbulence versus soliton turbulence: Rogue waves, probability density functions, and spectral features. Phys. Rev. E 2016, 94, 022212. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Devine, N.; Akhmediev, N. Integrable Turbulence and rogue waves: Breathers or solitons? Phys. Rev. Lett. 2016, 116, 103901. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Kuznetsov, E.A. Multi-scale expansions in the theory of systems integrable by the inverse scattering transform. Phys. D 1986, 18, 455–463. [Google Scholar] [CrossRef]
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011; p. 364. [Google Scholar]
- Fronberg, B. A Practical Guide to Pseudospectral Methods; Cambridge University Press: Cambridge, UK, 1998; p. 231. [Google Scholar]
- Miura, R.M.; Gardner, C.S.; Kruskal, M.D. Korteweg-de Vries equation and generalizations, II. Existence of conservation laws and constants of motion. J. Math. Phys. 1968, 9, 1204–1209. [Google Scholar] [CrossRef]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics; MIT Press: Cambridge, MA, USA, 1971; p. 769. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).