Abstract
Pairwise interactions of particle-like waves (such as solitons and breathers) are important elementary processes that play a key role in the formation of the rarefied soliton gas statistics. Such waves appear in different physical systems such as deep water, shallow water waves, internal waves in the stratified ocean, and optical fibers. We study the features of different regimes of collisions between a soliton and a breather in the framework of the focusing modified Korteweg–de Vries equation, where cubic nonlinearity is essential. The relative phase of these structures is an important parameter determining the dynamics of soliton–breather collisions. Two series of experiments with different values of the breather’s and soliton’s relative phases were conducted. The waves’ amplitudes resulting from the interaction of coherent structures depending on their relative phase at the moment of collision were analyzed. Wave field moments, which play a decisive role in the statistics of soliton gases, were determined.
1. Introduction
Solitons and breathers are a part of different wave systems’ dynamics, primarily hydrodynamics and optics [1,2]. Such waves have a particle-like behavior. In accordance with the analytical theory, solitons restore their shape after interaction and continue to propagate without loss of their identity, except for some phase shifts. Breathers are periodically pulsating or oscillating isolated wave forms. They are not waves of permanent form, unlike solitons, but they also propagate without loss of energy for a long time. If a wave field consists primarily of such waves, then this physical system can be considered as soliton turbulence or soliton gas, usually studied within the integrable equations (such as the nonlinear Schrödinger equation (NLS) or the Korteweg–de Vries equation (KdV) and its modifications). Thus, so-called integrable soliton turbulence takes place, actively studied in the last few years [3]. Two particles placed in the periodical domain correspond to the case of highly rarefied gas. Analysis of two soliton interactions as an elementary act of soliton turbulence has shown the key role of such processes in rarefield soliton gas statistics within the KdV-like models: [4]—within the KdV equation, [5,6]—within the modified KdV equation, [7,8,9]—within the extended KdV equation (Gardner equation). Several works have been devoted to the study of such processes within the NLS equation and its non-integrable analogue—the Dyachenko–Zakharov equation [10,11,12]. Three soliton collisions in warm magnetized plasmas were investigated in [13]. An increase in the number of interacting particles leads to rarefied and dense soliton gases [14,15,16,17,18,19,20,21,22,23,24,25]. An ensemble of interacting solitons can appear from the evolution of some initial conditions or as a result of modulation instability driven by random perturbations of an unstable plane wave. Multiple soliton and breather interactions may lead to the abnormally large wave appearance (so-called rogue or freak waves) [26,27,28,29,30]. Analytical solutions of solitons and breathers optimal focusing into rogue wave were obtained in [31,32] for mKdV and Gardner equation.
Solitons and breathers are usually observed in internal wave records in symmetrically stratified fluids and may play a significant role in the wave field dynamics [33,34,35]. The classical model of internal wave description is the extended Korteweg–de Vries model, which includes quadratic and cubic nonlinear terms. The breather’s explicit expression was obtained from the inverse scattering transform in [36], and later in [37] from the coalescence of two solitons with complex parameters, using the Darboux transformation. The expressions describing the interaction of a soliton and a breather within the focusing Gardner equation using the Hirota bilinear transform were obtained in [38]. While the quadratic nonlinearity is much smaller than the cubic one, the Gardner equation can be reduced to the modified KdV equation with the exact soliton and breather solutions [39,40]. A breather has more difficult dynamics than a soliton in some sense [41].
In this paper, we conduct a series of numerical experiments of the interaction between a soliton and a breather in the framework of the modified Korteweg–de Vries equation for different initial wave phases. The structure of the work is as follows. The exact breather and soliton solutions of the mKdV equation are given in Section 2. In Section 3, we consider soliton–breather interaction properties, such as the maximum wave amplitude in the interaction moment, the shapes of resulting pulses, and the higher wave field moments which play a decisive role in the statistics of soliton gases. Section 4 is the concluding one.
2. Breather and Soliton Solutions of the mKdV Equation
We use the canonical form of the modified Korteweg–de Vries equation:
Its exact soliton solution is:
where the soliton velocity is (A is soliton amplitude) and is soliton’s polarity, is soliton initial phase.
Its exact breather solution has the following form:
where:
are the free parameters. Initial phases R0 and f0 can be removed by the appropriate coordinate and time conversions. The physical meaning of the other constants is as follows: p affects the number of waves in a packet, and q determines the breather’s amplitude. If the q >> p, a breather has few cycles and resembles the superposition of the two mKdV solitons (2). A breather containing many oscillations can be interpreted as an envelope soliton of the nonlinear Schrödinger equation.
In general case, nonlinear «phase» and «group» velocities can be easily determined from Equations (4) and (5):
A more complicated expression for the multi-soliton breather solution was obtained in [31].
3. Breather’s Extrema
We study soliton–breather interactions as an elementary act of soliton–breather turbulence. Such collisions are the most frequent in the rarefied soliton gases [27].
The two series of numerical experiments with different soliton’s phases were conducted. Two breathers with q >> p and q << p took part in the interaction processes with the same soliton. The series consist of 29 and 57 experiments differ by the soliton initial phase. These numbers of experiments allowed covering all variants of the soliton–breather interactions with given parameters. The periodical boundary conditions were used. In each experiment, a soliton and a breather initially were separated by the level 10−5 and the calculations stopped when the distance between waves after their interactions became the same as at t = 0. During the calculations, the maximum amplitude of the resulting pulse, and higher moments of the wave field () were registered.
Equation (1) is solved numerically by the pseudo-spectral method [42]. Numerical simulations are controlled by retaining of the first and second moments with precision of 10−14 and 10−7, respectively.
3.1. Interaction Process
The first series of experiments demonstrates the interaction process between soliton (A = 1) and breather (p = 2, q = 0.25, ). According to (6) and (7), the breather moves to the left, and the soliton always moves to the right. We change the soliton’s initial phase from −39.8 to −42.6. This scatter of phases corresponds to all the possible soliton–breather interactions with given parameters, and covers one period of maximum maximorum function (as well as relative variations of wave field moments functions)—see below. In total, 29 experiments were conducted for the first series of experiments.
The breather, participated in the second series of experiments, has the following parameters: p = 0.05, q = 0.25, . The soliton again has an amplitude A = 1. In this case, the phase of soliton was changed from −30 to −120. The soliton overtakes the breather moving the same direction.
The snapshots of the soliton–breather interactions from both series of experiments are presented in Figure 1.
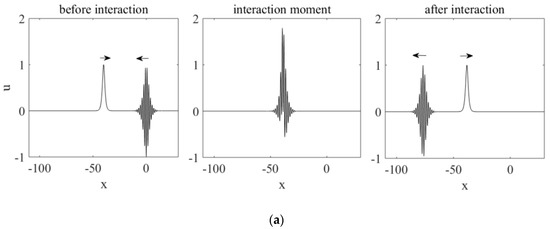
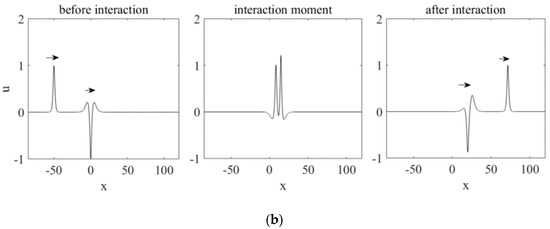
Figure 1.
Soliton–breather interaction with breather parameters: (a) p = 2, q = 0.25, (b) p = 0.05, q = 0.25.
3.2. Extrema of the Wave Fields
“Optimal” focusing gives the sum of initial waves’ amplitudes in the interacting moment, as it was shown in [31]. In both series of experiments, the maximum wave amplification is equal to 2 (x0 = −41.1 and x0 = −99 correspondingly), see Figure 2. Since the two regimes differ significantly, the horizontal scale is different in the two panels on the Figure. The pulse’s shapes at the “optimal” interacting moment are shown in Figure 3. These graphs are symmetrical unlike the other experiments.
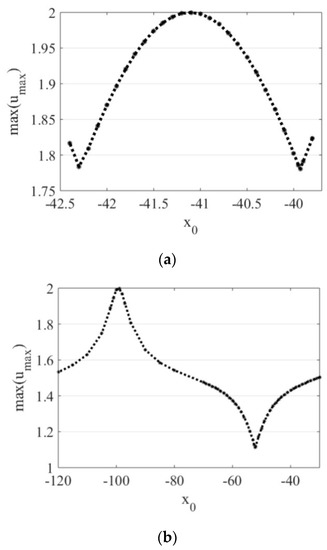
Figure 2.
Maximum maximorum of the wave fields on the soliton phase shift x0: (a) in the first series of experiments (p = 2, q = 0.25), (b) in the second series of experiments (p = 0.05, q = 0.25).
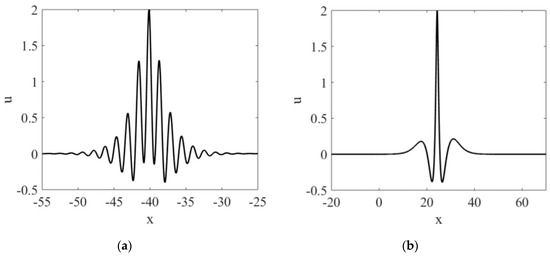
Figure 3.
The shapes of the resulting pulse during the “optimal” soliton–breather interaction: (a) in the first series of experiments (p = 2, q = 0.25), (b) in the second series of experiments (p = 0.05, q = 0.25).
The graphs from Figure 2 have periodical behavior. There is a slight change in the maximum wave amplitude during the soliton–breather interaction when the breather has many oscillations (from 1.78 to 2). On the contrary, when the “N-shape” breather with a few cycles participates in the interaction, there is a huge deviation in the resultant pulse’s amplitude: from 1.1 to 2. In the “optimal interaction”, the resultant wave has a shape of high thin pulse with two adjacent small hills of elevation (Figure 3b (right)). The waves attract each other in the collision moment and the amplitude significantly increases. When the wave field has the minimum amplification during the soliton–breather interaction, waves’ repelling plays a dominant role. The resultant wave has decreased amplitude and a shape of two almost equal positive pulses surrounded by two small hills of depression (see Figure 1b).
3.3. Moments of the Wave Fields
The collisions of solitons and breathers change the statistics of integrable turbulence. Their impact on the statistics of the rarefied soliton and breather gases is the most significant. In this section, we study the wave field moments, defined as , corresponding to skewness and kurtosis in the turbulence theory. The first two moments, corresponding to mean and variance, are invariants of the Korteweg–de Vries equation and constant in time. We use them to control numerical simulations.
The significant increase in wave moments was observed in the dominant interaction region of two waves (Figure 4). The initial values of non-interacting waves can be found analytically [41]. The third moment of symmetrical individual breather is equal to zero. Thus, only the soliton contributes to M3 = M3_sol in the initial moment and it is equal to 1.57. The fourth moment consists of both, soliton and breather components: M4 = M4_sol + M4_br = 2.3 (Figure 4a). Since, the breather is not horizontally symmetric in the initial moment in the second series of experiments, the analytical expressions satisfy the time moment t = 30.75, when the soliton and the breather are still far from each other, and the breather is represented by the sum of two identical solitons with different polarity. The moments are M3 = 1.57, M4 = 1.73 (Figure 4b).
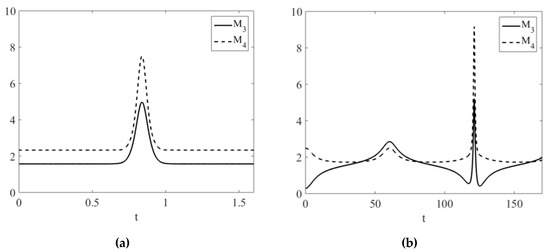
Figure 4.
3rd and 4th wave field moments during one experiment with the maximum wave field amplification from: (a) the first series of experiments (p = 2, q = 0.25), (b) from the second series of experiments (p = 0.05, q = 0.25).
The moments of the breather with many oscillations change very slightly in time, so the total moments are almost constant before and after the soliton–breather collision (Figure 4a). On the other hand, the moments of the N-shape breather change significantly and they contribute to the strong variations in Figure 4b.
Relative variations of the 3rd and 4th wave field moments (Mn* = (Mn_max − Mn_min)/Mn_max, n = 3, 4) for the first set of the experiments showed that the maximum variations correspond to the optimal focusing case (Figure 5a). For some wave phases, the tails of M3* are even higher than those of M4*. The behavior of these variations is non-monotonic in the second series of experiments (Figure 5b). Deviations of M3* are always larger than M4*. When the maximum elevation of resultant pulse is the smallest in the series, there is huge depression of M4*. Its biggest variation corresponds to the “optimal interaction” case.
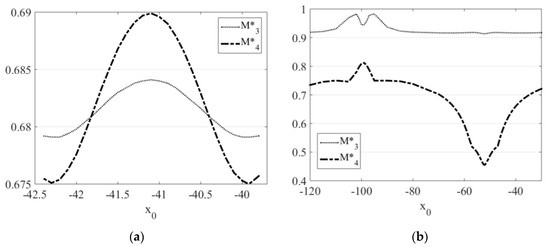
Figure 5.
Relative variations of the 3rd and 4th wave field moments on the soliton phase shift: (a) in the first series of experiments (p = 2, q = 0.25), (b) in the second series of experiments (p = 0.05, q = 0.25).
4. Conclusions
Various scenarios of interaction between a soliton and a breather were considered within the modified Korteweg–de Vries equation. Two series of experiments with limited breather’s shapes (when a breather has many oscillations, p >> q, and when an N-shape breather has a few cycles, p << q) were conducted. It is shown that an important parameter that determines the dynamics of collisions between breathers and solitons is the relative phase of these structures. The influence of the relative soliton’s phases on the wave field amplification during the interaction was investigated. The maximum wave field amplification corresponds to the linear sum of initial waves’ amplitudes, as was predicted analytically. The wave field moments, corresponding to skewness and kurtosis in the turbulence theory, and their relative variations have shown maximum increase during the “optimal interaction”. This research will be used further to describe the complex dynamics of wave fields consisting of many solitons and breathers (so-called soliton–breather turbulence).
Author Contributions
Conceptualization, E.P.; Investigation, E.D. and E.P.; Methodology, E.D.; Writing—original draft, E.D.; Writing—review & editing, E.P. All authors have read and agreed to the published version of the manuscript.
Funding
The work was funded by RFBR grant No. 19-35-60022. Studies are partially supported by Laboratory of Dynamical Systems and Applications NRU HSE, of the Ministry of science and higher education of the RF grant ag. No. 075-15-2019-1931, and the Foundation for the Advancement of Theoretical Physics and Mathematics “BASIS” No. 20-1-3-3-1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Drazin, P.G.; Johnson, R.S. Solitons: An Introduction; Cambridge University Press: Cambridge, UK, 1993; p. 226. [Google Scholar]
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011; p. 364. [Google Scholar]
- Agafontsev, D.S.; Zakharov, V.E. Integrable turbulence generated from modulational instability of cnoidal waves. Nonlinearity 2016, 29, 3551–3578. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.G.; Sergeeva, A.V.; Talipova, T.G.; El, G.A.; Grimshaw, R.H.J. Two-soliton interaction as an elementary act of soliton turbulence in integrable systems. Phys. Lett. A 2013, 377, 272–275. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.G. Two-soliton interaction in the frameworks of modified Korteweg–de Vries equation. Radiophys. Quantum Electron. 2015, 57, 737–744. [Google Scholar] [CrossRef]
- Anco, S.C.; Ngatat, N.T.; Willoughby, M. Interaction properties of complex modified kortewegde Vries (mKdV) solitons. Physics D 2011, 240, 1378–1394. [Google Scholar] [CrossRef]
- Shurgalina, E.G. The features of the paired soliton interactions within the framework of the Gardner equation. Radiophys. Quantum Electron. 2018, 60, 703–708. [Google Scholar] [CrossRef]
- Shurgalina, E.G. The mechanism of the formation of freak waves in the result of interaction of internal waves in stratified basin. Fluid Dyn. 2018, 53, 59–64. [Google Scholar] [CrossRef]
- Slyunyaev, A.V.; Pelinovskii, E.N. Dynamics of large-amplitude solitons. J. Exp. Theor. Phys. 1999, 89, 173–181. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Gelash, A. Interactions of coherent structures on the surface of deep water. Fluids 2019, 4, 83. [Google Scholar] [CrossRef]
- Kachulin, D.; Gelash, A. On the phase dependence of the soliton collisions in the Dyachenko–Zakharov envelope equation. Nonlinear Process. Geophys. 2018, 25, 553–563. [Google Scholar] [CrossRef]
- Xu, G.; Gelash, A.; Chabchoub, A.; Zakharov, V.; Kibler, B. Breather Wave Molecules. Phys. Rev. Lett. 2019, 122, 084101. [Google Scholar] [CrossRef] [PubMed]
- Ali, R.; Chatterjee, P. Three-Soliton Interaction and Soliton Turbulence in Superthermal Dusty Plasmas. Zeitschrift für Naturforschung A 2019, 74, 757–766. [Google Scholar] [CrossRef]
- El, G.A. Critical density of a soliton gas. Chaos 2016, 26, 023105. [Google Scholar] [CrossRef] [PubMed]
- Gelash, A.; Agafontsev, D.; Zakharov, V.; El, G.; Randoux, S.; Suret, P. Bound State Soliton Gas Dynamics Underlying the Spontaneous Modulational Instability. Phys. Rev. Lett. 2019, 123, 234102. [Google Scholar] [CrossRef] [PubMed]
- Gelash, A.A.; Agafontsev, D.S. Strongly interacting soliton gas and formation of rogue waves. Phys. Rev. E 2018, 98, 1–11. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Dremov, S. Multiple Soliton Interactions on the Surface of Deep Water. Fluids 2020, 5, 65. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Zakharov, V. Soliton Turbulence in Approximate and Exact Models for Deep Water Waves. Fluids 2020, 5, 67. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Shurgalina, E. KDV soliton gas: Interactions and turbulence. In Challenges in Complexity: Dynamics, Patterns, Cognition; Aronson, I., Pikovsky, A., Rulkov, N., Tsimring, L., Eds.; Series: Nonlinear Systems and Complexity; Springer: Berlin, Germany, 2017; Volume 20, pp. 295–306. [Google Scholar]
- Didenkulova, E.G.; Pelinovsky, E.N. The Role of a Thick Soliton in the Dynamics of the Soliton Gas Within the Framework of the Gardner Equation. Radiophys. Quantum Electron. 2019, 61, 623–632. [Google Scholar] [CrossRef]
- Shurgalina, E.G.; Pelinovsky, E.N. Nonlinear dynamics of a soliton gas: Modified Korteweg-de Vries equation framework. Phys. Lett. A 2016, 380, 2049–2053. [Google Scholar] [CrossRef]
- Dutykh, D.; Pelinovsky, E. Numerical simulation of a solitonic gas in KdV and KdV–BBM equations. Phys. Lett. A 2014, 378, 3102–3110. [Google Scholar] [CrossRef]
- El, G.; Tovbis, A. Spectral theory of soliton and breather gases for the focusing nonlinear Schrödinger equation. Phys. Rev. E 2020, 101, 052207. [Google Scholar] [CrossRef]
- El, G.A.; Kamchatnov, A.M. Kinetic equation for a dense soliton gas. Phys. Rev. Lett. 2005, 95, 1–4. [Google Scholar] [CrossRef] [PubMed]
- El, G.A.; Kamchatnov, A.M.; Pavlov, M.V.; Zykov, S.A. Kinetic equation for a soliton gas and its hydrodynamic reductions. J. Nonlinear Sci. 2011, 21, 151–191. [Google Scholar] [CrossRef]
- Pelinovsky, E.N.; Shurgalina, E.G. Formation of freak waves in a soliton gas described by the modified Korteweg–de Vries equation. Dokl. Phys. 2016, 61, 423–426. [Google Scholar] [CrossRef]
- Didenkulova (Shurgalina), E.G. Numerical modeling of soliton turbulence within the focusing Gardner equation: Rogue wave emergence. Physics D 2019, 399, 35–41. [Google Scholar] [CrossRef]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photonics 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.M.; Devine, N. Breather turbulence versus soliton turbulence: Rogue waves, probability density functions, and spectral features. Phys. Rev. E 2016, 94, 022212. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Devine, N.; Akhmediev, N. Integrable Turbulence and Rogue Waves: Breathers or Solitons? Phys. Rev. Lett. 2016, 116, 103901. [Google Scholar] [CrossRef]
- Slunyaev, A.V.; Pelinovsky, E.N. Role of multiple soliton interactions in the generation of rogue waves: The modified korteweg-de vries framework. Phys. Rev. Lett. 2016, 117, 214501. [Google Scholar] [CrossRef]
- Slunyaev, A. On the optimal focusing of solitons and breathers in long-wave models. Stud. Appl. Math. 2019, 142, 385–413. [Google Scholar] [CrossRef]
- Lamb, G.L. Elements of Soliton Theory; Wiley: New York, NY, USA, 1980; p. 289. [Google Scholar]
- Lamb, K.G.; Polukhina, O.; Talipova, T.; Pelinovsky, E.; Xiao, W.; Kurkin, A. Breather generation in fully nonlinear models of a stratified fluid. Phys. Rev. E 2007, 75, 046306. [Google Scholar] [CrossRef]
- Talipova, T.; Kurkina, O.; Kurkin, A.; Didenkulova, E.; Pelinovsky, E. Internal Wave Breathers in the Slightly Stratified Fluid. Microgravity Sci. Technol. 2020, 32, 69–77. [Google Scholar] [CrossRef]
- Pelinovsky, D.; Grimshaw, R. Structural transformation of eigenvalues for a perturbed algebraic soliton potential. Phys. Lett. A 1997, 229, 165–172. [Google Scholar] [CrossRef]
- Slyunyaev, A.V. Dynamics of localized waves with large amplitude in a weakly dispersive medium with a quadratic and positive cubic nonlinearity. J. Exp. Theor. Phys. 2001, 92, 529–534. [Google Scholar] [CrossRef]
- Chow, K.W.; Grimshaw, R.H.J.; Ding, E. Interactions of breathers and solitons in the extended Korteweg–de Vries equation. Wave Motion 2005, 43, 158–166. [Google Scholar] [CrossRef]
- Zhang, D.-J.; Zhao, S.-L.; Sun, Y.-Y.; Zhou, J. Solutions to the modified Korteweg–de Vries equation. Rev. Math. Phys. 2014, 26, 1430006. [Google Scholar] [CrossRef]
- Alejo, M.A.; Munoz, C. Nonlinear stability of mKdV breathers. Commun. Math. Phys. 2013, 324, 233–262. [Google Scholar] [CrossRef]
- Didenkulova, E.; Pelinovsky, E. Breather’s Properties within the Framework of the Modified Korteweg–de Vries Equation. Symmetry 2020, 12, 638. [Google Scholar] [CrossRef]
- Fronberg, B. A Practical Guide to Pseudospectral Methods; Cambridge University Press: Cambridge, UK, 1998; p. 231. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).