The Split Equality Fixed Point Problem of Demicontractive Operators with Numerical Example and Application

Abstract

This paper aims to propose a new reckoning method for solving the split equality fixed point problem of demicontractive operators in Hilbert spaces, and to establish a theorem with regard to the strong convergence of this new scheme. As an application, we also consider quasi-pseudo-contractive operators and obtain a result on the solution to the split equality fixed point problem in the framework of Hilbert spaces. A numerical example is also provided.

1. Introduction

Consider three Hilbert spaces, ${\mathcal{H}}_1$, ${\mathcal{H}}_2$, and ${\mathcal{H}}_3$, and two nonempty, closed, and convex sets $C\subset {\mathcal{H}}_1$ and $Q\subset {\mathcal{H}}_2$. In addition, consider a bounded linear mapping $\mathcal{A}:{\mathcal{H}}_1\to {\mathcal{H}}_2$, and $S:{\mathcal{H}}_1\to {\mathcal{H}}_1$, $T:{\mathcal{H}}_2\to {\mathcal{H}}_2$ be mappings.

The split feasibility problem (SFP) appeared first in 1994, in a work of Censor and Elfving [1]; it refers to determining an element in the set

$$\Gamma =\{x\in C:\mathcal{A}x\in Q\}\ne \varnothing .$$

Subsequently, signal processing and the reconstruction of images have benefited by the development of iterative methods for solving the SFP; see [2,3,4].

The split common fixed point problem (SCFP) appeared in a paper of Censor and Segal [5]; it refers to determining a point x satisfying

$$\begin{array}{c}\hfill x\in F(S)\mathrm{so}\mathrm{that}\mathcal{A}x\in F(T),\end{array}$$

(1)

where the mappings S and T are nonlinear, and $\mathcal{A}$ is as above. Here, $F(S)$ and $F(T)$ are formed by all the fixed points of S and T, respectively. It can be observed that the SFP can be obtained by an adequate choice, namely considering orthogonal projections as operators S and T. In the recent years, the reconstruction of images or the radio-therapy have used, as a beneficial tool, the SCFP (1) [6,7,8,9,10,11,12,13,14].

In [5], in order to study the SCFP (1), the next reckoning algorithm was designed by Censor and Segal. For $x_1\in {\mathcal{H}}_1$, define

$$\begin{array}{c}\hfill x_{n+1}=S(x_n-\gamma {\mathcal{A}}^{\ast }(I-T)\mathcal{A}{x}_n),n\in \mathbb{N},\end{array}$$

where S and T are directed mappings, I is the identity operator on ${\mathcal{H}}_2$ and $\gamma \in (0,2/{\parallel \mathcal{A}\parallel }^2)$. They also obtained a result concerning the weak convergence with regard to the SCFP (1). Meanwhile, their statement was further developed to mappings endowed with properties such as quasi-nonexpansiveness [7,15] or demicontractility [8], with the same weakly convergence of $\{x_n\}$ to an element satisfying the SCFP (1).

Recently, Moudafi [16] has addressed the split equality fixed point problem (SEFP on short):

$$\begin{array}{c}\hfill \mathrm{Determine}x\in F(S),\mathrm{and}y\in F(T)\mathrm{for}\mathrm{which}\mathcal{A}x=\mathcal{B}y,\end{array}$$

(2)

where $\mathcal{A}:{\mathcal{H}}_1\to {\mathcal{H}}_3$ and $\mathcal{B}:{\mathcal{H}}_2\to {\mathcal{H}}_3$ are characterized by boundedness and linearity, S and T are characterized by firmly quasi-nonexpansiveness. (2)-type problems allow a symmetric and partial relation with respect to both variables. The goal is the cover of a wide number of situations, such as applications in game theory, decomposition methods for differential equations or radio-therapy. In the case when $\mathcal{B}=I$ and ${\mathcal{H}}_2={\mathcal{H}}_3$, the SEFP (2) reduces to the SCFP (1).

In order to solve the SEFP (2), a simultaneous numerical method was proposed by Moudafi and Al-Shemas [17]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{n+1}=S(x_n-{\gamma }_n{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n)),\hfill \\ y_{n+1}=T(y_n+{\gamma }_n{\mathcal{B}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n)),n\in \mathbb{N},\hfill \end{array}\right.\end{array}$$

where the operators S and T are endowed with the firmly quasi-nonexpansiveness property, and ${\gamma }_k\in (ϵ,\frac{2}{{\lambda }_{\mathcal{A}}+{\lambda }_{\mathcal{B}}}-ϵ)$, and ${\lambda }_{\mathcal{A}}$, ${\lambda }_{\mathcal{B}}$ symbolize the spectral radii of ${\mathcal{A}}^{\ast }\mathcal{A}$ and ${\mathcal{B}}^{\ast }\mathcal{B}$, respectively.

In the above work, the step sizes relate to the norm $\parallel \mathcal{A}\parallel$ or the norm $\parallel \mathcal{B}\parallel$, which are generally not easily computable in practice. To overcome this difficulty, variable step sizes which ultimately have no relation with the norm are considered (see, e.g., [11,18,19,20,21]). Regarding their step sizes, Wang and Xu [21] dealt with

$$\begin{array}{c}\hfill {\tau }_n=\frac{{\rho }_n}{\parallel x_n-S{x}_n+{\mathcal{A}}^{\ast }(I-T)\mathcal{A}{x}_n\parallel },\end{array}$$

(3)

where ${\rho }_n\ge 0$, $n\in \mathbb{N}$, and

$$\begin{array}{c}\hfill \sum _{n=0}^{\infty }{\rho }_n=\infty \mathrm{and}\sum _{n=0}^{\infty }{\rho }_n^2<\infty ,\end{array}$$

(4)

and they proposed the following numerical formula to find a solution to the SCFP (1):

$$\begin{array}{c}\hfill x_{n+1}=x_n-{\tau }_n(x_n-S{x}_n+{\mathcal{A}}^{\ast }(I-T)\mathcal{A}{x}_n),n\in \mathbb{N}.\end{array}$$

By imposing suitable hypotheses, they stated a weak convergence result. Obviously, the step sizes chosen here are not based on the norm $\parallel \mathcal{A}\parallel$.

In 2018, Cui et al. [22] widened the result in [21] from nonexpansiveness to demicontractive continuous operators under assumptions (3) and (4). Furthermore, they have used their result in order to propose a solution to the SEFP with the following variable step size:

$$\begin{array}{c}\hfill {\tau }_n=\frac{{\rho }_n}{(\parallel x_n-S{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2+\parallel y_n-T{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n){{\parallel }^2)}^{\frac{1}{2}}}.\end{array}$$

(5)

On the other hand, inspired by the work of Attouch [23], Moudafi [16] proposed a viscosity approximation method for nonexpansive mappings to obtain strong results in Hilbert spaces. This viscosity approximation method has been an object of study for many authors e.g., see [24,25,26,27].

In this paper, we consider a new reckoning scheme to determine a solution to the SEFP of operators featuring the demicontractility, by using viscosity approximation methods in Hilbert spaces. A result with respect to the strong convergence of this scheme is stated and proved. As an application, we consider quasi pseudo-contractive operators and apply our result to solve the associated SEFP problem.

2. Preliminaries

Along this work, we need a Hilbert space $\mathcal{H}$ with the scalar product $⟨·,·⟩$, and norm $\parallel ·\parallel$. $\mathbb{R}$ designates the set of all real numbers. The strong (weak) convergence of a sequence from $\mathcal{H}$ to a point in $\mathcal{H}$, is designated by → (⇀). Along the paper $C\subset \mathcal{H}$ is a nonempty, closed, convex set, T is an operator defined on C into $\mathcal{H}$, and $F(T)$ is the set of the fixed points of T.

In order to prove our main results, we recollect the following definitions.

Definition 1.

A selfmapping T on $\mathcal{H}$ is called

(i) 

contractive if there can be found $\sigma \in (0,1)$ with the property

$$\parallel Ta-Tb\parallel \le \sigma \parallel a-b\parallel ,\mathrm{for}\mathrm{all}a,b\in \mathcal{H};$$

(ii) 

nonexpansive if

$$\parallel Ta-Tb\parallel \le \parallel a-b\parallel ,\mathrm{for}\mathrm{all}a,b\in \mathcal{H};$$

(iii) 

quasi-nonexpansive if

$$\parallel Ta-c\parallel \le \parallel a-c\parallel ,\mathrm{for}\mathrm{all}(a,c)\in \mathcal{H}\times F(T);$$

(iv) 

directed (firmly quasi-nonexpansive) if

$${\parallel Ta-c\parallel }^2\le {\parallel a-c\parallel }^2-{\parallel a-Ta\parallel }^2,\mathrm{for}\mathrm{all}(a,c)\in \mathcal{H}\times F(T);$$

(v) 

σ-demicontractive if there can be found a constant $\sigma \in (-\infty ,1)$ such that

$${\parallel Ta-c\parallel }^2\le {\parallel a-c\parallel }^2+\sigma {\parallel a-Ta\parallel }^2,\mathrm{for}\mathrm{all}(a,c)\in \mathcal{H}\times F(T),$$

which is the same as

$$\begin{array}{c}\hfill {\displaystyle ⟨a-Ta,a-c⟩\ge \frac{1-\sigma }{2}{\parallel a-Ta\parallel }^2,\mathrm{for}\mathrm{all}(a,c)\in \mathcal{H}\times F(T);}\end{array}$$

(6)

(vi) 

quasi-pseudo-contractive if

$${\parallel Ta-c\parallel }^2\le {\parallel a-c\parallel }^2+{\parallel a-Ta\parallel }^2,\mathrm{for}\mathrm{all}(a,c)\in \mathcal{H}\times F(T).$$

It can be observed that the class of operators endowed with demicontractility contains other classes, for example those of quasi-nonexpansive mappings or directed mappings.

Remark 1.

Every σ-demicontractive operator ($\sigma \le 0$) is characterized by quasi-nonexpansiveness. In addition, every directed mapping is (−1)-demicontractive.

Example 1

([28]; see Example 2.5). Take $\mathcal{H}=l_2$ and $T:l_2\to l_2$, $Tx=-kx$, $x\in l_2$, $k>1$. Then, $F(T)=\{0\}$ and T is an operator endowed with the demicontractility property, but not with the quasi-nonexpansiveness.

The orthogonal projection $P_C$ from $\mathcal{H}$ onto C,

$$P_{C}u:={\mathrm{argmin}}_{v\in C}\{\parallel u-v\parallel \},u\in \mathcal{H},$$

provides an example of a mapping endowed with firmly nonexpansiveness. It is known (please see [29]) that $P_{C}u$ is characterized by the inequality

$$\begin{array}{c}\hfill ⟨u-P_{C}u,v-P_{C}u⟩\le 0,v\in C.\end{array}$$

Recollect that $I-T$ is characterized by demiclosedness at 0 if for any $\{y_n\}\subset \mathcal{H}$ and $y^{\ast }\in \mathcal{H}$,

$$\begin{array}{c}\hfill \left.\begin{array}{c}{y}_n\rightharpoonup y^{\ast }\hfill \\ (I-T)y_n\to 0\hfill \end{array}\right\}\Rightarrow y^{\ast }=T{y}^{\ast }.\end{array}$$

If $C\subset \mathcal{H}$ is a nonempty, closed, and convex set, and $T:C\to \mathcal{H}$ is nonexpansive, according to [30], the operator $I-T$ is demiclosed on C. Nevertheless, the same is not true if T features quasi-nonexpansiveness instead of nonexpansiveness as the following example shows.

Example 2

([28]; see Example 2.11). The operator

$$\begin{array}{c}\hfill \mathcal{T}:[0,1]\to [0,1],\mathcal{T}x=\left\{\begin{array}{cc}\frac{x}{5},\hfill & x\in [0,\frac{1}{2}],\hfill \\ xsin\pi x,\hfill & x\in (\frac{1}{2},1].\hfill \end{array}\right.\end{array}$$

features the quasi-nonexpansiveness, but $I-\mathcal{T}$ is not characterized by the demiclosedness at 0.

$T:\mathcal{H}\to \mathcal{H}$ is called semi-compact if, for any bounded sequence $\{x_n\}\subset \mathcal{H}$ with $\parallel x_n-T{x}_n\parallel \to 0$, there can be found $\{x_{n_i}\}\subset \{x_n\}$ such that $x_{n_i}\to x\in \mathcal{H}$.

In the following, we recollect some lemmas needed in our main results. The first one provides conditions on which a sequence with adequate properties converges to zero.

Lemma 1.

[31] Presume that $a_n>0$, $n\in \mathbb{N}$, such that

$$a_{n+1}\le (1-{\gamma }_n)a_n+{\gamma }_n{\Delta }_n+{ϵ}_n,n\ge 0,$$

where $\{{\gamma }_n\}\subset (0,1)$ and $\{{\Delta }_n\}\subset \mathbb{R}$ for which

(i) 

${\sum }_{n=0}^{\infty }{\gamma }_n=\infty ;$

(ii) 

${ϵ}_n\ge 0(n\ge 0)$ and ${\sum }_{n=0}^{\infty }{ϵ}_n<\infty ;$

(iii) 

${lim\; sup}_{n\to \infty }{\Delta }_n\le 0$ or ${\Sigma }_{n=1}^{\infty }{\gamma }_n\left|{\Delta }_n\right|<\infty .$

Then ${lim}_{n\to \infty }{a}_n=0.$

The next lemma recalls properties of a mapping which satisfies demicontractive properties.

Lemma 2

([32]; see Proposition 2.1). Presume that $T:C\to C$ is a μ-demicontractive operator. Then, $F(T)$ is characterized by closedness and convexity.

Eventually, we also use the demiclosedness property of nonexpansive mappings.

Lemma 3

([33]). If $V:\mathcal{H}\to \mathcal{H}$ is a nonexpansive operator, then $I-V$ is characterized by demiclosedness at 0.

3. Main Results

Unless otherwise specified, in the sequel, we presume that ${\mathcal{H}}_1$, ${\mathcal{H}}_2$, and ${\mathcal{H}}_3$ are real Hilbert spaces. Here, $S:{\mathcal{H}}_1\to {\mathcal{H}}_1$ and $T:{\mathcal{H}}_2\to {\mathcal{H}}_2$ are demicontractive operators of constants $\beta$, $\mu \in (0,1)$, respectively. Let $f_1:{\mathcal{H}}_1\to {\mathcal{H}}_1$ and $f_2:{\mathcal{H}}_2\to {\mathcal{H}}_2$ be two contractive operators with constants ${\alpha }_1,{\alpha }_2\in (0,\frac{1}{\sqrt{2}})$, respectively. Consider two operators $\mathcal{A}:{\mathcal{H}}_1\to {\mathcal{H}}_3$ and $\mathcal{B}:{\mathcal{H}}_2\to {\mathcal{H}}_3$ characterized by boundedness and linearity, with their adjoints ${\mathcal{A}}^{\ast }$ and ${\mathcal{B}}^{\ast }$, respectively. Set $\gamma =max\{\beta ,\mu \}$ and $\alpha =max\{{\alpha }_1,{\alpha }_2\}$.

$\Omega$ designates the set of the solutions to problem (2), more precisely

$$\Omega =\{(x,y)\in {\mathcal{H}}_1\times {\mathcal{H}}_2:x\in F(S),y\in F(T)\mathrm{and}\mathcal{A}x=\mathcal{B}y\}.$$

Presume that $\Omega \ne \varnothing$. Denote by ${\mathcal{H}}^{\ast }={\mathcal{H}}_1\times {\mathcal{H}}_2$. We endow this set with the scalar product:

$$⟨(x_1,y_1),(x_2,y_2)⟩=⟨x_1,x_2⟩+⟨y_1,y_2⟩,\mathrm{for}\mathrm{all}(x_1,y_1),(x_2,y_2)\in {\mathcal{H}}^{\ast }.$$

Observe that ${\mathcal{H}}^{\ast }$ can be organized as a real Hilbert space and

$$\parallel (x,y)\parallel ={(\parallel x\parallel }^2+{\parallel y\parallel }^2{)}^{\frac{1}{2}},\mathrm{for}\mathrm{all}(x,y)\in {\mathcal{H}}^{\ast }.$$

We propose the algorithm below to determine the solutions to problem (2).

Algorithm 1.Let $x_1\in {\mathcal{H}}_1$, and $y_1\in {\mathcal{H}}_2$ be arbitrarily given.

The algorithm becomes   Step 1. If $$\parallel x_n-S{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2+{\parallel y_n-T{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n)\parallel }^2=0,$$ then stop, and $(x_n,y_n)$ fulfills problem (2); otherwise, move on to the next step.   Step 2. Define $x_{n+1}$ and $y_{n+1}$, $$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{n+1}={\alpha }_n{f}_1(x_n)+(1-{\alpha }_n)[x_n-{\tau }_n(x_n-S{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n)],\hfill \\ y_{n+1}={\alpha }_n{f}_2(y_n)+(1-{\alpha }_n)[y_n-{\tau }_n(y_n-T{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n)],\hfill \end{array}\right.\end{array}$$ where the step size ${\tau }_n$ is taken as in relation (5), and return to Step 1.

Lemma 4.

$(x^{\ast },y^{\ast })\in {\mathcal{H}}_1\times {\mathcal{H}}_2$ checks problem (2) if and only if

$$\begin{array}{c}\hfill \parallel x^{\ast }-S{x}^{\ast }+{\mathcal{A}}^{\ast }(\mathcal{A}{x}^{\ast }-\mathcal{B}{y}^{\ast }){\parallel }^2+{\parallel y^{\ast }-T{y}^{\ast }+{\mathcal{B}}^{\ast }(\mathcal{B}{y}^{\ast }-\mathcal{A}{x}^{\ast })\parallel }^2=0.\end{array}$$

(7)

Proof. 

Suppose that $(x^{\ast },y^{\ast })$ solves problem (2). Then, $x^{\ast }=S{x}^{\ast },y^{\ast }=T{y}^{\ast }$ and $\mathcal{A}{x}^{\ast }=\mathcal{B}{y}^{\ast }$. It is obvious that $\parallel x^{\ast }-S{x}^{\ast }+{\mathcal{A}}^{\ast }(\mathcal{A}{x}^{\ast }-\mathcal{B}{y}^{\ast }){\parallel }^2+{\parallel y^{\ast }-T{y}^{\ast }+{\mathcal{B}}^{\ast }(\mathcal{B}{y}^{\ast }-\mathcal{A}{x}^{\ast })\parallel }^2=0.$

To prove the converse statement, presume that (7) holds. Since S and T are demicontractive, for any

$(x,y)\in \Omega$, inequality (6) compels

$$\begin{array}{c}\hfill ⟨x^{\ast }-S{x}^{\ast },x^{\ast }-x⟩\ge \frac{1-\beta }{2}{\parallel x^{\ast }-S{x}^{\ast }\parallel }^2,\end{array}$$

(8)

$$\begin{array}{c}\hfill ⟨y^{\ast }-T{y}^{\ast },y^{\ast }-y⟩\ge \frac{1-\mu }{2}{\parallel y^{\ast }-T{y}^{\ast }\parallel }^2.\end{array}$$

(9)

Taking advantage of inequalities (8) and (9), and $\mathcal{A}x=\mathcal{B}y$, we obtain

$$\begin{array}{ccc}\hfill 0& =& \parallel x^{\ast }-S{x}^{\ast }+{\mathcal{A}}^{\ast }(\mathcal{A}{x}^{\ast }-\mathcal{B}{y}^{\ast })\parallel \parallel x^{\ast }-x\parallel +\parallel y^{\ast }-T{y}^{\ast }+{\mathcal{B}}^{\ast }(\mathcal{B}{y}^{\ast }-\mathcal{A}{x}^{\ast })\parallel \parallel y^{\ast }-y\parallel \hfill \\ & \ge & ⟨x^{\ast }-S{x}^{\ast }+{\mathcal{A}}^{\ast }(\mathcal{A}{x}^{\ast }-\mathcal{B}{y}^{\ast }),x^{\ast }-x⟩+⟨y^{\ast }-T{y}^{\ast }+{\mathcal{B}}^{\ast }(\mathcal{B}{y}^{\ast }-\mathcal{A}{x}^{\ast }),y^{\ast }-y⟩\hfill \\ & =& ⟨x^{\ast }-S{x}^{\ast },x^{\ast }-x⟩+⟨\mathcal{A}{x}^{\ast }-\mathcal{B}{y}^{\ast },\mathcal{A}{x}^{\ast }-\mathcal{A}x⟩+⟨y^{\ast }-T{y}^{\ast },y^{\ast }-y⟩+⟨\mathcal{B}{y}^{\ast }-\mathcal{A}{x}^{\ast },\mathcal{B}{y}^{\ast }-\mathcal{B}y⟩\hfill \\ & \ge & \frac{1-\beta }{2}\parallel x^{\ast }-S{x}^{\ast }{\parallel }^2+\frac{1-\mu }{2}\parallel y^{\ast }-T{y}^{\ast }{\parallel }^2+{\parallel \mathcal{A}{x}^{\ast }-\mathcal{B}{y}^{\ast }\parallel }^2,\hfill \end{array}$$

which implies that $x^{\ast }\in F(S)$, $y^{\ast }\in F(T)$ and $\mathcal{A}{x}^{\ast }=\mathcal{B}{y}^{\ast }$, completing the proof. □

By Lemma 4, we may assume that Algorithm 1 produced, by and large, an infinite sequence $\{x_n\}$. If the algorithm requires only a finite number of iterations, a solution is obviously reached.

Lemma 5.

Suppose $\{x_n\}$ and $\{y_n\}$ are sequences endowed with a boundedness property, and

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_n-S{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n)\parallel =\underset{n\to \infty }{lim}\parallel y_n-T{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n)\parallel =0.\end{array}$$

Then, ${lim}_{n\to \infty }\parallel x_n-S{x}_n\parallel =0$, ${lim}_{n\to \infty }\parallel y_n-T{y}_n\parallel =0$, and ${lim}_{n\to \infty }\parallel \mathcal{A}{x}_n-\mathcal{B}{y}_n\parallel =0.$

Proof. 

Set $z_n=x_n-S{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n),$ $w_n=y_n-T{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n)$. For any $(x^{\ast },y^{\ast })\in \Omega$, by relation (6), we obtain

$$\begin{array}{cc}& ⟨z_n,x_n-x^{\ast }⟩+⟨w_n,y_n-y^{\ast }⟩\hfill \\ =& ⟨x_n-S{x}_n,x_n-x^{\ast }⟩+⟨\mathcal{A}{x}_n-\mathcal{B}{y}_n,\mathcal{A}{x}_n-\mathcal{A}{x}^{\ast }⟩+⟨y_n-T{y}_n,y_n-y^{\ast }⟩+⟨\mathcal{B}{y}_n-\mathcal{A}{x}_n,\mathcal{B}{y}_n-\mathcal{B}{y}^{\ast }⟩\hfill \\ \ge & \frac{1-\beta }{2}\parallel (I-S)x_n{\parallel }^2+\frac{1-\mu }{2}\parallel (I-T)y_n{\parallel }^2+{\parallel \mathcal{A}{x}_n-\mathcal{B}{y}_n\parallel }^2.\hfill \end{array}$$

Since $\parallel z_n\parallel \to 0$, $\parallel w_n\parallel \to 0$, the boundedness of $\{x_n\}$ and $\{y_n\}$ compels

$$\begin{array}{cc}& \frac{1-\beta }{2}\parallel (I-S)x_n{\parallel }^2+\frac{1-\mu }{2}\parallel (I-T)y_n{\parallel }^2+{\parallel \mathcal{A}{x}_n-\mathcal{B}{y}_n\parallel }^2\hfill \\ \le & ⟨z_n,x_n-x^{\ast }⟩+⟨w_n,y_n-y^{\ast }⟩\le \parallel z_n\parallel \parallel x_n-x^{\ast }\parallel +\parallel w_n\parallel \parallel y_n-y^{\ast }\parallel \to 0.\hfill \end{array}$$

Due to the fact that $\beta$, $\mu \in (0,1)$, the conclusion has been proved. □

The next theorem refers to the strong convergence of the scheme designed previously; it links it also to a variational inequality.

Theorem 1.

Let $\{{\alpha }_n\}\subseteq (0,1)$ and $\{{\rho }_n\}\subseteq (0,+\infty )$ be two sequences. Assume that the following conditions are satisfied:

(a) 

$I-S$ and $I-T$ are demiclosed at 0;

(b) 

${\sum }_{n=1}^{\infty }{\rho }_n^2<\infty$;

(c) 

${lim}_{n\to \infty }{\alpha }_n=0$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$;

(d) 

${lim}_{n\to \infty }\frac{{\alpha }_n}{{\rho }_n}=0.$

Then, $\{(x_n,y_n)\}$ in Algorithm 1 is strongly convergent to $(x^{\ast },y^{\ast })\in \Omega$, the unique solution to the following variational inequality problem (VIP):

$$\begin{array}{c}\hfill ⟨((I-f_1)x^{\ast },(I-f_2)y^{\ast }),(x,y)-(x^{\ast },y^{\ast })⟩\ge 0,\mathrm{for}\mathrm{all}(x,y)\in \Omega .\end{array}$$

(10)

Proof. 

Lemma 2 ensures the closedness and convexity of $F(S)$ and $F(T)$. The boundedness and linearity of the operators $\mathcal{A}$ and B imply the closedness and the convexity of $\Omega$. Similarly to Step 1 in the proof of Theorem 3.3 in [34], the uniqueness of the solution to the VIP (10) follows; denote this solution by $(x^{\ast },y^{\ast })\in \Omega$.

Next, we have divided the proof into two stages.

Step 1. We prove that the boundedness characterizes the sequence $\{(x_n,y_n)\}$.

Set $z_n=x_n-S{x}_n+{\mathcal{B}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n)$, $w_n=y_n-T{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n)$, $p_n=x_n-{\tau }_n{z}_n$, and $q_n=y_n-{\tau }_n{w}_n$. Since $(x^{\ast },y^{\ast })\in \Omega$, by (6), we obtain

$$\begin{array}{cc}\hfill & ⟨z_n,x_n-x^{\ast }⟩+⟨w_n,y_n-y^{\ast }⟩\hfill \\ =& ⟨x_n-S{x}_n,x_n-x^{\ast }⟩+⟨\mathcal{A}{x}_n-\mathcal{B}{y}_n,\mathcal{A}{x}_n-\mathcal{A}{x}^{\ast }⟩+⟨y_n-T{y}_n,y_n-y^{\ast }⟩+⟨\mathcal{B}{y}_n-\mathcal{A}{x}_n,\mathcal{B}{y}_n-\mathcal{B}{y}^{\ast }⟩\hfill \\ \ge & \frac{1-\beta }{2}\parallel x_n-S{x}_n{\parallel }^2+\frac{1-\mu }{2}\parallel y_n-T{y}_n{\parallel }^2+{\parallel \mathcal{A}{x}_n-\mathcal{B}{y}_n\parallel }^2\hfill \\ \ge & \frac{1-\gamma }{2}\parallel x_n-S{x}_n{\parallel }^2+\frac{1-\gamma }{2}{\parallel y_n-T{y}_n\parallel }^2\hfill \\ & +\frac{1}{2\parallel {\mathcal{A}}^{\ast }{\parallel }^2}\parallel {\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2+\frac{1}{2\parallel {\mathcal{B}}^{\ast }{\parallel }^2}{\parallel {\mathcal{B}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n)\parallel }^2\hfill \\ \ge & \frac{1}{2}min\{1-\gamma ,\frac{1}{max\{\parallel {\mathcal{A}}^{\ast }{\parallel }^2,\parallel {\mathcal{B}}^{\ast }{\parallel }^2\}}\}(\parallel x_n-S{x}_n{\parallel }^2+{\parallel y_n-T{y}_n\parallel }^2\hfill \\ & +\parallel {\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2+\parallel {\mathcal{B}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2)\hfill \\ \ge & \frac{1}{4}min\{1-\gamma ,\frac{1}{max\{\parallel {\mathcal{A}}^{\ast }{\parallel }^2,\parallel {\mathcal{B}}^{\ast }{\parallel }^2\}}\}(\parallel x_n-S{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2\hfill \\ & +\parallel y_n-T{y}_n+{\mathcal{B}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2)\hfill \\ =& \tau (\parallel z_n{\parallel }^2+\parallel w_n{\parallel }^2),\hfill \end{array}$$

(11)

where $\tau =\frac{1}{4}min\left\{1-\gamma ,\frac{1}{max\{\parallel {\mathcal{A}}^{\ast }{\parallel }^2,\parallel {\mathcal{B}}^{\ast }{\parallel }^2\}}\right\}$.

Denote by $s_n=\parallel x_n-x^{\ast }{\parallel }^2+{\parallel y_n-y^{\ast }\parallel }^2$. From (5), we have ${\rho }_n={\tau }_n(\parallel z_n{\parallel }^2+\parallel w_n{{\parallel }^2)}^{\frac{1}{2}}$. Then, relation (11) leads us to

$$\begin{array}{ccc}\hfill \parallel p_n-x^{\ast }{\parallel }^2+{\parallel q_n-y^{\ast }\parallel }^2& =& \parallel x_n-x^{\ast }-{\tau }_n{z}_n{\parallel }^2+{\parallel y_n-y^{\ast }-{\tau }_n{w}_n\parallel }^2\hfill \\ & =& \parallel x_n-x^{\ast }{\parallel }^2+\parallel y_n-y^{\ast }{\parallel }^2+{\tau }_n^2(\parallel z_n{\parallel }^2+\parallel w_n{\parallel }^2)\hfill \\ & & -2{\tau }_n(⟨z_n,x_n-x^{\ast }⟩+⟨w_n,y_n-y^{\ast }⟩)\hfill \\ & \le & s_n-2\tau {\tau }_n(\parallel z_n{\parallel }^2+\parallel w_n{\parallel }^2)+{\tau }_n^2(\parallel z_n{\parallel }^2+\parallel w_n{\parallel }^2)\hfill \\ & =& s_n-2\tau {\rho }_n(\parallel z_n{\parallel }^2+\parallel w_n{{\parallel }^2)}^{\frac{1}{2}}+{\rho }_n^2\hfill \end{array}$$

(12)

$$\begin{array}{cc}\le & s_n+{\rho }_n^2.\hfill \end{array}$$

(13)

According to Algorithm 1, it follows

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{\ast }{\parallel }^2\le ({\alpha }_n\parallel f_1(x_n)-x^{\ast }\parallel +(1-{\alpha }_n)\parallel p_n-x^{\ast }{\parallel )}^2\hfill \\ =& {\alpha }_n^2\parallel f_1(x_n)-x^{\ast }{\parallel }^2+{(1-{\alpha }_n)}^2{\parallel p_n-x^{\ast }\parallel }^2+2{\alpha }_n(1-{\alpha }_n)\parallel f_1(x_n)-x^{\ast }\parallel \parallel p_n-x^{\ast }\parallel \hfill \\ \le & {\alpha }_n^2\parallel f_1(x_n)-x^{\ast }{\parallel }^2+{(1-{\alpha }_n)}^2{\parallel p_n-x^{\ast }\parallel }^2+{\alpha }_n(1-{\alpha }_n)(\parallel f_1(x_n)-x^{\ast }{\parallel }^2+\parallel p_n-x^{\ast }{\parallel }^2)\hfill \\ =& {\alpha }_n\parallel f_1(x_n)-x^{\ast }{\parallel }^2+(1-{\alpha }_n){\parallel p_n-x^{\ast }\parallel }^2\hfill \\ \le & {\alpha }_n(\parallel f_1(x_n)-f_1(x^{\ast })\parallel +\parallel f_1(x^{\ast })-x^{\ast }{\parallel )}^2+(1-{\alpha }_n){\parallel p_n-x^{\ast }\parallel }^2\hfill \\ \le & 2{\alpha }_n({\alpha }^2\parallel x_n-x^{\ast }{\parallel }^2+\parallel f_1(x^{\ast })-x^{\ast }{\parallel }^2)+(1-{\alpha }_n){\parallel p_n-x^{\ast }\parallel }^2.\hfill \end{array}$$

(14)

Analogously, we have

$$\begin{array}{c}\hfill \parallel y_{n+1}-y^{\ast }{\parallel }^2\le 2{\alpha }_n({\alpha }^2\parallel y_n-y^{\ast }{\parallel }^2+\parallel f_2(y^{\ast })-y^{\ast }{\parallel }^2)+(1-{\alpha }_n){\parallel q_n-y^{\ast }\parallel }^2.\end{array}$$

(15)

Relations (13)–(15) compel

$$\begin{array}{ccc}\hfill s_{n+1}& \le & 2{\alpha }^2{\alpha }_n{s}_n+2{\alpha }_n(\parallel f_1(x^{\ast })-x^{\ast }{\parallel }^2+\parallel f_2(y^{\ast })-y^{\ast }{\parallel }^2)+(1-{\alpha }_n)(\parallel p_n-x^{\ast }{\parallel }^2+\parallel q_n-y^{\ast }{\parallel }^2)\hfill \\ & \le & 2{\alpha }^2{\alpha }_n{s}_n+2{\alpha }_n(\parallel f_1(x^{\ast })-x^{\ast }{\parallel }^2+\parallel f_2(y^{\ast })-y^{\ast }{\parallel }^2)+(1-{\alpha }_n)(s_n+{\rho }_n^2)\hfill \\ & \le & [1-(1-2{\alpha }^2){\alpha }_n]s_n+{\rho }_n^2\hfill \\ & & +(1-2{\alpha }^2){\alpha }_n\frac{2(\parallel f_1(x^{\ast })-x^{\ast }{\parallel }^2+\parallel f_2(y^{\ast })-y^{\ast }{\parallel }^2)}{1-2{\alpha }^2}.\hfill \end{array}$$

Mathematical induction ensures us that the next inequality holds true

$$s_{n+1}\le max\{s_1,\frac{2(\parallel f_1(x^{\ast })-x^{\ast }{\parallel }^2+\parallel f_2(y^{\ast })-y^{\ast }{\parallel }^2)}{1-2{\alpha }^2}\}+\sum _{i=1}^n{\rho }_i^2.$$

Taking also into account condition (b) of the theorem, we get that $\{s_n\}$ is bounded, so do $\{(x_n,y_n)\}$, $\{x_n\}$, $\{y_n\}$. Relation (11) implies the boundedness of $\{z_n\}$ and $\{w_n\}$.

Step 2. We prove now the strong convergence of $\{(x_n,y_n)\}$ to $(x^{\ast },y^{\ast })$.

In fact, since $f_1$ and $f_2$ are contractions, the next relations hold true:

$$\begin{array}{cc}\hfill & 2⟨f_1(x_n)-x^{\ast },p_n-x^{\ast }⟩+2⟨f_2(y_n)-y^{\ast },q_n-y^{\ast }⟩\hfill \\ \le & 2\alpha \parallel x_n-x^{\ast }\parallel \parallel p_n-x^{\ast }\parallel +2\alpha \parallel y_n-y^{\ast }\parallel \parallel q_n-y^{\ast }\parallel \hfill \\ & +2⟨f_1(x^{\ast })-x^{\ast },p_n-x^{\ast }⟩+2⟨f_2(y^{\ast })-y^{\ast },q_n-y^{\ast }⟩\hfill \\ \le & {\alpha }^2{s}_n+\parallel p_n-x^{\ast }{\parallel }^2+{\parallel q_n-y^{\ast }\parallel }^2+2(⟨f_1(x^{\ast })-x^{\ast },p_n-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },q_n-y^{\ast }⟩).\hfill \end{array}$$

(16)

Algorithm 1, (12) and (16) lead us to

$$\begin{array}{ccc}\hfill s_{n+1}& =& \parallel (1-{\alpha }_n)(p_n-x^{\ast })+{\alpha }_n(f_1(x_n)-x^{\ast }){\parallel }^2+{\parallel (1-{\alpha }_n)(q_n-y^{\ast })+{\alpha }_n(f_2(y_n)-y^{\ast })\parallel }^2\hfill \\ & =& {(1-{\alpha }_n)}^2(\parallel p_n-x^{\ast }{\parallel }^2+\parallel q_n-y^{\ast }{\parallel }^2)+{\alpha }_n^2(\parallel f_1(x^{\ast })-x^{\ast }{\parallel }^2+\parallel f_2(y^{\ast })-y^{\ast }{\parallel }^2)\hfill \\ & & +2{\alpha }_n(1-{\alpha }_n)(⟨f_1(x_n)-x^{\ast },p_n-x^{\ast }⟩+⟨f_2(y_n)-y^{\ast },q_n-y^{\ast }⟩)\hfill \\ & \le & {(1-{\alpha }_n)}^2(\parallel p_n-x^{\ast }{\parallel }^2+\parallel q_n-y^{\ast }{\parallel }^2)+{\alpha }_n^2(\parallel f_1(x^{\ast })-x^{\ast }{\parallel }^2+\parallel f_2(y^{\ast })-y^{\ast }{\parallel }^2)\hfill \\ & & +{\alpha }_n(1-{\alpha }_n)[{\alpha }^2{s}_n+\parallel p_n-x^{\ast }{\parallel }^2+{\parallel q_n-y^{\ast }\parallel }^2\hfill \\ & & +2(⟨f_1(x^{\ast })-x^{\ast },p_n-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },q_n-y^{\ast }⟩)]\hfill \\ & =& (1-{\alpha }_n)(\parallel p_n-x^{\ast }{\parallel }^2+\parallel q_n-y^{\ast }{\parallel }^2)+{\alpha }_n(1-{\alpha }_n){\alpha }^2{s}_n+{\alpha }_n^{2}M\hfill \\ & & +2{\alpha }_n(1-{\alpha }_n)(⟨f_1(x^{\ast })-x^{\ast },p_n-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },q_n-y^{\ast }⟩)\hfill \\ & \le & (1-{\alpha }_n)(s_n-2\tau {\rho }_n(\parallel z_n{\parallel }^2+\parallel w_n{\parallel }^2{)}^{\frac{1}{2}}+{\rho }_n^2)+{\alpha }_n(1-{\alpha }_n){\alpha }^2{s}_n+{\alpha }_n^{2}M\hfill \\ & & +2{\alpha }_n(1-{\alpha }_n)(⟨f_1(x^{\ast })-x^{\ast },p_n-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },q_n-y^{\ast }⟩)\hfill \\ & \le & [1-{\alpha }_n(1-(1-{\alpha }_n){\alpha }^2)]s_n+{\rho }_n^2+{\alpha }_n(1-(1-{\alpha }_n){\alpha }^2)·\hfill \\ & & [\frac{2(1-{\alpha }_n)}{1-(1-{\alpha }_n){\alpha }^2}(⟨f_1(x^{\ast })-x^{\ast },p_n-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },q_n-y^{\ast }⟩)\hfill \\ & & -\frac{2\tau (1-{\alpha }_n)}{1-(1-{\alpha }_n){\alpha }^2}\frac{{\rho }_n}{{\alpha }_n}(\parallel z_n{\parallel }^2+\parallel w_n{{\parallel }^2)}^{\frac{1}{2}}+\frac{{\alpha }_{n}M}{1-(1-{\alpha }_n){\alpha }^2}]\hfill \\ & =& [1-{\alpha }_n(1-(1-{\alpha }_n){\alpha }^2)]s_n+{\alpha }_n(1-(1-{\alpha }_n){\alpha }^2)b_n+{\rho }_n^2,\hfill \end{array}$$

(17)

where

$$\begin{array}{ccc}\hfill M& =& \parallel f_1(x^{\ast })-x^{\ast }{\parallel }^2+{\parallel f_2(y^{\ast })-y^{\ast }\parallel }^2,\hfill \\ \hfill b_n& =& \frac{2(1-{\alpha }_n)}{1-(1-{\alpha }_n){\alpha }^2}(⟨f_1(x^{\ast })-x^{\ast },p_n-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },q_n-y^{\ast }⟩)\hfill \\ & & -\frac{2\tau (1-{\alpha }_n)}{1-(1-{\alpha }_n){\alpha }^2}\frac{{\rho }_n}{{\alpha }_n}(\parallel z_n{\parallel }^2+\parallel w_n{{\parallel }^2)}^{\frac{1}{2}}+\frac{{\alpha }_{n}M}{1-(1-{\alpha }_n){\alpha }^2}.\hfill \end{array}$$

From condition $(b)$, we get that

$$\begin{array}{c}\hfill \parallel p_n-x_n\parallel =\parallel {\tau }_n{z}_n\parallel \le {\tau }_n(\parallel z_n{\parallel }^2+\parallel w_n{{\parallel }^2)}^{\frac{1}{2}}={\rho }_n\to 0,\\ \hfill \parallel q_n-y_n\parallel =\parallel {\tau }_n{w}_n\parallel \le {\tau }_n(\parallel z_n{\parallel }^2+\parallel w_n{{\parallel }^2)}^{\frac{1}{2}}={\rho }_n\to 0.\end{array}$$

Since $\{s_n\}$ is bounded, from (13) and condition $(b)$, it follows that $\{p_n\}$ and $\{q_n\}$ are bounded. Hence, $\{b_n\}$ is bounded from above, that is, ${lim\; sup}_{n\to \infty }{b}_n$ is finite. By consequence, there can be found a subsequence $\{n_k\}\subseteq \{n\}$ such that

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim\; sup}{b}_n=\underset{k\to \infty }{lim}{b}_{n_k}& =& \underset{k\to \infty }{lim}[\frac{2(1-{\alpha }_{n_k})}{1-(1-{\alpha }_{n_k}){\alpha }^2}(⟨f_1(x^{\ast })-x^{\ast },p_{n_k}-x_{n_k}+x_{n_k}-x^{\ast }⟩\hfill \\ & & +⟨f_2(y^{\ast })-y^{\ast },q_{n_k}-y_{n_k}+y_{n_k}-y^{\ast }⟩)\hfill \\ & & -\frac{2\tau (1-{\alpha }_{n_k})}{1-(1-{\alpha }_{n_k}){\alpha }^2}\frac{{\rho }_{n_k}}{{\alpha }_{n_k}}(\parallel z_{n_k}{\parallel }^2+\parallel w_{n_k}{{\parallel }^2)}^{\frac{1}{2}}+\frac{{\alpha }_{n_k}M}{1-(1-{\alpha }_{n_k}){\alpha }^2}]\hfill \\ & =& \underset{k\to \infty }{lim}[\frac{2(1-{\alpha }_{n_k})}{1-(1-{\alpha }_{n_k}){\alpha }^2}(⟨f_1(x^{\ast })-x^{\ast },x_{n_k}-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },y_{n_k}-y^{\ast }⟩)\hfill \\ & & -\frac{2\tau (1-{\alpha }_{n_k})}{1-(1-{\alpha }_{n_k}){\alpha }^2}\frac{{\rho }_{n_k}}{{\alpha }_{n_k}}(\parallel z_{n_k}{\parallel }^2+\parallel w_{n_k}{{\parallel }^2)}^{\frac{1}{2}}]\hfill \end{array}$$

(18)

The boundedness of $\{(x_n,y_n)\}$ allows us to assume, with no loss of generality, that $\{(x_{n_k},y_{n_k})\}$ is weakly convergent to $(\widehat{x},\widehat{y})$. It follows that

$$\begin{array}{cc}\hfill & \underset{k\to \infty }{lim}(⟨f_1(x^{\ast })-x^{\ast },x_{n_k}-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },y_{n_k}-y^{\ast }⟩)\hfill \\ =& ⟨f_1(x^{\ast })-x^{\ast },\widehat{x}-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },\widehat{y}-y^{\ast }⟩.\hfill \end{array}$$

(19)

It follows from (18) and (19), and ${\alpha }_n\to 0$ that

$$\underset{k\to \infty }{lim}\frac{{\rho }_{n_k}}{{\alpha }_{n_k}}(\parallel z_{n_k}{\parallel }^2+\parallel w_{n_k}{{\parallel }^2)}^{\frac{1}{2}}$$

exists in $\mathbb{R}$. Hence, condition $(d)$ implies

$$\begin{array}{c}\hfill (\parallel z_{n_k}{\parallel }^2+\parallel w_{n_k}{\parallel }^2{)}^{\frac{1}{2}}=\frac{{\alpha }_{n_k}}{{\rho }_{n_k}}\frac{{\rho }_{n_k}}{{\alpha }_{n_k}}(\parallel z_{n_k}{\parallel }^2+\parallel w_{n_k}{{\parallel }^2)}^{\frac{1}{2}}\to 0,\end{array}$$

that is,

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel z_{n_k}\parallel =\underset{k\to \infty }{lim}\parallel w_{n_k}\parallel =0.\end{array}$$

(20)

Equalities (20) and Lemma 5 lead to

$$\begin{array}{cc}\hfill & \underset{k\to \infty }{lim}\parallel x_{n_k}-S{x}_{n_k}\parallel =\underset{k\to \infty }{lim}\parallel y_{n_k}-T{y}_{n_k}\parallel =0,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & \underset{k\to \infty }{lim}\parallel \mathcal{A}{x}_{n_k}-\mathcal{B}{y}_{n_k}\parallel =0.\hfill \end{array}$$

(22)

Since $x_{n_k}\rightharpoonup \widehat{x}$, $y_{n_k}\rightharpoonup \widehat{y}$, from condition $(a)$ and (21), we obtain that $\widehat{x}\in F(S)$ and $\widehat{y}\in F(T)$. Since the boundedness and linearity characterize the operators $\mathcal{A}$ and $\mathcal{B}$, we have $\mathcal{A}{x}_{n_k}-\mathbb{B}{y}_{n_k}\rightharpoonup \mathcal{A}\widehat{x}-\mathcal{B}\widehat{y}$. Taking advantage of the semicontinuity which characterizes the norm and of (22), we obtain

$$\parallel \mathcal{A}\widehat{x}-\mathcal{B}\widehat{y}\parallel \le \underset{k\to \infty }{lim\; inf}\parallel \mathcal{A}{x}_{n_k}-\mathcal{B}{y}_{n_k}\parallel =0.$$

Thus, $(\widehat{x},\widehat{y})\in \Omega .$ Then, by ${\alpha }_n\to 0$, (10), (18), and (19), we obtain

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim\; sup}{b}_n& \le & \frac{2}{1-{\alpha }^2}\underset{k\to \infty }{lim}(⟨f_1(x^{\ast })-x^{\ast },x_{n_k}-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },y_{n_k}-y^{\ast }⟩)\hfill \\ & =& \frac{2}{1-{\alpha }^2}(⟨f_1(x^{\ast })-x^{\ast },\widehat{x}-x^{\ast }⟩+⟨f_2(y^{\ast })-y^{\ast },\widehat{y}-y^{\ast }⟩)\hfill \\ & =& \frac{2}{1-{\alpha }^2}⟨((I-f_1)x^{\ast },(I-f_2)y^{\ast }),(x^{\ast },y^{\ast })-(\widehat{x},\widehat{y})⟩\le 0.\hfill \end{array}$$

(23)

By the use of (17) and (23), condition $(b)$, and Lemma 1, it follows that $s_n\to 0$, so $\{(x_n,y_n)\}$ is strongly convergent to $(x^{\ast },y^{\ast })$. □

Remark 2.

Theorem 1 enlarges ([21], Theorem 3.1) on the following issues:

(I) 

The split common fixed point problem is generalized to the SEFP problem; the nonexpansive mappings are extended to the demicontractive operators;

(II) 

The weak convergence in ([21], Theorem 3.1) is extended to the strong convergence.

4. Numerical Example

In order to illustrate the usability of the algorithm of Theorem 1, we consider the following example in $(\mathbb{R},|·|)$.

Example 3

(Numerical Example). Let ${\mathcal{H}}_1={\mathcal{H}}_2={\mathcal{H}}_3=\mathbb{R}$. Let $f_1$, $f_2:\mathbb{R}\to \mathbb{R}$, $f_1(x)=f_2(x)=\frac{1}{2}sinx.$ Let $\mathcal{A}$, $\mathcal{B}:\mathbb{R}\to \mathbb{R}$, $\mathcal{A}x=\mathcal{B}x=-x.$ Let S, $T:\mathbb{R}\to \mathbb{R}$, $Sx=-2x$ and $Tx=-3x$, respectively. Let $\{(x_n,y_n)\}$ be the sequence generated iteratively by Algorithm 1, where ${\alpha }_n=\frac{1}{n}$, ${\rho }_n=\frac{1}{n^{\frac{3}{4}}}$, $n\ge 1$. Then, $\{(x_n,y_n)\}$ is strongly convergent to (0,0).

Solution: For any x, $y\in \mathbb{R}$, define ${\mathcal{A}}^{\ast }x=-x$ and ${\mathcal{B}}^{\ast }y=-y$. Example 1 ensures that $F(S)=F(T)=\{0\}$ and $\mathcal{A}0=0=\mathcal{B}0$. Obviously, $\Omega =\{(0,0)\}\ne \varnothing$. $I-S$ and $I-T$ are characterized by demiclosedness at 0. All the assumptions of Theorem 1 are accomplished.

Algorithm 1 becomes, in this case,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{n+1}=\frac{1}{2n}sin{x}_n+(1-\frac{1}{n})[x_n-{\tau }_n(4x_n-y_n)],\hfill \\ y_{n+1}=\frac{1}{2n}sin{y}_n+(1-\frac{1}{n})[y_n-{\tau }_n(5y_n-x_n)],\hfill \end{array}\right.\end{array}$$

(24)

where the step size ${\tau }_n$ is as follows:

$${\tau }_n=\frac{1}{n^{\frac{3}{4}}(|4x_n-y_n{|}^2+|5y_n-x_n{{|}^2)}^{1/2}}.$$

By using scheme (24), we obtained the numerical results in Table 1. Figure 1 also illustrates the usefulness of Theorem 1.

Table 1. The convergence of $\{(x_n,y_n)\}$ with initial values (0.3,0.1).

n		${\mathit{x}}_{\mathit{n}}$	${\mathit{y}}_{\mathit{n}}$
1		0.300000000000000	0.100000000000000
2		0.147760103330670	0.049916708323414
3		−0.181488306475344	−0.017546156041863
4		0.138858140885285	−0.052994167458393
5		−0.099484842363747	0.100270304873921
...		...	...
197		0.004448866036788	−0.007198416659655
198		−0.005472189665092	0.008854189036970
199		0.004414260565043	−0.007142423823788
200		−0.005432678586300	0.008790258763243

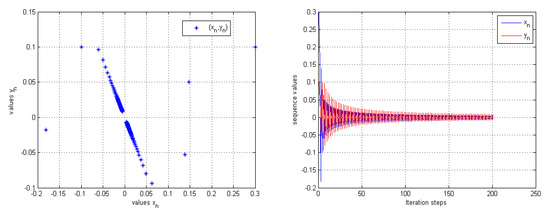
Figure 1. The convergence of $\{(x_n,y_n)\}$ with initial values (0.3,0.1).

5. Application

In this section, Theorem 1 will be applied to the study of the SEFP problem in the case of quasi pseudo-contractive operators, a more general class than the class of demicontractive mappings in Hilbert spaces.

In 2015, the following iterative method for solving the SEFP (2) was taken into consideration by Chang et al. [35]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_n=x_n-{\gamma }_n{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n),\hfill \\ x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)((1-\xi )I+\xi S((1-\eta )I+\eta S))u_n,\hfill \\ v_n=y_n+{\gamma }_n{\mathcal{B}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n),\hfill \\ y_{n+1}={\alpha }_n{y}_n+(1-{\alpha }_n)((1-\xi )I+\xi T((1-\eta )I+\eta T))v_n,\hfill \end{array}\right.\end{array}$$

(25)

where S and T are quasi-pseudocontractive, and ${\gamma }_n\in \left(0,min\left\{\frac{1}{{\parallel \mathcal{A}\parallel }^2},\frac{1}{{\parallel \mathcal{B}\parallel }^2}\right\}\right)$. Furthermore, the weak convergence of the sequence generated by (25) to a solution to the SEFP (2) under some mild assumptions was proved. If S and T are both semi-compact, they obtained a strong convergence result.

Consider the next hypotheses:

$(A1)$ Let S and T be two $L-$Lipschitzian quasi-pseudo-contractive mappings with $L>1;$

$(A2)$ Let $0<\xi <\eta <\frac{1}{1+\sqrt{1+L^2}}.$ Consider the mappings K and W,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}K=(1-\xi )I+\xi S((1-\eta )I+\eta S),\hfill \\ W=(1-\xi )I+\xi T((1-\eta )I+\eta T).\hfill \end{array}\right.\end{array}$$

Algorithm 2.Let $x_1\in {\mathcal{H}}_1$, $y_1\in {\mathcal{H}}_2$ be arbitrarily given.

The algorithm becomes   Step 1. If $$\parallel x_n-K{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2+{\parallel y_n-W{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n)\parallel }^2=0,$$ then stop, and $(x_n,y_n)$ is a solution to (2); if not, move on to the next step.   Step 2. Define $x_{n+1}$ and $y_{n+1}$, $$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{n+1}={\alpha }_n{f}_1(x_n)+(1-{\alpha }_n)[x_n-{\tau }_n(x_n-K{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n)],\hfill \\ y_{n+1}={\alpha }_n{f}_2(y_n)+(1-{\alpha }_n)[y_n-{\tau }_n(y_n-W{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n)],\hfill \end{array}\right.\end{array}$$ where the step size ${\tau }_n$ is chosen as follows: $$\begin{array}{c}\hfill {\tau }_n=\frac{{\rho }_n}{(\parallel x_n-K{x}_n+{\mathcal{A}}^{\ast }(\mathcal{A}{x}_n-\mathcal{B}{y}_n){\parallel }^2+\parallel y_n-W{y}_n+{\mathcal{B}}^{\ast }(\mathcal{B}{y}_n-\mathcal{A}{x}_n){{\parallel }^2)}^{\frac{1}{2}}},\end{array}$$ (26) and return to Step 1.

We need the following lemma which helps us to prove our result.

Lemma 6.

[35] Let $\mathcal{H}$ be a real Hilbert space and T be a Lipschitzian mapping with $L\ge 1$. Denote by

$$K=(1-\xi )I+\xi T((1-\eta )I+\eta T),$$

where $0<\xi <\eta <\frac{1}{1+\sqrt{1+L^2}}$. The next statements hold true:

(1) 

$F(T)=F(T((1-\eta )I+\eta T))=F(K)$.

(2) 

If $I-T$ is demiclosed at 0, then so is $I-K$.

(3) 

Additionally, if T is quasi-pseudo-contractive, K is quasi-nonexpansive.

The next theorem proves that the algorithm is strongly convergent to the solution to a variational inequality.

Theorem 2.

Let ${\mathcal{H}}_1,{\mathcal{H}}_2,{\mathcal{H}}_3$ be three real Hilbert spaces. Assume that $\mathcal{A}$, B, $f_1$, $f_2$, Ω are the same as in Theorem 1, and assumptions $(A1)$ and $(A2)$ hold. If the following conditions are satisfied:

(a) 

$I-S$ and $I-T$ are demiclosed at 0;

(b) 

${\sum }_{n=0}^{\infty }{\rho }_n^2<\infty$;

(c) 

${lim}_{n\to \infty }{\alpha }_n=0$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$;

(d) 

${lim}_{n\to \infty }\frac{{\alpha }_n}{{\rho }_n}=0,$

then $\{(x_n,y_n)\}$ generated by Algorithm 2 converges strongly to the unique solution to problem (10).

Proof. 

By Lemma 6 and the conditions imposed here, we obtain that $I-K$ and $I-W$ are endowed with demiclosedness at 0, and K and W are quasi-nonexpansive. Therefore, K and W are demicontractive. It follows from Theorem 1 that the conclusion holds. □

6. Conclusions

Along this work, we study the SEFP (2), a generalization of the SCFP (1). With the purpose of obtaining a strong convergence result, a new numerical scheme was introduced, combining viscosity approximation methodologies for the SEFP (2) of adequate operators in Hilbert spaces. Meanwhile, we applied our main result to the SEFP (2) of quasi pseudo-contractive mappings. We would like to note the following:

(1)

Theorem 1 mainly enlarge the ones in ([21], Theorem 3.1) and ([22], Theorem 14) from the following issues: (i) we extend the weak convergence result ([21], Theorem 3.1) for the SCFP (1) involving nonexpansive mappings to the strong convergent result for the SEFP (2) involving demicontractive operators; we improve and extend the weak convergence result ([22], Theorem 14) to the strong convergence result and remove the Lipschitz continuous conditions of the operators S and T; the proof of the strong convergence in Theorem 1 is different from the technique used to prove the weak convergence used in ([21], Theorem 3.1) and ([22], Theorem 14) because we use viscosity approximation methods.

(2)

Theorem 2 improves and extends ([35], Theorem 3.2) from the following points of view: (i) we remove the conditions of semi-compactness on the operators S and T, and still obtain a strong convergence result by using viscosity approximation methods; (ii) the choice $\{{\gamma }_n\}\in (0,min\{\frac{1}{{\parallel \mathcal{A}\parallel }^2},\frac{1}{{\parallel \mathcal{B}\parallel }^2}\})$ in proving the convergence of Algorithm 3.1 in [35] requires the computation of the related operator norms, which is a complicated task to be accomplished. Thus, our choice (26) of the step sizes is more efficient and desirable.

(3)

We give a numerical example to demonstrate the usefulness and convergence of our algorithm.