Abstract
Chaotic systems have attracted considerable attention and been applied in various applications. Investigating simple systems and counterexamples with chaotic behaviors is still an important topic. The purpose of this work was to study a simple symmetrical system including only five nonlinear terms. We discovered the system’s rich behavior such as chaos through phase portraits, bifurcation diagrams, Lyapunov exponents, and entropy. Interestingly, multi-stability was observed when changing system’s initial conditions. Chaos of such a system was predicted by applying a machine learning approach based on a neural network.
1. Introduction
The study of chaos in nonlinear systems has attracted significant attention in recent research [1,2,3,4]. Interestingly, new chaotic systems have continued to be proposed. A memristor-based chaotic circuit showing multi-stability was constructed by Song et al. [1]. Azar and Serrano [2] designed port Hamiltonian systems with chaos while Askar and Al-khedhairi mentioned a chaos of duopoly game for a player’s actions [5]. Chaos appeared in fractional systems, fractional-order maps, and discrete-time systems [6,7,8]. Chen et al. discovered entropy for indicating early-warning signals of zero-eigenvalue chaotic systems [9]. Disturbance observer control was applied to synchronize a chaotic system having one constant term and no equilibrium [10]. The special characteristics of chaos provide useful applications such as cryptography, transmission, security, and fractional chaotic memory [11,12,13]. Image encryption was developed by using a chaos of Farhan’s system [11] while a combination of compressed sensing and chaos in encryption scheme was introduced in [14]. Parallel mode of chaotic cryptography provided a transmission efficiency and resisted dangerous attacks [15]. Xie et al. developed image restoration for chaos-based transmission, which is effective to reduce devices’ consumption [12]. S-boxes were constructed with special systems’ chaos [16,17]. Ouannas et al. investigated MIMO communications using chaos synchronization [18]. By applying constant phase elements, Petrzela implemented chaotic memory [13].
Increased interest in symmetry in chaotic system has been reported in recent works [19]. Zhu and Du presented a chaotic system with a symmetrical curve equilibrium [20]. Chaotic oscillators were built with asymmetrical logic functions, illustrating the feasibility for integrated circuits [21]. It is noted that a symmetrical hyperchaotic attractor was able to control [19]. Especially, Li et al. examined comprehensively the evolution of symmetry [22]. From the viewpoint of information security, the vital roles of symmetry are verified by the improvement of substitution box structures [23], image encryption [24], and symmetric key encryption [25]. Discovering symmetrical chaotic systems is still an open topic.
When studying chaotic systems, discovering simple systems and counterexamples with chaotic behaviors is a vital research topic [26]. Common three-dimensional chaotic systems often have more than six terms and five-term chaotic systems are the most elegant ones [26]. Moreover, chaotic systems without linear terms have rarely been reported [27]. The purpose of our work was to investigate a novel five-term chaotic system without a linear term. Table 1 is provided for comparison with the results of recent studies.

Table 1.
Numbers of linear and nonlinear terms in some three-dimensional chaotic systems.
2. System without Linearity
We investigate a system with no linear terms:
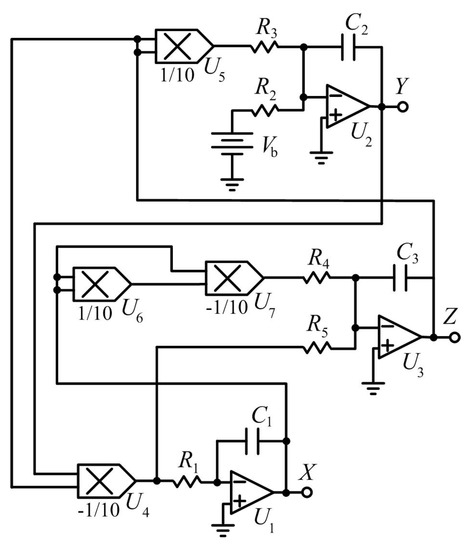
In system (1), a and b are positive parameters . Interestingly, five terms of the system (1) are nonlinear ones. Only few systems without linear terms have been studied [27]. Simple chaotic systems/circuits have attracted considerable attention because of their elegance [26]. From the viewpoint of terms, the simplest chaotic systems are five-term ones [26]. Therefore, we would like to consider system (1), which includes five nonlinear terms. In addition, the system can be implemented physically by using common electronic elements such as resistors, capacitors, operational amplifiers, and analog multipliers. A practical implementation of system (1) is illustrated in Figure 1. In the design, the circuit of system (1) includes five resistors, three capacitors, three operational amplifiers, and four analog multipliers. However, corresponding equations of the system do not describe certain events.
Considering coordinate transformation (2)
system (1) is invariant. Therefore, system (1) is symmetric. It is worth noting that symmetry in nonlinear systems has attracted interest in recent years [19,20,21].
The Jacobian matrix of system (1) is given by
Because of symmetry, by considering the Jacobian matrix at the equilibrium , we get the characteristic equation
and two eigenvalues
Therefore, this calculation shows that the system (1) is at a critical case for and .
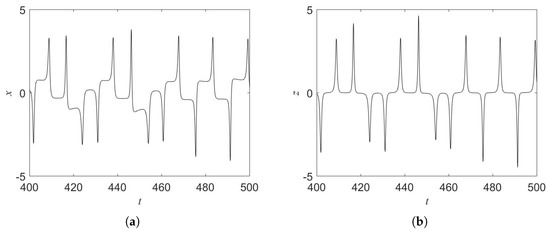
System (1) displays rich dynamics when varying a. The bifurcation diagram in Figure 2 shows windows of chaos, which are also verified by maximum Lyapunov exponents (see Figure 3). Chaos can be found in ranges, for example , and . Illustration of chaos is presented in Figure 4 for , and . The maximum Lyapunov exponent equals to 0.02714. Chaotic dynamics is similar to the observed chaotic one of the Lorenz system [29]. The Lorenz system describes the atmospheric convection and includes seven terms (with five linear terms). Our system has five terms (without linear terms).The waveforms of the variables x and z in Figure 5 display slow–fast dynamics. Slow–fast dynamics are important to get the autowaves [30].
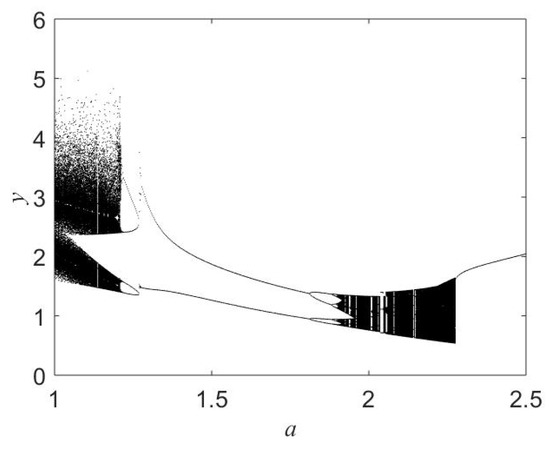
Figure 2.
Bifurcation diagram. We change parameter a while keeping , and initial conditions .
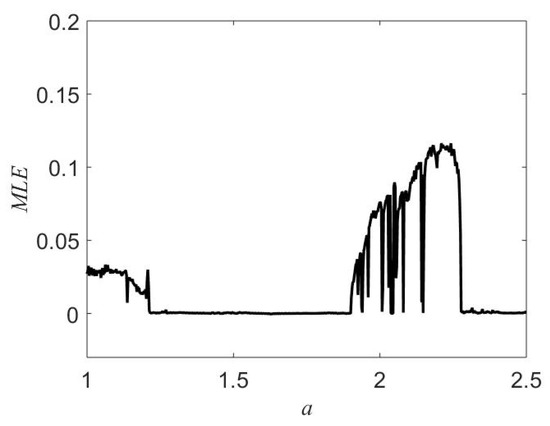
Figure 3.
Maximum Lyapunov exponents. We change a while keeping , and initial conditions .

Figure 4.
Attractors observed in three planes illustrating chaos in system (1) for : (a) , (b) , and (c) .
The symmetrical property of system (1) leads to the appearance of multistabily, which has been investigated in Figure 6. We plot simultaneously two bifurcation diagrams for initial conditions . Different coexisting attractors are reported in Figure 7.
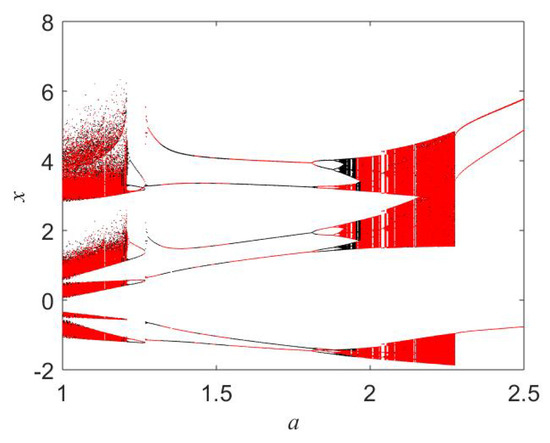
Figure 6.
Bifurcation diagrams for initial conditions (black) and (red) while keeping .
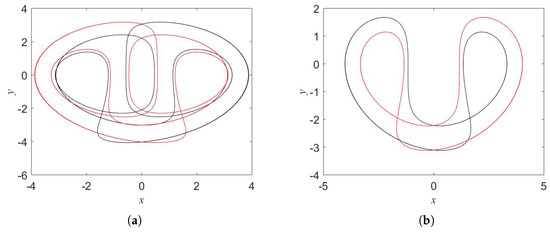
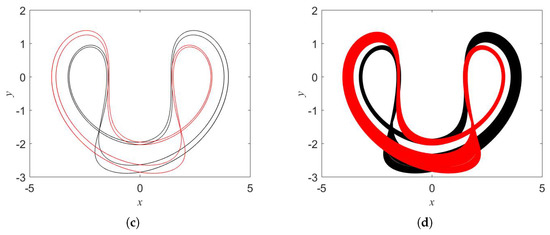
Figure 7.
Coexisting attractors in system (1) for (black) and (red): (a) , (b) , (c) , and (d) .
3. System’s Entropy
Entropy is an important tool not only in information theory but also in nonlinear works [31]. Entropy represents quantifies of information in a particular information system. It is useful for researches to describe nonlinear system’s complexity with entropy. Interestingly, entropy measurement has been witnessed for chaotic systems for last years [28,32]. Memristor-based chaotic oscillator has been developed by Liu et al. to achieve a high spectral entropy [3]. Chen et al. has indicated the usage of entropy as early warning indexes of chaotic signals [9].
We calculate entropy of system (1) to consider its complexity. The approximate entropy (ApEn) is measured for x variable. ApEn highlights advantages such as small samples demand, simple computation, and noise reduction [33].
Approximate entropy calculation [33] is presented briefly as follows. Firstly, we take a set of data from system (1). Vectors for are constructed by with a given m. The distance between vectors and is given by . As a result, we get the relative frequency of being similar to :
where K is the number of j satisfying for a given .
We obtain the approximate entropy
in which
Figure 8 depicts the approximate entropy [33] for parameter a. ApEn measures regularity and unpredictability of x. Significantly small values of ApEn indicate regular signals. As shown in Figure 8, system’s complex behavior can be witnessed for two ranges of a (, and ). Table 2 reports three examples of calculated ApEn values for a. The values of ApEn in the case 1 (0.2162), and the case 3 (0.3526) verify the complexity of system (1). Tiny value of ApEn confirms the periodical behavior of the system in the case 2.
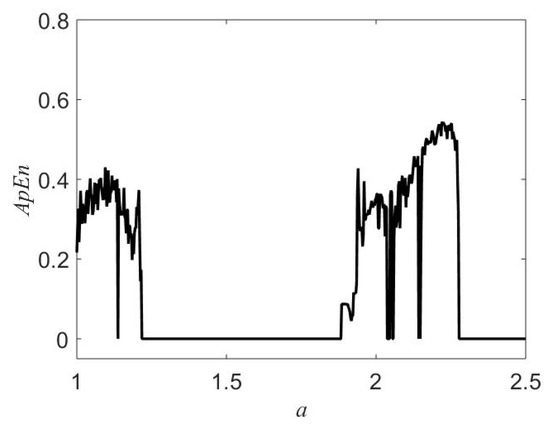
Figure 8.
Approximate entropy (ApEn) of system (1) calculated for .

Table 2.
Examples of calculated ApEn values.
4. Chaos Prediction
Artificial neuron network is constructed by connecting many neurons [34,35]. Numerous applications of neural networks in practice have been found in computer vision, pattern recognition, natural language processing, and robotics [36,37]. Ability of neuron network to represent nonlinear system has been investigated and attracted considerable interest [38,39,40]. Predicting chaotic system is challenge due to its sensitivity with initial conditions.
In this section, we build a simple feed-forward neural network (see Figure 9) to predict signals of system (1). As illustrated in Figure 9, the artificial neuron network includes four layers: input layer, two hidden layers, and output layer. It is considered as a deep neural network because there are multiple layers before the output layer [41]. The input layer includes three neurons. Each hidden layer is composed of ten neurons while there are only three neurons in the output layer. The numbers of hidden neurons and hidden layers are selected by considering the specific dynamics of the system such as multistability, and slow-fast dynamics. The computational roles of hidden layers are similar in order to model the dynamical system from its time series. It is worth noting that the hardest task of machine learning, choosing the suitable balance between model complexity and simplicity, must be considered seriously. The effective and robust architecture of the neural network as well as the optimization of network’s parameters guarantee the good performance of the network. In this work, we construct a simple feed-forward neural network. Compared with advanced networks, for example convolutional neural network, recurrent neural network, liquid state machine, and echo state network, the proposed architecture is effective and robust when being applied to system (1).
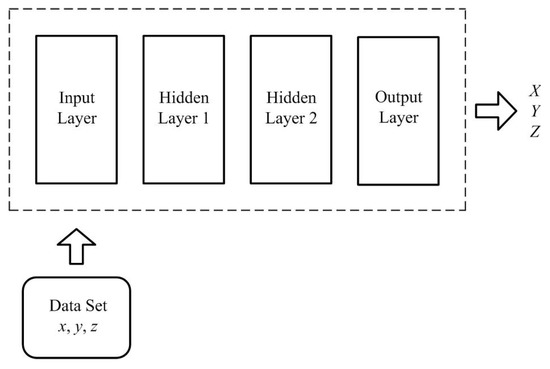
Figure 9.
Neuron network includes four layers. Data set is provided by system (1) and is used for training.
A dataset is generated by running system (1) with different initial conditions. The proposed neural network is trained with the data set by applying the Levenberg–Marquardt algorithm. It is noted that there are different training algorithms such as the Levenberg–Marquardt algorithm, Bayesian Regularization algorithm, Scaled Conjugate Gradient algorithm, and the Fletcher–Powell Conjugate Gradient [37,42]. In this work, we use the Levenberg–Marquardt algorithm because of its good convergence and robustness. The obtained performance is . After the training process, we achieve a network matching with the data set. Outputs of the network present expected signals. Figure 10 illustrates the prediction results compared with actual data . The agreement of the prediction results with the actual data shows the capability of the network for predicting chaos of system (1) in short term. In comparison to other works [43,44,45], the neural network is simple and displays good performance.
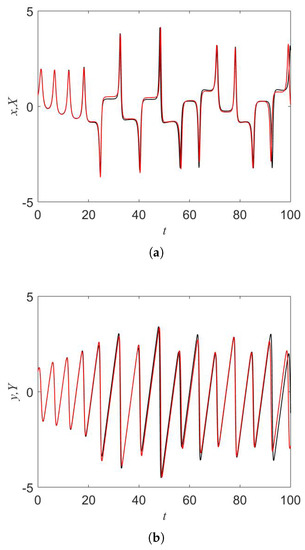
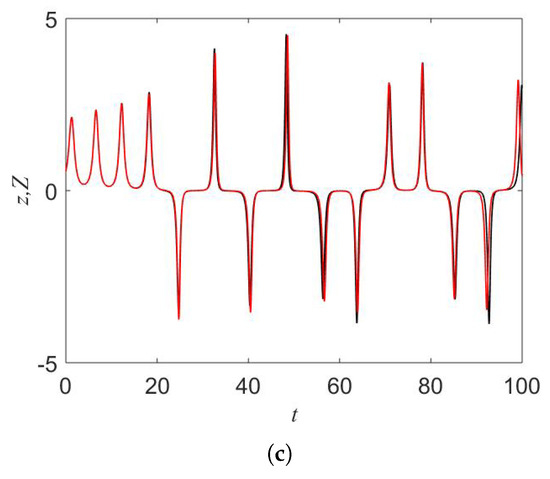
Figure 10.
Signals of system (1) (black color) and desired signals at the output of the neural network (red color): (a) x and X, (b) y and Y, (c) z and Z.
5. Conclusions
Our work introduces a symmetry nonlinear system with remarkable dynamics. There are only five nonlinear terms in the system, which generates chaos. By considering the initial conditions, we find coexisting attractors in the system verifying its multistability feature. Entropy measurement also indicates the system’s complexity. We believe that our work contributes to the known list of chaotic systems with algebraic simplicity. It is possible for us to apply a modified version of such a system to describe turbulent flows [46,47]. We implemented a neural-based approach to predict a system’s chaos in short-term. Long-term prediction of such chaotic signals should be considered. In addition, prediction results will be applied to control chaos in our future investigation. In addition, realization of the system for practical chaos-based applications will be studied in our future works.
Author Contributions
Data curation, V.V.H.; Formal analysis, V.P.T.; Funding acquisition, M.S.K.; Investigation, V.P.T. and V.V.H.; Methodology, A.O. and V.-T.P.; Project administration, M.S.K.; Resources, V.-T.P.; Software, M.S.K.; Supervision, A.O.; Visualization, V.V.H.; Writing—original draft, V.P.T. and A.O.; Writing—review & editing, V.-T.P. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Song, Y.; Yuan, F.; Li, Y. Coexisting attractors and multistability in a simple memristive Wien-Bridge chaotic circuit. Entropy 2019, 21, 678. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E. Stabilization of port Hamiltonian chaotic systems with hidden attractors by adaptive terminal sliding mode control. Entropy 2020, 22, 122. [Google Scholar] [CrossRef]
- Liu, L.; Du, C.; Liang, L.; Zhang, X. A high Spectral Entropy (SE) memristive hidden chaotic system with multi-type quasi-periodic and its circuit. Entropy 2019, 21, 1026. [Google Scholar] [CrossRef]
- Danca, M.F. Puu system of fractional order and its chaos suppression. Symmetry 2020, 12, 340. [Google Scholar] [CrossRef]
- Askar, S.S.; Al-khedhairi, A. Dynamic effects arise due to consumers’ preferences depending on past choices. Entropy 2020, 22, 173. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Bendoukha, S.; Vo, T.P.; Pham, V.T.; Huynh, V.V. The fractional form of the Tinkerbell map is chaotic. Appl. Sci. 2018, 8, 2640. [Google Scholar] [CrossRef]
- Huynh, V.V.; Ouannas, A.; Wang, X.; Pham, V.T.; Nguyen, X.Q.; Alsaadi, F.E. Chaotic map with no fixed points: Entropy, implementation and control. Entropy 2019, 21, 279. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Grassi, G.; Pham, V.T. Chaos and control of a three-dimensional fractional order discrete-time system with no equilibrium and its synchronization. AIP Adv. 2020, 10, 045310. [Google Scholar] [CrossRef]
- Chen, L.; Nazarimehr, F.; Jafari, S.; Tlelo-Cuautle, E.; Hussain, I. Investigation of early warning indexes in a three-dimensional chaotic system with zero eigenvalues. Entropy 2020, 22, 341. [Google Scholar] [CrossRef]
- Wang, S.; Yousefpour, A.; Yusuf, A.; Jahanshahi, H.; Alcaraz, R.; He, S.; Munoz-Pacheco, J.M. Synchronization of a non-equilibrium four-dimensional chaotic system using a disturbance-observer-based adaptive terminal sliding mode control method. Entropy 2020, 22, 271. [Google Scholar] [CrossRef]
- Farhan, A.K.; Al-Saidi, N.M.; Maolood, A.T.; Nazarimehr, F.; Hussain, I. Entropy analysis and image encryption application based on a new chaotic system crossing a cylinder. Entropy 2019, 21, 958. [Google Scholar] [CrossRef]
- Xie, Y.; Yu, J.; Chen, X.; Ding, Q.; Wang, E. Low-element image restoration based on an out-of-order elimination algorithm. Entropy 2020, 22, 1192. [Google Scholar] [CrossRef]
- Petrzela, J. Fractional-order chaotic memory with wideband constant phase elements. Entropy 2020, 22, 422. [Google Scholar] [CrossRef]
- Xie, Y.; Yu, J.; Guo, S.; Ding, Q.; Wang, E. Image encryption scheme with compressed sensing based on new three-dimensional chaotic system. Entropy 2019, 21, 819. [Google Scholar] [CrossRef]
- Yu, J.; Guo, S.; Song, X.; Xie, Y.; Wang, E. Image parallel encryption technology based on sequence generator and chaotic measurement matrix. Entropy 2020, 22, 76. [Google Scholar] [CrossRef]
- Wang, X.; Akgul, A.; Cavusoglu, U.; Pham, V.T.; Hoang, D.V.; Nguyen, X.Q. A chaotic system with infinite equilibria and its S-Box constructing application. Appl. Sci. 2018, 8, 2132. [Google Scholar] [CrossRef]
- Wang, X.; Cavusoglu, U.; Kacar, S.; Akgul, A.; Pham, V.T.; Jafari, S.; Alsaadi, F.E.; Nguyen, X.Q. S-Box based image encryption application using a chaotic system without equilibrium. Appl. Sci. 2019, 9, 781. [Google Scholar] [CrossRef]
- Ouannas, A.; Debbouche, N.; Wang, X.; Pham, V.T.; Zehrour, O. Secure Multiple-Input Multiple-Output communications based on F-M synchronization of fractional-order chaotic systems with non-identical dimensions and orders. Appl. Sci. 2018, 8, 1746. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Lei, T.; Liu, Z.; Tao, C. A symmetric controllable hyperchaotic hidden attractor. Symmetry 2020, 12, 550. [Google Scholar] [CrossRef]
- Zhu, X.; Du, W.S. New chaotic systems with two closed curve equilibrium passing the same point: Chaotic behavior, bifurcations, and synchronization. Symmetry 2019, 11, 951. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; García-Chávez, T.; Gonzalez-Diaz, V.R.; de La Fuente-Cortes, G.; del Carmen Gómez-Pavón, L. Two new asymmetric Boolean chaos oscillators with no dependence on incommensurate time-delays and their circuit implementation. Symmetry 2020, 12, 506. [Google Scholar] [CrossRef]
- Li, C.; Sun, J.; Lu, T.; Lei, T. Symmetry evolution in chaotic system. Symmetry 2020, 12, 574. [Google Scholar] [CrossRef]
- Artuǧer, F.; Özkaynak, F. A novel method for performance improvement of chaos-based substitution Boxes. Symmetry 2020, 12, 571. [Google Scholar] [CrossRef]
- Zhang, G.; Ding, W.; Li, L. Image encryption algorithm based on tent delay-sine cascade with logistic map. Symmetry 2020, 12, 355. [Google Scholar] [CrossRef]
- Stoyanov, B.; Nedzhibov, G. Symmetric key encryption based on rotation-translation equation. Symmetry 2020, 12, 73. [Google Scholar] [CrossRef]
- Sprott, J.C. Elegant Chaos Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Mobayen, S.; Kingni, S.T.; Pham, V.T.; Nazarimehr, F.; Jafari, S. Analysis, synchronisation and circuit design of a new highly nonlinear chaotic system. Int. J. Syst. Sci. 2018, 49, 617–630. [Google Scholar] [CrossRef]
- Xu, G.; Shekofteh, Y.; Akgul, A.; Li, C.; Panahi, S. A new chaotic system with a self-excited attractor: Entropy measurement, signal encryption, and parameter estimation. Entropy 2018, 20, 86. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Arena, P.; Caponetto, R.; Fortuna, L.; Manganaro, G. Cellular neural networks to explore complexity. Soft Comput. 1997, 1, 120–136. [Google Scholar] [CrossRef]
- Volos, C.K.; Jafari, S.; Kengne, J.; Munoz-Pacheco, J.M.; Rajagopal, K. Nonlinear dynamics and entropy of complex systems with hidden and self-excited attractors. Entropy 2019, 21, 370. [Google Scholar] [CrossRef]
- Liu, L.; Du, C.; Zhang, X.; Li, J.; Shi, S. Dynamics and entropy analysis for a new 4-D hyperchaotic system with coexisting hidden attractors. Entropy 2019, 21, 287. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Lytton, W.W. From Computer to Brain: Foundations of Computational Neuroscience; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Haykin, S.O. Neural Networks and Learning Machines; Pearson: London, UK, 2008. [Google Scholar]
- Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms And Applications; Pearson: London, UK, 1993. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Cai, F.; Zidan, M.A.; Ma, W.; Lee, S.H.; Lu, W.D. Reservoir computing using dynamic memristors for temporal information processing. Nat. Commun. 2017, 8, 2204. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.; Ma, W.; Shin, J.H.; Cai, F.; Du, C.; Lee, S.H.; Lu, W.D. Temporal data classification and forecasting using a memristor-based reservoir computing system. Nat. Electron. 2019, 2, 480–487. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Du, K.L.; Swamy, M.N.S. Neural Networks and Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Woolley, J.W.; Agarwal, P.K.; Baker, J. Modeling and prediction of chaotic systems with artificial neural networks. Int. J. Numer. Methods Fluids 2010, 63, 989–1004. [Google Scholar] [CrossRef]
- Lamamra, K.; Vaidyanathan, S.; Azar, A.T.; Salah, C.B. Chaotic System Modelling Using a Neural Network with Optimized Structure. In Fractional Order Control and Synchronization of Chaotic Systems; Azar, A.T., Vaidyanathan, S., Ouannas, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 833–856. [Google Scholar]
- Lellep, M.; Prexl, J.; Linkmann, M.; Eckhardt, B. Using machine learning to predict extreme events in the Hénon map. Chaos 2019, 30, 013113. [Google Scholar] [CrossRef]
- McDonough, J.M. Three-dimensional poor man’s Navier-Stokes equation: A discrete dynamical system exhibiting k−5/3 inertial subrange energy scaling. Phys. Rev. E 2009, 79, 065302. [Google Scholar] [CrossRef]
- Alberti, T.; Consolini, G.; Carbone, V. A discrete dynamical system: The poor man’s magnetohydrodynamic (PMMHD) equations. Chaos 2019, 29, 103107. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).