Abstract
This work proposes a modified logistic map based on the system previously proposed by Han in 2019. The constructed map exhibits interesting chaos related phenomena like antimonotonicity, crisis, and coexisting attractors. In addition, the Lyapunov exponent of the map can achieve higher values, so the behavior of the proposed map is overall more complex compared to the original. The map is then successfully applied to the problem of random bit generation using techniques like the comparison between maps, , and bit reversal. The proposed algorithm passes all the NIST tests, shows good correlation characteristics, and has a high key space.
1. Introduction
Chaos theory has found numerous applications over the last 50 years, including, but not limited to, encryption, engineering, secure communications, robotics, biology, and economics—see, for example, Refs. [1,2,3,4] and the references cited therein. Nonlinear systems with chaotic properties are deterministic systems with high sensitivity to small changes in initial conditions and parameters which lead to completely different solution trajectories. This sensitivity, combined with their deterministic nature, makes chaotic systems a perfect basis for designs that require high complexity and increased security.
Due to their abovementioned usability, there is an ongoing demand for constructing novel chaotic systems. Moreover, it is of interest to develop minimal chaotic systems that can provide high performance when implemented on FPGA [5,6]. Most of constructed chaotic maps are modifications of known chaotic systems. These modifications usually follow simple techniques, such as introducing additional nonlinear terms in the system’s differential/difference equations, changing an existing term to a higher-order term, or even by adding new variables to make the system hyperchaotic that is, having at least two positive Lyapunov exponents, which can only happen for four-dimensional systems or higher.
The logistic map [7,8] is one of the most well-known one-dimensional discrete time systems with chaotic behavior. Originally considered as a population model, it eventually found numerous applications in encryption, due to its simple and elegant form. This has also lead to many subsequent modifications of the map—see, for example, [9,10,11,12,13,14,15,16,17].
In this study, we consider a modification of the logistic map considered in [9]. The proposed modification is obtained by combining the map [9] with the conventional logistic map. This is done by multiplying the values of the map in [9] by the values of the logistic map computed from the decimal part of the same map, yielding a more complex behavior. The original map [9] exhibits a symmetric bifurcation diagram and constant chaos with a constant Lyapunov exponent, yet the proposed chaotic map showcases a plethora of chaos related phenomena, like antimonotonicity, crisis, and coexisting attractors, and the symmetric bifurcation diagram is now modified. In addition, the Lyapunov exponent of the new map can reach higher values, so overall the proposed map has a more complex chaotic behavior compared to the original map, and consequently compared to the classic logistic map as well. The emergence of many chaos related phenomena in the proposed system is an indication that the method of combining a given map with the logistic map derived from its decimal part can be generally utilized as a technique to make the behavior of a given system more complex.
Moreover, the proposed map is applied to the problem of pseudo-random bit generation [2,3,10,11,13,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. The term pseudo comes from the fact that a deterministic system is used to generate the sequence, rather than a random process, which is the case in true random bit generators. If the generator is properly designed though, the resulting sequence will have the characteristics of a random sequence. The method used utilizes various simple techniques like combinations of multiple maps, the comparison between different decimal parts of a number, bit reversal, and the operator. The sequences obtained by the pseudo-random bit generator based on the new map passes all 15 of the NIST statistical tests, shows good correlation and cross-correlation characteristics, and has a satisfactory key space. Thus, it is suitable for encryption related applications.
The rest of the work is structured as follows: In Section 2, the proposed modification of the well-known logistic map is presented and studied. In Section 3, the considered chaotic system is applied to the problem of random bit generation. Finally, Section 4 concludes the work with a discussion on future research topics.
2. The Proposed Map
In [9], the following modified logistic map was proposed:
The behavior of one-dimensional map Equation (1) depends on a single parameter . This map exhibits constant chaos for all values of its parameter, with a full mapping of the state values on provided that . Its symmetric bifurcation diagram is shown in Figure 1 and the diagram of its Lyapunov exponent in Figure 2.
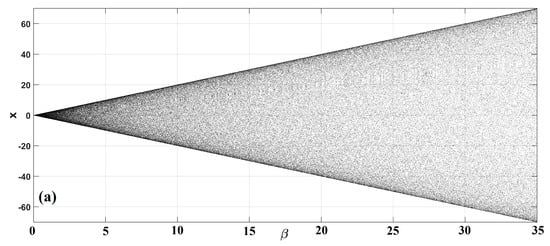
Figure 1.
Bifurcation diagram of Equation (1), with respect to parameter .
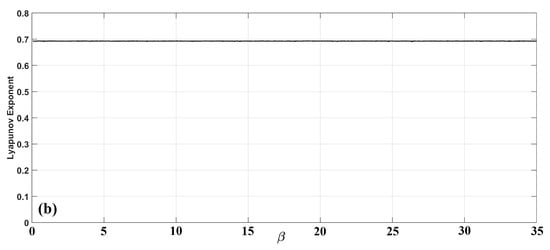
Figure 2.
Diagram of the Lyapunov exponent of Equation (1), with respect to parameter .
Here, a modified version of Equation (1) is proposed, given by
where . With the above modification, the values of the chaotic map Equation (1) are multiplied by the value which is actually the classic logistic map with bifurcation parameter r, computed using the decimal part of , instead of . The mod operator is used here to take the decimal part of , so that is bounded on the interval .
The bifurcation diagram of map Equation (2) with respect to parameter and is shown in Figure 3. The initial condition in each iteration is chosen as . From Figure 3, it can be seen that the system exhibits a similar but more complex behavior compared to Label (1), with small periodic windows appearing. This behavior can be seen more clearly in the zoomed subures. It is observed that the system exhibits crisis phenomena, where it exists abruptly from chaos and reenters it following a period doubling route. What is also interesting is that there are small windows where the phenomenon of antimonotonicity appears. This is when the system enters chaos by following a period doubling route, and then exists from chaos by following a reverse period halving route. This is observed in the subfigures around the value of . The chaotic oscillation mode is verified by the diagram of the Lyapunov exponent shown in Figure 4. In addition, Figure 5 shows a full plot for the Lyapunov exponent up to . From this figure, it can be seen that the Lyapunov exponent slowly increases to reach a value higher than 5, while there are also very small periodic windows appearing.
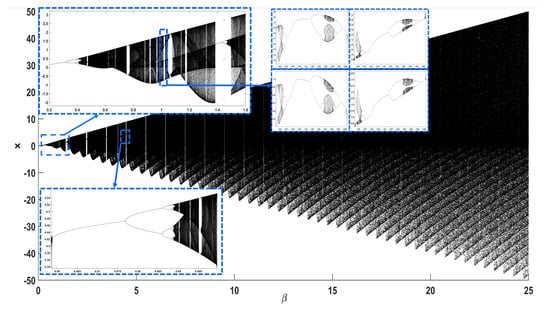
Figure 3.
Bifurcation diagram of Equation (2), with respect to parameter , for .
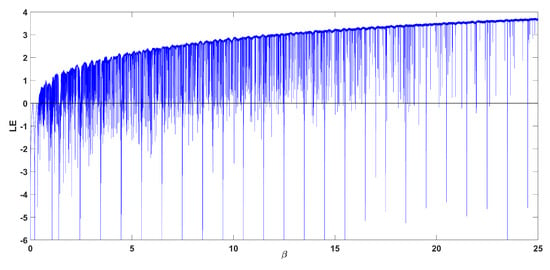
Figure 4.
Diagram of the Lyapunov exponent Equation (2), with respect to parameter , for .
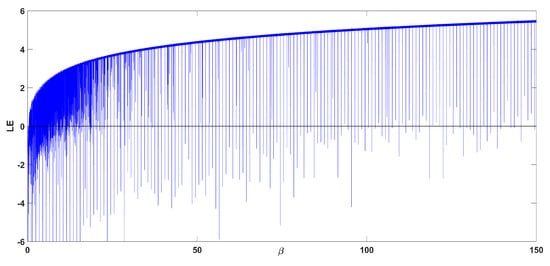
Figure 5.
Wider diagram of the Lyapunov exponent Equation (2), with respect to parameter , for .
Similar phenomena can be observed for different values of the parameter r. For example, the bifurcation diagram and the curve of the Lyapunov exponent with respect to for can be seen in Figure 6 and Figure 7. Again, antimonotonicity appears around the value of . The system also exits abruptly from chaos and re-enters it through a period doubling route.
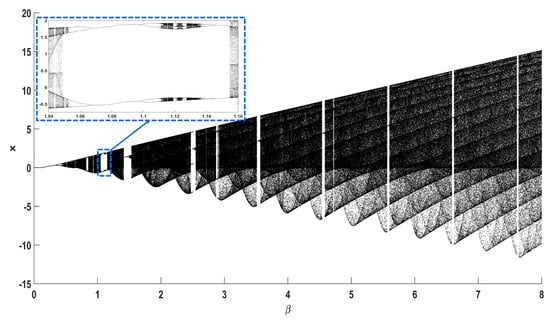
Figure 6.
Bifurcation diagram of Equation (2), with respect to parameter , for .
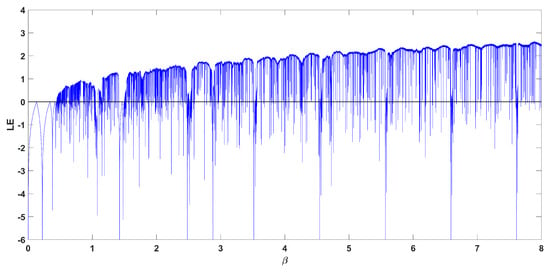
Figure 7.
Diagram of the Lyapunov exponent Equation (2), with respect to parameter , for .
In addition to the rich dynamical behavior with respect to parameter , the proposed map also exhibits chaotic oscillations with respect to parameter r, as seen in Figure 8 and Figure 9 where . The system here exhibits crisis phenomena again.
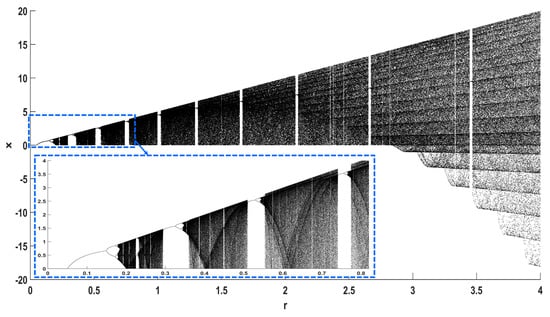
Figure 8.
Bifurcation diagram of Equation (2), with respect to parameter r, for .
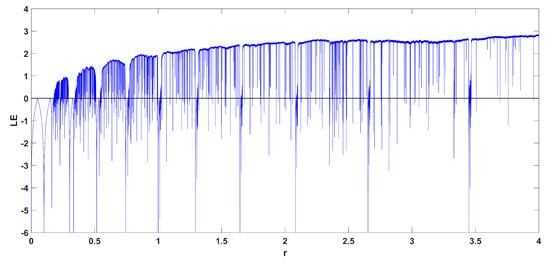
Figure 9.
Diagram of the Lyapunov exponent Equation (2), with respect to parameter r, for .
Moreover, as can be seen from Figure 4, Figure 5, Figure 7 and Figure 9, it is important to note that the system can achieve a Lyapunov exponent value that is higher than that of the system in [9] and also the classic logistic map, which both achieve the higher value at around 0.7.
To study the existence of coexisting attractors in the system, its continuation diagram is plotted. The continuation diagram is similar to the bifurcation diagram, with the difference that, in each iteration, the initial value of the chaotic map is taken to be equal to the final value of its previous simulation. The continuation diagram can thus be computed as the bifurcation parameter increases or decreases. Figure 10 shows the bifurcation diagram (black, .) of the map with respect to with , overlapping with its forward (red) and backward (green) continuation diagrams. This plot reveals coexisting attractors for the system around the value of . This means that, depending on the initial condition of the system, its steady-state behavior may converge to different attracting regions.
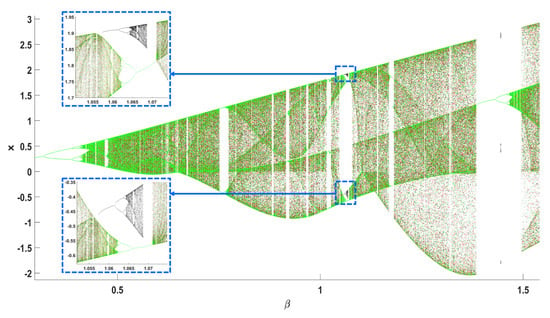
Figure 10.
Bifurcation diagram (black), forward continuation diagram (red), and backward continuation diagram (green) for Equation (2), with respect to parameter , for .
3. Application to Random Bit Generation
To apply the proposed map to pseudo-random bit generation, an algorithm was devised with the aim of having pseudo-random properties, weak correlation, and high key space. The proposed algorithm utilizes the techniques of comparing different decimal parts from different maps, as was performed in [23] for one map, the technique of bit reversal [19,22], performed here in a chaotic way, depending on the values of a logistic map, and also the operator, which is commonly used in PRBGs [19,20,21,31,37].
The algorithm is outlined as follows:
- Step 1.
- First, two modified logistic maps , one classic logistic map , as well as two bit sequences are initialized, and the maps’ parameters are chosen.
- Step 2.
- In every iteration, the decimal part of is compared to the decimal part of and depending on the result a 0 or 1 is produced and saved in . Similarly, the decimal part of is compared to the decimal part of and depending on the result a 0 or 1 is produced and saved in .
- Step 3.
- For every 10 iterations, the value of the logistic map is compared to the decimal part of . Depending on the result, a bit reversal is performed on the last ten digits of b or d.
- Step 4.
- Once the desired bitstream length is reached, the obtained sequence is computed using .
A full description of the proposed technique is described in Algorithm 1. Note that, when the decimal part is computed in each iteration, its sign is discarded, so a positive value is always returned. The modulo operation is performed using the command in Matlab.
| Algorithm 1 The Proposed Random Bit Generator. |
| Data: Initialize initial conditions: , parameter values: , Bit subsequences and bitstream length: ℓ. |
|
The proposed technique was tested using the National Institute of Standards and Technology (NIST) statistical test package [38]. The suite consists of 15 tests that are used to test the randomness of a sequence. For each test, a p-value is calculated. If the value exceeds a significance value a, the test is passed. A set of 50 bit sequences of bits each was considered, for parameter values , and arbitrarily chosen initial values. The results are shown in Table 1, where it can be seen that all the tests are passed. For tests that have multiple case runs, only the last p-value is printed.

Table 1.
NIST statistical test results, with .
In addition, Figure 11 depicts the autocorrelation and cross-correlation plots for a bit sequence of length , generated for parameter values , . For pseudo-random sequences, the auto-correlation should have a delta like form, and the cross-correlation should be close to zero [3,13], which is verified in Figure 11a. For the cross-correlation, two bit sequences were generated for the same parameter values and initial conditions, with the only difference taken as follows: In (b), the initial condition of the first map was chosen as and . In (c), the parameter of the first map is chosen as and . In (d), the parameter of the first map is chosen as and .
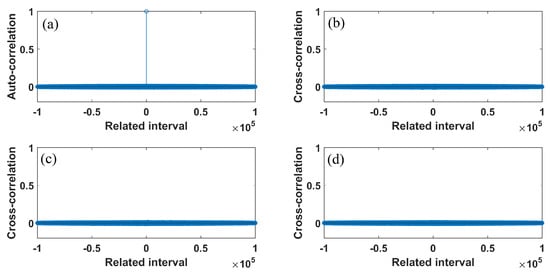
Figure 11.
(a) auto-correlation; (b) cross-correlation, with the initial condition of the first map being chosen as and ; (c) cross-correlation, with the parameter of the first map is chosen as and ; (d) cross-correlation, with the parameter of the first map being chosen as and .
As for the key space, the proposed technique utilizes two modified logistic maps and one logistic map, each with different initial conditions and parameters. Thus, in the case of the floating-point data type with double precision [39], there are overall eight key parameters, so the upper bound for the key space is . This is higher than the value of that is required to resist brute force attacks, as reported in [40].
4. Conclusions
In the present work, the modified version of the logistic map proposed in [9] was presented. The extensive dynamical analysis has shown that the proposed system exhibits phenomena like crisis, antimonotonicity, and coexisting attractors. This technique to increase the complexity of a map can be tested on other systems in the future. The map was then applied to constuct the chaos-based pseudo-random bit generator, utilizing techniques like multiple map comparison, bit reversal, and . In addition, the key space of the proposed algorithm is much higher than the indicated threshold of . Future aspects of this work will consider the application of the proposed PRBG to image encryption, the generation of multiple bits per iteration, as well as fractional versions of the map. It is of interest to develop the adaptive chaotic maps with controllable symmetry of a higher order based on the proposed map. It was previously shown that such systems are prospective for stream encryption algorithms [29,41]. Moreover, the obtained results can be applied to other cryptographic problems, including encoding multimedia data, creating watermarks and QR codes, generating checksums using chaotic hash functions, etc.
Author Contributions
C.V., L.M., A.T., D.B., J.M.M.-P. and H.N. contributed equally to this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research is co-financed by Greece and the European Union (European Social Fund- ESF) through the Operational Programme <<Human Resources Development, Education and Lifelong Learning>> in the context of the project “Reinforcement of Postdoctoral Researchers—2nd Cycle” (MIS-5033021), implemented by the State Scholarships Foundation (IKY).
Acknowledgments
The authors would like to thank the anonymous reviewers for theis comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. Image encryption process based on chaotic synchronization phenomena. Signal Process. 2013, 93, 1328–1340. [Google Scholar] [CrossRef]
- Huang, X.; Liu, L.; Li, X.; Yu, M.; Wu, Z. A New Pseudorandom Bit Generator Based on Mixing Three-Dimensional Chen Chaotic System with a Chaotic Tactics. Complexity 2019, 6567198. [Google Scholar] [CrossRef]
- Moysis, L.; Petavratzis, E.; Volos, C.; Nistazakis, H.; Stouboulos, I. A chaotic path planning generator based on logistic map and modulo tactics. Robot. Auton. Syst. 2020, 124, 103377. [Google Scholar] [CrossRef]
- Nepomuceno, E.G.; Lima, A.M.; Arias-García, J.; Perc, M.; Repnik, R. Minimal digital chaotic system. Chaos Solitons Fractals 2019, 120, 62–66. [Google Scholar] [CrossRef]
- Wang, H.; Song, B.; Liu, Q.; Pan, J.; Ding, Q. FPGA design and applicable analysis of discrete chaotic maps. Int. J. Bifurc. Chaos 2014, 24, 1450054. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Ausloos, M.; Dirickx, M. The Logistic Map and the Route to Chaos: From the Beginnings to Modern Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Han, C. An image encryption algorithm based on modified logistic chaotic map. Optik 2019, 181, 779–785. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Ma, J.; He, H. A pseudorandom number generator based on piecewise logistic map. Nonlinear Dyn. 2016, 83, 2373–2391. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.; Cruz-Hernández, C.; Cardoza-Avendaño, L.; Méndez-Ramírez, R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. 2017, 87, 407–425. [Google Scholar] [CrossRef]
- Radwan, A.G. On some generalized discrete logistic maps. J. Adv. Res. 2013, 4, 163–171. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S.; Hu, H.; Deng, Y. Pseudorandom bit generator based on non-stationary logistic maps. IET Inf. Secur. 2016, 10, 87–94. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. A new image encryption algorithm based on logistic chaotic map with varying parameter. SpringerPlus 2016, 5, 289. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.L.; Hwang, T.; Lin, W.W. Randomness enhancement using digitalized modified logistic map. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 996–1000. [Google Scholar]
- Borujeni, S.E.; Ehsani, M.S. Modified logistic maps for cryptographic application. Appl. Math. 2015, 6, 773. [Google Scholar] [CrossRef]
- Li, S.; Yin, B.; Ding, W.; Zhang, T.; Ma, Y. A nonlinearly modulated logistic map with delay for image encryption. Electronics 2018, 7, 326. [Google Scholar] [CrossRef]
- Irfan, M.; Ali, A.; Khan, M.A.; Ehatisham-ul Haq, M.; Mehmood Shah, S.N.; Saboor, A.; Ahmad, W. Pseudorandom Number Generator (PRNG) Design Using Hyper-Chaotic Modified Robust Logistic Map (HC-MRLM). Electronics 2020, 9, 104. [Google Scholar] [CrossRef]
- Ahmad, M.; Doja, M.; Beg, M.S. A new chaotic map based secure and efficient pseudo-random bit sequence generation. In Proceedings of the International Symposium on Security in Computing and Communication, Bangalore, India, 19–22 September 2018; pp. 543–553. [Google Scholar]
- Ge, R.; Yang, G.; Wu, J.; Chen, Y.; Coatrieux, G.; Luo, L. A Novel Chaos-Based Symmetric Image Encryption Using Bit-Pair Level Process. IEEE Access 2019, 7, 99470–99480. [Google Scholar] [CrossRef]
- François, M.; Grosges, T.; Barchiesi, D.; Erra, R. Pseudo-random number generator based on mixing of three chaotic maps. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 887–895. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.; Teh, J.S. Enhanced digital chaotic maps based on bit reversal with applications in random bit generators. Inf. Sci. 2020, 512, 1155–1169. [Google Scholar] [CrossRef]
- Wang, X.Y.; Xie, Y.X. A design of pseudo-random bit generator based on single chaotic system. Int. J. Mod. Phys. C 2012, 23, 1250024. [Google Scholar] [CrossRef]
- Patidar, V.; Sud, K.K.; Pareek, N.K. A pseudo random bit generator based on chaotic logistic map and its statistical testing. Informatica 2009, 33, 441–452. [Google Scholar]
- Stojanovski, T.; Kocarev, L. Chaos-based random number generators-part I: analysis [cryptography]. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2001, 48, 281–288. [Google Scholar] [CrossRef]
- Volos, C.; Kyprianidis, I.; Stouboulos, I. Experimental investigation on coverage performance of a chaotic autonomous mobile robot. Robot. Auton. Syst. 2013, 61, 1314–1322. [Google Scholar] [CrossRef]
- Hamza, R. A novel pseudo random sequence generator for image-cryptographic applications. J. Inf. Secur. Appl. 2017, 35, 119–127. [Google Scholar] [CrossRef]
- Nepomuceno, E.G.; Nardo, L.G.; Arias-Garcia, J.; Butusov, D.N.; Tutueva, A. Image encryption based on the pseudo-orbits from 1D chaotic map. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 061101. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Nepomuceno, E.G.; Karimov, A.I.; Andreev, V.S.; Butusov, D.N. Adaptive chaotic maps and their application to pseudo-random numbers generation. Chaos Solitons Fractals 2020, 133, 109615. [Google Scholar] [CrossRef]
- Akgül, A.; Arslan, C.; Arıcıoğlu, B. Design of an Interface for Random Number Generators based on Integer and Fractional Order Chaotic Systems. Chaos Theory Appl. 2019, 1, 1–18. [Google Scholar]
- Khanzadi, H.; Eshghi, M.; Borujeni, S.E. Image encryption using random bit sequence based on chaotic maps. Arab. J. Sci. Eng. 2014, 39, 1039–1047. [Google Scholar] [CrossRef]
- Andrecut, M. Logistic map as a random number generator. Int. J. Mod. Phys. B 1998, 12, 921–930. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, H. Pseudo-Random Number Generator Based on Logistic Chaotic System. Entropy 2019, 21, 960. [Google Scholar] [CrossRef]
- Meranza-Castillón, M.; Murillo-Escobar, M.; López-Gutiérrez, R.; Cruz-Hernández, C. Pseudorandom number generator based on enhanced Hénon map and its implementation. AEU-Int. J. Electron. Commun. 2019, 107, 239–251. [Google Scholar] [CrossRef]
- Persohn, K.; Povinelli, R.J. Analyzing logistic map pseudorandom number generators for periodicity induced by finite precision floating-point representation. Chaos Solitons Fractals 2012, 45, 238–245. [Google Scholar] [CrossRef]
- Phatak, S.; Rao, S.S. Logistic map: A possible random-number generator. Phys. Rev. E 1995, 51, 3670. [Google Scholar] [CrossRef] [PubMed]
- Volos, C.K.; Kyprianidis, I.; Stouboulos, I. Text Encryption Scheme Realized with a Chaotic Pseudo-Random Bit Generator. J. Eng. Sci. Technol. Rev. 2013, 6, 9–14. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Technical Report; Booz-Allen and Hamilton Inc.: Mclean, VA, USA, 2001. [Google Scholar]
- Kahan, W. IEEE standard 754 for binary floating-point arithmetic. Lect. Notes Status IEEE 1996, 754, 11. [Google Scholar]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Butusov, D.N.; Karimov, A.I.; Pyko, N.S.; Pyko, S.A.; Bogachev, M.I. Discrete chaotic maps obtained by symmetric integration. Phys. A Stat. Mech. Its Appl. 2018, 509, 955–970. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).