The Effect of a Non-Local Fractional Operator in an Asymmetrical Glucose-Insulin Regulatory System: Analysis, Synchronization and Electronic Implementation
Abstract
1. Introduction
2. Fractional-Order Glucose-Insulin Regulatory System
3. Stability Analysis of Fractional-Order Glucose-Insulin Model
- (i)
- If , , , , then the equilibrium point is locally asymptotically stable .
- (ii)
- is the necessary condition for the equilibrium point to be locally asymptotically stable.
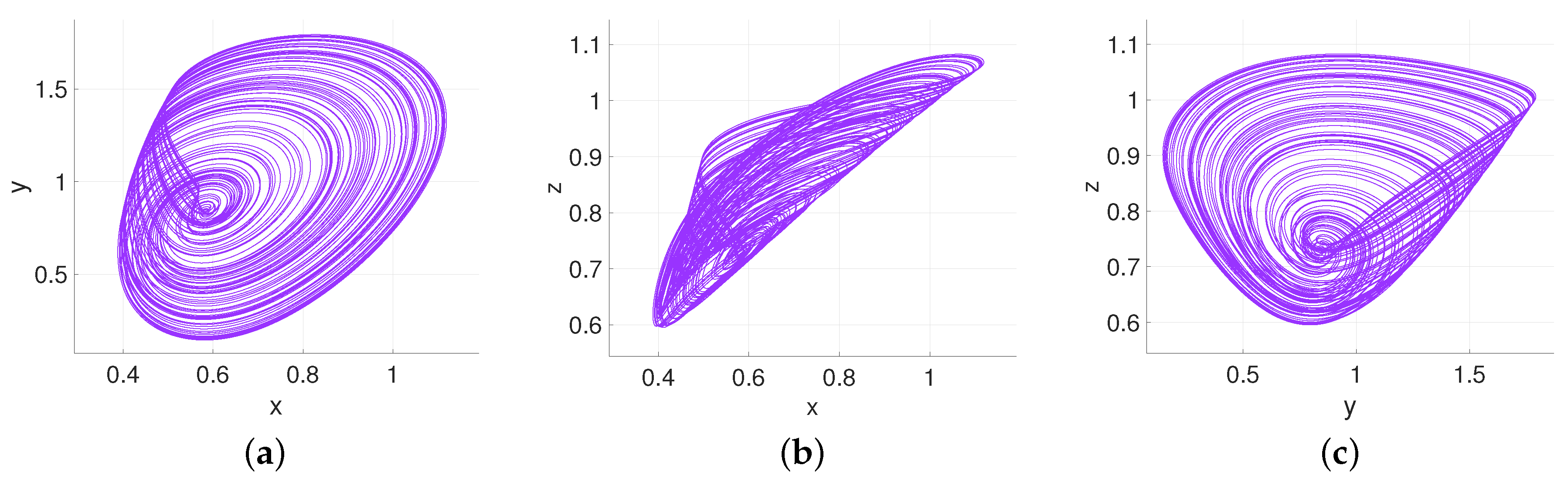
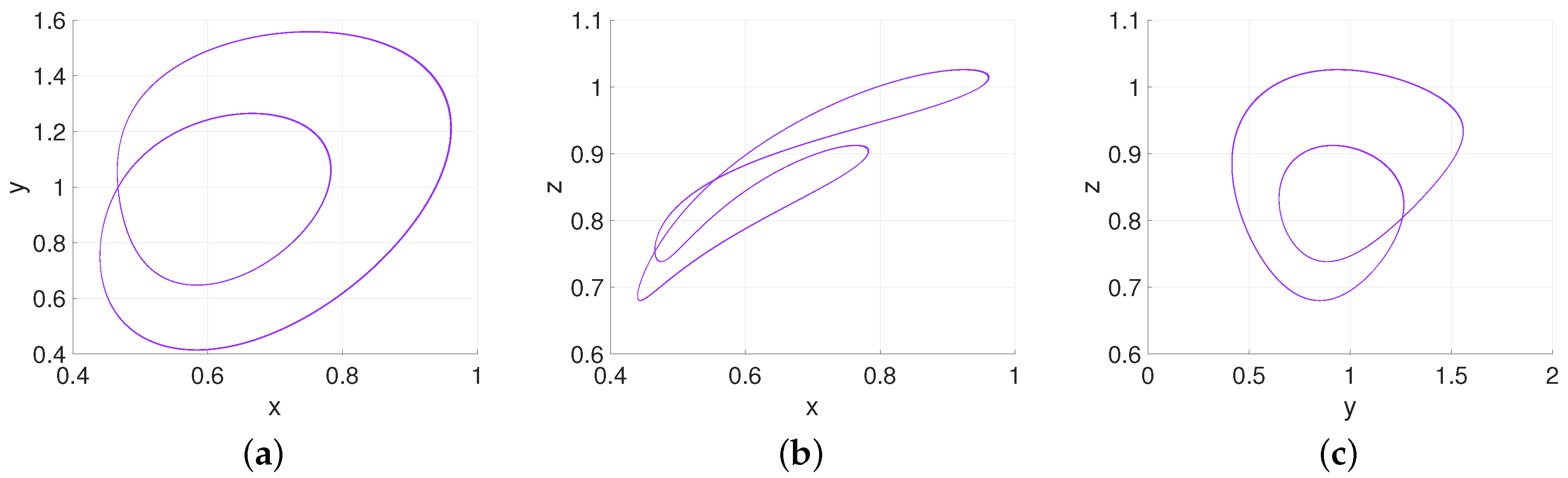
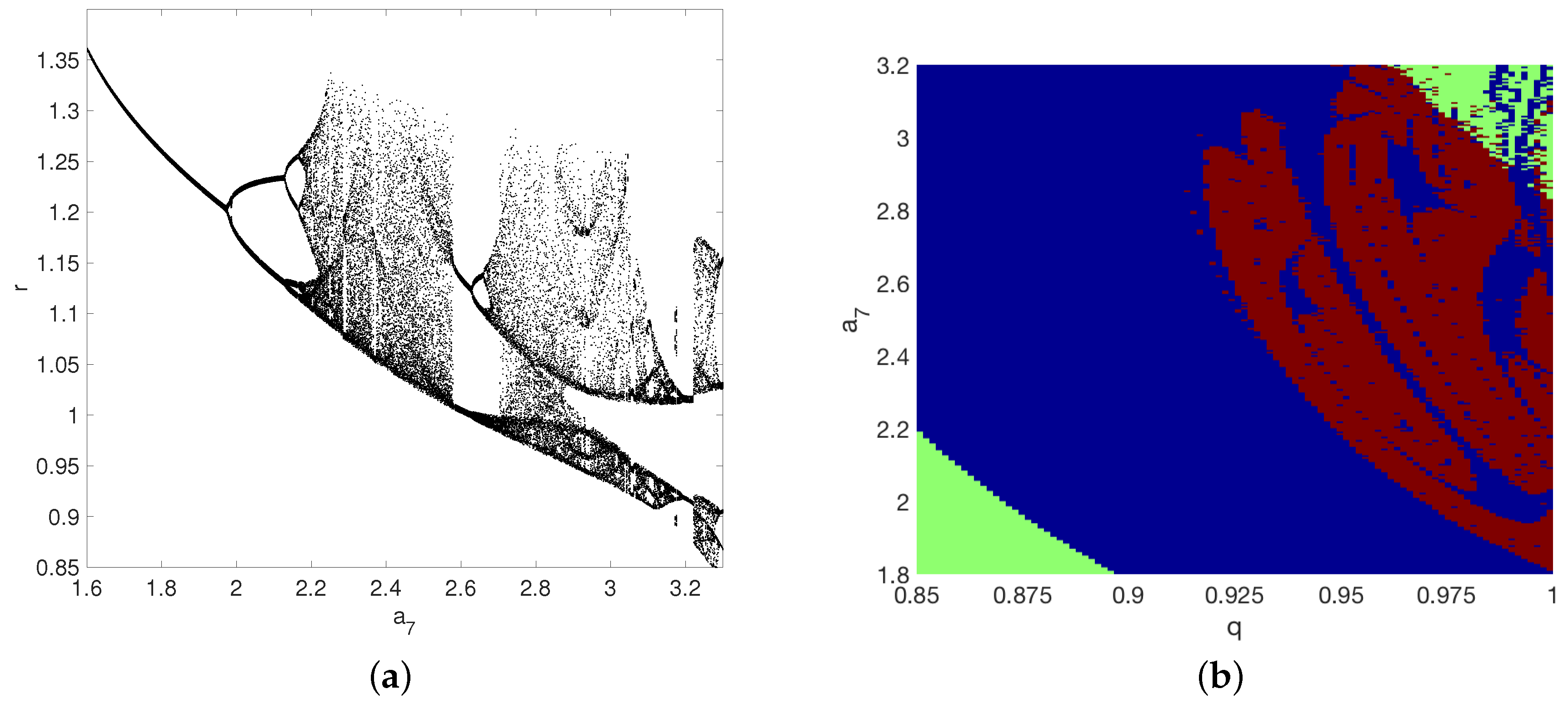
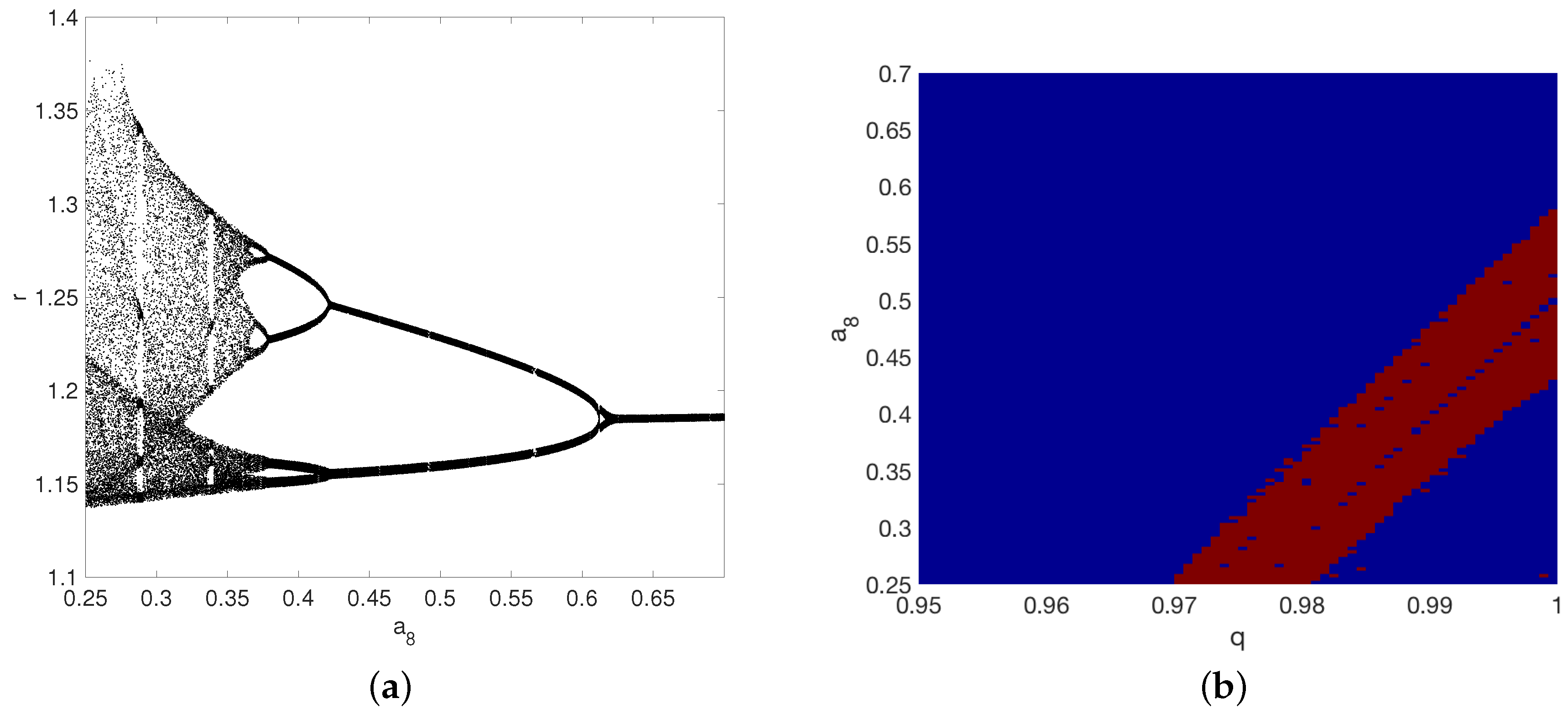
4. Numerical Analysis of the Non-Local Fractional Operators on Hypoglycemia, Hyperinsulinemia, T1DM, and T2DM
4.1. Hypoglycemia: Parameter as a Function of Fractional-Order q
4.2. Hyperinsulinemia: Parameter as a Function of Fractional-Order q
4.3. Type-2 Diabetes Mellitus: Parameter as a Function of Fractional-Order q
4.4. Type-1 Diabetes Mellitus: Parameter as a Function of Fractional-Order q
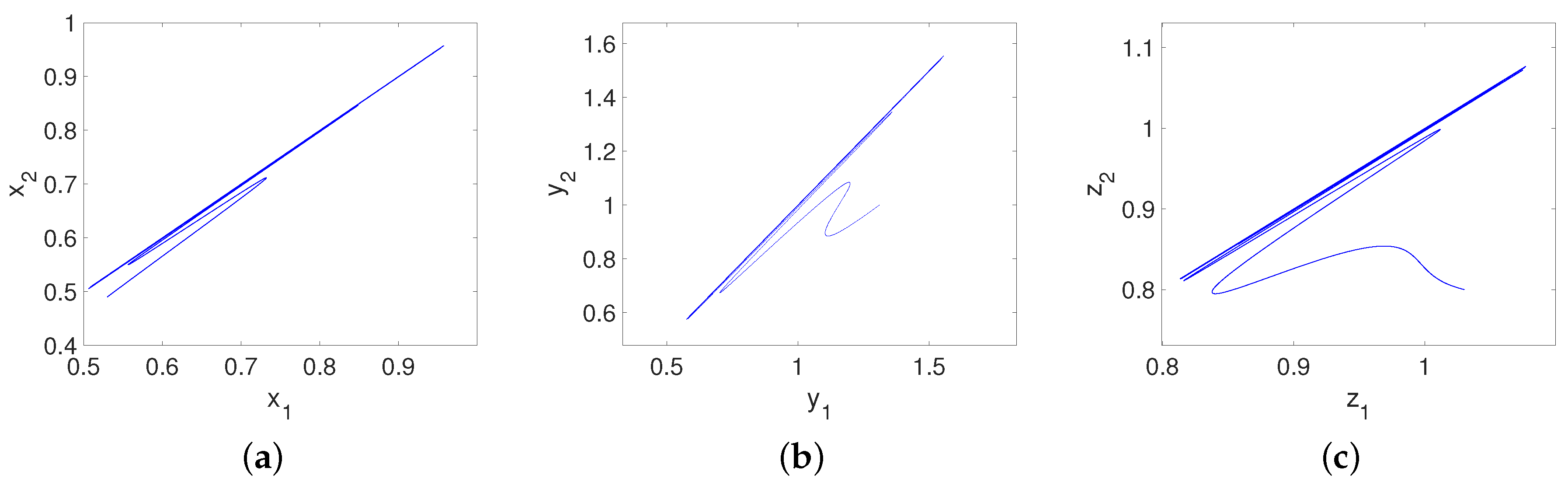
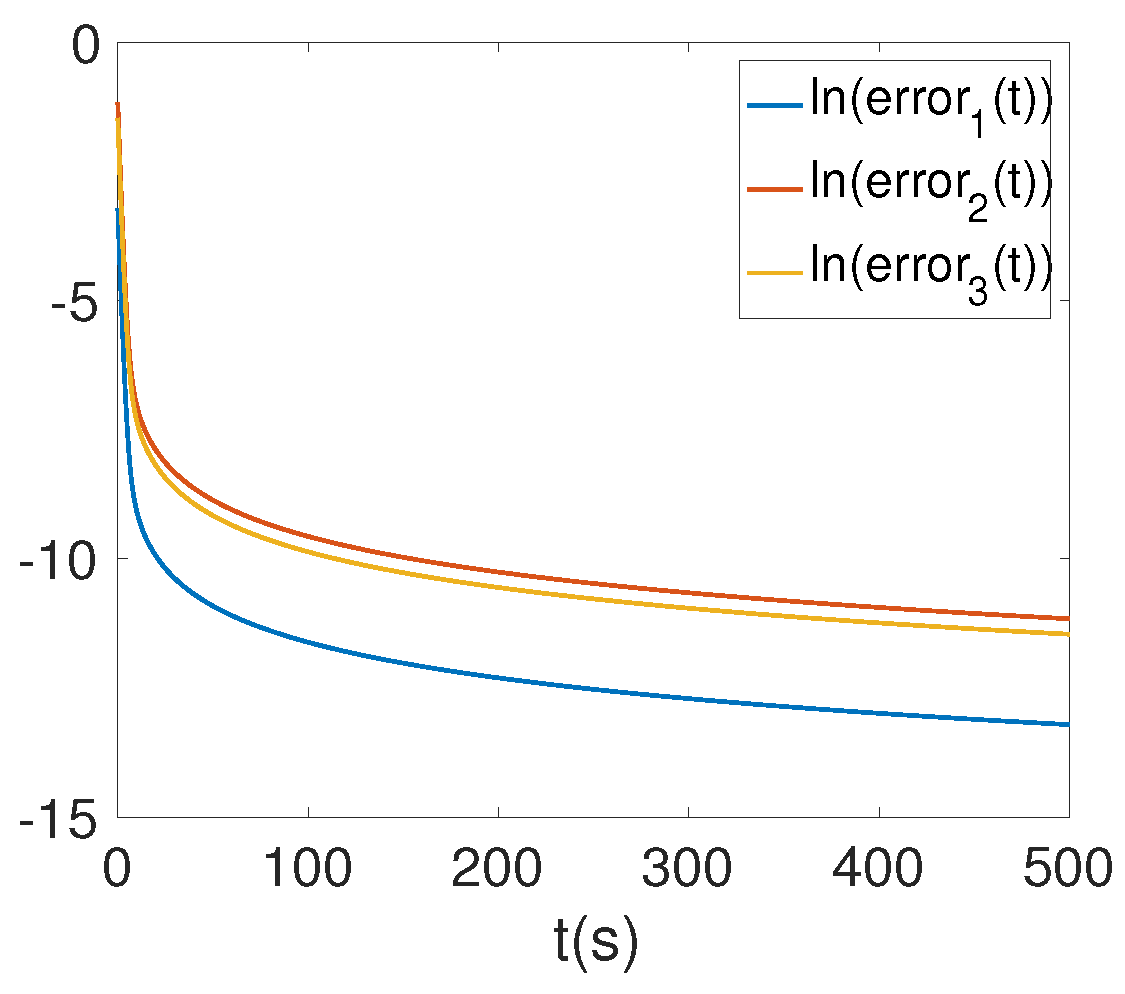
5. Synchronization between Fractional-Order Glucose Insulin Systems
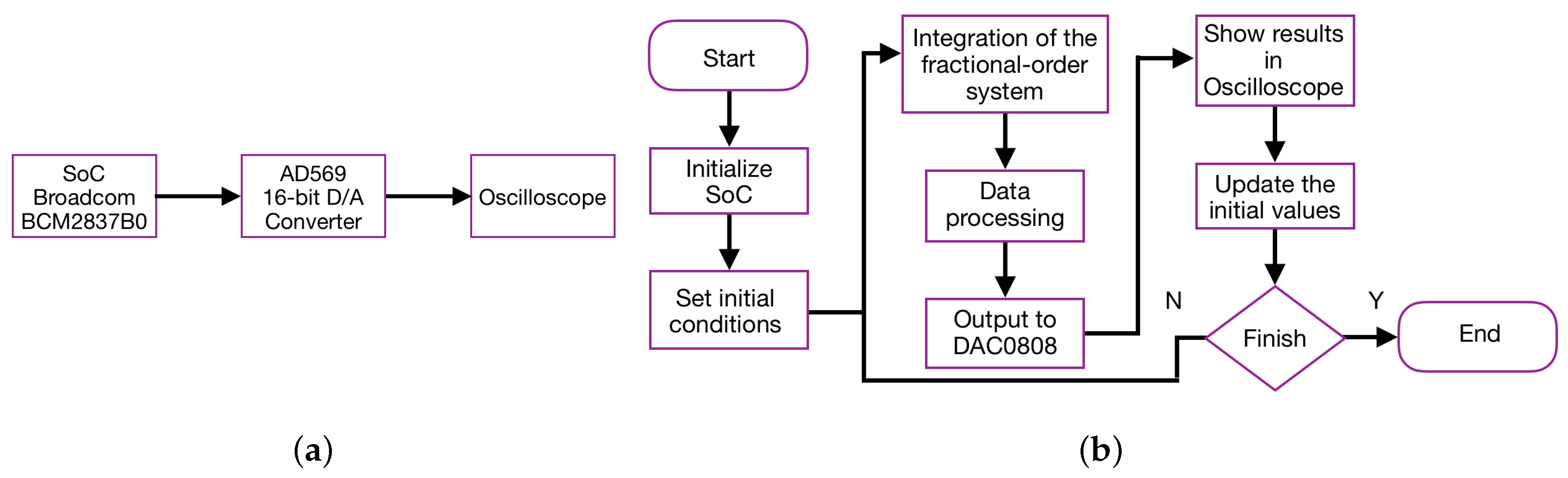
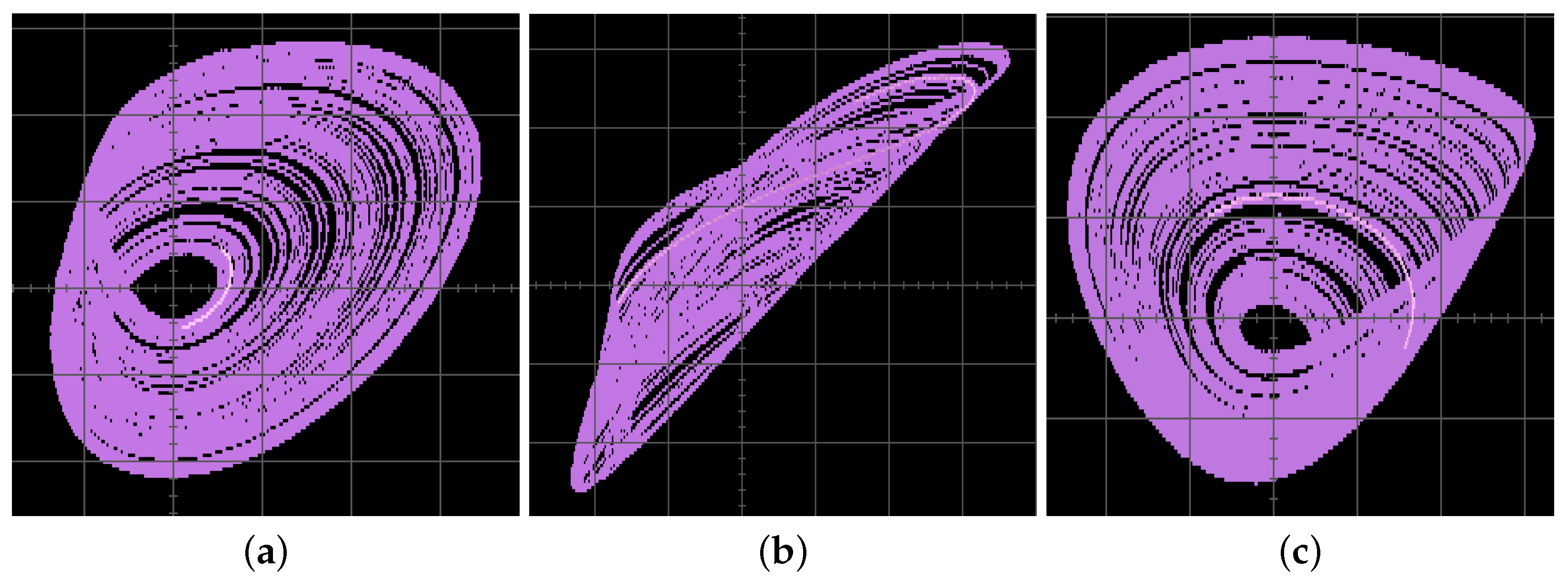
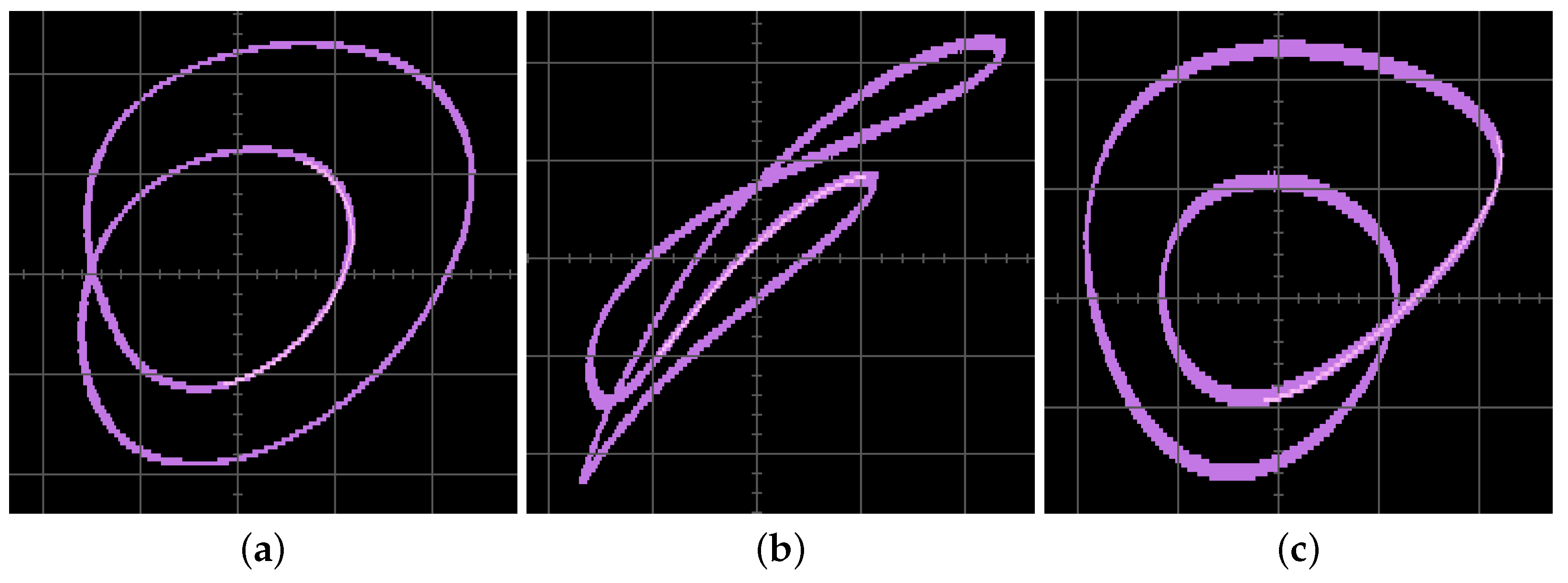
6. Physical Realization of the Fractional-Order Glucose-Insulin System Based on an ARM Processor
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Röder, P.V.; Wu, B.; Liu, Y.; Han, W. Pancreatic regulation of glucose homeostasis. Exp. Mol. Med. 2016, 48, e219. [Google Scholar] [CrossRef] [PubMed]
- Puglianiello, A.; Cianfarani, S. Central control of glucose homeostasis. Rev. Diabet. Stud. 2006, 3, 54. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Palumbo, P.; Ditlevsen, S.; Bertuzzi, A.; De Gaetano, A. Mathematical modeling of the glucose–insulin system: A review. Math. Biosci. 2013, 244, 69–81. [Google Scholar] [CrossRef] [PubMed]
- Roglic, G. WHO Global report on diabetes: A summary. Int. J. Noncommun. Dis. 2016, 1, 3. [Google Scholar] [CrossRef]
- Andrianov, I.; Starushenko, G.; Kvitka, S.; Khajiyeva, L. The Verhulst-Like Equations: Integrable OΔE and ODE with Chaotic Behavior. Symmetry 2019, 11, 1446. [Google Scholar] [CrossRef]
- Rathee, S. ODE models for the management of diabetes: A review. Int. J. Diabetes Dev. Ctries. 2017, 37, 4–15. [Google Scholar] [CrossRef]
- Cruz-Duarte, J.M.; Rosales-García, J.J.; Correa-Cely, C.R. Entropy Generation in a Mass-Spring-Damper System Using a Conformable Model. Symmetry 2020, 12, 395. [Google Scholar] [CrossRef]
- Solís-Pérez, J.E.; Gómez-Aguilar, J.F. Novel Fractional Operators with Three Orders and Power-Law, Exponential Decay and Mittag–Leffler Memories Involving the Truncated M-Derivative. Symmetry 2020, 12, 626. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.L.; Huerta-Cuellar, G.; Jaimes-Reátegui, R.; García-López, J.H.; Aboites, V.; Cassal-Quiroga, B.B.; Gilardi-Velázquez, H.E. Multistability Emergence through Fractional-Order- Derivatives in a PWL Multi-Scroll System. Electronics 2020, 9, 880. [Google Scholar] [CrossRef]
- Danca, M.F. Puu system of fractional order and its chaos suppression. Symmetry 2020, 12, 340. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Rihan, F.A. Numerical modeling of fractional-Order biological systems. Abstr. Appl. Anal. 2013, 2013, 816803. [Google Scholar] [CrossRef]
- Kheiri, H.; Jafari, M. Stability analysis of a fractional order model for the HIV/AIDS epidemic in a patchy environment. J. Comput. Appl. Math. 2019, 346, 323–339. [Google Scholar] [CrossRef]
- Teka, W.W.; Upadhyay, R.K.; Mondal, A. Spiking and bursting patterns of fractional-order Izhikevich model. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 161–176. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Munoz-Pacheco, J.; Gomez-Pavon, L.; Luis-Ramos, A.; Chen, G. Synchronization in a fractional-order model of pancreatic β-cells. Eur. Phys. J. Spec. Top. 2018, 227, 907–919. [Google Scholar] [CrossRef]
- Bodo, B.; Mvogo, A.; Morfu, S. Fractional dynamical behavior of electrical activity in a model of pancreatic β-cells. Chaos Solitons Fractals 2017, 102, 426–432. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Wei, H.; Chen, Y. A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. Top. 2011, 193, 185. [Google Scholar] [CrossRef]
- Saeedian, M.; Khalighi, M.; Azimi-Tafreshi, N.; Jafari, G.; Ausloos, M. Memory effects on epidemic evolution: The susceptible-infected-recovered epidemic model. Phys. Rev. E 2017, 95, 022409. [Google Scholar] [CrossRef]
- Lundstrom, B.N.; Higgs, M.H.; Spain, W.J.; Fairhall, A.L. Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 2008, 11, 1335. [Google Scholar] [CrossRef]
- Lifshitz, R.; Cross, M. Response of parametrically driven nonlinear coupled oscillators with application to micromechanical and nanomechanical resonator arrays. Phys. Rev. B 2003, 67, 134302. [Google Scholar] [CrossRef]
- Bitar, D.; Kacem, N.; Bouhaddi, N. Investigation of modal interactions and their effects on the nonlinear dynamics of a periodic coupled pendulums chain. Int. J. Mech. Sci. 2017, 127, 130–141. [Google Scholar] [CrossRef]
- Chikhaoui, K.; Bitar, D.; Kacem, N.; Bouhaddi, N. Robustness analysis of the collective nonlinear dynamics of a periodic coupled pendulums chain. Appl. Sci. 2017, 7, 684. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. Synchronization approach to analysis of biological systems. Fluct. Noise Lett. 2004, 4, L53–L62. [Google Scholar] [CrossRef]
- Stožer, A.; Gosak, M.; Dolenšek, J.; Perc, M.; Marhl, M.; Rupnik, M.S.; Korošak, D. Functional connectivity in islets of Langerhans from mouse pancreas tissue slices. PLoS Comput. Biol. 2013, 9, e1002923. [Google Scholar] [CrossRef] [PubMed]
- Loppini, A.; Cherubini, C.; Filippi, S. On the emergent dynamics and synchronization of β-cells networks in response to space-time varying glucose stimuli. Chaos Solitons Fractals 2018, 109, 269–279. [Google Scholar] [CrossRef]
- Barua, A.K.; Goel, P. Isles within islets: The lattice origin of small-world networks in pancreatic tissues. Phys. D Nonlinear Phenom. 2016, 315, 49–57. [Google Scholar] [CrossRef]
- Kotani, K.; Takamasu, K.; Ashkenazy, Y.; Stanley, H.E.; Yamamoto, Y. Model for cardiorespiratory synchronization in humans. Phys. Rev. E 2002, 65, 051923. [Google Scholar] [CrossRef]
- Bartsch, R.; Kantelhardt, J.W.; Penzel, T.; Havlin, S. Experimental evidence for phase synchronization transitions in the human cardiorespiratory system. Phys. Rev. Lett. 2007, 98, 054102. [Google Scholar] [CrossRef]
- Satin, L.S.; Butler, P.C.; Ha, J.; Sherman, A.S. Pulsatile insulin secretion, impaired glucose tolerance and type 2 diabetes. Mol. Asp. Med. 2015, 42, 61–77. [Google Scholar] [CrossRef]
- Ravier, M.A.; Güldenagel, M.; Charollais, A.; Gjinovci, A.; Caille, D.; Söhl, G.; Wollheim, C.B.; Willecke, K.; Henquin, J.C.; Meda, P. Loss of connexin36 channels alters β-cell coupling, islet synchronization of glucose-induced Ca2+ and insulin oscillations, and basal insulin release. Diabetes 2005, 54, 1798–1807. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B. Backstepping based stabilization and synchronization of a class of fractional order chaotic systems. Chaos Solitons Fractals 2017, 102, 274–284. [Google Scholar] [CrossRef]
- Singh, A.K.; Yadav, V.K.; Das, S. Synchronization between fractional order complex chaotic systems with uncertainty. Optik 2017, 133, 98–107. [Google Scholar] [CrossRef]
- Bai, E.W.; Lonngren, K.E. Synchronization of two Lorenz systems using active control. Chaos Solitons Fractals 1997, 8, 51–58. [Google Scholar] [CrossRef]
- Shah, D.K.; Chaurasiya, R.B.; Vyawahare, V.A.; Pichhode, K.; Patil, M.D. FPGA implementation of fractional-order chaotic systems. AEU-Int. J. Electron. Commun. 2017, 78, 245–257. [Google Scholar] [CrossRef]
- Soriano-Sánchez, A.; Posadas-Castillo, C.; Platas-Garza, M.A.; Arellano-Delgado, A. Synchronization and FPGA realization of complex networks with fractional–order Liu chaotic oscillators. Appl. Math. Comput. 2018, 332, 250–262. [Google Scholar]
- Rajagopal, K.; Akgul, A.; Jafari, S.; Karthikeyan, A.; Koyuncu, I. Chaotic chameleon: Dynamic analyses, circuit implementation, FPGA design and fractional-order form with basic analyses. Chaos Solitons Fractals 2017, 103, 476–487. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Complexity analysis and DSP implementation of the fractional-order Lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- Wang, H.; Sun, K.; He, S. Characteristic analysis and DSP realization of fractional-order simplified Lorenz system based on Adomian decomposition method. Int. J. Bifurc. Chaos 2015, 25, 1550085. [Google Scholar] [CrossRef]
- Evans, J.R.; Arslan, T. Enhanced image detection on an ARM based embedded system. Des. Autom. Embed. Syst. 2002, 6, 477–487. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Rangel-Magdaleno, J.; Pano-Azucena, A.; Obeso-Rodelo, P.; Nuñez-Perez, J.C. FPGA realization of multi-scroll chaotic oscillators. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 66–80. [Google Scholar] [CrossRef]
- Chen, H.; He, S.; Azucena, A.D.P.; Yousefpour, A.; Jahanshahi, H.; López, M.A.; Alcaraz, R. A Multistable Chaotic Jerk System with Coexisting and Hidden Attractors: Dynamical and Complexity Analysis, FPGA-Based Realization, and Chaos Stabilization Using a Robust Controller. Symmetry 2020, 12, 569. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; García-Chávez, T.; Gonzalez-Diaz, V.R.; de La Fuente-Cortes, G.; del Carmen Gómez-Pavón, L. Two new asymmetric Boolean chaos oscillators with no dependence on incommensurate time-delays and their circuit implementation. Symmetry 2020, 12, 506. [Google Scholar] [CrossRef]
- Montero-Canela, R.; Zambrano-Serrano, E.; Tamariz-Flores, E.I.; Muñoz-Pacheco, J.M.; Torrealba-Meléndez, R. Fractional chaos based-cryptosystem for generating encryption keys in Ad Hoc networks. Ad Hoc Netw. 2020, 97, 102005. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Munoz-Pacheco, J.; Campos-Cantón, E. Chaos generation in fractional-order switched systems and its digital implementation. AEU-Int. J. Electron. Commun. 2017, 79, 43–52. [Google Scholar] [CrossRef]
- Shabestari, P.S.; Panahi, S.; Hatef, B.; Jafari, S.; Sprott, J.C. A new chaotic model for glucose-insulin regulatory system. Chaos Solitons Fractals 2018, 112, 44–51. [Google Scholar] [CrossRef]
- Letellier, C.; Denis, F.; Aguirre, L.A. What can be learned from a chaotic cancer model? J. Theor. Biol. 2013, 322, 7–16. [Google Scholar] [CrossRef]
- Jafari, S.; Baghdadi, G.; Golpayegani, S.R.H.; Towhidkhah, F.; Gharibzadeh, S. Is attention deficit hyperactivity disorder a kind of intermittent chaos? J. Neuropsychiatry Clin. Neurosci. 2013, 25, E02. [Google Scholar] [CrossRef]
- Khajanchi, S.; Perc, M.; Ghosh, D. The influence of time delay in a chaotic cancer model. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 103101. [Google Scholar] [CrossRef]
- Shabestari, P.S.; Rajagopal, K.; Safarbali, B.; Jafari, S.; Duraisamy, P. A Novel Approach to Numerical Modeling of Metabolic System: Investigation of Chaotic Behavior in Diabetes Mellitus. Complexity 2018, 2018, 6815190. [Google Scholar] [CrossRef]
- Ginoux, J.M.; Ruskeepää, H.; Perc, M.; Naeck, R.; Di Costanzo, V.; Bouchouicha, M.; Fnaiech, F.; Sayadi, M.; Hamdi, T. Is type 1 diabetes a chaotic phenomenon? Chaos Solitons Fractals 2018, 111, 198–205. [Google Scholar] [CrossRef]
- Rajagopal, K.; Bayani, A.; Jafari, S.; Karthikeyan, A.; Hussain, I. Chaotic dynamics of a fractional order glucose-insulin regulatory system. Front. Inf. Technol. Electron. Eng. 2019, 21, 1108–1118. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Campos-Cantón, E.; Muñoz-Pacheco, J.M. Strange attractors generated by a fractional order switching system and its topological horseshoe. Nonlinear Dyn. 2016, 83, 1629–1641. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Mittag–Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Odibat, Z.; Corson, N.; Aziz-Alaoui, M.; Alsaedi, A. Chaos in fractional order cubic Chua system and synchronization. Int. J. Bifurc. Chaos 2017, 27, 1750161. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.; El-Saka, H.A. Equilibrium points, stability and numerical solutions of fractional-order predator–prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Tavazoei, M.; Haeri, M. Unreliability of frequency-domain approximation in recognising chaos in fractional-order systems. IET Signal Process. 2007, 1, 171–181. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. A necessary condition for double scroll attractor existence in fractional- order systems. Phys. Lett. A 2007, 367, 102–113. [Google Scholar] [CrossRef]
- Danca, M.F. Hidden chaotic attractors in fractional-order systems. Nonlinear Dyn. 2017, 89, 577–586. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Chaotic attractors in incommensurate fractional order systems. Phys. D Nonlinear Phenom. 2008, 237, 2628–2637. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.; El-Saka, H.A. On some Routh–Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems. Phys. Lett. A 2006, 358, 1–4. [Google Scholar] [CrossRef]
- Sprott, J.C. Simplest chaotic flows with involutional symmetries. Int. J. Bifurc. Chaos 2014, 24, 1450009. [Google Scholar] [CrossRef]
- Tourkmani, A.M.; Alharbi, T.J.; Rsheed, A.M.B.; AlRasheed, A.N.; AlBattal, S.M.; Abdelhay, O.; Hassali, M.A.; Alrasheedy, A.A.; Al Harbi, N.G.; Alqahtani, A. Hypoglycemia in Type 2 Diabetes Mellitus patients: A review article. Diabetes Metab. Syndr. Clin. Res. Rev. 2018, 12, 791–794. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Effah-Poku, S.; Obeng-Denteh, W.; Dontwi, I. A Study of Chaos in Dynamical Systems. J. Math. 2018, 2018, 1808953. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Time-varying linearization and the Perron effects. Int. J. Bifurc. Chaos 2007, 17, 1079–1107. [Google Scholar] [CrossRef]
- Lee, Y.; Fluckey, J.D.; Chakraborty, S.; Muthuchamy, M. Hyperglycemia-and hyperinsulinemia-induced insulin resistance causes alterations in cellular bioenergetics and activation of inflammatory signaling in lymphatic muscle. FASEB J. 2017, 31, 2744–2759. [Google Scholar] [CrossRef] [PubMed]
- Shanik, M.H.; Xu, Y.; Škrha, J.; Dankner, R.; Zick, Y.; Roth, J. Insulin resistance and hyperinsulinemia: Is hyperinsulinemia the cart or the horse? Diabetes Care 2008, 31, S262–S268. [Google Scholar] [CrossRef] [PubMed]
- Erion, K.A.; Corkey, B.E. Hyperinsulinemia: A cause of obesity? Curr. Obes. Rep. 2017, 6, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Corkey, B.E. Banting lecture 2011: Hyperinsulinemia: Cause or consequence? Diabetes 2012, 61, 4–13. [Google Scholar] [CrossRef] [PubMed]
- Glaser, B. Type 2 diabetes: Hypoinsulinism, hyperinsulinism, or both? PLoS Med. 2007, 4, e148. [Google Scholar] [CrossRef] [PubMed]
- Dawson, S.P.; Grebogi, C.; Yorke, J.A.; Kan, I.; Koçak, H. Antimonotonicity: Inevitable reversals of period-doubling cascades. Phys. Lett. A 1992, 162, 249–254. [Google Scholar] [CrossRef]
- Kengne, J.; Jafari, S.; Njitacke, Z.; Khanian, M.Y.A.; Cheukem, A. Dynamic analysis and electronic circuit implementation of a novel 3D autonomous system without linear terms. Commun. Nonlinear Sci. Numer. Simul. 2017, 52, 62–76. [Google Scholar] [CrossRef]
- Signing, V.F.; Kengne, J.; Pone, J.M. Antimonotonicity, chaos, quasi-periodicity and coexistence of hidden attractors in a new simple 4-D chaotic system with hyperbolic cosine nonlinearity. Chaos Solitons Fractals 2019, 118, 187–198. [Google Scholar] [CrossRef]
- Pandey, A.; Chawla, S.; Guchhait, P. Type-2 diabetes: Current understanding and future perspectives. IUBMB Life 2015, 67, 506–513. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Dey, D.; Roy, S.S. Molecular mechanism of insulin resistance. J. Biosci. 2007, 32, 405–413. [Google Scholar] [CrossRef][Green Version]
- Quan, W.; Jo, E.K.; Lee, M.S. Role of pancreatic β-cell death and inflammation in diabetes. Diabetes Obes. Metab. 2013, 15, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.; Li, Y.; Xu, W.; Shi, L.; Zhang, Q.; Zhu, D.; Hu, Y.; Zhou, Z.; Yan, X.; Tian, H.; et al. Effect of intensive insulin therapy on β-cell function and glycaemic control in patients with newly diagnosed type 2 diabetes: A multicentre randomised parallel-group trial. Lancet 2008, 371, 1753–1760. [Google Scholar] [CrossRef]
- Pearson, J.A.; Agriantonis, A.; Wong, F.S.; Wen, L. Modulation of the immune system by the gut microbiota in the development of type 1 diabetes. Hum. Vaccines Immunother. 2018, 14, 2580–2596. [Google Scholar] [CrossRef] [PubMed]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Kacar, S.; Pham, V.T.; Alsaadi, F.E. A new fractional-order hyperchaotic memristor oscillator: Dynamic analysis, robust adaptive synchronization, and its application to voice encryption. Appl. Math. Comput. 2020, 383, 125310. [Google Scholar] [CrossRef]
- Nasteska, D.; Hodson, D.J. The role of beta cell heterogeneity in islet function and insulin release. J. Mol. Endocrinol. 2018, 61, R43–R60. [Google Scholar] [CrossRef]
- Reinbothe, T.M.; Safi, F.; Axelsson, A.S.; Mollet, I.G.; Rosengren, A.H. Optogenetic control of insulin secretion in intact pancreatic islets with β-cell-specific expression of Channelrhodopsin-2. Islets 2014, 6, e28095. [Google Scholar] [CrossRef]





| Equilibrium Point | Eigenvalues | |
|---|---|---|
| , | ||
| , |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munoz-Pacheco, J.M.; Posadas-Castillo, C.; Zambrano-Serrano, E. The Effect of a Non-Local Fractional Operator in an Asymmetrical Glucose-Insulin Regulatory System: Analysis, Synchronization and Electronic Implementation. Symmetry 2020, 12, 1395. https://doi.org/10.3390/sym12091395
Munoz-Pacheco JM, Posadas-Castillo C, Zambrano-Serrano E. The Effect of a Non-Local Fractional Operator in an Asymmetrical Glucose-Insulin Regulatory System: Analysis, Synchronization and Electronic Implementation. Symmetry. 2020; 12(9):1395. https://doi.org/10.3390/sym12091395
Chicago/Turabian StyleMunoz-Pacheco, Jesus M., Cornelio Posadas-Castillo, and Ernesto Zambrano-Serrano. 2020. "The Effect of a Non-Local Fractional Operator in an Asymmetrical Glucose-Insulin Regulatory System: Analysis, Synchronization and Electronic Implementation" Symmetry 12, no. 9: 1395. https://doi.org/10.3390/sym12091395
APA StyleMunoz-Pacheco, J. M., Posadas-Castillo, C., & Zambrano-Serrano, E. (2020). The Effect of a Non-Local Fractional Operator in an Asymmetrical Glucose-Insulin Regulatory System: Analysis, Synchronization and Electronic Implementation. Symmetry, 12(9), 1395. https://doi.org/10.3390/sym12091395







