Unified Inflation and Late-Time Accelerated Expansion with Exponential and R² Corrections in Modified Gravity

Abstract

Modified gravity models with and exponential function of curvature and $R^2$ corrections are proposed. At low curvature, the model explains the matter epoch and the late time accelerated expansion while at the inflation epoch the leading term is $R^2$. At $R\to 0$ the cosmological constant disappears, giving unified description of inflation and dark energy in pure geometrical context. The models satisfy the stability conditions, pass local tests and are viable in the $(r,m)$-plane, where the trajectories connect the saddle matter dominated critical point ($r=-1$, $m=0$) with the late time de Sitter attractor at $r=-2$ and $0<m\le 1$. Initial conditions were found, showing that the density parameters evolve in a way consistent with current cosmological observations, predicting late time behavior very close to the $\mathsf{\Lambda }$CDM with future universe evolving towards the de Sitter attractor.

1. Introduction

The possibilities of unification of the early time inflationary era with late time accelerated expansion of the universe is one of the attractive facts of modified gravity theories; this captured the attention of the researchers in this field. This approach, based on geometrical grounds, avoids the introduction of additional degrees of freedom for the inflation or dark energy.

The modified gravity models represent an appealing alternative to a dynamical explanation of dark energy (for review see [1,2,3,4]), despite the success of the cosmological constant as the source of dark energy, but which is clouded by the known fine tuning problem. These theories introduce additional non-linear corrections to the Einstein model, which are subject to local systems tests and cosmological observational constraints that determine the viability of the model (see [5,6,7,8,9,10,11] for reviews). A variety of models for modified gravity were proposed and some of them are [6,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. Models that can satisfy both cosmological and local gravity constraints were proposed in [31,33,34,35,36,37], and exact cosmological solutions were studied in [38,39,40,41,42,43,44]. Modified gravity with arbitrary function of the 4-dimensional Gauss-Bonnet invariant was introduced in [45,46,47]. There are also models that attempt to unify early time inflation with late time acceleration, among which we can highlight: [15] in which negative and positive powers of curvature were introduced in order to unify inflation and cosmic acceleration, in [48] an extension of the Hu-Sawyki model [31] was proposed that includes inflation and late-time accelerated expansion, in [49] a modified gravity that unifies power-law curvature inflation with late-time $\mathsf{\Lambda }$CDM epoch was considered, in [36] a class of exponential modified gravity models was introduced, in which the inflation and accelerated expansion are present, a simple modified model with exponential gravity was considered in [37,50], a model with exponential and logarithmic corrections was considered in [51] and constant roll inflation with exponential modified gravity was studied in [52]. Unified models of inflation and dark energy with modified Gauss-Bonnet contribution were studied in [45,46,47,53,54]. In [55] a comprehensive study of the cosmological constraints for general $f\left(R\right)$ theory was performed, where a classification of $f\left(R\right)$ models was proposed, depending on the existence of the standard matter era and on the final accelerated state. The viability of several models was also analyzed by using the autonomous system approach. In [56], local and cosmological constraints are discussed and the evolution of matter density perturbations was studied. A dynamical analysis and study of critical points for locally anisotropic cosmological models of modified gravity were carried out in [57,58].

The aim of this paper is to propose a simple viable model of $f\left(R\right)$ gravity that consistently describes both the inflationary epoch and the late time accelerated expansion of the universe, while satisfies the stringent local gravity constraints. This model contains a new exponential gravity correction that gives compatible with observations description of the cosmic evolution, mimicking the $\mathsf{\Lambda }$CDM model, and $R^2$ term [32] that becomes relevant at high curvature and gives successful explanation of the early-time inflation. The viability of the model is shown in the ($m,r$) diagram which describes trajectories connecting the matter dominated saddle point at $r=-1$, $m=0$ with late-time de Sitter attractor at $r=-1$ and $0<m\le 1$. The model also satisfies the more stringent local gravity constraints.

This paper is organized as follows. In Section 2 we present the general features of the $f\left(R\right)$ models, including the autonomous system and the relevant critical points for our study in terms of the $(r,m)$ parameters. In Section 3 we present the model, showing the conditions for viability and its trajectories in the ($r,m$)-plane, including some numerical cases of cosmic evolution. In Section 4 we present some discussion.

2. Field Equations

The modified gravity can be the described by the following action

$$S=\int d^{4}x\sqrt{-g}\left[\frac{1}{2{\kappa }^2}f\left(R\right)+{\mathcal{L}}_m\right]$$

(1)

where ${\kappa }^2=8\pi G$ and ${\mathcal{L}}_m$ is the Lagrangian density for the matter component which satisfies the usual continuity equation. The equation of motion is given by

$$f_{,R}\left(R\right)R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }f\left(R\right)+\left(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)f_{,R}\left(R\right)={\kappa }^2{T}_{\mu \nu }^{\left(m\right)}$$

(2)

where $T_{\mu \nu }^{\left(m\right)}$ is the matter energy-momentum tensor assumed as

$$T_{\mu \nu }^m=\left(\rho +p\right)u^{\mu }{u}^{\nu }+p{g}_{\mu \nu }$$

and $f_{,R}\equiv \frac{df}{dR}$. The trace of Equation (2) gives

$$R{f}_{,R}\left(R\right)-2f\left(R\right)+3\square f_{,R}\left(R\right)={\kappa }^2{T}^{\left(m\right)}={\kappa }^2\left(3p-\rho \right)$$

(3)

Extracting the time and spatial components of Equation (2) gives by the expressions

$$3H^2{f}_{,R}=\frac{1}{2}\left(R{f}_{,R}-f\right)-3H{\dot{f}}_{,R}+{\kappa }^2\rho$$

(4)

and

$$-2\dot{H}{f}_{,R}={\ddot{f}}_{,R}-H{\dot{f}}_{,R}+{\kappa }^2\left(\rho +p\right)$$

(5)

where dot represents derivative with respect to cosmic time. The effective equation of state (EoS) from these expressions is

$$w_{eff}=-1-\frac{2\dot{H}}{3H^2}=-1+\frac{{\ddot{f}}_{,R}-H{\dot{f}}_{,R}+{\kappa }^2\left(\rho +p\right)}{\frac{1}{2}\left(R{f}_{,R}-f\right)-3H{\dot{f}}_{,R}+{\kappa }^2\rho },$$

(6)

where $\rho$ and p include both matter and radiation components, i.e., $\rho ={\rho }_m+{\rho }_r$ and $p=p_m+p_r$. The viability conditions begin with the stability which demands that

$$f_{,R}>0,f_{,RR}>0$$

(7)

where the first condition is necessary to avoid change of sign in the effective Newtonian coupling, and the second is necessary in order to avoid tachyonic behavior of the scalaron and is also a condition of stability under perturbations, especially at the matter dominated epoch. In fact, the scalar particle associated with $f\left(R\right)$, dubbed scalaron with mass

$$M^2=\frac{1}{3}\left(\frac{f_{,R}}{f_{,RR}}-R\right)$$

(8)

which in matter epoch or in the regime $M^2>>R$, when $R{f}_{,RR}<<1$ and $f_{,R}\simeq 1$ can be reduced to

$$M^2\simeq \frac{1}{3f_{,RR}},$$

(9)

which requires $f_{,RR}>0$. Apart from that, the model must be compatible with the observational evidence at both local and cosmological scales. The mass M plays an important role in local gravity constraints since it defines the range of the force mediated by the scalaron which determines the Compton wavelength ${\lambda }_C=2\pi M^{-1}$. If ℓ is the typical size of a local gravitational system, then the local gravity constraints on $f\left(R\right)$ are satisfied whenever $\ell >>{\lambda }_C$ or $M\ell >>1$ [55,56]. On the other hand, to demonstrate the viability of modified gravity as cosmological model it is useful to consider the autonomous system with the following dimensionless variables that can be obtained from Equation (4) [55] (we will use indistinctly $f_{,R}$ or $F=f_{,R}$)

$$x=-\frac{\dot{F}}{HF},y=-\frac{f}{6H^{2}F},z=\frac{R}{6H^2}=\frac{\dot{H}}{H^2}+2,w=\frac{{\kappa }^2{\rho }_r}{3H^{2}F},{\mathsf{\Omega }}_m=\frac{{\kappa }^2{\rho }_m}{3H^{2}F}$$

(10)

which lead to the following dynamical system

$$x+y+z+w+{\mathsf{\Omega }}_m=1$$

(11)

$$\frac{dx}{dN}=x^2-xz-3y-z+w-1$$

(12)

$$\frac{dy}{dN}=xy+\frac{xz}{m}-2y(z-2)$$

(13)

$$\frac{dz}{dN}=-\frac{xz}{m}-2z(z-2)$$

(14)

$$\frac{dw}{dN}=xw-2zw$$

(15)

where $N=lna$, $w={\mathsf{\Omega }}_r$ is the density parameter of the radiation component, and m is given by

$$m=\frac{R{f}_{,RR}}{f_{,R}}.$$

(16)

Along with the parameter m there is another useful parameter r defined as

$$r=-\frac{R{f}_{,R}}{f}.$$

(17)

These parameters are useful to analyze the cosmological viability of $f\left(R\right)$ models and characterize the deviation of a given $f\left(R\right)$ model from the standard $\mathsf{\Lambda }$CDM model, which corresponds to the line $m=0$. In terms of the dynamical variables the effective EoS (6) is written as

$$w_{eff}=-\frac{1}{3}\left(2z-1\right),$$

(18)

while the dark energy equation of state from (4) and (5) can be written as [55,56]

$$w_{DE}=-\frac{1}{3}\frac{2z-1+(F/F_0)w}{1-(F/F_0)(1-x-y-z)},$$

(19)

where $F_0$ is the current value of $f_{,R}$.

The critical points of the dynamical system (11)–(15), that are the solutions of the equations ([55,56])

$$\frac{dx}{dN}=0,\dots \frac{dw}{dN}=0,$$

(20)

allow analyzing asymptotic cosmological solutions of the model (1) and their stability properties. Among the solutions of the system (20) there are three important critical points that we will consider to analyze the viability of our models (in this analysis we do not consider the contribution of radiation, which does not change the stability properties of the critical points).

The first critical point corresponds to scaling solutions which include the matter dominated era, has the following coordinates in terms of the parameter m

$$P_S=(x_c,y_c,z_c)=\left(\frac{3m}{1+m},-\frac{1+4m}{2{(1+m)}^2},\frac{1+4m}{2(1+m)}\right),$$

(21)

with eigenvalues

$$EV\left(P_S\right):\left(3(1+m^{\prime }),\frac{-3m\pm \sqrt{m(256m^3+160m^2-31m-16)}}{4m(m+1)}\right),$$

(22)

where m is given by (16) and prime represents derivative with respect to r. At this point the matter density parameter and the effective EoS take the form

$${\mathsf{\Omega }}_m=1-\frac{m(7+10m)}{2{(1+m)}^2},w_{eff}=-\frac{m}{1+m},$$

(23)

The second point has the coordinates

$$P_{deS}=(x_c,y_c,z_c)=(0,-1,2),$$

(24)

with eigenvalues

$$EV\left(P_{deS}\right):\left(-3,-\frac{3}{2}\pm \frac{\sqrt{25-16/m(r=-2)}}{2}\right),$$

(25)

and lead to the de Sitter solution with

$${\mathsf{\Omega }}_m=0,w_{eff}=-1$$

(26)

The third critical point, that leads to accelerated expansion scenarios, has the coordinates

$$P_C=(x_c,y_c,z_c)=\left(\frac{2(1-m)}{1+2m},\frac{1-4m}{m(1+2m)},-\frac{(1-4m)(1+m)}{m(1+2m)}\right),$$

(27)

with the eigenvalues

$$EV\left(P_C\right):\left(-4+\frac{1}{m},\frac{2-3m-8m^2}{m(1+2m)},-\frac{2(m^2-1)(1+m^{\prime })}{m(1+2m)}\right).$$

(28)

The matter density parameter and effective EoS corresponding to this point are

$${\mathsf{\Omega }}_m=0,w_{eff}=\frac{2-5m-6m^2}{3m(1+2m)},$$

(29)

From the coordinates y and z for the points $P_S$ and $P_C$ it can be seen that they are connected by the line $m\left(r\right)=-1-r$, where the relation

$$r\left(N\right)=\frac{z\left(N\right)}{y\left(N\right)}$$

(30)

is used.

From (21) follows that the matter dominated point corresponds to $(r,m)$=$(-1,0)$. The existence of a viable saddle matter era requires $m(r\to -1)>0$ and $-1<dm/dr(r\to -1)\le 0$. This last condition implies that all the $m\left(r\right)$ trajectories must be between the lines $m=0$ and $m=-r-1$. In order to be viable, the trajectory of a given $f\left(R\right)$ model in the $(r,m)$ plane should be such that it contains the matter dominated point $P_M=(-1,0)$ and starting from $P_M$ intersects the line $r=-2$ in the region $0<m\le 1$ [55]. The $\mathsf{\Lambda }$CDM model, for instance, connect the points $P_M=(-1,0)$ and $P_{dS}=(-2,0)$. There are also viable trajectories connecting the saddle matter point $P_M=P_S(m\to 0)$ with the curvature dominated point that leads to stable accelerated expansion $P_C$, whenever $m^{\prime }>-1$.

3. The Models

The following model, as will be shown satisfies all above discussed conditions of stability and viability

$$f\left(R\right)=R-2{\lambda }_1{\mu }^2{e}^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}+\frac{{\lambda }_2}{{\mu }^2}{R}^2$$

(31)

where the dimensionless constants $\eta$, ${\lambda }_1$ and ${\lambda }_2$ are positive, and $0<\eta \le 1$. This function is well defined for any R and describes the physical regimes related to the crucial cosmological epochs epochs of the universe: the inflationary regime where the relevant contribution comes from the $R^2$ Starobinsky term and the small curvature regime covering from the matter era to the current stage of accelerated expansion, where gravity is described mainly by the first two terms in (31). The Lagrangian composed of

$$R+\frac{{\lambda }_2}{{\mu }^2}{R}^2,$$

(32)

which is the dominant sector of the model (31) for large curvature, typical of the inflationary epoch, gives the well known and still consistent with observational data Starobinsky inflation. Hence, these two corrections are of different nature and are introduced for different purposes. Then to analyze the viability of the model to explain the late time accelerated expansion, the $R^2$ term should be irrelevant, which imposes restrictions on the parameter ${\lambda }_2$. In fact the scale ${\mu }^2$ was introduced in the last term with the sole objective to make ${\lambda }_2$ dimensionless, since at the end ${\lambda }_2$ must satisfy the restrictions imposed by the curvature at the inflationary period. The properties of the model (31) must be reflected in the behavior of the autonomous system, as we show below. First we note that the exponential function satisfies the limits

$$\underset{R\to 0}{lim}{e}^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}=0,\underset{R\to \infty }{lim}{e}^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}=1.$$

(33)

The first limit allows the existence of flat spacetime solutions and the second is necessary for consistency with high redshift CMB observations.

To check the stability conditions (7) we analyze the corresponding expressions for $f_{,R}$ and $f_{,RR}$

$$f_{,R}=1-2{\lambda }_1\eta {\left(\frac{{\mu }^2}{R}\right)}^{1+\eta }{e}^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}+\frac{2{\lambda }_{2}R}{{\mu }^2},$$

(34)

$$f_{,RR}=\frac{2\eta {\lambda }_1}{{\mu }^2}{\left(\frac{{\mu }^2}{R}\right)}^{2+\eta }\left[1+\eta -\eta {\left(\frac{{\mu }^2}{R}\right)}^{\eta }\right]e^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}+\frac{2{\lambda }_2}{{\mu }^2}.$$

(35)

The condition $f_{,R}>0$ can be easily meet under the assumption ${\mu }^2<R$ and taking into account that $0<\eta \le 1$. Since the last term in (34) is positive and the R-dependent terms are always less than 1, it can be satisfied under the following restriction on ${\lambda }_1$

$${\lambda }_1<\frac{1}{2\eta }.$$

(36)

From (35) follows that $f_{,RR}>0$ is always true for ${\mu }^2<R$ and $0<\eta \le 1$. This is compatible with the criteria we will use below to redefine the stability conditions, by setting ${\lambda }_1$ such that the de Sitter critical point takes place at $R=R_1$.

The r and m parameters for the model (31), that determine its cosmological viability, are obtained from (17) and (16) respectively and are given by

$$r=-\frac{\frac{R}{{\mu }^2}\left(2{\lambda }_1\frac{R}{{\mu }^2}-2\eta {\lambda }_2{e}^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}{\left(\frac{{\mu }^2}{R}\right)}^{\eta +1}+1\right)}{\frac{R}{{\mu }^2}+{\lambda }_1{\left(\frac{R}{{\mu }^2}\right)}^2-2{\lambda }_2{e}^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}}$$

(37)

and

$$m=\frac{2{\lambda }_1{e}^{{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}{\left(\frac{R}{{\mu }^2}\right)}^2+2\eta {\lambda }_2{\left(\frac{{\mu }^2}{R}\right)}^{\eta }\left(1+\eta \left(1-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }\right)\right)}{\frac{R}{{\mu }^2}{e}^{{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}+2{\lambda }_1{\left(\frac{R}{{\mu }^2}\right)}^2{e}^{{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}-2\eta {\lambda }_2{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}.$$

(38)

where the expressions for $f_{,R}$ and $f_{,RR}$ from (34) and (35) were used.

To analyze the stability at the de Sitter point $0<m(r=-2)\le 1$, we fix ${\lambda }_1$ in such a way that the de Sitter point $r=-2$ takes place at $R=R_1$. From (37) it is found

$${\lambda }_1=\frac{\frac{R_1}{{\mu }^2}{e}^{{\left(\frac{{\mu }^2}{R_1}\right)}^{\eta }}}{2\left[2-\eta {\left(\frac{{\mu }^2}{R_1}\right)}^{\eta }\right]}.$$

(39)

Please note that this value does not depend on ${\lambda }_2$ because de de Sitter solution is automatically satisfied by the $R^2$-model. The restriction ${\lambda }_1>0$ can be solved by imposing

$${\left(\frac{{\mu }^2}{R_1}\right)}^{\eta }<\frac{2}{\eta }$$

(40)

And for the stability condition at the de sitter point $0<m(r=-2)\le 1$, using the above value for $\lambda -1$, leads to

$$0<\frac{\eta {\left(\frac{{\mu }^2}{R_1}\right)}^{\eta }\left(1+\eta \left(1-{\left(\frac{{\mu }^2}{R_1}\right)}^{\eta }\right)\right)+2{\lambda }_2\frac{R_1}{{\mu }^2}\left(2-\eta {\left(\frac{{\mu }^2}{R_1}\right)}^{\eta }\right)}{2\left(1-\eta {\left(\frac{{\mu }^2}{R_1}\right)}^{\eta }\right)+2{\lambda }_2\frac{R_1}{{\mu }^2}\left(2-{\left(\frac{{\mu }^2}{R_1}\right)}^{\eta }\right)}\le 1$$

(41)

This inequality cannot be solved explicitly in terms of $R_1$, but it we choose the parametrization

$$\frac{{\mu }^2}{R_1}={\left(\frac{1}{p\eta }\right)}^{1/\eta },p>1$$

(42)

which satisfies (40), then the inequality (41) becomes

$$0<\frac{\eta {\left(\frac{1}{p\eta }\right)}^{1+1/\eta }\left(1+\eta -1/p\right)+2{\lambda }_2\left(2-1/p\right)}{2{\left(\frac{1}{p\eta }\right)}^{1/\eta }\left(1-1/p\right)+2{\lambda }_2\left(2-1/p\right)}\le 1$$

(43)

that is satisfied by

$$p\ge \frac{\eta +3}{4}+\frac{1}{4}\sqrt{{\eta }^2+6\eta +1},0<\eta \le 1.$$

(44)

In fact, given that $0<\eta \le 1$, this inequality is always satisfied by any $p\ge 1+1/\sqrt{2}$ which is consistent with (42).

Turning to the stability conditions and taking into account ${\lambda }_1$ from (39) and $R_1$ from (42), we find after replacing in (34)

$$f_{,R}=1-\frac{e^{\frac{1}{p\eta }-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}}{(2p-1){\left(p\eta \right)}^{1/\eta -1}}{\left(\frac{{\mu }^2}{R}\right)}^{1+\eta }+2{\lambda }_2\frac{R}{{\mu }^2}$$

(45)

as ${\lambda }_2>0$, then a sufficient condition to satisfy the inequality $f_{,R}>0$ is

$$\frac{e^{\frac{1}{p\eta }-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}}{(2p-1){\left(p\eta \right)}^{1/\eta -1}}{\left(\frac{{\mu }^2}{R}\right)}^{1+\eta }<1.$$

(46)

From the fact that $R>R_1$ follows that ${\mu }^2/R<{\mu }^2/R_1$ or

$$\frac{{\mu }^2}{R}<{\left(\frac{1}{p\eta }\right)}^{1/\eta },$$

then the inequality (46) also takes place if we assume the maximum value for ${\mu }^2/R$, which reduces to

$$\left(2p-1\right){\left(p\eta \right)}^{2/\eta }>1$$

(47)

which takes place if additionally to $p>1$, we impose the restriction $p\eta \ge 1$. For the second derivative $f_{,RR}$ we obtain

$$f_{,RR}=\frac{1}{(2p-1){\mu }^2}{\left(p\eta \right)}^{1+1/\eta }{e}^{\frac{1}{p\eta }-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}{\left(\frac{{\mu }^2}{R}\right)}^{2+\eta }\left(1+\eta -\eta {\left(\frac{{\mu }^2}{R}\right)}^{\eta }\right)+\frac{2{\lambda }_2}{{\mu }^2}$$

(48)

And the stability condition $f_{,RR}$ is automatically satisfied since $p>1$ and $R>{\mu }^2$ (we can also use the maximum value of ${\mu }^2/R$ coming from the inequality $R>R_1$ to find that $1+\eta -1/p>0$, which leads to $f_{,RR}>0$). Thus, we found the conditions for stability without compromising the constant ${\lambda }_2$ which will be useful in adjusting the Starobinsky $R^2$ term with the scale of inflation. It is worth noticing that the stability condition $f_{,RR}>0$ holds for any $R>R_1$, and there are not any instability problems related to the matter epoch and at local systems scales. Note also that the stability conditions derived after fixing ${\lambda }_1$ maintain the consistency with the general stability conditions derived for $f_{,R}$ and $f_{,RR}$ given by the expressions (34) and (35) respectively. The restriction (36) on ${\lambda }_1$ can be satisfied assuming, for instance, $p\eta =1$ (i.e., ${\mu }^2/R_1=1$) one finds

$$\eta <\frac{2}{e+1}.$$

(49)

To analyze the viability of the model in the $(r,m)$-plane we resort to the parametric plot of some trajectories, since m cannot be expressed analytically in terms of r. Using (37) and (38) and defining the variable $y=R/{\mu }^2$ with de Sitter value $y_1=R_1/{\mu }^2$ (see (42)) we can write the corresponding expressions for r and m as follows

$$r=-\frac{(2p-1)\left(1+2{\lambda }_{2}y\right)y^{\eta +1}-{\left(p\eta \right)}^{1+1/\eta }{e}^{\frac{1}{p\eta }-\frac{1}{y^{\eta }}}}{(2p-1)\left(1+{\lambda }_{2}y\right)y^{\eta +1}-p{\left(p\eta \right)}^{1/\eta }{y}^{\eta }{e}^{\frac{1}{p\eta }-\frac{1}{y^{\eta }}}}$$

(50)

$$m=\frac{2{\lambda }_2(2p-1)y^{2\eta +2}+{\left(p\eta \right)}^{1+1/\eta }\left(\left(1+\eta \right)y^{\eta }-\eta \right)e^{\frac{1}{p\eta }-\frac{1}{y^{\eta }}}}{(2p-1)\left(1+2{\lambda }_{2}y\right)y^{2\eta +1}-{\left(p\eta \right)}^{1+1/\eta }{y}^{\eta }{e}^{\frac{1}{p\eta }-\frac{1}{y^{\eta }}}}$$

(51)

where we used the expression for ${\lambda }_1$ from (39). It can be confirmed that at $y={\left(p\eta \right)}^{1/\eta }$, r takes the value $r=-2$. To simplify the numerical analysis, in what follows we assume the restriction

$$p\eta =1,$$

(52)

that satisfies all above restrictions and, according to (42), gives $R_1={\mu }^2$.

On the other hand, the value of ${\lambda }_2$ must be chosen in such a way that

$$\frac{{\lambda }_2}{{\mu }^2}\sim \frac{6}{M^2}$$

(53)

where $M\sim {10}^{13}Gev$, which is the typical value required for inflation. If $R_i$ is the typical curvature during inflation, then the coefficient ${\lambda }_2/{\mu }^2$ should be of the order of

$$\lambda /{\mu }^2\sim 1/R_i$$

to ensure that in the small curvature regime, when $R<<R_i$, it is verified that

$$R>>\frac{R^2}{R_i},$$

(54)

necessary to avoid the effect of the $R^2$-term in the small curvature regime. Thus, for the model (31) the physical criteria to establish the value of ${\lambda }_2$ involves the curvature (mass) scale $\mu$. At the same time, this scale is set so that local gravity constraints are satisfied. In any case since, after the restriction (52), the de Sitter curvature satisfies $R_1={\mu }^2$, then this scale should be smaller than the current curvature $R_0\sim H_0^2$, i.e., ${\mu }^2<H_0^2$, which implies, according to (53), that

$${\lambda }_2<\frac{H_0^2}{6M^2}\sim {10}^{-112}$$

(55)

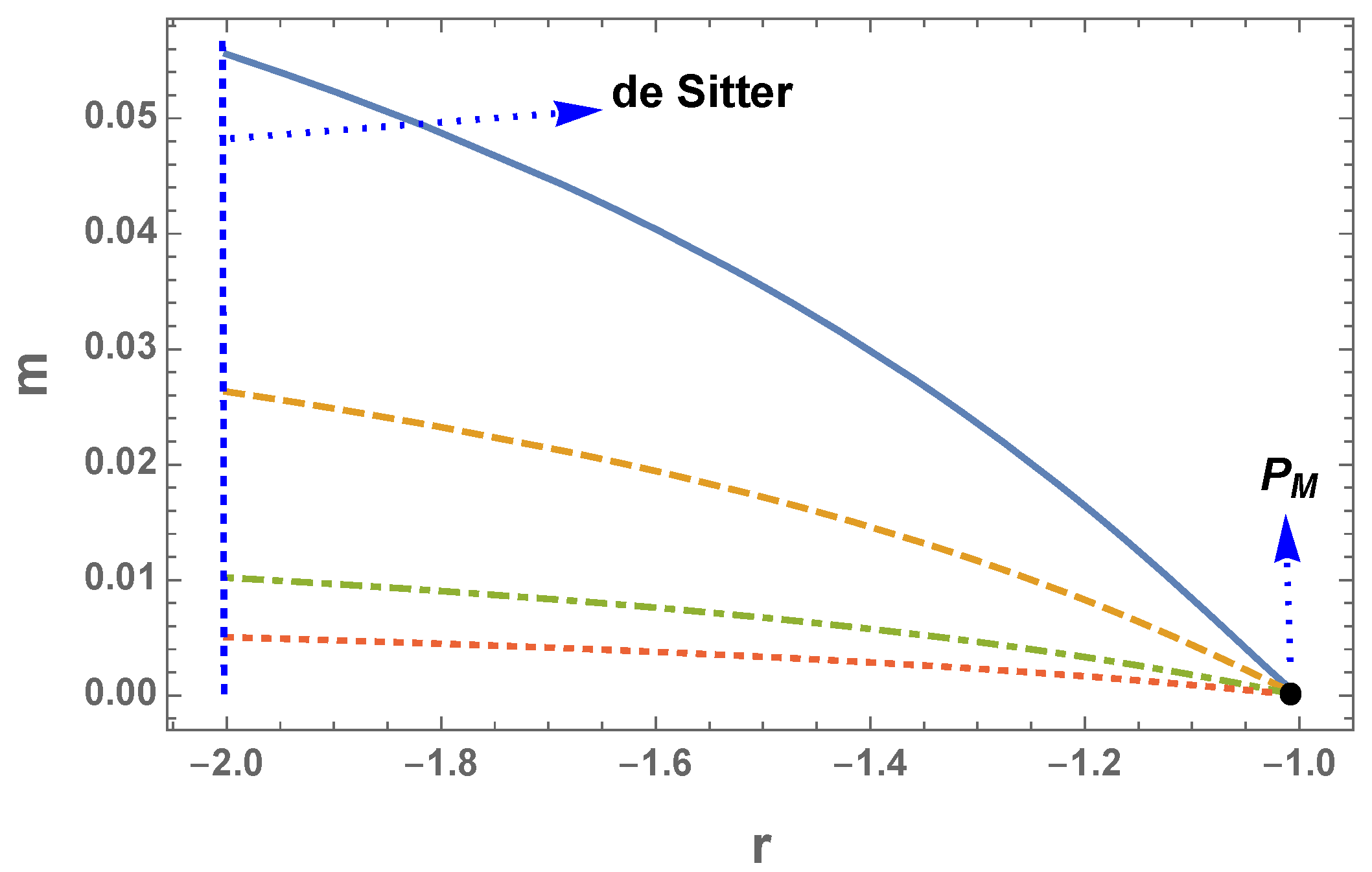
In Figure 1 we present some trajectories in the $(r,m)$-plane. The model contains the matter dominated point $P_M=(-1,0)$ and cosmologically viable trajectories that connect the matter era with the final de Sitter attractor at $r=-2$. As can be seen from Figure 1 the value of ${\lambda }_2$ is such that it avoids the effects of the $R^2$ term during the matter era. Nevertheless numerical calculations show that the curves in Figure 1 practically remain unchanged for any ${\lambda }_2<{10}^{-7}$, which reflects the fact that the scale $\mu$ is not relevant for the cosmological trajectories in the $(r,m)$-plane. The real stringent restrictions on $\mu$, and therefore on ${\lambda }_2$ through (53), come from the local gravity tests.

Local Gravity Constraints.

The effective mass corresponding to the modified gravity $f\left(R\right)$ model is given by

$$M^2=\frac{R}{3}\left(\frac{f_{,R}}{R{f}_{,RR}}-1\right)=\frac{R}{3m}\left(1-m\right).$$

(56)

This mass characterizes the range of the force mediated by the scalaron and defines the Compton wavelength ${\lambda }_C=2\pi /M$. To avoid the propagation of this scalar degree of freedom and satisfy the local gravity constraints, this Compton length must be negligible small compared to the typical size of the system ℓ, ${\lambda }_C<<\ell$. Thus, to satisfy the local gravity constraints it is necessary that

$$M\ell >>1.$$

(57)

If we use the approximation for the local curvature $R_s\sim {\ell }^{-2}$, then using this in (56) we can write

$$M^2\sim \frac{{\ell }^{-2}}{3m}\left(1-m\right)$$

(58)

then from (57) it follows that

$$\frac{\sqrt{1-m}}{\sqrt{3m}}>>1\Rightarrow m<<1,$$

(59)

which gives from (56)

$$M^2\simeq \frac{R}{3m}.$$

(60)

This allows us to write the constraint (57) as

$$m\left(R_s\right)<<{\ell }^2{R}_s.$$

(61)

Making use of the relationship $R\sim H^2\sim 8\pi G\rho$ applied to the current universe ($R_0,{\rho }_0$) and to the local structure ($R_s,{\rho }_s$), we can write $R_s\sim H_0^2{\rho }_s/{\rho }_0$ and the above constraint becomes [56]

$$m\left(R_s\right)<<\frac{{\rho }_s}{{\rho }_0}{\left(\frac{\ell }{H_0^{-1}}\right)}^2.$$

(62)

For the solar system with ${\rho }_s\sim {10}^{-23}$ gr/cm${}^3$ and $\ell \sim {10}^{13}$ cm one finds that $m<<{10}^{-24}$, where we used $H_0^{-1}\sim {10}^{28}$ cm.

Applied to the model (31) the local gravity constraints can be addressed using the representation for m given by (51). For the solar system one has $y_s=R_s/{\mu }^2$, where $R_s\simeq {10}^6{H}_0^2$. For the parameters $\eta$ and p used in Figure 1, we will set ${\mu }^2={10}^{-16}{H}_0^2$, which gives $y_s={10}^{22}$ and ${\lambda }_2\sim {10}^{-127}$ (assuming $m\sim {10}^{13}Gev$ in (53)

$$\begin{array}{c}(\eta =0.1,p=10)\Rightarrow m=9.8\times {10}^{-26}\hfill \\ (\eta =0.05,p=20)\Rightarrow m=5.3\times {10}^{-25}\hfill \\ (\eta =0.02,p=50)\Rightarrow m=7\times {10}^{-25}\hfill \\ (\eta =0.01,p=100)\Rightarrow m=4.5\times {10}^{-25}\hfill \end{array}$$

Hence, the model (31) can pass solar system tests, assuming $\mu \sim {10}^{-8}{H}_0$ for the viable trajectories depicted in Figure 1. If we consider larger values of $\eta$ then the results for local systems improve as shown bellow.

$$\begin{array}{c}(\eta =1/5,p=5)\Rightarrow m=1.4\times {10}^{-27}\hfill \\ (\eta =1/4,p=4)\Rightarrow m=1.5\times {10}^{-28}\hfill \\ (\eta =1/3,p=3)\Rightarrow m=3.4\times {10}^{-30}\hfill \\ (\eta =1/2,p=2)\Rightarrow m=1.4\times {10}^{-33}\hfill \end{array}$$

(63)

It is worth noting that the above numerical values for local restrictions on m can be obtained for ${\lambda }_2\lesssim {10}^{-55}$, even though ${\lambda }_2$ is subject to the restriction (53) which results in much smaller values than this limit.

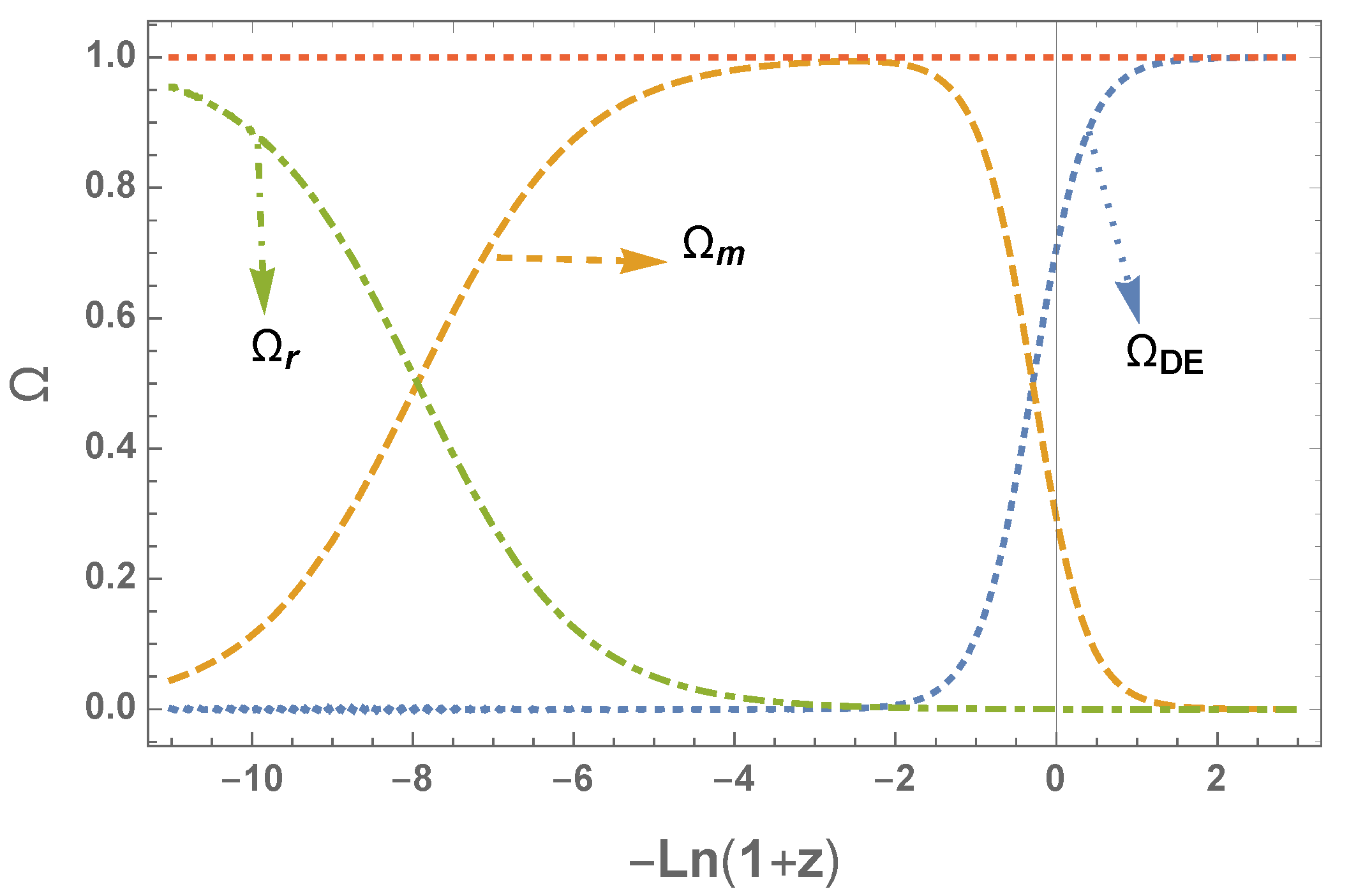
In Figure 2 we present the evolution of the density parameters for the radiation ${\mathsf{\Omega }}_r$, matter ${\mathsf{\Omega }}_m$ and the geometrical dark energy ${\mathsf{\Omega }}_{DE}$, with parameters $\eta$ and p that satisfy cosmological constraints. Since there is no explicit expression for $m\left(r\right)$, we used a polynomial fit to the paths depicted in Figure 1. Taking, for instance, the cosmological scenario with $\mu =0.01$ and $p=100$, the corresponding trajectory in Figure 1 can be approximated by the following function of the dynamical variables $y\left[t\right]$ and $z\left[t\right]$ ($t=-ln(1+z)$)

$$m=c_0+c_1\sqrt{-\frac{z\left[t\right]}{y\left[t\right]}}+c_2\frac{z\left[t\right]}{y\left[t\right]}$$

(64)

with

$$c_0=-{0.0339961}^{\prime },c_1={0.0495968}^{\prime },c_2={0.0155756}^{\prime }$$

where (${}^{\prime }$) represents more digits taken into account for the numerical calculations.

Numerical calculations show that as in the case of the $(r,m)$-plane in Figure 1, the evolution of the densities does not substantially change if we choose ${\lambda }_2<{10}^{-7}$ (including ${\lambda }_2\sim {10}^{-127}$ obtained after inflationary restrictions). This indicates that cosmological constraints on ${\lambda }_2$ are not as stringent as local gravity constraints. In Figure 3 we show the behavior of the effective and geometrical dark energy equations of state for this numerical sample.

Please note that these numerical results are consistent with those obtained in [59], showing that the $R^2$ corrections in the matter era are negligible. The $R^2$ term is also consistent with local gravity tests according to the above numerical values of m. It is worth noting that if we continue lowering the values of $\eta$, the model becomes practically undistinguishable from $\mathsf{\Lambda }$CDM, but the local gravity constraints become more relaxed in the sense that the scale $\mu$ does not have to be so small compared to $H_0$. Thus, we find the following behavior

$$\begin{array}{c}(\eta ={10}^{-8},p={10}^8,\mu ={10}^{-5}{H}_0)\Rightarrow m=5\times {10}^{-25}\hfill \\ (\eta ={10}^{-10},p={10}^{10},\mu ={10}^{-4}{H}_0)\Rightarrow m=5\times {10}^{-25}\hfill \\ (\eta ={10}^{-10},p={10}^{10},\mu ={10}^{-5}{H}_0)\Rightarrow m=5\times {10}^{-27}\hfill \\ (\eta ={10}^{-12},p={10}^{12},\mu ={10}^{-3}{H}_0)\Rightarrow m=5\times {10}^{-25}\hfill \\ (\eta ={10}^{-12},p={10}^{12},\mu ={10}^{-4}{H}_0)\Rightarrow m=5\times {10}^{-27}\hfill \end{array}$$

(65)

In this case, the local restrictions on m can be obtained for ${\lambda }_2\lesssim {10}^{-45}$.

Model 2.

A viable model with characteristics similar to those of the model (31) has the following form

$$f\left(R\right)=R-\left(2{\lambda }_1{\mu }^2-\frac{{\lambda }_2}{{\mu }^2}{R}^2\right)e^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}$$

(66)

where as in the case of the model (31), ${\lambda }_1,{\lambda }_2>0$ and $0<\mu \le 1$. This model satisfies the limits

$$\underset{R\to \infty }{lim}f\left(R\right)=R-2{\lambda }_1{\mu }^2,\underset{R\to 0}{lim}f\left(R\right)=0.$$

(67)

showing closeness to $\mathsf{\Lambda }$CDM model with the cosmological constant vanishing in the flat spacetime. Let us first look at the model’s ability to produce inflation. To this end we consider the model

$$f_1\left(R\right)=R+\frac{{\lambda }_2}{{\mu }^2}{e}^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}{R}^2$$

(68)

where the second term in (66) was neglected. The corresponding scalar field in the Einstein frame has the form

$$\varphi =\sqrt{\frac{3}{2}}ln\left[1+e^{-{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}\lambda \left(\frac{{\mu }^2}{R}\right)\left(2+\eta {\left(\frac{{\mu }^2}{R}\right)}^{\eta }\right)\right].$$

(69)

The scalar potential in the Einstein frame for $f\left(R\right)$ models

$$V\left(R\left(\varphi \right)\right)=\frac{M_p^2}{2}\frac{R{f}_1{\left(R\right)}_{,R}-f_1\left(R\right)}{{\left(f_{1,R}\right)}^2},$$

(70)

gives for the model (68)

$$V=\frac{{\mu }^2{M}_p^2}{2}\frac{{\lambda }_2{\left(\frac{R}{{\mu }^2}\right)}^2\left[1+\eta {\left(\frac{{\mu }^2}{R}\right)}^{\eta }\right]e^{{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}}{2{\left[{\lambda }_2\left(\frac{R}{{\mu }^2}\right)\left(2+\eta {\left(\frac{{\mu }^2}{R}\right)}^{\eta }\right)+e^{{\left(\frac{{\mu }^2}{R}\right)}^{\eta }}\right]}^2}$$

(71)

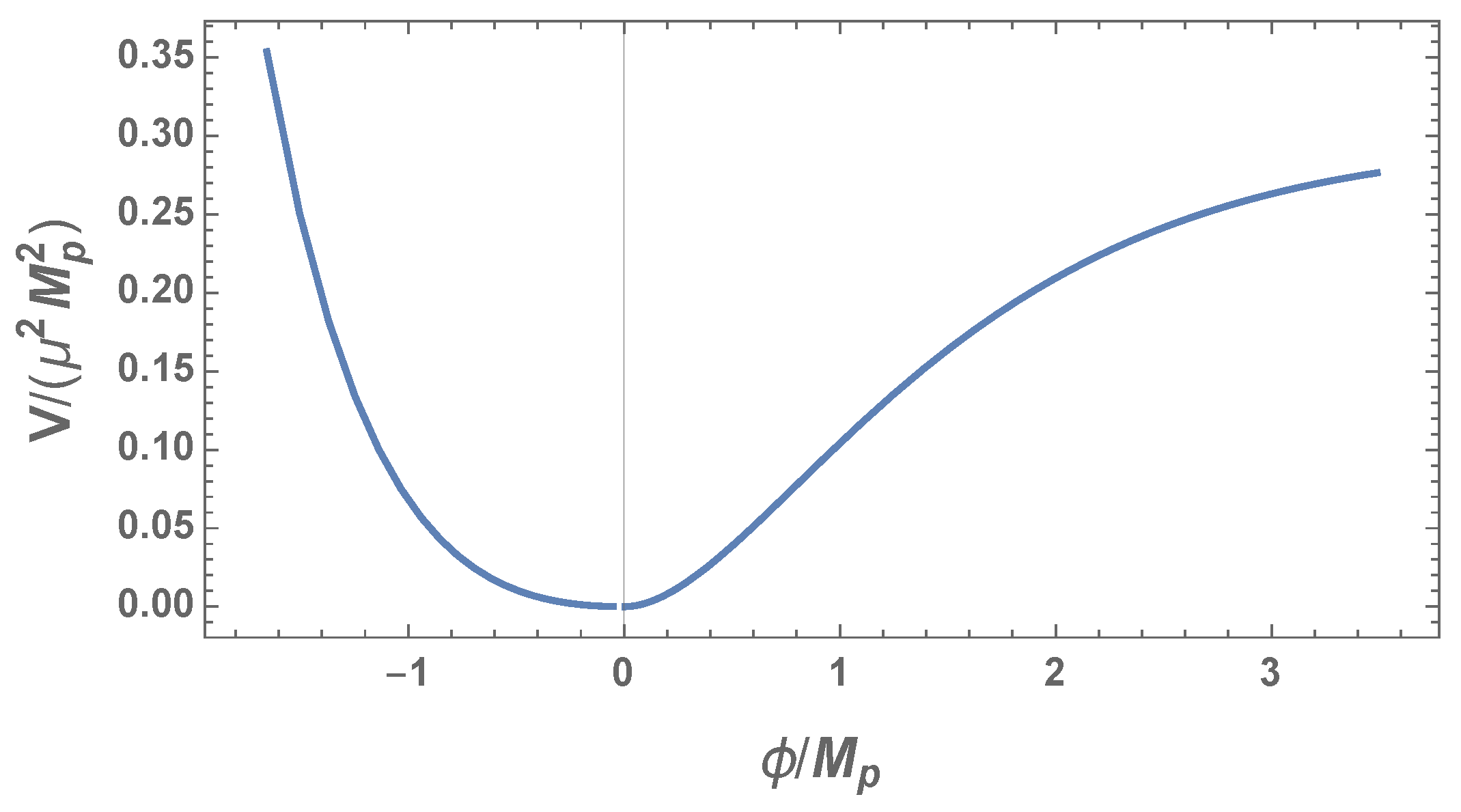
Using parametric method, in Figure 4 we show the shape of the potential, which maintains similarity with the Starobinsky potential and is appropriate for slow-roll inflation. The slow-roll parameters defined for the potential

$${ϵ}_v=\frac{M_p^2}{2}{\left(\frac{V_{,\varphi }}{V}\right)}^2\mathit{and}{\eta }_v=M_p^2\frac{V_{,\varphi \varphi }}{V},$$

(72)

take the following form using the variable $y=R/{\mu }^2$

$${ϵ}_v=\frac{\left(e^{1/y^{\eta }}-\eta {\lambda }_2{y}^{1-\eta }\right)}{3{\lambda }_2^2{y}^2{\left(1+\eta y^{-\eta }\right)}^2},$$

(73)

$${\eta }_v=\frac{2e^{2/y^{\eta }}-2{\lambda }_{2}y{e}^{1/y^{\eta }}\left(4+2\eta y^{-\eta }\left(7-3\eta (1-y^{-\eta })\right)\right)+2{\eta }^2{\lambda }_2^2{y}^{2-\eta }\left(2+(2-\eta )y^{-\eta }+\eta y^{-2\eta }\right)}{3{\lambda }_2^2{y}^2\left(1+\eta y^{-\eta }\right)\left(2+\eta y^{-\eta }\left(3-\eta (1-y^{-\eta })\right)\right)}.$$

(74)

These parameters are evaluated at the horizon crossing where the curvatures takes the value $R_i$, i.e., $y=y_i$. The inflaton value at the end of inflation is found from the condition ${ϵ}_v\left(y_e\right)\simeq 1$, which leads to the approximate equation for $y_e$

$$1-\eta \lambda y^{1-\eta }\simeq \sqrt{3}\lambda y\left(1+\eta y^{-\eta }\right)$$

(75)

where we neglected the exponential for $y>>1$. Additionally if we consider $\eta <<1$, then $y^{1-\eta }\sim y$ and we ca appreciate the magnitude of the curvature at the end of inflation from

$$y_e\sim \frac{1}{\eta +\sqrt{3}(1+\eta )}\frac{1}{{\lambda }_2}\sim \frac{1}{\sqrt{3}{\lambda }_2}.$$

(76)

In the slow-roll approximation the duration of inflation is measured by the e-folding number N

$$N\simeq \frac{1}{M_p^2}{\int }_{{\varphi }_e}^{{\varphi }_i}\frac{V}{V_{,\varphi }}d\varphi =\frac{3}{2}{\lambda }_2^2{\int }_{y_e}^{y_i}\frac{y\left(1+\eta y^{-\eta }\right)\left(2+\eta y^{-\eta }\left(3-\eta (1-y^{-\eta })\right)\right)}{\left(1-\eta {\lambda }_2{y}^{1-\eta }\right)\left(1+{\lambda }_{2}y\left(2+\eta y^{-\eta }\right)\right)}dy,$$

(77)

where $y_i$ is the curvature at the horizon crossing. Numerical integration gives $y_i$ for a given number of e-foldings before the end of inflation, sufficient to prove the viability of the model to predict the values of inflationary observables. The spectral index of scalar perturbations and the tensor-to-scalar ratio are among the most important observables and for the potential driven inflation are given in therms of the slow-roll parameters by

$$n_s=1-6{ϵ}_v+2{\eta }_v,\mathit{and}r=16{ϵ}_0.$$

(78)

To evaluate $n_s$ and r we will consider the case with numerical parameters that were used to obtain the evolution of density parameters in Figure 2 ($\eta =0.01$) (dotted line in Figure 1) and that satisfy local gravity constraints ($\mu ={10}^{-8}{H}_0$) and ${\lambda }_2={10}^{-127}$ from (53). We can use these results from the model (31) because the intermediate matter era and the late time behavior is the same for both models, including the local gravity restrictions. After numerical calculations, taking $y_e=6.06\times {10}^{126}$ (suggested by (76)) and $N\approx 55$ we find that $y_i\approx 3.87\times {10}^{128}$ which gives, after replacing in (73) and (74),

$$n_s\approx 0.963\mathit{and}r\approx 0.0038,$$

(79)

which are in good agreement with the current Planck observations. From (69) we find ${\varphi }_e\approx 0.93M_p$ and ${\varphi }_i\approx 5.28M_p$. The corresponding Hubble parameter during inflation is $H_i\approx 5.7\times {10}^{13}Gev\sim 2.3\times {10}^{-5}{M}_p$. Then the model is capable of describing inflation, matter era and late time accelerated expansion.

To analyze the stability conditions we first define the constant ${\lambda }_1$ in such a way that the de Sitter solution at $r=-2$ is reached at $R=R_1$. The r and m parameters take the form

$$r=-\frac{y^{1+\eta }{e}^{1/y^{\eta }}-2\eta {\lambda }_1+{\lambda }_2{y}^2\left(\eta +2y^{\eta }\right)}{y^{1+\eta }{e}^{1/y^{\eta }}-2{\lambda }_1{y}^{\eta }+{\lambda }_2{y}^{2+\eta }}$$

(80)

$$m=\frac{2\eta {\lambda }_1\left((1+\eta )y^{\eta }-\eta \right)+{\lambda }_2\left(2y^{2\eta +2}+3\eta y^{\eta +2}+{\eta }^2{y}^2\left(1-y^{\eta }\right)\right)}{y^{\eta }\left({\lambda }_2{y}^2\left(2y^{\eta }+\eta \right)+y^{\eta +1}{e}^{1/y^{\eta }}-2\eta {\lambda }_1\right)}$$

(81)

where $y=R/{\mu }^2$. The equation $r=-2$ at $R=R_1$ ($y=y_1$) gives

$${\lambda }_1=\frac{y_1^{\eta +1}{e}^{1/y_1^{\eta }}-\eta {\lambda }_2{y}_1^2}{4y_1^{\eta }-2\eta },$$

(82)

which lead to ${\lambda }_1>0$ for

$$y_1^{\eta }>\frac{\eta }{2},\mathit{and}{\lambda }_2<\frac{1}{\eta }{y}_1^{\eta -1}{e}^{1/y_1^{\eta }}.$$

(83)

Replacing ${\lambda }_1$ in m (81), the stability condition for de Sitter point, $0<m(r=-2)\le 1$ leads to the inequality

$$0<\frac{\eta e^{1/y_1^{\eta }}\left((1+\eta )y_1^{\eta }-\eta \right)+2{\lambda }_2{y}_1\left(2y_1^{2\eta }+\eta (2-\eta )y_1^{\eta }-{\eta }^2\right)}{2y_1^{\eta }\left(e^{1/y_1^{\eta }}\left(y_1^{\eta }-\eta \right)+2{\lambda }_2{y}_1^{1+\eta }\right)}\le 1.$$

(84)

To facilitate the numerical analysis, in what follows we will set $y_1=1$, equivalent to $R_1={\mu }^2$. Setting $y_1=1$ in (84) we find

$$0<\frac{e\eta +4{\lambda }_2\left(1+\eta -{\eta }^2\right)}{2e(1-\eta )+4{\lambda }_2}\le 1\Rightarrow 0<\eta \le \frac{3e+4{\lambda }_2}{8{\lambda }_2}-\frac{1}{8{\lambda }_2}\sqrt{9e^2-8e{\lambda }_2+16{\lambda }_2^2}$$

(85)

which given the fact that $0<\eta \le 1$, is satisfied by any ${\lambda }_2>0$. The first derivative of $f\left(R\right)$, after replacing ${\lambda }_1$ and setting $y_1=1$ becomes

$$f_{,R}=e^{-1/y^{\eta }}\left[e^{1/y^{\eta }}+{\lambda }_{2}y\left(\frac{\eta }{y^{\eta }}+2\right)+\frac{{\eta }^2{\lambda }_2}{(2-\eta )y^{\eta }}-\frac{e\eta }{(2-\eta )y^{\eta }}\right]$$

(86)

Since all the terms, except the last one, are positive then to satisfy the condition $f_{,R}>0$ it is enough that it is fulfilled

$$e^{1/y^{\eta }}-\frac{e\eta }{(2-\eta )y^{\eta }}>0$$

(87)

Since $e^{1/y^{\eta }}>1$, and $y>1$ then the sufficient condition to satisfy $f_{,R}>0$ is

$$\eta <\frac{2}{1+e}.$$

(88)

Repeating the same procedure with $f_{,RR}$ we find

$$f_{,RR}=\frac{1}{{\mu }^2}{e}^{-\frac{1}{y^{\eta }}}\left[{\lambda }_2\left({\eta }^2\frac{1}{y^{2\eta }}+\eta (3-\eta )\frac{1}{y^{\eta }}+2\right)+\frac{\eta (e-\eta {\lambda }_2)}{2-\eta }\left(1+\eta -\eta \frac{1}{y^{\eta }}\right)\frac{1}{y^{2+\eta }}\right]$$

(89)

which automatically satisfies $f_{,RR}>0$ since $0<\eta \le 1$, $y>1$ and, according to (83), ${\lambda }_2<e/\eta$. Then the model (66) satisfies all conditions of stability and cosmological viability.

Concerning the local gravity restrictions, for the solar system the model gives the same values for m shown in (63) and (65). Likewise the density parameters and the equation of state, present the same behavior as shown in Figure 2 and Figure 3. As is the case for most of the realistic models, the stringent local gravity constraints forces the models (31) and (66) to be practically indistinguishable form $\mathsf{\Lambda }$CDM. The possibility remains that further analysis of matter perturbations allows finding a departure from $\mathsf{\Lambda }$CDM.

The exponential term in the models (31) and (66) is useful to avoid some type of singularities. Excluding the last term in (31) and (66) we can see that $f\left(R\right)\to R-2{\mu }^2\mathsf{\Lambda }$ as $R\to \infty$, $f_{,R}(R\to \infty )$ tends to 1 and $f_{,RR},f_{,RRR},\dots .\to 0$ at $R\to \infty$. Then the r.h.s. of Equation (4), excluding the matter density, for the models (31) and (66), which gives the corresponding ${\rho }_{eff}$, tends to a constant value on singular solutions with $R\to \infty$, avoiding in this way the appearance of type I and type III future singularities [37]. From Figure 1 and Figure 2 it is clear also that the inflationary term in the models (31) and (66) does not have any influence on the stability of matter era.

4. Discussion

Two models of modified gravity that are able to explain early time inflation and late time accelerated expansion were studied. The models include an exponential function of de form $e^{-{({\mu }^2/R)}^{\eta }}$ and the $R^2$ term. The factor $e^{-{({\mu }^2/R)}^{\eta }}$, which is present in both models, leads to the limit $f\left(R\right)\to 0$ at $R\to 0$ implying the disappearance of the cosmological constant. i.e., the models contain the flat space-time solution. The stability, cosmological viability and local gravity restrictions were studied. The dynamical system was solved under appropriate initial conditions, and the cosmological evolution for the density parameters corresponding to radiation, matter and (geometrical) dark energy was obtained, which is closely adjusted to current observations. Consequently, the equation of state evolves according to observations with $w_{eff}$ showing the transition to the accelerated phase at the currently observed $z_t\sim 0.5$, and $w_{DE}\simeq -1$.

The local gravity constraints, as expected, impose very stringent conditions for m to achieve values of the order $m\lesssim {10}^{-24}$, which demand very small values for the scale $\mu$ ($\mu \sim {10}^{-8}{H}_0$), although this scale may increase as we take smaller values of $\eta$. However, at the same time, making $\eta$ smaller brings the model closer to $\mathsf{\Lambda }$CDM, making it practically indistinguishable from it. In any case the general result is that the stronger the local gravity restrictions are, the further in the future the final de Sitter attractor of the system is. It is also interesting to note that the numerical results for local restrictions on m can be obtained for ${\lambda }_2\lesssim {10}^{-55}$, even though ${\lambda }_2$ is subject to the restriction (53) which results in much smaller values than this limit. On the other hand, the cosmological constraints, which do not depend on the scale $\mu$, impose softer conditions on ${\lambda }_2$, being sufficient to consider ${\lambda }_2\lesssim {10}^{-7}$.

The expressions for m given by (51) for the model (31) and by (81) for the model (66) suggest a correlation between the curvature dependent parameter m and ${\lambda }_2$, which could be useful to fix ${\lambda }_2$ by local gravity constraints on m. This is an interesting alternative mechanism to fix ${\lambda }_2$, other than the condition (53) where the mass $M^2$ is determined from the amplitude of the scalar power spectrum. On the other hand, at high curvature typical of inflation, the model (31) leads to the Starobinsky inflation while the model (66) gives a new potential with the appropriate behavior to develop successful slow-roll inflation. A peculiarity of this potential is its dependence on $\eta$ and ${\lambda }_2$ that is transferred to the slow-roll parameters, allowing exploring a wider region of possibilities for the inflationary observables, compared to the Starobinsky potential.

A more detailed analysis of local gravity restrictions is necessary, particularly to test whether local gravity constraints can independently and uniquely determine a value of ${\lambda }_2$ that is consistent with inflation. Further study of cosmological effects that distinguish the models form $\mathsf{\Lambda }$CDM is needed, for instance, the evolution of the background and matter density perturbations which could give patterns in the growth of structures that mark the difference with $\mathsf{\Lambda }$CDM.