Abstract
Wood is a natural composite, having a porous structure, with a complex elastic symmetry specific to orthotropic solid, influenced by three mutually perpendicular planes of elastic symmetry. The classical guitar is obtained from different wooden species, each of them having their own elastic properties and, as a whole, forming a lignocellulosic composite structure. Generally, some constructive parts of the classical guitar body are based on symmetry, starting from the structural features of wooden plates, which are symmetrically cut, and some patterns of the stiffening bars. The other elements, such as the strings system, are not symmetric. This study aims to evaluate the frequency responses of the guitar body as a symmetrical mechanical system from constructive points of view. Because theoretical results (analytic and numeric) regarding the symmetrical systems cannot be applied to quasi-symmetric systems, the dynamic response was analyzed from experiments performed on four types of classical guitar body (without neck), different from each other by the pattern of stiffening bars placed inside of the top plate. The experiments were performed using a Brüel&Kjær mini-shaker to excite the structure, and the signal was captured with accelerometers. The symmetric behavior of coupled plates from the guitar body was noticed in the case of an applied dynamic force of 110 Hz and 440 Hz, but in the case of 146 Hz, 588 Hz, 720 Hz, quasi skew symmetrical modes were recorded.
1. Introduction
The frequency response of the lignocelluloses plates with different structural and material characteristics offers useful information about the way in which the frequency of the excitation force overlaps with the plate’s normal frequency. The modal shapes show the elastically behavior of the plate, respectively, the areas in which are formed the node and the amplitude loops for different vibration modes. One of the most important characteristics of the stringed instruments is the possibility of resonating at excitation frequency of the strings. On this line, the amplification box made up of the ligno-cellulose plates takes over this function, being the reason of the necessity of analyzing the frequency response of the plates with FEM. The resonating domain of the plates takes shape between the bridge (the force’s application point) and the sound hole. The musical instruments with strings, such as the guitar, represent a complex mechanical structure that has seen numerous improvements over time, especially in case of bracing patterns of the soundboard, which has a significant effect on its mode shapes [1]. The application of different strutting (bracing) systems on the soundboard of the guitar aim to improve the vibrating capacity of the guitar, while maintaining its structural integrity under the tension of the strings during playing. Several studies have analyzed how different bracing patterns change the modal properties of the top plate using Chladni’s method, through numerical or experimental methods [2,3]. Very few scientific studies have been performed to explain the effect of bracing patterns in producing specific modal patterns [1,2,3].
In the computation mechanics of the classical guitar, the couplings between the various parts of the guitar are treated like a mass-spring system, so each bracing pattern adds its own additional mass to the soundboard of the guitar, which leads to changes in the eigenvalues of the guitar body [4,5]. On the other hand, Jansson [6,7,8] noticed that the bracing systems play an important role concerning the thickness modulation of top plates, with the effect of a fine adjustment on guitar tone. The connection between science and luthiers is assured by theoretical and experimental researches made on different types of guitars, in different stages of guitar construction [4,5]. Thus, regarding the dynamic behavior of the guitar body, many researchers studied the modal analysis and vibration behavior of classical guitar both experimentally and with FEM (Finite Element Method). Some of them, like [8,9,10], performed the modal analysis, and the vibration behavior on the classical guitar in its different construction stages using FEM, highlighting the symmetrical and antisymmetric modes of coupled plates of the guitar body. Others [11,12,13,14] tried, using numerical simulation and experimental methods, to establish the influence of the individual components, monitoring the quantitative and qualitative contributions on the dynamic response of the guitar body. The authors of [15] researched the influence of the Russian strutting system on the dynamic behavior of the plates and managed to improve the quality of the sound of the guitar according to the design and the dimensions of the fan bracing. For [14], the simulation coupling between the inner fluid and the structure represented one of the theoretical studies. The authors of [16] focused on the modeling of the different types of classical guitar manufactured in their country, and on analyzing the dynamic behavior of the plates as free structures and as parts of the guitar body. The authors of [17] conducted acoustical measurements on guitars and identified the essential difference between a bad and good timbre of a guitar tone. Thus, the sounds of a good guitar are characterized by a longer duration of tones and the flexibility of the acoustic emission between quiet or loud tones, in comparison with a bad guitar, which presents poor dynamic capability, frequently buzz tone, wolf tone in case of high tone. The authors of [18,19,20] brought the physical sounds of the instruments from a musicological point of view into focus. He approached the difference between continuum and discrete mechanics, elaborating an interesting theory about the impedance of second-order to solve the problem of overtones. The fact that the guitar is a complex acoustical system is proven by the numerous studies, which have been focusing on how the structural elements of the guitar influence the vibrations and, automatically, the tone and the tonal quality of the guitar [21,22,23,24,25]. Therefore, it will certainly help the design process if the symmetry approach ends up reducing the complexity of the vibration analysis. Even though there are many studies on the body of the guitar, the approaches regarding the symmetrical behavior of the body of the guitar, the relations between the symmetry of the construction and the responses of the guitar to the forced vibrations are insufficient, or not at all addressed. The challenge of interdisciplinary researchers is to find a better approach in the design and construction of classical guitar in correlation with the development of mathematical models of dynamic and acoustic behavior [4,5,26]. Under this challenge, the paper aims to establish the structural differences reflected on the dynamical behavior of guitar bodies with different bracing systems, both through analytical, numerical and experimental investigation. The novelty of the paper consists of the applied mathematical problem of forced vibration, starting from the hypothesis that the guitar body is a symmetrical mechanical structure, and the correlation of mathematical models with numerical and experimental ones. For musical instruments makers, this research is useful to choose the proper type of guitar, in accordance with the musical style of players (musicians), and to develop new bracing patterns of guitars, with minimum consumption of wood materials.
2. The Mathematical Model of the Guitar as a Symmetrical System
It is known that different mathematical solutions are based on symmetry hypotheses to solve the static and dynamical problems of engineering structures, such as civil engineering, mechanical and biomechanical systems, acoustic bodies or even medical structures. In the last decades, such systems were analyzed by researchers. When considering mechanical systems with symmetries, the main challenge of researches in the field of structural mechanics and vibrations is to solve the mathematical problems of symmetrical systems with different asymmetric loading [27,28,29]. Generally, designing such a mechanical system with structural symmetries is easier and cheaper to do, but aesthetic reasons also play an important role in the design process [30]. A study of a system having two identical parts is a particular case in this field of study. Interesting free vibration properties of this case are presented in the literature [29,31]. The eigenmodes can be classified into two classes: symmetrical and skew-symmetrical eigenmodes. The properties of the symmetric systems were less used in the field of applied mechanics, but some papers study applications in the field [32,33,34].
If we consider the longitudinal axis, it is easy to identify a symmetry plane on in the geometric model (without the strings) of a classical guitar body; therefore, the guitar can be included as part of symmetrical systems, and the properties determined for other symmetrical systems can be applied to it (Figure 1). Some results which presented the properties of the eigenfrequencies and eigenmode of guitar plate’s vibration can be found in a previous study [32,35]. These properties help us ease the calculation and increase its accuracy in such problems. The symmetrical shape of a guitar induces vibration properties that determine the specific tone quality of this instrument. The classical guitar body, without strings, has a plane of symmetry, the one that passes through the means of the two plates of the guitar box, and a plane of quasi-symmetry, the one that separates the lower part from the upper part of the guitar. Properties of the resonant frequencies of a guitar have been presented in previous papers [36,37,38]. Depending on the frequencies and the size of the vibrating surface of the guitar body’s eigenmodes, the sounds produced by the strings are amplified more or less. Additionally, the damping velocity of the forced vibrations produced by the strings depends on the dynamic behavior of the guitar body. Thus, there is a close connection between the parts of the guitar as a mechanical structure that ensures the propagation of vibrations from the strings (the excitation system) to the guitar body. From a dynamic point of view, the guitar body behaves like a Helmholz resonator [39,40,41].
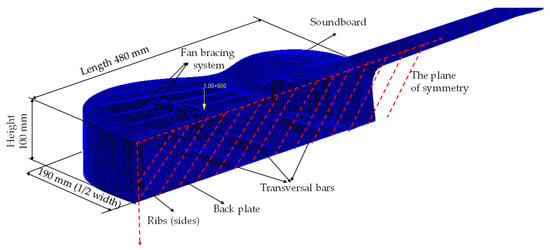
Figure 1.
The structural symmetry of guitar body, without strings systems—case of seven fan bracing systems.
It was noticed that a basic condition of the resonance boxes of the guitar is that of not being selective, respectively, of not favoring some sounds. In addition to that, the damping must have a high value. The sounds’ non-selectivity can be obtained through complex geometrical shapes of the resonance box (as it is the case for the guitar’s shape). This phenomenon is explained through the theory of division for irregular air volume contained by the box into a sum of numerous small simple volumes with a normal resonance frequency [42,43]. The combination of these small volumes, and their capacity to resonate, offers the conditions of amplification of all the sounds emitted by the string and, ideally, offers the conditions of even amplification. The properties of a symmetrical mechanical system in the case of forced vibrations are presented in this paper. A quasi-symmetrical system behaves very close to a symmetrical system. Theoretical results regarding symmetrical systems cannot be applied to quasi-symmetric systems, but the fact that the properties are very close is shown experimentally for this instrument. The guitar has a plane of symmetry, the one that passes through the means of the two plates of the guitar box, and a plane of quasi-symmetry, the one that separates the lower part from the upper part of the guitar.
For mathematical modeling, the guitar body is considered as consisting of two identical parts. In this case, if a finite element model is used to study the vibrations of this instrument and the equations of motion are obtained in the form [28,31,44]:
where the symmetry of the system is highlighted in the structure of the equations. Some notations are made:
In Equation (2), the vector {x} contains the independent coordinates of the first (left) subsystem, the independent coordinates of the second (right) subsystem and the other independent coordinates of the system. If we consider the vibrating system as a whole, the equations of the free undamped vibrations in Equation (1) can be written in compact form:
where represents the total vector of independent coordinates, being the matrix of inertia and being the stiffness matrix.
As we said, we consider the guitar consisting of two identical parts. For half the body of the guitar, the equations of the free vibrations are:
In some previous papers [45,46,47,48] the following property, which describes the symmetrical systems, has been established:
Theorem T1.
The eigenvalues for the system (4) are also eigenvalues for the system (1). In our case, it means that the solutions of polynomial equations:
are also polynomial solutions:
so, we can write:
It denotes that:
The characteristic equation for the whole system (6) can be written:
We will consider being the natural frequencies of a half part of the guitar and being the natural frequencies of the whole system (n1 is the dimension of one single part, n is the total dimension of the system).
This property is a particular case of Proposition 1 demonstrated in [48] described below.
Proposition 1:
If we consider the square polynomial matrices with complex coefficients, of size n, noted A, B, C, L, Z=On and matrixthen det (M) is dividable by det(A). In the case of our symmetrical system, using the notation (8) we have:
The theorem T1 implies some interesting properties of the natural modes of vibration. To obtain the natural modes of vibration it means to solve the linear homogenous system:
The following 2 theorems are valid (12) and (13) [48,49,50]:
Theorem T2.
The system (11) has, forsolutions such as (skew-symmetrical eigenmodes):
Theorem T3.
The system (11) has, for(), solutions such as (symmetrical eigenmodes):
Forced Vibrations in Systems with Symmetries
We assume that the two identical subsystems are excited in the same way. The vector of the forces acting on the system has the form:
where partitioning was done according to the three subsystems. The motion of the non-damped excited system is given by Equation (7).
If is the modal matrix and are the modes of vibrations for the system:
and if we consider being the canonic coordinates, then we have:
We define:
with nonzero diagonal elements are :
with nonzero diagonal elements: and:
where: . The coupled differential equations describing the vibration response of the system (3) will be decoupled into n second-order uncoupled differential equations with constant coefficients:
or:
If we divide with and if we consider that: , we have:
We get the following result:
Theorem T4.
The system (21) has, for, the homogeneous system solution (excitation does not influence the movement of the system).
Proof:
Let us consider that in the modal matrix the first n1 vectors correspond to eigenfrequencies . Then:
(the mode of vibration is orthogonal to the excitation). The system becomes:
and the solution of the forced vibration becomes:
□
We also have the following property:
Theorem T5.
The amplitudes of the vibrations of the forced particular solutions have, for each harmonic, the form:
(the excitation symmetry is kept in the response’s symmetry).
Proof:
For a harmonic p where the excitation is , the amplitude of the forced vibrations is given by:
or:
or, in other words:
□
From here it results that Equations (29) and (30) have the same solution. The property is also preserved for damped vibrations with proportional damping and, generally, if the damping matrix can be decomposed in Caughey form.
3. Finite Element Analysis (FEA) of the Resonance Body of the Guitar
3.1. Geometrical and Structural Models
In the first step, the modeling and the dynamic analysis of the three types of guitar body from the bracing system’s point of view were performed, aiming to determine the frequency response of these structures at the periodic load of a unitary concentrated harmonic force with a frequency in the range of 20–1000 Hz. The numerical models consist of: a guitar body without the bracing system, just three transversal bars (coded C3BT), as can be noticed in Figure 2a; a guitar body with a three fans bracing system and two transversal bars (coded C3BR2T), as can be seen in Figure 2b; a guitar body with five fan bars system and two transversal bars (coded C5BR2T), as shown in Figure 2c. The geometrical sizes and materials properties of all models are the same, and they can be seen in Table 1.

Figure 2.
Different types of guitar bodies: (a) C3BT—without fan bracing system and three transversal bars; (b) C3BR2T—with three radial (fan) bars and two transversal bars; (c) C5BR2T—with five radial (fan) bars and two transversal bars.

Table 1.
Physical and Mechanical properties of wood plates from the guitar body.
The values for spruce (used for the top plate) and maple (used for backplate and sides) are selected starting from values of Young’s moduli E and shear moduli G from references [51,52], and applying the ratio between the directions L:R:T account for 9.8:1.7:1 for MOEs and of the shear moduli in the shearing planes LT:LR:RT for 4.5:2.9:1 in accordance with [52]. The anisotropy depends on the internal structure of the material and perceived as the variation in material response with the direction of the applied stress. The complex elastic symmetry of orthotropic solid lies when constants are influenced by three mutually perpendicular planes of elastic symmetry. The number of constants for various types of anisotropic materials is 21 for monoclinic materials, 13 for triclinic materials, nine for orthotropic materials, five for hexagonal or transversely isotropic materials and two for isotropic materials [51]. In the construction of stringed musical instruments, such as the guitar, the wood for the top plate is compulsorarily cut in a longitudinal–radial direction (Figure 3a,b). The regularity and the same sizes of the annual rings— with the zone of early wood and late wood— assure the sound transmission in the wood at maximum velocity. For the back plate, the maple wood (in the studied cases) is also cut in radial direction, in order to emphasize the grain of wood, which tends to be a flamed or curly figure (Figure 3c). Due to the small thickness of guitar plate (2.5 mm) reported to the length (480 mm) and witdh (380 mm), the anisotropic features of wood can be neglected.
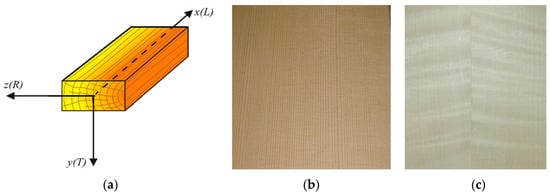
Figure 3.
The section of wood used in guitar construction: (a) the main orthogonal section (R—radial, T—tangential, L—longitudinal); (b) resonance spruce wood (Picea Abies L) for the top plate of the guitar, cut in the longitudinal-radial direction; (c) curly maple (Acer Pseudoplatanus) for the back plate of the guitar, cut in the longitudinal-radial direction.
3.2. Discretization of Models and Loading
The models were meshed with QUAD4 shell finite elements, the number of degrees of freedom on the element node being 6. For all the nodes on the contour, all the degrees of freedom were fixed. Modeling and simulation were done using the Patran Nastran 2004 package as also were presented in previous work [53]. The unitary harmonic force (F=1N) was applied in the nodes in the bridge area (the area where the vibration from the strings is actually transmitted to the acoustic plate and the soundbox), respectively in node P1, according to Figure 4a–c. The dynamic response of each structure was analyzed at the points on the front plate, back and sides (ribs) of the guitar body as shown in Figure 4d–f. Being a symmetrical structure, the analysis was performed on half the body of the guitar, as can be seen in Figure 5.

Figure 4.
The placement of the analyzed nodes: (a) C3BT; (b) C3BR2T; (c) C5BR2T; (d) the measured points of dynamic response on the soundboard of the guitar body; (e) the measured points of dynamic response on the backplate of guitar body; (f) the measured points of dynamic response on ribs of the guitar body.
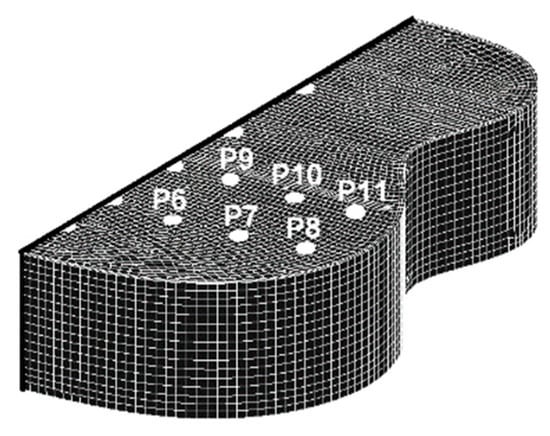
Figure 5.
The Finite Element Analysis (FEA) model for half the body of the guitar.
3.3. FEA Results and Discussion
From the analysis of the frequency response of the points on the C3BT guitar body (regardless of how the ribs are deposited), it was found that the first resonance frequency of the frontal plate of the box is between 200 and 220 Hz, depending on the ribbing system of the plate; the second resonant frequency is 300 Hz; The maximum amplitude is obtained in the neighboring points (P3) of the force application point (P1) and the area between the impedance point and the acoustic hole. The frequencies in the range of 0–700 Hz are shown in Figure 6a. The amplitude of the vibration decreases both along the length and along the width of the axis of the box (Figure 6b). The vibration amplitudes of the back of the acoustic box are approximately four times lower than that of the soundboard (Figure 7).
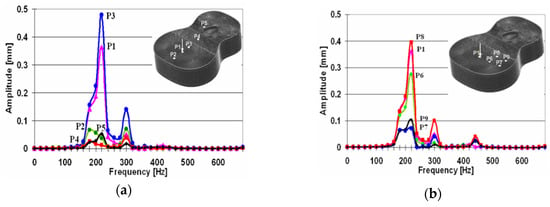
Figure 6.
The variation of amplitudes in the analyzed points on the front plate of the acoustic box, according to the excitation frequency: (a) along the axis of the structure; (b) transversally on the axis.
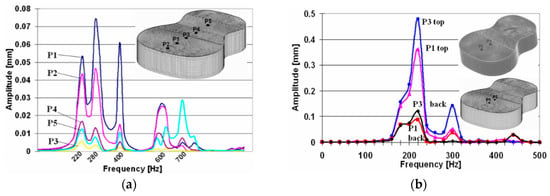
Figure 7.
The variation of vibration amplitudes for the back of the acoustic box: (a) along the axis of the structure; (b) comparison with the top plate.
The analyzed nodes on the plates of the guitar body responded differently to force vibrations, in accordance with its position related to force point application (Figure 8). The maximum amplitude for the top plate corresponds to a frequency of 300 Hz (obtained in the point P3), while the one for the backplate corresponds to 280 Hz (found in P1). For the sides, a maximum frequency of 200 Hz could be found in the points P1 and P4.
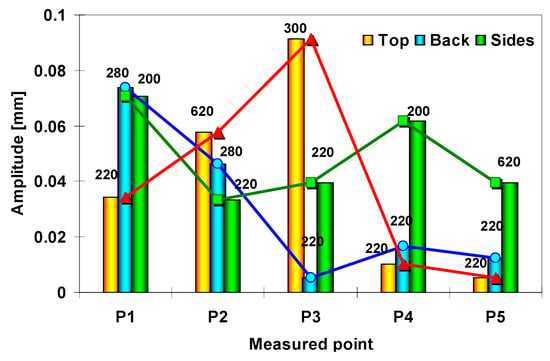
Figure 8.
The resonance frequencies of the coupled plates of the guitar body.
Concerning the comparison of dynamic responses of guitar bodies with different bracing systems, it can be noticed that the major differences are obtained for the guitar body without fan bracing systems (designation C3BT) (Figure 9). Comparing the two models of guitar bodies with three (C3BR2T) and five fan bars (C5BR2T), it can be observed that both have the similar amplitude spectra in near of load points (Figure 9a–f), but, with increasing the distance between the loading application point and the measured point on the soundboard, the guitar body with five radial bars (C5BR2T) recorded higher amplitudes than a guitar with three radial bars (C3BR2T) (Figure 9g,h). As can be seen the amplitude spectra in Figure 9 and in the resonance frequency for each analyzed structure in Table 2, the bracing caused higher and more resonant frequencies. The authors of [3] remarked that the bracing results in good sound from top boards in the high-frequency range.
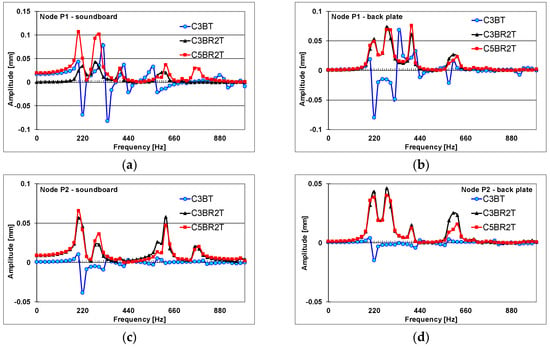
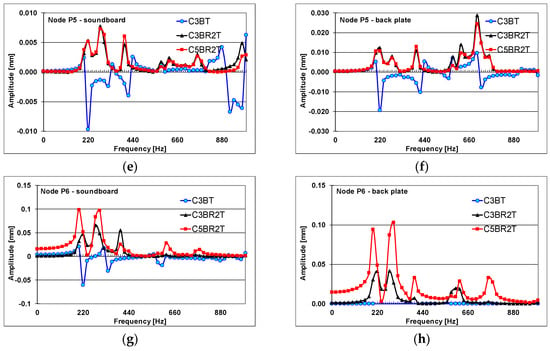
Figure 9.
Comparison of dynamic responses of different guitar bodies: (a) the captured vibration of node P1, the same point of applied force, in the case of the soundboard; (b) the captured vibration of node P1, in the case of the backplates; (c) the captured vibration of node P2, the near point of P1, in the case of the soundboard; (d) the captured vibration of node P1, in the case of the backplates; (e) the captured vibration of node P5, the point near the soundhole, in the case of the soundboard; (f) the captured vibration of node P5, in the case of the backplates; (g) the captured vibration of node P6, in the case of the soundboard; (h) the captured vibration of node P6, in the case of the backplates.

Table 2.
Resonance frequencies (in Hz).
Connecting the FEA results with mathematical models, the symmetric and skew-symmetric responses are obtained for all types of the guitar body. On these principles [26], deliberate create asymmetric modes to maximizes acoustic radiation, observing that some eigenmodes cannot radiate due to their symmetric shapes. As an effect of fixing the faces of the soundbox, the standing waves appear by overlapping the direct waves over the reflected ones. These generate higher harmonics. The dynamics of the guitar body differs from that of the individually analyzed plates presented in previous papers [34,36,37]. This is due to the new bordering conditions created by attaching the sides to the top and back plates, as well as due to the aerodynamic phenomena inside the cavity that leads to delaying the transmission of vibration from the top plate to the backplate and to the sides [17,39]. The modeling of the guitar body approximates the simulation of vibrations with the real phenomenon. The FEM analysis was performed to make a comparison with the experimentally obtained values.
4. The Experimental Analysis to Forced Vibrations
Experimental Set-Up
The experimental method consists in fixing the impedance head of the vibration generator on the structure (body of the guitar)—the B&K mini-shaker provided with a force transducer (Figure 10). The exciter was located in the bridge area, according to studies in the literature [36,37,38]. The vibrating mass puts the structure under harmonic vibrations through the signal generator and the amplifier. The input size (of the excitation force) was measured with the force transducer, and the output signals were captured with the B&K accelerometers 4517-002. In order to capture the input and output signals, in the first stage of the experimental research, a DAQ type acquisition plate was used, and then the Pulse 12 platform was attached to the data processing software, thus replacing part of the installation components, such as the conditioner, the acquisition plate and the program for visualization and basic data processing. In order to determine the vibrational shapes, the plates were coated with a thin, uniform layer of sand with granulation of 100–150 microns. The resulting Chladni figures were captured using a digital camera. From the preliminary investigations, it was found that it is difficult to excite the plate with sufficient amplitude to identify all the modes of vibration, as well as the existence of a variation of the response of the structures at different frequencies. For this purpose, tests were carried out on all types of structures in order to establish the corresponding input parameters of the system. Subsequently, in all experimental determinations, the same input data for the excitation frequency signal amplification, voltage and amperage were used (Table 3).
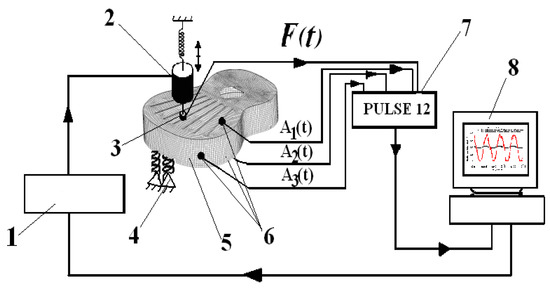
Figure 10.
The experimental set-up: 1—frequency generator; 2—B&K mini-shaker; 3—force transmitter; 4—supports; 5—guitar box; 6—accelerometers; 7—the Pulse 12 platform; 8—computer for data visualization and processing.

Table 3.
The values of the input parameters of the system.
In the experimental study, four classical guitar bodies were analyzed: type C3BT; C5BR2T and an additional guitar body with seven radial bars (coded C7BR2T) and a guitar body with three radial bars and two disposed of in V, coded C3BR2V. In order to compare the vibration modes and determine how the bar system influences the structure’s response, the structures were excited at the same frequencies, under the same laboratory conditions. In the technological process of producing the manufactured guitars, various bar systems are used, depending on the type, size and quality of the guitar in which they are integrated. The number of scientific studies on how the stiffening system influences the acoustic quality of the guitar is relatively low [16,26,40,53], and the studies are generally not exhaustive, given the interaction of the many factors that contribute to the acoustic quality of the guitar. Moreover, the approaches aim to analyze aspects of the particular bar systems. Numerous and various forms and modes of vibration were obtained, of which the most significant were selected and presented in Table 4. The configuration of the resulting vibration modes on the plates with different ribs shows both similarities and differences.

Table 4.
The symmetrical and skew-symmetric modes related to strutting systems of the guitar body.
5. Discussion
At relatively low frequencies (between 110–246 Hz) the behavior of the plate structures–guitar body is similar, regardless of the bar system used, obtaining symmetric modes. The influence that the bar system exerts on the dynamic response of guitar bodies is observed at higher frequencies, through two aspects: the formation of particular modes of vibrations, which are not found in the other structures; the sequence of vibration modes that differ from one structure to another. During vibrations, each pattern of strutting system characteristically has nodes and antinodes at various locations on the body of the guitar. The largest differences occur between the guitar body with three stiffening cross-bars (C3BT) and the other types of structures. Additionally, the dynamic response, in terms of Chladni patterns for C5BR2T, C7BR2T structures, differs from C3BR2T and C3BR2V structures in the case of a frequency of 146 Hz. For a frequency of 246 Hz, 588 Hz and 720 Hz, as can be observed in Table 4, quasi skew-symmetric modes with different nodal lines are in all types of the guitar body. Additionally, skew-symmetric modes are obtained for a loading frequency of 329 Hz, 413 Hz and 440 Hz. All studied guitar bodies respond harmonically (Figure 11a–d). At low frequencies, for example, 110 Hz, the front and back plates vibrate in phase with amplitudes close in value for all cases of bar systems (Figure 11). At the same input parameters (voltage and amperage, excitation frequency, contour conditions), the plates of the bodies with different bar systems respond with different amplitudes (Figure 11). Thus, at the frequency of 146 Hz, the plates of the bodies with five resonance bars (in the variants C5BR2T and C3BR2V) have the largest amplitudes, compared to the other analyzed structures. The C5BR2T and C3BR2V guitar bodies show a complex vibration mode resulting from the addition of the fundamental frequency with its first two harmonics. The response of the backplates in all cases considered is also a complex vibration. As the frequencies increase between the top and backplate of the guitar body, vibration shifts occur. At the frequency of 146 Hz, it can be seen the influence of the stiffening systems for the front plates on the dynamic behavior of the whole body (Figure 12a–e).
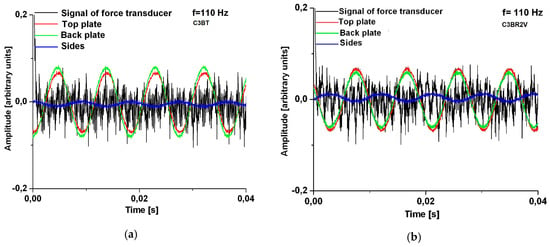
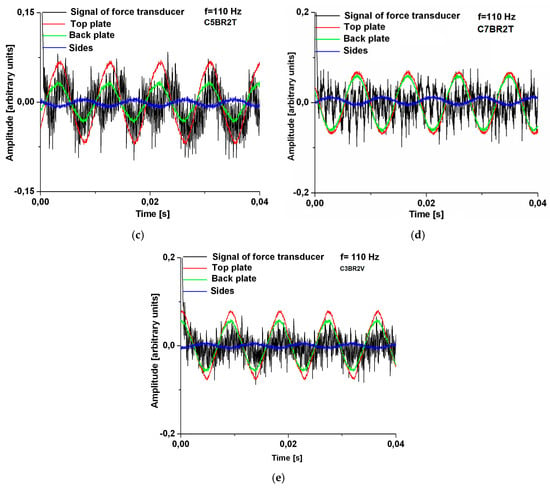
Figure 11.
Comparisons regarding the dynamic response in the time domain of guitar bodies with different bar systems, for frequency of 110 Hz: (a) body type C3BT; (b) guitar body type C3BR2T; (c) guitar body type C5BR2T; (d) body type C7BR2T; (e) body type 3BR2V.
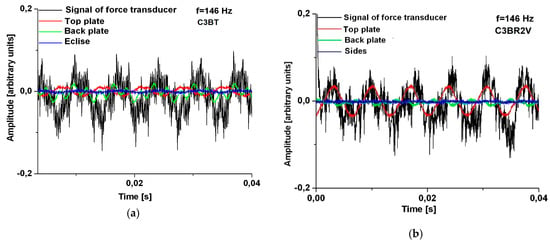
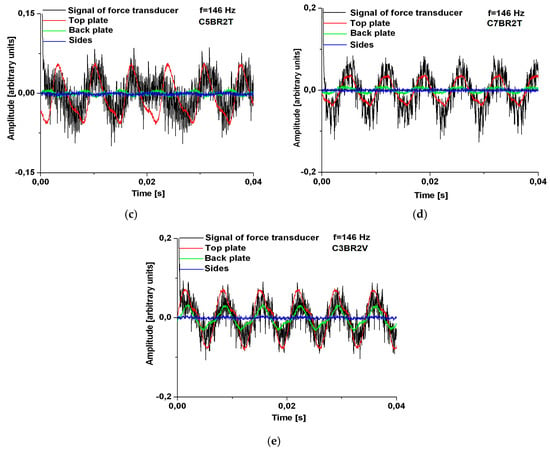
Figure 12.
Comparisons regarding the dynamic response in the time domain of guitar bodies with different bar systems, for frequency of 146 Hz: (a) body type C3BT; (b) guitar body type C3BR2T; (c) guitar body type C5BR2T; (d) body type C7BR2T; (e) body type 3BR2V.
Thus, the vibration amplitudes of the plates differ in the five analyzed cases, the largest being recorded for the box with five radial bars. Except in the case of structure C3BR2V, in all the others it is found that the top and back plates vibrate in anti-phase. At the frequency of 146 Hz, due to the anti-phase motion, the sides vibrate with small amplitudes—the extinction of the air volume takes place in the z-direction (Figure 12). At the frequency of 246 Hz, a phase shift of the top and back plates is observed, depending on their degree of stiffness. Thus, if, at the frequency of 110 Hz (Figure 11), the plates of all the guitar bodies vibrate in phase, with the increase of frequency, these phenomena of "breathing" of the air inside the box became different, due to the internal geometry of the box and the stiffness of plates. The plates of the box with three radial bars and two oblique bars vibrate in phase at the frequency of 246 Hz and in the other cases, there is a phase gap between the plates. At 440 Hz, the dynamic behavior of the plates with different stiffening structures is similar for the C3BR2T, C3BR2V and C5BR2T—the top and back plates of the guitar body vibrating in phase, as opposed to the guitar body C7BR2T, which show a slight phase gap between the two plates (Figure 13).
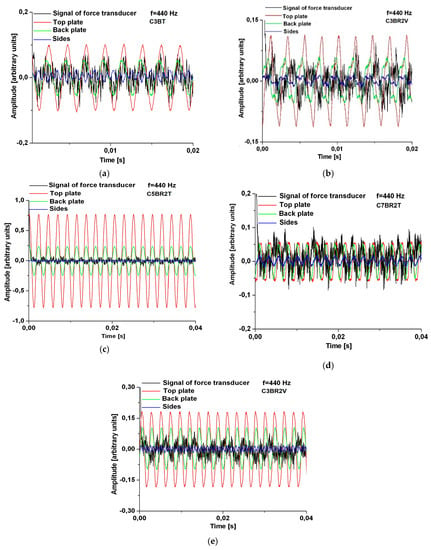
Figure 13.
Comparisons regarding the dynamic response in the time domain of guitar bodies with different bar systems, for a frequency of 440 Hz: (a) body type C3BT; (b) guitar body type C3BR2T; (c) guitar body type C5BR2T; (d) body type C7BR2T; (e) body type 3BR2V.
There are differences in the response of the guitar coupled plates in terms of the amplitude and complexity of the vibrations. The symmetric and antisymmetric modes were noticed by Huber et al. [42], which applied the non-contact method to measure the modal analysis and dynamic response of classical guitar. So, [42] noticed that around frequency of 205 Hz, symmetric deflection of modal shape was captured by the ultrasonic method since antisymmetric modes were captured around 232 Hz and 685 Hz. Each of these bracing systems is a carrier of inertia (mass acceleration), influencing the equilibrium state (stresses and deformation) and the vibrational surface with effect on the acoustic radiation of the guitar. By including these characteristics, a rigid model is transformed into a nonlinear system that can be subjected to something more than a modal analysis, as was noticed by [24].
In Figure 14, the Fast Fourier Transform (FFT) analyses are presented for each type of studied structures, in case of applied force of 440 Hz. It can be noticed that, in case of the guitar bodies C5BR2T C7BR2T and C3BR2V, the constructed waveform will consist of more than three different frequency components (overtones of the 440 Hz dominant frequency, as 880 Hz; 1320 Hz; 1760 Hz), in comparison with other studied structures, which FFT reveals just two main peaks (440 Hz and 1320 Hz).
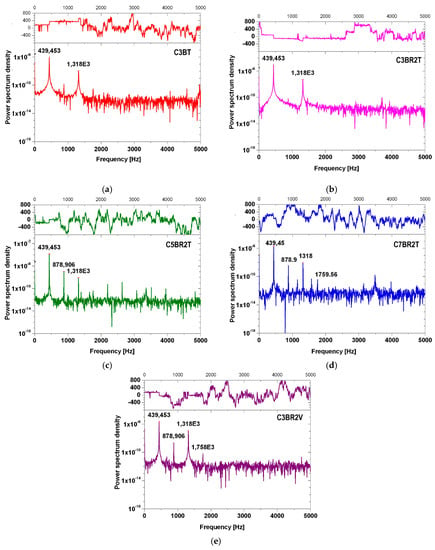
Figure 14.
Fast Fourier Transform (FFT) for an excitation frequency of 440 Hz: a) body type C3BT; (b) guitar body type C3BR2T; (c) guitar body type C5BR2T; (d) body type C7BR2T; (e) body type 3BR2V.
6. Conclusions
The body of the guitar has an obvious plane of symmetry, which passes through the means of the two sides of the guitar, but can also be considered to have a quasi-symmetry plane, which separates the top plate from the bottom plate. In the calculations made, we considered only the perfect symmetry plan, which makes the results in terms of frequencies, of half the body of the guitar, to be rigorously found between the dynamic responses of the whole guitar body calculated with FEM, but also, during the experiments, the quasi-symmetry of the top and bottom was observed at the frequencies of 146 Hz, 588 Hz and 720 Hz (see Table 2). First, it could be noticed that the dynamical behaviour of guitar body is governed by the same harmonic law as the excitation force, regardless of strutting system. In spite of the same values of harmonic excitations which were applied during the experiments, different resonance frequencies for the acoustic bodies of classical guitars with different braces patterns were recprded. For the perfect symmetrical system considered, the two types of vibration modes can be identified: the symmetrical mode and the skew-symmetric mode. The influences of different bracing systems can be highlighted:
- Each type of bracing system from guitar body generates the nodal patterns, which overlap with the patterns found from modal analysis (Table 4);
- The first resonance is noticed first, with higher amplitude, then the second, third, etc. All appear at a specific frequency, their resonant frequency and all have different patterns in accordance with bracing systems applied on soundboards;
- In case of forced vibration of 110 Hz, all analyzed structures has one vibration antinode, in a symmetric mode. For 146 Hz, the quasi skew symmetric vibration modes are recorded, has three vibration antinodes with two vertical nodal lines, with vibrating surfaces more or less extended according to bracing patterns;
- The amplitude spectra becomes more complex with increasing the frequency. With increasing the number of bars from bracing systems, the overtones increases too.
Author Contributions
Conceptualization, M.D.S., M.M. and SV; methodology, S.V., M.M. and M.D.S.; investigation and software M.D.S.; validation, M.M.; formal analysis, S.V; resources, M.D.S., S.V.; data curation, M.D.S.; writing—original draft preparation, S.V.; writing—review and editing, M.D.S and M.M.; visualization, M.D.S.; supervision, S.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was accomplished under the following grants: TD cod 182, no. 222/2007, UEFISCDI, project responsible: Ph.D. Eng. Stanciu Mariana Domnica and Program partnership in priority domains -PNIII under the aegis of MECS -UEFISCDI, project no. PN-III-P2-2.1-BG-2016-0017/85 SINOPTIC, project manager Stanciu M.D.
Acknowledgments
The authors would like to thank the company SC Hora S.A., Reghin, Romania for providing the patterns and geometry of the guitar plates involved in this study. We are grateful to Professor Ioan Curtu (1942–2016), who was the supervisor of the above-mentioned projects, for a life dedicated to wood science.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dumond, P.; Baddour, N. Effects ofa Scalloped and RectangularBrace on the Modeshapes of a Brace-Plate System. Int. J. Mech. Eng. Mechat. 2012, 1. [Google Scholar] [CrossRef]
- Dumond, P.; Baddour, N. Effects of using scalloped shape braces on the natural frequencies of a brace-soundboard system. App. Acoust. 2012, 73, 1168–1173. [Google Scholar] [CrossRef]
- Okuda, A.; Ono, T. Bracing effect in a guitar top board by vibration experiment and modal analysis. Acoust. Sci. Technol. 2008, 29, 103–105. [Google Scholar] [CrossRef]
- Bader, R. Computational Mechanics of the Classical Guitar; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Hurtado, E.G.; Pedraza-Ortega, J.C.; Ramos-Arreguin, J.-M.; Sotomayor-Olmedo, A.; Perez-Meneses, J. Vibration analysis in the design and construction of an acoustic guitar. Int.J. Phys. Sci. 2012, 7, 1986–1997. [Google Scholar]
- Jansson, E. Acoustics for violin and guitar makers. The Function, Tone, and Tonal Quality of Guitar—Chapter VI, 4th ed. 2002. Available online: http://www.speech.kth.se/music/acviguit4/index.html (accessed on 20 September 2019).
- Christensen, O.; Vistisen, B.B. Simple model for low-frequency guitar function. Catgut Acoust. Soc. Newslett. 1981, 36, 21–27. [Google Scholar]
- Jansson, E.V. A study of the acoustical and hologram interferometric measurements on the top plate vibrations of a guitar. Acustica 1971, 25, 95–100. [Google Scholar]
- Christensen, O. An oscillator model for analysis of guitar sound pressure response. Acustica 1984, 54, 289–295. [Google Scholar]
- Rodríguez, S.E. Numerical Analysis of the Modal Coupling at low resonances in a Colombian Andean Bandola in C using the Finite Element Method. Ph.D. Thesis, Universidad EAFIT, Antioquia, Colombia, 2012. [Google Scholar]
- Stanciu, M.D.; Curtu, I. Analytical and numerical simulation of structures of classical guitar. In Dinamica Structurii Chitarei Clasice (Ro); Printhouse of Transylvania University of Brașov: Brașov, România, 2012; pp. 51–120. Available online: https://www.researchgate.net/publication/272822983_Carte_Dinamica_structurii_chitarei_clasice (accessed on 27 May 2019).
- Ezcurra, A.; Elejabarrieta, M.; Jesús Santamaría, C. Internal Fluid Influence on the Dynamic Behavior of the Resonance Box of the Guitar. Available online: http://www.sea-acustica.es/fileadmin/publicaciones/Sevilla02_mus06015.pdf (accessed on 14 October 2019).
- Elejabarrieta, M.J.; Ezcurra, A.; Santamaría, C. Resonance Box of the Guitar Structure-Fluid Interactio. In Proceedings of the 19th International Congress on Acoustics, Madrid, Spain, 2–7 September 2007. [Google Scholar]
- Elejabarrieta, M.J.; Ezcurra, A.; Santamaria, C. Coupled modes of the resonance box of the guitar. J. Acoust. Soc. Am. 2002, 111, 2283–2292. [Google Scholar] [CrossRef]
- Vladimirovici, S. Calculation Method for the Component Elements of Guitar. Ph.D. Thesis, Technical State Institute Mari, Yoshkar-Ola, Russia, 2004. [Google Scholar]
- Richardson, B.E.; Walker, G.P.; Brooke, M. Synthesis of guitar tones from fundamental parameters relating to construction. Proc. Inst. Acoust. 1990, 12, 757–764. [Google Scholar]
- Šali, S.; Kopač, J. Measuring the quality of guitar tone. Exp. Mech. 2000, 40, 242–247. [Google Scholar] [CrossRef]
- Russell, D. Modal analysis of an Acoustic Folk Guitar. Ph.D. Thesis, Applied Physics, Kettering University, Flint, MI, USA, 1998. [Google Scholar]
- Russel, D.; Pedersen, P. Modal Analyses of an Electric Guitar; Kettering University: Flint, MI, USA, 1999. [Google Scholar]
- Wright, H. The Acoustics and Psychoacoustics of the Guitar. Ph.D. Thesis, University of Wales, College of Cardiff, Cardiff, UK, 1996. [Google Scholar]
- Bécache, E.; Chaigne, A.; Derveaux, G.; Joly, P. Numerical simulation of a guitar. Comput. Struct. 2005, 83, 107–126. [Google Scholar] [CrossRef]
- Torres, J.A.; Boullosa, R.R. Influence of the bridge on the vibrations of the top plate of a classical guitar. Appl. Acoust. 2009, 70, 1371–1377. [Google Scholar] [CrossRef]
- Skrodzka, E.; Łapa, A.; Linde, B.B.J.; Rosenfeld, E. Modal parameters of two incomplete and complete guitars differing in the bracing pattern of the soundboard. J. Acoust. Soc. Am. 2011, 130, 2186–2194. [Google Scholar] [CrossRef] [PubMed]
- Bielski, P.M.; Kujawa, M.; Lubowiecka, I. Modelling and measurement of folk guitar: Truss rod and strings in numerical analysis of tone. Arch. Acoust. 2019, 44, 35–49. [Google Scholar] [CrossRef]
- French, M. Structural modification of stringed instruments. Mech. Syst. Signal Process. 2007, 21, 98–107. [Google Scholar] [CrossRef]
- Besnainou, C.; Frelat, J.; Buys, K. A new concept for string instrument sound board: The splitting board. In Proceedings of the International Symposium on Music Acoustics, Sydney, Australia, 25–27 August 2010; Available online: http://www.lam.jussieu.fr/Publications/Conferences/ISMA2010_Besnainou.pdf (accessed on 11 February 2020).
- Zingoni, A. Group-theoretic exploitations of symmetry in computational solid and structural mechanics. Int. J. Numer. Meth. Eng. 2009, 79, 253–289. [Google Scholar] [CrossRef]
- Mangeron, D.; Goia, I.; Vlase, S. Symmetrical Branched Systems Vibrations. Sci. Mem. Rom. Acad. Buchar. 1991, 12, 232–236. [Google Scholar]
- Vlase, S.; Năstac, D.C.; Marin, M.; Mihălcică, M. A method for the study of the vibration of mechanical bars systems with symmetries. Acta Tech.l Napoc. Ser. Appl. Math. Mech. Eng. 2017, 60, 539. [Google Scholar]
- Alcayde, A.; Velilla, C.; San-Antonio-Gómez, C.; Peña-Fernández, A.; Pérez-Romero, A.; Manzano-Agugliaro, F. Basket-Handle Arch and Its Optimum Symmetry Generation as a Structural Element and Keeping the Aesthetic Point of View. Symmetry 2019, 11, 1243. [Google Scholar] [CrossRef]
- Vlase, S.; Paun, M. Vibration Analysis of a Mechanical System consisting of Two Identical Parts. Ro. J. Techn. Sci. Appl. Mech. 2015, 60, 216–230. [Google Scholar]
- Chen, Y.; Feng, J. Generalized Eigenvalue Analysis of Symmetric Prestressed Structures using Group Theory. J. Comput. Civil. Eng. 2012, 26, 488–497. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Scutaru, M.L.; Munteanu, R. Coupled transverse and torsional vibrations in a mechanical system with two identical beams. AIP Adv. 2017, 7, 065301. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Vlase, S.; Marin, M. Vibration Analysis of a Guitar considered as a Symmetrical Mechanical System. Symmetry 2019, 11, 727. [Google Scholar] [CrossRef]
- Holm, D.D.; Stoica, C.; Ellis, D.C.P. Group Actions, Symmetries and reduction. In Geometric Mechanics and Symmetry, 1st ed.; Oxford University Press: Oxford, UK, 2009; pp. 184–211. [Google Scholar]
- Curtu, I.; Stanciu, M.D.; Grimberg, R. Correlations between the Plates’ Vibrations from the Guitar’s Structure and the Physical, Mechanical and Elastically Characteristics of the Composite Materials. In Proceedings of the 9th International Conference on Acoustics & Music: Theory & Applications (Amta ’08), Bucharest, Romania, 24–26 June 2008. [Google Scholar]
- Curtu, I.; Stanciu, M.D.; Itu, C.; Grimberg, R. Numerical Modelling of the Acoustic Plates as Constituents of Stringed Instruments. In Proceedings of the 6th International Conference Baltic Industrial Engineering, Tallinn, Estonia, 24–26 April 2008; pp. 53–58. [Google Scholar]
- Curtu, I.; Stanciu, M.D.; Savin, A. The propagation of forced vibrations in coupled plates of guitars. In Proceedings of the 19th International DAAAM Symposium “Intelligent Manufacturing & Automation: Focus on Next Generation of Intelligent Systems and Solutions”, Trnava, Slovakia, 22–25 October 2008; pp. 345–346. [Google Scholar]
- French, M.R. Engineering of Guitar—Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Lee, M.K.; Fouladi, M.H.; Namasivayam, S.N. Mathematical modelling and acoustical analysis of classical guitars and their soundboards. Adv. Acoust. Vib. 2016, 6084230. [Google Scholar] [CrossRef]
- Boullosa, R.R. Vibration measurements in the classical guitar. Appl. Acoust. 2002, 63, 311–322. [Google Scholar] [CrossRef]
- Huber, T.M.; Beaver, N.; Helps, J.R. Noncontact modal excitation of a classical guitar using ultrasound radiation force. Exp. Tech. 2013, 37, 38–46. [Google Scholar] [CrossRef]
- Urma, D. Acoustic and Music; (print book); Scientific Printhouse: Bucharest, Romania, 1983. (In Romanian) [Google Scholar]
- Ganghoffer, J.F.; Mladenov, I. Similarity, Symmetry and Group Theoretical Methods in Mechanics; Lectures at the International Centre for Mechanical Sciences; CISM: Udine, Italy, 2015. [Google Scholar]
- Lopatin, A.V.; Morozov, E.V. Symmetrical vibration modes of composite sandwich plates. J. Sandw. Struct. Mater. 2010, 13, 189–211. [Google Scholar] [CrossRef]
- Vlase, S. Elimination of Lagrangean Multipliers. Mech. Res. Commun. 1987, 14, 17–20. [Google Scholar] [CrossRef]
- Negrean, I. New Formulations in Analytical Dynamics of Systems. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2017, 60, 49–56. [Google Scholar]
- Douglas, T. Eigenvalues and Eigenvectors. In Structural Dynamics and Vibrations in Practice: An Engineering Handbook, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2008; pp. 159–180. [Google Scholar]
- Le, K.C.; Nguyen, L.T.K. Energy Methods in Dynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Le, K.C. Vibrations of Shells and Rods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bucur, V. Chapter 7- Wood species for musical instruments. In Acoustics of Wood; Springer: Berlin/Heidelberg, Germany, 2006; pp. 171–214. [Google Scholar]
- Sonderegger, W.; Martienssen, A.; Nitsche, C.; Ozyhar, T.; Kaliske, M.; Niemz, P. Investigations on the physical and mechanical behavior of sycamore maple (Acer pseudoplatanus L.). Eur. J. Wood Prod. 2013, 71, 91–99. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Curtu, I.; Itu, C. Influence of strengthening bars of guitar’s plates on the normal modes of vibrations using. In Proceedings of the 19th International DAAAM Symposium “Intelligent Manufacturing & Automation: Focus on Next Generation of Intelligent Systems and Solutions”, Trnava, Slovakia, 22–25 October 2008; pp. 1295–1296. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).